Abstract
A fundamental challenge in robotics is to reason with incomplete domain knowledge to explain unexpected observations and partial descriptions extracted from sensor observations. Existing explanation generation systems draw on ideas that can be mapped to a multidimensional space of system characteristics, defined by distinctions, such as how they represent knowledge and if and how they reason with heuristic guidance. Instances in this multidimensional space corresponding to existing systems do not support all of the desired explanation generation capabilities for robots. We seek to address this limitation by thoroughly understanding the range of explanation generation capabilities and the interplay between the distinctions that characterize them. Towards this objective, this paper first specifies three fundamental distinctions that can be used to characterize many existing explanation generation systems. We explore and understand the effects of these distinctions by comparing the capabilities of two systems that differ substantially along these axes, using execution scenarios involving a robot waiter assisting in seating people and delivering orders in a restaurant. The second part of the paper uses this study to argue that the desired explanation generation capabilities corresponding to these three distinctions can mostly be achieved by exploiting the complementary strengths of the two systems that were explored. This is followed by a discussion of the capabilities related to other major distinctions to provide detailed recommendations for developing an explanation generation system for robots.
1. Introduction
Robots (we use the term interchangeably with “agents” in this paper) equipped with multiple sensors are increasingly used to interact and collaborate with humans in different applications. These robots receive an incomplete and inaccurate description of the domain based on the information extracted from the sensor data they acquire. They also receive useful common sense information that holds in all, but a few exceptional situations, but it is challenging to represent and reason with such information. Furthermore, humans interacting with the robots may not be able to interpret raw data or to provide comprehensive and accurate information. To truly collaborate with humans, robots thus need the ability to represent and reason with different descriptions of domain knowledge to generate explanations for unexpected observations (e.g., of action outcomes) and partial descriptions (e.g., of the scene) extracted by processing sensor data.
Consider, for instance, a robot waiter that assists in seating people and delivering orders in a restaurant. The robot may be given default knowledge, such as “plates are usually in the kitchen, but used plates may be on the tables in the dining room” and “unattended guests usually wait in the entrance area”. The robot also receives information by processing its sensor observations. Now, consider the scenario in which the robot is asked to seat two regular guests waiting in the entrance area. The robot goes to the entrance area, but does not see the guests there. The robot can explain this unexpected observation by inferring some exogenous actions (actions not performed by the robot), e.g., the guests left the restaurant. Continuing with this example, assume that on the way back to the kitchen, the robot observes the two guests seated at a table, an unexpected observation that also falsifies the previous explanation. The robot can explain (and resolve) this inconsistency by inferring other exogenous actions, e.g., the guests had a pre-existing reservation at a specific table or another waiter seated the two guests. The focus of this paper is on the robot’s ability to consider all suitable options and infer the occurrence of one or more actions that best explain the unexpected observations. This is a fundamental open problem in robotics, especially when robots are used in complex, dynamically-changing domains. As a more formal description of this explanation generation task, consider its inputs and output:
- Inputs: (a) a description of the relevant symbols of the domain; (b) a knowledge base expressed in terms of these symbols; and (c) an encoding of the observations to be explained;
- Output: a finite collection of statements, defined in terms of the available symbols, which accounts for the observations in terms of available knowledge.
The specific instances of the domain symbols are obtained by processing sensor data (e.g., images), and a knowledge base typically comprises relations between domain objects (i.e., specific instances of domain symbols) and axioms that characterize the actions that can be performed on these objects. This knowledge base can, for instance, be represented as logic statements. The output may take the form of relational logic expressions, a graph of objects (nodes) and relations between them (edges) or some other representation. The explanation generation task thus involves efficiently processing the inputs to describe how (and why) the observations were generated. Some applications may require real-time operation, while others may not.
Despite decades of research, existing explanation generation systems in the artificial intelligence (AI) and robotics literature do not provide all of the desired capabilities, such as default reasoning and the ability to interactively and incrementally generate explanations from partial information. It is challenging to support these capabilities because existing systems generate and evaluate possible explanations based on ideas that map to a complex multidimensional space of system characteristics defined by various distinctions, such as how they represent and reason with domain knowledge (e.g., hierarchical structures and relational representations), if and how they use heuristic guidance (e.g., using heuristics to introduce new objects and rank candidate explanations) and if and how they use models inspired by human cognition and behaviour (e.g., models of mental states, goals and intentions). The work described in this paper is a step towards a thorough understanding of the distinctions defining this complex multidimensional space. Towards this objective, this paper makes the following contributions:
- (1)
- It describes three fundamental distinctions that can be used to characterize the multidimensional space of explanation generation systems (Section 3.1) and two systems that are substantially different along these three dimensions (Section 3.2 and Section 3.3).
- (2)
- It compares the capabilities of the two chosen systems in a series of execution scenarios of a robot assistant in a restaurant, to explore and understand the three distinctions characterizing the space of explanation generation systems (Section 4).
- (3)
- It provides detailed recommendations for developing an explanation generation system for robots based on the comparative study and the capabilities related to other key distinctions that characterize such systems (Section 5).
For our comparative study, we select two systems: (1) KRASP, which supports non-monotonic logical reasoning and generates explanations based on the system specification, observations of system behaviour and minimal use of heuristics; and (2) UMBRA, which does not support non-monotonic logical reasoning, but interpolates observations and background information with domain axioms and constraints and uses heuristic rules to incrementally generate explanations. This study highlights the need for reliable, efficient and incremental generation of partial explanations in robotics. It also suggests that although neither system fully supports these capabilities, which is also true of other existing systems, they possess complementary strengths that can be exploited. Finally, we build on this idea to provide insights and recommendations for the development of an explanation generation system for robots that considers the other major distinctions defining the multidimensional space of explanation generation systems.
An initial version of this paper was presented at the the 2016 ACM/SIGAPP (Association for Computing Machinery; Special Interest Group on Applied Computing) Symposium on Applied Computing [1]; this paper substantially extends and expands upon our previous work, as discussed in the following section.
2. Related Work
The task of explanation generation has been formulated in many different ways in various branches of the robotics and artificial intelligence (AI) research communities. It is equated with diagnostics in the logic programming community, while it is considered an application of abductive inference in the broader AI community. Existing approaches are based on ideas drawn from a multidimensional space of system characteristics defined by various distinctions, many of which we focus on in this paper. For instance, two fundamental distinctions are: (1) how these systems represent and reason with knowledge in domains that may feature other agents; and (2) how and to what extent they use heuristic guidance. Some systems use elaborate system descriptions and observations of system behaviour, with minimal heuristics, to explain unexpected occurrences [2,3]. Other systems are limited in their ability to represent and reason with system descriptions and depend more on heuristic representation of experience and intuition to generate explanations [4,5]. Many explanation generation systems have also been developed by drawing subsets of ideas along these dimensions.
Existing approaches for explanation generation have used ideas from different disciplines to represent and reason with domain knowledge in domains involving one or more agents. A large number of existing systems have used first-order logic to construct their primary representation of domain knowledge and axioms for explanation generation; some other approaches have used probabilistic representations. Since approaches based on first-order logic cannot support non-monotonic reasoning, some approaches have used declarative programming and non-monotonic logical reasoning to infer the outcomes of plans [6,7]. However, these approaches require comprehensive knowledge about the domain and tasks, and find it difficult to reason with probabilistic information. Other research has focused on representing and recognizing activities and plans to discern agents’ observed behaviour within some setting and the goals that produced this behaviour [5,8,9]. These approaches often focus on identifying a high-level task or goal rather than providing comprehensive information about a sequence of world states, mental states and actions. Consequently, these approaches tend to emphasize hierarchical structures [8,10], interleaving the actions of one or more agents [8] or capitalizing on prior knowledge by associating weights with rule components [11]. Many modern approaches use probabilistic representations, but then find it challenging to reason with common sense knowledge. Researchers have thus developed algorithms that combine probabilistic and first-order logic representations for abductive reasoning [12] or combine probabilistic and non-monotonic logical reasoning for generating explanations [13,14].
In the context of multiagent collaboration, some approaches have jointly represented the knowledge of agents in the pursuit of shared goals, to explain the observation sequence [15,16]. Other algorithms have explained observations by constructing joint plans for multiple agents and explicitly modeling and reasoning about the intentions of other agents [17]. These algorithms often include ways to model and reason about the mental states of agents [18]. More recent work on reasoning about other agents’ mental states includes computational analyses of deception [19] and work on cognitive architectures, such as Scone [20] and Polyscheme [21], that are able to use default reasoning by inheritance to support inference over problem state descriptions.
Explanation generation approaches differ in the extent and manner in which they use heuristic guidance. For instance, approaches based on declarative programming languages, such as Answer Set Prolog (ASP), are typically limited to using heuristics for prioritizing the rules that may be used to explain the observations. Recent research has eliminated the need to solve ASP programs entirely anew when the problem specification changes [22], allowing: (a) new information to expand existing programs; and (b) reuse of ground rules to support interactive theory exploration. However, these approaches cannot generate explanations incrementally and focus on generating complete models, which makes it challenging to operate efficiently. On the other hand, approaches that have developed sophisticated heuristics to reason with domain knowledge have focused on finding low-cost proofs to explain observations [23] and on developing search strategies based on criteria, such as parsimony, consilience and coherence [5,24]. They may seek to formulate explanation generation as inference of a common sense nature that involves creating a “web of plausible conjectures” [25].
In robotics and AI research, many algorithms and architectures have been developed for knowledge representation and reasoning, and some of them have included the ability to explain (or analyze the reasons for) observations. For instance, the Oro framework creates a sophisticated ontology and uses it to justify observed inconsistencies on a robot [26]. The KnowRob architecture for service robots uses knowledge bases created from different sources to perform limited analysis of the reasons for unexpected observations [27]. Other examples include the use of ASP for planning and diagnostics by one or more simulated robot housekeepers [28] and mobile robot teams [29] and by robots reasoning about domain knowledge learned through natural language interactions with humans [30]. More recent architectures that support logic-based reasoning and probabilistic reasoning with common sense knowledge, also include the ability to generate explanations. One example is a three-layered organization of knowledge and reasoning for planning and diagnostics based on first-order logic and probabilistic reasoning in open worlds [31]. Another example is a general refinement-based architecture for robots that represents and reasons with incomplete domain knowledge and uncertainty at different levels of granularity, combining non-monotonic logical reasoning and probabilistic reasoning for planning and diagnostics [32,33]. Researchers have also combined non-monotonic logical reasoning with relational reinforcement learning to discover domain axioms in response to failures that cannot be explained with existing knowledge [34]. Among these systems, those that do not support advanced explanation generation capabilities are outside the scope of this paper, and those that do generate sophisticated explanations map to the multidimensional space of the distinctions considered in this paper.
The approaches discussed above demonstrate that explanation generation systems populate a complex multidimensional space defined by many distinctions. Since a thorough understanding of this space is still lacking, existing systems continue to face many common challenges. For instance, many approaches involve an exhaustive search of the space of ground literals or some transformation of that space, making it difficult to scale to large knowledge bases and complex explanations. It is also difficult to represent and reason with different (e.g., symbolic and probabilistic) descriptions of knowledge and uncertainty. Existing systems also do not fully support one or more of the desired capabilities, such as efficient and incremental addition of knowledge, generating partial explanations with incomplete information, default reasoning and the use of heuristics for interactive explanation generation. This paper seeks to promote better understanding of the multidimensional space and, thus, the development of a system that supports a comprehensive set of reasoning abilities for robots. Our recent paper compared a representative system from each of two broad distinctions of the space of explanation generation systems [1]. In this paper, we first describe three fundamental distinctions that characterize the multidimensional space, and compare two representative systems that differ substantially based on these distinctions. We then use this study and consider other major distinctions to provide detailed recommendations for the design of an explanation generation system for robots.
As an illustrative example that we will return to throughout the paper, consider a robot waiter that seats people at tables and delivers orders in a restaurant (as described in Section 1). Figure 1 provides an example map of this domain: humans and the robot waiter can be located in different areas of this map. The sorts of the domain are arranged hierarchically, e.g., and are subsorts of ; and are subsorts of ; and are subsorts of ; is a subsort of ; and , , and are subsorts of . We include specific rooms, e.g., and , and consider objects of sorts, such as , and , to be characterized by attributes, such as , , and . The sort is used for temporal reasoning. The focus in this paper is on explanation generation, i.e., on the robot’s ability to explain unexpected observations and partial scene descriptions by hypothesizing the occurrence of exogenous actions. For instance, if the robot waiter believes that is unattended and is unoccupied at a specific time step, but observes at within a few time steps, it may infer that another waiter seated at in between. To fully explore the key distinctions that characterize the multidimensional space of systems that generate such explanations, we make two simplifying assumptions for the first part of our paper that include a comparative study:
- (1)
- The robot does not create joint plans or model communication with other agents.
- (2)
- The robot does not consider probabilistic representations of uncertainty.
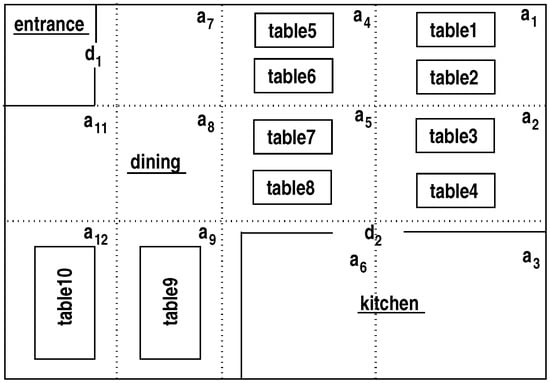
Figure 1.
Map of the illustrative domain used for discussion, with rooms, doors and tables; the s denote areas in rooms. Humans and the robot can appear in any location and are not shown for simplicity.
The first assumption eliminates the need to model the beliefs or capabilities of other agents: the robot reasons about possible actions of other agents (humans or robots) only to explain unexpected observations. The second assumption focuses our attention on high-level cognition without having to consider the uncertainty in processing sensor inputs. We relax these assumptions in the second part of our paper, particularly where we make broader recommendations in Section 5.
3. System Descriptions
We begin our exploration of the multidimensional space populated by explanation generation systems by first describing three fundamental distinctions, along with the associated distinct characteristics, underlying assumptions and behaviors (Section 3.1). Next, Section 3.2 and Section 3.3 describe two specific systems that differ substantially along these three dimensions. Specifically, we investigate KRASP, a system that uses an elaborate description of domain knowledge and observations of system behaviour to generate explanations (Section 3.2). We also explore UMBRA, which uses heuristic abductive inference for explanation generation (Section 3.3). In our exploration of these three distinctions, we initially make some limiting assumptions, as described in Section 2 in the context of the illustrative example. For instance, our description of KRASP and UMBRA does not consider any extensions that use probabilities for representing uncertainty. We also do not consider an agent’s ability to jointly plan actions with other agents: the agent only reasons about other agents to explain an observation sequence. These limitations are relaxed in our subsequent discussion in Section 5, which provides recommendations for designing a comprehensive explanation generation system for robots.
3.1. Distinctions between Explanation Generation Systems
We introduce the following three fundamental distinctions to characterize, in terms of components, capabilities and approaches, the multidimensional space populated by existing explanation generation systems:
- (1)
- Methodical/heuristic distinction: Systems at one end of this axis primarily rely on extensive domain information to compute explanations under different situations. They build models methodically from domain axioms and observations of system behaviour, possibly using other predefined domain rules to deal with anomalies. These systems include guarantees about the quality of the explanations found. They may also define a preference relation over the domain axioms and use this relation to determine minimal explanations. Systems at the other end of this axis, on the other hand, use heuristic guidance, which is typically organized hierarchically at different levels of abstraction and is often dependent on experimentally-established numeric constants, to generate explanations. These systems engage in forms of reasoning that usually do not provide guarantees about the quality of the explanation found.
- (2)
- Non-specialized/cognitive distinction: Systems on one end of this axis have broad, general problem-solving capabilities. These capabilities are non-specialized in that they do not intrinsically encode prior assumptions about specific types of task or domain characteristics. Since domain-specific assumptions must be explicitly encoded, these systems cannot make inferences beyond those implied by the domain information provided. One class of systems (amongst many) that is quite distinct to these general frameworks are cognitive systems that use methods informed by human behaviors and can draw on prior internal representations of high-level concepts, such as beliefs, mental models, time symbols, other agents and persistent constraints. While there are many other classes of specialized systems, we focus on cognitively-inspired systems because they are particularly relevant to robotics and human-robot interaction.
- (3)
- Full-model/incremental-cyclic distinction: systems at one extreme of this dimension typically seek to produce a complete explanation. They report failure when a full model is not found, but may perform non-monotonic belief revision to address inconsistencies. These systems typically only use temporal information described in axioms, rather than having preconceptions about time built into the system framework itself. On the other hand, systems corresponding to a different point along this dimension operate incrementally through repeated “cognitive cycles” that are usually linked to an internal notion of time that may be used to process input observations. They use high-level rules to determine when a set of input literals have been sufficiently explained and may pause the processing if the state is unchanged.
It is important to emphasize that while we consider these three distinctions to be fundamental, we do not seek to provide a complete taxonomy of distinctions or explanation generation systems. Instead, the objective of this paper is to identify and use certain key distinctions as stepping stones towards a more comprehensive approach for explanation generation in robotics. Towards this objective, we next describe the representations and operations of two systems that differ substantially along these dimensions.
3.2. System I: KRASP
KRASP, or Knowledge Representation for Robots using ASP, is based on Answer Set Prolog (ASP), a declarative language that can represent recursive definitions, causal relations, defaults, special forms of self-reference and language constructs that occur frequently in non-mathematical domains and are difficult to express in classical logic formalisms. ASP is based on the stable model (answer set) semantics of logic programs and research in non-monotonic logics [2,35]. ASP can draw conclusions from a lack of evidence to the contrary, using concepts such as default negation (negation by failure) and epistemic disjunction. For instance, unlike “¬a”, which implies that “a is believed to be false”, “not a” only implies that “a is not believed to be true”; and unlike “p p” in propositional logic, “p or ¬p” is not tautologous. The key novelty here is that if a statement is not believed to be true, it does not automatically mean the statement is believed to be false; there may just not be sufficient evidence to believe one way or the other. Statements in an ASP program define beliefs of an agent associated with this program, and the agent does not believe anything that it is not forced to believe, which is in accordance with KRASP being a non-specialized system with regard to the non-specialized/cognitive distinction.
ASP supports non-monotonic reasoning, i.e., adding a statement to the program can reduce the set of inferred consequences, which is a desired capability in robotics. ASP also supports reasoning in large knowledge bases [36] and reasoning with quantifiers. These capabilities have led to widespread use of ASP-based architectures in robotics by an international community of researchers [29,37,38]. In the remainder of this paper, any mention of KRASP refers to the use of these capabilities of ASP; where appropriate, we highlight the differences between KRASP and a standard ASP formulation. A pictorial representation of KRASP’s structure and operation is given in Figure 2.
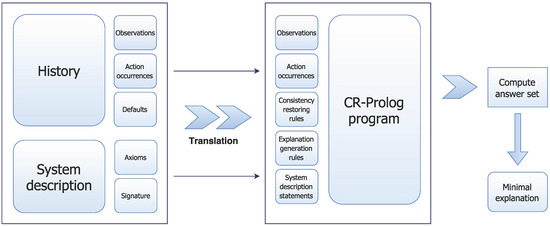
Figure 2.
KRASP uses a description of domain knowledge and observations of system behaviour, reducing planning, explanation generation and inference to computing answer sets of an ASP program.
Knowledge representation: The domain representation in KRASP consists of a system description and a history containing initial state defaults. KRASP has no prior understanding of symbols in either or . The domain content cannot influence the process of explanation generation, e.g., through heuristic judgements based on cognitive or social facets of the domain, unless instances of these facets are encoded in the system description for the domain under consideration. This representation corresponds to a non-specialized system with regard to the non-specialized/cognitive distinction.
The system description has (a) a sorted signature that defines the names of objects, functions, and predicates available for use and (b) axioms that describe the corresponding transition diagram τ. To obtain , τ is described in an action language. For instance, action language AL has a sorted signature containing , domain properties whose values cannot be changed by actions; , domain properties whose values are changed by actions; and are those that may be executed in parallel [2]. AL supports causal laws, which describe the effects of actions when certain conditions are met, state constraints, which are constraints on the values of combinations of fluents, and executability conditions, which are conditions under which one or more actions cannot be executed. KRASP’s system description is a collection of these AL statements.
The domain fluents are defined in terms of the sorts (similar to classes) of their arguments, e.g., . There are two types of fluents. Basic fluents obey laws of inertia and are directly changed by actions. Defined fluents do not obey inertia laws and cannot be changed directly by actions; they are described in terms of other relations. The system description includes relations that define statics, e.g., relations between stationary objects and connections between rooms. In addition, the relation implies that a specific fluent holds at a time step, and the relation is used to reason about a specific action occurring at a specific time step. Each action is also defined in terms of the sorts of its arguments, e.g., action causes a robot to move to a specific location, and action causes a robot to pick up a specific object. Domain dynamics are defined by the causal laws, state constraints and executability conditions.
The history of a dynamic domain typically contains records of the form , which encode specific actions happening at specific time steps, and , which encode the observation of specific fluents at specific time steps. Unlike a standard ASP-based formulation, KRASP expands the notion of history to include prioritized defaults describing the values of fluents in their initial states and any exceptions that may exist [33]. Default statements represent beliefs of the form: “elements of a class C typically have property P”. For instance, the robot may initially believe that unused plates are typically on a table between the kitchen and the dining room, and if not there, they are typically on a table in the kitchen; dirty plates are an exception and are stacked on a different table. KRASP allows us to elegantly represent and reason with such default knowledge.
The domain representation is translated into a program in CR-Prolog, which incorporates Consistency Restoring (CR) rules in ASP [2,39]. These CR rules represent exceptions to defaults that are triggered only under exceptional circumstances. For instance, we may want to state that “elements of class C can be an exception to the default and may not have property P, but such a possibility is very rare and is to be ignored whenever possible”. Π includes the causal laws of and inertia axioms that assert that a basic fluent retains its truth value between steps unless there is evidence to the contrary. Π also includes the closed world assumption for actions and defined fluents, reality checks and records of observations, actions and defaults from . Every default is turned into an ASP rule and a CR rule; when there is an inconsistency because an observation does not match expectations, the system tries to restore consistency by identifying and invoking a CR rule to falsify the conclusion of the corresponding ASP rule (i.e., default statement). For instance, a robot waiter that initially believes that unused plates are on the table between the kitchen and the dining room will continue to believe this (due to the rules of inertia) in subsequent time steps. However, if the robot then sees an unused plate in some other location after some time, this creates an inconsistency. Invoking the CR rule corresponding to this default will enable the robot to assume that the observed plate is an exception to the initial state default, propagate this belief through inertia and have a consistent model (of the world) at the current time step.
Planning and diagnosis: Given the CR-Prolog program Π, which includes domain axioms and observations of system behaviour, the ground literals in an answer set obtained by solving Π is guaranteed to represent the beliefs of an agent associated with Π. Statements that hold in all such answer sets are program consequences, i.e., the result of inference using the available knowledge. It has been shown that planning can be reduced to computing answer sets of program Π by adding a goal, a constraint stating that the goal must be achieved and a rule generating possible future actions [2]. KRASP’s approach to planning and diagnosis thus is that of a methodical system with regard to the al system with regard to the methodical/heuristic distinction.
An ASP-based architecture can also be designed to support the explanation of unexpected observations [40,41] by reasoning about exogenous actions and partial descriptions. For instance, to reason about a door between the kitchen and the dining room being locked by another agent and to reason about a person moving away from a known location, we augment the program Π (i.e., input knowledge base) by introducing and as exogenous actions and add (or revise) the corresponding axioms. The expected observations of the values of attributes (e.g., colour and shape) of domain objects can also be encoded in the CR-Prolog program Π. To support the generation of explanations, the program Π is augmented by introducing: (a) an explanation generation rule that hypothesizes the occurrence of exogenous actions; (b) awareness axioms, which require the value of each fluent to be known; and (c) reality check axioms that produce inconsistencies when observations do not match expectations (i.e., agent’s current beliefs); see [2,41] for specific examples. In essence, KRASP can hypothesize the occurrence of one or more exogenous actions to restore consistency by explaining the unexpected observations. Consistency can be restored by: (1) using the explanation generation rule to provide all explanations; or (2) generating the minimal explanation by invoking CR-rules. In KRASP, we pursue the second option by defining a partial ordering over sets of CR rules, also called a “preference relation”. This ordering can be set-theoretic (a set that is a subset of another is preferred) or it can be based on the cardinality of sets (the set with smaller cardinality is preferred). For any unexpected observation or partial description extracted from observations, KRASP considers sets of CR rules that can be triggered, picking the set with the lowest cardinality as the minimal explanation [41].
Computing answer sets: The processes for computing answer sets of a logic program are generate and test reasoning algorithms. In their first step, they replace the program Π with its ground instantiation. Sophisticated methods for grounding exist, e.g., using algorithms from deductive databases, but grounding a program containing variables over large domains is still computationally expensive. The second step recursively computes the consequences of the grounded program and its partial interpretations. The algorithm used by KRASP takes as input the domain knowledge specified as a CR-Prolog program, including the sequence of observations. For simplicity, in the case studies in this paper, all observations are given concurrently and analyzed incrementally as required. This program is solved using DLV, which uses disjunctive logic programming and a satisfiability solver [42]. The output (i.e., answer set) represents all of the current beliefs of the agent associated with program Π, including the minimal explanation for the observations; if the program includes a planning task, the answer set also includes a minimal set of actions. KRASP is thus a full-model system in accordance with the full-model/incremental-cyclic distinction discussed in Section 3.1.
Although not included in this study, it is possible to model heuristics and numerical costs in an ASP program. Recent answer set solvers also improve computational efficiency through partial grounding and heuristic ordering of variables and rules, allow new information to expand existing programs, reuse ground rules and support interactive query answering and theory exploration [22]. However, grounding and computing all consequences of a program is still expensive for complex domains, and better heuristics are needed for optimized explanation generation. The design of such systems can be informed by the insights gained from the study of systems such as UMBRA that rely on heuristic guidance for incremental explanation generation.
3.3. System II: UMBRA
UMBRA is a cognitive system that leverages abductive inference to generate explanations for observations. Prior work has discussed its performance on cognitive tasks involving social understanding [43], dialogue [44] and planning [4]. This section describes UMBRA’s semantic representation and the processes that operate over it.
Working memory representation: UMBRA has a working memory that stores the system’s inferences and information arriving from the external environment, e.g., statements about an agent’s behaviour. The discrete components of this memory are mental states, including beliefs regarding factual statements, and goals comprising views about things the agent intends to achieve. These elements are stated as logical literals with propositional attitudes. Each working memory element specifies: (a) the agent holding the belief or goal; (b) its content ; (c) the start time, denoting when first entertained ; and (d) the end time, denoting when stopped believing or abandoned its intention towards . Unbound variables (implemented as Skolem constants, ) in the last two arguments denote unknown times.
For fluents that hold over a temporal interval, the relevant times may be unknown. For such literals, UMBRA has a third form of mental state predicate, constraint, which specifies relations, such as inequalities or temporal orderings. For example, during(interval(skol, time(1)), interval(skol, skol)) encodes that the time period between skol and Time 1 is contained within a time period from skol to skol. Working memory elements may refer to domain-level literals, e.g., at-location(person1, area1, time(2)), but may also be embedded, i.e., a mental state may refer to another mental state rather than a domain predicate. For example, belief(robot1, goal(waiter1, seat(person1, table1, skol), time(3), skol), time(4), skol) implies that robot1 believes from Time 4 to time skol that the waiter has the goal (from Time 3 to time skol) to seat person1 at table1 at time skol. Such embeddings could in principle be arbitrarily deep, but studies suggest that people cannot readily use more than the fourth-order mental state nesting that UMBRA models [45]. Constraint components are assumed to have a much lower heuristic demand for explanation than more content-rich literals. This representation of working memory, which assumes that any domain encountered will be relational, populated by agent(s), and sensitive to temporal changes, is typical of a cognitive system in accordance with the non-specialized/cognitive distinction.
Axiom representation: UMBRA also has a long-term memory containing skills and conceptual rules that encode generalized knowledge about states and actions. A conceptual rule is equivalent to a Horn clause associating a predicate in the head with a relational situation described in the body. A skill is similar, but associates the head with a set of literals that are sorted into preconditions, postconditions, invariants, constraints, subtasks, and operators. This distinction is not always considered during processing. Higher-level predicates are defined in terms of lower-level ones, such that representation of long-term memory is similar to a hierarchical task network or a concept grammar. Axioms often include logical constraints that specify orderings on times associated with antecedents, or assert the non-equivalence of two elements. Much of an agent’s axiomatic knowledge deals with goals and beliefs directly about the environment. However, social axioms may include goal-directed evaluation and alteration of others’ mental models [43]. While non-specialized systems such as KRASP can encode such knowledge in relational expressions, these systems will not attach any “meaning” to these symbols beyond what is encoded in their knowledge base. UMBRA’s direct access to relevant high-level concepts based on these symbols (e.g., embedded mental states) within its machinery defines its position on the cognitively-focused side of the non-specialized/cognitive distinction. It is difficult to encode prioritized defaults (and exceptions) in UMBRA due to its: (a) binary truth values; (b) focus on structural knowledge; and (c) emphasis on (default) assumption as a process (used to generate explanations) instead of content encoded in its knowledge base.
Explanation: UMBRA is implemented in SWI-Prolog [46], but does not use the language’s built-in engine for inference. Rather, it builds on Prolog’s support for relational logic and embedded structures to perform directed abductive inference governed by heuristic rules, and to make plausible assumptions instead of strict derivations. The system receives a sequence of observations as inputs and uses them to construct an explanation. Since robots receive observations sequentially, the explanation mechanism is designed to operate in an incremental manner, building on earlier inferences by chaining from observations and heads of rules, rather than Prolog-style top-down chaining from queries. However, as before, observations are provided concurrently and analyzed incrementally (as required) in the case studies for simplicity. This approach builds on earlier work on incremental approaches to plan recognition, and indicates that UMBRA is closely associated with the incremental-cyclic side of the third distinction described in Section 3.1. It makes repeated reconstructions of the explanation or extensive belief revision unnecessary, and the explanation at any given time may include fewer than or more than a single top-level activity; there is no notion of a “complete model”. The domain rules, when bound to elements in the working memory, explain observed events; since a memory element may be used in multiple rule applications, an explanation can be viewed as an acyclic proof lattice.
Processing: UMBRA operates over a series of input cycles in which it first adds input observations to its working memory as system-level beliefs (with start times equivalent to the current world time). It then enacts one or more low-level inference cycles, each of which involves a rule application that may add further beliefs to working memory. In addition to this preference for an incremental-cyclic approach, as a cognitive system, much of UMBRA’s architecture emulates (or is inspired by) cognitively plausible processes and structures. A representation of UMBRA’s structure and operation is given in Figure 3.
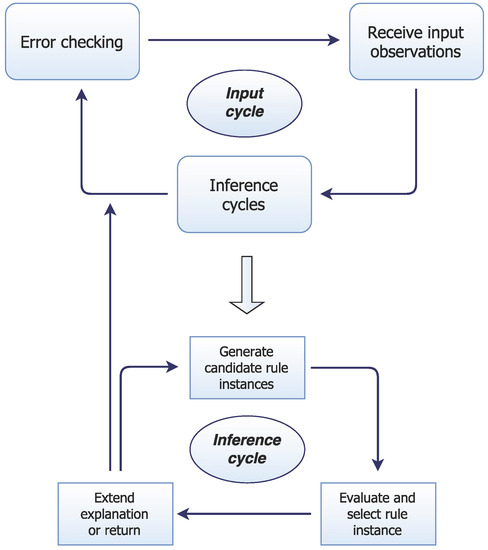
Figure 3.
UMBRA operates over a number of input cycles, each of which first attempts to perform one or more inference cycles, then checks for explanation consistency and finally receives new perceived inputs.
In an inference cycle, UMBRA first identifies each piece of axiomatic knowledge (rule) with at least one component that can unify with some element in working memory. For each such - pair, it generates the partially instantiated rule head produced by the unification of with . The system creates a set of candidate rule instances for each partial instance , unifying as many rule components with working memory elements as possible, and making the minimum number of default assumptions to complete . If ’s components include unbound variables, UMBRA inserts Skolem constants into component literals, e.g., to denote unknown times that satisfy a temporal relation in a constraint. When these variables are instantiated, any rule instance with a literal inconsistent with working memory is eliminated.
Candidate rule instances are pruned using heuristic rules that determine which domain axioms to apply. Heuristic rules also determine whether search should continue in the current stage or a new cycle should begin. The system will retain rules that: (a) incorporate currently unexplained elements; (b) improve explanation by incorporating multiple rule elements that are otherwise disparate; or (c) can be applied deductively without assumptions. These rule instances are ranked by cost, using an evaluation function that considers the proportion and number of ’s antecedents that the system needs to assume, as well as the proportion of candidate explanation elements not yet explained by other rule instances. The explanation is then extended by adding inferences from the lowest-cost rule instance to the working memory. Since the system directs its attention based on heuristic decisions about what needs explanation, it is a heuristic system with regard to the heuristic/methodical distinction.
UMBRA builds an explanation step by step using lower-level heuristics, and a separate set of high-level strategic heuristic rules that determine whether and how to proceed with this process. These strategic rules perform tasks such as determining the next focus of explanation, considering whether to wait for more observations, and deciding whether or not to apply a rule instance once it has been selected. Crucially, these rules take into account a number of factors that are not explicitly encoded in the domain. UMBRA operates by measuring things such as the connectivity of the explanation graph, the number of conditions of different types in axioms, weights on different origins of literals in working memory, and numeric evaluations of the connectivity of the explanation graph. It uses these extracted values, together with experimentally-established constants, in rules that then influence the system’s overall behaviour in generating an explanation.
The input cycle ends if the rule instance exceeds a limit on the total number of assumptions per cycle. Since each cycle incrementally extends the explanation to account for the observations, the output is an account of the input observations in terms of the instantiated axioms. Candidate literals are generated in a local manner highly analogous to a heuristic search with rules for a one-step look-ahead. UMBRA is thus not guaranteed to find a minimal explanation or to refrain from unnecessary inferences. Since explanations are expanded by extending working memory monotonically, it also does not fully support non-monotonic reasoning. In the performance tasks we will discuss in Section 4, we have used a standard parameterization [4] of UMBRA (in particular, an assumption limit of two, with runs limited to 12 input cycles, and no additional strategic rules). Since the system’s core ability to reason over nested expressions has been explored extensively elsewhere [4], this paper considers test cases that usually involve only direct beliefs about the world.
4. Discussion of Scenarios
In this section, we compare the strengths and limitations of KRASP and UMBRA, using scenarios in the robot waiter domain in Section 2. This study illustrates how these two systems exemplify different characteristics defined by the three distinctions described in Section 3.1, and helps identify some desired explanation generation capabilities for robots. Figure 1 provides a map of this domain with rooms, doors, and tables; the s denote areas in rooms. Humans and the robot can be in any location, and are not shown for simplicity.
4.1. Basic Approach to Explanation
We first consider the following scenario to illustrate the operation of the two systems.
Scenario 1.
The first scenario presents a basic anomaly:
- At Time 2: believes is unattended, and that is unoccupied.
- At Time 3: observes that is at .
We can construct a KRASP program that contains these beliefs, observations, and the system description. Inference then identifies an inconsistency because the expected observations, obtained by propagating the initial beliefs with inertia axioms, do not match actual observations. Consistency is restored by invoking a CR rule that provides a minimal explanation: , i.e., by assuming the occurrence of an exogenous action that a waiter seated at .
UMBRA is able to combine its beliefs table(table1) and person(person1) with the observations provided and apply the conceptual rule for the exogenous action, needing only to assume that the action did occur in the world. Since this incorporates all working memory elements, no more inputs are given, there are no other extremely low-cost inferences to be made (which might be made even in the absence of an anomaly demanding an explanation), and no further reasoning is attempted.
As a variant of Scenario 1, assume that has prior (default) knowledge that unattended people usually wait near the entrance (in in Figure 1), and the robot knows that is initially unattended (at Time 0). If is asked to seat at Time 2, a plan generated by inference in KRASP will have the robot go to because it continues to believe that is still next to the entrance. Now, when is observed at at Time 3, one possible explanation is that directly walked to to meet friends, and is thus an exception to the initial state default. The non-monotonic reasoning capability of KRASP enables the robot to draw such conclusions, and to build a different model of history to revise the result of previous inferences. UMBRA does not fully support such default reasoning or non-monotonic reasoning.
Scenario 1 gives us a starting point for a list of key criteria for high-quality explanation generation. It illustrates that computational efficiency, accuracy (including both precision and recall), and the ability to revise previous beliefs, are important abilities.
4.2. Multiple Concurrent Goals
Although considerable work in explanation generation has focused on identifying a top-level goal that activity is directed towards, a robot in social scenarios must maintain coherent beliefs about actors who may follow separate plans. We consider two scenarios that involve anomalies with tasks performed concurrently.
Scenario 2.
Consider a scenario that is a variation of Scenario 1:
- At Time 2: believes is unattended, and that is unoccupied.
- At Time 2: searches unsuccessfully for in .
- At Time 3: is greeted by at .
As before, KRASP’s inference process invoked a CR rule to infer that was seated at by a waiter at Time 2: , and reasoned to account for other observations. UMBRA also produced the correct “search” and “greet person” rule instances but, in the following cycles, preferred conceptual rules that it was able to prove cheaply, e.g., to explain why was considered occupied. It also inferred variations of rule instances with different time constraints as arguments, because it does not implement axiomatic constraints encoding concepts such as “adding an action differing only by time values does not extend the explanation”. This phenomenon was also observed in some other scenarios. When run for additional cycles, UMBRA eventually ran out of cheap conceptual rules and correctly inferred . This behaviour contrasts with the operation of KRASP, which assumes that a fluent holds at the earliest possible time and then holds by inertia. If a reality check axiom fails at a subsequent time step (because observations do not match expectations), the assumption regarding the corresponding fluent is revised in a way that suitably resolves the inconsistency.
Scenario 3.
Consider another variation of Scenario 1 which features a second, unrelated anomaly:
- At Time 2: believes is unattended, and is empty and at unoccupied in .
- At Time 2: travels from the kitchen door to with the goal of clearing .
- At Time 3: observes at , and observes that is not at .
These observations represent an inconsistency, but make sense if a waiter cleared and seated at . Computing the answer set of the corresponding KRASP program restores consistency by invoking two exogenous actions: and , i.e., the correct explanations are generated. UMBRA also generated most of the correct inferences, but was again distracted by making conceptual rule applications that were perceived to be cheaper than inferring . As an incremental-cyclic and heuristic system according to the full-model/incremental-cyclic and methodical/heuristic distinctions, UMBRA uses high-level heuristic strategies encoding a certain level of preference for cheaper axiom applications. When we varied its strategic rules to relax this preference, UMBRA quickly made the right inferences.
Scenarios 2–3 help identify a key criterion for explanation generation: leveraging knowledge effectively to explain multiple simultaneous behaviors or events.
4.3. Strategies for Explanation Selection
Explanation generation searches for a plausible model of the world that is as similar as possible to the ground truth. UMBRA guides search with heuristic measures of this similarity, e.g., coherence and consilience. Approaches such as KRASP, on the other hand, search the space of all relevant objects and axioms to find a minimal model. As the number of literals and ground instances increases, inference in KRASP becomes computationally expensive. Even with recent work in ASP-based systems that support interactive exploration, generating incremental and partial explanations is challenging. Scaling to complex domains is a challenge for both KRASP and UMBRA (and other explanation generation systems), but heuristic measures improve tractability of the search for explanations.
A strategy for belief maintenance is required when the system receives input dynamically, especially when observations contradict the system’s assumptions. Such a strategy is also necessary if the explanation generation is incremental and non-complete. Approaches for belief maintenance typically re-run the process anew, or maintain multiple competing hypotheses. KRASP, as a full-model system, performs a more elaborate search through all ground terms. Standard usage would thus require re-planning, or at least the generation of complete solutions, for incremental inputs. UMBRA, on the other hand, is a non-rigorous, heuristic, and incremental-cyclic system. It delays deciding in the face of ambiguity, seeking the lowest-hanging fruit, and committing when its parameterization allows. This strategy for belief maintenance also means that UMBRA can reach a point where its only option is to rebuild an explanation completely. The following scenario illustrates these differences.
Scenario 4.
Consider the following beliefs and observations:
- At Time 0: believes that is located in , and travels from the to .
- At Time 1: observes that is not in .
An important point is that at Times 0 and 1, does not know whether is unattended or seated at a table, making it difficult to arrive at a single explanation. For instance, may not have been in , or may have been in and then moved away. Inference in the corresponding KRASP program provides these two explanations: or . The explanations correspond to two possible worlds that require the same number of rules to be triggered and thus have a similar value. Unlike UMBRA’s fine-grained approach, KRASP does not include variable heuristic costs of relaxing different rules. The first explanation implies that was not really waiting to be seated to begin with, and the second explanation implies that has moved away from the previous location. The dynamics of these exogenous actions need to be modeled explicitly in KRASP, by adding suitable statements in the corresponding program, before they can be used to generate explanations.
UMBRA’s approach, on the other hand, is somewhat analogous to local greedy search with one-step look-ahead and monotonic commitments. Due in large part to its incremental-cyclic nature, it cannot generate and directly compare different multiple-step explanations. For this scenario, UMBRA explained the absence of by assuming that had been there, but left the restaurant. Based on UMBRA’s heuristics, this assumption resulted in as cheap and coherent an explanation as the possible alternatives.
Scenario 4 suggests that an explanation generation system should have a formal model of explanations, and be flexible to decide when and how to maintain competing hypotheses or to revise baseline beliefs.
4.4. Including Different Assumptions
Providing a meaningful explanation frequently involves making assumptions about different aspects of the world. In robotics applications, this is important because the information extracted from sensors is often incomplete (e.g., includes false negatives).
Scenario 5.
The following scenario illustrates the process of making a range of assumptions.
- At Time 1: is in the , and believes is seated at in ; also believes that has ordered . At this time, picks up a dish believing it to contain .
- At Time 2: observes its own location to be .
- At Time 3: observes that is not at .
In this scenario, coming up with a valid explanation, e.g., that has moved and left the restaurant, requires that the system reason about: (a) an exogenous event; (b) a domain object (a dish containing ); and (c) a movement action ( moving from to ).
As a methodical system (under the methodical/heuristic distinction), KRASP can only reason about actions that have been modeled, and cannot reason about object instances that have not been specified in advance. Inference in the KRASP program for this scenario generates the explanation to explain the unexpected absence of at . If, in addition to the standard action, the KRASP program includes an action () to reason about the robot being moved to a specific location, inference in the corresponding KRASP program also generates as an explanation. However, there is no further reasoning about the dish that has been picked up, and such reasoning is not necessary in this scenario.
UMBRA, on the other hand, may assume any literal; it actively seeks out symbols that can be used to construct rule instances. For instance, if a new identifier or an entirely new domain predicate are introduced, UMBRA will try to incorporate them as appropriate. For instance, introducing allows UMBRA to infer statements such as . However, this ability also causes it to sometimes make unnecessary or irrelevant assumptions, since UMBRA is constrained only by limits on cognitive cycles, the quality of its cost function, and the sparsity of the input observations. In Scenario 5, UMBRA inferred that traveled from the to , identified the abnormality, and explained that left the restaurant. In the same scenario, instead of assuming a new dish and its properties (), the lower cost option was to assume that was a . This scenario is thus another instance where constraint-like axioms, especially if incorporated into concept rule definitions, would improve representational power and accuracy.
4.5. Explanations with Inconsistent Inputs
Observations received by the robot may include false positives, as well as false negatives. For instance, a robot’s sensors are imperfect, and other agents may communicate incorrect information.
Scenario 6.
Consider the following situation, which includes irrelevant and incorrect literals.
- At Time 1: believes has ordered , believes contains , observes is empty, and travels from to in .
- At Time 2: is in , it observes seated at , observes is at and contains , and observes to be seated at .
Possible explanations of this scenario are that the wrong dish () has been delivered to , or that the initial belief about was incorrect.
Inference in the KRASP program, which includes these beliefs and observations (and other domain axioms), only explains the state of ; nothing else needs explanation. The corresponding explanation invokes an exogenous action, i.e., , to imply that has been mixed up and the wrong dish has been delivered to instead of . The other possibility is not considered because the domain knowledge does not include any measure of uncertainty for the initial belief about the state of . Interestingly, if the number of time steps is increased between the initial belief and final observation of , KRASP generates multiple explanations by hypothesizing that the dish got mixed up at different time steps during this interval.
For UMBRA, this scenario was one of the least accurate cases, and the explanation process mainly consisted of applying cheap conceptual rules. The system assumed that was a who had left the restaurant, i.e., the key anomaly went unexplained. This outcome was a failure of the high-level strategic rules. It is often difficult to establish why a reasoning process guided by heuristics made an error in a particular scenario, but any explanation based on an incomplete search can only be as good as the heuristic it uses for inference choice. Furthermore, as a cognitive system (under the non-specialized/cognitive distinction), UMBRA aims to produce a set of reasonable assumptions given reliable partial inputs, rather than create a maximally consistent explanation given unreliable inputs. The corresponding design choices contribute in part to the fact that UMBRA cannot easily redact beliefs.
A robot may encounter inputs that are more problematic than the type of false positives considered above, as illustrated by the following three scenarios.
Scenario 7.
Consider a baseline scenario which states that:
- At Time 2: believes that is unoccupied, is on in , and is empty.
- At Time 3: has moved to to clear , but observes that there is no on .
Inference in the corresponding KRASP program generates the explanation: , i.e., that a waiter cleared at Time 2, which is a correct explanation. For this scenario, UMBRA is able to generate the correct explanation. Next, we examine two variants of this scenario that feature unexpected inputs.
Scenario 8.
First, consider the inclusion of new literals in the input, e.g., to describe a previously unknown attribute of or a previously unknown relationship between and .
KRASP cannot deal with such new additions that have not been defined in its domain description. UMBRA, on the other hand, ignores the foreign literals until an opportunity comes up to incorporate those observations.
Scenario 9.
The second variant of Scenario 7 adds contradictory observations:
- At Time 3: is both observed to have state , and observed to have state .
Inference in the KRASP program cannot deal with this inconsistency and no solutions are provided. UMBRA has similar problems, but is able to construct a partial explanation when provided the inputs incrementally; it only fails at the point where the contradictory input is received.
Scenarios 7–9 highlight some key criteria for explanation generation systems: (a) robustness with respect to observed false positives and false negatives; (b) the ability to decide what observations to focus on; and (c) graceful failure (when failure is unavoidable). Based on all the criteria identified above, we will now turn our attention to eliciting and discussing the desired capabilities of a general explanation generation system for robots.
4.6. Domain Size and Complexity
We end our comparative study with a brief description of the size and complexity of the robot waiter domain. Most of the specific details are provided in the context of KRASP (the corresponding counts for UMBRA are somewhat different due to differences in representations and encoding, but not substantially so). The domain contains 19 sorts (or class symbols) of various levels of abstraction, such as , , and . It also has nine object properties that contribute to the system’s state, e.g., a door can be , and a customer can be . There are 12 higher-level predicates for static domain properties (e.g., , ) and meta-level objects and events (e.g., for action occurrence, and ). The remaining symbols include 12 fluents (nine basic and three defined), seven actions, 10 exogenous events, and 20 constant object names (excluding identifiers for time steps). The axioms in the knowledge base given to KRASP for this domain include 17 causal laws, 18 state constraints, 10 executability conditions, and additional axioms that implement the closed world assumption, rules of inertia, reality checks, default statements, CR rules, and rules that trigger inference to achieve a given goal (see Section 3.2).
During explanation generation (with KRASP, UMBRA, or other systems), we expect that as the number of domain concepts modeled increases, the computation effort (i.e., time and thus cost) also increase. We also expect reasoning time to scale disproportionately in the number of ground instances (i.e., specific instances of various classes) because every such new instance must be considered in conjunction with all other literals and relevant axioms during the search for an explanation. Although scaling is challenging for KRASP, UMBRA and other systems, it is more pronounced in systems such as KRASP, which search through the space of all literals and axioms, than in systems such as UMBRA, which are more selective in their search for an explanation.
Note that the objective of the comparative study (above) is to illustrate some key desired explanation generation capabilities, and the relationship between these capabilities and the distinctions characterizing the space of explanation generation systems. A quantitative analysis of the (space or time) complexity of these two systems will not help achieve this objective; such analyses have also been documented in other papers and books [2,4]. Furthermore, although the complexity can vary between different explanation generation systems, scaling to large, complex domains is challenging for all of them.
5. Recommendations
This section first revisits the three distinctions introduced in Section 3.1 to characterize the space of explanation generation systems, and discusses the effect of these distinctions on the capabilities of the two systems that differ substantially along these three dimensions (Section 5.1). Next, the comparative study in Section 4 is used to emphasize how the complementary strengths of these two (and other similar) systems can support important explanation generation capabilities for robots (Section 5.2). Finally, other key distinctions and the associated capabilities are considered to provide additional recommendations for the design of a system that supports efficient, incremental and reliable explanation generation from partial information (Section 5.3).
5.1. Distinctions Revisited
With regard to the methodical/heuristic distinction, methodical systems like KRASP compute high-quality explanations, using domain rules to deal with anomalies. Such approaches provide appealing guarantees, e.g., correctness or minimality of the explanations generated, while also supporting non-monotonic reasoning with default knowledge. Heuristic systems like UMBRA forgo such guarantees to generate explanations with heuristic guidance; they also do not fully support desired capabilities such as non-monotonic reasoning and reasoning with default knowledge. However, heuristic processing scales more efficiently, and can be used to explain anomalies by operating over both domain-specific information and conceptual rules.
The non-specialized/cognitive distinction suggests that more general systems like KRASP can draw inferences in any domain without prior assumptions. Such systems can be used in different settings, including those that do not need to reason about time, without having to make any changes in their processing behaviour. Cognitively-inspired systems such as UMBRA, on the other hand, generate explanations and promote understanding using their cognitive biases and preconceptions about high-level structures; representing these preconceptions in a system such as KRASP may be difficult. These biases and preconceptions can lead UMBRA (and similar systems) to draw incorrect or inefficient conclusions in some situations. At the same time, they enable inferences beyond the ones implied by domain information, and support the use of such systems for tasks involving mental state understanding and social cognition. Furthermore, these systems may be better able to emulate plausible human reasoning in some situations, thus improving interaction with other agents.
With regard to the full-model/incremental-cyclic distinction, full-model systems like KRASP run to completion, i.e., they generate complete (and consistent) models of the set of current beliefs. They may also resolve observed inconsistencies with non-monotonic belief revision. Conversely, incremental-cyclic systems like UMBRA operate online by iterating through problem solving cycles until high-level heuristic rules deem the explanation sufficient. Allowing operation with different combinations of such rules provides significant flexibility. Systems like UMBRA may also use predetermined symbols for time that match those in domain axioms and observations, giving them greater temporal reasoning power at the cost of generality.
5.2. Coupling KRASP and UMBRA
The comparative study performed in Section 4 showed that the three distinctions we introduced in Section 3.1 are closely related to some key desired capabilities of an explanation generation system for robots. In this section, we investigate the extent to which an explanation generation system that couples a non-specialized solver like KRASP with a cognitive system such as UMBRA, will support these desired explanation generation capabilities. Table 1 lists the capabilities identified based on the scenarios explored in Section 4, and documents the extent to which KRASP and UMBRA individually support these capabilities; we observe that KRASP and UMBRA mostly complement each other. The three partitions of Table 1, each of which presents three capabilities, are discussed below.

Table 1.
Comparison of KRASP and UMBRA in terms of their support for some desired explanatory capabilities.
The top partition in Table 1 lists capabilities related to how systems process information to generate explanations, and the types of information they can represent and reason with:
- (1)
- An explanation generation system should provide accurate inferences in complex domains with large knowledge bases. One example is the KRASP architecture, which generates explanations from first principles using the system description and observations of system behaviour. Such a system should also explain multiple concurrent activities, e.g., Scenario 3 in Section 4. Both KRASP and UMBRA support this capability, although KRASP provides a more expressive and rigorous means for generating explanations.
- (2)
- A high-quality explanation generation system should make good use of a knowledge base containing domain axioms with varying semantics, e.g., default rules, concept hierarchies, and hierarchical task networks (HTNs). Although both KRASP and UMBRA are able to demonstrate this ability, there are some differences. KRASP provides better representation and reasoning capabilities for default knowledge and concepts, but UMBRA, as a cognitive system, is designed to support varying semantics, and thus may be somewhat better than KRASP in this area in some situations.
- (3)
- An explanation system should be able to effectively apply and maintain constraints, either in the form of explicit, reified elements in memory, as supported by UMBRA, or in the form of axioms, as supported by KRASP. The ability to support an axiomatic description of constraints makes KRASP more expressive and powerful, e.g., in Scenario 2, UMBRA would be more effective if it could use axiomatic constraints. At the same time, reified constraints are also useful, especially when partial information is available and temporal reasoning is necessary, situations which an explanation generation system for robots will often encounter.
Combining the capabilities in the first partition will thus result in a broad and flexible model of explanation. We next turn our attention to the central partition of Table 1, which considers capabilities related to truth maintenance and the ability to handle different forms of uncertainty:
- (4)
- KRASP provides an elegant and expressive approach for modeling ambiguity and maintaining beliefs. It supports non-monotonic logical reasoning by computing answers sets of a program containing axioms and domain knowledge, including default knowledge. This behaviour is demonstrated by multiple scenarios in Section 4, and is a useful capability for an explanation generation system. UMBRA’s approach for belief maintenance is heuristic, much simpler, and not as expressive.
- (5)
- An explanation generation system for robots should have strategies to maintain concurrent hypotheses, and to deal with uncertainty, ambiguity, and evidence that becomes available over time. These strategies should be general, i.e., applicable to any context the robot encounters. UMBRA only has a simplistic method of delayed commitment that allows the generation of a new explanation only when the system hits a dead end. KRASP does not support multiple strategies, but it elegantly reduces planning, diagnostics and inference to computing answer sets. This behaviour was illustrated by multiple scenarios in Section 4.
- (6)
- KRASP is formally well-defined and provides satisfying guarantees about the inferences it draws, which is an appealing feature for an explanation generation system. It also allows certainty about various facets of its behaviour in various contexts. Many reasoning frameworks, including UMBRA, do not provide any such guarantees, often trading it for improved efficiency. Sometimes this is by design, when cognitive systems aim to emulate informal human cognition. The ideal system should be able to revise its operation to support the desired guarantees when it is advantageous to have such guarantees.
Together, the features in the second partition of Table 1 will produce an explanation framework that is adaptable and powerful. Next, the bottom partition lists capabilities related to scalable and incremental explanation:
- (7)
- The search for explanations should be scalable, as discussed in Section 4.6. KRASP’s approach can become computationally expensive if inference is not done selectively, as the number of relations and ground object instances grows very large. UMBRA generates explanations more efficiently using low-level heuristics for local search with abductive inference, and high-level (strategic) rules to decide which elements in memory have the highest demand for explanation. Although domain-specific heuristic rules can be encoded in KRASP, the innate cognitive biases and preconceptions of UMBRA can model mental states, social cognition and human behaviour, which cannot be encoded in KRASP. However, UMBRA’s efficiency is relative and may come with accuracy trade-offs, e.g., see Scenario 3. For robotics applications, well-designed heuristics can support desirable real-time operation.
- (8)
- Incremental incorporation of sensor data to generate explanations is a desired feature. New observations should be used to reliably and efficiently build on existing explanations. This capability is an underlying part of UMBRA’s structure, building on earlier inferences by chaining from observations and heads of rules, and making repeated reconstructions or extensive belief revision unnecessary. KRASP, on the other hand, focuses on building complete models by (re)computing all the beliefs each time the solver is invoked. Incremental processing is thus a challenging problem for KRASP and other ASP-based architectures, although research is currently being performed in this area [22].
- (9)
- Sensor information may contain false negatives (i.e., partial information) and false positives (i.e., incorrect information). UMBRA and KRASP are both able to deal with partial information, as in Scenario 5. KRASP can also handle false positives in cases where it can restore consistency by, for instance, reasoning about exogenous actions; see Scenario 6. UMBRA, on the other hand, has no process to actively detect and remove false positives. It can ignore noise in input symbols, relations and objects that have not been defined (see Scenario 8), but may also try to incorporate unrelated literals in unexpected ways. Ideally, an explanation generation system should make inferences that are robust to both noise and omissions, and identify and handle examples of unreliable inputs.
The abilities described in the third partition of Table 1 thus complete the set of capabilities expected in an advanced explanation generation system for robots.
5.3. Additional Desiderata
The previous section discussed some desirable capabilities of an explanation generation system for robots. These capabilities were identified by comparing KRASP and UMBRA in the set of scenarios in Section 4. However, as stated in Section 3.1 where we introduced three fundamental distinctions, the space of explanation generation systems is characterized by other distinctions and thus other capabilities. In addition, KRASP and UMBRA have some capabilities that were not explored in our comparative study. Based on our review of KRASP, UMBRA, other existing explanation generation systems, and the needs of robotics applications, this section makes some additional, more speculative recommendations. We summarize our central desiderata, including those not illustrated by the systems we have considered, in Figure 4.
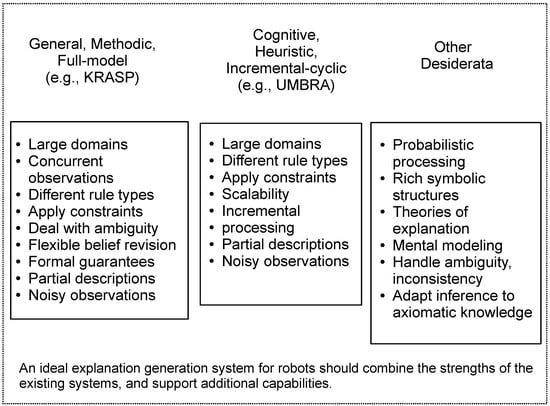
Figure 4.
Desired capabilities of an explanation generation system for robots. Capabilities that are supported by KRASP and UMBRA, as examples of systems that differ substantially along the three fundamental distinctions, are grouped together. Additional capabilities are listed separately.
- Probabilistic information: An explanation system should be able to incorporate probabilistic descriptions of knowledge and uncertainty (i.e., degrees of belief) into its model(s) in conjunction with logical reasoning. Recent work in this direction has been reported in the context of using ASP and probabilistic graphical models for planning and diagnostics in robotics [33,38,41]. A sophisticated explanation system could extend KRASP-like representations to hypothesize and evaluate different possible worlds [13,14], but incrementally guide the reasoning using well-designed heuristics, to generate explanatory structures that tightly couple probabilistic and logic-based representations of knowledge.
- Representational richness for symbolic structures: An explanation generation system should provide system-level access to symbols for high-level domain concepts. For example, it is useful for a system to reason directly about concepts such as time [47], especially as its specifics are unlikely to change between domains. Also, computationally intractable problems in temporal reasoning should be avoided, e.g., deciding consistency of the interval algebra and computing its minimal network are both NP-complete problems [48]. Furthermore, robots should be able to present information in human-readable encodings. Existing systems such as KRASP and UMBRA support such encodings to some extent; KRASP also supports a relational and distributed encoding. However, different levels of abstraction may be preferable for encoding truth values, time, quantification, and mental states, in addition to the basic semantic content of a domain [49]. Designing such a representation will require consideration of tasks such as explanation generation, planning, learning, and question answering, along the lines of KRASP.
- Multiple approaches to explanation: Any computational agent should use a formal theory to draw inferences and provide explanations. The systems we have discussed have somewhat differing models of explanation. KRASP has its roots in “explanation as diagnosis from first principles” and focuses on the minimality and correctness of explanations as deviations from a standard (expected) model. UMBRA’s roots are in “explanation as plan recognition” and focuses on working memory interconnectedness and minimizing search effort. A sophisticated system should be able to operate according to varying accounts of the observations in terms of different mappings between axiomatic knowledge, prior beliefs, and input observations. A proof lattice should be able to contain inferences from different paradigms, e.g., “agent(n) can be deduced from the syllogism robot(X) → agent(X) holding for ground instance of X”; “the plates were in the kitchen at time , so it is credible that the plates were in the kitchen at time with a default inductive probability ”; “robot rob1 had the goal for door d1 to be open, so rob1 opening d1 was an intentional action”; and so on.
- Mental modeling: A system with prior knowledge of high-level symbolic structures and domain knowledge that refers to those structures, will be able to perform sophisticated mental modeling [50]. To infer other agents’ beliefs and intentions, a key task for multiagent systems, it is important to capitalize on system-level access to symbols (e.g., belief, goal), types (e.g., agents, mental states), and concepts (e.g., negation, time) that are general across the domains each agent may be expected to operate in. UMBRA allows an agent to automatically construct such mental models [43], using beliefs about its mental states to infer the explanations that other agents are generating; any differences from its own explanation emerge from its beliefs about how other agents’ beliefs differ from its own. UMBRA incorporates mental models into its explanation at multiple levels of recursion. KRASP, and other similar systems, can reproduce similar behaviour, i.e., reason about other agents’ beliefs, given relevant domain knowledge, but the process is not integrated at the system level. An explanation generation system for robots will benefit significantly from the ability to understand and reason about mental states during processing, without requiring special axioms in its knowledge base.
- Handling ambiguity and inconsistency: An explanation generation system should have strategies for dealing with uncertainty and inconsistency, and be able to adapt its behaviour by selecting between these strategies as appropriate. Based on existing work, we would expect such strategies to include methods for maintaining concurrent hypotheses about the world, revising existing hypotheses, or for transforming mental models in light of new data [51]. This flexibility will allow a robot to understand other agents, reason about situations with low certainty, create contingency plans for different variations of the true state of the world, reach mutual understanding of the world with another agent, deal with humans’ possibly inconsistent beliefs by creating conflicting models of their mental states, and so on.
- Adapting inference to axiomatic knowledge: Explanation generation systems typically operate over axiomatic knowledge in the form of logical structures that encode relationships. These structures may be expressed in different syntactic forms designed to encapsulate different semantic constructions, e.g., axiomatic constraints, hierarchical methods, process models, defaults or norms, and dispositional beliefs. Computational frameworks tend to support some subset of these structures, and thus only capitalize on the advantages of that representation. Instead, inference should be adapted to the axiomatic knowledge available; explanation is then a search through the space of possible sets of ground axioms for a set that best matches reality. Axiom characteristics can also inform higher-level heuristics that guide this search, e.g., UMBRA uses strategic rules to determine its next focus of explanation based on the origins of existing beliefs (e.g., observations, inferences, assumptions, and constraint implications) and the edges between them in the explanation graph.
Taken in conjunction with the recommendations in Section 5.2, these abilities describe a sophisticated system for explanation generation in robotics.
6. Conclusions
Explanation generation systems populate a complex, multidimensional space defined by a wide range of distinctions. This paper first introduced three fundamental distinctions in the multidimensional space. Next, we compared the capabilities of two systems that differ substantially along the axes defined by these three distinctions, using scenarios involving a robot waiter assisting in a restaurant. This comparative study helped identify important criteria for high-quality explanation generation systems in robotics. We have also confirmed that KRASP and UMBRA face some common challenges, such as scaling to very large domains and reasoning with different descriptions of uncertainty. Exploiting the complementary strengths of the two systems may provide solutions to these challenges, and this paper opens up several directions for further research.
An initial step will be to couple the complementary strengths of the two systems, as described in Section 5.2. Towards this objective, we will improve UMBRA by focusing on computational efficiency, scalable search, failure recovery and improved guidance by heuristic knowledge. Specifically, we will include a better theory of explanation, using lessons learned from KRASP to support reasoning with default knowledge and a preferential hierarchy of elements to explain. It will also employ better cost functions for improved efficiency and use control rules to determine when to prune hypotheses and how to choose between belief revision and hypothesis replacement. We will also apply lessons learned from the study of UMBRA’s heuristic approach to improve the scalability of KRASP for large domains and more complex explanations. We will explore this design of improved heuristics while retaining the appealing capabilities of KRASP, such as non-monotonic logical reasoning and guarantees about the inferences drawn.
We are considering, for both KRASP and UMBRA, incorporating the other recommendations discussed in Section 5.3. For instance, we are exploring the introduction of the probabilistic description of knowledge and uncertainty in conjunction with the logical reasoning. We hope to build on recent work that has been reported in this direction in the general context of using ASP and probabilistic planning with robots [33,38]. Furthermore, we are exploring the extension of KRASP and UMBRA to explicitly model communication between agents and to use this model for generating explanations. The long-term objective is to provide a reliable, efficient and formally well-defined approach for explanation generation, as a fundamental capability required for human-robot collaboration in complex domains.
Acknowledgments
The authors thank Pat Langley and Michael Gelfond for discussions related to the systems discussed in this paper. This work was supported in part by the U.S. Office of Naval Research Science of Autonomy Award N00014-13-1-0766. Opinions and conclusions described in this paper are those of the authors.
Author Contributions
M.S., with input from B.M. and Z.C., conceived of and designed the scenarios. M.S. and Z.C. designed and built the KRASP system and the programs for scenarios. B.M. designed and built the UMBRA system and translated the scenarios into its representation. B.M., M.S. and Z.C. performed the experimental analysis. B.M. and M.S. wrote the paper.
Conflicts of Interest
The authors declare no conflict of interest. The sponsors had no role in the design of the study, in the collection, analyses or interpretation of data, in the writing of the manuscript; nor in the decision to publish the results.
Abbreviations
The following abbreviations are used in this manuscript:
| ASP | Answer Set Prolog |
| KRASP | Knowledge Representation for Robots using ASP |
| UMBRA | Understanding Mechanism for aBductive Reasoning Agents |
| AL | Action Language |
| CR | Consistency-Restoring |
References
- Sridharan, M.; Meadows, B.; Colaco, Z. A Tale of Many Explanations: Towards An Explanation Generation System for Robots. In Proceedings of the Intelligent Robotics and Multiagent Systems (IRMAS) track of the ACM/SIGAPP Symposium on Applied Computing (SAC), Pisa, Italy, 4–8 April 2016; pp. 260–267.
- Gelfond, M.; Kahl, Y. Knowledge Representation, Reasoning and the Design of Intelligent Agents; Cambridge University Press: New York, NY, USA, 2014. [Google Scholar]
- Reiter, R. A Theory of Diagnosis from First Principles. Artif. Intell. 1987, 32, 57–95. [Google Scholar] [CrossRef]
- Meadows, B.; Langley, P.; Emery, M. Seeing Beyond Shadows: Incremental Abductive Reasoning for Plan Understanding; AAAI Plan, Activity, and Intent Recognition Workshop; AAAI Press: Bellevue, WA, USA, 2013; Volume 13, pp. 24–31. [Google Scholar]
- Ng, H.T.; Mooney, R. Abductive Plan Recognition and Diagnosis: A Comprehensive Empirical Evaluation. In Proceedings of the International Conference on Principles of Knowledge Representation and Reasoning, Cambridge, MA, USA, 26–29 October 1992; pp. 499–508.
- Baral, C.; Gelfond, G.; Son, T.C.; Pontelli, E. Using answer set programming to model multi-agent scenarios involving agents’ knowledge about other’s knowledge. In Proceedings of the Ninth International Conference on Autonomous Agents and Multiagent Systems, Toronto, ON, Canada, 9–14 May 2010; pp. 259–266.
- Pontelli, E.; Son, T.C.; Baral, C.; Gelfond, G. Answer Set Programming and Planning with Knowledge and World-Altering Actions in Multiple Agent Domains. In Correct Reasoning: Essays on Logic-Based AI in Honour of Vladimir Lifschitz; Springer: New York, NY, USA, 2012; pp. 509–526. [Google Scholar]
- Goldman, R.; Geib, C.; Miller, C. A New Model of Plan Recognition. In Proceedings of the International Conference on Uncertainty in Artificial Intelligence, Stockholm, Sweden, 30 July–1 August 1999; pp. 245–254.
- Ramirez, M.; Geffner, H. Probabilistic Plan Recognition Using Off-the-Shelf Classical Planners. In Proceedings of the Twenty-Fourth AAAI Conference on Artificial Intelligence, Atlanta, GA, USA, 11–15 July 2010; pp. 1121–1126.
- Kautz, H.; Allen, J.F. Generalized Plan Recognition. In Proceedings of the Fifth National Conference on Artificial Intelligence, Philadelphia, PA, USA, 11–15 August 1986; pp. 32–38.
- Appelt, D.; Pollack, M. Weighted Abduction for Plan Ascription. User Model. User-Adapt. Interact. 1992, 2, 1–25. [Google Scholar] [CrossRef]
- Raghavan, S.; Mooney, R. Abductive Plan Recognition by Extending Bayesian Logic Programs. In Proceedings of the European Conference on Machine Learning and Principles and Practice of Knowledge Discovery in Databases, Athens, Greece, 5–9 September 2011; pp. 629–644.
- Baral, C.; Gelfond, M.; Rushton, N. Probabilistic Reasoning with Answer Sets. Theory Pract. Log. Program. 2009, 9, 57–144. [Google Scholar] [CrossRef]
- Lee, J.; Wang, Y. A Probabilistic Extension of the Stable Model Semantics. In Proceedings of the Twelfth International Symposium on Logical Formalizations of Commonsense Reasoning, Stanford, CA, USA, 23–25 March 2015; pp. 96–102.
- Cohen, P.R.; Levesque, H.J. Intention is choice with commitment. Artif. Intell. 1990, 42, 213–261. [Google Scholar] [CrossRef]
- Sycara, K. Multiagent Systems. AI Mag. 1998, 19, 79–92. [Google Scholar]
- Rao, A.; Georgeff, M.; Sonenberg, E. Social plans. In Proceedings of the Fourth European Workshop on Modeling Autonomous Agents in a Multi-Agent World, Martino al Cimino, Italy, 29–31 July 1992; pp. 57–76.
- Castelfranchi, C. Modelling Social Action for AI Agents. Artif. Intell. 1998, 103, 157–182. [Google Scholar] [CrossRef]
- Bridewell, W.; Langley, P. A computational account of everyday abductive inference. In Proceedings of the Thirty-Third Annual Meeting of the Cognitive Science Society, Boston, MA, USA, 20–23 July 2011; pp. 2289–2294.
- Fahlman, S.E. Using Scone’s multiple-context mechanism to emulate human-like reasoning. In Proceedings of the AAAI Fall Symposium on Advances in Cognitive Systems, Arlington, VA, USA, 4–6 November 2011; pp. 98–105.
- Bello, P. Shared Representations of Belief and their Effects on Action Selection: A Preliminary Computational Cognitive Model. In Proceedings of the Thirty-Third Annual Meeting of the Cognitive Science Society, Boston, MA, USA, 20–23 July 2011; pp. 2997–3002.
- Gebser, M.; Janhunen, T.; Jost, H.; Kaminski, R.; Schaub, T. ASP Solving for Expanding Universes. In Proceedings of the Thirteenth International Conference on Logic Programming and Nonmonotonic Reasoning, Lexington, KY, USA, 27–30 September 2015; pp. 354–367.
- Leake, D. Focusing Construction and Selection of Abductive Hypotheses. In Proceedings of the International Joint Conference on Artificial Intelligence, San Francisco, CA, USA, 28 August–3 September 1993; pp. 24–29.
- Thagard, P. The Best Explanation: Criteria for Theory Choice. J. Philos. 1978, 75, 76–92. [Google Scholar] [CrossRef]
- Perkins, D.; Allen, R.; Hafner, J. Difficulties In Everyday Reasoning. In Thinking: The Expanding Frontier; Franklin Institute Press: Philadelphia, PA, USA, 1983; pp. 177–189. [Google Scholar]
- Lemaignan, S.; Ros, R.; Mösenlechner, L.; Alami, R.; Beetz, M. ORO, a Knowledge Management Platform for Cognitive Architectures in Robotics. In Proceedings of the 2010 IEEE International Conference on Intelligent Robots and Systems (IROS), Taipei, Taiwan, 18–22 October 2010; pp. 3548–3553.
- Tenorth, M.; Beetz, M. KnowRob: A Knowledge Processing Infrastructure for Cognition-Enabled Robots. Int. J. Robot. Res. 2013, 32, 566–590. [Google Scholar] [CrossRef]
- Erdem, E.; Aker, E.; Patoglu, V. Answer Set Programming for Collaborative Housekeeping Robotics: Representation, Reasoning, and Execution. Intell. Serv. Robot. 2012, 5, 275–291. [Google Scholar] [CrossRef]
- Saribatur, Z.; Erdem, E.; Patoglu, V. Cognitive Factories with Multiple Teams of Heterogeneous Robots: Hybrid Reasoning for Optimal Feasible Global Plans. In Proceedings of the IEEE/RSJ International Workshop on Intelligent Robots and Systems, Chicago, IL, USA, 14–18 September 2014; pp. 2923–2930.
- Chen, X.; Xie, J.; Ji, J.; Sui, Z. Toward Open Knowledge Enabling for Human-Robot Interaction. Hum-Robot Interact. 2012, 1, 100–117. [Google Scholar] [CrossRef]
- Hanheide, M.; Gobelbecker, M.; Horn, G.; Pronobis, A.; Sjoo, K.; Jensfelt, P.; Gretton, C.; Dearden, R.; Janicek, M.; Zender, H.; et al. Robot Task Planning and Explanation in Open and Uncertain Worlds. Artif. Intell. 2015. [Google Scholar] [CrossRef]
- Sridharan, M.; Gelfond, M. Using Knowledge Representation and Reasoning Tools in the Design of Robots. In Proceedings of the IJCAI Workshop on Knowledge-based Techniques for Problem Solving and Reasoning (KnowProS), New York, NY, USA, 10 July 2016; pp. 1288–1302.
- Zhang, S.; Sridharan, M.; Gelfond, M.; Wyatt, J. Towards an Architecture for Knowledge Representation and Reasoning in Robotics. In Social Robotics; Springer International Publishing: Sydney, Australia, 2014; pp. 400–410. [Google Scholar]
- Sridharan, M.; Meadows, B. Should I do that? Using Relational Reinforcement Learning and Declarative Programming to Discover Domain Axioms. In Proceedings of the International Conference on Developmental Learning and Epigenetic Robotics (ICDL-EpiRob), Paris, France, 19–22 September 2016.
- Gelfond, M.; Lifschitz, V. The Stable Model Semantics for Logic Programming. In Proceedings of the Fifth International Conference on Logic Programming, Seattle, WA, USA, 15–19 August 1988; pp. 1070–1080.
- Terracina, G.; Leone, N.; Lio, V.; Panetta, C. Experimenting with Recursive Queries in Database and Logic Programming Systems. Theory Pract. Log. Program. 2008, 8, 129–165. [Google Scholar] [CrossRef]
- Balduccini, M.; Regli, W.; Nguyen, D. Towards an ASP-Based Architecture for Autonomous UAVs in Dynamic Environments (Extended Abstract). In Proceedings of the Thirtieth International Conference on Logic Programming (ICLP), Vienna, Austria, 19–22 July 2014.
- Zhang, S.; Sridharan, M.; Wyatt, J. Mixed Logical Inference and Probabilistic Planning for Robots in Uncertain Worlds. IEEE Trans. Robot. 2015, 31, 699–713. [Google Scholar] [CrossRef]
- Balduccini, M.; Gelfond, M. Logic programs with Consistency-Restoring Rules. In Proceedings of the International Symposium on Logical Formalizations of Commonsense Reasoning, Stanford, CA, USA, 24–26 March 2003; pp. 9–18.
- Balduccini, M.; Gelfond, M. Diagnostic Reasoning with A-Prolog. Theory Pract. Log. Program. 2003, 3, 425–461. [Google Scholar] [CrossRef]
- Colaco, Z.; Sridharan, M. What Happened and Why? A Mixed Architecture for Planning and Explanation Generation in Robotics. In Proceedings of the Australasian Conference on Robotics and Automation, Canberra, Australia, 2–4 December 2015.
- Leone, N.; Pfeifer, G.; Faber, W.; Eiter, T.; Gottlob, G.; Perri, S.; Scarcello, F. The DLV System for Knowledge Representation and Reasoning. ACM Trans. Comput. Log. 2006, 7, 499–562. [Google Scholar] [CrossRef]
- Meadows, B.; Langley, P.; Emery, M. Understanding Social Interactions Using Incremental Abductive Inference. In Proceedings of the International Conference on Advances in Cognitive Systems, Baltimore, MD, USA, 12–14 December 2013; pp. 39–56.
- Langley, P.; Meadows, B.; Gabaldon, A.; Heald, R. Abductive Understanding of Dialogues about Joint Activities. Interact. Stud. 2014, 15, 426–454. [Google Scholar]
- Dunbar, R. On the Origin of Human Mind. In Evolution and the Human Mind: Modularity, Language, and Meta-Cognition; Cambridge University Press: Cambridge, UK, 2000. [Google Scholar]
- Wielemaker, J.; Schrijvers, T.; Triska, M.; Lager, T. SWI-Prolog. Theory Pract. Log. Program. 2012, 12, 67–96. [Google Scholar] [CrossRef]
- Allen, J.F. Maintaining knowledge about temporal intervals. Commun. ACM 1983, 26, 832–843. [Google Scholar] [CrossRef]
- Vilain, M.; Kautz, H. Constraint propagation algorithms for temporal reasoning. In Proceedings of the Fifth National Conference on Artificial Intelligence, Philadelphia, PA, USA, 11–15 August 1986; pp. 377–382.
- Laird, J.E.; Newell, A.; Rosenbloom, P.S. SOAR: An Architecture for General Intelligence. Artif. Intell. 1987, 33, 1–64. [Google Scholar] [CrossRef]
- Bello, P. Cognitive Foundations for a Computational Theory of Mindreading. Adv. Cogn. Syst. 2012, 1, 59–72. [Google Scholar]
- Chi, M. Three types of conceptual change: Belief revision, mental model transformation, and categorical shift. In International Handbook of Research on Conceptual Change; Routledge: New York, NY, USA, 2008; pp. 61–82. [Google Scholar]
© 2016 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC-BY) license (http://creativecommons.org/licenses/by/4.0/).