Drive the Drive: From Discrete Motion Plans to Smooth Drivable Trajectories
Abstract
:1. Introduction
2. Related Work
3. Generating Smooth Trajectories On-Line
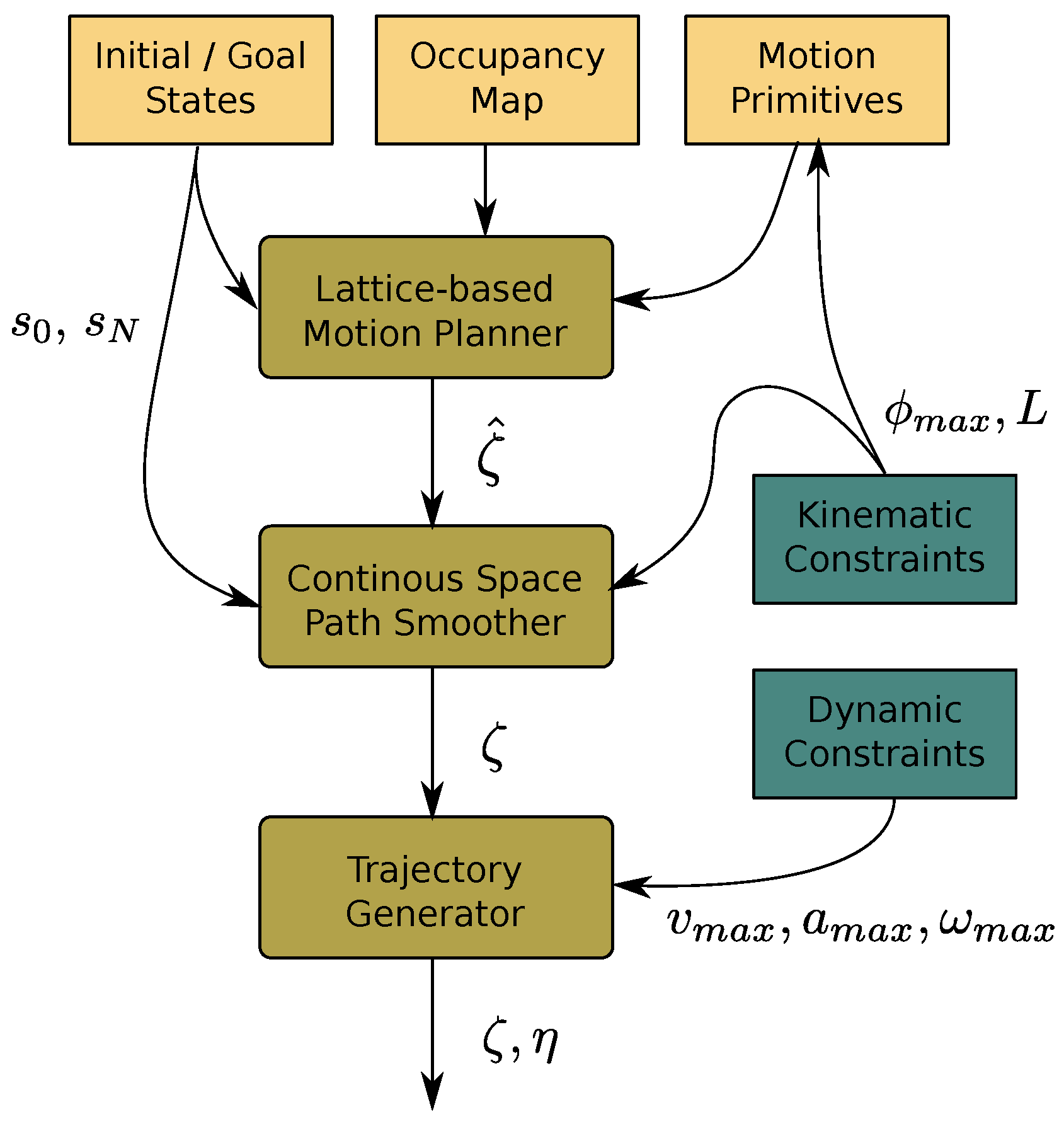
3.1. Problem Formulation
3.2. Lattice-Based Motion Planner
| Mean (s) | Std (s) | Max (s) | |
|---|---|---|---|
| Motion planning | 0.105 | 0.085 | 0.680 |
| Path smoothing | 1.095 | 0.222 | 1.868 |
3.3. Continuous Space Path Smoother
3.4. Trajectory Generator
3.5. Model Predictive Controller
4. Experimental Evaluation

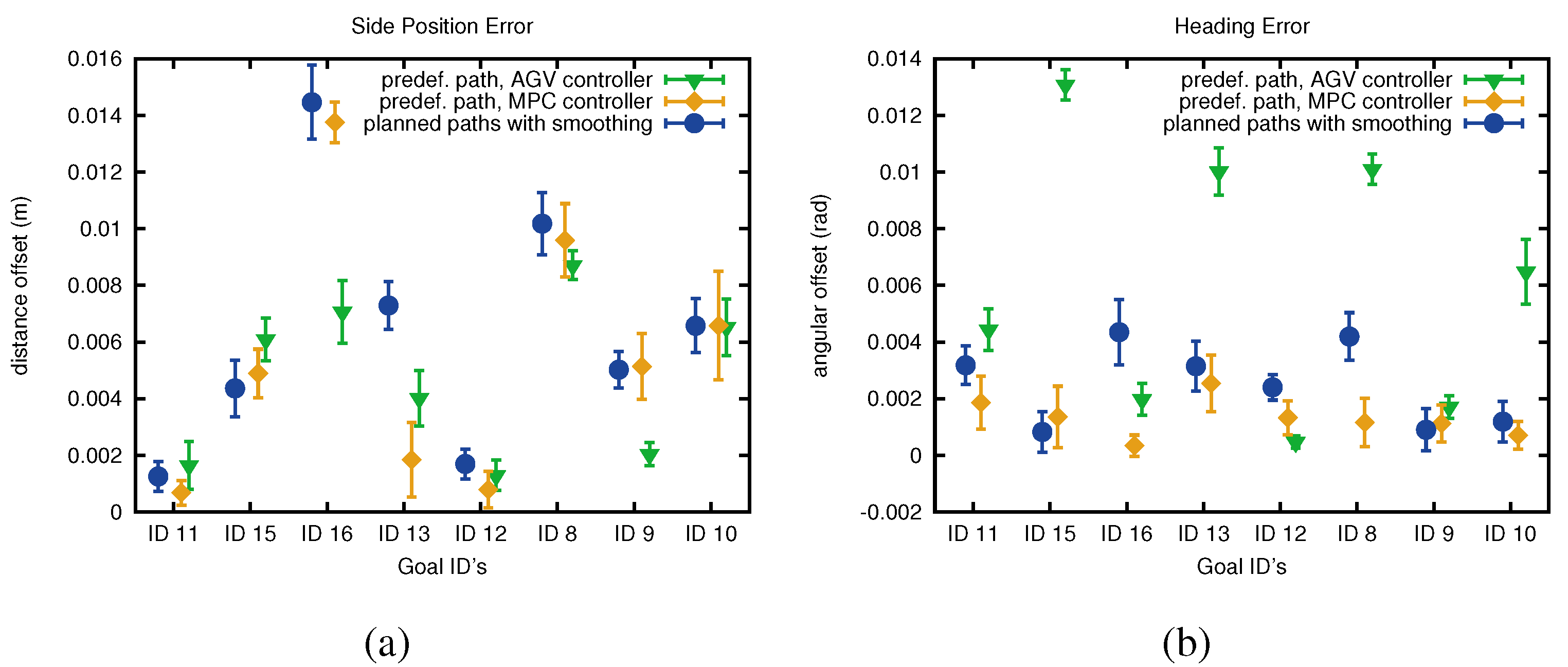
4.1. Controller Comparison
| Method | Forward | Std (m) | Max (m) | Side | Std (m) | Max (m) | Heading | Std (rad) | Max (rad) |
|---|---|---|---|---|---|---|---|---|---|
| Error (m) | Error (m) | Error (rad) | |||||||
| predef. path, AGV controller | 0.0168 | 0.0027 | 0.0224 | 0.0047 | 0.0028 | 0.0098 | 0.0060 | 0.0044 | 0.0138 |
| predef. path, MPC controller | 0.0025 | 0.0018 | 0.0080 | 0.0054 | 0.0044 | 0.0150 | 0.0013 | 0.0010 | 0.0041 |
| planned path with smoothing | 0.0018 | 0.0016 | 0.0080 | 0.0063 | 0.0042 | 0.0172 | 0.0025 | 0.0016 | 0.0062 |
| planned path without smoothing | 0.0273 | 0.0299 | 0.0886 | 0.0521 | 0.0211 | 0.1116 | 0.0621 | 0.0602 | 0.1783 |
| 60 random goals | 0.0036 | 0.0036 | 0.0259 | 0.0084 | 0.0048 | 0.0231 | 0.0014 | 0.0013 | 0.0069 |

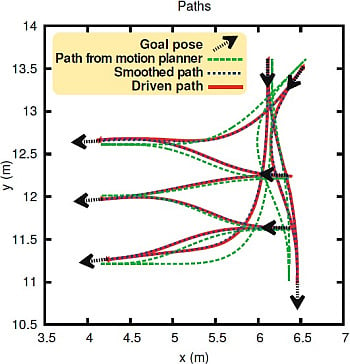
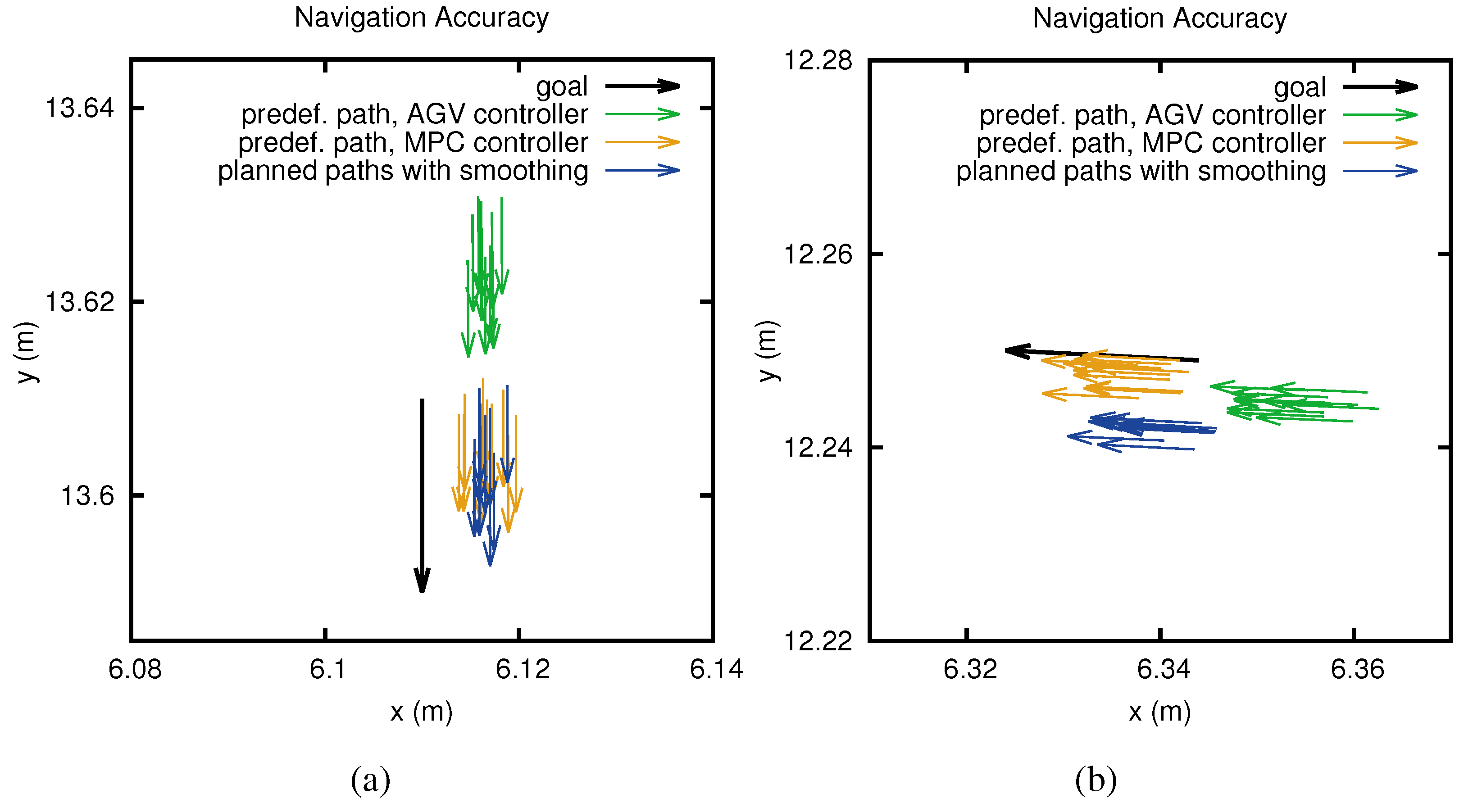
4.2. Path Smoothing of Automatically Generated Paths
4.3. Evaluation over Randomly Chosen Goals

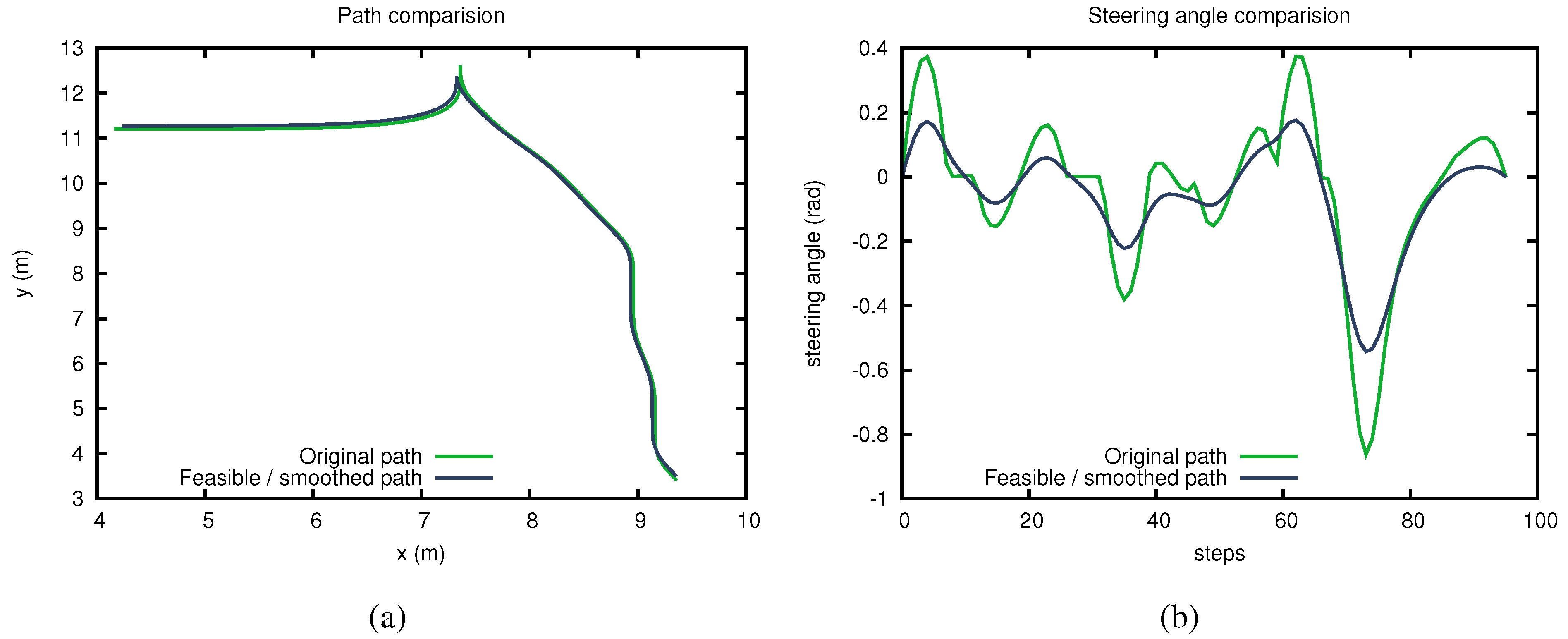
4.4. Evaluation of Discretization Effect on Longer Paths
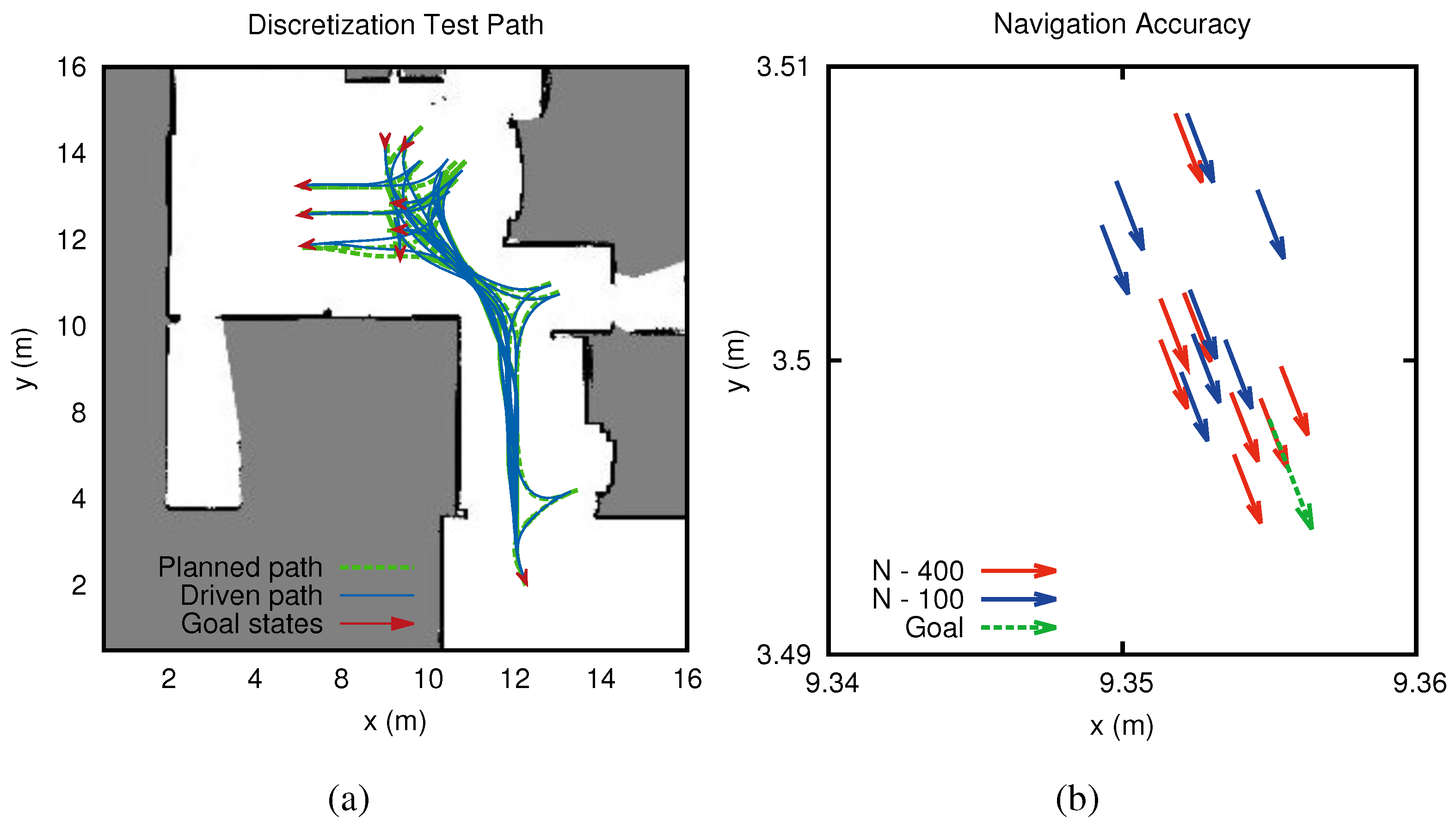
| Dist (m) | Std (m) | Computation Time (s) | Std (s) | |
|---|---|---|---|---|
| 0.0103 | 0.0091 | 1.5286 | 0.1668 | |
| 0.0079 | 0.0034 | 8.2057 | 1.0059 |
5. Conclusions and Future Work
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Bouguerra, A.; Andreasson, H.; Lilienthal, A.J.; Åstrand, B.; Rögnvaldsson, T. MALTA: A System of Multiple Autonomous Trucks for Load Transportation. In Proceedings of the European Conference on Mobile Robots (ECMR), Mlini/Dubrovnik, Croatia, 23–25 September 2009.
- Magnusson, M.; Almqvist, H. Consistent Pile-Shape Quantification for Autonomous Wheel Loaders. In Proceedings of the IEEE/RSJ International Conference on Intelligent Robots and Systems (IROS), San Francisco, CA, USA, 25–30 September 2011.
- Kollmorgen web page. Available online: http:www.kollmorgen.com (accessed on 10 December 2014).
- Cheng, P.; Frazzoli, E.; LaValle, S. Improving the performance of sampling-based motion planning with symmetry-based gap reduction. IEEE Trans. Robot. 2008, 24, 488–494. [Google Scholar] [CrossRef]
- Seiler, K.M.; Singh, S.P.; Sukkarieh, S.; Durrant-Whyte, H. Using Lie group symmetries for fast corrective motion planning. Int. J. Robot. Res. 2012, 31, 151–166. [Google Scholar] [CrossRef]
- Hellstrom, T.; Ringdahl, O. Follow the past: A path-tracking algorithm for autonomous vehicles. Int. J. Veh. Auton. Syst. 2006, 4, 216–224. [Google Scholar] [CrossRef]
- Marshall, J.; Barfoot, T.; Larsson, J. Autonomous underground tramming for center-articulated vehicles. J. Field Robot. 2008, 25, 400–421. [Google Scholar] [CrossRef]
- LaValle, S.M. Planning Algorithms; Cambridge University Press: Cambridge, UK, 2006. [Google Scholar]
- Kavraki, L.; Svestka, P.; Latombe, J.; Overmars, M. Probabilistic roadmaps for path planning in high-dimensional configuration spaces. IEEE Trans. Robot. Autom. 1996, 12, 566–580. [Google Scholar] [CrossRef]
- LaValle, S.M. Rapidly-Exploring Random Trees: A New Tool for Path Planning; Technical Report, TR 98-11; Computer Science Department, Iowa State University: USA, 1998. [Google Scholar]
- Karaman, S.; Frazzoli, E. Sampling-based algorithms for optimal motion planning. Int. J. Robot. Res. 2011, 30, 846–894. [Google Scholar] [CrossRef]
- Islam, F.; Nasir, J.; Malik, U.; Ayaz, Y.; Hasan, O. RRT*-Smart: Rapid convergence implementation of RRT* towards optimal solution. In Proceedings of the International Conference on Mechatronics and Automation (ICMA), Chengdu, China, 5–8 August 2012.
- Ferguson, D.; Likhachev, M. Efficiently using cost maps for planning complex maneuvers. In Proceedings of the ICRA Workshop on Planning with Cost Maps, Pasadena, California, USA, 19–23 May 2008.
- Pivtoraiko, M.; Kelly, A. Fast and Feasible Deliberative Motion Planner for Dynamic Environments. In Proceedings of the ICRA Workshop on Safe Navigation in Open and Dynamic Environments: Application to Autonomous Vehicles, Kobe, Japan, 12–17 May 2009.
- Koenig, S.; Likhachev, M. D* Lite. In Proceedings of the National Conference on Artificial Intelligence (AAAI), Edmonton, Alberta, Canada, 28 July–1 August 2002.
- Lau, B.; Sprunk, C.; Burgard, W. Kinodynamic Motion Planning for Mobile Robots Using Splines. In Proceedings of the IEEE/RSJ International Conference on Intelligent Robots and Systems (IROS), St.Louis, MO, USA, 11–15 October 2009.
- Walther, M.; Steinhaus, P.; Dillmann, R. Using B-Splines for Mobile Robot Path Representation and Motion Control. In Proceedings of the European Conference on Mobile Robots (ECMR), Ancona, Italy, 7–10 September 2005.
- Sprunk, C.; Lau, B.; Burgard, W. Improved Non-linear Spline Fitting for Teaching Trajectories to Mobile Robots. In Proceedings of the IEEE International Conference on Robotics and Automation (ICRA), St. Paul, MN, USA, 14–18 May 2012.
- Wilde, D.K. Computing clothoid segments for trajectory generation. In Proceedings of the IEEE/RSJ International Conference on Intelligent Robots and Systems (IROS), St. Louis, MO, USA, 11–15 October 2009.
- Brezak, M.; Petrovic, I. Path Smoothing Using Clothoids for Differential Drive Mobile Robots. In Proceedings of the 18th IFAC World Congress, Milano, Italy, 28 August–2 September 2011.
- Sprunk, C.; Lau, B.; Pfaff, P.; Burgard, W. Online Generation of Kinodynamic Trajectories for Non-Circular Omnidirectional Robots. In Proceedings of the IEEE International Conference on Robotics and Automation (ICRA), Shanghai, China, 9–13 May 2011.
- Cirillo, M.; Uras, T.; Koenig, S.; Andreasson, H.; Pecora, F. Integrated Motion Planning and Coordination for Industrial Vehicles. In Proceedings of the 24th International Conference on Automated Planning and Scheduling, Portsmouth, NH, USA, 21–26 June 2014.
- Pecora, F.; Cirillo, M.; Dimitrov, D. On Mission-Dependent Coordination of Multiple Vehicles under Spatial and Temporal Constraints. In Proceedings of the IEEE/RSJ International Conference on Intelligent Robots and Systems (IROS), Algarve, Portugal, 7–12 October 2012.
- Cirillo, M.; Uras, T.; Koenig, S. A Lattice-Based Approach to Multi-Robot Motion Planning for Non-Holonomic Vehicles. In Proceedings of the IEEE/RSJ International Conference on Intelligent Robots and Systems (IROS), Chicago, IL, USA, 14–18 September 2014.
- Pivtoraiko, M.; Knepper, R.A.; Kelly, A. Differentially Constrained Mobile Robot Motion Planning in State Lattices. J. Field Robot. 2009, 26, 308–333. [Google Scholar] [CrossRef]
- Pivtoraiko, M.; Kelly, A. Kinodynamic motion planning with state lattice motion primitives. In Proceedings of the IEEE/RSJ International Conference on Intelligent Robots and Systems (IROS), San Francisco, CA, USA, 25–30 September 2011.
- Likhachev, M.; Gordon, G.; Thrun, S. ARA*: Anytime A* with provable bounds on sub-optimality. Adv. Neural Inf. Process. Syst. 2003, 16, 767–774. [Google Scholar]
- Knepper, R.A.; Kelly, A. High Performance State Lattice Planning Using Heuristic Look-Up Tables. In Proceedings of the IEEE/RSJ International Conference on Intelligent Robots and Systems (IROS), Beijing, China, 9–15 October 2006.
- Houska, B.; Ferreau, H.; Diehl, M. ACADO Toolkit—An Open Source Framework for Automatic Control and Dynamic Optimization. Optim. Control Appl. Methods 2011, 32, 298–312. [Google Scholar] [CrossRef]
- Bock, H.; Plitt, K. A Multiple Shooting algorithm for direct solution of optimal control problems. In Proceedings of the 9th IFAC World Congress, Budapest, Hungary, 2–6 July 1984; pp. 242–247.
- Munoz, V.F.; Ollero, A. Smooth trajectory planning method for mobile robots. In Proceedings of the Conference on Computational Engineering in Systems Applications, Lille, France, 9–12 July 1996.
© 2014 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Andreasson, H.; Saarinen, J.; Cirillo, M.; Stoyanov, T.; Lilienthal, A.J. Drive the Drive: From Discrete Motion Plans to Smooth Drivable Trajectories. Robotics 2014, 3, 400-416. https://doi.org/10.3390/robotics3040400
Andreasson H, Saarinen J, Cirillo M, Stoyanov T, Lilienthal AJ. Drive the Drive: From Discrete Motion Plans to Smooth Drivable Trajectories. Robotics. 2014; 3(4):400-416. https://doi.org/10.3390/robotics3040400
Chicago/Turabian StyleAndreasson, Henrik, Jari Saarinen, Marcello Cirillo, Todor Stoyanov, and Achim J. Lilienthal. 2014. "Drive the Drive: From Discrete Motion Plans to Smooth Drivable Trajectories" Robotics 3, no. 4: 400-416. https://doi.org/10.3390/robotics3040400
APA StyleAndreasson, H., Saarinen, J., Cirillo, M., Stoyanov, T., & Lilienthal, A. J. (2014). Drive the Drive: From Discrete Motion Plans to Smooth Drivable Trajectories. Robotics, 3(4), 400-416. https://doi.org/10.3390/robotics3040400