Extended Operational Space Kinematics, Dynamics, and Control of Redundant Non-Serial Compound Robotic Manipulators

Abstract

An extended operational space kinematics and dynamics formulation is presented for the control of redundant non-serial compound robotic manipulators. A broad spectrum of high-load-capacity non-serial manipulators used in earth moving, material handling, and construction applications is addressed. Departing from conventional approaches that rely on Jacobian pseudoinverses and local null-space projections, a globally valid, differential-geometry-based, multi-valued inverse kinematic mapping is defined at the configuration level, with the explicit self-motion parameterization of manipulator redundancy. The formulation yields coupled second-order ordinary differential equations of manipulator dynamics on the product space of task variables and self-motion coordinates. This enables the direct integration of system dynamics with control strategies, such as model predictive control or feedback design, while maintaining task constraint compliance. The methods presented are validated through the simulation and control of a non-serial compound material loader manipulator with multiple degrees of redundancy, demonstrating advantages in generality, numerical accuracy, and trajectory smoothness.

1. Introduction

Redundant robotic manipulators offer flexibility for achieving tasks such as obstacle avoidance, joint limit avoidance, and posture optimization. However, classical modeling and control strategies have been limited to serial manipulators and rely on velocity-level inverse kinematics using Jacobian pseudoinverses and null-space projection techniques [1,2,3,4,5,6]. These approaches are inherently local and can suffer from numerical drift, instability near singularities, and difficulties in maintaining secondary objectives over extended trajectories. Recent papers by the authors have employed differential geometry and modern methods of multibody dynamics that avoid the use of Lagrange multipliers and resolve these deficiencies for redundant robotic manipulators [7,8,9]. This paper extends these results to a dynamically consistent approach that is globally valid on singularity-free components of a non-serial compound manipulator configuration space. Building on a configuration-level inverse kinematic mapping that presents all inverse kinematic solutions as functions of operational space parameters, coupled second-order ordinary differential equations (ODEs) of dynamics are constructed in the product space of task variables and self-motion coordinates. This framework eliminates the need for projection-based redundancy resolution and provides a control-ready ODE formulation that is applicable for a broad spectrum of non-serial compound manipulator architectures.

The goals of this paper are twofold: (i) to present a new dynamics and control formulation in an accessible style for researchers and control engineers; and (ii) to benchmark its performance using a multi-degree-of-redundancy example. This work aims to bridge a significant gap between the geometric modeling of redundant non-serial compound manipulators and their application in planning and control.

2. Background on Redundant Non-Serial Compound Manipulator Modeling and Control

2.1. Methods Adapted from Redundant Serial Manipulators

In redundant serial manipulators, an explicit input–output forward kinematic relation exists in the following form [2,9]:

$$\mathit{z}=\mathit{G}\mathbf{(}\mathit{y}\mathbf{)}$$

(1)

where input and output coordinates are denoted $\mathit{y}\in R^n \mathrm{and} \mathit{z}\in R^m$, with $n>m$. Here, ${\mathrm{R}}^{\mathrm{k}}$ is k-dimensional Euclidean space with elements $\mathit{x}\in R^k$ in the form of column vectors $\mathit{x}={\left[\begin{array}{ccc}{x}_1& \dots & x_k\end{array}\right]}^T$. The symbols in bold are vectors and matrices.

The inverse kinematics problem associated with Equation (1) has infinitely many solutions. Classical approaches resolve this redundancy by operating at the velocity level [1,10]:

$$\dot{\mathit{y}}={\mathit{J}}^{†}\dot{\mathit{z}}+\left(\mathit{I}-{\mathit{J}}^{†}\mathit{J}\right){\dot{\mathit{y}}}^0$$

(2)

where ${\mathit{J}}^{†}$ is the Moore–Penrose pseudoinverse [2,11] of $\mathit{J}=\left[\partial G_i\mathbf{(}\mathit{y}\mathbf{)}/\partial y_{\mathrm{j}}\right]$, and ${\dot{\mathit{y}}}^0$ is arbitrary. Although effective in some non-serial settings, such methods are differential in nature and require integration to recover configurations. They can exhibit numerical instability and are often sensitive to singularities. This velocity space generalized inverse approach has been adapted for use in parallel redundant manipulators, but without notable success [12,13]. A more recent approach to such systems [14] is based on classical mechanics [15].

Task priority methods and control in operational space originated in the serial manipulator setting, e.g., [16,17], provide hierarchical frameworks for multiple objectives, but rely on local Jacobian-based approximations and projections that lead to serious problems, especially in non-serial compound manipulators.

The concept of self-motion of serial manipulators introduced in [1] has been adapted in the present research for use with non-serial compound manipulator applications.

2.2. Constrained Operational Space Dynamics

In a formulation introduced in [18], the multiplier form of the constrained equation of motion is mapped into a task space using the dynamically consistent inverse of a Jacobian that characterizes both the task and constraint spaces. The resulting task space equation of motion is then partitioned into an equation corresponding to the motion and an equation corresponding to the constraint forces. One begins by expressing the multiplier form of the constrained equation of motion. The d’Alembert variational equation of motion for the manipulator with holonomic constraints $\mathit{\Phi }\mathbf{(}\mathit{q}\mathbf{)}=0$ is as follows:

$$\delta {\mathit{q}}^{\mathrm{T}}\left[\mathit{M}\mathbf{(}\mathit{q}\mathbf{)}\ddot{\mathit{q}}-\mathit{S}\mathbf{(}\mathit{q},\dot{\mathit{q}}\mathbf{)}-{\mathit{Q}}^{\mathrm{A}}\mathbf{(}\mathit{q},\dot{\mathit{q}},\mathrm{t}\mathbf{)}-{\mathit{P}}^{\mathit{q}}\right]=0$$

for all $\delta \mathit{q}\in \ker \mathbf{(}{\mathit{\Phi }}_{\mathit{q}}\mathbf{)}$; i.e., for all $\delta \mathit{q}$ such that ${\mathit{\Phi }}_{\mathit{q}}\delta \mathit{q}=0$ [7,15]. This implies the following:

$${\mathit{P}}^{\mathit{q}}=\mathit{M}\mathbf{(}\mathit{q}\mathbf{)}\ddot{\mathit{q}}-\mathit{S}\mathbf{(}\mathit{q},\dot{\mathit{q}}\mathbf{)}-{\mathit{Q}}^{\mathrm{A}}\mathbf{(}\mathit{q},\dot{\mathit{q}},t\mathbf{)}-{\mathit{\Phi }}_{\mathit{q}}{\mathbf{(}\mathit{q}\mathbf{)}}^{\mathit{T}}\mathit{\lambda }$$

(3)

which is subject to the following holonomic constraints:

$$\mathit{\Phi }\mathbf{(}\mathit{q}\mathbf{)}=0$$

(4)

where $\mathit{\lambda }$ is a vector of Lagrange multipliers that determine constraint forces. The task velocity relationship is as follows:

$$\mathrm{z} \dot{}= \mathit{J}\dot{\mathit{q}}$$

(5)

and the constraint velocity condition is as follows:

$$\dot{\mathit{\Phi }}= {\mathit{\Phi }}_{\mathit{q}}\dot{\mathit{q}}= 0.$$

(6)

Concatenating these relationships into a single matrix relation results in the following:

$$\dot{\stackrel{⌣}{\mathit{z}}}=\left[\begin{array}{c}\dot{\mathit{z}}\\ \dot{\mathit{\Phi }}\end{array}\right]=\left[\begin{array}{c}\mathit{J}\\ {\mathit{\Phi }}_{\mathit{q}}\end{array}\right]\dot{\mathit{q}}=\stackrel{⌣}{\mathit{J}}\dot{\mathit{q}}$$

(7)

where the notation $\stackrel{⌣}{\square }$ represents a quantity that is formed from the composition of task and constraint terms. The applied generalized force can be decomposed into a task/constraint space component and a null-space component, as in [18] as follows:

$${\mathit{P}}^{\mathit{q}}={\stackrel{⌣}{\mathit{J}}}^{\mathit{T}}{\stackrel{⌣}{\mathit{P}}}^{\mathit{z}}+{\stackrel{⌣}{\mathit{N}}}^{\mathit{T}}{\mathit{P}}_{\mathit{o}}^{\mathit{q}}=\left[\begin{array}{cc}{\mathit{J}}^{\mathit{T}}& {\mathit{\Phi }}_{\mathit{q}}^{\mathit{T}}\end{array}\right]\left[\begin{array}{c}{\mathit{P}}^{\mathit{z}}\\ {\mathit{P}}_{\mathit{C}}^{\mathit{z}}\end{array}\right]+{\stackrel{⌣}{\mathit{N}}}^{\mathit{T}}{\mathit{P}}_{\mathit{o}}^{\mathit{q}}$$

(8)

where ${\mathit{P}}_{\mathit{C}}^{\mathit{z}}$ is the component of applied task space force acting along the constraint direction. Equation (8) can thus be written as follows:

$${\stackrel{⌣}{\mathit{J}}}^{\mathit{T}}\left[\begin{array}{c}{\mathit{P}}^{\mathit{z}}\\ {\mathit{P}}_{\mathit{C}}^{\mathit{z}}\end{array}\right]+{\stackrel{⌣}{\mathit{N}}}^{\mathit{T}}{\mathit{P}}_{\mathit{o}}^{\mathit{q}}=\mathit{M}\ddot{\mathit{q}}-\mathit{S}-{\mathit{Q}}^{\mathit{A}}-{\stackrel{⌣}{\mathit{J}}}^{\mathit{T}}\left[\begin{array}{c}\mathbf{0}\\ \mathit{\lambda }\end{array}\right]$$

(9)

Mapping Equation (9) into the task space by premultiplying by $\stackrel{⌣}{\mathit{\Gamma }}\stackrel{⌣}{\mathit{J}}{\mathit{M}}^{-1}$ results in the following:

$$\underset{\mathit{I}}{\underbrace{\stackrel{⌣}{\mathit{\Gamma }}\stackrel{⌣}{\mathit{J}}{\mathit{M}}^{-1}{\stackrel{⌣}{\mathit{J}}}^{\mathit{T}}}}\left[\begin{array}{c}{\mathit{P}}^{\mathit{z}}\\ {\mathit{P}}_{\mathit{C}}^{\mathit{z}}\end{array}\right]+\underset{0}{\underbrace{\stackrel{⌣}{\mathit{\Gamma }}\stackrel{⌣}{\mathit{J}}{\mathit{M}}^{-1}{\stackrel{⌣}{\mathit{N}}}^{\mathit{T}}}}{\mathit{P}}_0^{\mathit{q}}=\stackrel{⌣}{\mathit{\Gamma }}\stackrel{⌣}{\mathit{J}}{\mathit{M}}^{-1}\left(\mathit{M}\ddot{\mathit{q}}-\mathit{S}-{\mathit{Q}}^{\mathit{A}}\right)-\underset{\mathit{I}}{\underbrace{\stackrel{⌣}{\mathit{\Gamma }}\stackrel{⌣}{\mathit{J}}{\mathit{M}}^{-1}{\stackrel{⌣}{\mathit{J}}}^{\mathit{T}}}}\left[\begin{array}{c}\mathbf{0}\\ \mathit{\lambda }\end{array}\right]$$

(10)

This yields the following:

$$\begin{array}{cc}\left[\begin{array}{c}{\mathit{P}}^{\mathit{z}}\\ {\mathit{P}}_{\mathit{C}}^{\mathit{z}}\end{array}\right]& =\stackrel{⌣}{\mathit{\Gamma }}\stackrel{⌣}{\mathit{J}}\ddot{\mathit{q}}-\stackrel{⌣}{\mathit{\Gamma }}\stackrel{⌣}{\mathit{J}}{\mathit{M}}^{-1}\mathit{S}-\stackrel{⌣}{\mathit{\Gamma }}\stackrel{⌣}{\mathit{J}}{\mathit{M}}^{-1}{\mathit{Q}}^{\mathit{A}}-\left[\begin{array}{c}\mathbf{0}\\ \mathit{\lambda }\end{array}\right]\hfill \\ & =\stackrel{⌣}{\mathit{\Gamma }}\left[\begin{array}{c}\ddot{\mathit{z}}-\dot{\stackrel{⌣}{\mathit{J}}}\dot{\mathit{q}}\\ \dot{\mathit{\Phi }}-{\dot{\mathit{\Phi }}}_{\mathit{q}}\dot{\mathit{q}}\end{array}\right]-\stackrel{⌣}{\mathit{\Gamma }}\stackrel{⌣}{\mathit{J}}{\mathit{M}}^{-1}\mathit{S}-\stackrel{⌣}{\mathit{\Gamma }}\stackrel{⌣}{\mathit{J}}{\mathit{M}}^{-1}{\mathit{Q}}^{\mathit{A}}-\left[\begin{array}{c}\mathbf{0}\\ \mathit{\lambda }\end{array}\right]\hfill \end{array}$$

(11)

and

$$\left[\begin{array}{c}{\mathit{P}}^{\mathit{z}}\\ {\mathit{P}}_{\mathit{C}}^{\mathit{z}}\end{array}\right]=\stackrel{⌣}{\mathit{\Gamma }}\mathbf{(}\mathit{q}\mathbf{)}\left[\begin{array}{c}\ddot{\mathit{z}}\\ \mathbf{0}\end{array}\right]+\stackrel{⌣}{\mathit{\mu }}\mathbf{(}\mathit{q},\dot{\mathit{q}}\mathbf{)}+\stackrel{⌣}{\mathit{p}}\mathbf{(}\mathit{q}\mathbf{)}-\left[\begin{array}{c}\mathbf{0}\\ \mathit{\lambda }\end{array}\right]$$

(12)

where the constraint condition, $\ddot{\mathit{\Phi }}=0$, has been imposed. This yields the following identities:

$$\begin{array}{c}\stackrel{⌣}{\mathit{\Gamma }}\mathbf{(}\mathit{q}\mathbf{)}={\left[\begin{array}{cc}\mathit{J}{\mathit{M}}^{-1}{\mathit{J}}^{\mathit{T}}& \mathit{J}{\mathit{M}}^{-1}{\mathit{\Phi }}_{\mathit{q}}^{\mathit{T}}\\ {\mathit{\Phi }}_{\mathit{q}}{\mathit{M}}^{-1}{\mathit{J}}^{\mathit{T}}& {\mathit{\Phi }}_{\mathit{q}}{\mathit{M}}^{-1}{\mathit{\Phi }}_{\mathit{q}}^{\mathit{T}}\end{array}\right]}^{-1}\\ \stackrel{⌣}{\mathit{\mu }}\mathbf{(}\mathit{q},\dot{\mathit{q}}\mathbf{)}=\stackrel{⌣}{\mathit{\Gamma }}\left[\begin{array}{c}-\mathit{J}{\mathit{M}}^{-1}\mathit{S}-\dot{\stackrel{⌣}{\mathit{J}}}\dot{\mathit{q}}\\ \hspace{0.17em}-{\mathit{\Phi }}_{\mathit{q}}{\mathit{M}}^{-1}\mathit{S}-{\dot{\mathit{\Phi }}}_{\mathit{q}}\dot{\mathit{q}}\end{array}\right]\\ \stackrel{⌣}{\mathit{p}}\mathbf{(}\mathit{q}\mathbf{)}=\stackrel{⌣}{\mathit{\Gamma }}\left[\begin{array}{c}-\mathit{J}{\mathit{M}}^{-1}{\mathit{Q}}^{\mathit{A}}\\ \hspace{0.17em}-{\mathit{\Phi }}_{\mathit{q}}{\mathit{M}}^{-1}{\mathit{Q}}^{\mathit{A}}\end{array}\right]\end{array}$$

(13)

While Equation (12) expresses system task constraint dynamics, it is useful to partition it in the following manner:

$$\left[\begin{array}{c}{\mathit{P}}^{\mathit{z}}\\ {\mathit{P}}_{\mathit{C}}^{\mathit{z}}\end{array}\right]=\left[\begin{array}{cc}{\stackrel{⌣}{\mathit{\Gamma }}}_{11}& {\stackrel{⌣}{\mathit{\Gamma }}}_{12}\\ {\stackrel{⌣}{\mathit{\Gamma }}}_{21}& {\stackrel{⌣}{\mathit{\Gamma }}}_{22}\end{array}\right]\left[\begin{array}{c}\ddot{\mathit{z}}\\ \mathbf{0}\end{array}\right]+\left[\begin{array}{c}{\stackrel{⌣}{\mathit{\mu }}}_1\\ {\stackrel{⌣}{\mathit{\mu }}}_2\end{array}\right]+\left[\begin{array}{c}{\stackrel{⌣}{\mathit{p}}}_1\\ {\stackrel{⌣}{\mathit{p}}}_2\end{array}\right]-\left[\begin{array}{c}\mathbf{0}\\ \mathit{\lambda }\end{array}\right]$$

(14)

This partitioning yields an equation corresponding to the task space control force as follows:

$${\mathit{P}}^{\mathit{z}}={\stackrel{⌣}{\mathit{\Gamma }}}_{11}\ddot{\mathit{z}}+{\stackrel{⌣}{\mathit{\mu }}}_1+{\stackrel{⌣}{\mathit{p}}}_1$$

(15)

and an equation corresponding to the constraint forces as follows:

$${\mathit{P}}_{\mathit{C}}^{\mathit{z}}+\mathit{\lambda }={\stackrel{⌣}{\mathit{\Gamma }}}_{21}\ddot{\mathit{z}}+{\stackrel{⌣}{\mathit{\mu }}}_2+{\stackrel{⌣}{\mathit{p}}}_2$$

(16)

The constraint force vector $\mathit{\lambda }$ will always arise so as to satisfy Equation (15), as dictated by constraint consistency. The component of the applied task space force, ${\mathit{P}}_{\mathit{C}}^{\mathit{z}}$, acting along the constraint direction has no impact on the motion of the task. Its only effect is on constraint forces (values of λ) that arise. Thus, all choices for ${\mathit{P}}_{\mathit{C}}^{\mathit{z}}$ result in equivalent motion of the system.

The dynamics are derived from Equations (15) and (16), as demonstrated in [18]:

$${\mathit{P}}^{\mathit{q}}={\mathit{\Theta }}^{\mathit{T}}{\mathit{J}}^{\mathit{T}}\left({\mathit{\Gamma }}_{\mathit{c}}\ddot{\mathit{z}}+{\mathit{\mu }}_{\mathit{c}}+{\mathit{p}}_{\mathit{c}}\right)+{\mathit{\Phi }}_{\mathit{q}}^{\mathit{T}}\left(\mathit{\alpha }+\mathit{\rho }\right)+{\mathit{N}}_{\mathit{c}}^T{\mathit{P}}_{\mathit{o}}^{\mathit{q}}-{\mathit{\Phi }}_{\mathit{q}}^{\mathit{T}}\mathit{\lambda }$$

(17)

The term $\mathit{\Theta }\left(\mathit{q}\right)\in {\mathit{R}}^{\mathit{k}\times \mathit{k}}$ is the constraint null-space matrix, ${\mathit{\Gamma }}_{\mathit{c}}\left(\mathit{q}\right)\in {\mathit{R}}^{\mathit{m}\times \mathit{m}}$ is the task/constraint space mass matrix, ${\mathit{\mu }}_{\mathit{c}}\left(\mathit{q}, \mathit{q}\dot{}\right)\in {\mathit{R}}^{\mathit{m}}$ is the task/constraint space centrifugal and Coriolis force vector, ${\mathit{p}}_{\mathit{c}}\left(\mathit{q}\right)\in {\mathit{R}}^{\mathit{m}}$ is the task/constraint space gravity vector, and ${\mathit{N}}_{\mathit{c}}{\left(\mathit{q}\right)}^{\mathit{T}}\in {\mathit{R}}^{\mathit{n}\times \mathit{n}}$ is the task/constraint null-space projection matrix. These terms are given in [18] as follows:

$$\mathit{\Theta }\mathbf{(}\mathit{q}\mathbf{)}=1-{\mathit{M}}^{-1}{\mathit{\Phi }}_{\mathit{q}}^{\mathit{T}}{\mathit{L}}^{\mathit{T}}{\mathit{\Phi }}_{\mathit{q}}$$

$${\mathit{\Gamma }}_{\mathit{c}}\mathbf{(}\mathit{q}\mathbf{)}={\left(\mathit{J}{\mathit{M}}^{-1}{\mathit{\Theta }}^{\mathit{T}}{\mathit{J}}^{\mathit{T}}\right)}^{-1}$$

(18)

$${\mathit{\mu }}_{\mathit{c}}\mathbf{(}\mathit{q},\dot{\mathit{q}}\mathbf{)}=-{\mathit{\Gamma }}_{\mathit{c}}\mathit{J}{\mathit{M}}^{-1}{\mathit{\Theta }}^{\mathit{T}}\mathit{S}-{\mathit{\Gamma }}_{\mathit{c}}\left(\dot{\mathit{J}}-\mathit{J}{\mathit{M}}^{-1}{\mathit{\Phi }}_{\mathit{q}}^{\mathit{T}}\mathit{L}{\dot{\mathit{\Phi }}}_{\mathit{q}}\right)\dot{\mathit{q}}$$

(19)

$${\mathit{p}}_{\mathit{c}}\mathbf{(}\mathit{q}\mathbf{)}=-{\mathit{\Gamma }}_{\mathit{c}}\mathit{J}{\mathit{M}}^{-1}{\mathit{\Theta }}^{\mathit{T}}{\mathit{Q}}^{\mathit{A}}$$

(20)

$${\mathit{N}}_{\mathit{c}}{\mathbf{(}\mathit{q}\mathbf{)}}^{\mathit{T}}={\mathit{\Theta }}^{\mathit{T}}\left(1-{\mathit{J}}^{\mathit{T}}{\mathit{\Gamma }}_{\mathit{c}}\mathit{J}\mathit{\Theta }{\mathit{M}}^{-1}\right)$$

(21)

The term $\mathit{L}\mathbf{(}\mathit{q}\mathbf{)}\in {\mathit{R}}^{\mathit{k}-\mathit{n}\times \mathit{k}-\mathit{n}}$ is the constraint space mass matrix, which reflects the system inertia projected onto the constraint, $\mathit{\alpha }\left(\mathit{q}, \mathit{q}\dot{}\right)\in {\mathit{R}}^{\mathit{k}-\mathit{n}}$ is the vector of centrifugal and Coriolis forces projected onto the constraint, and $\mathit{\rho }\mathbf{(}\mathit{q}\mathbf{)}\in {\mathit{R}}^{\mathit{k}-\mathit{n}}$ is the vector of gravity forces projected onto the constraint.

$$\mathit{L}={\left({\mathit{\Phi }}_{\mathit{q}}{\mathit{M}}^{-1}{\mathit{\Phi }}_{\mathit{q}}^{\mathit{T}}\right)}^{-1}$$

(22)

$$\mathit{\alpha }=-\mathit{L}{\mathit{\Phi }}_{\mathit{q}}{\mathit{M}}^{-1}\mathit{S}-\mathit{L}{\dot{\mathit{\Phi }}}_{\mathit{q}}\dot{\mathit{q}}$$

(23)

$$\mathit{\rho }=-\mathit{L}{\mathit{\Phi }}_{\mathit{q}}{\mathit{M}}^{-1}{\mathit{Q}}^{\mathit{A}}$$

(24)

2.3. Redundant Parallel Manipulators

Redundant manipulators comprising a single moving platform as output with six spatial degrees of freedom, whose position and orientation are controlled by parallel legs with more than six input coordinates, have received significant attention in the engineering literature [12,13,16,17,18], using theoretical and computational methods of ODE [19,20]. Inverse kinematics approaches in these applications have, however, been ad hoc or adaptations of problematic generalized inverse velocity approaches adapted from the serial manipulator literature. A contribution to the redundant parallel manipulator literature [21] has established the reality that excess generalized coordinates are required to treat this class of redundant manipulator. This reality is addressed in the redundant non-serial compound manipulators herein.

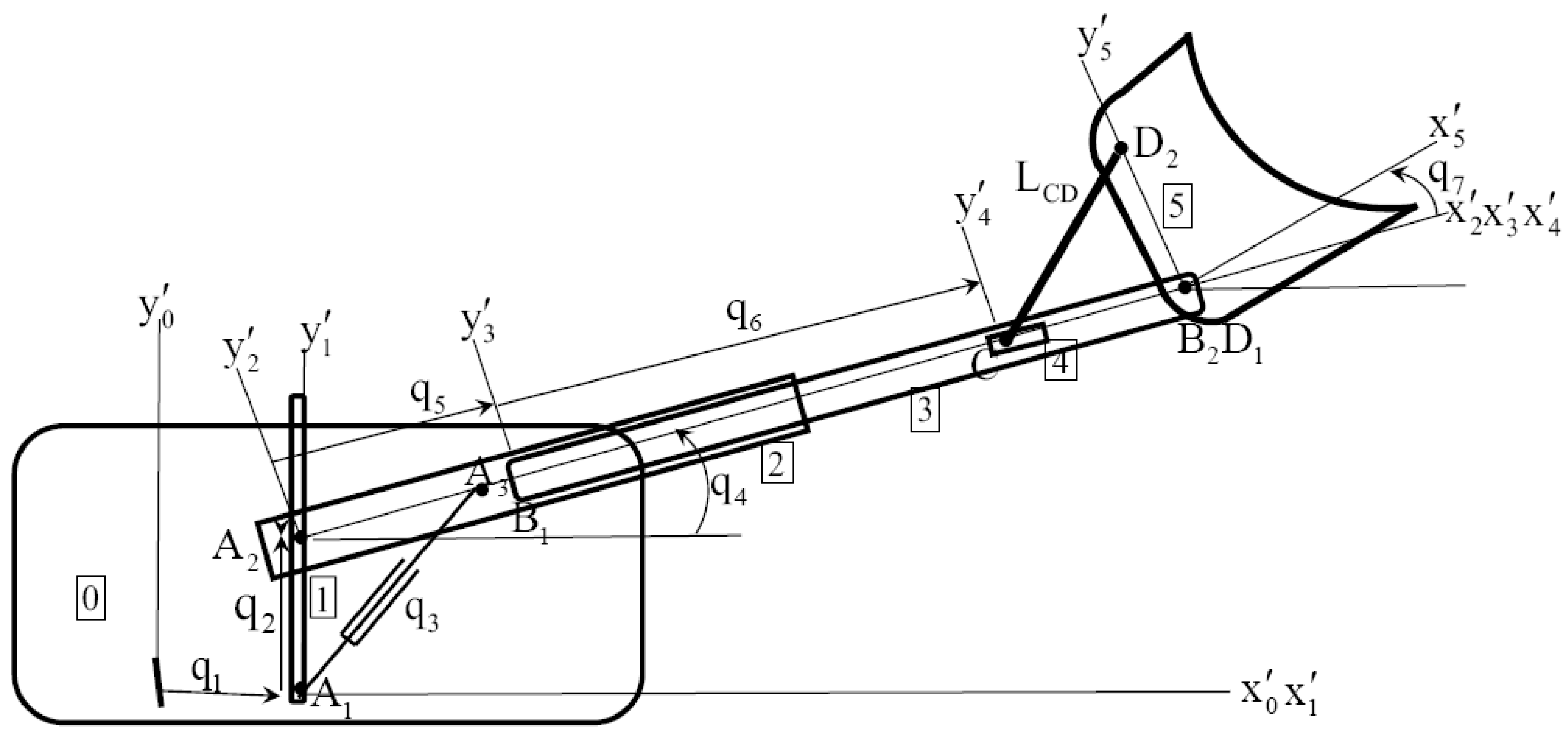
3. A Redundant Non-Serial Compound Material Loader Manipulator

In contrast, the approach presented in this paper constructs an explicit inverse kinematic mapping at the position/configuration level. A unified approach is employed for redundant non-serial compound manipulators, allowing the full set of inverse kinematic solutions to be represented analytically [8]. This enables the direct formulation of dynamics in a form that is suitable for the implementation of control laws in the space of task and self-motion redundancy coordinates, without projection into a Jacobian null space. The unified approach presented herein for non-serial redundant manipulators is an extension of prior developments that used idealized small-scale manipulators to illustrate the formulation [8]. A multi-degree-of-redundancy example is used herein to demonstrate the approach, presented in the form of a tutorial, with numerical results that verify the accuracy and practicality of the approach.

The kinematics of a material loading compound manipulator [8] in Figure 1 are defined by unit vectors ${\mathit{u}}_{\mathit{x}} \mathrm{and} {\mathit{u}}_{\mathit{y}}$ and the following vectors in the global $x_{\mathbf{0}}^{\mathbf{\prime }}-y_{\mathbf{0}}^{\mathbf{\prime }}$ frame as functions of generalized coordinates $q_1 \mathrm{through} q_7$:

$$\begin{array}{l}{\mathit{r}}_{{\mathit{A}}_{\mathbf{1}}}=q_1{\mathit{u}}_{\mathit{y}}, {\mathit{r}}_{{\mathit{A}}_{\mathbf{2}}}=q_1{\mathit{u}}_{\mathit{x}} +q_2{\mathit{u}}_{\mathit{y}}\\ {\mathit{r}}_{{\mathit{A}}_{\mathbf{3}}}=q_1{\mathit{u}}_{\mathit{x}} +q_2{\mathit{u}}_{\mathit{y}}+s_{A_2{A}_3}\mathbf{(}\mathit{cos}{q}_4{\mathit{u}}_{\mathit{y}}+\mathit{sin}{q}_4{\mathit{u}}_{\mathit{y}}\mathbf{)}\\ {\mathit{r}}_{{\mathit{B}}_{\mathbf{1}}}=q_1{\mathit{u}}_{\mathit{x}} +q_2{\mathit{u}}_{\mathit{y}}+q_5\mathbf{(}\mathit{cos}{q}_4{\mathit{u}}_{\mathit{y}}+\mathit{sin}{q}_4{\mathit{u}}_{\mathit{y}}\mathbf{)}\\ {\mathit{r}}_{\mathit{C}}={\mathit{r}}_{{\mathit{B}}_{\mathbf{1}}}+q_6\mathbf{(}\mathit{cos}{q}_4{\mathit{u}}_{\mathit{y}}+\mathit{sin}{q}_4{\mathit{u}}_{\mathit{y}}\mathbf{)}\\ {\mathit{r}}_{{\mathit{B}}_{\mathbf{2}}}={\mathit{r}}_{{\mathit{B}}_{\mathbf{1}}}+L_3\mathbf{(}\mathit{cos}{q}_4{\mathit{u}}_{\mathit{y}}+\mathit{sin}{q}_4{\mathit{u}}_{\mathit{y}}\mathbf{)}\\ {\mathit{r}}_{{\mathit{D}}_{\mathbf{2}}}={\mathit{r}}_{{\mathit{B}}_{\mathbf{2}}}+\mathit{A}\mathbf{(}{q}_4+q_7\mathbf{)}{s}_{D_1{D}_2}{\mathit{u}}_{\mathit{y}}\end{array}$$

(25)

where $s_{\mathit{AB}}$ is the distance between points A and B, $L_3$ is the length of body 3, and $\mathit{A}(q_4+q_7\mathbf{)}=\left[\begin{array}{cc}\mathit{cos}(q_4+q_7\mathbf{)}& -\mathit{sin}(q_4+q_7\mathbf{)}\\ \mathit{sin}(q_4+q_7\mathbf{)}& \mathit{cos}(q_4+q_7\mathbf{)}\end{array}\right]$.

Loops comprising

(1)

bodies 0, 1, and 2, and slider $A_2$ that define the length of actuator $q_3$, which is not contained in a joint;

(2)

bodies 3, 4, and 5 that define the fixed length of bar ${\mathit{L}}_{\mathit{CD}}$ are written in algebraic form as follows:

$$\mathit{\Phi }\mathbf{(}\mathit{q}\mathbf{)}=\mathbf{(}1/2\mathbf{)}\left[\begin{array}{c}{\mathbf{(}{\mathit{r}}_{{\mathit{A}}_{\mathbf{2}}}-{\mathit{r}}_{{\mathit{A}}_{\mathbf{1}}}\mathbf{)}}^{\mathit{T}}\mathbf{(}{\mathit{r}}_{{\mathit{A}}_{\mathbf{2}}}-{\mathit{r}}_{{\mathit{A}}_{\mathbf{1}}}\mathbf{)}-q_3^2\\ {\mathbf{(}{\mathit{r}}_{{\mathit{D}}_{\mathbf{2}}}-{\mathit{r}}_{\mathit{C}}\mathbf{)}}^{\mathrm{T}}\mathbf{(}{\mathit{r}}_{{\mathit{D}}_{\mathbf{2}}}-{\mathit{r}}_{\mathit{C}}\mathbf{)}-L_{\mathit{CD}}^2\end{array}\right]=\mathbf{0}$$

(26)

The input and output coordinates $\mathit{y}\in R^5$ and $\mathit{z}\in R^3$ are functions of $\mathit{q}\in R^7$:

$$\begin{array}{l}\mathit{y}=\mathit{r}\mathbf{(}\mathit{q}\mathbf{)}={\left[\begin{array}{ccccc}{q}_1& q_2& q_3& q_4& q_5\end{array}\right]}^{\mathit{T}}\\ \mathit{z}=\mathit{s}\mathbf{(}\mathit{q}\mathbf{)}=\left[\begin{array}{c}{q}_1+(q_5+L_3)\mathit{cos}{q}_4\\ q_2+(q_5+L_3)\mathit{sin}{q}_4\\ q_7\end{array}\right]\end{array}$$

(27)

where z is the vector of the generalized coordinates of the bucket. The manipulator has two degrees of redundancy, and its kinematics cannot be reduced to the form of Equation (1) that defines the kinematics of a serial manipulator.

4. Redundant Compound Manipulator Kinematics, Dynamics, and Control

4.1. Basics of Compound Redundant Manipulator Kinematics

Many important redundant compound manipulators contain kinematic or actuator closed loops. They also arise when Euler parameters with excess variables are employed that are subject to a normalization constraint to define orientation in space [20]. Their kinematics are defined by input coordinates $\mathit{y}\in R^n$, output coordinates $\mathit{z}\in R^m$, $\mathrm{m}<\mathrm{n}$, and generalized coordinates $\mathit{q}\in R^k$, $k>n$. The generalized coordinates satisfy $\mathrm{k}-\mathrm{n}$ twice continuously differentiable constraints:

$$\mathit{\Phi }\mathbf{(}\mathit{q}\mathbf{)}=\mathbf{0}$$

(28)

and determine the input and output coordinates as follows:

$$\begin{array}{l}\mathit{y}=\mathit{r}\mathbf{(}\mathit{q}\mathbf{)}\\ \mathit{z}=\mathit{s}\mathbf{(}\mathit{q}\mathbf{)}\end{array}$$

(29)

where $\mathit{r}\mathbf{(}\mathit{q}\mathbf{)} \mathrm{and} \mathit{s}\mathbf{(}\mathit{q}\mathbf{)}$ are twice continuously differentiable functions.

There are few studies in the literature on redundant compound manipulators [8,16,17,18,22,23]. While some results have been obtained using the velocity approach [17,18], much remains to be done.

4.1.1. Manipulator Configuration Space

Compound manipulator configuration coordinates are defined as $\mathit{x}={\left[\begin{array}{ccc}{\mathit{y}}^T& {\mathit{q}}^{\mathrm{T}}& {\mathit{z}}^{\mathrm{T}}\end{array}\right]}^{\mathrm{T}}\in R^{\mathrm{n}+\mathrm{k}+\mathrm{m}}$ and form the compound manipulator configuration space

$$X=\left\{\mathit{x}\in {\mathit{R}}^{\mathrm{n}+\mathrm{k}+\mathrm{m}}: \mathit{\Phi }\mathbf{(}\mathit{q}\mathbf{)}=\mathbf{0}, \mathit{r}\mathbf{(}\mathit{q}\mathbf{)}-\mathit{y}=\mathbf{0}, \mathrm{and} \mathit{s}\mathbf{(}\mathit{q}\mathbf{)}-\mathit{z}=\mathbf{0}\right\}$$

(30)

which may contain singular configurations. This configuration space contains important information that defines the differential geometry and topology of the manipulator [24,25,26].

4.1.2. Assembly Components

It is shown in [8] that if ${\mathit{\Phi }}_{\mathit{q}}\mathbf{(}\mathit{q}\mathbf{)}$ has full rank, X in Equation (30) is a topological space. It may thus be partitioned into maximal, disjoint, and path connected assembly components $A{C}_i$ that cover X, as shown schematically in Figure 2.

4.1.3. Forward and Inverse Kinematics

The compound manipulators’ kinematics are defined by composite equations:

$$\mathit{\Omega }\mathbf{(}\mathit{q},\mathit{y}\mathbf{)}=\left[\begin{array}{c}\mathit{\Phi }\mathbf{(}\mathit{q}\mathbf{)}\\ \mathit{r}\mathbf{(}\mathit{q}\mathbf{)}-\mathit{y}\end{array}\right] =\mathbf{0}$$

(31)

$$\mathit{\Lambda }\mathbf{(}\mathit{q},\mathit{z}\mathbf{)}=\left[\begin{array}{c}\mathit{\Phi }\mathbf{(}\mathit{q}\mathbf{)}\\ \mathit{s}\mathbf{(}\mathit{q}\mathbf{)}-\mathit{z}\end{array}\right]=\mathbf{0}$$

(32)

If $\left|{\mathit{\Omega }}_{\mathit{q}}\mathbf{(}\overline{\mathit{q}},\overline{\mathit{y}}\mathbf{)}\right|\ne 0$ for $\overline{\mathit{x}}\in X$, the implicit function theorem [27] implies the existence of a unique twice continuously differentiable solution

$$\mathit{q}=\mathit{f}\mathbf{(}\mathit{y}\mathbf{)}$$

(33)

for Equation (31) in a neighborhood of $\overline{\mathit{y}}$. Combining this with the second of Equations (29) results in the following:

$$\mathit{z}=\mathit{s}\mathbf{(}\mathit{f}\mathbf{(}\mathit{y}\mathbf{)}\mathbf{)}$$

(34)

which is a twice continuously differentiable forward kinematic mapping in a neighborhood of $\overline{\mathit{y}}$. While the mapping of Equation (34) cannot generally be analytically defined, it can be evaluated accurately using Newton–Raphson iteration [28].

In contrast with the foregoing single-valued forward kinematic mapping, if $\mathrm{rank}\mathbf{(}{\mathit{\Lambda }}_{\mathit{q}}\mathbf{(}\overline{\mathit{q}},\overline{\mathit{z}}\mathbf{)}\mathbf{)}=k-\mathbf{(}\mathrm{n}-\mathrm{m})<k$ for $\mathit{x}\in X$, the implicit function theorem implies the existence of a twice continuously differentiable multi-valued solution

$$\mathit{q}=\mathit{g}\mathbf{(}\mathit{z},\mathit{v}\mathbf{)}$$

(35)

for Equation (32), where $\mathit{v}\in R^{\mathrm{n}-\mathrm{m}}$ is arbitrary, in a neighborhood of $\mathit{z}=\overline{\mathit{z}}$ and $\mathit{v}=\mathbf{0}$. Combining this result with the first of Equation (29)

$$\mathit{y}=\mathit{r}\mathbf{(}\mathit{g}\mathbf{(}\mathit{z},\mathit{v}\mathbf{)}\mathbf{)}$$

(36)

is a twice continuously differentiable multi-valued inverse kinematic mapping in a neighborhood of $\mathit{z}=\overline{\mathit{z}} \mathrm{and} \mathit{v}=\mathbf{0}$. This theoretical result can seldom be implemented analytically. It is implemented numerically in the following.

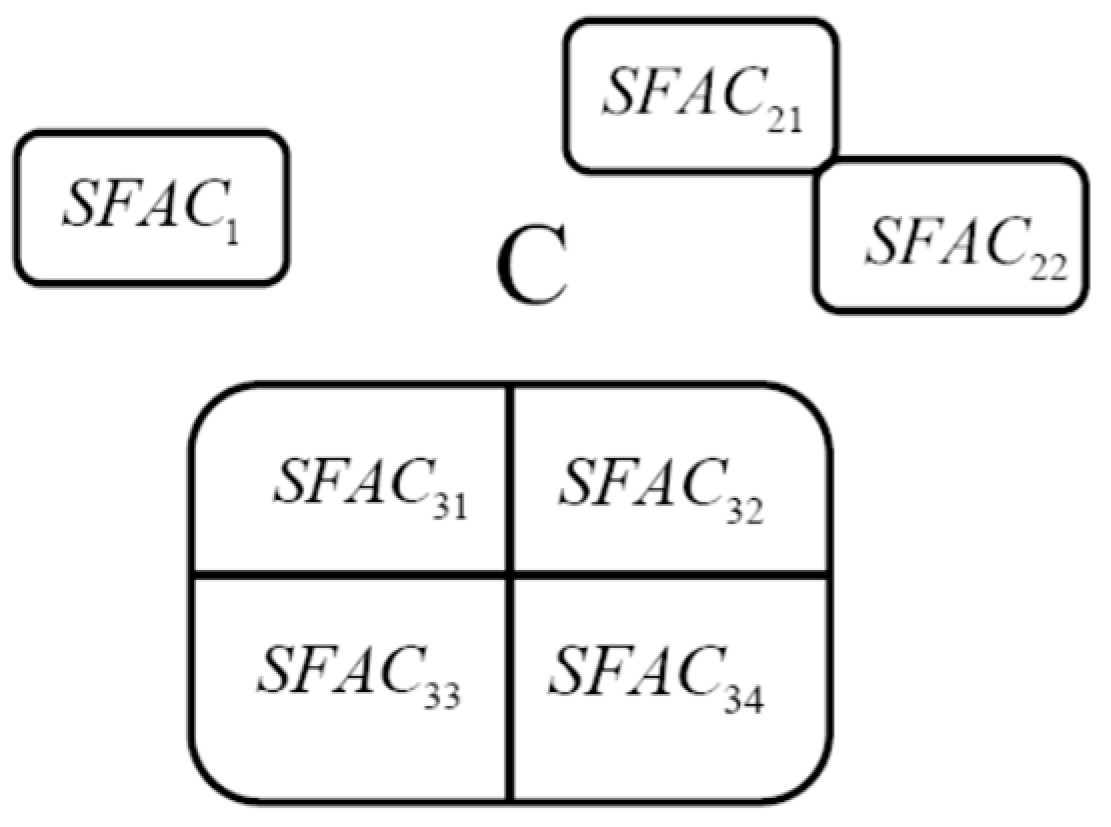
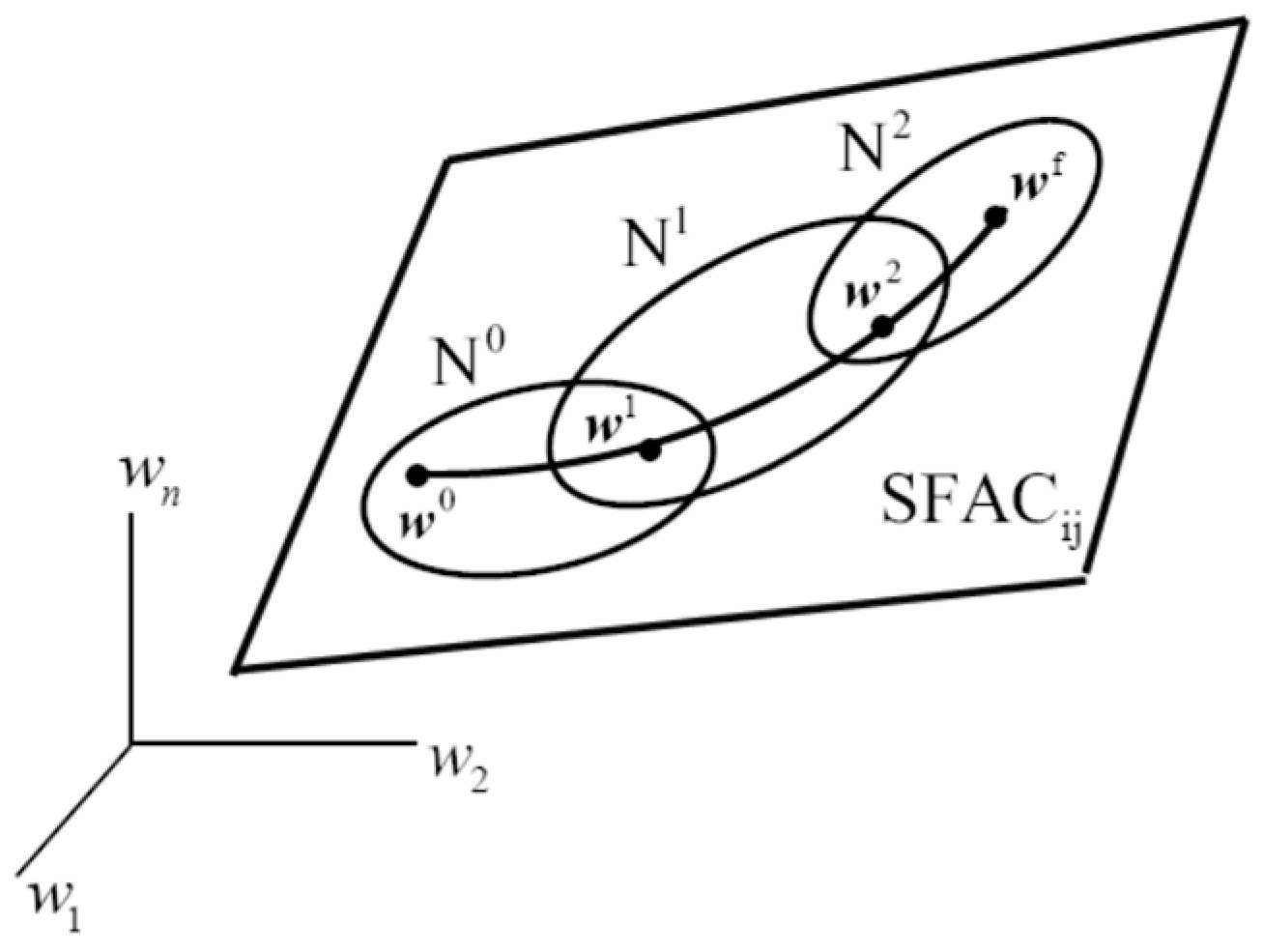
4.1.4. Singularity-Free Assembly Components

It is shown in [8] that the regular compound manipulator configuration space

$$C=\left\{\mathit{x}\in \mathit{X}:\left|{\mathit{\Omega }}_{\mathit{q}}\mathbf{(}\mathit{q},\mathit{y}\mathbf{)}\right|\ne 0, \mathrm{rank}\mathbf{(}{\mathit{\Lambda }}_{\mathit{q}}\mathbf{(}\overline{\mathit{q}},\overline{\mathit{z}}\mathbf{)}\mathbf{)}=k-\mathbf{(}\mathrm{n}-\mathrm{m})\right\}$$

(37)

is a differentiable manifold that is partitioned into singularity-free, path connected, and assembly components $\mathit{SFA}{C}_{\mathit{ij}}\subset A{C}_i$ that cover C, as shown schematically in Figure 3. It is impossible to connect configurations in different $\mathit{SFA}{C}_{\mathit{ij}}$ with singularity-free continuous paths in C. These important results cannot be obtained in velocity space.

4.1.5. Numerical Construction of a Multi-Valued Inverse Kinematic Mapping

To construct an inverse kinematic mapping on a subset ${\mathrm{N}}^{\mathrm{j}}$ of $\mathit{SFA}{C}_{\mathit{ij}}$ with base point ${\overline{\mathit{x}}}^{\mathrm{j}}\in {\mathrm{N}}^{\mathrm{j}}$, define constant matrices ${\mathit{U}}^{\mathrm{j}}$ and ${\mathit{V}}^{\mathrm{j}}$ on ${\mathbf{N}}^{\mathrm{j}}$ such that

$${\mathit{U}}^{\mathrm{j}}={\mathit{\Lambda }}_{\mathit{q}}^T\mathbf{(}{\overline{\mathit{q}}}^{\mathrm{j}},{\overline{\mathit{z}}}^{\mathrm{j}}\mathbf{)} {\mathit{\Lambda }}_{\mathit{q}}\mathbf{(}{\overline{\mathit{q}}}^{\mathrm{j}},{\overline{\mathit{z}}}^{\mathrm{j}}\mathbf{)}{\mathit{V}}^{\mathrm{j}}=\mathbf{0} {\mathit{V}}^{\mathrm{j}\mathrm{T}}{\mathit{V}}^{\mathrm{j}}=\mathit{I}$$

(38)

The matrix ${\mathit{V}}^{\mathrm{j}}$ is computed using singular value decomposition [11,28]. The k linearly independent columns of ${\mathit{U}}^{\mathrm{j}} \mathrm{and} {\mathit{V}}^{\mathrm{j}}$ span ${\mathrm{R}}^{\mathrm{k}}$, so every solution q of Equation (32) in a neighborhood of ${\overline{\mathit{q}}}^{\mathrm{j}}$ may be represented as follows:

$$\mathit{q}={\overline{\mathit{q}}}^{\mathrm{j}}+{\mathit{V}}^{\mathrm{j}}\mathbf{(}\mathit{v}-{\overline{\mathit{v}}}^{\mathrm{j}}\mathbf{)}-{\mathit{U}}^{\mathrm{j}}\mathbf{(}\mathit{u}-{\overline{\mathit{u}}}^{\mathrm{j}}\mathbf{)}$$

(39)

where $\mathit{v}\in {\mathit{R}}^{\mathit{n}-\mathit{m}}$ and $\mathit{u}\in {\mathit{R}}^{\mathit{k}-\mathit{n}+\mathit{m}}$. At $\mathit{q}={\overline{\mathit{q}}}^{\mathit{j}}$, $\mathit{v}={\overline{\mathit{v}}}^{\mathrm{j}}$, and $\mathit{u}={\overline{\mathit{u}}}^{\mathrm{j}}$.

The goal is to solve Equation (32) with q in Equation (39), i.e.,:

$$\mathit{\Lambda }\mathbf{(}{\overline{\mathit{q}}}^{\mathrm{j}}+{\mathit{V}}^{\mathrm{j}}\mathbf{(}\mathit{v}-{\overline{\mathit{v}}}^{\mathrm{j}}\mathbf{)}-{\mathit{U}}^{\mathrm{j}}\mathbf{(}\mathit{u}-{\overline{\mathit{u}}}^{\mathrm{j}}\mathbf{)},\mathit{z}\mathbf{)}=\mathbf{0}$$

(40)

for u as a function of z and v in a neighborhood of $\mathit{z}={\overline{\mathit{z}}}^{\mathrm{j}} \mathrm{and} \mathit{v}={\overline{\mathit{v}}}^{\mathrm{j}}$. The derivative of the left side of Equation (40) with respect to u at ${\overline{\mathit{x}}}^{\mathrm{j}}$ is $-{\mathit{\Lambda }}_{\mathit{q}}\mathbf{(}{\overline{\mathit{q}}}^{\mathrm{j}},{\overline{\mathit{z}}}^{\mathrm{j}}\mathbf{)}{\mathit{U}}^{\mathrm{j}}=-{\mathit{U}}^{\mathrm{j}\mathrm{T}}{\mathit{U}}^{\mathrm{j}}$, which is nonsingular. The implicit function theorem [27] implies the existence of a unique, twice continuously differentiable solution

$$\mathit{u}={\mathit{h}}^{\mathrm{j}}\mathbf{(}\mathit{z},\mathit{v}\mathbf{)}$$

(41)

of Equation (40) in a neighborhood of $\mathit{z}={\overline{\mathit{z}}}^{\mathrm{j}} \mathrm{and} \mathit{v}={\overline{\mathit{v}}}^{\mathrm{j}}$.

In the space of operational coordinates $\mathit{w}={\left[\begin{array}{cc}{\mathit{z}}^{\mathrm{T}}& {\mathit{v}}^{\mathrm{T}}\end{array}\right]}^{\mathrm{T}}$, substituting u in Equation (41) into Equation (39) results in the following:

$$\mathit{q}\mathbf{(}\mathit{w}\mathbf{)}={\overline{\mathit{q}}}^{\mathrm{j}}+{\mathit{V}}^{\mathrm{j}}\mathbf{(}\mathit{v}-{\overline{\mathit{v}}}^{\mathrm{j}}\mathbf{)}-{\mathit{U}}^{\mathrm{j}}\mathbf{(}{\mathit{h}}^{\mathrm{j}}\mathbf{(}\mathit{z},\mathit{v}\mathbf{)}-{\overline{\mathit{u}}}^{\mathrm{j}}\mathbf{)}$$

(42)

Using the first of Equation (29),

$$\mathit{y}\mathbf{(}\mathit{w}\mathbf{)}=\mathit{y}\mathbf{(}\mathit{z},\mathit{v}\mathbf{)}=\mathit{r}\mathbf{(}{\overline{\mathit{q}}}^{\mathrm{j}}+{\mathit{V}}^{\mathrm{j}}\mathbf{(}\mathit{v}-{\overline{\mathit{v}}}^{\mathrm{j}}\mathbf{)}-{\mathit{U}}^{\mathrm{j}}\mathbf{(}{\mathit{h}}^{\mathrm{j}}\mathbf{(}\mathit{z},\mathit{v}\mathbf{)}-{\overline{\mathit{u}}}^{\mathrm{j}}\mathbf{)}\mathbf{)}\equiv {\mathit{\psi }}^{\mathrm{j}}\mathbf{(}\mathit{w}\mathbf{)}$$

(43)

is a twice continuously differentiable, multi-valued, inverse kinematic mapping in a neighborhood of $\mathit{z}={\overline{\mathit{z}}}^{\mathrm{j}} \mathrm{and} \mathit{v}={\overline{\mathit{v}}}^{\mathrm{j}}$. Multiplying Equation (43) on the left by ${\mathit{V}}^{j\mathit{T}}$ and using Equation (34) yields a twice continuously differentiable, one-to-one relation between $\mathit{w} \mathrm{and} \mathit{y}$ as follows:

$$\mathit{w}={\left[\begin{array}{cc}{\mathit{z}}^{\mathit{T}}& {\mathit{v}}^{\mathit{T}}\end{array}\right]}^{\mathit{T}}={\left[\mathit{s}{\mathbf{(}\mathit{f}\mathbf{(}\mathit{y}\mathbf{)}\mathbf{)}}^{\mathit{T}} {\mathbf{(}{\overline{\mathit{v}}}^j+{\mathit{V}}^{j\mathit{T}}\mathbf{(}\mathit{y}-{\overline{\mathit{y}}}^j\mathbf{)}\mathbf{)}}^{\mathit{T}}\right]}^{\mathit{T}}={\mathit{\psi }}^{j\mathbf{(}-1\mathbf{)}}\mathbf{(}\mathit{y}\mathbf{)}$$

(44)

Analysis in the set $\mathit{SFA}{C}_{\mathit{ij}}$ must be carried out on individual charts and transitioned to adjacent charts as the manipulator configurations progress along a trajectory in $\mathit{SFA}{C}_{\mathit{ij}}$, as shown schematically in Figure 4.

.

Note that if $\mathit{v}\mathbf{(}t\mathbf{)} \mathrm{and} \mathit{z}\mathbf{(}t\mathbf{)}$ are periodic functions of time, so is $\mathit{y}\mathbf{(}\mathit{v}\mathbf{(}t\mathbf{)},\mathit{z}\mathbf{(}t\mathbf{)}\mathbf{)}$; i.e., this inverse kinematic mapping is locally cyclic, a property not enjoyed by inverse kinematics based on generalized matrix inverses [29,30,31].

With the output fixed as z and $\mathit{v}\in {\mathit{R}}^{\mathrm{n}-\mathrm{m}}$ arbitrary in a neighborhood of $\mathit{v}={\overline{\mathit{v}}}^{\mathrm{j}}$, Equation (43) defines the manipulator self-motion manifold [1,26]:

$$\begin{array}{l}\mathit{SMM}\mathbf{(}\mathit{z}\mathbf{)}=\{\mathit{y}=\mathit{r}\mathbf{(}{\overline{\mathit{q}}}^{\mathrm{j}}+{\mathit{V}}^{\mathrm{j}}\mathbf{(}\mathit{v}-{\overline{\mathit{v}}}^{\mathrm{j}}\mathbf{)}-{\mathit{U}}^{\mathrm{j}}\mathbf{(}{\mathit{h}}^{\mathrm{j}}\mathbf{(}\mathit{z},\mathit{v}\mathbf{)}-{\overline{\mathit{u}}}^{\mathrm{j}}\mathbf{)}\mathbf{)}:\\ \mathrm{for} \mathrm{all} \mathit{v} \mathrm{in} \mathrm{a} \mathrm{neighborhood} \mathrm{of} {\overline{\mathit{v}}}^{\mathrm{j}}\}\end{array}$$

(45)

4.2. Compound Manipulator Dynamics

4.2.1. Input Space ODE of Dynamics

The d’Alembert variational equation of motion for the manipulator is as follows:

$$\delta {\mathit{q}}^T\left[\mathit{M}\mathbf{(}\mathit{q}\mathbf{)}\ddot{\mathit{q}}-\mathit{S}\mathbf{(}\mathit{q},\dot{\mathit{q}}\mathbf{)}-{\mathit{Q}}^{\mathrm{A}}\mathbf{(}\mathit{q},\dot{\mathit{q}},\mathrm{t}\mathbf{)}\right]-\delta {\mathit{y}}^{\mathrm{T}}{\mathit{P}}^{\mathit{y}}\mathbf{(}\mathit{y},\dot{\mathit{y}}\mathbf{)}-\delta {\mathit{z}}^{\mathrm{T}}{\mathit{P}}^{\mathit{z}}\mathbf{(}\mathit{z},\dot{\mathit{z}}\mathbf{)}=\mathbf{0}$$

(46)

for all $\delta \mathit{q}, \delta \mathit{y}, \mathrm{and} \delta \mathit{z}$ that are consistent with linearized Equations (28) and (29) [20].

In $\mathit{SFA}{C}_{\mathit{ij}}$, the solution $\mathit{q}=\mathit{f}\mathbf{(}\mathit{y}\mathbf{)}$ of Equation (31) satisfies $\mathit{\Omega }\mathbf{(}\mathit{f}\mathbf{(}\mathit{y}\mathbf{)},\mathit{y}\mathbf{)}=\mathbf{0}$. Differentiating with respect to y, ${\mathit{\Omega }}_{\mathit{q}}\mathbf{(}\mathit{f}\mathbf{(}\mathit{y}\mathbf{)},\mathit{y}\mathbf{)}{\mathit{f}}^{\prime }\mathbf{(}\mathit{y}\mathbf{)}+{\mathit{\Psi }}_{\mathit{y}}\mathbf{(}\mathit{f}\mathbf{(}\mathit{y}\mathbf{)},\mathit{y}\mathbf{)}=\mathbf{0}$ so ${\mathit{f}}^{\prime }\mathbf{(}\mathit{y}\mathbf{)}=-{\mathit{\Omega }}_{\mathit{q}}^{-1}\mathbf{(}\mathit{f}\mathbf{(}\mathit{y}\mathbf{)},\mathit{y}\mathbf{)}{\mathit{\Omega }}_{\mathit{y}}\mathbf{(}\mathit{f}\mathbf{(}\mathit{y}\mathbf{)},\mathit{y}\mathbf{)}$, which has full rank, since ${\mathit{\Omega }}_{\mathit{q}}^{-1}\mathbf{(}\mathit{f}\mathbf{(}\mathit{y}\mathbf{)},\mathit{y}\mathbf{)}$ is nonsingular in $\mathit{SFA}{C}_{\mathit{ij}}$ and ${\mathit{\Omega }}_{\mathit{y}}\mathbf{(}\mathit{f}\mathbf{(}\mathit{y}\mathbf{)},\mathit{y}\mathbf{)}$ has full rank. Thus, the following is obtained:

$$\dot{\mathit{q}}={\mathit{f}}^{\prime }\mathbf{(}\mathit{y}\mathbf{)}\dot{\mathit{y}}=-{\mathit{\Omega }}_{\mathit{q}}^{-1}\mathbf{(}\mathit{f}\mathbf{(}\mathit{y}\mathbf{)},\mathit{y}\mathbf{)}{\mathit{\Omega }}_{\mathit{y}}\mathbf{(}\mathit{f}\mathbf{(}\mathit{y}\mathbf{)},\mathit{y}\mathbf{)}\dot{\mathit{y}}$$

(47)

Differentiating this result with respect to t yields the following:

$$\ddot{\mathit{q}}={\mathit{f}}^{\prime }\mathbf{(}\mathit{y}\mathbf{)}\ddot{\mathit{y}}-{\dot{\mathit{\Omega }}}_{\mathit{q}}^{-1}{\mathit{\Omega }}_{\mathit{y}}\dot{\mathit{y}}-{\mathit{\Omega }}_{\mathit{q}}^{-1}\left[{\left({\mathit{\Omega }}_{\mathit{y}}\mathbf{(}\mathit{q},\widehat{\mathit{y}}\mathbf{)}\widehat{\dot{\mathit{y}}}\right)}_{\mathit{q}}\dot{\mathit{q}}+{\left({\mathit{\Omega }}_{\mathit{y}}\mathbf{(}\widehat{\mathit{q}},\mathit{y}\mathbf{)}\widehat{\dot{\mathit{y}}}\right)}_{\mathit{y}}\dot{\mathit{y}}\right]$$

(48)

Since ${\mathit{\Omega }}_{\mathit{q}}\mathbf{(}\mathit{q},\mathit{y}\mathbf{)}{\mathit{\Omega }}_{\mathit{q}}^{-1}\mathbf{(}\mathit{q},\mathit{y}\mathbf{)}\mathit{\beta }=\mathit{\beta }$, with $\mathit{\beta }$ kept constant, differentiation with respect to t and manipulating [8] yields the following:

$$\begin{array}{l}\ddot{\mathit{q}}={\mathit{f}}^{\prime }\mathbf{(}\mathit{y}\mathbf{)}\ddot{\mathit{y}}+\mathit{K}\mathbf{(}\mathit{y},\dot{\mathit{y}}\mathbf{)}\\ \mathit{K}\mathbf{(}\mathit{y},\dot{\mathit{y}}\mathbf{)}={\mathit{\Omega }}_{\mathit{q}}^{-1}\left[\begin{array}{l}{\left({\mathit{\Omega }}_{\mathit{q}}\mathbf{(}\mathit{q},\widehat{\mathit{y}}\mathbf{)}{\widehat{\mathit{\Omega }}}_{\mathit{q}}^{-1}{\widehat{\mathit{\Psi }}}_{\mathit{y}}\widehat{\dot{\mathit{y}}}\right)}_{\mathit{q}}\dot{\mathit{q}}\\ +{\left({\mathit{\Omega }}_{\mathit{q}}\mathbf{(}\widehat{\mathit{q}},\mathit{y}\mathbf{)}{\widehat{\mathit{\Omega }}}_{\mathit{q}}^{-1}{\widehat{\mathit{\Omega }}}_{\mathit{y}}\widehat{\dot{\mathit{y}}}\right)}_{\mathit{y}}\dot{\mathit{y}}\end{array}\right]-{\mathit{\Omega }}_{\mathit{q}}^{-1}\left[\begin{array}{l}{\left({\mathit{\Omega }}_{\mathit{y}}\mathbf{(}\mathit{q},\widehat{\mathit{y}}\mathbf{)}\widehat{\dot{\mathit{y}}}\right)}_{\mathit{q}}\dot{\mathit{q}}\\ +{\left({\mathit{\Omega }}_{\mathit{y}}\mathbf{(}\widehat{\mathit{q}},\mathit{y}\mathbf{)}\widehat{\dot{\mathit{y}}}\right)}_{\mathit{y}}\dot{\mathit{y}}\end{array}\right]\end{array}$$

(49)

where $\mathit{q}=\mathit{f}\mathbf{(}\mathit{y}\mathbf{)}$ and $\dot{\mathit{q}}={\mathit{f}}^{\prime }\mathbf{(}\mathit{y}\mathbf{)}\dot{\mathit{y}}$.

Substituting $\ddot{\mathit{q}}$ in Equation (49), $\mathit{q}=\mathit{f}\mathbf{(}\mathit{y}\mathbf{)}$ in Equations (33) and (47), $\delta \mathit{z}={\mathit{s}}^{\prime }\mathbf{(}\mathit{f}\mathbf{(}\mathit{y}\mathbf{)}\mathbf{)}{\mathit{f}}^{\prime }\mathbf{(}\mathit{y}\mathbf{)}\delta \mathit{y}$ from Equation (34), and $\delta \mathit{q}={\mathit{f}}^{\prime }\mathbf{(}\mathit{y}\mathbf{)}\delta \mathit{y}$ into Equation (46), $\delta {\mathit{y}}^T\left\{{{\mathit{f}}^{\prime }}^T\mathit{M}{\mathit{f}}^{\prime }+{{\mathit{f}}^{\prime }}^T\left(\mathit{M}\mathit{K}-\mathit{S}-{\mathit{Q}}^{\mathrm{A}}\right)-{\mathit{P}}^{\mathit{y}}-{{\mathit{f}}^{\prime }}^T{{\mathit{s}}^{\prime }}^T{\mathit{P}}^{\mathit{z}}\right\}=\mathbf{0}$. Since $\delta \mathit{y}$ is arbitrary, the compound manipulator input space ODE of motion is as follows:

$${{\mathit{f}}^{\prime }}^T\mathit{M}{\mathit{f}}^{\prime } \ddot{\mathit{y}}+{{\mathit{f}}^{\prime }}^{\mathrm{T}}\left(\mathit{M}\mathit{K}-\mathit{S}-{\mathit{Q}}^{\mathrm{A}}\right)-{\mathit{P}}^{\mathit{y}}-{{\mathit{f}}^{\prime }}^{\mathrm{T}}{{\mathit{s}}^{\prime }}^{\mathrm{T}}{\mathit{P}}^{\mathit{z}}=\mathbf{0}$$

(50)

Since ${\mathit{\Phi }}_{\mathit{q}}\delta \mathit{q}={\mathit{\Phi }}_{\mathit{q}}{\mathit{f}}^{\prime }\delta \mathit{y}=\mathbf{0}$ and $\delta \mathit{y}$ is arbitrary, ${\mathit{\Phi }}_{\mathit{q}}{\mathit{f}}^{\prime }=\mathbf{0}$ and the columns of ${\mathit{f}}^{\prime }$ span the null space of ${\mathit{\Phi }}_{\mathit{q}}$, ${{\mathit{f}}^{\prime }}^T\mathit{M}{\mathit{f}}^{\prime }$ is positive definite, hence nonsingular, so the ODE of Equation (50) is well posed [19,20].

4.2.2. Operational Space Velocity and Acceleration Kinematics

Differentiating Equation (42) with respect to t, we obtain the following:

$$\dot{\mathit{q}}=\mathit{V}\dot{\mathit{v}}-\mathit{U}\dot{\mathit{h}}$$

(51)

Differentiating the identity $\mathit{\Lambda }\mathbf{(}\overline{\mathit{q}}+\mathit{V}\mathbf{(}\mathit{v}-\overline{\mathit{v}}\mathbf{)}-\mathit{U}\mathbf{(}\mathit{h}-\overline{\mathit{u}}\mathbf{)},\mathit{z}\mathbf{)}=\mathbf{0}$ with respect to t, yields the following:

$${\mathit{\Lambda }}_{\mathit{q}}\mathbf{(}\mathit{q},\mathit{z}\mathbf{)}\mathbf{(}\mathit{V}\dot{\mathit{v}}-\mathit{U}\dot{\mathit{h}}\mathbf{)}+{\mathit{\Lambda }}_{\mathit{z}}\mathbf{(}\mathit{q},\mathit{z}\mathbf{)}\dot{\mathit{z}}=\mathbf{0}$$

(52)

In Equation (38), $-{\mathit{\Lambda }}_{\mathit{q}}\mathbf{(}\overline{\mathit{q}},\overline{\mathit{z}}\mathbf{)}\mathit{U}=-{\mathit{U}}^T\mathit{U}$ is nonsingular. Since ${\mathit{\Lambda }}_{\mathit{q}}\mathbf{(}\mathit{q},\mathit{z}\mathbf{)}$ is continuous, ${\mathit{\Lambda }}_{\mathit{q}}\mathbf{(}\mathit{q},\mathit{z}\mathbf{)}\mathit{U}$ is nonsingular in a neighborhood of $\overline{\mathit{x}}\in \mathit{SFA}{C}_{\mathrm{j}}$ and

$$\mathit{B}\mathbf{(}\mathit{q},\mathit{z}\mathbf{)}={\left({\mathit{\Lambda }}_{\mathit{q}}\mathbf{(}\mathit{q},\mathit{z}\mathbf{)}\mathit{U}\right)}^{-1}$$

(53)

is continuously differentiable in a neighborhood of $\overline{\mathit{x}}\in \mathit{SFA}{C}_{\mathrm{j}}$.

Using Equation (53) in Equation (52),

$$\dot{\mathit{h}}=\mathit{B}\mathbf{(}\mathit{q},\mathit{z}\mathbf{)}\left({\mathit{\Lambda }}_{\mathit{q}}\mathbf{(}\mathit{q},\mathit{z}\mathbf{)}\mathit{V}\dot{\mathit{v}}+{\mathit{\Lambda }}_{\mathit{z}}\mathbf{(}\mathit{q},\mathit{z}\mathbf{)}\dot{\mathit{z}}\right)$$

(54)

In Equation (51), this yields the following:

$$\begin{array}{ll}\dot{\mathit{q}}& =-\mathit{U}\mathit{B}\mathbf{(}\mathit{q},\mathit{z}\mathbf{)}{\mathit{\Lambda }}_{\mathit{z}}\mathbf{(}\mathit{q},\mathit{z}\mathbf{)}\dot{\mathit{z}}+\left(\mathit{I}-\mathit{U}\mathit{B}\mathbf{(}\mathit{q},\mathit{z}\mathbf{)}{\mathit{\Lambda }}_{\mathit{q}}\mathbf{(}\mathit{q},\mathit{z}\mathbf{)}\right)\mathit{V}\dot{\mathit{v}}\\ & =-\mathit{U}\mathit{B}\mathbf{(}\mathit{q},\mathit{z}\mathbf{)}{\mathit{\Lambda }}_{\mathit{z}}\mathbf{(}\mathit{q},\mathit{z}\mathbf{)}\dot{\mathit{z}}+\mathit{D}\mathbf{(}\mathit{q},\mathit{z}\mathbf{)}\dot{\mathit{v}}=\mathit{H}\mathbf{(}\mathit{w}\mathbf{)}\dot{\mathit{w}}\end{array}$$

(55)

where

$$\begin{array}{l}\mathit{D}\mathbf{(}\mathit{q},\mathit{z}\mathbf{)}\equiv \left(\mathit{I}-\mathit{U}\mathit{B}\mathbf{(}\mathit{q},\mathit{z}\mathbf{)}{\mathit{\Lambda }}_{\mathit{q}}\mathbf{(}\mathit{q},\mathit{z}\mathbf{)}\right)\mathit{V}\\ \mathit{H}\mathbf{(}\mathit{w}\mathbf{)}\equiv {\left[-\mathit{U}\mathit{B}\mathbf{(}\mathit{q},\mathit{z}\mathbf{)}{\mathit{\Lambda }}_{\mathit{z}}\mathbf{(}\mathit{q},\mathit{z}\mathbf{)}\mathit{D}\mathbf{(}\mathit{q},\mathit{z}\mathbf{)}\right]}_{\mathit{k}\times \mathit{n}}\end{array}$$

In terms of differentials, this can be written as follows:

$$\mathit{\delta }\mathit{q}=-\mathit{U}\mathit{B}\mathbf{(}\mathit{q},\mathit{z}\mathbf{)}{\mathit{\Lambda }}_{\mathit{z}}\mathbf{(}\mathit{q},\mathit{z}\mathbf{)}\mathit{\delta }\mathit{z}+\mathit{D}\mathbf{(}\mathit{q},\mathit{z}\mathbf{)}\mathit{\delta }\mathit{v}=\mathit{H}\mathbf{(}\mathit{w}\mathbf{)}\mathit{\delta }\mathit{w}$$

(56)

Suppressing arguments and manipulating the product on the left yields the following:

$$\left[\begin{array}{c}-{\mathit{\Lambda }}_{\mathit{z}}^{-1}{\mathit{\Lambda }}_{\mathit{q}}\\ {\mathit{V}}^T\end{array}\right]\mathit{H}=\left[\begin{array}{c}-{\mathit{\Lambda }}_{\mathit{z}}^{-1}{\mathit{\Lambda }}_{\mathit{q}}\\ {\mathit{V}}^T\end{array}\right]\left[-\mathit{U}\mathit{B}{\mathit{\Lambda }}_{\mathit{z}} \mathit{D}\right]=\left[\begin{array}{c}\mathit{I}{\mathit{\Lambda }}_{\mathit{z}}^{-1}\mathbf{(}{\mathit{\Lambda }}_{\mathit{q}}-{\mathit{\Lambda }}_{\mathit{q}}\mathbf{)}\mathit{V}\\ \mathbf{0}{\mathit{V}}^T\mathit{V}\end{array}\right]=\left[\begin{array}{cc}\mathit{I}& \mathbf{0}\\ \mathbf{0}& \mathit{I}\end{array}\right]=\mathit{I}$$

Thus, $\mathit{H}\mathbf{(}\mathit{w}\mathbf{)}$ has full column rank, with the left inverse as follows:

$${\mathit{H}}^{-L}\mathbf{(}\mathit{w}\mathbf{)}=\left[\begin{array}{c}-{\mathit{\Lambda }}_{\mathit{z}}^{-1}\mathbf{(}\mathit{q}\mathbf{(}\mathit{w}\mathbf{)},\mathit{z}\mathbf{)}{\mathit{\Lambda }}_{\mathit{q}}\mathbf{(}\mathit{q}\mathbf{(}\mathit{w}\mathbf{)},\mathit{z}\mathbf{)}\\ {\mathit{V}}^T\end{array}\right]$$

(57)

Differentiating Equation (55) with respect to t yields the following:

$$\begin{array}{l}\ddot{\mathit{q}}=\mathit{H}\mathbf{(}\mathit{w}\mathbf{)}\ddot{\mathit{w}}-\mathit{U}\dot{\mathit{B}}{\mathit{\Lambda }}_{\mathit{z}}\dot{\mathit{z}}-\mathit{U}\dot{\mathit{B}}{\mathit{\Lambda }}_{\mathit{q}}\mathit{V}\dot{\mathit{v}}-\mathit{U}\mathit{B}\left({\mathbf{(}{\mathit{\Lambda }}_{\mathit{z}}\mathbf{(}\mathit{q},\widehat{\mathit{z}}\mathbf{)}\widehat{\dot{\mathit{z}}}\mathbf{)}}_{\mathit{q}}\dot{\mathit{q}}+{\mathbf{(}{\mathit{\Lambda }}_{\mathit{z}}\mathbf{(}\widehat{\mathit{q}},\mathit{z}\mathbf{)}\widehat{\dot{\mathit{z}}}\mathbf{)}}_{\mathit{z}}\dot{\mathit{z}}\right)\\ -\mathit{U}\mathit{B}\left({\mathbf{(}{\mathit{\Lambda }}_{\mathit{q}}\mathbf{(}\mathit{q},\widehat{\mathit{z}}\mathbf{)}\mathit{V}\widehat{\dot{\mathit{v}}}\mathbf{)}}_{\mathit{q}}\dot{\mathit{q}}+{\mathbf{(}{\mathit{\Lambda }}_{\mathit{q}}\mathbf{(}\widehat{\mathit{q}},\mathit{z}\mathbf{)}\mathit{V}\widehat{\dot{\mathit{v}}}\mathbf{)}}_{\mathit{z}}\dot{\mathit{z}}\right)\end{array}$$

(58)

where, from Equation (55), $\dot{\mathit{q}}=\mathit{H}\mathbf{(}\mathit{w}\mathbf{)}\dot{\mathit{w}}$. Writing Equation (53) in the form ${\mathit{\Lambda }}_{\mathit{q}}\mathbf{(}\mathit{q},\mathit{z}\mathbf{)}\mathit{U}\mathit{B}\mathbf{(}\mathit{q},\mathit{z}\mathbf{)}\mathit{\beta }=\mathit{\beta }$, with $\mathit{\beta }$ kept constant, differentiating with respect to t, and manipulating [8] yields the following:

$$\begin{array}{l}\ddot{\mathit{q}}=\mathit{H}\mathbf{(}\mathit{w}\mathbf{)}\ddot{\mathit{w}}+\mathit{E}\mathbf{(}\mathit{w},\dot{\mathit{w}}\mathbf{)}\\ \mathit{E}\mathbf{(}\mathit{w},\dot{\mathit{w}}\mathbf{)}=\mathit{U}\mathit{B}\left(\begin{array}{l}\left[\begin{array}{l}{\left({\mathit{\Lambda }}_{\mathit{q}}\mathbf{(}\mathit{q},\widehat{\mathit{z}}\mathbf{)}\mathit{U}\widehat{\mathit{B}}\mathbf{(}{\widehat{\mathit{\Lambda }}}_{\mathit{z}}\widehat{\dot{\mathit{z}}}+{\widehat{\mathit{\Lambda }}}_{\mathit{q}}\mathit{V}\widehat{\dot{\mathit{v}}}\mathbf{)}\right)}_{\mathit{q}}\dot{\mathit{q}}\\ +{\left({\mathit{\Lambda }}_{\mathit{q}}\mathbf{(}\widehat{\mathit{q}},\mathit{z}\mathbf{)}\mathit{U}\widehat{\mathit{B}}\mathbf{(}{\widehat{\mathit{\Lambda }}}_{\mathit{z}}\widehat{\dot{\mathit{z}}}+{\widehat{\mathit{\Lambda }}}_{\mathit{q}}\mathit{V}\widehat{\dot{\mathit{v}}}\mathbf{)}\right)}_{\mathit{z}}\dot{\mathit{z}}\end{array}\right]\\ -\left[\begin{array}{l}\left({\mathbf{(}{\mathit{\Lambda }}_{\mathit{z}}\mathbf{(}\mathit{q},\widehat{\mathit{z}}\mathbf{)}\widehat{\dot{\mathit{z}}}\mathbf{)}}_{\mathit{q}}\dot{\mathit{q}}+{\mathbf{(}{\mathit{\Lambda }}_{\mathit{z}}\mathbf{(}\widehat{\mathit{q}},\mathit{z}\mathbf{)}\widehat{\dot{\mathit{z}}}\mathbf{)}}_{\mathit{z}}\dot{\mathit{z}}\right)\\ +\left({\mathbf{(}{\mathit{\Lambda }}_{\mathit{q}}\mathbf{(}\mathit{q},\widehat{\mathit{z}}\mathbf{)}\mathit{V}\widehat{\dot{\mathit{v}}}\mathbf{)}}_{\mathit{q}}\dot{\mathit{q}}+{\mathbf{(}{\mathit{\Lambda }}_{\mathit{q}}\mathbf{(}\widehat{\mathit{q}},\mathit{z}\mathbf{)}\mathit{V}\widehat{\dot{\mathit{v}}}\mathbf{)}}_{\mathit{z}}\dot{\mathit{z}}\right)\end{array}\right]\end{array}\right)\end{array}$$

(59)

Differentiating y in Equation (43) with respect to t and using Equation (54) yields the following:

$$\begin{array}{ll}\dot{\mathit{y}}& ={\mathit{r}}^{\prime }\mathbf{(}\left(\mathit{q}\right)\left[{\mathit{V}}^{\mathit{j}}\dot{\mathit{v}}-{\mathit{U}}^{\mathit{j}}\left(\mathit{B}\mathbf{(}\mathit{q},\mathit{z}\mathbf{)}\left({\mathit{\Lambda }}_{\mathit{q}}\mathbf{(}\mathit{q},\mathit{z}\mathbf{)}{\mathit{V}}^{\mathit{j}}\dot{\mathit{v}}+{\mathit{\Lambda }}_{\mathit{z}}\mathbf{(}\mathit{q},\mathit{z}\mathbf{)}\dot{\mathit{z}}\right)\right)\right]\\ & ={\mathit{r}}^{\prime }\mathbf{(}\left(\mathit{q}\right)\left[-{\mathit{U}}^{\mathit{j}}\mathit{B}\mathbf{(}\mathit{q},\mathit{z}\mathbf{)}{\mathit{\Lambda }}_{\mathit{z}}\mathbf{(}\mathit{q},\mathit{z}\mathbf{)}\dot{\mathit{z}}+\left(\mathit{I}-{\mathit{U}}^{\mathit{j}}\mathit{B}\mathbf{(}\mathit{q},\mathit{z}\mathbf{)}{\mathit{\Lambda }}_{\mathit{q}}\mathbf{(}\mathit{q},\mathit{z}\mathbf{)}\right){\mathit{V}}^{\mathit{j}}\dot{\mathit{v}}\right]\\ & ={\mathit{r}}^{\prime }\mathbf{(}\left(\mathit{q}\right)\left[-{\mathit{U}}^{\mathit{j}}\mathit{B}\mathbf{(}\mathit{q},\mathit{z}\mathbf{)}{\mathit{\Lambda }}_{\mathit{z}}\mathbf{(}\mathit{q},\mathit{z}\mathbf{)}\dot{\mathit{z}}+\mathit{D}\mathbf{(}\mathit{q},\mathit{z}\mathbf{)}\dot{\mathit{v}}\right]={\mathit{r}}^{\prime }\mathbf{(}\left(\mathit{q}\right)\mathit{H}\mathbf{(}\mathit{w}\mathbf{)}\dot{\mathit{w}}\end{array}$$

(60)

In terms of differentials, this can be written as follows:

$$\mathit{\delta }\mathit{y}={\mathit{r}}^{\prime }\mathbf{(}\left(\mathit{q}\right)\left[-{\mathit{U}}^{\mathit{j}}\mathit{B}\mathbf{(}\mathit{q},\mathit{z}\mathbf{)}{\mathit{\Lambda }}_{\mathit{z}}\mathbf{(}\mathit{q},\mathit{z}\mathbf{)}\mathit{\delta }\mathit{z}+\mathit{D}\mathbf{(}\mathit{q},\mathit{z}\mathbf{)}\mathit{\delta }\mathit{v}\right]={\mathit{r}}^{\prime }\mathbf{(}\left(\mathit{q}\right)\mathit{H}\mathbf{(}\mathit{w}\mathbf{)}\mathit{\delta }\mathit{w}$$

(61)

4.2.3. Operational Space ODE of Dynamics

In Equations (56) and (61) and $\mathit{w}={\left[\begin{array}{cc}{\mathit{z}}^T& {\mathit{v}}^T\end{array}\right]}^T$, $\delta \mathit{q}=\mathit{H}\mathbf{(}\mathit{w}\mathbf{)}\delta \mathit{w}$, $\delta \mathit{y}={\mathit{r}}^{\prime }\mathbf{(}\mathit{q}\mathbf{(}\mathit{w}\mathbf{)}\mathbf{)}\mathit{H}\mathbf{(}\mathit{w}\mathbf{)}\delta \mathit{w}$, and $\delta \mathit{z}=\left[\begin{array}{cc}\mathit{I}& \mathbf{0}\end{array}\right]\delta \mathit{w}$. Substituting these relations and Equation (59) into Equation (46), $\delta {\mathit{w}}^T\left[{\mathit{H}}^T\mathit{M}\mathit{H}\ddot{\mathit{w}}+{\mathit{H}}^T\left(\mathit{M}\mathit{E}-\mathit{S}-{\mathit{Q}}^A-{{\mathit{r}}^{\prime }}^T{\mathit{P}}^{\mathit{y}}\right)-{\left[\begin{array}{cc}\mathit{I}& 0\end{array}\right]}^T{\mathit{P}}^{\mathit{z}}\right]=0$. Since $\delta \mathit{w}$ is arbitrary, the compound manipulator operational space ODE of motion is

$${\mathit{H}}^T\mathit{M}\mathit{H}\ddot{\mathit{w}}+{\mathit{H}}^T\left(\mathit{M}\mathit{E}-\mathit{S}-{\mathit{Q}}^A-{{\mathit{r}}^{\prime }}^T{\mathit{P}}^{\mathit{y}}\right)-{\left[\begin{array}{cc}\mathit{I}& \mathbf{0}\end{array}\right]}^T{\mathit{P}}^{\mathit{z}}=\mathbf{0}$$

(62)

Since M is positive definite in the null space of ${\mathit{\Phi }}_{\mathit{q}}$ [20] and ${\mathit{\Phi }}_{\mathit{q}}\delta \mathit{q}={\mathit{\Phi }}_{\mathit{q}}\mathit{H}\delta \mathit{w}=\mathbf{0}$ for arbitrary $\delta \mathit{w}$, the linearly independent columns of the matrix H are in the null space of ${\mathit{\Phi }}_{\mathit{q}}$ and ${\mathit{H}}^T\mathit{M}\mathit{H}$ is positive definite, hence nonsingular. Thus, the operational space ODE of Equation (62) is well posed [19,20].

For manipulator control, it may be helpful to write second-order ODE in terms of z and v. Substituting $\ddot{\mathit{q}}$ in Equation (58) and manipulating [8] yields the following:

$$\begin{array}{l}-{\mathit{\Lambda }}_{\mathit{z}}^T{\mathit{B}}^T{\mathit{U}}^T\mathit{M}\mathit{U}\mathit{B}{\mathit{\Lambda }}_{\mathit{z}}\ddot{\mathit{z}}+{\mathit{\Lambda }}_{\mathit{z}}^T{\mathit{B}}^T{\mathit{U}}^T\mathit{M}\mathit{D}\ddot{\mathit{v}}+{\mathit{\Lambda }}_{\mathit{z}}^T{\mathit{B}}^T{\mathit{U}}^T\left(\mathit{M}\mathit{E}+\mathit{S}+{\mathit{Q}}^A-{\mathit{P}}^{\mathit{y}}\right)-{\mathit{P}}^{\mathit{z}}=\mathbf{0}\\ {\mathit{D}}^T\mathit{M}\mathit{U}\mathit{B}{\mathit{\Lambda }}_{\mathit{z}}\ddot{\mathit{z}}-{\mathit{D}}^T\mathit{M}\mathit{D}\ddot{\mathit{v}}-{\mathit{D}}^T\left(\mathit{M}\mathit{E}+\mathit{S}+{\mathit{Q}}^A-{\mathit{P}}^{\mathit{y}}\right)=\mathbf{0}\end{array}$$

(63)

This operational space ODE of compound manipulator dynamics forms the foundation for a new approach to the control of compound manipulators.

4.2.4. Computation of $\mathit{h}\mathbf{(}\mathit{z},\mathit{v}\mathbf{)}$ and $\mathit{B}\mathbf{(}\mathit{q},\mathit{z}\mathbf{)}$

At $\overline{\mathit{x}}\in \mathit{SFA}{\mathit{C}}_{\mathrm{j}}$, $\mathit{B}(\overline{\mathit{q}},\overline{\mathit{z}})={\left({\mathit{\Lambda }}_{\mathit{q}}\mathbf{(}\overline{\mathit{q}},\overline{\mathit{z}}\mathbf{)}\mathit{U}\right)}^{-1}={\left({\mathit{U}}^T\mathit{U}\right)}^{-1}$ is numerically evaluated. For $\mathbf{(}{\mathit{q}}^{\mathrm{i}},{\mathit{z}}^{\mathrm{i}}\mathbf{)}$ at time ${\mathit{t}}^{\mathit{i}}$, $\mathit{B}\mathbf{(}{\mathit{q}}^{\mathrm{i}},{\mathit{z}}^{\mathrm{i}}\mathbf{)}$ satisfies Equation (53) with the following form:

$${\mathit{\Lambda }}_{\mathit{q}}\mathbf{(}\mathit{q},\mathit{z}\mathbf{)}\mathit{U}\mathit{B}\mathbf{(}\mathit{q},\mathit{z}\mathbf{)}-\mathit{I}=\mathbf{0}$$

(64)

With an approximation ${\mathit{B}}^{\left(1\right)}\approx \mathit{B}({\mathit{q}}^{\mathrm{i}-1},{\mathit{z}}^{\mathrm{i}-1})$ of the solution of Equation (64), a matrix version of Newton–Raphson iteration in the solution of Equation (64) is [8] as follows:

$${\mathit{B}}^{(\mathrm{j}+1)}=2{\mathit{B}}^{\left(\mathrm{j}\right)}-{\mathit{B}}^{\left(\mathrm{j}\right)}{\mathit{\Lambda }}_{\mathit{q}}\mathit{U}{\mathit{B}}^{\left(\mathrm{j}\right)}, \mathrm{j}=1, 2,\dots , \mathrm{until} ‖{\mathit{\Lambda }}_{\mathit{q}}\mathit{U}{\mathit{B}}^{(\mathrm{j}+1)}-\mathit{I}‖\le \mathrm{Btol}$$

(65)

where Btol is an error tolerance.

Similarly, $\mathit{h}({\mathit{z}}^{\mathrm{i}},{\mathit{v}}^{\mathrm{i}})$ can be efficiently evaluated as accurately as desired using Newton–Raphson iteration to solve Equation (40) for $\mathit{u}=\mathit{h}\mathbf{(}{\mathit{z}}^{\mathrm{i}},{\mathit{v}}^{\mathrm{i}}\mathbf{)}$:

$$\begin{array}{l}{\mathit{u}}^{(\mathrm{j}+1)}={\mathit{u}}^{\left(\mathrm{j}\right)}+\mathit{B}\mathit{\Lambda }\mathbf{(}\overline{\mathit{q}}+\mathit{V}\mathit{v}-\mathit{U}{\mathit{u}}^{\left(\mathrm{j}\right)},\mathit{z}\mathbf{)}, \mathrm{j}=1, 2,\dots \\ \mathrm{until} ‖\mathit{\Lambda }\mathbf{(}\overline{\mathit{q}}+\mathit{V}\mathit{v}-\mathit{U}{\mathit{u}}^{(\mathrm{j}+1)},\mathit{z}\mathbf{)}‖\le \mathrm{utol}\end{array}$$

(66)

where utol is a specified error tolerance.

5. Material Loader Dynamics and Control

5.1. Material Loader Input and Operational Space Dynamics

The equivalence of input space dynamics and extended operational space dynamics is demonstrated next for the loader example. For input space dynamics, the differential-algebraic equation (DAE) form of the constrained equations of motion (Equation (3)) is as follows:

$${\mathit{P}}^{\mathit{q}}+{\mathit{\Phi }}_{\mathit{q}}{\mathbf{(}\mathit{q}\mathbf{)}}^{\mathit{T}}\mathit{\lambda }=\mathit{M}\mathbf{(}\mathit{q}\mathbf{)}\ddot{\mathit{q}}-\mathit{S}\mathbf{(}\mathit{q},\dot{\mathit{q}}\mathbf{)}-{\mathit{Q}}^A\mathbf{(}\mathit{q},\dot{\mathit{q}},t\mathbf{)}-{\mathit{P}}^{\mathit{j}}+10{\nabla }_{\mathit{q}}T$$

subject to the following holonomic constraint:

$$\mathit{\Phi }\mathbf{(}\mathit{q}\mathbf{)}=0$$

where a structural joint limit response force ${\mathit{P}}^{\mathit{j}}$ is specified to prevent the hyper-extension of the actuator cylinders. A dissipative force ${\nabla }_{\mathit{q}}T$ associated with the gradient of the kinetic energy has also been added to the standard input space forces. This represents a set of DAEs. These DAEs can be represented as a set of ODEs by differentiating the constraint equations twice and solving for $\ddot{\mathit{q}}$, yielding the following:

$$\ddot{\mathit{q}}=\mathit{\Theta }{\mathit{M}}^{-1}\left(\mathit{S}+{\mathit{Q}}^A+{\mathit{P}}^{\mathit{j}}-10{\nabla }_{\mathit{q}}T\right)-{\overline{\mathit{\Phi }}}_{\mathit{q}}{\dot{\mathit{\Phi }}}_{\mathit{q}}\dot{\mathit{q}}-{\overline{\mathit{\Phi }}}_{\mathit{q}}\mathbf{(}\mathit{\alpha }\mathit{\Phi }+\mathit{\beta }{\mathit{\Phi }}_{\mathit{q}}\dot{\mathit{q}}\mathbf{)}$$

where ${\overline{\mathit{\Phi }}}_{\mathit{q}}\equiv {\mathit{M}}^{-1}{\mathit{\Phi }}_{\mathit{q}}^{\mathit{T}}{\left({\mathit{\Phi }}_{\mathit{q}}{\mathit{M}}^{-1}{\mathit{\Phi }}_{\mathit{q}}^{\mathit{T}}\right)}^{-1}$ and $\mathit{\alpha }=100$ and $\mathit{\beta }=20$ are Baumgarte stabilization constants [32]. Specifying the following initial conditions

$$\begin{array}{l}{\mathit{q}}_0={\left[\begin{array}{ccccccc}0& 2& \sqrt{5}& 0& 0.5& 1.1725& 0\end{array}\right]}^{\mathit{T}}\\ {\dot{\mathit{q}}}_0=0\end{array}$$

and an integration procedure yields [33] as follows:

$$\begin{array}{l}\mathrm{For} \mathit{i}=0 \mathrm{to} \mathit{n},\\ {\left.{\ddot{\mathit{q}}}_{\mathit{i}}=\mathit{\Theta }{\mathit{M}}^{-1}\left(\mathit{S}+{\mathit{Q}}^A+{\mathit{P}}^{\mathit{j}}-10{\nabla }_{\mathit{q}}T\right)-{\overline{\mathit{\Phi }}}_{\mathit{q}}{\dot{\mathit{\Phi }}}_{\mathit{q}}\dot{\mathit{q}}-{\overline{\mathit{\Phi }}}_{\mathit{q}}\mathbf{(}\mathit{\alpha }\mathit{\Phi }+\mathit{\beta }{\mathit{\Phi }}_{\mathit{q}}\dot{\mathit{q}}\mathbf{)}\right|}_{\mathit{i}}\\ {\dot{\mathit{q}}}_{\mathit{i}+1}={\dot{\mathit{q}}}_{\mathit{i}}+{\ddot{\mathit{q}}}_{\mathit{i}}\mathbf{\Delta }\mathit{t}\\ {\mathit{q}}_{\mathit{i}+1}={\mathit{q}}_{\mathit{i}}+{\dot{\mathit{q}}}_{\mathit{i}}\mathbf{\Delta }\mathit{t}+{\displaystyle \frac{1}{2}}{\ddot{\mathit{q}}}_{\mathit{i}}\mathbf{\Delta }\mathit{t}\end{array}$$

Running this simple second-order integrator for three seconds yields the results shown in Figure 5 and Figure 6. Each image in Figure 5 depicts the manipulator configuration at a specific time. The images occur at regular intervals, with the earliest images fading away; i.e., becoming more transparent. Figure 6 displays generalized coordinates over the three-second interval. Comparable results could be obtained by solving Equation (50) for $\mathit{y}\mathbf{(}t\mathbf{)} \mathrm{and} \dot{\mathit{y}}\mathbf{(}t\mathbf{)}$ and using $\mathit{q}=\mathit{f}\mathbf{(}\mathit{y}\mathbf{)} \mathrm{and} \dot{\mathit{q}}={\mathit{f}}^{\prime }\mathbf{(}\mathit{y}\mathbf{)}\dot{\mathit{y}}$ to recover $\mathit{q} \mathrm{and} \dot{\mathit{q}}$.

The operational space differential equation of motion [34] of Equation (62) is as follows:

$${\mathit{H}}^T\mathit{M}\mathit{H}\ddot{\mathit{w}}+{\mathit{H}}^T\left(\mathit{M}\mathit{E}-\mathit{S}-{\mathit{Q}}^{\mathrm{A}}-{\mathit{P}}^{\mathit{j}}+10{\nabla }_{\mathit{q}}T\right)=\mathbf{0}$$

This is a set of ODEs. With the same initial conditions and integration procedure [22], the following is obtained:

$$\begin{array}{l}\mathrm{For} \mathit{i}=0 \mathrm{to} \mathit{n}\\ {\ddot{\mathit{w}}}_{\mathit{i}}={\left.-{\mathbf{(}{\mathit{H}}^T\mathit{M}\mathit{H}\mathbf{)}}^{-1}{\mathit{H}}^T\left(\mathit{M}\mathit{E}-\mathit{S}-{\mathit{Q}}^A-{\mathit{P}}^{\mathit{j}}+10{\nabla }_{\mathit{q}}T\right)\right|}_{\mathit{i}}\\ {\ddot{\mathit{q}}}_{\mathit{i}}={\left.\mathit{H}\ddot{\mathit{w}}+\mathit{E}\right|}_{\mathit{i}}\\ {\dot{\mathit{q}}}_{\mathit{i}+1}={\dot{\mathit{q}}}_{\mathit{i}}+{\ddot{\mathit{q}}}_{\mathit{i}}\mathbf{\Delta }\mathit{t}\\ {\mathit{q}}_{\mathit{i}+1}={\mathit{q}}_{\mathit{i}}+{\dot{\mathit{q}}}_{\mathit{i}}\mathbf{\Delta }\mathit{t}+{\displaystyle \frac{1}{2}}{\ddot{\mathit{q}}}_{\mathit{i}}\mathbf{\Delta }\mathit{t}\end{array}$$

where the acceleration is computed in extended operational space coordinates and transformed to generalized accelerations, for comparison with the foregoing input space integration results.

Running this simple second-order integrator for three seconds yields the results shown in Figure 7. The results are essentially identical to the input space results, demonstrating the equivalence of input space and extended operational space dynamics.

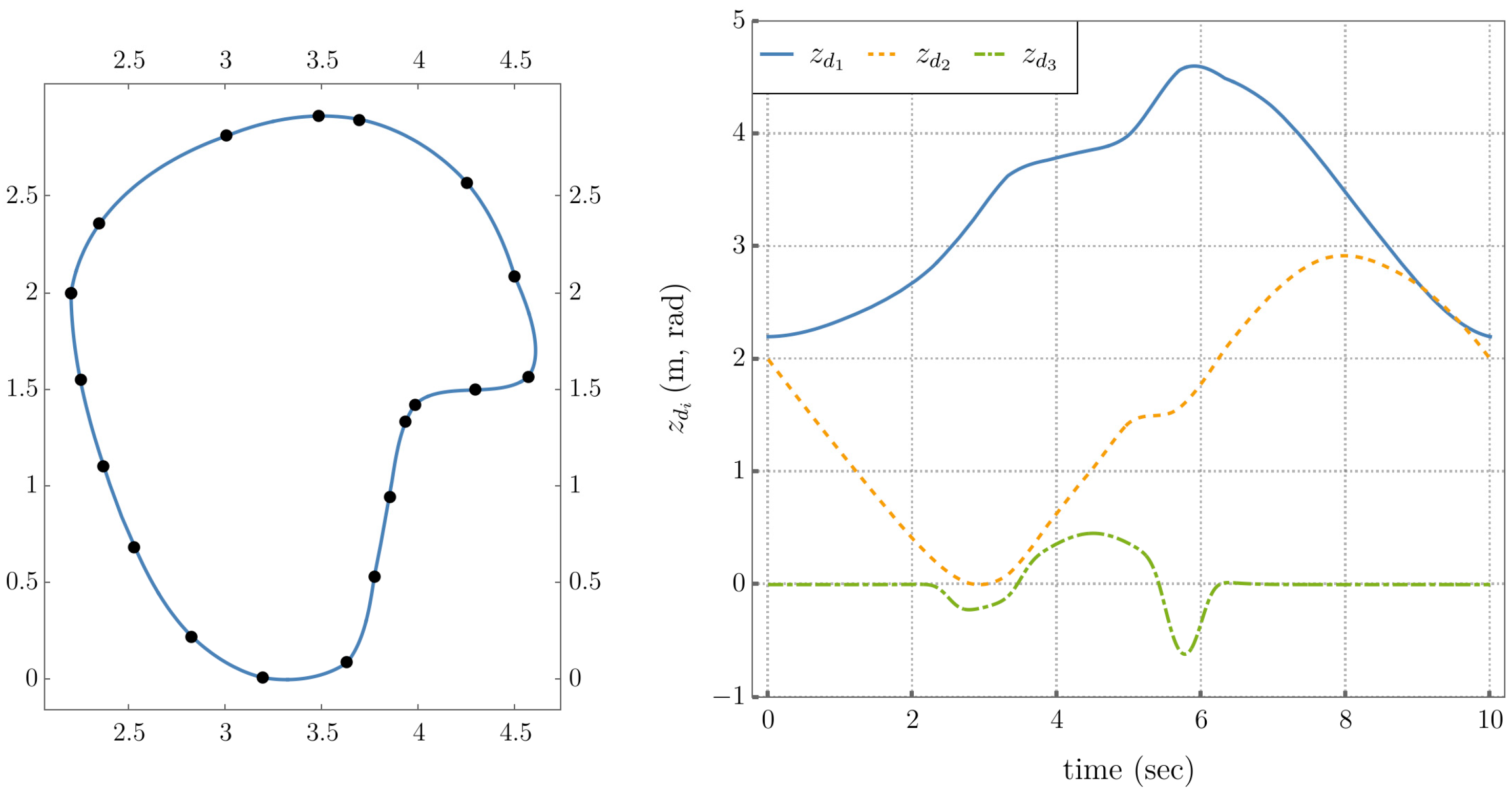
5.2. Tracking Task Trajectory with Kinetic Energy Minimization and Joint Limit Avoidance

Two operational space controllers will be compared in tracking a desired task trajectory z_d. For both traditional and extended operational space control, the initial conditions of the manipulator are as follows:

$$\begin{array}{l}\mathit{q}\mathbf{(}0\mathbf{)}={\left[\begin{array}{ccccccc}0& 2& \sqrt{5}& 0& 0.5& 1.1725& 0\end{array}\right]}^{\mathit{T}}\\ \dot{\mathit{q}}\left(0\right)={\left[\begin{array}{c}\mathit{J}\\ \mathit{\Phi }\end{array}\right]}^{+}\left[\begin{array}{c}{\dot{\mathit{x}}}_{\mathit{d}}\\ 0\end{array}\right]\end{array}$$

The desired task trajectory is shown on the left in Figure 8, with output coordinate time histories on the right.

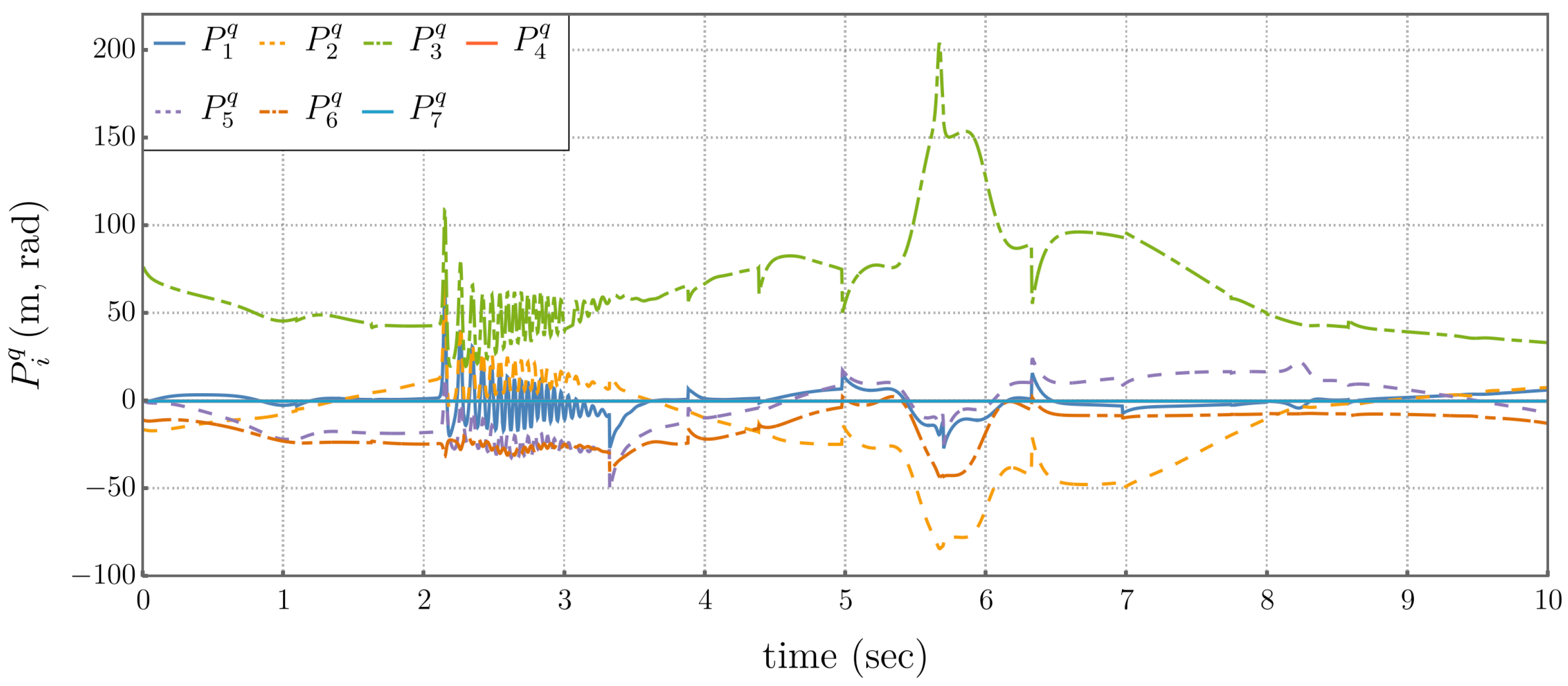
5.2.1. Traditional Operational Space Control

The multiplier form of the constrained operational space equations is restated from Equation (17) as follows:

$${\mathit{P}}^{\mathit{q}}+{\mathit{\Phi }}_{\mathit{q}}^{\mathit{T}}\mathit{\lambda }={\mathit{\Theta }}^{\mathit{T}}{\mathit{J}}^{\mathit{T}}\left({\mathit{\Gamma }}_{\mathit{c}}\ddot{\mathit{z}}+{\mathit{\mu }}_{\mathit{c}}+{\mathit{p}}_{\mathit{c}}\right)+{\mathit{\Phi }}_{\mathit{q}}^{\mathit{T}}\left(\mathit{\alpha }+\mathit{\rho }\right)+{\mathit{N}}_{\mathit{c}}^T{\mathit{P}}_{\mathit{o}}^{\mathit{q}}$$

where the terms are defined in Equations (18)–(24). These equations need to be complemented by the passivity condition on the unactuated joints [18] as follows:

$${\mathit{S}}_{\mathit{p}}{\mathit{P}}^{\mathit{q}}=0$$

where ${\mathit{S}}_{\mathit{p}}\in {\mathit{R}}^{\mathit{k}-\mathit{n}\times \mathit{k}}$ is the selection matrix that specifies the unactuated joints. For example, in this case, the following is obtained:

$${\mathit{S}}_{\mathit{p}}=\left[\begin{array}{ccccccc}0& 0& 0& 1& 0& 0& 0\\ 0& 0& 0& 0& 0& 0& 1\end{array}\right]$$

which indicates that the fourth and seventh generalized coordinates are unactuated.

The control input to the plant is then obtained as follows:

$$\left[\begin{array}{c}{\mathit{P}}^{\mathit{q}}\\ \mathit{\lambda }\end{array}\right]={\left[\begin{array}{cc}1& {\mathit{\Phi }}_{\mathit{q}}^{\mathit{T}}\\ {\mathit{S}}_{\mathit{p}}& 0\end{array}\right]}^{-1}\left[\begin{array}{c}{\mathit{\Theta }}^{\mathit{T}}{\mathit{J}}^{\mathit{T}}\left({\mathit{\Gamma }}_{\mathit{c}}{\mathit{P}}^{\ast }+{\mathit{\mu }}_{\mathit{c}}+{\mathit{p}}_{\mathit{c}}\right)+{\mathit{\Phi }}_{\mathit{q}}^{\mathit{T}}\left(\mathit{\alpha }+\mathit{\rho }\right)+{\mathit{N}}_{\mathit{c}}^T{\mathit{P}}_{\mathit{o}}^{\mathit{q}}\\ 0\end{array}\right]$$

where

$${\mathit{P}}^{\ast }=100\mathbf{(}{\mathit{z}}_d-\mathit{z}\mathbf{)}+20\mathbf{(}{\dot{\mathit{z}}}_d-\dot{\mathit{z}}\mathbf{)}+{\ddot{\mathit{z}}}_d \mathrm{and} {\mathit{P}}_{\mathit{o}}^{\mathit{q}}={\mathit{P}}^{\mathit{j}}-10{\nabla }_{\dot{\mathit{q}}}T$$

The joint limit avoidance forces ${\mathit{P}}^{\mathit{j}}$, modeled using exponential springs, are specified. These forces are filtered through the null-space projection matrix to ensure that they are dynamically decoupled from the task control. Additionally, a kinetic energy minimization term $10{\nabla }_{\mathit{q}}T$ is added.

The application of this controller generates the results shown in Figure 9, Figure 10, Figure 11 and Figure 12. Each image in Figure 9 depicts the manipulator configuration at a specific time. The high-frequency artifacts in Figure 11 and Figure 12 are due to joint limits repeatedly being hit.

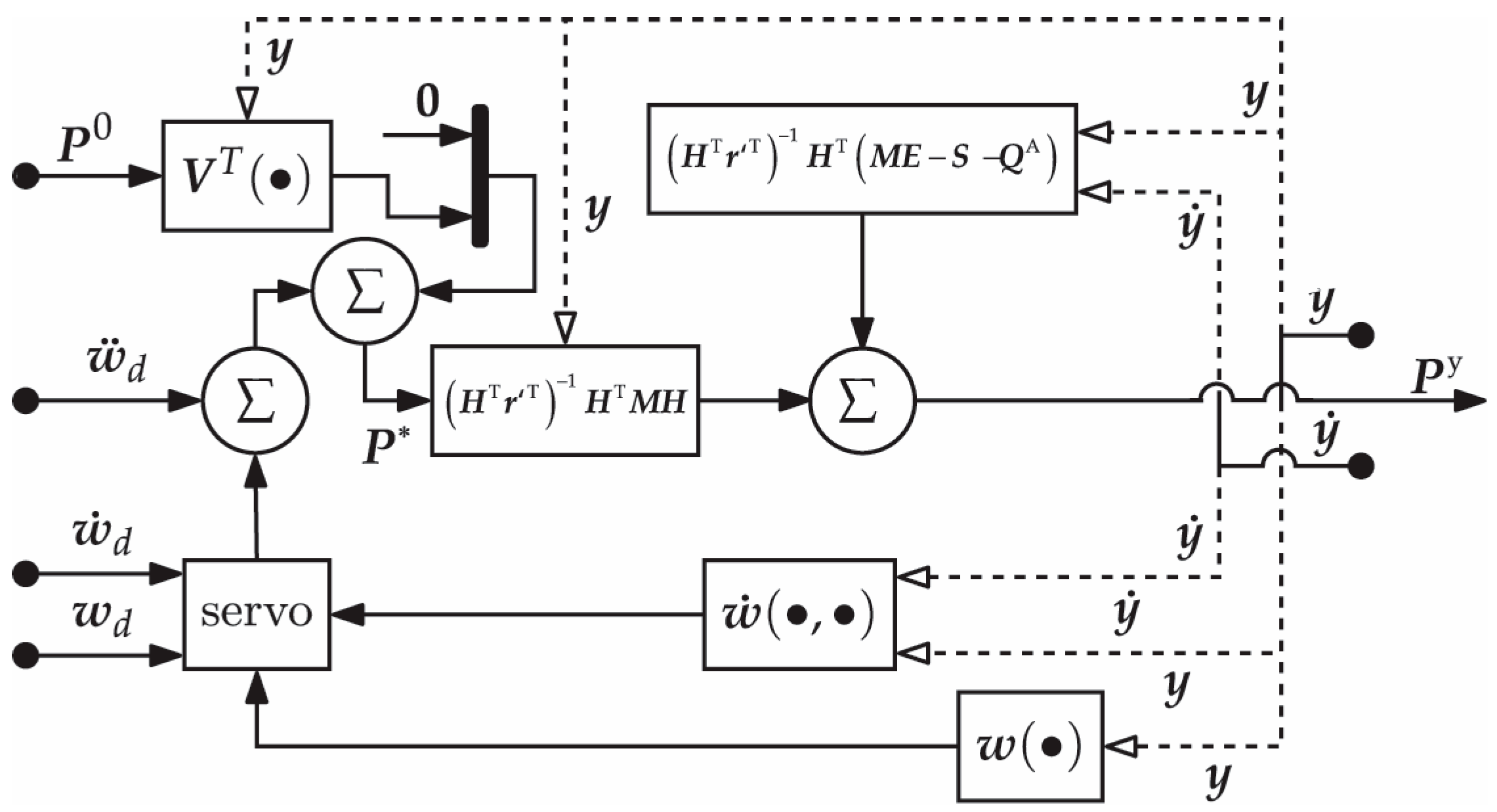
5.2.2. Extended Operational Space Control

The compound extended operational space equations are restated from Equation (62) as ${\mathit{P}}^{\mathrm{y}}={\left({\mathit{H}}^{\mathrm{T}}{{\mathit{r}}^{\prime }}^{\mathrm{T}}\right)}^{-1}{\mathit{H}}^{\mathrm{T}}\mathit{M}\mathit{H}\ddot{\mathit{w}}+{\left({\mathit{H}}^{\mathrm{T}}{{\mathit{r}}^{\prime }}^{\mathrm{T}}\right)}^{-1}{\mathit{H}}^{\mathrm{T}}\left(\mathit{M}\mathit{E}-\mathit{S}-{\mathit{Q}}^{\mathrm{A}}\right)$. The control input to the plant is then obtained as follows:

$${\mathit{P}}^{\mathrm{y}}={\left({\mathit{H}}^{\mathrm{T}}{{\mathit{r}}^{\prime }}^{\mathrm{T}}\right)}^{-1}{\mathit{H}}^{\mathrm{T}}\mathit{M}\mathit{H}{\mathit{P}}^{*}+{\left({\mathit{H}}^{\mathrm{T}}{{\mathit{r}}^{\prime }}^{\mathrm{T}}\right)}^{-1}{\mathit{H}}^{\mathrm{T}}\left(\mathit{M}\mathit{E}-\mathit{S}-{\mathit{Q}}^{\mathrm{A}}\right)$$

where

$${\mathit{P}}^{\ast }=\left[\begin{array}{c}100\mathbf{(}{\mathit{z}}_d-\mathit{z}\mathbf{)}+20\mathbf{(}{\dot{\mathit{z}}}_d-\dot{\mathit{z}}\mathbf{)}+{\ddot{\mathit{z}}}_d\\ {\mathit{V}}^{\mathit{T}}\mathbf{(}{\mathit{P}}^{\mathit{j}}-10{\nabla }_{\dot{\mathit{q}}}T\mathbf{)}\end{array}\right]$$

The same joint limit avoidance forces and kinetic energy minimization forces are applied as in the previous example. This extended operational space control algorithm is presented in the block diagram of Figure 13. An analysis showing that the real-time implementation of this algorithm can be achieved on modern microprocessors is presented in [8].

The application of this controller has led to the results shown in Figure 14, Figure 15 and Figure 16, indicating that high-frequency artifacts are not present (or are significantly reduced).

Given that the assembly is driven by a human operator, it is assumed the operator would not control the actuators directly but would rather specify a task motion. Thus, the bucket would follow a trajectory prescribed by the operator and controlled with the redundant motion being resolved naturally. The system could theoretically operate completely autonomously without the need for a human operator, in which case task motion would be prescribed based on the knowledge of some objective. Redundant motion would be resolved naturally or could be directly prescribed based on the objective.

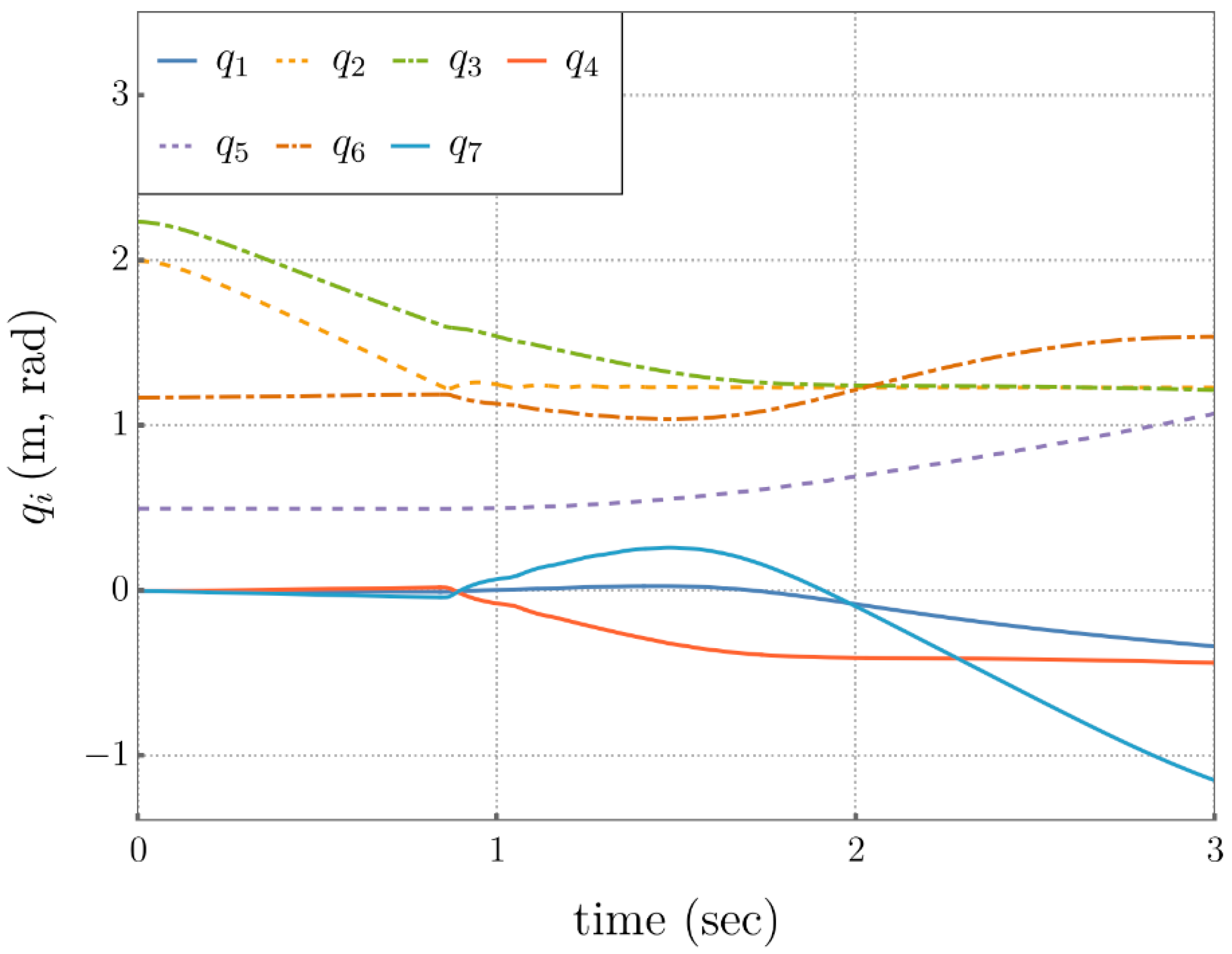
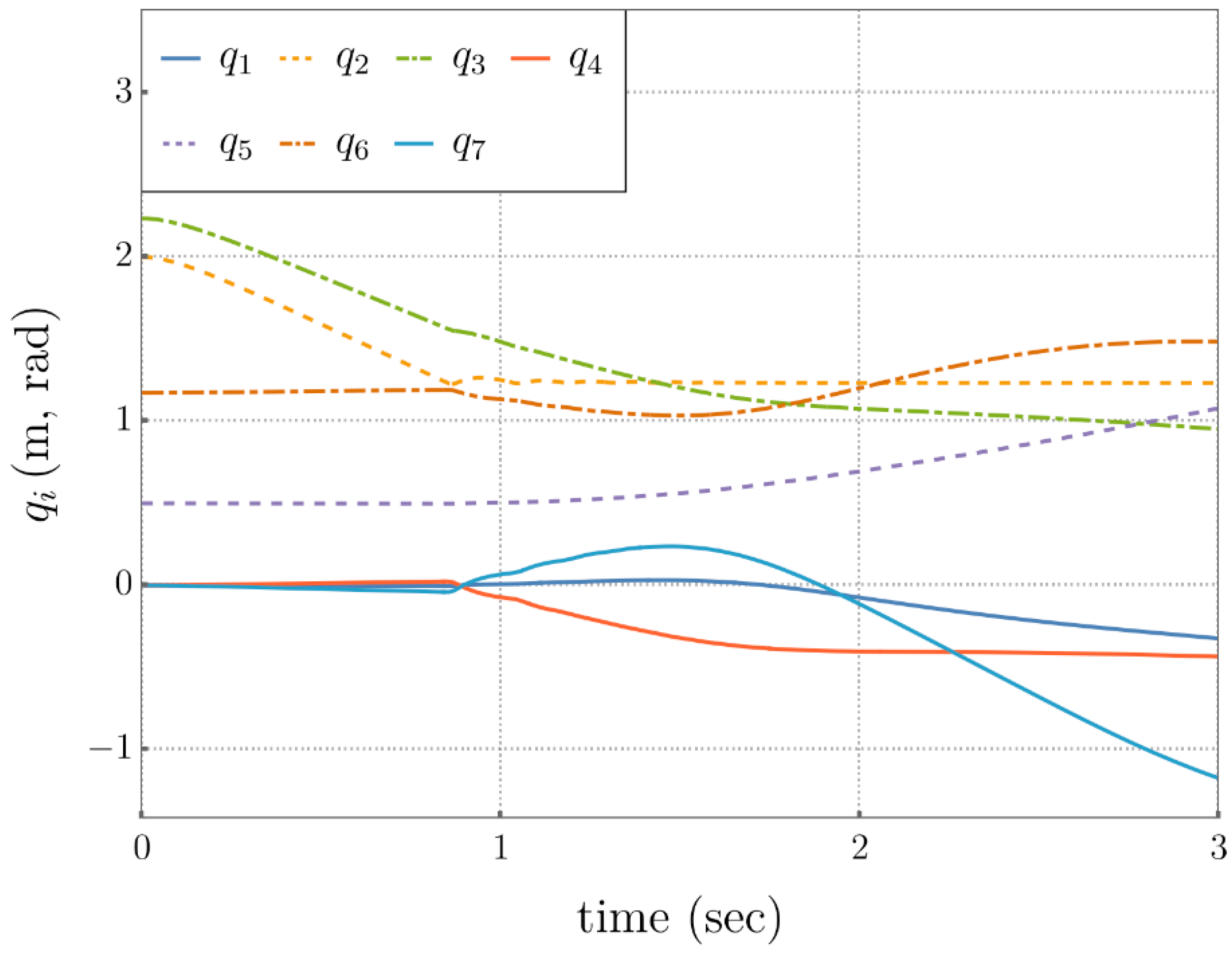
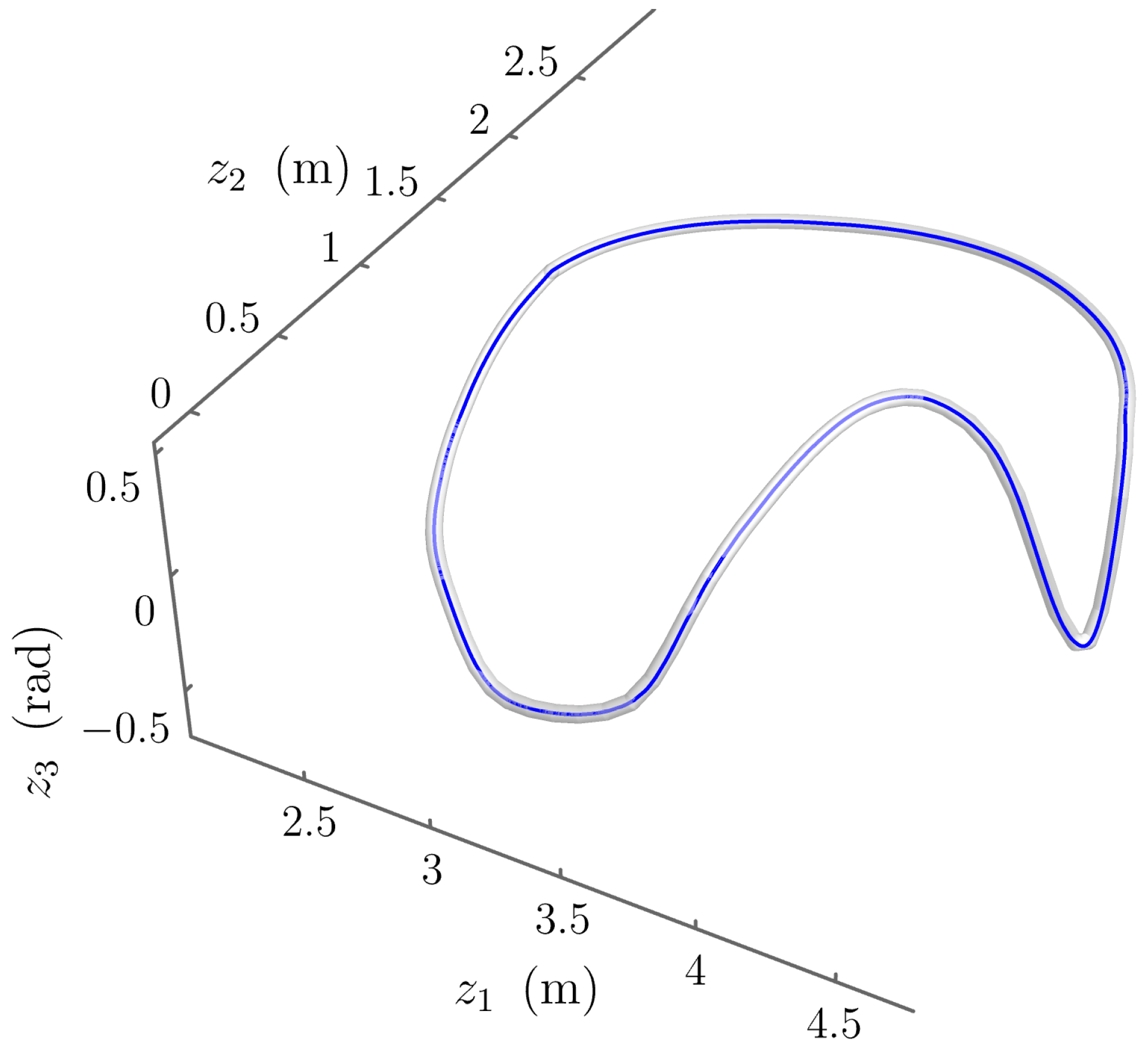
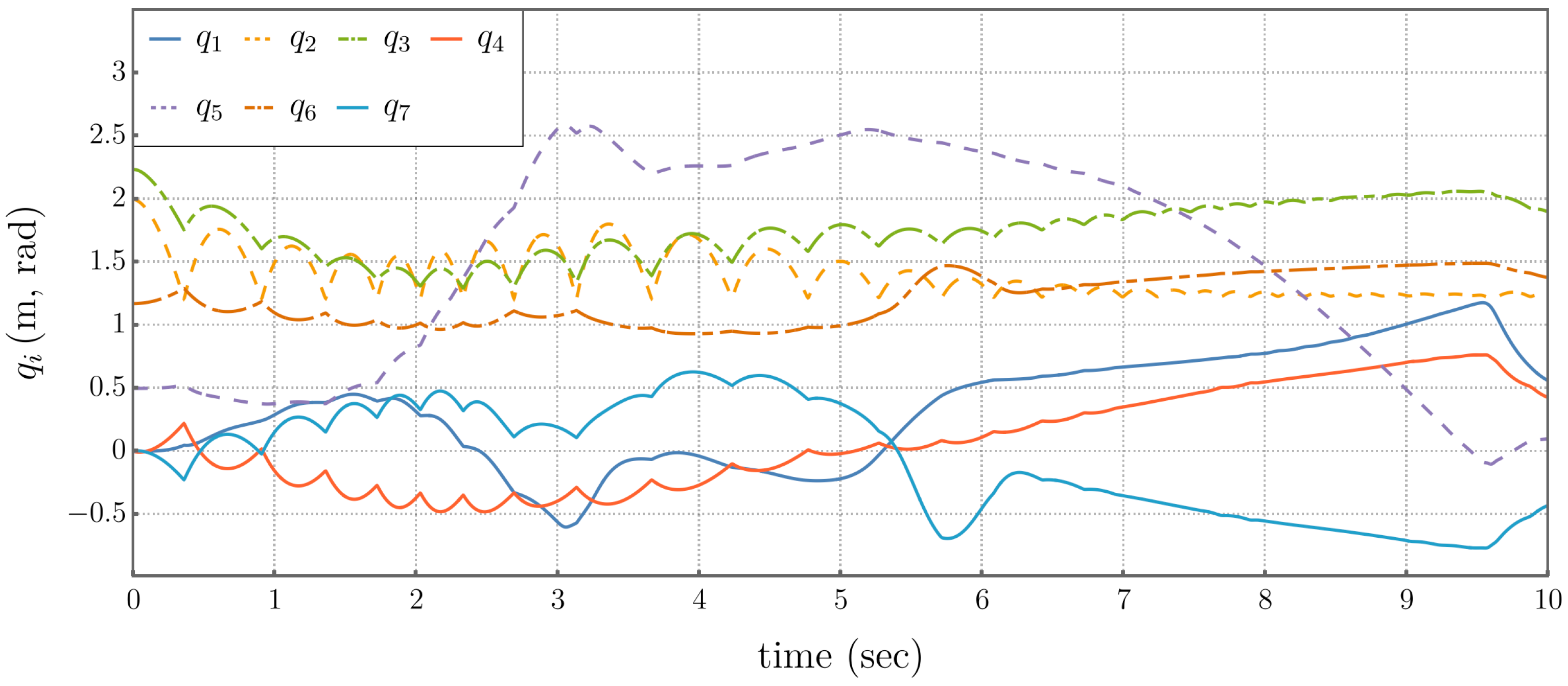
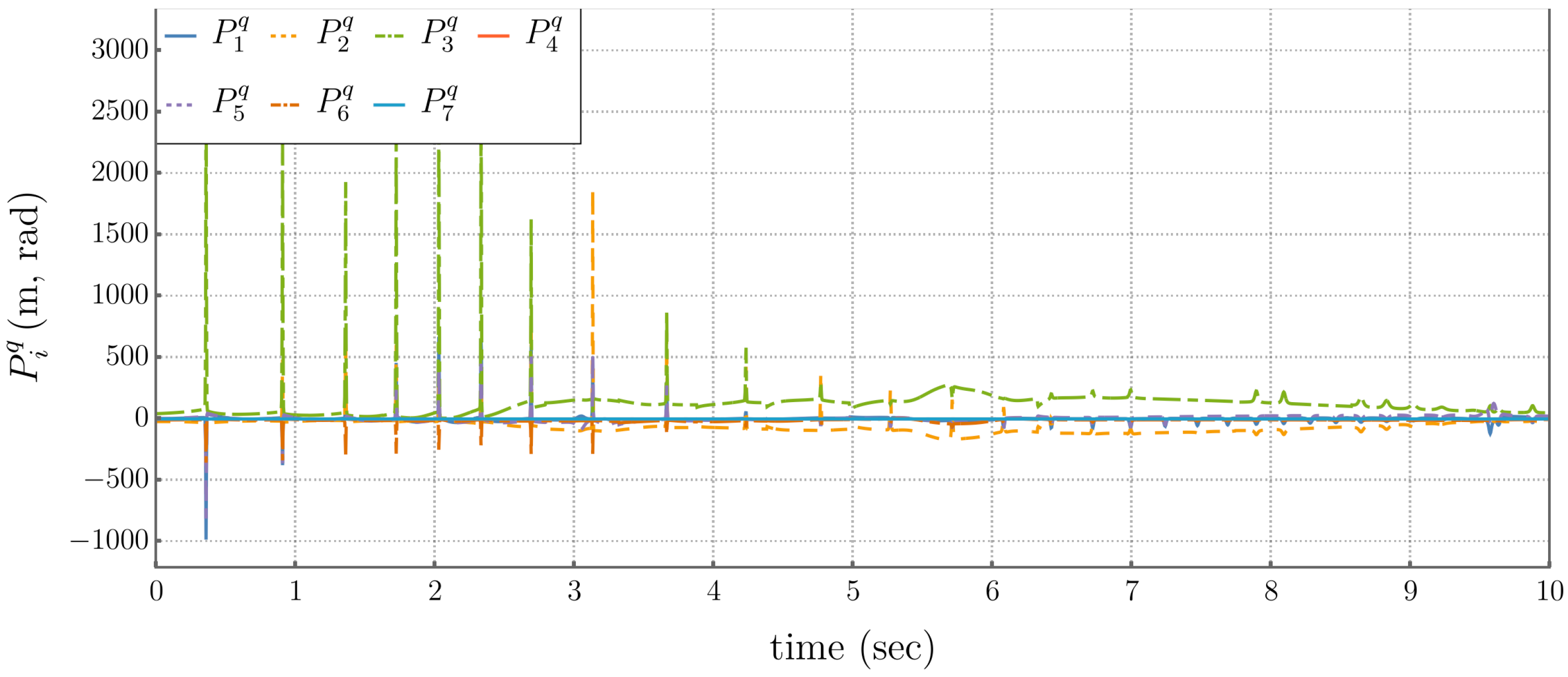
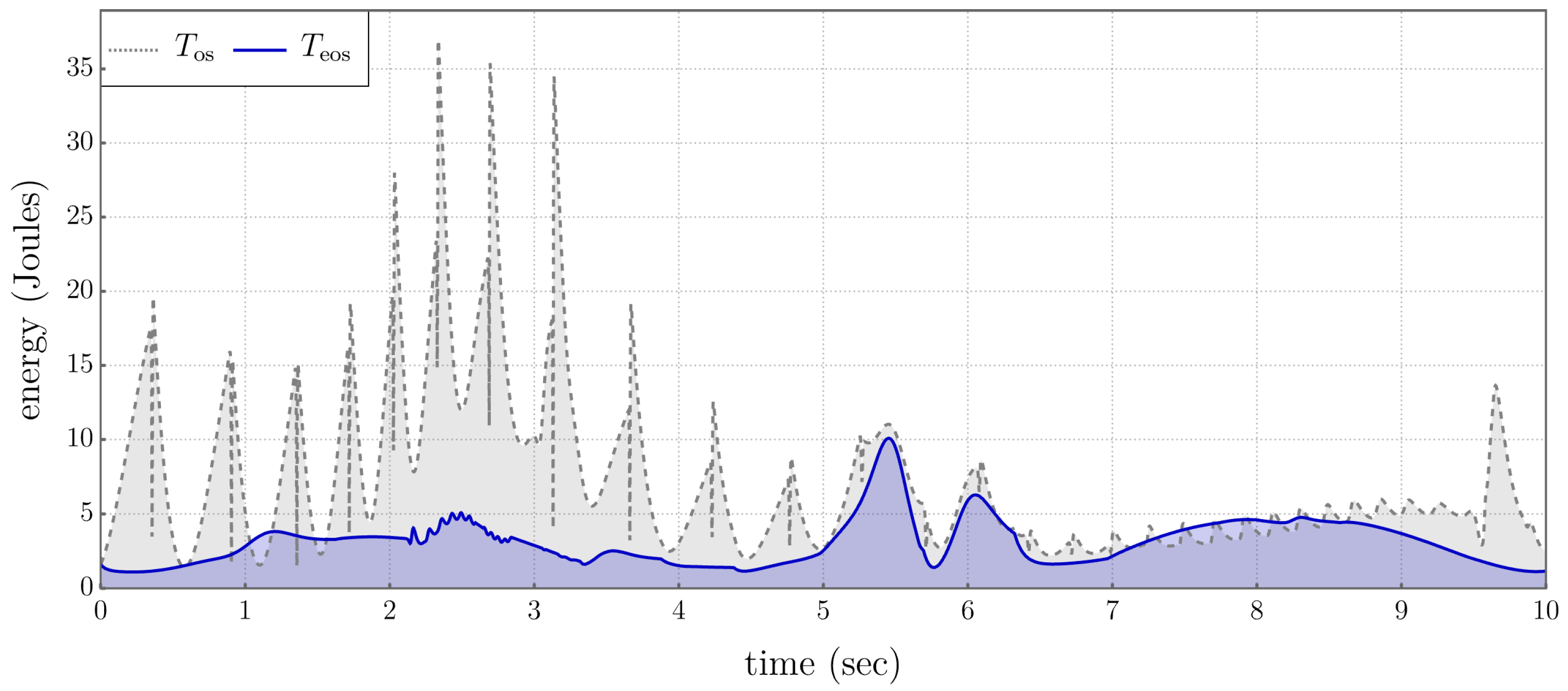
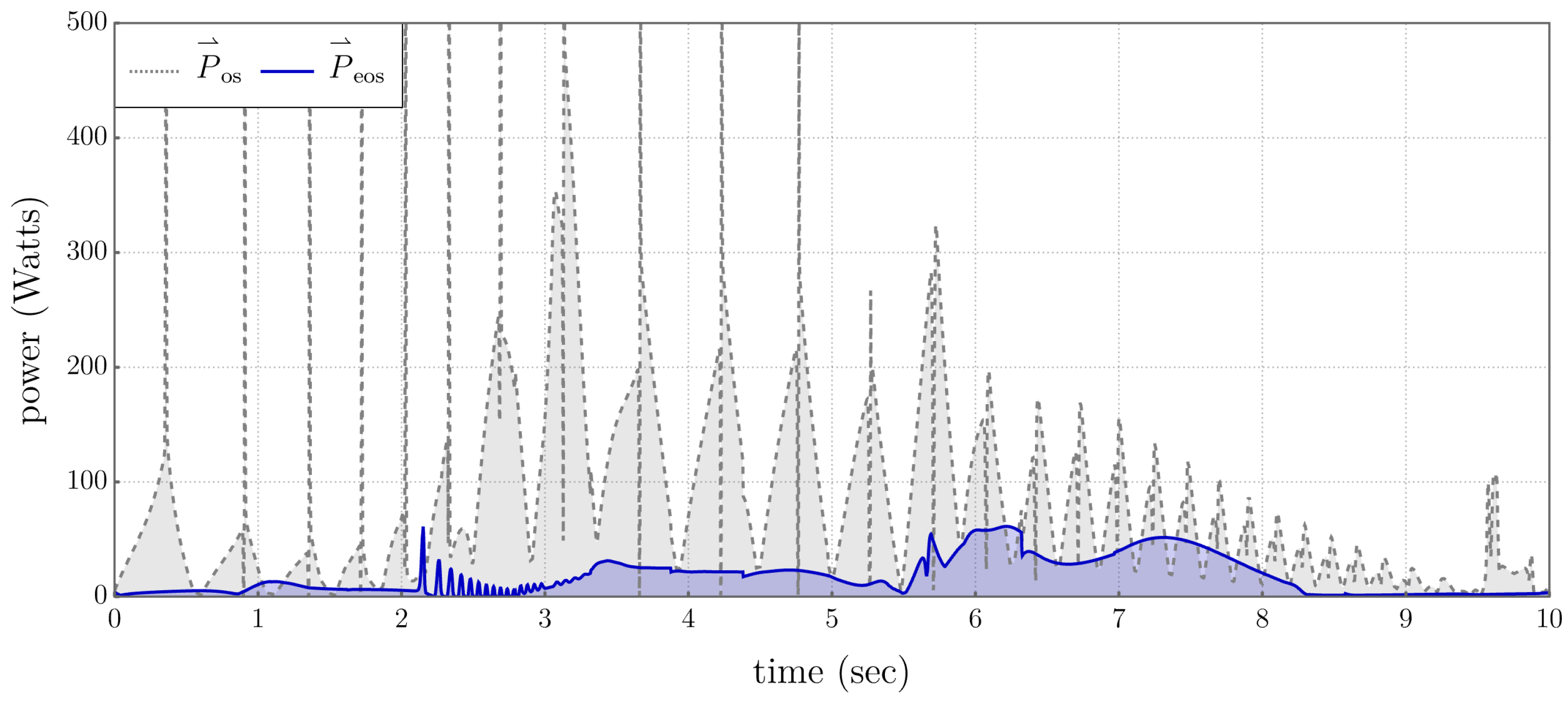
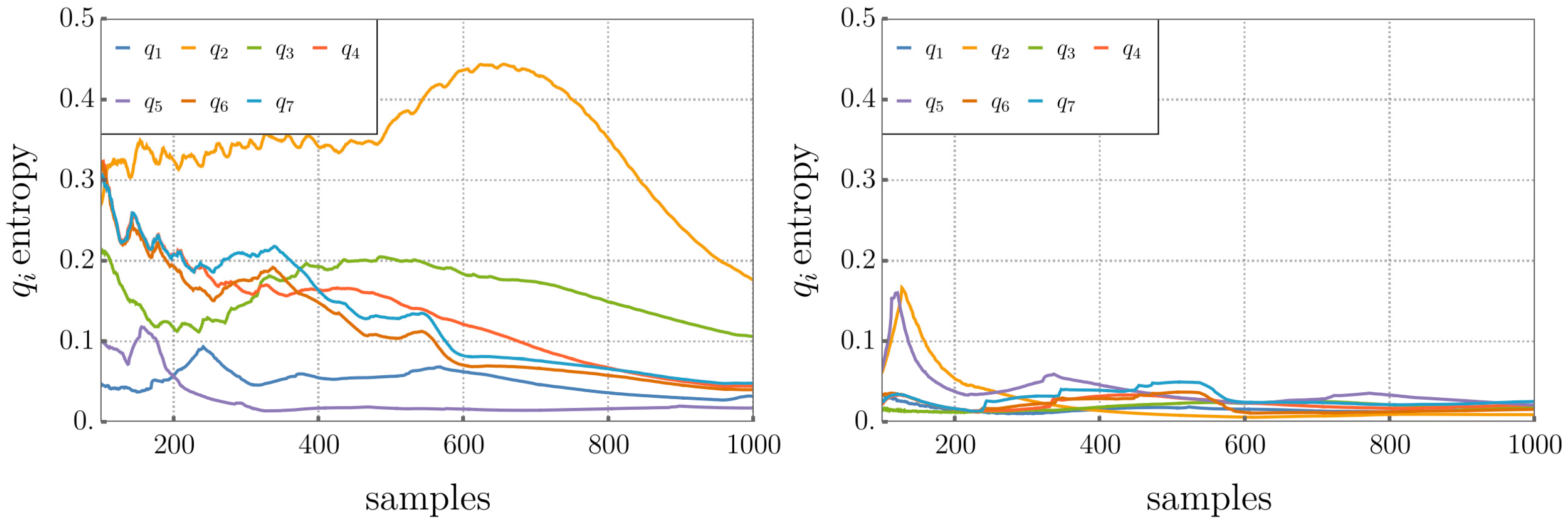
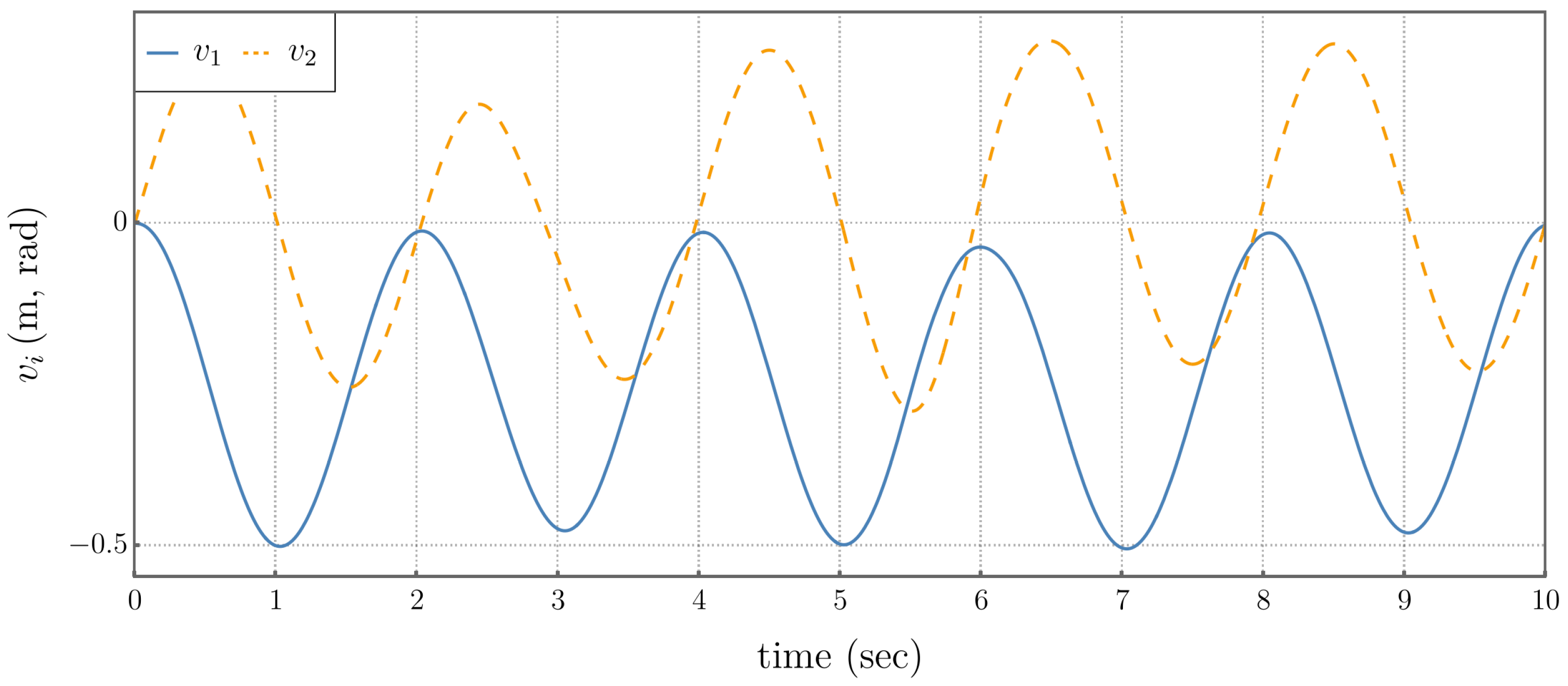
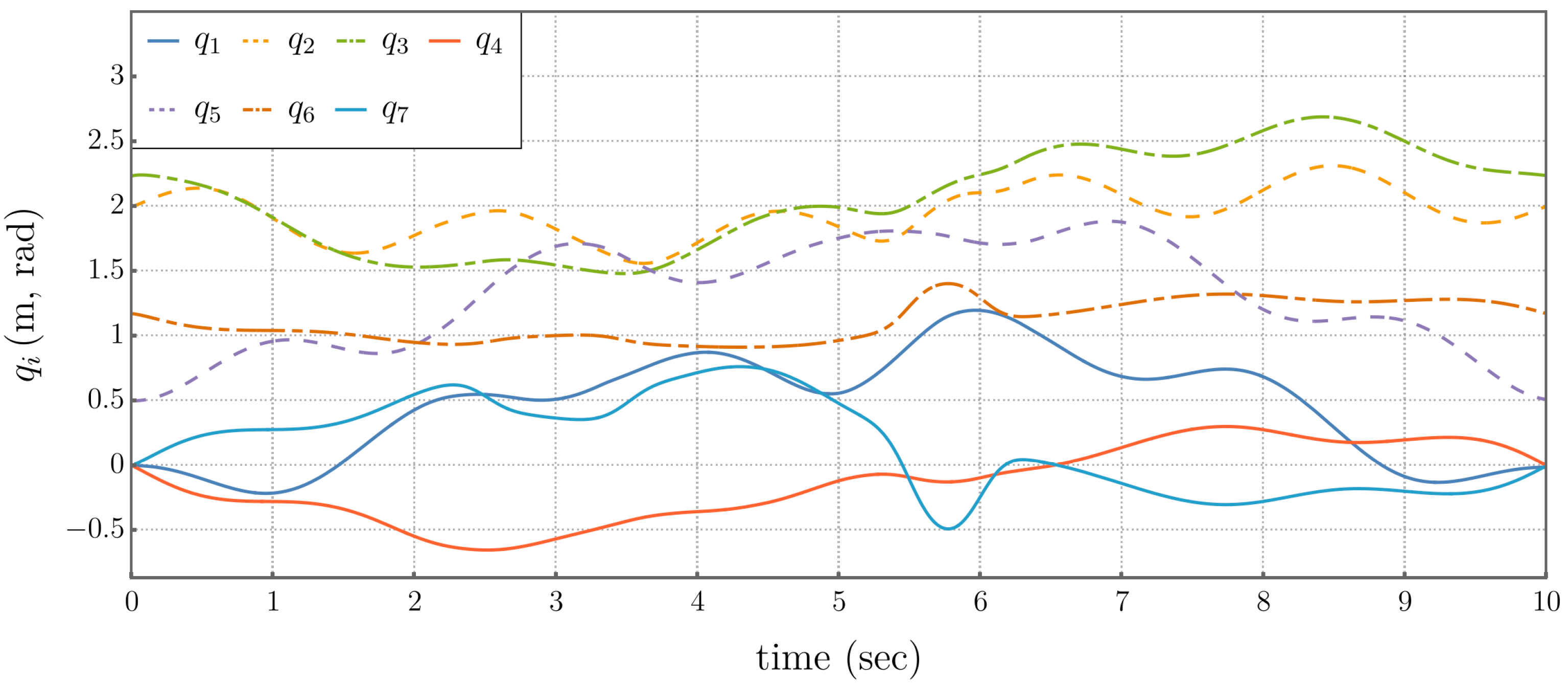
5.3. Comparison of Performance Metrics

A number of performance metrics have been implemented to establish an objective comparison between the extended operational space control formulation presented herein and the traditional operational space control approaches [35,36]. These metrics include the kinetic energy, defined as follows:

$$\mathit{T}={\displaystyle \frac{1}{2}}{\dot{\mathit{q}}}^{\mathit{T}}\mathit{M}\dot{\mathit{q}}\hspace{0.17em}$$

and plotted in Figure 17, showing a significantly greater system kinetic energy $T_{\mathit{os}}$ throughout the entire time history in the traditional operational space controller, compared to the small stored kinetic energy $T_{\mathit{eos}}$ in the extended operational space controller.

The power is the product of input space force and input space velocity. If this product is positive, the flow of power is from the actuator to the joint, and from the joint to the actuator if the product is negative. If the actuator is perfectly regenerative, then all power flowing to it from the joint is recovered. Actuators that are not regenerative will be considered, in which case, the power is given by the following:

$$\stackrel{\rightharpoonup }{P}=\hspace{0.17em}{\displaystyle \sum _{i=1}^{\mathit{n}}\mathit{Ramp}\mathbf{(}{\mathit{P}}_{\mathit{i}}^{\mathit{q}}{\dot{q}}_i\mathbf{)}}\hspace{0.17em} \mathrm{where} \mathit{Ramp}\mathbf{(}\mathit{x}\mathbf{)}=\left\{\begin{array}{c}\mathit{x} \mathrm{if} \mathit{x}>0\\ 0 \mathrm{if} \mathit{x}\le 0\end{array}\right.$$

The plot of Figure 18 shows the significantly greater level of system power ${\overline{P}}_{\mathit{os}}$ generated by the actuators throughout the entire time history in the traditional operational space controller, compared with the lower level of power ${\overline{P}}_{\mathit{eos}}$ in the extended operational space controller.

Sample entropy is a measure of complexity [35,36]. It is used here to characterize the disorder of the internal motion of the manipulator under different control approaches. Given a continuous time series $\mathit{x}\mathbf{(}\mathit{t}\mathbf{)}$ over the interval $[0,{\mathit{t}}_{\mathit{f}}]$, the discrete time series is defined as follows:

$${\mathit{X}}^{\mathit{N}}=\left.\left\{\mathit{x}\mathbf{(}{\mathit{t}}_{\mathit{f}}\mathbf{/}\mathit{N}\mathbf{)}\mathbf{,}\mathit{x}\mathbf{(}\mathbf{2}{\mathit{t}}_{\mathit{f}}\mathbf{/}\mathit{N}\mathbf{)}\mathbf{,}\mathbf{\dots }\mathbf{,}\mathit{x}\mathbf{(}{\mathit{t}}_{\mathit{f}}\mathbf{)}\right.\right\}$$

where $\mathit{N}$ is the number of time samples. The sample entropy is given by the numerical procedure $\mathit{SampEn}\mathbf{(}\mathit{m}\mathbf{,}\mathit{r}\mathbf{,}{\mathit{X}}^{\mathit{N}}\mathbf{)}$, where $\mathit{m}$ is the embedding dimension that is usually taken to be equal to two. The term $\mathit{r}$ is the tolerance, usually taken to be equal to $0.2\mathit{\sigma }$, where $\mathit{\sigma }$ is the standard deviation of the time series samples. The cumulative entropy of the time series is as follows:

$$\left\{\mathit{SampEn}\mathbf{(}\mathit{m},\mathit{r},{\mathit{X}}^{\mathit{N}}\mathbf{(}1\mathbf{)},\mathit{SampEn}\mathbf{(}\mathit{m},\mathit{r},{\mathit{X}}^{\mathit{N}}\mathbf{(}1,\dots ,2\mathbf{)},\mathit{SampEn}\mathbf{(}\mathit{m},\mathit{r},{\mathit{X}}^{\mathit{N}}\mathbf{(}1,\dots ,\mathit{N}\mathbf{)}\right\}$$

For the input space time series ${\mathit{q}}_i\mathbf{(}\mathit{t}\mathbf{)}$, the following is obtained:

$$\begin{array}{l}\left\{\mathit{SampEn}\mathbf{(}\mathit{m},\mathit{r},{\mathit{Q}}_{\mathit{i}}^{\mathit{N}}\mathbf{(}1\mathbf{)},\mathit{SampEn}\mathbf{(}\mathit{m},\mathit{r},{\mathit{Q}}_{\mathit{i}}^{\mathit{N}}\mathbf{(}1,\dots ,2),\mathit{SampEn}\mathbf{(}\mathit{m},\mathit{r},{\mathit{Q}}_{\mathit{i}}^{\mathit{N}}\mathbf{(}1,\dots ,\mathit{N})\right\}\\ \mathrm{for} \mathit{i}=1,2,\dots ,7\end{array}$$

As shown in Figure 19, a higher general level of entropy, reflecting greater disorder, occurs in the traditional operational space controller (left) compared to the lower level of entropy in the extended operational space controller (right).

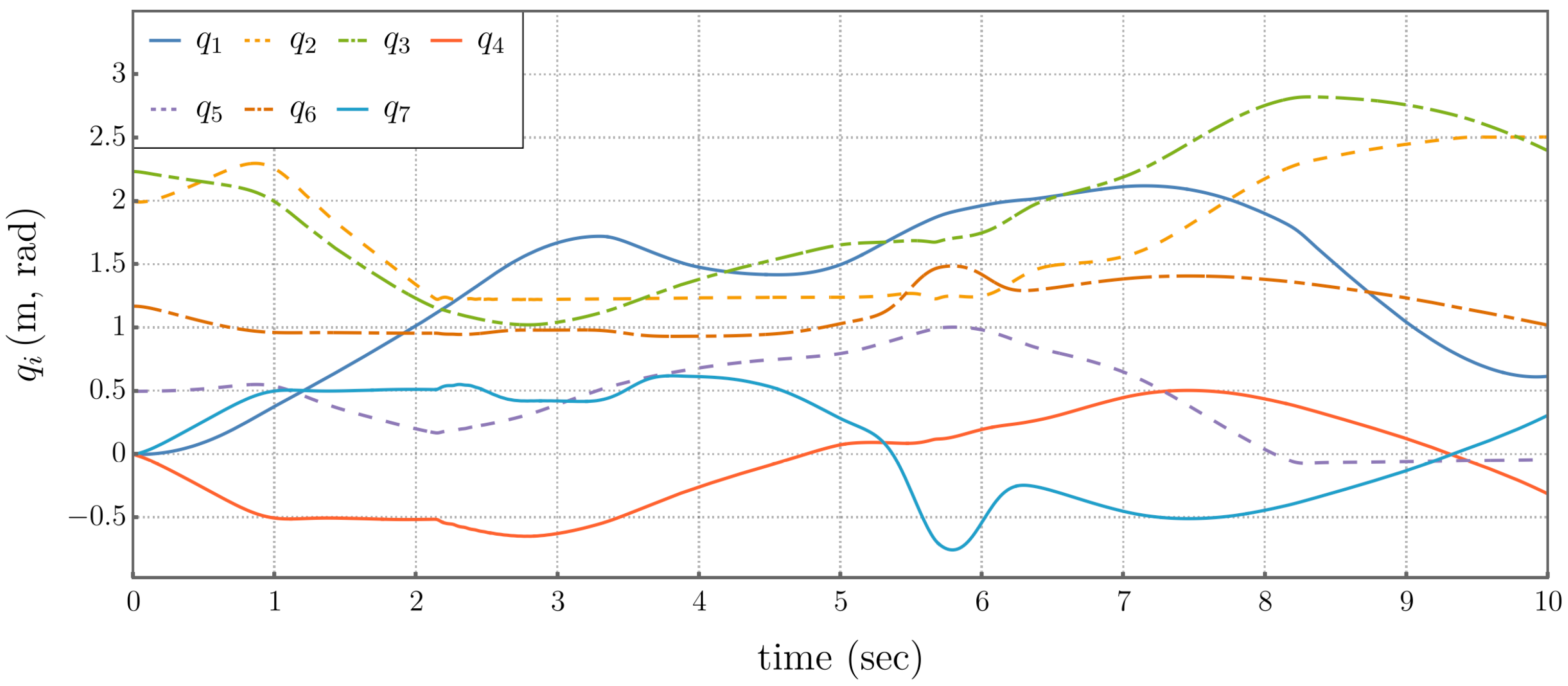
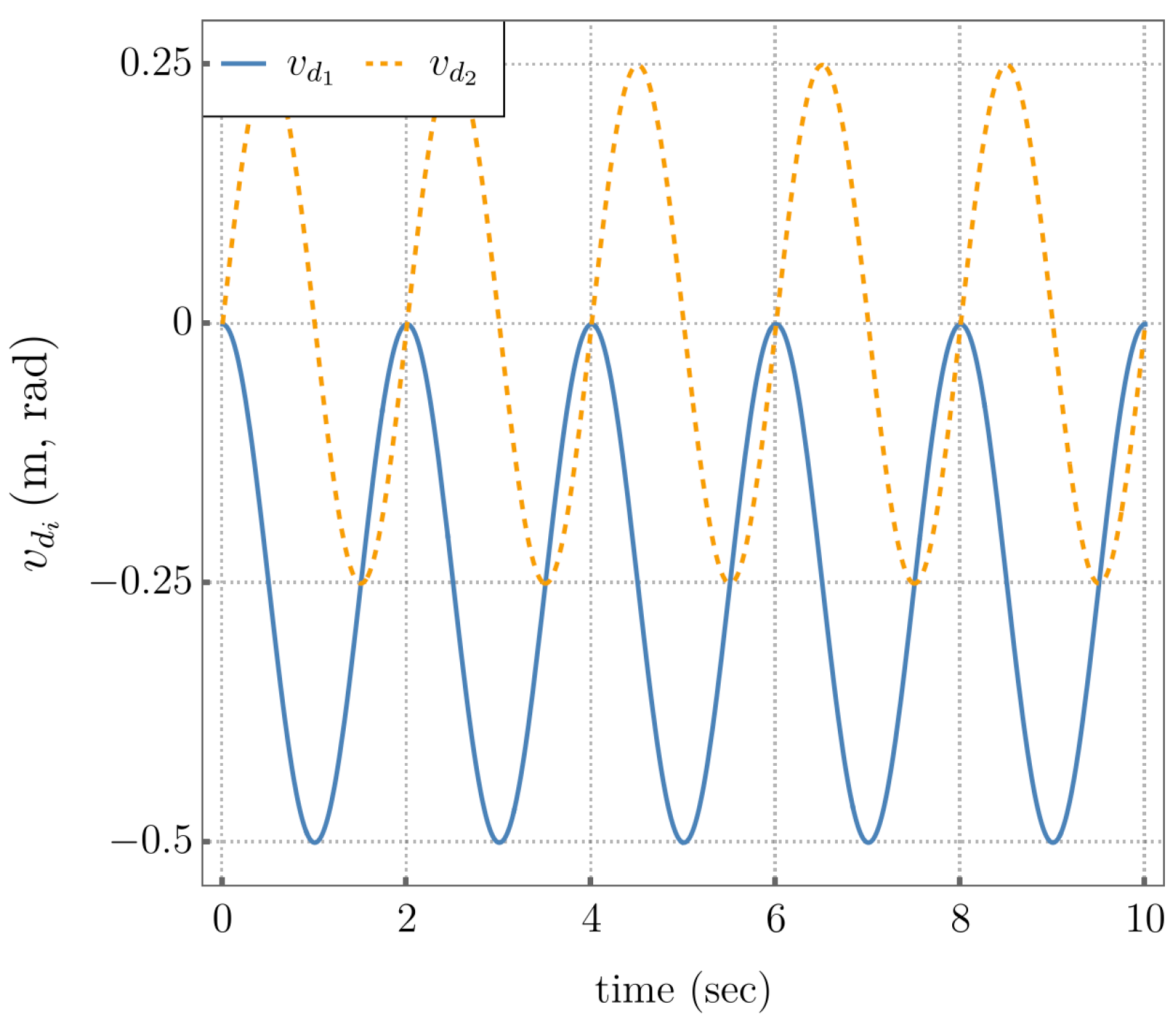
5.4. Self-Motion Coordinate Tracking

Next, self-motion coordinate tracking, in addition to task coordinate tracking, is demonstrated. The reference trajectories used are shown in Figure 20. Note that these are used only for extended operational space control, since traditional operational space control does not allow for the control of self-motion coordinates. The initial conditions are $\mathit{q}\mathbf{(}0\mathbf{)}={\left[\begin{array}{ccccccc}0& 2& \sqrt{5}& 0& 0.5& 1.1725& 0\end{array}\right]}^{\mathit{T}}$ and $\dot{\mathit{q}}\left(0\right)=-\mathit{U}{\mathbf{(}{\mathit{\Lambda }}_{\mathit{q}}\mathit{U}\mathbf{)}}^{-1}{\mathit{\Lambda }}_{\mathit{z}}{\mathit{z}}_{\mathit{d}}+\mathbf{(}{1}_7-\mathit{U}{\mathbf{(}{\mathit{\Lambda }}_{\mathit{q}}\mathit{U}\mathbf{)}}^{-1}{\mathit{\Lambda }}_{\mathit{q}}\mathit{V}{\dot{\mathit{v}}}_{\mathit{d}}$.

The compound extended operational space equations are restated from Equation (62) as ${\mathit{P}}^{\mathrm{y}}={\left({\mathit{H}}^{\mathrm{T}}{{\mathit{r}}^{\prime }}^{\mathrm{T}}\right)}^{-1}{\mathit{H}}^{\mathrm{T}}\mathit{M}\mathit{H}\ddot{\mathit{w}}+{\left({\mathit{H}}^{\mathrm{T}}{{\mathit{r}}^{\prime }}^{\mathrm{T}}\right)}^{-1}{\mathit{H}}^{\mathrm{T}}\left(\mathit{M}\mathit{E}-\mathit{S}-{\mathit{Q}}^{\mathrm{A}}\right)$. The control input to the plant is then ${\mathit{P}}^{\mathrm{y}}={\left({\mathit{H}}^{\mathrm{T}}{{\mathit{r}}^{\prime }}^{\mathrm{T}}\right)}^{-1}{\mathit{H}}^{\mathrm{T}}\mathit{M}\mathit{H}{\mathit{P}}^{\ast }+{\left({\mathit{H}}^{\mathrm{T}}{{\mathit{r}}^{\prime }}^{\mathrm{T}}\right)}^{-1}{\mathit{H}}^{\mathrm{T}}\left(\mathit{M}\mathit{E}-\mathit{S}-{\mathit{Q}}^{\mathrm{A}}\right)$, where ${\mathit{P}}^{\ast }=\left[\begin{array}{c}100\mathbf{(}{\mathit{z}}_d-\mathit{z}\mathbf{)}+20\mathbf{(}{\dot{\mathit{z}}}_d-\dot{\mathit{z}}\mathbf{)}+{\ddot{\mathit{z}}}_d\\ 100\mathbf{(}{\mathit{v}}_d-\mathit{v}\mathbf{)}+20\mathbf{(}{\dot{\mathit{v}}}_d-\dot{\mathit{v}}\mathbf{)}+{\ddot{\mathit{v}}}_d+{\mathit{V}}^{\mathit{T}}\mathbf{(}{\mathit{P}}^{\mathit{j}}-10{\nabla }_{\dot{\mathit{q}}}T\mathbf{)}\end{array}\right]$.

The same joint limit avoidance forces and kinetic energy minimization forces are applied as in the previous example. The application of this controller has led to the results shown in Figure 21, Figure 22, Figure 23 and Figure 24, indicating the tracking of the self-motion coordinates.

6. Summary and Conclusions

The results from the previous sections have demonstrated the effectiveness of the extended operational space control formulation in tracking both self-motion and task coordinates. Additionally, the gradient minimization of kinetic energy has been demonstrated. Most importantly, in the absence of the direct specification of self-motion coordinates, the extended operational formulation achieved lower levels of kinetic energy, power consumption, and sample entropy than the traditional operational space formulation.

It is important to note that a dynamically consistent generalized inverse of the task Jacobian for a serial manipulator is defined [3,18] to minimize the kinetic energy of the solution of the velocity kinematic equation. In fact, the dynamically consistent inverse has the property of yielding the least velocity norm solution. The mass-weighted inverse solution of the velocity equation is precisely the lowest kinetic energy (analogous to the lowest norm). Despite this property of the dynamically consistent inverse, it can be seen in Figure 17 that control based on dynamic consistency does not produce minimal kinetic energy over a time series, for either serial or compound manipulators. As discussed in [9] for serial manipulators, it should not be expected to do so, since the kinetic energy property that it satisfies is an instantaneous one that is dependent upon the specific configuration.

Future investigations should establish global properties for the extended operational control formulation, based on the analysis of the differential geometry of self-motion manifolds. For example, Hertz’s principle of least curvature [33] reveals that under certain conditions, motion on the constraint manifold is restricted to geodesic (the most straight) paths. Without the specification of explicit control for the self-motion space, the manner in which the extended operational space approach implicitly controls self-motion is worthy of future investigation.