Robust Optimization and Workspace Enhancement of a Reconfigurable Delta Robot via a Singularity-Sensitive Index

Abstract

This study investigates the kinematic behavior of a reconfigurable Delta parallel robot aiming to enhance its performance in real industrial applications such as high-speed packaging, precision pick-and-place operations, automated inspection, and lightweight assembly tasks. While Delta robots are widely recognized for their speed and accuracy, their practical use is often limited by workspace constraints and singularities that compromise motion stability and control safety. Through a detailed analysis, it is shown that classical Jacobian-based performance indices are unsuitable for resolving the redundancy introduced by geometric reconfiguration, as they may lead the system toward singular or ill-conditioned configurations. To overcome these limitations, this work introduces an adjustable singularity-sensitive performance index designed to penalize extreme velocity and force singular values and enables tuning between velocity and force performance. Simulation results demonstrate that optimizing the reconfiguration parameter using this index increases the usable workspace by approximately 82% and improves the uniformity of manipulability across the workspace. These findings suggest that the proposed approach provides a robust framework for enhancing the operational range and kinematic safety of reconfigurable Delta robots, while remaining adaptable to different design priorities.

1. Introduction

Despite the recent surge in popularity of parallel robots for their ease of construction, lightweight design, and capability to achieve high velocities and accelerations in applications such as packaging, a potential drawback lies in their low cost-efficiency [1,2,3]. The complex kinematics and expensive control systems, coupled with a limited workspace relative to their size, contribute to this issue. However, their inherent strengths suggest potential for design optimization to minimize these drawbacks and improve efficiency. In particular, reconfigurable designs offer a promising solution to address challenges such as limited workspaces [2,4,5] while improving performance, thus extending the range of practical applications for parallel robots [6,7]. Reconfiguration of parallel robots can involve changes in the geometrical parameters of the arms, the orientation of the kinematic chains, or the position of the mobile platform relative to the fixed base. These changes can be made manually or automatically by employing intelligent control systems. The implementation of a reconfigurable robot in which the reconfiguration is executed by a mechanical system controllable during operation makes the robot redundant and requires an even more sophisticated control strategy [8,9]. Redundancy in parallel robots offers several advantages, such as an increased workspace, avoidance of or reduction in singularities, greater payload capacity, improved mechanism dynamics, and elimination of backlash [10,11,12,13,14]. However, these benefits come at the cost of higher kinematic and dynamic model complexity, challenges in control design, and increased energy consumption due to additional actuators and internal forces/torques [15]. Moreover, extra actuators also contribute to higher costs and friction losses in the active joints. There are several types of redundancy in parallel robots, the most significant being kinematic redundancy and actuator redundancy [16,17,18]. Kinematic redundancy consists of the addition of active joints to the kinematic chains, resulting in an infinite number of joint velocity combinations that produce the same end-effector motion. In contrast, actuator redundancy consists of having more kinematic chains than are needed to connect the fixed and mobile platforms. The analysis of singular configurations is a fundamental aspect of the kinematic analysis of parallel robots. In such configurations, the end-effector of the mechanism instantly gains or loses degrees of freedom. This implies that the end-effector loses the ability to generate motion in certain directions or may exhibit infinitesimal uncontrolled movements even when the actuators are locked [19,20,21]. The most common approach for singularity analysis involves the robot’s Jacobian matrix, which relates joint velocities to the Cartesian velocities of the end-effector. In [22], a general framework for the analysis of singularities in closed-loop kinematic chains was established, along with a classification scheme for three main types of singular configurations.

In this work, we analyze the effect of implementing a reconfiguration strategy in a Delta-type parallel robot by comparing the original non-reconfigurable architecture with its reconfigurable counterpart, focusing on differences in workspace volume, singularities, and kinematic performance. To this end, a singularity-sensitive performance index is proposed. This new index is designed to penalize extreme velocity and force singular values and should allow for careful tuning between velocity and force performance. Finally, this work also presents simulation results which demonstrate that optimization under this index increases the usable workspace of the robot by approximately 82% while improving manipulability across the workspace.

This article is organized as follows: Section 2 describes the reconfigurable Delta robot, including its kinematic and inverse geometric models. Section 3 presents the traditional performance indices based on the Jacobian matrix. Section 4 provides an analysis of the robot’s singular configurations. Section 5 addresses the kinematic redundancy problem, demonstrates the inadequacy of traditional indices, and proposes a novel singularity-sensitive index. Section 6 presents a quantitative comparison of the kinematic performance, including workspace volume and manipulability, between the reconfigurable robot using the new index and its non-reconfigurable counterpart. Finally, Section 7 summarizes the conclusions of this work.

2. Reconfigurable Delta Robot

Consider the Delta robot shown in Figure 1, which consists of two platforms, one fixed and one moving, connected by three identical kinematic chains (indexed by $i=1,2,3$ throughout this document) and uniformly distributed around the vertical axis $Z_0$ of the fixed platform.

In the standard configuration, the fixed platform is at the top of the mechanism (horizontal element), and the moving platform (where the end-effector is attached) is a smaller horizontal element located at the bottom of the mechanism. Four reference frames are defined: the global fixed frame $\{X_0,Y_0,Z_0\}$ and three local frames $\{X_i,Y_i,Z_i\}$, each associated with one kinematic chain. The origins of all frames and the Z axes are coincident, while each $X_i$ axis points from the center of the fixed platform towards the first joint of the i-th kinematic chain. The $X_i$ axes are placed at constant angles ${\alpha }_i$ with respect to $X_0$, uniformly distributed around the $Z_0$ axis. The variables of the kinematic chains are expressed in their local frames $\{X_i,Y_i,Z_i\}$.

Each kinematic chain comprises two links: $L_{i1}$ and $L_{i2}$. One end of the first link $L_{i1}$ is connected to the fixed platform at point $A_i$ through an actuated revolute joint with joint variable ${\theta }_{i1}$. The other end connects to the second link $L_{i2}$ at point $B_i$ through a passive revolute joint characterized by angle ${\theta }_{i2}$. Link $L_{i1}$ has length $L_1$. The second link has a parallelogram configuration, with a passive revolute joint at each corner with mutually parallel axes that are perpendicular to the previous joint axis. The parallelogram has an associated passive joint variable ${\theta }_{i3}$ as shown in the figure. The other end of the second link is connected to the moving platform at point ${\mathbf{C}}_i$ by a revolute joint.

For the purpose of modeling the robot, the second link can be represented as a single rigid body of length $L_2$, with universal joints at both its ends. The equivalent universal joint connecting links 1 and 2 accounts for the passive angles ${\theta }_{i2}$ and ${\theta }_{i3}$. The use of joints with a parallelogram configuration, together with the robot’s architecture, ensures that the orientation of both platforms is the same at all times. This type of architecture was first introduced by Clavel in [24].

Point $\mathbf{P}$ is the center of the moving platform and its coordinates represent the position of the end effector with respect to the reference frame on the fixed platform. The distance between $\mathbf{P}$ and point ${\mathbf{C}}_i$ is called the moving platform radius and is denoted by r.

The distance between the origin O (center) of the fixed robot platform and point $A_i$ is called the radius of the fixed platform and is denoted by R. In the case of the Delta robot with geometric reconfiguration [10], a single additional actuator is introduced, enabling the adjustment of this parameter during operation. Consequently, the fixed platform can be interpreted as a set of three synchronized prismatic joints—each moving along its respective $X_i$ axis—whose coordinated motion changes the positions of points $A_i$. By design, the mechanism constrains all three radii to share the same magnitude at any time. When this fourth actuator is included within the robot control input, the geometric parameter R becomes an active joint variable.

In Figure 2, the geometric reconfiguration mechanism is shown, while the geometric parameters of the robot are presented in

Table 1. Geometric parameters for the reconfigurable Delta robot.

R	r	${\mathit{L}}_{\mathit{i}1}$	${\mathit{L}}_{\mathit{i}2}$
[0.138 m, 0.495 m]	0.065 m	0.200 m	0.400 m

; note that parameter R falls within an interval. This mechanism was presented in [10] as well as an analysis of the effect of geometric reconfiguration, for different links, on the workspace and static load. That work demonstrates the advantage of the geometric reconfiguration of the parameter R, that is, significant gains in the volume of the workspace, gains in the static load capacity, and its implementation feasibility. However, that work does not include a detailed analysis of the kinematic performance of the robot with the reconfiguration.

2.1. Kinematic Model

The Jacobian matrix of the reconfigurable robot is as follows:

$${\mathbf{J}}_{\mathbf{x}}\dot{\mathbf{x}}={\mathbf{J}}_{\mathbf{q}}\dot{\mathbf{q}}$$

(1)

where the configuration vector, whose components are the active joint variables, is defined as

$$\mathbf{q}=\left[\begin{array}{c}R\\ {\theta }_{11}\\ {\theta }_{21}\\ {\theta }_{31}\end{array}\right],$$

(2)

the Cartesian position of the end-effector is

$$\mathbf{x}=\mathbf{P}=\left[\begin{array}{c}{P}_x\\ P_y\\ P_z\end{array}\right],$$

(3)

$${\mathbf{J}}_{\mathbf{x}}=\left[\begin{array}{ccc}{a}_{1x}& a_{1y}& a_{1z}\\ a_{2x}& a_{2y}& a_{2z}\\ a_{3x}& a_{3y}& a_{3z}\end{array}\right]$$

(4)

with

$$\begin{array}{c}\hfill \begin{array}{cc}\hfill a_{ix}& =sin{\theta }_{i3}cos\left({\theta }_{i2}+{\theta }_{i1}\right)cos{\alpha }_i+cos{\theta }_{i3}sin{\alpha }_i\hfill \\ \hfill a_{iy}& =-sin{\theta }_{i3}cos\left({\theta }_{i2}+{\theta }_{i1}\right)sin{\alpha }_i+cos{\theta }_{i3}cos{\alpha }_i\hfill \\ \hfill a_{iz}& =-sin{\theta }_{i3}sin\left({\theta }_{i2}+{\theta }_{i1}\right)\hfill \end{array}\end{array}$$

(5)

is a Jacobian matrix associated with the work-space, and

$${\mathbf{J}}_{\mathbf{q}}=\left[\begin{array}{cccc}{b}_{11}& b_{12}& 0& 0\\ b_{21}& 0& b_{23}& 0\\ b_{31}& 0& 0& b_{34}\end{array}\right]$$

(6)

with

$$\begin{array}{c}\hfill \begin{array}{cc}\hfill b_{i1}& =sin\left({\theta }_{i3}\right)cos({\theta }_{i2}+{\theta }_{i1})\hfill \\ \hfill b_{i(i+1)}& =-L_{1}sin\left({\theta }_{i2}\right)sin\left({\theta }_{i3}\right)\hfill \end{array}\end{array}$$

(7)

is a Jacobian matrix associated with the joint-space.

Finally, the total Jacobian matrix is given by

$$\dot{\mathbf{x}}=\mathbf{J}\dot{\mathbf{q}}$$

(8)

where $\mathbf{J}={\mathbf{J}}_{\mathbf{x}}^{-1}{\mathbf{J}}_{\mathbf{q}}$. The reconfigurable robot was modeled as a redundant parallel robot and its kinematics analysis is presented in [23].

2.2. Inverse Geometric Model

The inverse geometric model is used to establish the correspondence between the end-effector position $\mathbf{x}$ and the associated configuration vector $\mathbf{q}$. In the case of parallel robots with kinematic redundancy, a given $\mathbf{x}$ vector can be associated with an infinite set of $\mathbf{q}$ vectors. Solving an optimization problem is necessary to determine a single vector $\mathbf{q}$. In this work, the algorithm previously introduced in [23] is used. The algorithm consists of systematically iterating the values of R at regular intervals. At each iteration, the values of the other three active joints are calculated using the inverse geometric model of the delta robot without reconfiguration. Subsequently, the vector of active joints is used to calculate different performance indices. At the end of all iterations, multiple pairs of vector $\mathbf{q}$ and performance index are obtained, where each index is optimized. In addition, the collected data can be used to analyze the variation in each performance index over the range of actuation of the reconfiguration mechanism.

3. Performance Indices Based on the Jacobian Matrix

The Jacobian matrix establishes the correspondence between the active joints velocity vector and the velocity vector of the moving platform. It also establishes the relationship between the forces and moments vector of the moving platform and the forces and moments vector of the active joints. For this reason, the Jacobian matrix is used as the basis for many performance indices. However, the properties of the Jacobian matrix depend on the scale and reference frame. Scale dependence implies that its value is significantly affected by the choice of measurement units. Changing the units can cause drastic changes in the Jacobian properties [25]. Moreover, the Jacobian matrix is not invariant with respect to the reference frame used [26]. Furthermore, combining translational and rotational DOF manipulations creates Jacobian inconsistency, indicating that it lacks clear physical meaning [27].

To carry out performance index measurements based on this matrix, a homogeneous Jacobian matrix was first determined. The hybrid nature of the joint velocities (as they include a mix of angular and linear) results in an inhomogeneous Jacobian matrix. For their homogenization, elements with units of length (columns 2, 3, and 4) are identified and divided by the characteristic length $L_1$, which is the length of the first link in each kinematic chain. This choice is based on the physical meaning of $L_1$ and the fact that it is present in every element of the Jacobian matrix. This procedure produces the following homogeneous Jacobian matrix with consistent units in each element:

$$\hat{\mathbf{J}}=\mathbf{J}\left[\begin{array}{cccc}1& 0& 0& 0\\ 0& 1/L_1& 0& 0\\ 0& 0& 1/L_1& 0\\ 0& 0& 0& 1/L_1\end{array}\right]$$

(9)

where $\hat{\mathbf{J}}$ is the Jacobian homogeneous matrix. Using this matrix ensures a correct comparison of the kinematic characteristics of the redundant delta robot compared to the robot without redundancy.

Performance Indices

The condition number if the Jacobian is given by

$$k\left(J\right)={\displaystyle \frac{{\sigma }_1}{{\sigma }_3}}$$

(10)

where ${\sigma }_1\ge {\sigma }_2\ge {\sigma }_3$ are the singular values of matrix $\mathbf{J}$. It has a value from 1 to infinity, where infinity is defined as a singular configuration. Alternatively, it can be expressed in terms of its reciprocal value, which has a range value of 0 to 1, where 0 indicates a singularity. The condition number of the Jacobian matrix is often considered a measure of kinematic dexterity and kinematic uniformity (isotropy) and is commonly used to avoid singularities.

The velocity minimum singular value

$${\sigma }_{min}^v={\sigma }_3$$

(11)

of the Jacobian matrix is a good indication of the minimum motion capability of the end-effector. The minimum singular value ${\sigma }_{min}$ of the entire workspace can be used as a global index and gives a notion of the worst mobility capability of the robot.

The force minimum singular value

$${\sigma }_{min}^f={\displaystyle \frac{1}{{\sigma }_1}}$$

(12)

is a good indication of the minimum static force capability of the end-effector.

Manipulability refers to the robot’s ability to amplify velocity and force from active joints. This index provides more detailed information about the amplification of velocity and force than the condition number. While condition number indicates the uniformity of velocity and force amplification, the manipulability index reports both the magnitude and uniformity of velocity and force amplification. Thus, manipulability is used as a measure of kinematic dexterity and transmission of motion and force.

The velocity manipulability index $\omega$ was first introduced by [28] as follows:

$${\omega }^v={\sigma }_1\ast {\sigma }_2\ast \dots \ast {\sigma }_n$$

(13)

where ${\sigma }_i$ with $i=1,2,\dots ,n$ correspond to the different singular values of the Jacobian matrix. Similarly, the manipulability of force is given by

$${\omega }^f={\displaystyle \frac{1}{{\sigma }_1}}\ast {\displaystyle \frac{1}{{\sigma }_2}}\ast \dots \ast {\displaystyle \frac{1}{{\sigma }_n}}$$

(14)

These are commonly represented by the ellipse or ellipsoid of velocity and force manipulability, respectively. In the case of the velocity manipulability ellipsoid, the dimensions of the axes represent both minimum and maximum velocity as well as velocity isotropy [29,30]. On the other hand, the volume of the ellipsoid indicates the manipulability value.

4. Singularities

In this section, an analysis of the singularities of the reconfigurable robot is presented, based on the Jacobian matrices ${\mathbf{J}}_{\mathbf{x}}$ and ${\mathbf{J}}_{\mathbf{q}}$.

As presented in Section 2.1, the matrix ${\mathbf{J}}_{\mathbf{x}}$ of the robot with geometric reconfiguration is the same as that of the robot without reconfiguration. This implies that, a priori, the singular configurations associated with ${\mathbf{J}}_{\mathbf{x}}$ are identical. However, the reconfiguration parameter R introduces specific geometric conditions for reaching them.

• Singularity 1: ${\theta }_{i3}=\pi /2$ and ${\theta }_{i1}+{\theta }_{i2}=\pi$ simultaneously for all kinematic chains. The $L_2$ links are coplanar with the platform, and the end-effector loses 1 DOF (vertical motion). This configuration is reached when the geometric constraint $R+L_1\ast cos\left({\theta }_{i1}\right)=r+L_2$ is satisfied. This equation highlights the direct influence of the active joint R; for a given $R>L_1+r$, a set of angles ${\theta }_{i1}$ exists that produces this singularity.
• Singularity 2: ${\theta }_{i3}=\pi /2$ and ${\theta }_{i1}+{\theta }_{i2}=\pi /2$ simultaneously for all kinematic chains. The $L_2$ links are perpendicular to the fixed platform, losing 2 DOF (horizontal motion). This condition requires $R\le L_1+r$, with ${\theta }_{i1}=arccos\left({\displaystyle \frac{r-R}{L_1}}\right)$. In the reconfigurable robot, this creates a continuum of singular configurations along the $Z_0$ axis.

  –

  A special case occurs at $R=r$, where the 3 kinematic chains are vertical, and all 3 DOF are lost. This boundary configuration is non-avoidable by reconfiguration.

Now let us consider the matrix ${\mathbf{J}}_{\mathbf{q}}$. In the non-reconfigurable case, a singularity occurs if ${\theta }_{i2}=0$ for any chain, where link $L_1$ and parallelogram $L_2$ become coplanar. This causes the end-effector to lose mobility in the direction of the $L_2$ link corresponding to that chain. For the reconfigurable robot, this condition becomes more specific:

• Singularity 3: ${\theta }_{i2}=0$ and ${\theta }_{i1}=\pi /2$ for one or more kinematic chains. The affected chains are coplanar in a vertical plane.
  • When one chain meets this condition, 1 DOF is lost (motion along its $L_2$ link).
  • If two chains meet this condition, 2 DOF are lost (motion in the plane formed by the two $L_2$ links).
  • If all three chains meet this condition, it requires $R=r$, coinciding with the special case of Singularity 2.
  These configurations correspond to the workspace boundary.
• Singularity 4: ${\theta }_{i2}=0$ for two kinematic chains (non-vertical case). The two chains are coplanar. The moving platform loses 2 DOF, constrained to move only perpendicularly to the plane formed by the $L_1$ links.

The singularity analysis reveals that by introducing R as a continuous active joint, the set of singular configurations becomes infinite. However, this same kinematic redundancy also provides, for a given end-effector position $\mathbf{x}$, an infinite set of non-singular joint configurations $\mathbf{q}$. This allows for the avoidance of most singularities (excluding specific boundary cases like $R=r$). Consequently, the control strategy for the reconfigurable robot must incorporate an optimization criterion to select non-singular configurations.

5. Solution of the Kinematic Redundancy Problem

In this section, an optimization criterion is developed to solve the inverse geometry and inverse kinematics problems. This approach aims to achieve optimal kinematic performance while avoiding singularities.

5.1. Performance Indices

As a first step, the known performance indices (${\omega }^v$, ${\omega }^f$, ${\sigma }_{min}^v$, ${\sigma }_{min}^f$, and $1/k$), derived from the Jacobian matrix, are evaluated. For non-reconfigurable architectures, these indices are commonly used both as performance measures in solving inverse geometry and inverse kinematics problems, and as optimization criteria during the design phase.

Particular attention is given to kinematic performance near singular configurations. This focus stems from the singularity analysis, which shows that geometric reconfiguration enables certain geometric parameters to function as active joints. As a result, singular configurations are influenced by these parameters. Thus, depending on the chosen optimization criterion, the solution to the inverse geometry and kinematics problems may lead to either regular or singular configurations.

To evaluate the effectiveness of each performance index, a set of target positions ${\mathbf{x}}_i$ was defined to uniformly cover the entire workspace using a grid of $401\times 401\times 300$ points, providing a spatial resolution of 0.002 m between adjacent positions. For each position, the inverse geometric problem was attempted by discretely sampling the base radius R within the interval [0.138, 0.495] m with a constant increment of 0.001 m. If a feasible solution was found, the point was considered part of the workspace and the Jacobian was computed while enforcing the physical constraints of the mechanism, specifically the actuated revolute joint limits ${\theta }_{i1}\in [-{40}^{\circ },{110}^{\circ }]$. After completing the sweep over R for a given position, the configuration corresponding to the maximum value of the performance index under evaluation was selected as the optimal solution.

Singularity detection is performed through a multi-step verification process. This includes monitoring the numerical rank deficiency of the Jacobian matrices ${\mathbf{J}}_{\mathbf{x}}$ and ${\mathbf{J}}_{\mathbf{q}}$ and evaluating the analytical conditions identified during the singularity analysis. Furthermore, a configuration is classified as near-singular or ill-conditioned based on specific numerical thresholds. Specifically, a configuration is penalized if the reciprocal of the condition number $1/k$ or the minimum singular values ${\sigma }^v$ and ${\sigma }^f$ fall below 0.1. Similarly, thresholds are set for the manipulability indices, where values of ${\omega }^v$ or ${\omega }^f$ lower than 0.001 are considered to represent a critical loss of mobility or force transmission capability. Regarding the computational complexity of the optimization process, the discrete search for the reconfiguration parameter R involved 385 iterations for each spatial position evaluated. To ensure computational efficiency during the analysis of the discretized workspace volume, parallel computing techniques were employed to distribute the workload of the 3D grid sweep. Consequently, the maximum runtime required to determine the optimal configuration and compute the associated performance indices was 1.11 ms per point (it was lower when, for some values of R there was no solution to the inverse geometric problem, thus no calculation of the Jacobian singular values was required), resulting in an average total duration of 33 min to complete the exploration of the entire workspace. This performance confirms the feasibility of the proposed method for extensive offline kinematic analysis, such as redundant robot kinematic performance characterization or robot design. All numerical simulations and workspace evaluations were conducted on a workstation equipped with an Ryzen 5 5600G processor (Advanced Micro Devices, Santa Clara, CA, USA) (6 cores, operating at 4.2 GHz) running the Windows 10 operating system. The algorithms were implemented in Python 3.10, utilizing the NumPy library for efficient numerical methods and matrix operations. Furthermore, to optimize processing time during the exhaustive grid search, the Numba library was employed to parallelize the execution across the available cores. The following Examples 1 and 2 serve as representative operational scenarios identified during the workspace exploration that illustrate cases where singular configurations arise under specific optimization criteria. It is important to note that for these specific examples, a finer resolution of 0.0001 m for the parameter R is utilized to enhance data resolution during the analysis of a single configuration.

5.1.1. Example 1

The configuration obtained for the Cartesian position $\mathbf{x}={(0.000,0.000,-0.200)}^T\mathrm{m}$, by optimizing the index ${\omega }^v$, is $\mathbf{q}={(0.465 \mathrm{m},{90.000}^{\circ },{90.000}^{\circ },{90.000}^{\circ })}^T$. According to the analysis presented in Section 4 (Singularity 1), this corresponds to a singular configuration.

Figure 3 shows the variation in the performance indices ${\omega }^v$ (velocity manipulability) and ${\sigma }_{\min }^v$ (minimum singular value for velocity) for the Cartesian position $\mathbf{x}={(0.000,0.000,-0.200)}^T\mathrm{m}$, as the geometric reconfiguration parameter R is varied. The horizontal axis represents R, ranging approximately from 0.13 m to 0.5 m; the left vertical axis (scale: 0–100) corresponds to the index ${\omega }^v$ (green line), while the right vertical axis (scale: 0.0–1.0) corresponds to the index ${\sigma }_{\min }^v$ (orange line).

It is observed that the index ${\omega }^v$, which indicates a good velocity transmission capability, shows low values for small R, but experiences an extremely sharp increase as R approaches 0.465 m. In fact, for $R=0.4649\mathrm{m}$, which is very close to the value of $R=0.465$,

Table 2. Performance indices for the (near singular) configuration $\mathbf{q}={(0.4649,90.000,90.000,90.000)}^T$.

${\mathit{\omega }}^{\mathit{v}}$	${\mathit{\omega }}^{\mathit{f}}$	${\mathit{\sigma }}_{\mathit{min}}^{\mathit{v}}$	${\mathit{\sigma }}_{\mathit{min}}^{\mathit{f}}$	$1/\mathit{k}$
$6.1584\times {10}^8$	$1.6237\times {10}^{-9}$	$8.1648\times {10}^{-1}$	$1.0825\times {10}^{-9}$	$8.8388\times {10}^{-10}$

indicates a value of ${\omega }^v=6.1584\times {10}^8$, which is a clear indicator of proximity to a singular configuration or an ill-conditioned system. On the other hand, index ${\sigma }_{\min }^v$, which reflects the minimum movement capability of the end-effector, also shows critical behavior in this same region. Although Table 2 reports ${\sigma }_{\min }^v=0.81648$ for the specific configuration that maximizes ${\omega }^v$ with $R=0.4649\mathrm{m}$, it is essential to note that the geometric singularity condition ${\theta }_{i1}={90}^{\circ }$ reached with this value of R implies that the robot effectively loses degrees of freedom, which manifests as an inability to generate velocities in certain directions, leading ${\sigma }_{\min }^v$ to become zero under this specific geometric singularity condition, even if the table shows a high point value from a different optimization.

The singularity condition of Example 1, associated with $R=0.465\mathrm{m}\mathrm{and}{\theta }_{i1}={90}^{\circ }$, is thus corroborated both by the rapid growth of ${\omega }^v$ and the effective nullification of ${\sigma }_{\min }^v$ under said singular geometric condition. The maximization of ${\omega }^v$ leads the system to this singular configuration, and the consideration of ${\sigma }_{\min }^v$ under the same critical geometric condition confirms the loss of mobility. Therefore, optimizing either of these two indices, seeking their maximum values for this coordinate x, leads the robot to operate at or very near a singularity. This scenario confirms that solving the inverse geometry problem by blindly optimizing ${\omega }^v$ or ${\sigma }_{\min }^v$ can result in the selection of singular configurations, justifying the need for more robust optimization criteria such as the one that will be proposed later.

Table 2 presents the values of the performance indices for a configuration very close to the one obtained. From the data, it can be observed how maximizing an index associated with velocity minimizes its counterpart in static force.

5.1.2. Example 2

Let us now consider the coordinate $x=(0.000,0.000,-0.116)\mathrm{m}$ from which, by maximizing the force manipulability index ${\omega }^f$, the following configuration is obtained: $\{x=(0.000,0.000,-0.1153)\mathrm{m}, q=(0.22842\mathrm{m},-{35.0297}^{\circ },-{35.0297}^{\circ },-{35.0297}^{\circ })\}$. When analyzing this configuration, it is found that the three passive joints ${\theta }_{i2}$ adopt a value of ${179.9}^{\circ }$, which is extremely close to the singularity condition of ${180}^{\circ }$.

Figure 4 graphically presents the variation in the indices ${\omega }^f$ (force manipulability), ${\sigma }_{\min }^f$ (force minimum singular value), and $1/k$ (reciprocal of the condition number) for this coordinate x while the reconfiguration parameter R is modified (X-axis, varying approximately from 0.12 m to 0.5 m). The left Y-axis (scale 0.0–1.0) corresponds to $1/k$ (purple line), while the right Y-axis (scale 0–100) is shared by ${\omega }^f$ (red line) and ${\sigma }_{\min }^f$ (brown line).

It is observed in Figure 4 that the indices ${\omega }^f$ and ${\sigma }_{\min }^f$ reach their maximum values (consistent with ${\omega }^f=2.8116\times {10}^8$ and ${\sigma }_{\min }^f=6.5274\times {10}^2$ from

Table 3. Measurements of the performance indices for the configuration $\{\mathbf{x}=(0.000,0.000,-0.1153)$, $\mathbf{q}=(0.22842,-35.0297355,-35.0297355,-35.0297355)\}$.

${\mathit{\omega }}^{\mathit{v}}$	${\mathit{\omega }}^{\mathit{f}}$	${\mathit{\sigma }}_{\mathit{min}}^{\mathit{v}}$	${\mathit{\sigma }}_{\mathit{min}}^{\mathit{f}}$	$1/\mathit{k}$
$3.5566\times {10}^{-9}$	$2.8116\times {10}^8$	$1.5236\times {10}^{-3}$	$6.5274\times {10}^2$	0.9946

) precisely at $R\approx 0.22842\mathrm{m}$. This value of R represents a lower bound of the feasible range to reach the given coordinate x; for smaller values of R, there is no solution to the inverse geometry problem. Immediately after this point, both indices (${\omega }^f$ and ${\sigma }_{\min }^f$) drop drastically towards zero, indicating a rapid loss of force transmission and generation capability.

Regarding the index $1/k$, it also exhibits a very high value (close to 1, specifically 0.9946 according to Table 3) at $R\approx 0.22842\mathrm{m}$, which would traditionally suggest excellent numerical conditioning (isotropy). However, this “optimal” conditioning occurs exactly in the identified geometrically singular configuration (${\theta }_{i2}\approx {180}^{\circ }$). As R increases slightly, $1/k$ drops abruptly to a value close to zero (around $R=0.3\mathrm{m}$), indicating severe ill-conditioning, before partially recovering.

The crucial point to highlight here is the apparent contradiction: the maximization of performance indices traditionally associated with good force capability (${\omega }^f$, ${\sigma }_{\min }^f$) and good conditioning ($1/k$) leads the system to a configuration that is, in fact, singular or extremely close to a geometric singularity (the boundary of the reachable space for that R, with ${\theta }_{i2}\approx {180}^{\circ }$). The high values of these indices at $R\approx 0.22842\mathrm{m}$ mask the singular nature of the configuration. This apparent paradox, where indicators of “good” performance coincide with a kinematically undesirable configuration, underscores the inadequacy of these classic indices as sole optimization criteria for resolving redundancy in the reconfigurable Delta robot. It is precisely this contradiction that motivates the need to develop and propose a new performance index that is sensitive to these conditions and can guide the selection of robust configurations far from singularities.

Table 3 presents the values of the performance indices for the obtained configuration. From the data, it can be observed how maximizing an index associated with static force minimizes its counterpart in velocity.

From the evaluation performed, the following conclusions can be drawn for the Delta robot with geometric reconfiguration:

• ${\omega }^v\in (0,\infty )$. When ${\omega }^v$ tends to a large value, ${\omega }^f$ tends to zero, ${\sigma }_{min}^f$ tends to zero, and $1/k$ tends to zero.
• ${\omega }^f\in (0,\infty )$. When ${\omega }^f$ tends to a large value, ${\omega }^v$ tends to zero, and ${\sigma }_{min}^v$ tends to zero.
• ${\sigma }^f\in (0,\infty )$. When ${\sigma }^f={\displaystyle \frac{1}{{\sigma }_1}}$ tends to a large value, ${\omega }^v={\sigma }_1{\sigma }_2{\sigma }_3$ tends to zero and ${\sigma }_{min}^v$ tends to zero since ${\sigma }_1>{\sigma }_3={\sigma }_{min}^v$. If, in addition, $1/k$ tends to one, then ${\sigma }_3={\sigma }_1$.
• ${\sigma }^v\in (0,\infty )$.

The results of this evaluation conclude that optimizing based on ${\omega }^v$, ${\omega }^f$, ${\sigma }_{min}^v$, ${\sigma }_{min}^f$, or $1/k$ generates singular configurations when they tend to very high values as well as to zero. It is important to clarify that Examples 1 and 2 are not worst-case scenarios but rather representative cases of common configurations. Extensive exploration across the workspace revealed that optimizing for the standard indices often leads to large singular regions. Therefore, these indices are not suitable for the Delta robot with geometric reconfiguration. Since none of the considered indices are appropriate, the need arises to propose an optimization criterion that is sensitive to singular configurations.

5.2. Singularity-Sensitive Performance Index

Considering the results obtained in the previous section, where it was shown that traditional performance indices can lead to singular configurations when used as optimization criteria for the reconfigurable Delta robot, a new performance index is proposed in this section. This index, denoted as $\tilde{k}$, is specifically designed to be sensitive to singularities and to overcome the limitations of classical criteria. The philosophy behind this new index is to penalize both very low values of the minimum singular values (indicative of an imminent singularity) and excessively high values, which can also be associated with problematic configurations or undesirable system sensitivity. The index ranges from 0 to 1; it approaches 0 as the minimum singular values approach very low or very high values; and it approaches 1 as the minimum singular values approach a pre-designed (adjustable) “sweet spot” or compromise of velocity and force performance.

The proposed index $\tilde{k}$ is based on the product of two normalized functions, one for the velocity minimum singular value (${\tilde{\sigma }}_{\min }^v$) and another for the force minimum singular value (${\tilde{\sigma }}_{\min }^f$):

$$\tilde{k}={\tilde{\sigma }}_{\min }^v·{\tilde{\sigma }}_{\min }^f$$

(15)

with

$${\tilde{\sigma }}_{\min }^v=\left\{\begin{array}{cc}1-{\left({\displaystyle \frac{{\sigma }_{\min }^v-a^v}{a^v}}\right)}^2\hfill & \mathrm{if}0\le {\sigma }_{\min }^v\le a^v\hfill \\ 1-{\left({\displaystyle \frac{{\sigma }_{\min }^v-a^v}{b^v-a^v}}\right)}^2\hfill & \mathrm{if}{a}^v<{\sigma }_{\min }^v\le b^v\hfill \\ 0\hfill & \mathrm{otherwise}\hfill \end{array}\right.$$

(16)

$${\tilde{\sigma }}_{\min }^f=\left\{\begin{array}{cc}1-{\left({\displaystyle \frac{{\sigma }_{\min }^f-a^f}{a^f}}\right)}^2\hfill & \mathrm{if}0\le {\sigma }_{\min }^f\le a^f\hfill \\ 1-{\left({\displaystyle \frac{{\sigma }_{\min }^f-a^f}{b^f-a^f}}\right)}^2\hfill & \mathrm{if}{a}^f<{\sigma }_{\min }^f\le b^f\hfill \\ 0\hfill & \mathrm{otherwise}\hfill \end{array}\right.$$

(17)

where $a^v=\beta \ast b^v$ and $a^f=(1-\beta )\ast b^f$, with $\beta \in (0,1)$.

There are 3 parameters that are used to design the behavior of the index, namely, $b^v$, the maximum tolerated value for the velocity minimum singular value, $b^f$, the maximum tolerated value for the force minimum singular value, and $\beta$, the adjustable weight to favor either velocity or force performance. When $\beta$ approaches 0, the velocity performance is sacrificed to favor force performance and when it approaches 1 the velocity performance is completely favored by sacrificing force performance. Note that parameters $a^v$ and $a^f$, defined in terms of $\beta$, $b^v$ and $b^f$, represent the selected “sweet spot” of the minimum singular values.

Function ${\tilde{\sigma }}_{\min }^v$ (Equation (16)) is constructed so that it approaches zero as ${\sigma }_{\min }^v$ approaches zero (an indicator of singularity, where mobility drops). As ${\sigma }_{\min }^v$ increases and approaches the selected value of $a^v$ (representative of the chosen mobility compromise), ${\tilde{\sigma }}_{\min }^v$ reaches its maximum value of 1. If ${\sigma }_{\min }^v$ continues to increase beyond the selected point $a^v$, up to ${\sigma }_{\min }^v=b^v$, the function ${\tilde{\sigma }}_{\min }^v$ continuously decreases to zero. For values of ${\sigma }_{\min }^v$ greater than $b^v$, the function remains at zero, penalizing configurations where the velocity minimum singular value is excessively high, which could be indicative of undesirable anisotropy or proximity to another type of problematic behavior not captured solely by the value of ${\sigma }_{\min }^v$.

Analogously, the function ${\tilde{\sigma }}_{\min }^f$ (Equation (17)) operates on the force minimum singular value. Thus, ${\tilde{\sigma }}_{\min }^f$ continuously approaches zero as ${\sigma }_{\min }^f$ approaches 0, reaches 1 when ${\sigma }_{\min }^f=a^f$, and returns to zero if ${\sigma }_{\min }^f$ reaches or exceeds $b^f$.

In this work, the following parameter values were used: $b^v=2$, $b^f=4.2$ and $\beta =0.5$. The weighting factor $\beta =0.5$ corresponds to a neutral setting, implying no specific prioritization of velocity over force. This value was selected to demonstrate the index’s capacity to achieve a natural balance of velocity and force performance, avoiding extreme configurations associated with singularities or ill-conditioned states. The limits for $b^v$ and $b^f$ were determined through a numerical evaluation across the robot’s workspace, progressively increasing them until the corresponding classical indices approached zero or exhibited abrupt increases near singular configurations (see, for instance, Figure 3 and Figure 4). Alternative criteria could be adopted, such as adjusting these limits for specific tasks or based on theoretical bounds of the Jacobian matrix.

To evaluate the effectiveness of this proposed index $\tilde{k}$ as an optimization criterion, the two scenarios from the previous examples are revisited. Figure 5 corresponds to Example 1 (coordinate $x=(0.000,0.000,-0.200)\mathrm{m}$). It shows the behavior of the new index $\tilde{k}$ (blue line) in comparison with ${\omega }^v$ and ${\sigma }_{\min }^v$. Notably, $\tilde{k}$ reaches its maximum value for a value of $R\approx 0.20465\mathrm{m}$. This choice of R is significantly different from the problematic $R=0.465\mathrm{m}$ where ${\omega }^v$ tended to infinity and the geometric singularity ${\theta }_{i1}={90}^{\circ }$ occurred. In the configuration selected by $\tilde{k}$, the values of ${\omega }^v=0.11063$ and ${\sigma }_{\min }^v=0.46054$ (

Table 4. Measurements of the performance indices for the configuration $\mathbf{x}=(0.000,0.000,-0.200)$, $\mathbf{q}=(0.20465,-3.39378,-3.39378,-3.39378)$.

${\mathit{\omega }}^{\mathit{v}}$	${\mathit{\omega }}^{\mathit{f}}$	${\mathit{\sigma }}_{\mathit{min}}^{\mathit{v}}$	${\mathit{\sigma }}_{\mathit{min}}^{\mathit{f}}$	$1/\mathit{k}$
$1.1063\times {10}^{-1}$	$9.0389\times {10}^0$	$4.6054\times {10}^{-1}$	$2.4592\times {10}^0$	0.8829

) are moderate and far from the extremes that characterized the singular configuration.

Similarly, Figure 6 analyzes Example 2 (coordinate $x=(0.000,0.000,-0.116)\mathrm{m}$). Here, the index $\tilde{k}$ (blue line) presents its maximum at $R\approx 0.24901\mathrm{m}$. This value of R differs from the $R\approx 0.22842\mathrm{m}$ that maximized the force indices (${\omega }^f,{\sigma }_{\min }^f$) and the reciprocal of the condition number ($1/k$), but which corresponded to the geometric singularity with ${\theta }_{i2}\approx {180}^{\circ }$. The configuration chosen by $\tilde{k}$ results in values of ${\omega }^f=25.9473$ and ${\sigma }_{\min }^f=1.6410$ (

Table 5. Measurements of the performance indices for the configuration $\{\mathbf{x}=(0.000,0.000,-0.1153)$, $\mathbf{q}=(0.24901,0.92940,0.92940,0.92940)\}$.

${\mathit{\omega }}^{\mathit{v}}$	${\mathit{\omega }}^{\mathit{f}}$	${\mathit{\sigma }}_{\mathit{min}}^{\mathit{v}}$	${\mathit{\sigma }}_{\mathit{min}}^{\mathit{f}}$	$1/\mathit{k}$
$3.8553\times {10}^{-2}$	$25.9473\times {10}^0$	$2.5148\times {10}^{-1}$	$1.6410\times {10}^0$	0.4127

), which are considerably more balanced and safer compared to the extreme values of Table 3, which were associated with the singularity. It is important to note that the peak of $\tilde{k}$ does not coincide with the initial peak of $1/k$ (which occurred at the singularity), demonstrating that $\tilde{k}$ identifies a different and safer compromise.

The main contribution of this new index $\tilde{k}$ lies in its ability to solve the inverse geometry and kinematics problem by selecting joint configurations that are not only reachable but also operationally safe. This is achieved by avoiding both direct singularities (where the ${\sigma }_{\min }$ are zero) and those configurations associated with extreme values (very high or very low) of traditional performance indices, which, as has been shown, can be misleading and lead to problematic conditions. The normalization functions ${\tilde{\sigma }}_{\min }^v$ and ${\tilde{\sigma }}_{\min }^f$ are fundamental in this process, as they penalize minimum singular values that deviate significantly from an intermediate range considered of “good behavior,” thus prioritizing a balance between mobility, force capability, and stability. As demonstrated by Figure 5 and Figure 6, and the corresponding values in Table 4 and Table 5, optimization based on $\tilde{k}$ effectively diverts the choice of the reconfiguration parameter R from the previously identified critical values, selecting configurations that result in moderate and well-behaved values for all performance indices. This validates $\tilde{k}$ as a robust and singularity-sensitive optimization criterion, suitable for the reconfigurable Delta robot.

6. Comparison of Kinematic Performance

Building upon the robust optimization criterion $\tilde{k}$ established in the previous section for resolving kinematic redundancy in the reconfigurable Delta robot, this section presents a quantitative and qualitative assessment of the impact and advantages derived from such reconfiguration capability. In particular, the influence of redundancy—introduced through the geometric reconfiguration of the parameter R—is analyzed with respect to two key aspects of the robot’s performance: (1) the range and morphology of the reachable workspace volume, and (2) the enhancement of kinematic performance indices, such as velocity manipulability, across that workspace.

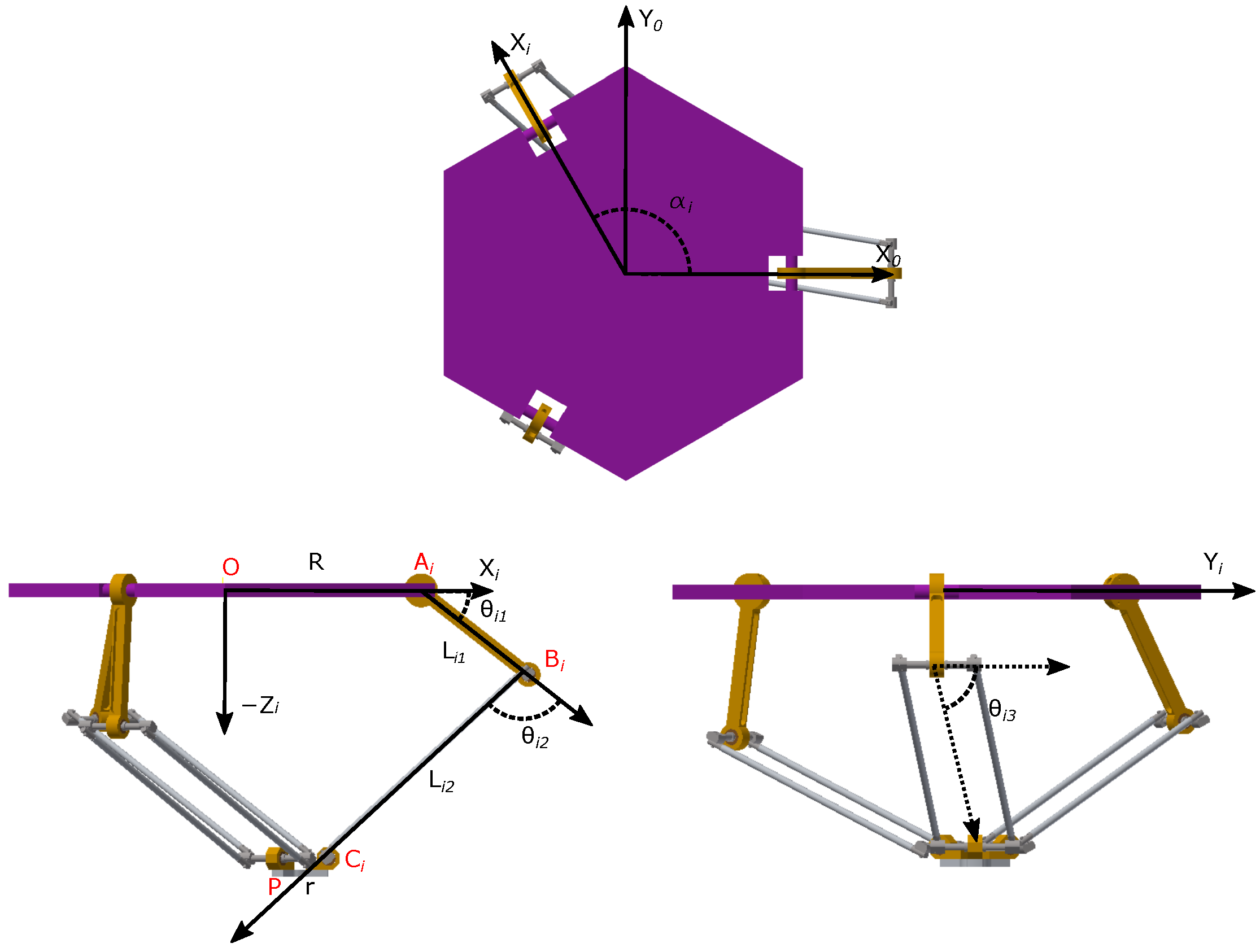
To this end, this section is dedicated to quantitatively and qualitatively evaluating the impact and benefits of said reconfiguration capability. Specifically, the effect of redundancy, enabled by the geometric reconfiguration of the parameter R, will be analyzed on two fundamental aspects of the robot’s performance: first, the extent and shape of the reachable workspace volume, and second, the potential improvement in kinematic performance indices, such as velocity manipulability, throughout said space. To do this, the results obtained for the Delta robot operating with its active reconfiguration capability (where R is variable and its value is selected using the $\tilde{k}$ index for each point in the workspace) will be contrasted with its non-reconfigurable counterpart. The latter is considered a particular case of the reconfigurable robot where the parameter R is kept fixed at $R=0.200\mathrm{m}$, a value representative of the original design or a standard non-reconfigurable configuration. This evaluation is fundamental to validate the hypothesis that reconfigurability not only expands the operational capabilities of the Delta robot but also allows for a significant optimization of its kinematic behavior.

6.1. Maximum Reachable Volume

To quantify the reachable workspace of the reconfigurable Delta robot, a numerical discretization approach was employed. The search space is bounded by an enclosing prism defined by the Cartesian coordinates $x,y\in [-0.400,0.400]$ m and $z\in [-0.000,-0.600]$ m. This volume was discretized into a high-resolution grid of $401\times 401\times 300$ points, corresponding to a spatial resolution of 0.002 m between adjacent positions. This resolution was selected based on a convergence analysis to ensure that the resulting volume measurements are numerically stable and independent of the grid density, while maintaining an efficient computational cost for the optimization process. The workspace volume is determined by evaluating the ratio between the number of points that satisfy the inverse kinematic constraints and the total number of points within the bounding prism and multiplying this ratio by the total volume of the prism.

The application of this methodology reveals a significant expansion of the operational range due to the reconfiguration capability. The workspace volume for the standard configuration (with fixed R) was measured at 0.075 m³, whereas the reconfigurable Delta robot achieved a volume of 0.137 m³. These results represent a 82% increase in the reachable workspace.

Figure 7a shows the workspace of the reconfigurable robot, while Figure 7b shows the case without reconfiguration. In these images, we can observe the shapes of the volumes and how the reconfigurable robot gains volume in all directions; in particular, a significant gain is observed in the upper part of the workspace.

6.2. Performance Comparison

To analyze the impact of geometric reconfiguration on the robot’s kinematic behavior, a comparative study is presented between the reconfigurable Delta robot (RDR) and its non-reconfigurable counterpart (ODR). The ODR serves as a baseline with a fixed base radius of $R=0.200\mathrm{m}$, while the RDR adapts its geometry at each point to maximize the singularity-sensitive index $\tilde{k}$.

The performance evaluation is conducted using the same grid-based discretization applied for the workspace volume estimation, consisting of $401\times 401\times 300$ points. For every reachable coordinate $(x,y,z)$ within this grid, the inverse geometric problem is solved. In the case of the RDR, this involves a systematic search for the optimal reconfiguration parameter R by sampling the range [0.138, 0.495] m with a high-resolution step of 0.001 m. At each configuration, Jacobian-based performance indices—such as velocity manipulability, minimum singular values, and the condition number—are computed and recorded. This methodology allows for a comprehensive mapping of kinematic dexterity across the entire workspace, providing a robust statistical basis for comparing the operational safety and mobility of both robot architecture.

Figure 8 shows heatmaps representing the distribution of the velocity manipulability index, ${\omega }^v$, over different $xy$ planes (cross-sections of the workspace at different z heights). The subfigures in the left column (a, b, c) correspond to the reconfigurable Delta robot, where for each point $(x,y,z)$, the value of R that maximizes the $\tilde{k}$ index has been selected. The subfigures in the right column (d, e, f) illustrate the behavior for the robot with a fixed $R=0.200\mathrm{m}$. In these maps, warmer colors (tending to red/yellow on the provided color scale) indicate higher values of ${\omega }^v$ (greater ability to transmit velocities), while colder colors (tending to dark blue) represent lower values.

Analyzing the planes at a height of $z=-0.300\mathrm{m}$ (comparing Figure 8a, reconfigurable, with Figure 8d, non-reconfigurable), it is observed that the reconfigurable robot not only covers a larger cross-sectional area but also presents extensive regions with high and more homogeneous values of ${\omega }^v$. For $z=-0.400\mathrm{m}$ (Figure 8b,e), the advantage of the reconfigurable robot in terms of area with good manipulability remains clear; the ability to adjust R allows it to maintain superior performance. Even in lower regions such as $z=-0.500\mathrm{m}$ (Figure 8f, non-reconfigurable), where the robot with a fixed R may have a very restricted operating space or significantly degraded manipulability, the reconfigurable robot (whose operability at this depth is inferred to be superior due to the general expansion of the workspace shown in Figure 7a) can select an R that allows it to operate with better performance.

In general, Figure 8 demonstrates that reconfigurability not only expands the geometrically reachable workspace but, when combined with the $\tilde{k}$ optimization criterion, allows the robot to operate with an improved or more consistently maintained velocity manipulability ${\omega }^v$ across a larger portion of this volume. The global quantitative data presented in

Table 6. Performance indices behavior for the Reconfigurable Delta Robot (RDR) and the Original (Non-Reconfigurable) Delta Robot (ODR) configurations throughout the entire (ODR) workspace.

Index	Robot	Min	Max	Mean
$1/k$	RDR	0.1505	0.9999	0.4988
	ODR	$8.93\times {10}^{-4}$	0.9994	0.4778
${\omega }^v$	RDR	0.0635	1.1538	0.6380
	ODR	$5.71\times {10}^{-4}$	1.1375	0.7036
${\omega }^f$	RDR	0.8666	15.7337	1.7976
	ODR	0.8790	1748.7	1.8231
${\sigma }^v$	RDR	0.2100	0.9963	0.5981
	ODR	$9.87\times {10}^{-4}$	0.8493	0.6008
${\sigma }^f$	RDR	0.3672	1.9724	0.8231
	ODR	0.4060	9.4800	0.7924

for ${\omega }^v$ (where RDR is Reconfigurable Delta Robot and ODR is Original/Non-Reconfigurable Delta Robot with $R=0.200\mathrm{m}$) support these observations. While the mean value of ${\omega }^v$ may be similar between both configurations (0.6380 for RDR vs. 0.7036 for ODR), the minimum value of ${\omega }^v$: for the RDR, it is 0.0635, while for the ODR with $R=0.200\mathrm{m}$, it is merely 0.0006. This indicates that the reconfigurable robot, thanks to the optimization of R using $\tilde{k}$, much more effectively avoids configurations of very low velocity manipulability. Additionally, the maximum value of ${\omega }^v$ reached by the RDR (1.1538) is marginally higher than that of the ODR (1.1375), suggesting a higher kinematic performance ceiling. Regarding the force performance, the mean value of ${\omega }^f$ is marginally lower (1.7976) for RDR vs. 1.82.31 for ODR), the minimum value of ${\omega }^f$ is 0.8666 for the RDR, while for the ODR, it is 0.8790. However, the maximum value of ${\omega }^f$ is 15.7337 for the RDR, while for the ODR is 1748.7 which is a very high value indicating an ill-conditioned configuration. This indicates that the reconfigurable robot, thanks to the optimization of R using $\tilde{k}$, much more effectively avoids ill-conditioned configurations.

When velocity performance is prioritized by setting $\beta =0.75$, the results in

Table 7. Performance behavior throughout the entire (ODR) workspace for $\beta =0.75$.

Index	Robot	Min	Max	Mean
$1/k$	RDR	0.1511	0.9999	0.4916
	ODR	$8.93\times {10}^{-4}$	0.9994	0.4778
${\omega }^v$	RDR	0.0881	1.3151	0.7197
	ODR	$5.71\times {10}^{-4}$	1.1375	0.7036
${\omega }^f$	RDR	0.7603	11.3387	1.5480
	ODR	0.8790	1748.7	1.8231
${\sigma }^v$	RDR	0.2409	0.9997	0.6204
	ODR	$9.87\times {10}^{-4}$	0.8493	0.6008
${\sigma }^f$	RDR	0.3534	1.2721	0.7769
	ODR	0.4060	9.4800	0.7924

indicate that the minimum, maximum, and mean values of ${\omega }^v$ are higher for the RDR robot than for the ODR robot, while force performance remains satisfactory. Conversely, setting $\beta =0.25$, which favors force performance at the expense of velocity, yields superior force performance for the RDR robot compared to the ODR robot, while maintaining acceptable velocity performance, as shown in

Table 8. Performance behavior throughout the entire (ODR) workspace for $\beta =0.25$.

Index	Robot	Min	Max	Mean
$1/k$	RDR	0.1443	0.9999	0.4598
	ODR	$8.93\times {10}^{-4}$	0.9994	0.4778
${\omega }^v$	RDR	0.0291	0.9751	0.5374
	ODR	$5.71\times {10}^{-4}$	1.1375	0.7036
${\omega }^f$	RDR	1.0254	34.3475	2.1525
	ODR	0.8790	1748.7	1.8231
${\sigma }^v$	RDR	0.1740	0.9435	0.5329
	ODR	$9.87\times {10}^{-4}$	0.8493	0.6008
${\sigma }^f$	RDR	0.4060	2.8499	0.8597
	ODR	0.4060	9.4800	0.7924

. These findings demonstrate that the proposed index can be tuned to emphasize either velocity or force performance according to design requirements.

The proposed index exhibits smooth and continuous variation across the workspace, as shown in the heat maps, indicating a continuous sensitivity relationship between the index and the parameters. Minor modeling errors or assembly tolerances would therefore induce only limited changes in the index value, consistent with the numerical robustness of Jacobian-based measures away from singular boundaries. While a formal sensitivity analysis could be addressed in future work, the observed behavior provides qualitative evidence of stability under small perturbations.

Based on the data shown in the tables and figures presented in this section, a substantial improvement can be observed in both the workspace volume and the performance indices for the reconfigurable robot when compared to a standard fixed configuration. The distribution of the velocity manipulability index values is also more favorable. Regarding the feasibility of the reconfiguration mechanism used in this work, it was previously demonstrated in [10], where the design of the mechanism was presented, and in [23] where several controls were proposed and subsequently validated through experimental testing. Taking these facts into account, it can be concluded that geometric reconfiguration, managed through the $\tilde{k}$ optimization criterion, is effective in improving both the reach and the kinematic characteristics of the Delta robot.

7. Conclusions

This work presents a simulation-based study on the optimization of a reconfigurable Delta robot using a novel singularity-sensitive index. The proposed index addresses the limitations of classical Jacobian-based criteria by penalizing configurations near singularities or ill-conditioned states and allowing adjustable weighting between velocity and force performance. Through extensive numerical evaluation, the index demonstrated its ability to select safe and balanced configurations across the entire workspace, avoiding extreme values for these indices which may appear when using traditional approaches. The simulation results indicate that geometric reconfiguration, combined with the proposed optimization criterion, can significantly expand the reachable workspace (by approximately 82%) and improve the distribution of manipulability indices, thereby enhancing operational flexibility. Although the current validation is limited to simulation, the methodology establishes a foundation for future experimental implementation and adaptation to specific tasks or theoretical bounds.

Future work will focus on experimental validation, which will follow two pathways. First, the practical workspace will be validated by commanding the robot to a set of target positions spanning the workspace; the volume will then be quantified based on the task completion success rate. This experiment will be conducted comparatively, solving the inverse geometric problem using both the proposed index $\tilde{k}$ and classical indices (e.g., ${\omega }^v,1/k$) to demonstrate the practical impact of the optimization criterion on reachability. Second, dynamic trajectory-tracking control laws will be designed to verify that the proposed index effectively prevents the control system from drifting toward singular or mechanically invalid configurations.