Neural Adaptive Nonlinear MIMO Control for Bipedal Walking Robot Locomotion in Hazardous and Complex Task Applications
Abstract
1. Introduction
- Unified adaptive control: Combines adaptation, learning, and real-time feedback within a cohesive architecture, addressing the fragmentation in prior methods.
- Robustness under critical failures: Maintains gait stability under severe conditions, including structural damage, disturbances, and system degradation.
- Real-time feedback and learning: Achieves fast correction using finite-time dynamic feedback and RBF-based online learning in hazardous tasks.
- Synergistic adaptation and learning integration: Combines MIMO adaptive control and neural approximation for precise trajectory tracking under uncertainty.
- Scalability and generalization: Applicable across diverse walking modes and robotic platforms, extending its use beyond the tested 5 DOF RABBIT robot.
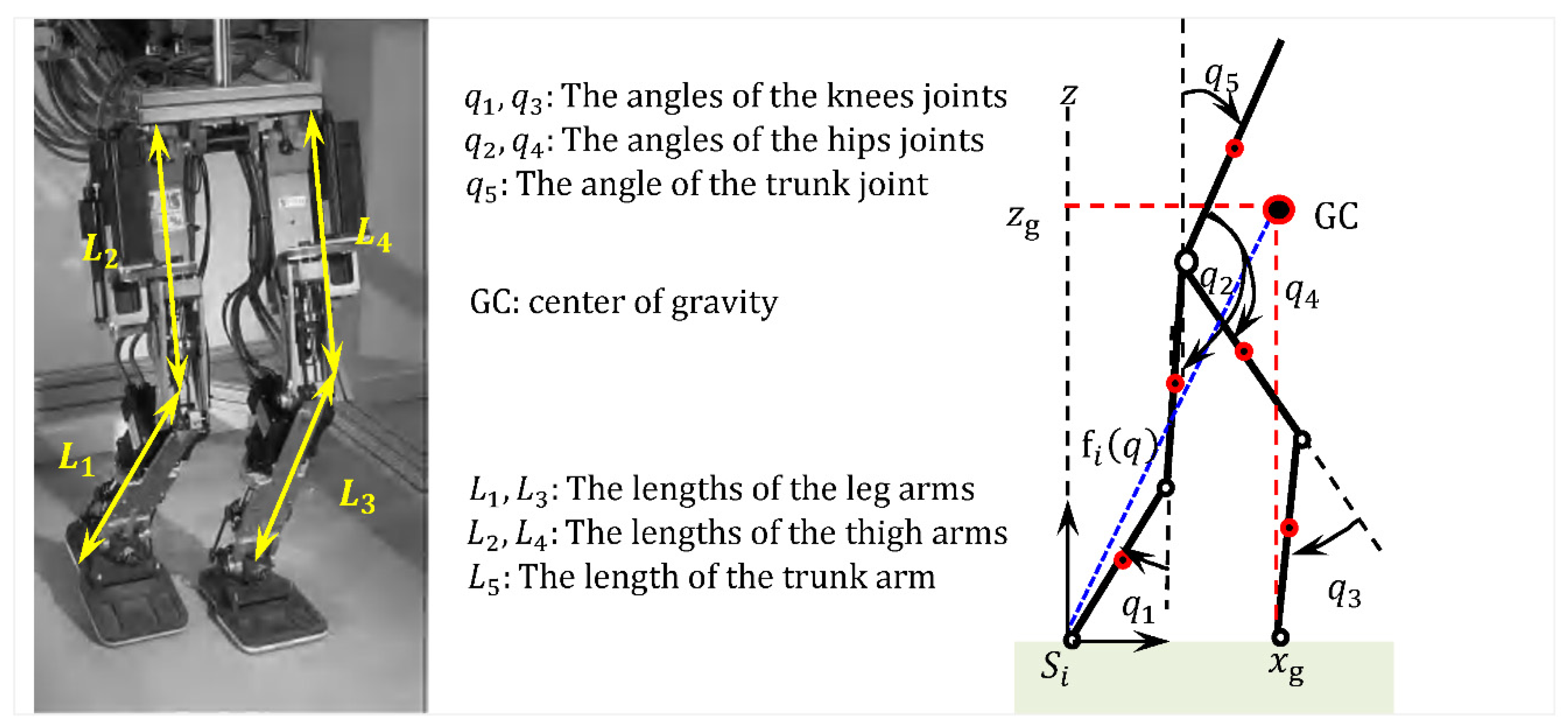
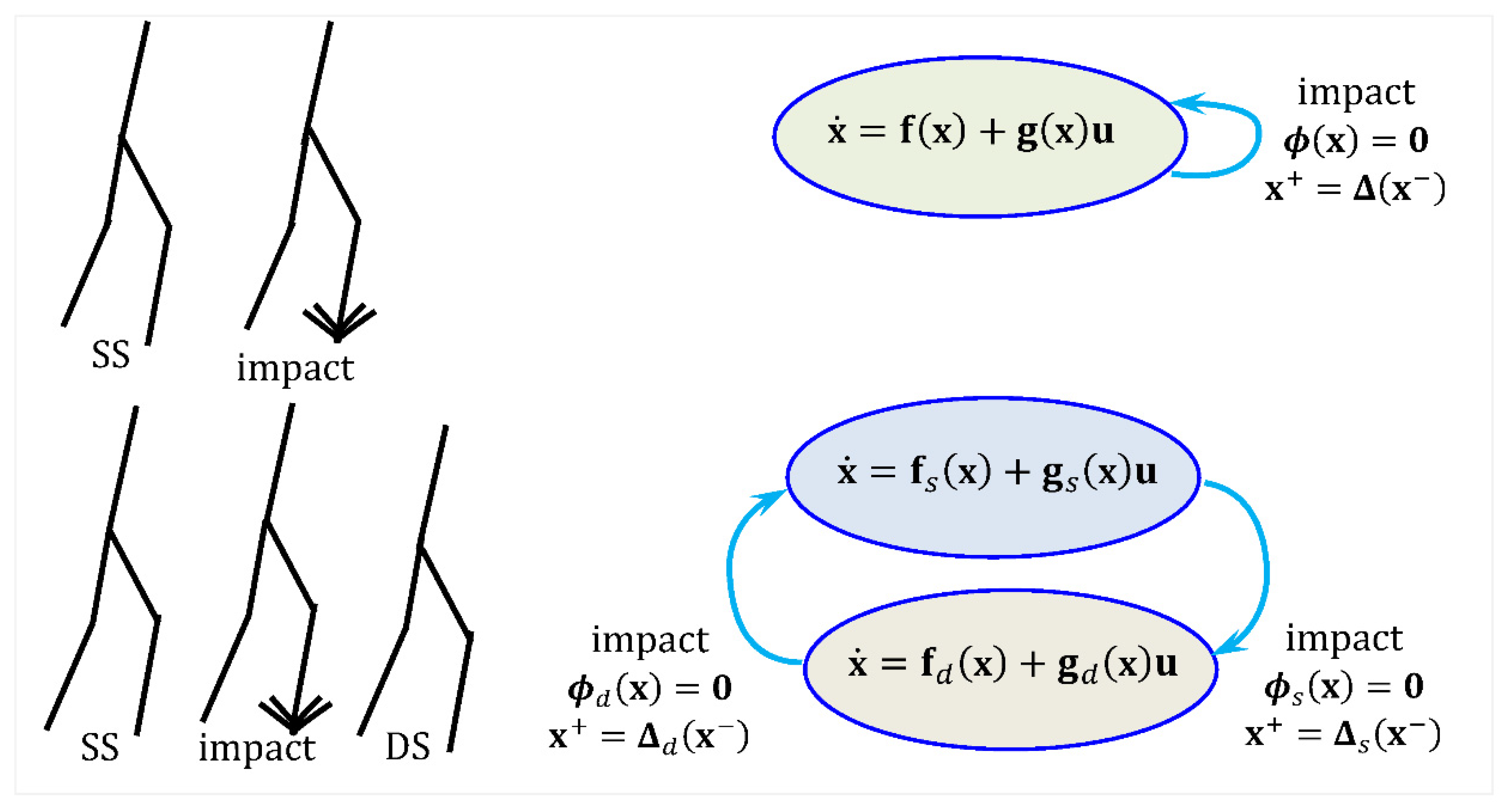
2. Mathematical Modeling of Bipedal Locomotion
- ▪
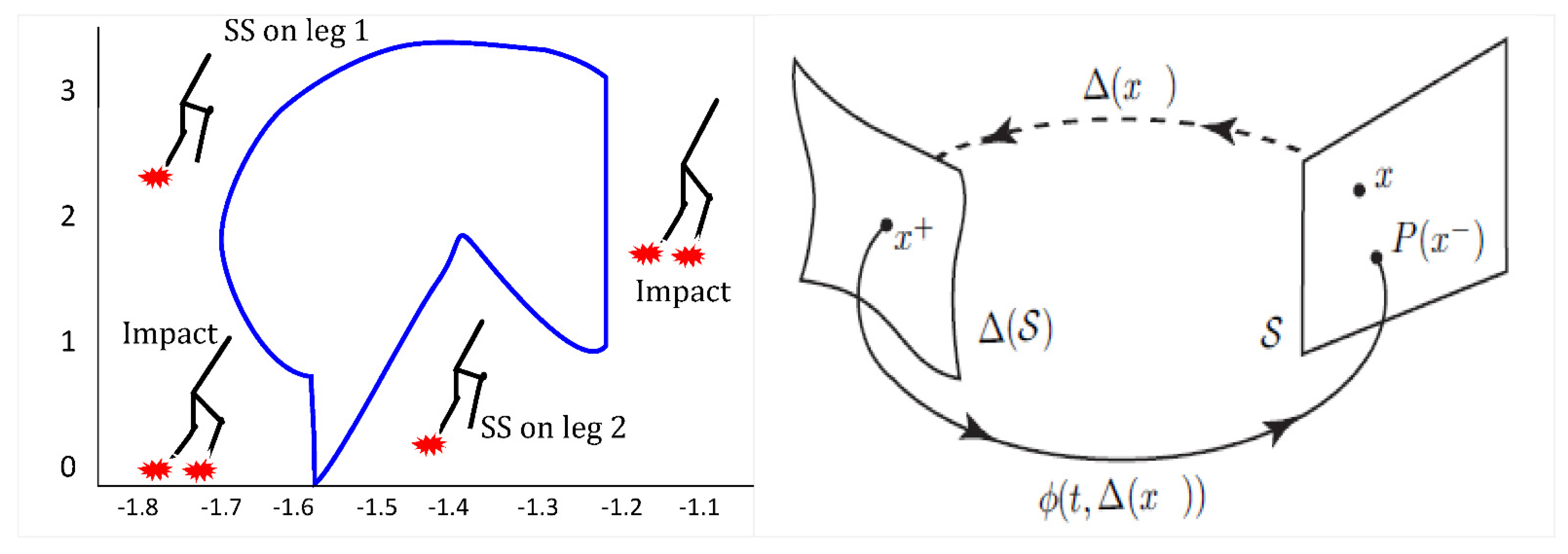
- Single-support phase or swing phase, during which the locomotion system evolves as an open kinematic chain (one foot on the ground and the other is free).
- ▪
- Double-support phase, during which the locomotion system moves as a closed kinematic loop (both feet on the ground).
2.1. Kinematic and Dynamic Modeling of Biped Robots (Diff Phases)
- ▪
- is the vector of generalized forces/torques;
- ▪
- is the of the system;
- ▪
- are the total kinetic and potential energies of the system;
- ▪
- are the vectors of the generalized positions and velocities.
- is the mass of the body (if we neglect feet, then ).
- is the moment of inertia at the center of gravity along axis .
- is the moment of inertia of motor around the axis.
- is the distance from body ’s center of gravity to its frame origin.
2.2. The Model of Impacts
2.3. Symbolic Calculations of the Model
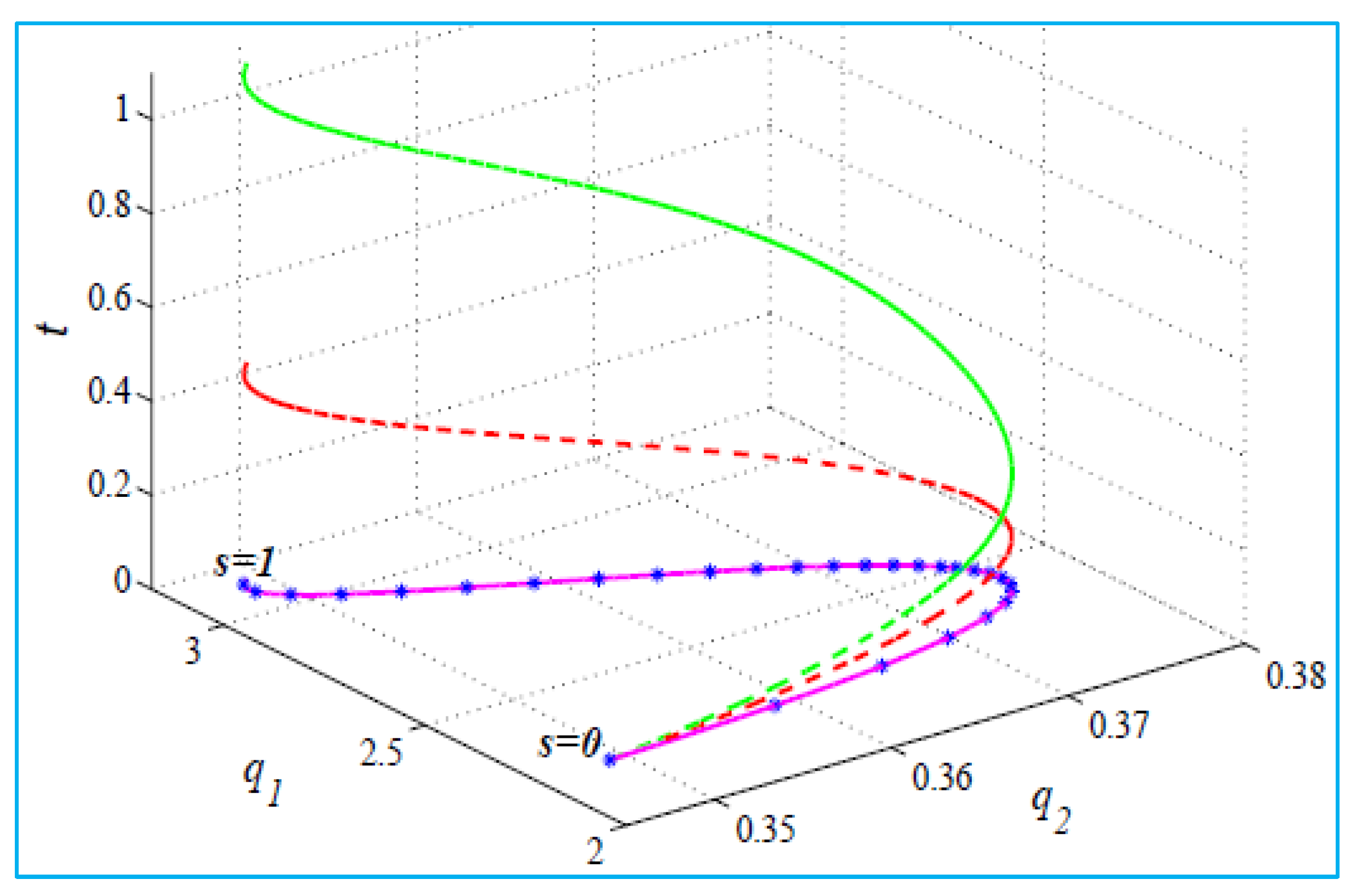
2.4. Optimal Trajectories Generation
- Here, = initial configuration, and = final configuration.
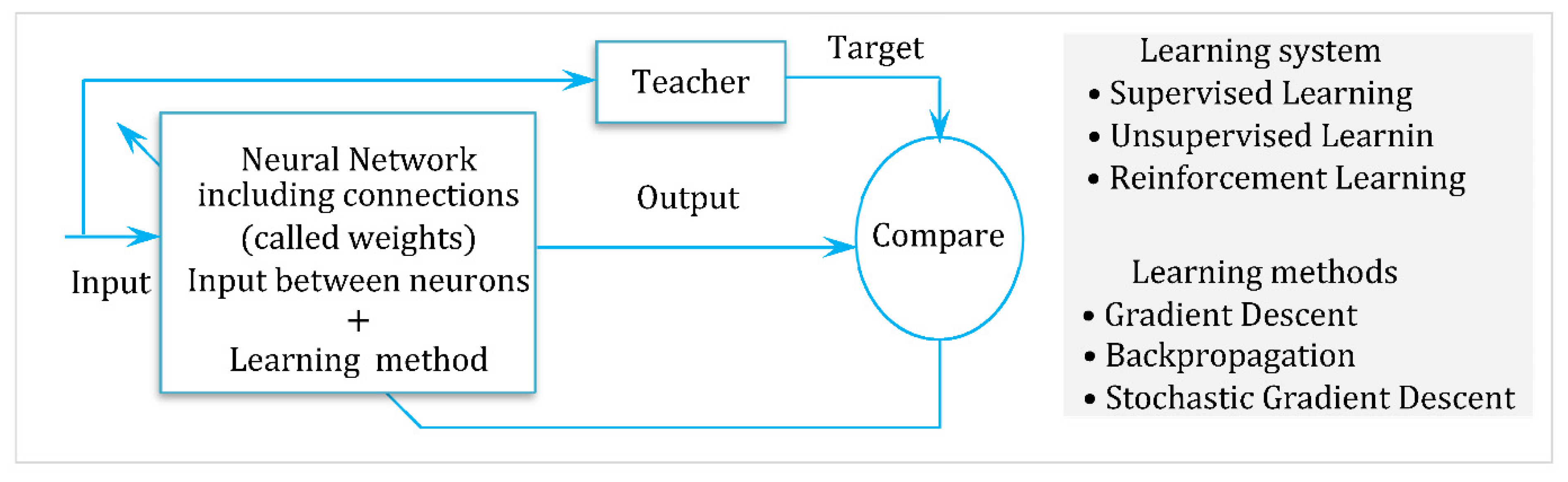
3. Basics of Intelligent Adaptive Control and Neural Networks
3.1. Neural Networks and Global Approximation Theory
- is a nonlinear function that acts element-wise on vectors;
- , , and are the approximator parameters;
- is an index of approximation.
| • Fuzzy neural networks. • Polynomial basis function network. • Gaussian RBF networks. | • Radial basis function networks. • Wavelet neural networks. • General form neural networks. |
- is the activation vector.
- is the output weight matrix.
- denotes nonlinear sigmoid activation functions (e.g., tanh, ReLUs, etc.).
- is the stacked weight matrix ( row is ); denotes biases.
- The exponential and division are element-wise.
3.2. Radial Basis Function Neural Networks and Training
- is the center of the basis function, ;
- is the width (spread), and it measures the similarity between and ;
- .
| Algorithm 1: RBF Neural Network Training via Gradient Descent |
 |
3.3. Adaptive Neural Network Control
- is the input vector (joint positions and velocities);
- is the RBF vector, defined by , ;
- is the ideal weight matrix.
4. Stability and Control of RABBIT Robot
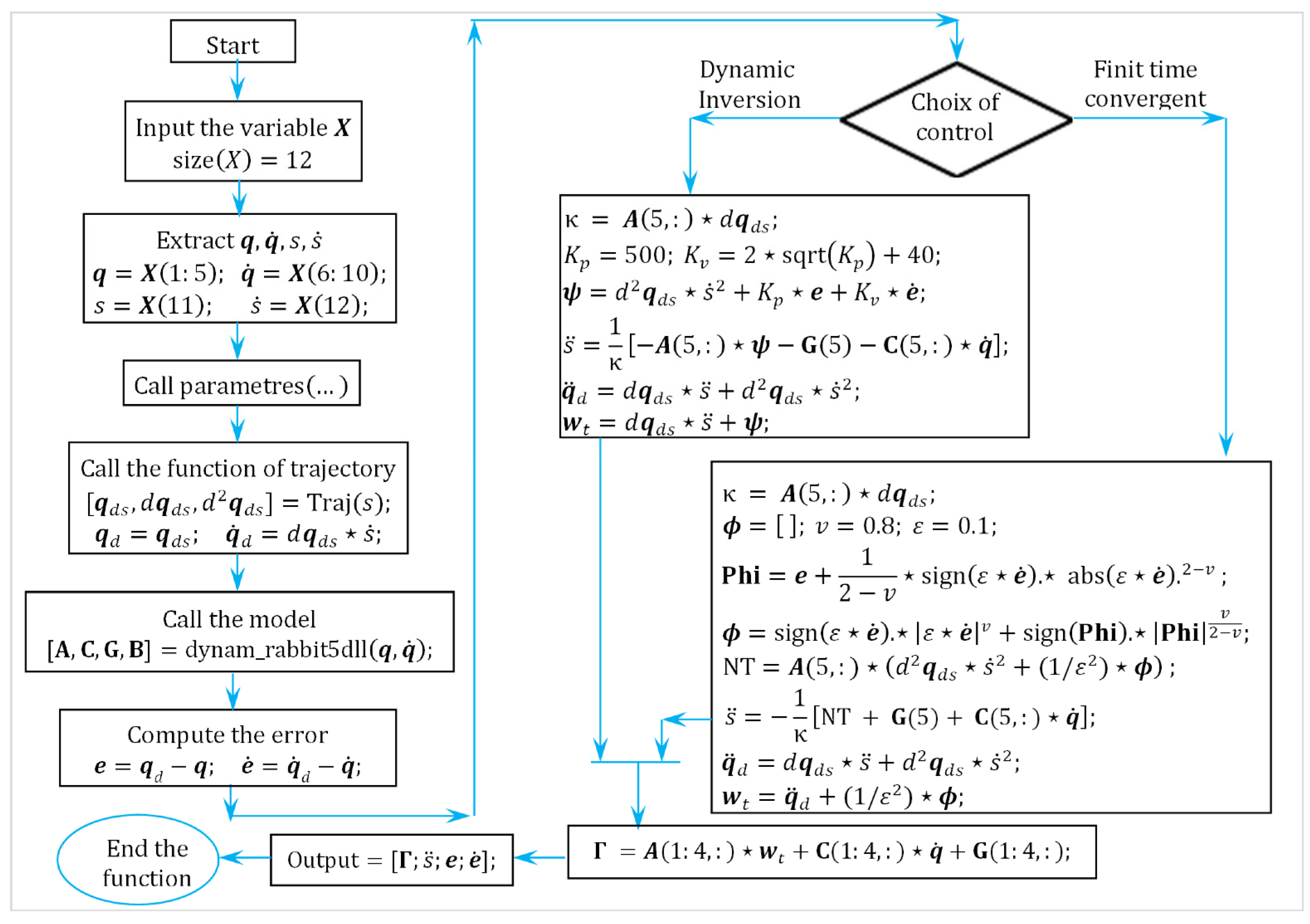
4.1. Nonlinear Decoupling Control
4.2. Finite-Time Convergent Control
4.3. The Proposed Adaptive Finite-Time Convergent Control
- If and , any initial value yields cyclic ref-motion.
- If and or if values and have different signs, then there is no cyclic reference motion.
- The previous equation has a unique solution if and only if values and have the same sign.
- Sampling and Discretization Framework: The control algorithm was implemented on a real-time platform with a fixed sampling rate of . To discretize the continuous-time controller, we adopted zero-order hold (ZOH) assumptions, which consider control inputs constant between samples. The state updates are computed at each sampling instant.
- Discretization of the Control Law: The control law includes the following:
- An FTC correction term (including the dynamic inversion);
- An adaptive RBF neural network compensation term
- includes fractional or high-gain error terms computed via FTCC logic;
- .
- 3.
- Numerical Differentiation: Velocity and acceleration are approximated by and . Given the sensitivity of numerical differentiation to noise, digital filters (e.g., low-pass filters, Kalman filter, or Savitzky–Golay filter) are employed to smooth the signals, ensuring accurate derivative estimation without amplifying measurement noise.
- 4.
- Neural Network Online Update: The RBF neural network is trained online using discrete adaptation: . This ensures real-time learning while keeping the update rate within the system’s computational limits.
- 5.
- Real-Time Execution: The full control loop is executed at each sampling instant on the dSPACE DS1103 platform. The timing constraints ( were met through:
- Efficient MATLAB/Simulink code generation;
- Pre-computation and lookup tables for RBF activations;
- Optimization of matrix operations and control scheduling.
- 6.
- Validation and Testing: Discrete implementation was tested via the following:
- Hardware-in-the-loop (HIL) simulation;
- Real-time experiments under various scenarios.
- 7.
- Performance Preservation: The discretized control law successfully preserved key properties of the original continuous-time formulation, including the following:
- FTC convergence through gain-tuned discretization framework;
- Robustness to uncertainties maintained via filtering and adaptive NN updates;
- Bounded control effort and tracking ensured through careful discretization and real-time computation strategies.
| Algorithm 2: The complete algorithm of the implemented discrete control law |
 |
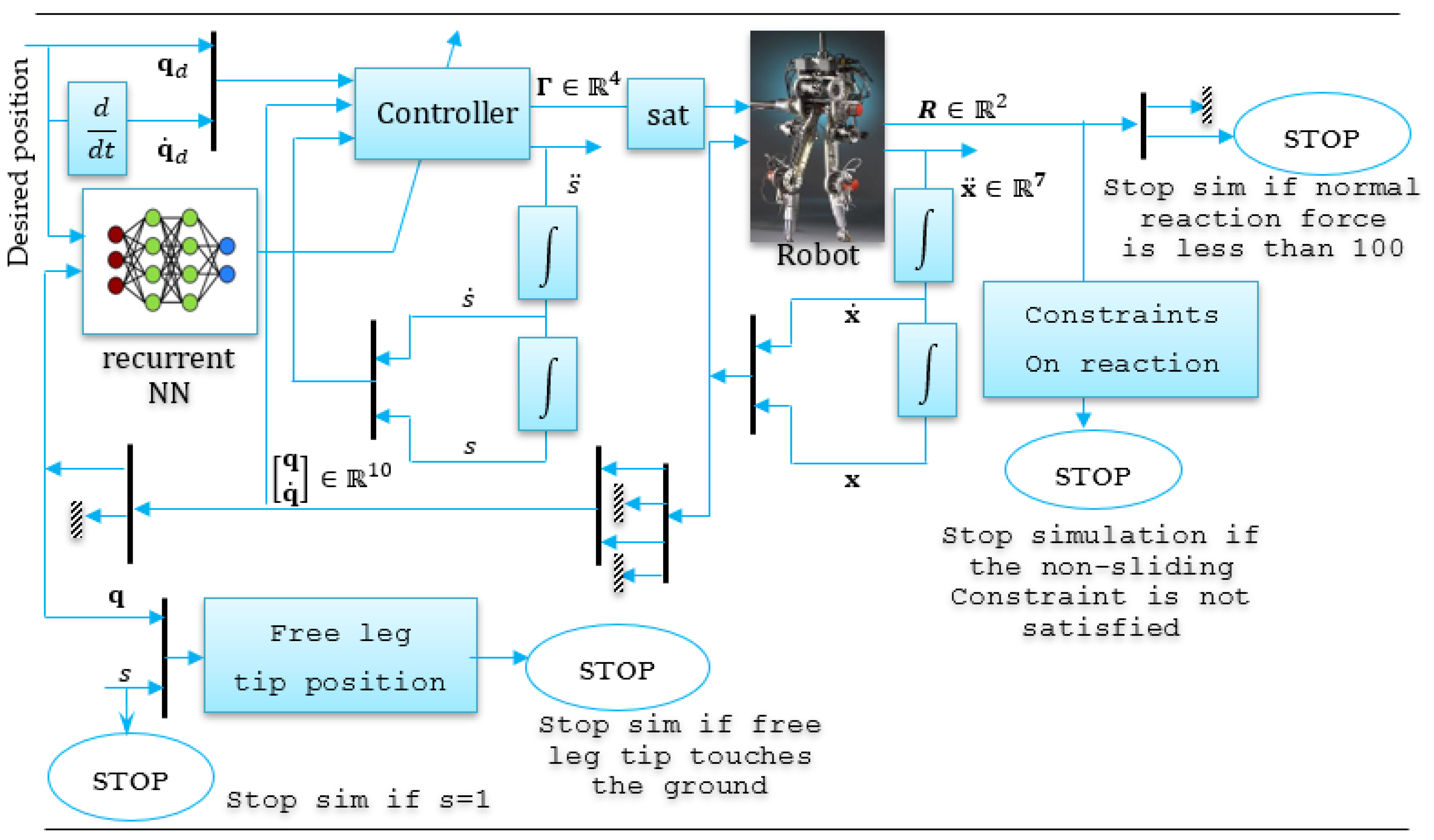
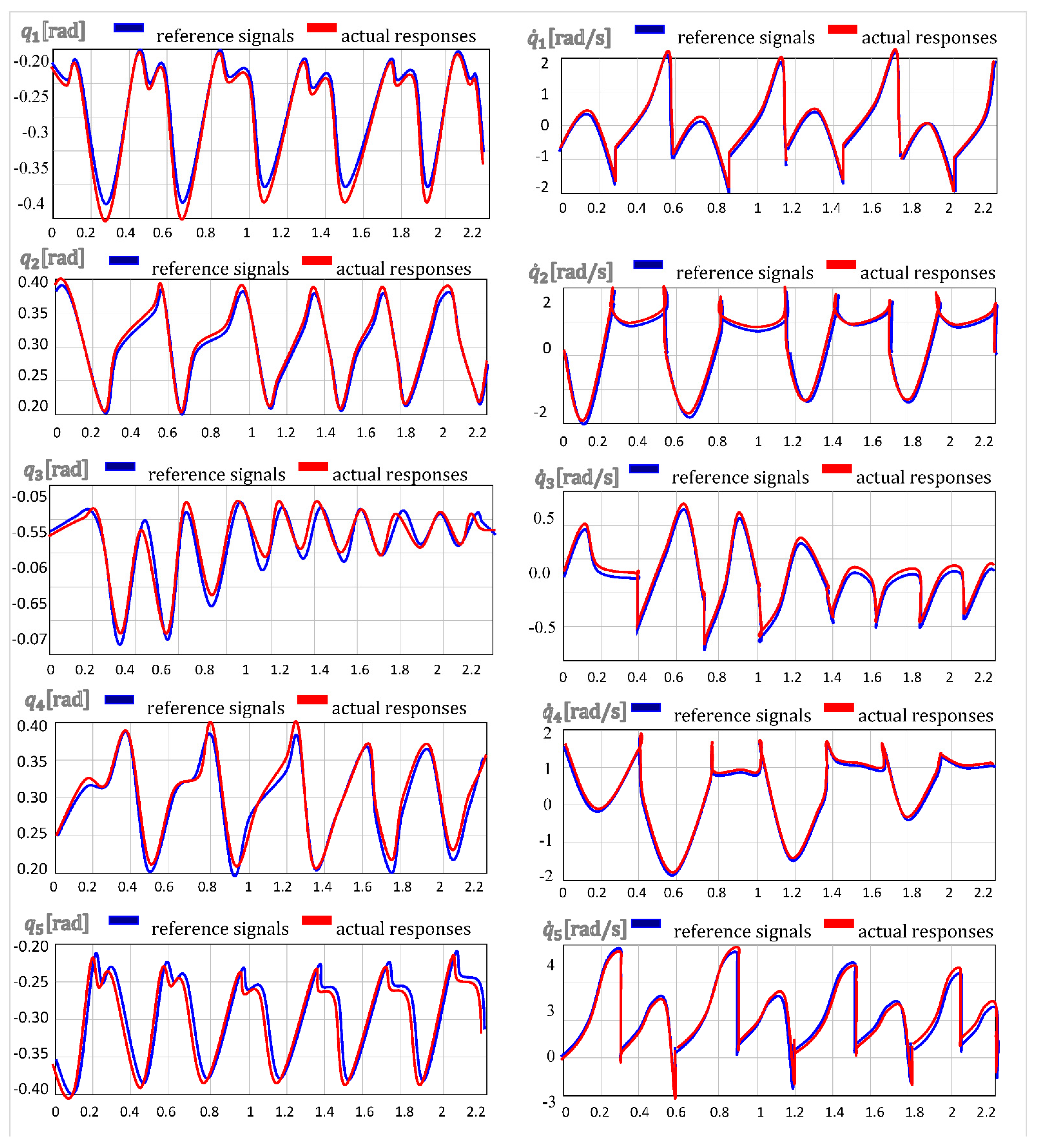
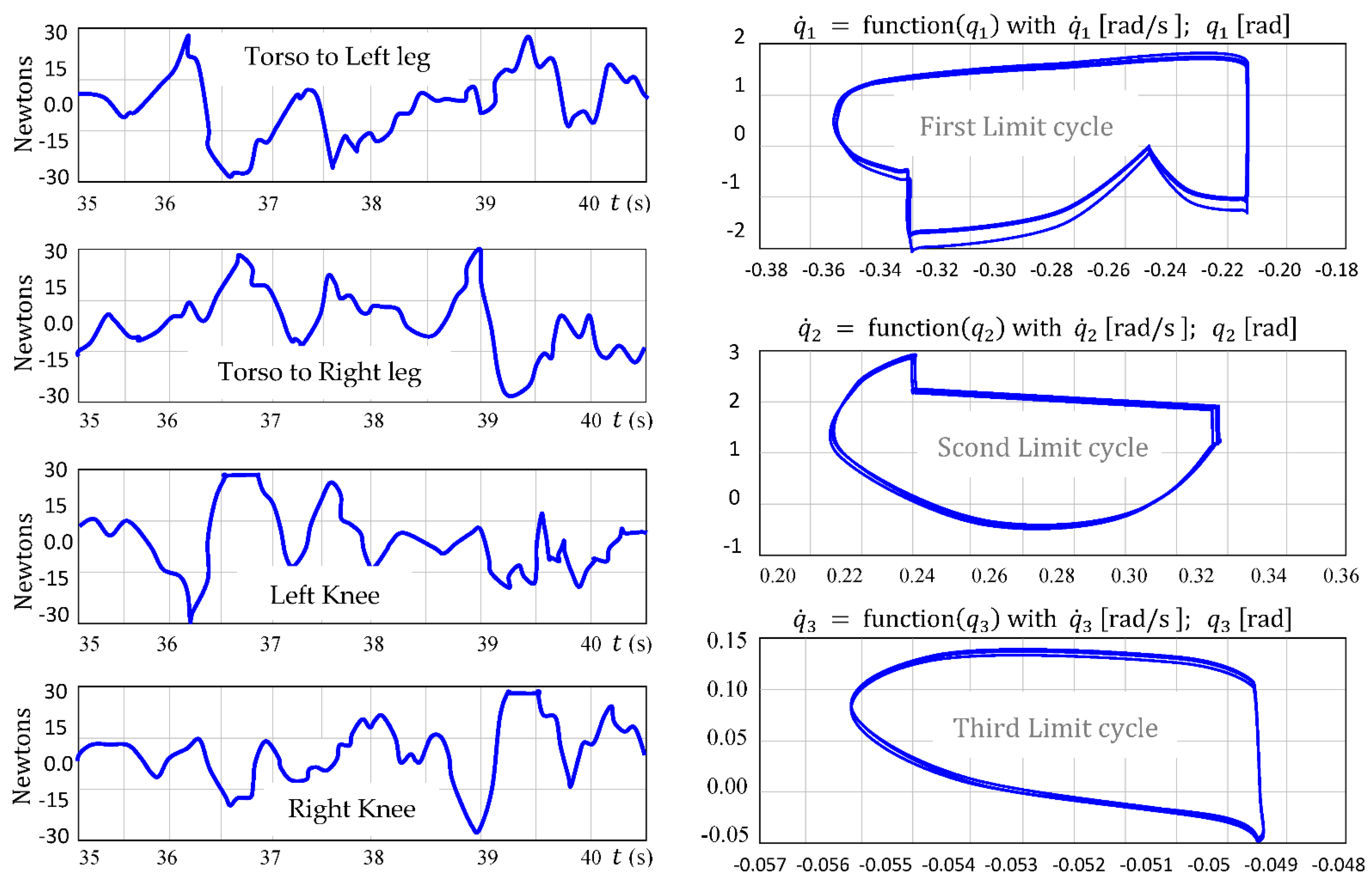
5. Experimental Results of the RABBIT Robot
- Friction in the motor–belt–gear assemblies and at the tower’s universal joint;
- Unmodeled flex dynamics due to cabling, gear torsion, and deformation;
- Inaccuracies due to poor estimates of link inertias + dSPACE + power electronics;
- Digital implementation limitations (e.g., sampling, quantization);
- Non-rigid impacts due to compliance at the end of the leg, etc.
- Joint Backlash Tolerance: ±0.8° due to slack and gear tolerances.
- Linkage Compliance: Up to 1.2 mm deflection under peak load.
- Assembly Misalignments: Errors up to ±0.5 mm between joint axes.
- Flexibility: ~2–3 mm compliance in the foot–ground interface, damping vibrations.
- Unmodeled Dynamics: 4–6% damping from residual friction stabilizes oscillations.
| •The 1 function: Main Program | The primary script coordinating the simulation. |
| •The 2 function: robot_parametres | Defines the physical parameters of the robot. |
| •The 3 function: [Out1] = dm7dof (Entree1) | Computes the dynamic equations of the 7 DOF robot. |
| •The 4 function: [Out] = reaction_forcesde (R1) | Calculates the ground reaction forces. |
| •The 5 function: [qp,Ir] = impact (qf,qpf) | Models the impact phase/computes post-impact velocities. |
| •The 6 function: [A,Ac1,Ac2] = dynam_impact (qf) | Computes dynamic matrices related to the impact. |
| •The 7 function: [qd_s,dqd_s,ddqd_s] = Traj (s) | Generates the desired trajectory. |
| •The 8 function: stick_inf (x) | Displays or manages the stick-figure representation. |
| •The 9 function: [Out] = pos_swing_leg (Entree) | Computes the position of the swing leg. |
| •The 10 function: [Out] = discrete_control _law (Entree) | Implements the discrete-time control law. |
| •The 11 function: [A,C,G,B,Ac1,hxs] = dyn_7dof_rabbit (q,dq) | Returns the full dynamic model of the 7 DOF RABBIT. |
| •The 12 function: [A,C,G,B] = dynam_5dof_rabbit (q,dq) | Provides the reduced 5 DOF dynamic model. |
| •The 13 function: [dqp,F] = post_impact_dynamics (q,dqm) | Calculates post-impact dynamics. |
| •The 14 function: dess (tout,ERR,ERRP,qp,qpp,R,pos_p,Gama) | Handles the graphical visualization of the results. |
- IAE: Integral of absolute error (total error over time; insensitive to early transients).
- ISE: Integral squared error (indicates large deviations; sensitive to overshoots).
- ITAE: Integral time absolute error (Weights late errors; sensitive to slow settling)
- Higher robustness under uncertainties, maintaining stable gait under actuator saturation, payload variation (>20%), and ground contact perturbations.
- Real-time adaptability, thanks to the online learning capability of RBF neural networks integrated within a finite-time control backbone.
6. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Abbreviations
| CPG | Central pattern generators; | NN | Neural network; |
| DOF | Degree of freedom; | IAE | Integral absolute error; |
| FTCC | Finite-time convergent control; | ISE | Integral square error; |
| MLP | Multi-layer perceptron; | ITAE | Integral time absolute error; |
| MIMO | Multi-input multi-output; | RBF | Radial basis function; |
| MRAC | Model reference adaptive control; | RBFNN | Radial basis function neural network; |
| NDC | Nonlinear decoupling control; | ZMP | Zero-moment point. |
Appendix A

Appendix B

References
- Gubina, F. On the Dynamic Stability of Biped Locomotion. IEEE Trans. Biomed. Eng. 1974, 21, 102–108. [Google Scholar] [CrossRef] [PubMed]
- Hemami, H. The Inverted Pendulum and Biped Stability. Math. Biosci. 1977, 34, 95–110. [Google Scholar] [CrossRef]
- Hemami, H. Postural Stability of Two Biped Models via Lyapunov Second Method. IEEE Trans Autom. Control. 1977, 22, 66–70. [Google Scholar] [CrossRef]
- Hemami, H. A Feedback On-Off Model of Biped Dynamics. In Proceedings of the International Conference on Cybernetics and Society, Denver, CO, USA, 8–10 October 1979. [Google Scholar]
- Hemami, H. Modeling and Control of Constrained Dynamic Systems with Application to Biped Locomotion. IEEE Trans. Autom. Control 1979, 24, 526–535. [Google Scholar] [CrossRef]
- Hemami, H. Stability of Planar Biped Models by Simultaneous Pole Assignment and Decoupling. Int. J. Syst. Sci. 1980, 11, 65–75. [Google Scholar] [CrossRef]
- Hemami, H. Initiation of Walk and Tiptoe of a Planar Nine-Link Biped. Math. Biosci. 1982, 61, 163–189. [Google Scholar] [CrossRef]
- Hemami, H. Some Aspects of Euler-Newton Equations of Motion. Ing. Arch. 1982, 52, 167–176. [Google Scholar] [CrossRef]
- Han, J.-Y.; Hemami, H. Nonlinear Adaptive Control of an N-Link Robot with Unknown Load. Int. J. Robot. Res. 1987, 6, 71–86. [Google Scholar] [CrossRef]
- Saleem, O.; Abbas, F.; Iqbal, J. Complex fractional-order LQIR for inverted-pendulum-type robotic mechanisms—Design and experimental validation. Mathematics 2023, 11, 913. [Google Scholar] [CrossRef]
- Afifa, R.; Ali, S.; Pervaiz, M.; Iqbal, J. Adaptive backstepping integral sliding mode control of a MIMO separately excited DC motor. Robotics 2023, 12, 105. [Google Scholar] [CrossRef]
- Cheng, M.Y.; Lin, C.S. Genetic Algorithm for Control Design of Biped Locomotion. J. Robot. Syst. 1997, 14, 365–373. [Google Scholar] [CrossRef]
- Kasiyanchuk, D.A. Planar Walking of a Five-Link Biped Robot over a Stepped Surface with Obstacles of Different Heights and Lengths. J. Phys. Conf. Ser. 2024, 2701, 012020. [Google Scholar] [CrossRef]
- Awan, Z.S.; Ali, K.; Iqbal, J.; Mehmood, A. Adaptive backstepping based sensor and actuator fault tolerant control of a manipulator. J. Electr. Eng. Technol. 2019, 14, 2497–2504. [Google Scholar] [CrossRef]
- Saleem, O.; Ali, S.; Iqbal, J. Robust MPPT control of stand-alone photovoltaic systems via adaptive fractional-order PID controller with self-adjusting fractional orders. Energies 2023, 16, 5039. [Google Scholar] [CrossRef]
- Behzad, D. Multi-Modal Analysis of Human Motion From External Measurements. Trans. ASME 2001, 123, 272–278. [Google Scholar]
- Chevallereau, C. Parameterized Control for an Under-Actuated Biped Robot. In Proceedings of the 15th Triennial World Congress, Barcelona, Spain, 21–26 July 2002; Volume 35, pp. 539–544. [Google Scholar]
- Chevallereau, C. RABBIT: A Testbed for Advanced Control Theory. IEEE Control. Syst. Mag. 2003, 23, 5. [Google Scholar]
- Chevallereau, C. Tracking a Joint Path for the Walk of an Underactuated Biped, Robotica; Cambridge University Press: Cambridge, UK, 2004; Volume 22, pp. 15–28. [Google Scholar]
- Grizzle, J.W. Nonlinear Control of Mechanical Systems with an Unactuated Cyclic Variable. IEEE Trans. Autom. Control 2005, 50, 5. [Google Scholar] [CrossRef]
- Djoudi, D. Optimal Reference Motions for Walking of a Biped Robot. In Proceedings of the 2005 IEEE International Conference on Robotics and Automation, Barcelona, Spain, 18–22 April 2005. [Google Scholar]
- Djoudi, D. Stability Analysis of a Walk of a Biped with Control of the ZMP. In Proceedings of the IEEE/RSJ International Conference on Intelligent Robots and Systems, Edmonton, AB, Canada, 2–6 August 2005. [Google Scholar]
- Djoudi, D. Feet Can Improve the Stability Property of a Control Law for a Walking Robot. In Proceedings of the 2006 IEEE International Conference on Robotics and Automation, Orlando, FL, USA, 15–19 May 2006. [Google Scholar]
- Choi, T.-Y. A Hybrid SOF-PID Controller for a MIMO Biped Robot. Artif. Life Robot. 2006, 10, 69–72. [Google Scholar] [CrossRef]
- Djoudi, D. Contribution à la Commande D’un Robot Bipède. Ph.D. Thesis, Central School of Nantes, Nantes, France, 2007. [Google Scholar]
- Yilei, W. Robust Recurrent Neural Network Control of Biped Robot. J. Intell. Robot. Syst. 2007, 49, 151–169. [Google Scholar]
- Vukobratovi, M.K. Contribution to the Integrated Control of Biped Locomotion Mechanisms. Int. J. Humanoid Robot. 2007, 4, 49–96. [Google Scholar] [CrossRef]
- Westervelt, E.R.; Chevallereau, C. Feedback Control of Dynamic Bipedal Robot Locomotion; CRC Press: Boca Raton, FL, USA, 2007. [Google Scholar]
- Djoudi, D. A Path-Following Approach to Stable Bipedal Walking and Zero Moment Point Regulation. In Proceedings of the 2007 IEEE International Conference on Robotics and Automation, Roma, Italy, 10–14 April 2007. [Google Scholar]
- Chevallereau, C. Stable Bipedal Walking with Foot Rotation Through Direct Regulation of the Zero Moment Point. IEEE Trans. Robot. 2008, 24, 390–401. [Google Scholar] [CrossRef]
- Chevallereau, C. Bipedal Robots Modeling, Design and Walking Synthesis; Wiley-ISTE: Hoboken, NJ, USA, 2009. [Google Scholar]
- Grizzle, J.W. Models, Feedback Control, and Open Problems of 3D Bipedal Robotic Walking. Automatica 2014, 50, 1955–1988. [Google Scholar] [CrossRef]
- Wang, T. Stable Walking Control of a 3D Biped Robot with Foot Rotation, Robotica; Cambridge Press: Cambridge, UK, 2014; Volume 32. [Google Scholar]
- Liu, Y. Human-Like Walking with Heel Off and Toe Support for Biped Robot. Appl. Sci. 2017, 7, 499. [Google Scholar] [CrossRef]
- Hemami, H. Human and Robotic Movement in the Air. Comput. Electr. Eng. 2020, 81, 106496. [Google Scholar] [CrossRef]
- Kim, D. Dynamic Locomotion for Passive-Ankle Biped Robots and Humanoids Using Whole-Body Locomotion Control. Int. J. Robot. Res. 2020, 39, 936–956. [Google Scholar] [CrossRef]
- Kakaei, M.M. New Robust Control Method Applied to the Locomotion of a 5-Link Biped Robot. Robotica 2020, 38, 2023–2038. [Google Scholar] [CrossRef]
- Martínez-Castelán, J.N.; Villarreal-Cervantes, M.G. Integrated Structure-Control Design of a Bipedal Robot Based on Passive Dynamic Walking. Mathematics 2021, 9, 1482. [Google Scholar] [CrossRef]
- Khoi, P.B.; Nguyen Xuan, H. Fuzzy Logic-Based Controller for Bipedal Robot. Appl. Sci. 2021, 11, 11945. [Google Scholar] [CrossRef]
- Li, Z.; Peng, X.B.; Abbeel, P.; Levine, S.; Berseth, G. Sreenath. Reinforcement learning for versatile, dynamic, and robust bipedal locomotion control. Int. J. Robot. Res. 2024, 44, 840–888. [Google Scholar] [CrossRef]
- Wu, Y.; Tang, B.; Qiao, S.; Pang, X. Bionic Walking Control of a Biped Robot Based on CPG Using an Improved Particle Swarm Algorithm. Actuators 2024, 13, 393. [Google Scholar] [CrossRef]
- Wu, Y.; Tang, B.; Tang, J.; Qiao, S.; Pang, X.; Guo, L. Stable Walking of a Biped Robot Controlled by Central Pattern Generator Using Multivariate Linear Mapping. Biomimetics 2024, 9, 626. [Google Scholar] [CrossRef] [PubMed]
- Gao, H.; Wang, S.; Shan, K.; Mu, C.; Wang, X.; Su, B.; Yu, H. Stable Rapid Sagittal Walking Control for Bipedal Robot Using Passive Tendon. Actuators 2024, 13, 240. [Google Scholar] [CrossRef]
- Yamano, J.; Kurokawa, M.; Sakai, Y.; Hashimoto, K. Realization of a Human-like Gait for a Bipedal Robot Based on Gait Analysis. Machines 2024, 12, 92. [Google Scholar] [CrossRef]
- Mou, H.; Tang, J.; Liu, J.; Xu, W.; Hou, Y.; Zhang, J. High Dynamic Bipedal Robot with Underactuated Telescopic Straight Legs. Mathematics 2024, 12, 600. [Google Scholar] [CrossRef]
- Xu, Z.; Xie, J.; Hashimoto, K. Human-Inspired Gait and Jumping Motion Generation for Bipedal Robots Using Model Predictive Control. Biomimetics 2025, 10, 17. [Google Scholar] [CrossRef] [PubMed]
- Yang, T.; Tong, Y.; Zhang, Z. Flexible Model Predictive Control for Bounded Gait Generation in Humanoid Robots. Biomimetics 2025, 10, 30. [Google Scholar] [CrossRef]
- Khalil, W.; Dombre, E. Modélisation, Identification et Commande des Robots; Hermes Science Publications: Cachan, France, 1999. [Google Scholar]
- Slotine, J.-J.E. Applied Nonlinear Control; Prentice-Hall: Hoboken, NJ, USA, 1991. [Google Scholar]
- Bhat, S.P. Continuous finite-time stabilization of the translational and rotational double integrators. IEEE Trans. Autom. Control 1998, 43, 678–682. [Google Scholar] [CrossRef]
- Nayfeh, A.H.; Mook, D.T. Nonlinear Oscillations; John Wiley and Sons: New York, NY, USA, 1976. [Google Scholar]
- Tejeda, Y.G. Deep Learning with Convolutional Neural Networks: A Compact Holistic Tutorial with Focus on Supervised Regression. Mach. Learn. Knowl. Extr. 2024, 6, 2753–2782. [Google Scholar] [CrossRef]
- Manca, V. Artificial Neural Network Learning, Attention, and Memory. Information 2024, 15, 387. [Google Scholar] [CrossRef]
- Mienye, I.D. Recurrent Neural Networks: A Comprehensive Review of Architectures, Variants, and Applications. Information 2024, 15, 517. [Google Scholar] [CrossRef]
- Cabello, J.G. Mathematical Neural Networks. Axioms 2022, 11, 80. [Google Scholar] [CrossRef]
- Yang, L.; Lai, G.; Chen, Y.; Guo, Z. Online Control for Biped Robot with Incremental Learning Mechanism. Appl. Sci. 2021, 11, 8599. [Google Scholar] [CrossRef]
- Alemayoh, T.T.; Lee, J.H.; Okamoto, S. A Deep Learning Approach for Biped Robot Locomotion Interface Using a Single Inertial Sensor. Sensors 2023, 23, 9841. [Google Scholar] [CrossRef] [PubMed]
- Wurzberger, F.; Schwenker, F. Learning in Deep Radial Basis Function Networks. Entropy 2024, 26, 368. [Google Scholar] [CrossRef]
- Yang, Y. A Novel Radial Basis Function Neural Network with High Generalization Performance for Nonlinear Process Modelling. Processes 2022, 10, 140. [Google Scholar] [CrossRef]
- Kuo, P.-H. Artificial rabbits optimization–based motion balance system for the impact recovery of a bipedal robot. Adv. Eng. Inform. 2025, 63, 102965. [Google Scholar] [CrossRef]
- Bekhiti, B. On Hyper-Stability Theory Based Multivariable Nonlinear Adaptive Control: Experimental Validation on Induction Motors. IET Electr. Power Appl. 2025, 19, e70035. [Google Scholar] [CrossRef]
- Scaldaferri, A.; Angelini, F. Learning to Walk with Adaptive Feet. Robotics 2024, 13, 113. [Google Scholar] [CrossRef]
- Marquez-Acosta, E. Experimental Validation of the Essential Model for a Complete Walking Gait with the NAO Robot. Robotics 2024, 13, 123. [Google Scholar] [CrossRef]








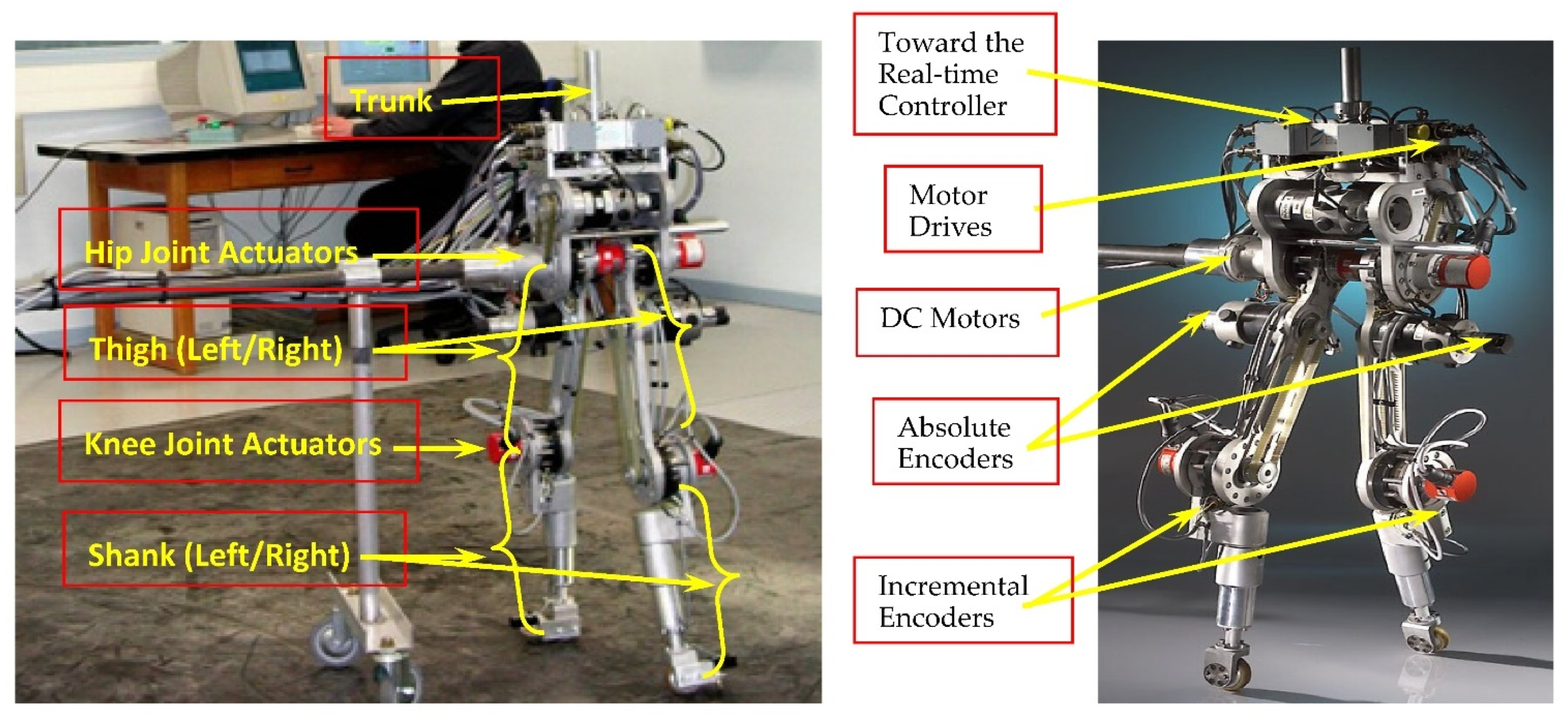






| Trunk | Thigh | Leg | Foot | Motors and Gears | ||
|---|---|---|---|---|---|---|
| 17.000 | 6.800 | 3.230 | 1.000 | Maximum torque [Nm] | 150 | |
| The length | 0.6000 | 0.400 | 0.472 | 0.250 | Reduction ratio | 50 |
| Inertia | 2.2200 | 0.250 | 0.400 | 0.012 | Gears’ inertia | |
| Center of inertia | 0.1434 | 0.163 | 0.127 | 0.000 | ||
| Component | Model and/or Size (Specification) | Manufacturer |
|---|---|---|
| DC motors | RS420J | Parvex SA, Dijon, France |
| Motor current drives | RS420 RTS10/20-60 | Parvex SA, Dijon, France |
| Incremental encoders (motors) | C4 (250 counts/rev) | Parvex SA, Dijon, France |
| Absolute encoders (joints) | CHM 506 P426R/8192/16 (8192 counts/rev) | Ideacod, Strasbourg, France |
| Incremental encoders (central tower) | GHM5 | Ideacod, Strasbourg, France |
| Gear reducers | HFUS-2UH, size: 25 (ratio: 1/50) | HDT T-Cup, Peabody, MA, USA |
| Real-time controller | DS1103 (400 MHz PowerPC 604e DSP) | dSpace, Paderborn, Germany |
| Stage | Difficulties Encountered | Solution Strategies |
|---|---|---|
| Establishing the Early Model | Complexity of system dynamics: • Nonlinear, high dimensional. • Coupled dynamics in bipedal and MIMO structure, leading to modeling challenges. Simplifications may cause inaccuracies. Parameter uncertainty and variations in mass, friction, and actuator parameters complicate precise modeling. | • We used high-fidelity simulation tools with advanced noise filters ( filter) and identification techniques for accurate models. • We incorporated intelligent adaptive and robust approaches to handle uncertainties. • We employed machine learning (i.e., networks) to approximate complex dynamics. |
| Method Design | Ensuring stability and convergence: Guaranteeing controller stability under uncertainties and disturbances. Real-time implementation constraints: Achieving fast computation for real-time control with complex algorithms like neural networks. | • We used techniques and adaptive networks for rapid, stable tracking. • We optimized algorithms for efficiency and tested them on platforms prior experiment. • We conducted extensive hardware-in-the-loop () tests to validate stability. |
| ExperimentalProcess | Hardware limitations and noise: • Sensor noise. • Actuator saturation. • Mechanical imperfections. Environmental disturbances and external factors: • Disturbances causing deviations. Safety concerns: risks of damage during testing. | • We implemented safety protocols such as soft limits and emergency stops and used sensor filtering and noise reduction techniques. • We adopted a phased testing approach: simulations → HIL → real-world experiments. • We incorporated robustness features into the control design to manage disturbances |
| Joint | Mean (Rad) | Std Dev (Rad) | 95% CI Lower | 95% CI Upper | Conv-Time(s) | Std Dev (s) | Mean (Nm) | Std Dev |
|---|---|---|---|---|---|---|---|---|
| Hip L | 0.02090 | 0.00149 | 0.01905 | 0.02275 | 0.77 | 0.016 | 38.43 | 3.53 |
| Knee L | 0.01504 | 0.00108 | 0.01370 | 0.01637 | 0.69 | 0.015 | 31.68 | 2.45 |
| Hip R | 0.02146 | 0.00138 | 0.01975 | 0.02317 | 0.78 | 0.014 | 40.36 | 4.28 |
| Knee R | 0.01739 | 0.00155 | 0.01546 | 0.01932 | 0.65 | 0.013 | 34.69 | 2.12 |
| Control Strategy | Settling | Overshoot | Comments | |||
|---|---|---|---|---|---|---|
| Classical MIMO nonlinear decoupling control [23] | 3.72 | 7.98 | 2.10 | 2.83 [s] | 14.65% | Slower settling, visible overshoot, and coupling between joints |
| Non-adaptive finite-time convergent control [19] | 2.48 | 5.10 | 1.32 | 1.95 [s] | 8.75% | Better transient performance, smoother adaptation |
| Proposed MIMO neural adaptive control | 1.36 | 2.43 | 0.68 | 1.24 [s] | 2.21% | Fast convergence, minimal overshoot, robust under foot-slip/noise |
| Neural fuzzy incremental learning mechanism [56] | 2.22 | 4.62 | 1.01 | 1.63 [s] | 6.36% | Robust to disturbances, though high complexity slightly increases ITAE. |
| Deep learning control for biped robot locomotion [57] | 2.80 | 6.50 | 1.85 | 2.47 [s] | 11.12% | Good steady state but poor adaptability to terrain change |
| Performance Indicator | FTCC1 [14] | FTCC2 [19] | NDC [23] | NF-ILM [39] | RLBM [40] | NNC [56] | DLC [57] | Proposed Scheme |
|---|---|---|---|---|---|---|---|---|
| • Error minimization • Global stability • Time of convergence • Control efficiency • Disturbance rejection • Chattering suppression • Math complexity • Computation load • Tuning difficulty | Good | Adequate | Good | Bad | Good | Fair | Good | Excellent |
| Yes | Yes | Yes | Yes | Yes | Difficult | Yes | Yes | |
| Fast | Fast | Slow | Delayed | Swift | Tardy | Poky | Very fast | |
| Medium | Low | Low | Medium | Fair | Low | Fair | High | |
| Good | Best | Better | Bad | Good | Fair | Good | Excellent | |
| Adequate | Adequate | Fair | Good | Good | Good | Better | High | |
| Medium | High | High | Low | High | High | Low | Adequate | |
| High | High | High | Low | High | High | Low | Medium | |
| High | Medium | High | Low | Low | High | Low | Medium |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Bekhiti, B.; Iqbal, J.; Hariche, K.; Fragulis, G.F. Neural Adaptive Nonlinear MIMO Control for Bipedal Walking Robot Locomotion in Hazardous and Complex Task Applications. Robotics 2025, 14, 84. https://doi.org/10.3390/robotics14060084
Bekhiti B, Iqbal J, Hariche K, Fragulis GF. Neural Adaptive Nonlinear MIMO Control for Bipedal Walking Robot Locomotion in Hazardous and Complex Task Applications. Robotics. 2025; 14(6):84. https://doi.org/10.3390/robotics14060084
Chicago/Turabian StyleBekhiti, Belkacem, Jamshed Iqbal, Kamel Hariche, and George F. Fragulis. 2025. "Neural Adaptive Nonlinear MIMO Control for Bipedal Walking Robot Locomotion in Hazardous and Complex Task Applications" Robotics 14, no. 6: 84. https://doi.org/10.3390/robotics14060084
APA StyleBekhiti, B., Iqbal, J., Hariche, K., & Fragulis, G. F. (2025). Neural Adaptive Nonlinear MIMO Control for Bipedal Walking Robot Locomotion in Hazardous and Complex Task Applications. Robotics, 14(6), 84. https://doi.org/10.3390/robotics14060084









