Analytical Modeling, Virtual Prototyping, and Performance Optimization of Cartesian Robots: A Comprehensive Review
Abstract
1. Introduction
State of the Art
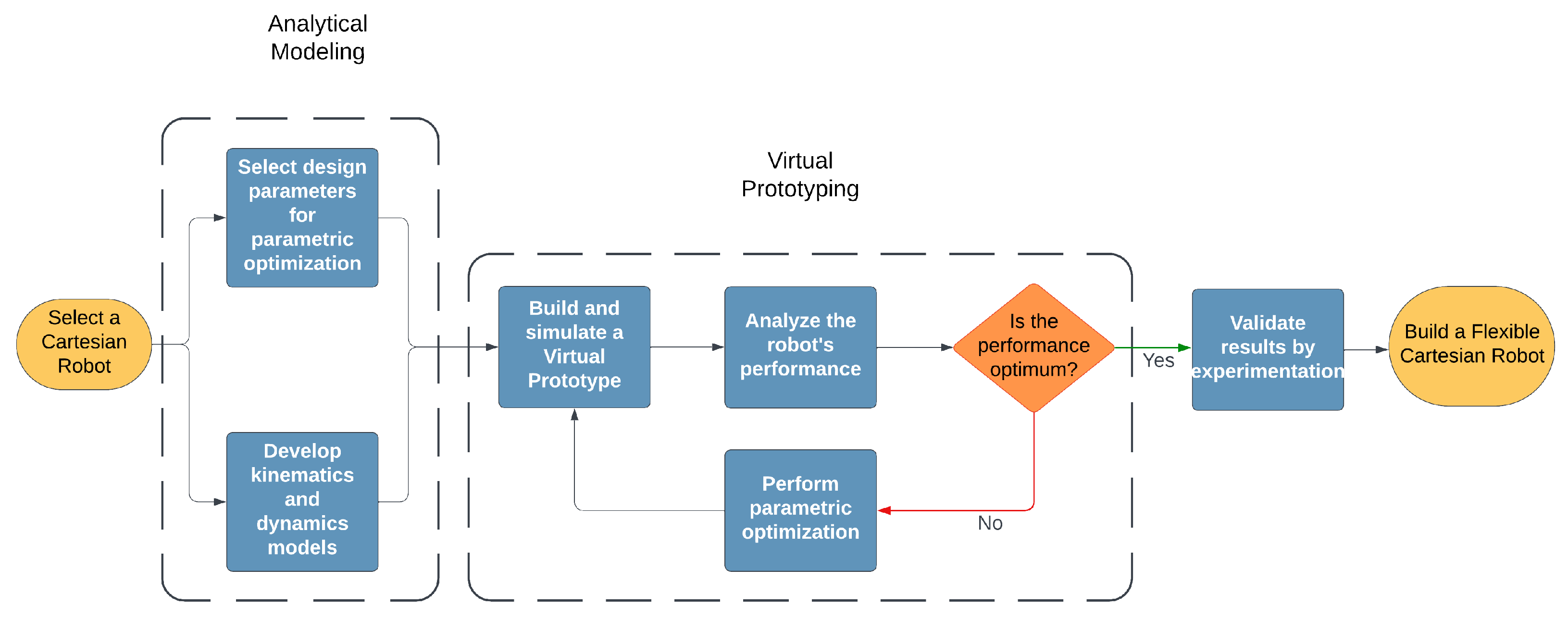
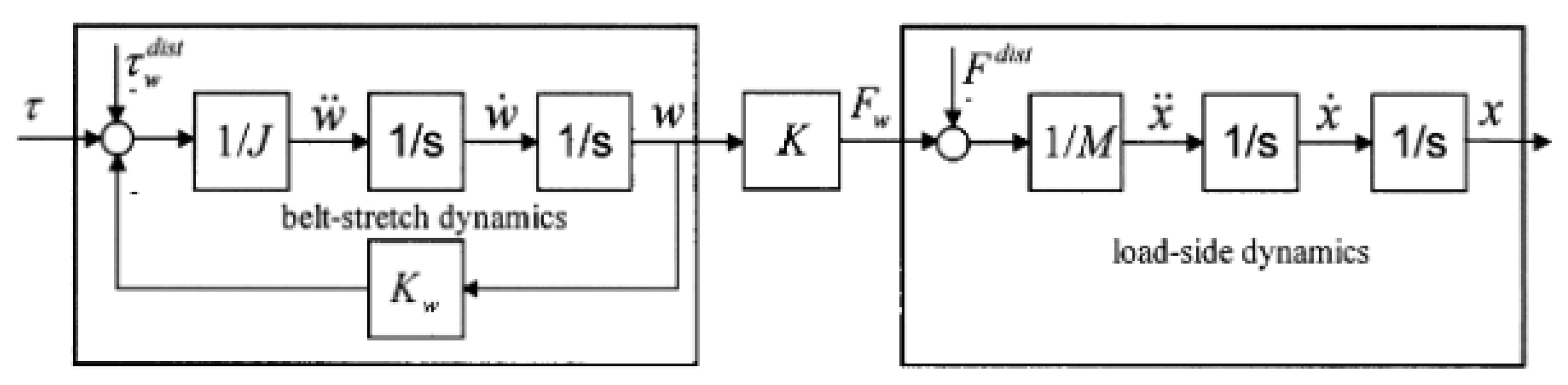
- Analytical Modeling: Recent research on Cartesian robots has focused on improving the kinematic and dynamic models of robots to account for flexible configurations and nonlinear elements, such as those in belt–pulley systems. These models provide solutions to challenges such as precision positioning of the drives and vibrations despite different problems, such as configuration flexibility, elasticity, and nonlinear friction of the drives. Advanced analytical modeling strategies can accurately predict robot behavior, which is very important for designing adaptable robotic systems. Vibration reduction strategies for both the structure and linear drive can improve stability and position accuracy of the system. Robust control strategies can efficiently handle the model uncertainties and disturbances, thus enabling precise positioning and reduced chattering. Trajectory planning enhances the performance by ensuring smooth time- and energy-optimal motion trajectories. Analytical models identify the key design parameters, constraints, and optimization goals that are useful for virtual prototype modeling and optimization of a robot.
- Virtual Prototyping: Nowadays, virtual prototyping is turning out to be an important and irreplaceable means for design optimization of industrial robots. Virtual prototyping can help in simulating both the kinematics and dynamics of a robot to test its different possible configurations, refine influencing design parameters, and predict the output response of the robot without building a physical prototype. With the help of V.P, an optimum design of a Cartesian robot with enhanced performance can be developed. The two main V.P techniques that are discussed here for modeling flexibly configured robots are multi-body dynamics and finite element methods. Multi-body analysis tools perform a detailed analysis of robot movement and its forces and interactions between its components. The assessment of the deformation, structural integrity, and stress distribution of a robot under operational loads is enabled by finite element analysis techniques. The design and performance of the robots can be optimized using these tools by changing different parameters while setting some design constraints and analyzing the output performance. This will help in reducing the time and cost associated with traditional design methods while it will ensure that the robot satisfies the required performance standards. Using virtual prototyping, robot designers can maximize the configuration flexibility, precision, and durability of the robot through repeated simulation and refinement of the robot design in software, especially in applications with HMLV production.
- Performance Optimization: The main objective of optimization in industrial robotics is to improve the design and performance of a robot through analytical modeling and virtual prototyping strategies. Each strategy addresses specific challenges and proposes solutions to them. Vibration analysis, controller design, and input trajectory modeling can enhance the robot’s overall performance by addressing different problems and proposing its solutions. The design optimization can be performed using virtual prototyping strategies, such as design study, design of experiments, and optimization. The design optimization process using V.P is accomplished by iteratively simulating the V.P of the robot in which single or multiple design variables vary while achieving an objective and satisfying some constraints. By following this thorough approach, robots can be customized to meet specific needs while remaining flexible and reliable.
2. Modeling of the Cartesian Robots
2.1. Dynamic Modeling of Linear Belt Drives
2.2. Modeling of Other Mechanical Drives
2.3. Vibration Analysis
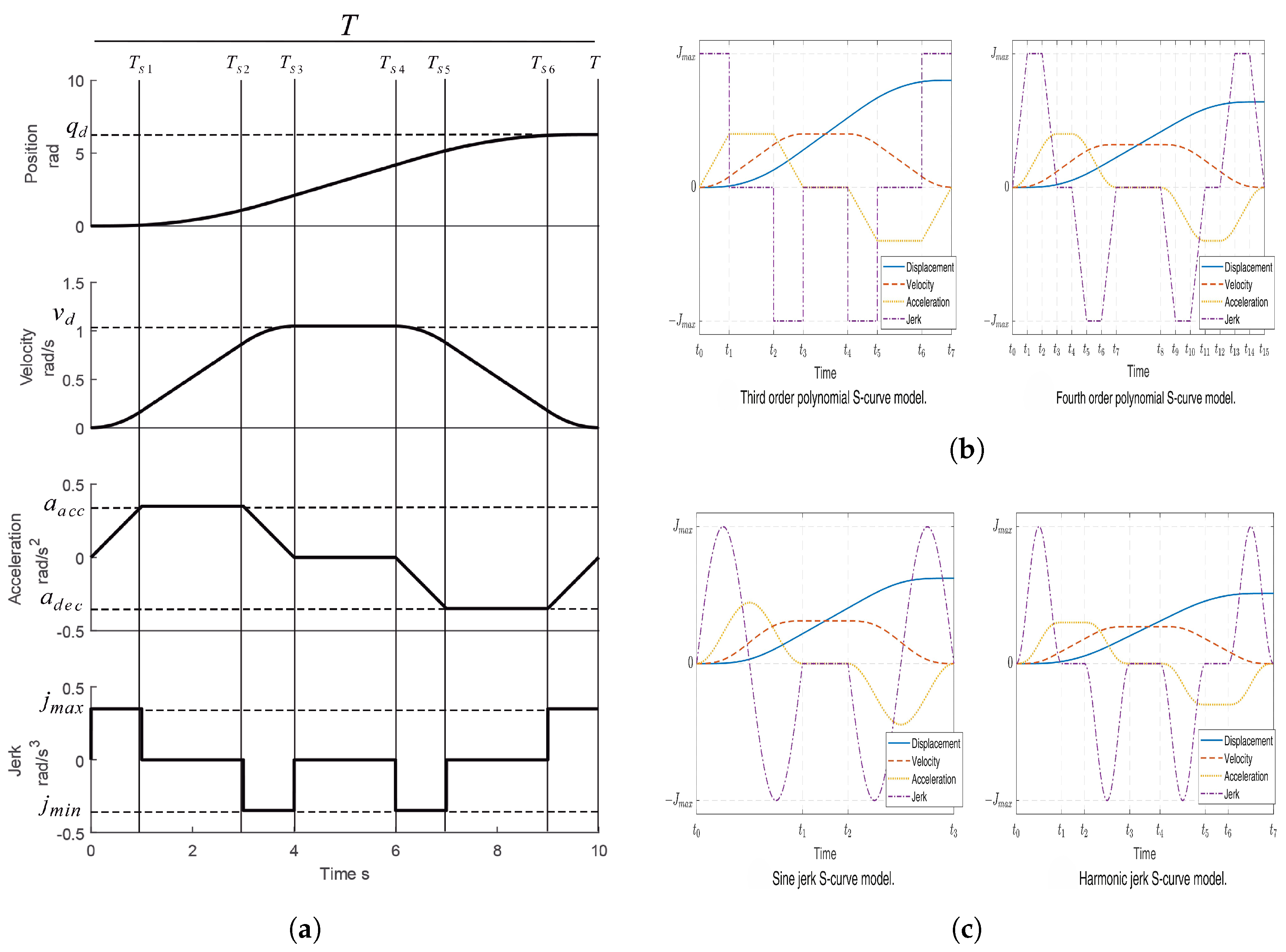
2.4. Trajectory Planning
2.5. Control Strategies for Cartesian Robots
3. Virtual Prototyping of the Cartesian Robot
3.1. Multi-Body Dynamics and Simulation
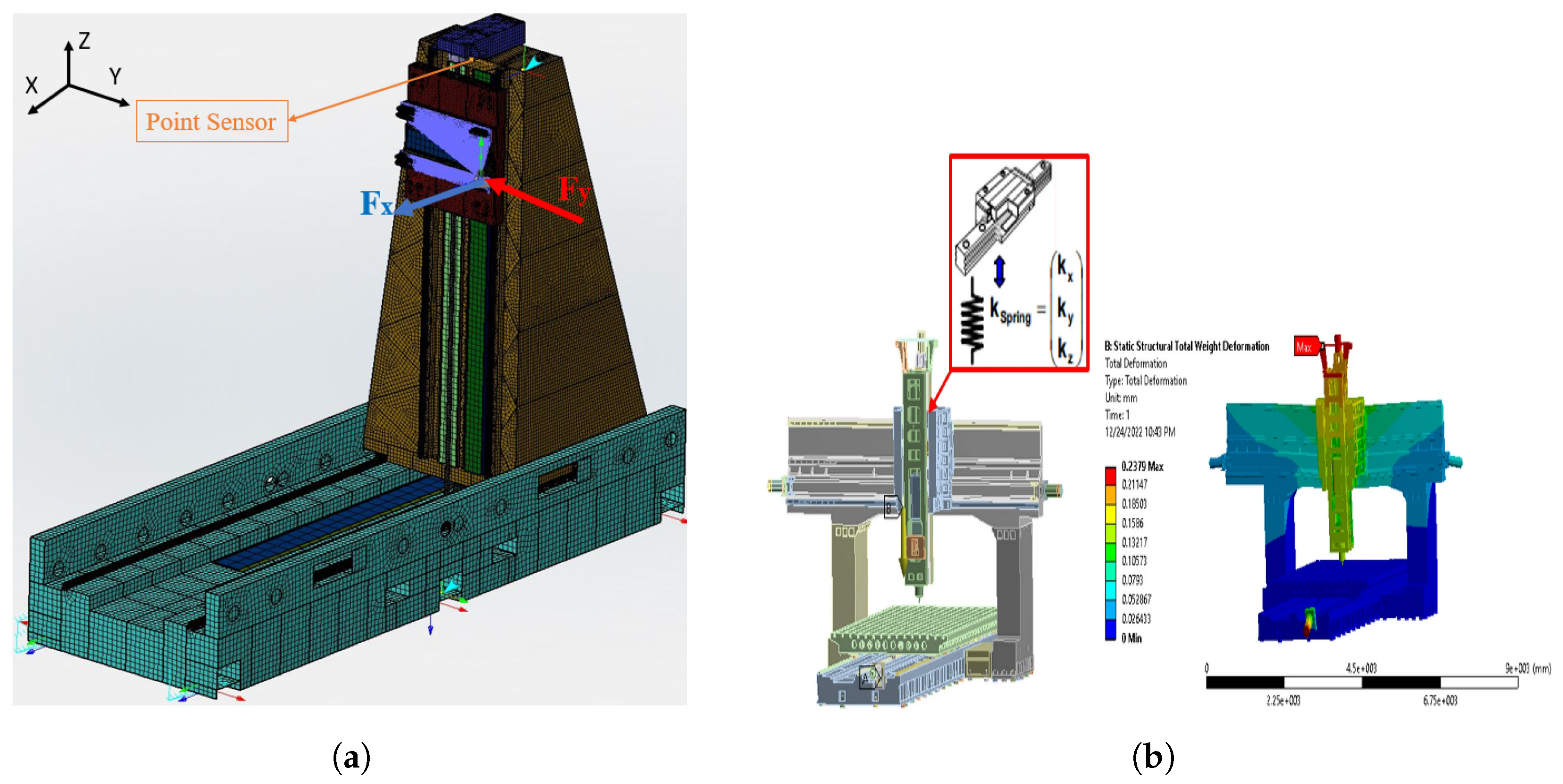
3.2. Finite Element Analysis
4. Optimization of Cartesian Robots
5. Conclusions
6. Future Work
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Conflicts of Interest
References
- Dressler, I. Modeling and Control of Stiff Robots for Flexible Manufacturing. Ph.D. Thesis, Lund University, Lund, Sweden, 2012. [Google Scholar]
- Gruninger, R.; Kus, E.; Huppi, R. Market study on adaptive robots for flexible manufacturing systems. In Proceedings of the 2009 IEEE International Conference on Mechatronics, Malaga, Spain, 14–17 April 2009; pp. 1–7. [Google Scholar] [CrossRef]
- Wang, G.G. Definition and Review of Virtual Prototyping. J. Comput. Inf. Sci. Eng. 2003, 2, 232–236. [Google Scholar] [CrossRef]
- Gibson, I.; Gao, Z.; Campbell, I. A comparative study of virtual prototyping and physical prototyping. Int. J. Manuf. Technol. Manag. 2004, 6, 503–522. [Google Scholar] [CrossRef]
- Callegari, M.; Cannella, F.; Monti, S.; Santolini, C.; Pagnanelli, P. Dynamic models for the re-engineering of a high-speed Cartesian robot. In Proceedings of the 2001 IEEE/ASME International Conference on Advanced Intelligent Mechatronics. Proceedings (Cat. No.01TH8556), Como, Italy, 8–12 July 2001; Volume 1, pp. 560–565. [Google Scholar] [CrossRef]
- Bottin, M.; Cipriani, G.; Tommasino, D.; Doria, A. Analysis and Control of Vibrations of a Cartesian Cutting Machine Using an Equivalent Robotic Model. Machines 2021, 9, 162. [Google Scholar] [CrossRef]
- Sharath, G.S.; Hiremath, N.; Manjunatha, G. Design and analysis of gantry robot for pick and place mechanism with Arduino Mega 2560 microcontroller and processed using pythons. Mater. Today Proc. 2021, 45, 377–384. [Google Scholar] [CrossRef]
- Jiang, Q.; Cai, K.; Xu, F. Obstacle-avoidance path planning based on the improved artificial potential field for a 5 degrees of freedom bending robot. Mech. Sci. 2023, 14, 87–97. [Google Scholar] [CrossRef]
- Gasparetto, A.; Rosati, G. Design and Implementation of a Cartesian Robot. In AMST’02 Advanced Manufacturing Systems and Technology; Kulianic, E., Ed.; International Centre for Mechanical Sciences: Vienna, Austria, 2002; pp. 539–544. [Google Scholar] [CrossRef]
- De Waas Tilakaratna, P.; Shirinzadeh, B.; Alici, G. Model Development and System Identification of a Cartesian Manipulator Using a Laser-Interferometry Based Measurement System. IFAC Proc. Vol. 2004, 37, 401–406. [Google Scholar] [CrossRef]
- Madani, P.; Mobaraki, M.; Jahromi, S.; Fakhari, V. Experiental Robustness Evaluation of PID Controller for Position Control of a Cartesian Robot. In Proceedings of the 2019 7th International Conference on Robotics and Mechatronics (ICRoM), Tehran, Iran, 20–21 November 2019; pp. 526–531. [Google Scholar] [CrossRef]
- Xu, F.; Jiang, Q.; Rong, L.; Zhou, P.; Hu, J. Structural model and dynamic analysis of six-axis Cartesian coordinate robot for sheet metal bending. Int. J. Adv. Robot. Syst. 2019, 16, 1729881419861568. [Google Scholar] [CrossRef]
- Shimada, N.; Yoshioka, T.; Ohishi, K.; Toshimasa, M.; Yokokura, Y. Reliable force-sensorless contact detection method for ball screw drive cartesian robot. In Proceedings of the 2013 IEEE International Symposium on Industrial Electronics, Taipei, Taiwan, 28–31 May 2013; pp. 1–6. [Google Scholar] [CrossRef]
- Lee, S.J.; Chung, W.J.; Ju, J.H.; Park, K.B. Monte-Carlo Simulation Technique for Repeatability Analysis of 3-Axis Cartesian Robot Using Position Resolution of a Ball Screw; Ministry of Commerce, Industry and Energy (MOCIE) and Korea Industrial Technology Foundation (KOTEF): Sejong, Republic of Korea, 2010. [Google Scholar]
- Sanchez-Sanchez, P.; Reyes-Cortes, F.; Sanchez-Sanchez, P.; Reyes-Cortes, F. Cartesian Control for Robot Manipulators. In Robot Manipulators Trends and Development; IntechOpen: London, UK, 2010. [Google Scholar] [CrossRef]
- González-Arriaga, D.M.; Vargas-Treviño, M.A.D.; Vergara-Limon, S.; De León, C.L.C.D.; López-Gómez, J.; Vargas-Treviño, M.; Guerrero-García, J. Design of a Software Platform to Generate Convolutional Neural Networks for the Parametric Identification of a Cartesian Robot. IEEE Access 2023, 11, 63371–63387. [Google Scholar] [CrossRef]
- Karabegovic, I.; Banjanovic-mehmedovic, L. (Eds.) Industrial Robots: Design, Applications and Technology; Nova Science Pub Inc.: New York, NY, USA, 2020. [Google Scholar]
- Bertin, C. Timing Belt Theory. Available online: https://www.academia.edu/35140327/Timing_Belt_Theory (accessed on 14 June 2023).
- Perneder, R.; Osborne, I. Handbook Timing Belts. Handbook Timing Belts: Principles, Calculations, Applications; Springer: Berlin/Heidelberg, Germany, 2012. [Google Scholar] [CrossRef]
- Pierleoni, P.; Belli, A.; Palma, L.; Sabbatini, L. Diagnosis and Prognosis of a Cartesian Robot’s Drive Belt Looseness. In Proceedings of the 2020 IEEE International Conference on Internet of Things and Intelligence System (IoTaIS), Bali, Indonesia, 27–28 January 2021; pp. 172–176. [Google Scholar] [CrossRef]
- Minh, V.T.; Tamre, M.; Sekhri, E. Modeling and robust control algorithms for a linear belt driven system. Open Comput. Sci. 2018, 8, 142–153. [Google Scholar] [CrossRef]
- Sabanovic, A.; Sozbilir, O.; Goktug, G.; Sabanovic, N. Sliding mode control of timing-belt servosystem. In Proceedings of the 2003 IEEE International Symposium on Industrial Electronics (Cat. No.03TH8692), Rio de Janeiro, Brazil, 9–11 June 2003; Volume 2, pp. 684–689. [Google Scholar] [CrossRef]
- Sollmann, K.; Jouaneh, M. Dynamic modelling of a single-axis belt-drive system. Int. J. Model. Identif. Control 2011, 12, 386–394. [Google Scholar] [CrossRef]
- Katsioula, A.G.; Karnavas, Y.L.; Boutalis, Y.S. An enhanced simulation model for DC motor belt drive conveyor system control. In Proceedings of the 2018 7th International Conference on Modern Circuits and Systems Technologies (MOCAST), Thessaloniki, Greece, 7–9 May 2018; pp. 1–4. [Google Scholar] [CrossRef]
- Hace, A.; Jezernik, K.; Sabanovic, A. A new robust position control algorithm for a linear belt-drive. In Proceedings of the IEEE International Conference on Mechatronics, ICM ’04, Istanbul, Turkey, 3–5 June 2004; pp. 358–363. [Google Scholar] [CrossRef]
- Hace, A.; Jezernik, K.; Sabanovic, A. Improved design of VSS controller for a linear belt-driven servomechanism. IEEE/ASME Trans. Mechatron. 2005, 10, 385–390. [Google Scholar] [CrossRef]
- Hace, A.; Jezernik, K.; Sabanovic, A. SMC With Disturbance Observer for a Linear Belt Drive. IEEE Trans. Ind. Electron. 2007, 54, 3402–3412. [Google Scholar] [CrossRef]
- Hace, A.; Jezernik, K.; Terbuc, M. VSS motion control for a laser-cutting machine. Control Eng. Pract. 2001, 9, 67–77. [Google Scholar] [CrossRef]
- Jokinen, M. Centralized Motion Control of a Linear Tooth Belt Drive: Analysis of the Performance and Limitations; Lappeenranta University of Technology: Lappeenranta, Finland, 2010. [Google Scholar]
- Parkkinen, J.; Jokinen, M.; Niemela, M.; Lindh, T.; Pyrhonen, J. Motion synchronization of two linear tooth belt drives using cross-coupled controller. In Proceedings of the 2013 15th European Conference on Power Electronics and Applications (EPE), Lille, France, 2–6 September 2013; pp. 1–7. [Google Scholar] [CrossRef]
- Nevaranta, N.; Parkkinen, J.; Niemelä, M.; Lindh, T.; Pyrhönen, O.; Pyrhönen, J. Recursive identification of linear tooth belt-drive system. In Proceedings of the 2014 16th European Conference on Power Electronics and Applications, Lappeenranta, Finland, 26–28 August 2014; pp. 1–8. [Google Scholar] [CrossRef]
- Nevaranta, N.; Parkkinen, J.; Lindh, T.; Niemelä, M.; Pyrhönen, O.; Pyrhönen, J. Online Estimation of Linear Tooth Belt Drive System Parameters. IEEE Trans. Ind. Electron. 2015, 62, 7214–7223. [Google Scholar] [CrossRef]
- Jokinen, M.; Saarakkala, S.; Niemela, M.; Pollanen, R.; Pyrhonen, J. Physical drawbacks of linear high-speed tooth belt drives. In Proceedings of the Automation and Motion 2008 International Symposium on Power Electronics, Electrical Drives, Ischia, Italy, 11–13 June 2008; pp. 872–877. [Google Scholar] [CrossRef]
- Autsou, S.; Vaimann, T.; Rassõlkin, A.; Asad, B.; Kudelina, K.; Hyunh, V.K. Fault Diagnosis of the Tooth Belt Transmission of Cartesian Robot. In Proceedings of the 2022 29th International Workshop on Electric Drives: Advances in Power Electronics for Electric Drives (IWED), Moscow, Russia, 26–29 January 2022; pp. 1–6. [Google Scholar] [CrossRef]
- Altintas, Y.; Verl, A.; Brecher, C.; Uriarte, L.; Pritschow, G. Machine tool feed drives. CIRP Ann. 2011, 60, 779–796. [Google Scholar] [CrossRef]
- Engelberth, T.; Apprich, S.; Friedrich, J.; Coupek, D.; Lechler, A. Properties of electrically preloaded rack-and-pinion drives. Prod. Eng. 2015, 9, 269–276. [Google Scholar] [CrossRef]
- Zenn, W.; Keck, A.; Beck, M.; Herold, S.; Melz, T. Automated backlash determination on rack-and-pinion drives. In Proceedings of the 2023 IEEE/ASME International Conference on Advanced Intelligent Mechatronics (AIM), Seattle, WA, USA, 28–30 June 2023; pp. 1202–1207. [Google Scholar] [CrossRef]
- Karim, A.; Lindner, P.; Verl, A. Control-based compensation of friction and backlash within rack-and-pinion drives. Prod. Eng. 2018, 12, 589–596. [Google Scholar] [CrossRef]
- Verl, A.; Engelberth, T. Adaptive preloading for rack-and-pinion drive systems. CIRP Ann. 2018, 67, 369–372. [Google Scholar] [CrossRef]
- Choi, Y.H.; Choi, E.Y.; Jang, S.H.; Park, H.M.; Ha, J.S. Vibration analysis and dynamic optimization of a rack and pinion typed feed drive system for a router machine. In Proceedings of the ICMIT 2005: Control Systems and Robotics, SPIE, Chongqing, China, 20–23 September 2006; Volume 6042, pp. 961–966. [Google Scholar] [CrossRef]
- Brecher, C.; Weck, M. Feed Axes in Machine Tools. In Machine Tools Production Systems 3; Springer: Wiesbaden, Germany, 2021; pp. 7–106. [Google Scholar] [CrossRef]
- Verl, A.; Frey, S. Correlation between feed velocity and preloading in ball screw drives. CIRP Ann. 2010, 59, 429–432. [Google Scholar] [CrossRef]
- Pritschow, G.; Philipp, W. Direct Drives for High-Dynamic Machine Tool Axes. CIRP Ann. 1990, 39, 413–416. [Google Scholar] [CrossRef]
- Zirn, O. Machine Tool Analysis: Modelling, Simulation and Control of Machine Tool Manipulators; ETH Zürich: Zürich, Switzerland, 2008. [Google Scholar] [CrossRef]
- Reynoso, A. Structural Dynamics Model of a Cartesian Robot. Doctoral Dissertation, Massachusetts Institute of Technology, Cambridge, MA, USA, 1985. [Google Scholar]
- Bottin, M.; Cipriani, G.; Tommasino, D.; Doria, A. Control of the Vibrations of a Cartesian Automatic Machine. In Mechanism Design for Robotics; Zeghloul, S., Laribi, M.A., Arsicault, M., Eds.; Mechanisms and Machine Science; Springer: Cham, Switzerland, 2021; pp. 236–243. [Google Scholar] [CrossRef]
- Yamamoto, T.; Tanaka, K.; Sumiyoshi, M. Vibration control for cartesian 3 axes robot. In Proceedings of the 4th IEEE International Workshop on Advanced Motion Control—AMC ’96—MIE, Mie, Japan, 18–21 March 1996; Volume 2, pp. 647–652. [Google Scholar] [CrossRef]
- Barre, P.J.; Bearee, R.; Borne, P.; Dumetz, E. Influence of a Jerk Controlled Movement Law on the Vibratory Behaviour of High-Dynamics Systems. J. Intell. Robot. Syst. 2005, 42, 275–293. [Google Scholar] [CrossRef]
- D’Imperio, S.; Berruti, T.M.; Gastaldi, C.; Soccio, P. Tunable Vibration Absorber Design for a High-Precision Cartesian Robot. Robotics 2022, 11, 103. [Google Scholar] [CrossRef]
- Benjamin, M.; Garcia-Reynoso, A.; Seering, W. Dynamic and vibration modeling of a cartesian robot. In Proceedings of the 1985 IEEE International Conference on Robotics and Automation Proceedings, St. Louis, MO, USA, 25–28 March 1985; Volume 2, pp. 990–995. [Google Scholar] [CrossRef]
- Zheng, L.; Guan, Q.; Wang, X.; Luo, Y.; Wu, Y. A Robust Resonance Suppression Method for Linear Tooth Belt Drive with Variable Resonance Frequency. IEEE Trans. Ind. Electron. 2024, 71, 10346–10355. [Google Scholar] [CrossRef]
- Basso, R.; Fanti, G. Vibration Monitoring for Local Fault Detection in Synchronous Belts; American Society of Mechanical Engineers Digital Collection: New York, NY, USA, 2009; pp. 577–583. [Google Scholar] [CrossRef]
- Autsou, S.; Vaimann, T.; Rassõlkin, A.; Kudelina, K. Fault Diagnosis System of Cartesian Robot for Various Belt Tension. In Proceedings of the 2022 International Conference on Diagnostics in Electrical Engineering (Diagnostika), Pilsen, Czech Republic, 6–8 September 2022; pp. 1–4. [Google Scholar] [CrossRef]
- Autsou, S.; Vaimann, T.; Rassõlkin, A.; Kudelina, K.; Asad, B. Influence of Different Tooth Belt Transmission Faults on the Work of a Cartesian Robot. In Proceedings of the 2022 20th International Conference on Mechatronics—Mechatronika (ME), Pilsen, Czech Republic, 7–9 December 2022; pp. 1–5. [Google Scholar]
- Zhao, Z.H.; Jiang, X.M.; Du, Y.H. Design of Gantry Robot for Dye Dispense and Analysis of Vibration of its Synchronous Belt Driven and Positioning System. Key Eng. Mater. 2011, 458, 313–318. [Google Scholar] [CrossRef]
- Chen, G.S.; Zhen, H.; Qatu, M. Noise Modeling of Synchronous Belts. Noise Vib. Worldw. 2013, 44, 14–27. [Google Scholar] [CrossRef]
- Sheng, G.; Zheng, H.; Qatu, M.; Dukkipati, R.V. Modelling of friction-induced noise of timing belt. Int. J. Veh. Noise Vib. 2008, 4, 285–303. [Google Scholar] [CrossRef]
- Sante, R.D.; Revel, G.M.; Rossi, G.L. Measurement techniques for the acoustic analysis of synchronous belts. Meas. Sci. Technol. 2000, 11, 1463. [Google Scholar] [CrossRef]
- Schnürer, D.; Holl, H.J. Transversal vibrations of a toothed belt in linear drives during operation. PAMM 2021, 20, e202000026. [Google Scholar] [CrossRef]
- Schnürer, D.; Holl, H.J. Frequency analysis of transversal vibrations of belt drives with time-varying belt lengths. PAMM 2021, 21, e202100186. [Google Scholar] [CrossRef]
- Liu, S. An on-line reference-trajectory generator for smooth motion of impulse-controlled industrial manipulators. In Proceedings of the 7th International Workshop on Advanced Motion Control, Proceedings (Cat. No. 02TH8623), Maribor, Slovenia, 3–5 July 2002; pp. 365–370. [Google Scholar] [CrossRef]
- Mu, H.; Zhou, Y.; Yan, S.; Han, A. Third-order trajectory planning for high accuracy point-to-point motion. Front. Electr. Electron. Eng. China 2009, 4, 83–87. [Google Scholar] [CrossRef]
- Blejan, M.; Blejan, R. Mathematics for Real-Time S-Curve Profile Generator. Hidraulica 2020, 4, 7–25. [Google Scholar]
- García-Martínez, J.R.; Rodríguez-Reséndiz, J.; Cruz-Miguel, E.E. A New Seven-Segment Profile Algorithm for an Open Source Architecture in a Hybrid Electronic Platform. Electronics 2019, 8, 652. [Google Scholar] [CrossRef]
- Fang, Y.; Hu, J.; Liu, W.; Shao, Q.; Qi, J.; Peng, Y. Smooth and time-optimal S-curve trajectory planning for automated robots and machines. Mech. Mach. Theory 2019, 137, 127–153. [Google Scholar] [CrossRef]
- Biagiotti, L.; Melchiorri, C. FIR filters for online trajectory planning with time- and frequency-domain specifications. Control Eng. Pract. 2012, 20, 1385–1399. [Google Scholar] [CrossRef]
- Biagiotti, L.; Melchiorri, C. Trajectory generation via FIR filters: A procedure for time-optimization under kinematic and frequency constraints. Control Eng. Pract. 2019, 87, 43–58. [Google Scholar] [CrossRef]
- Joy, M.P.M. Energy Optimal Motion Profile Generation for Cartesian Robot Driven by Linear Tooth Belt Drives. 2023. Available online: https://lutpub.lut.fi/handle/10024/166165 (accessed on 3 November 2023).
- Scalera, L.; Carabin, G.; Vidoni, R.; Gasparetto, A. Minimum-Energy Trajectory Planning for Industrial Robotic Applications: Analytical Model and Experimental Results. In Advances in Service and Industrial Robotics; Mechanisms and Machine Science; Springer: Cham, Switzerland, 2020; pp. 334–342. [Google Scholar] [CrossRef]
- Meckl, P.H.; Seering, W.P. Experimental Evaluation of Shaped Inputs to Reduce Vibration for a Cartesian Robot. J. Dyn. Syst. Meas. Control 1990, 112, 159–165. [Google Scholar] [CrossRef]
- Boscariol, P.; Richiedei, D. Energy-efficient design of multipoint trajectories for Cartesian robots. Int. J. Adv. Manuf. Technol. 2019, 102, 1853–1870. [Google Scholar] [CrossRef]
- Boscariol, P.; Caracciolo, R.; Richiedei, D. Energy Optimal Design of Jerk-Continuous Trajectories for Industrial Robots. In Advances in Italian Mechanism Science; Niola, V., Gasparetto, A., Eds.; Mechanisms and Machine Science; Springer: Cham, Swizerland, 2021; pp. 318–325. [Google Scholar] [CrossRef]
- Gruber, D. Self-Commissioning of Linear Toothed Belt Drives. Ph.D. Thesis, Technische Universität Wien, Vienna, Austria, 2017. [Google Scholar] [CrossRef]
- Meressi, T. Modeling and control of a three dimensional gantry robot. In Proceedings of the 37th IEEE Conference on Decision and Control (Cat. No.98CH36171), Tampa, FL, USA, 18 December 1998; Volume 2, pp. 1514–1515. [Google Scholar]
- Frank, H.; Barteit, D.; Meyer, M.; Mittnacht, A.; Novak, G.; Mahlknecht, S. Optimized Control Methods for Capturing Flying Objects with a Cartesian Robot. In Proceedings of the 2008 IEEE Conference on Robotics, Automation and Mechatronics, Chengdu, China, 21–24 September 2008; pp. 160–165. [Google Scholar] [CrossRef]
- Ferretti, G.; Magnani, G.; Rocco, P. Virtual prototyping of mechatronic systems. Annu. Rev. Control 2004, 28, 193–206. [Google Scholar] [CrossRef]
- Ferretti, G.; Lucchini, F.; Magnani, G.; Rocco, P. A mechatronic approach to the control of machine tools. IFAC Proc. Vol. 2005, 38, 228–233. [Google Scholar] [CrossRef]
- Scaglioni, B.; Ferretti, G. Towards digital twins through object-oriented modelling: A machine tool case study. IFAC-PapersOnLine 2018, 51, 613–618. [Google Scholar] [CrossRef]
- Groothuis, M.; Damstra, A.; Broenink, J. Virtual prototyping through co-simulation of a Cartesian plotter. In Proceedings of the 2008 IEEE International Conference on Emerging Technologies and Factory Automation, Hamburg, Germany, 15–18 September 2008; pp. 697–700. [Google Scholar] [CrossRef]
- Wang, H.; Yang, Z.; Zhang, Q.; Sun, Q.; Lim, E. A Digital Twin Platform Integrating Process Parameter Simulation Solution for Intelligent Manufacturing. Electronics 2024, 13, 802. [Google Scholar] [CrossRef]
- Yang, G.; Yang, L.; Cao, M. Simulation analysis of timing belt movement characteristics based on RecurDyn. Vibroeng. Procedia 2019, 22, 13–18. [Google Scholar] [CrossRef]
- Zhu, H.; Wang, B.; Chen, W. Dynamic performance analysis of truss robot based on RecurDyn and experimental research. In Proceedings of the 2016 Asia-Pacific Conference on Intelligent Robot Systems (ACIRS), Tokyo, Japan, 20–22 July 2016; pp. 31–35. [Google Scholar] [CrossRef]
- Mahir, A.I.I.; Deng, S.P.; Qi, Y.M. Gantry Robot Dynamic Analysis Based on Lagrange’s Motion Equation. Key Eng. Mater. 2016, 693, 1741–1746. [Google Scholar] [CrossRef]
- Pisoni, A.; Santolini, C.; Tomasini, E. Modal Analysis of a Cartesian Robot: Noise and Non-lineax Effeas. In Proceedings of the Proceedings—SPIE the International Society for Optical Engineering, Kona, HI, USA, 17–18 March 1994. [Google Scholar]
- Fan, C.W.; Tu, T.Y.; Chen, C.W. Modal Analysis and Static Structure Analysis for 3-Axis Cartesian Robot Used in Injection Molding Machine; American Society of Mechanical Engineers Digital Collection: New York, NY, USA, 2023. [Google Scholar] [CrossRef]
- Xu, G. The dynamic characteristic analysis on Cartesian coordinate robot. IOP Conf. Ser. Earth Environ. Sci. 2020, 474, 032003. [Google Scholar] [CrossRef]
- Chan, T.C.; Ullah, A.; Roy, B.; Chang, S.L. Finite element analysis and structure optimization of a gantry-type high-precision machine tool. Sci. Rep. 2023, 13, 13006. [Google Scholar] [CrossRef]
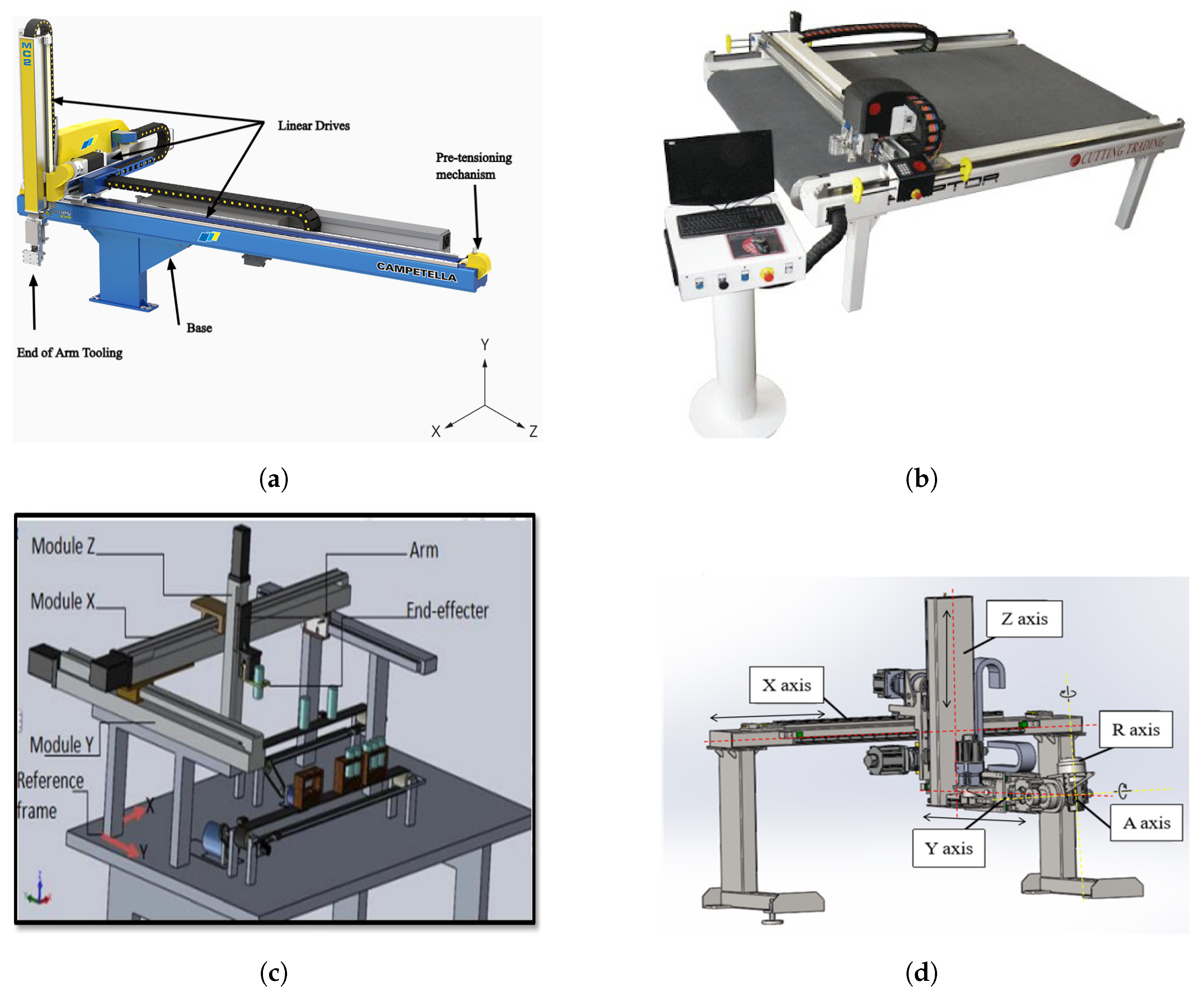
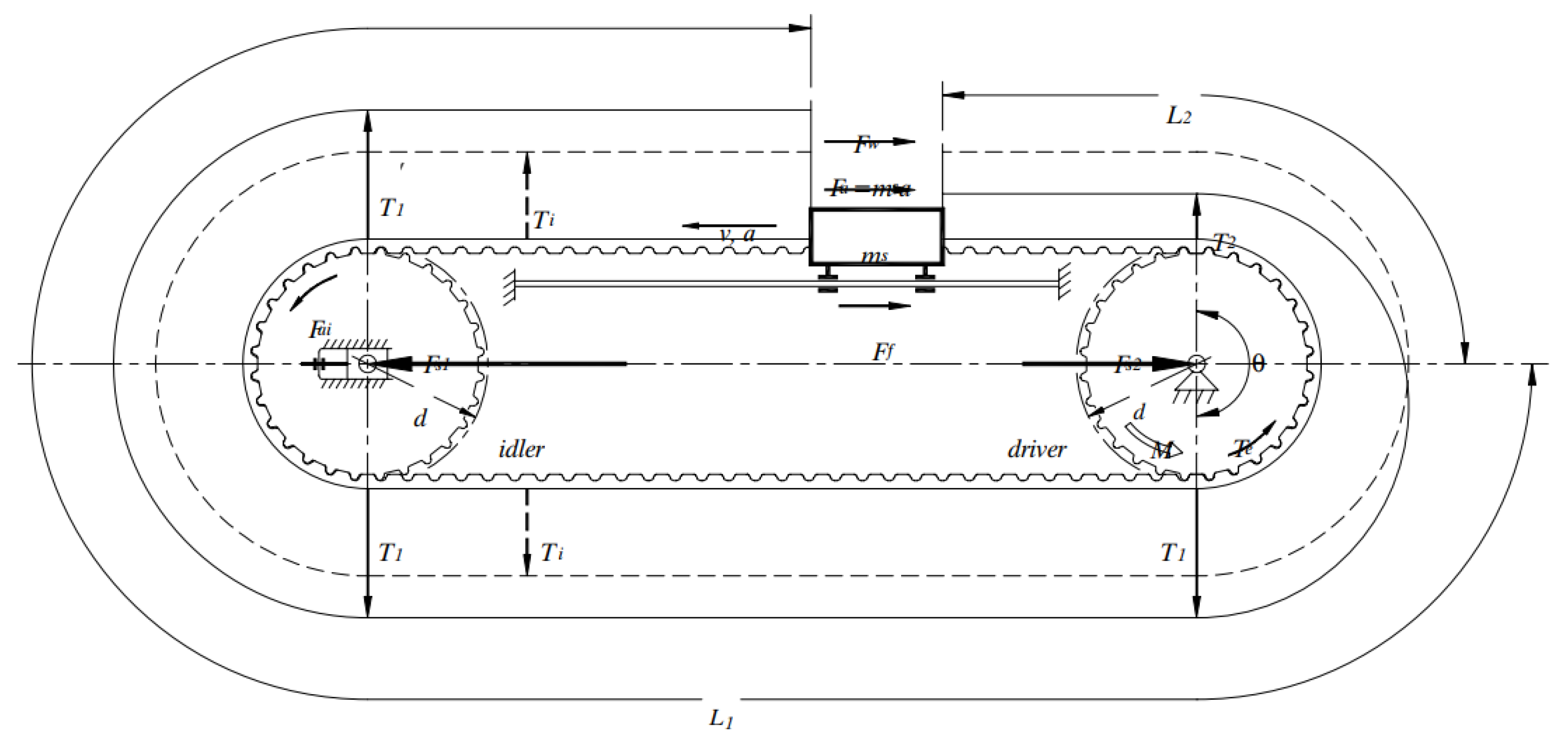
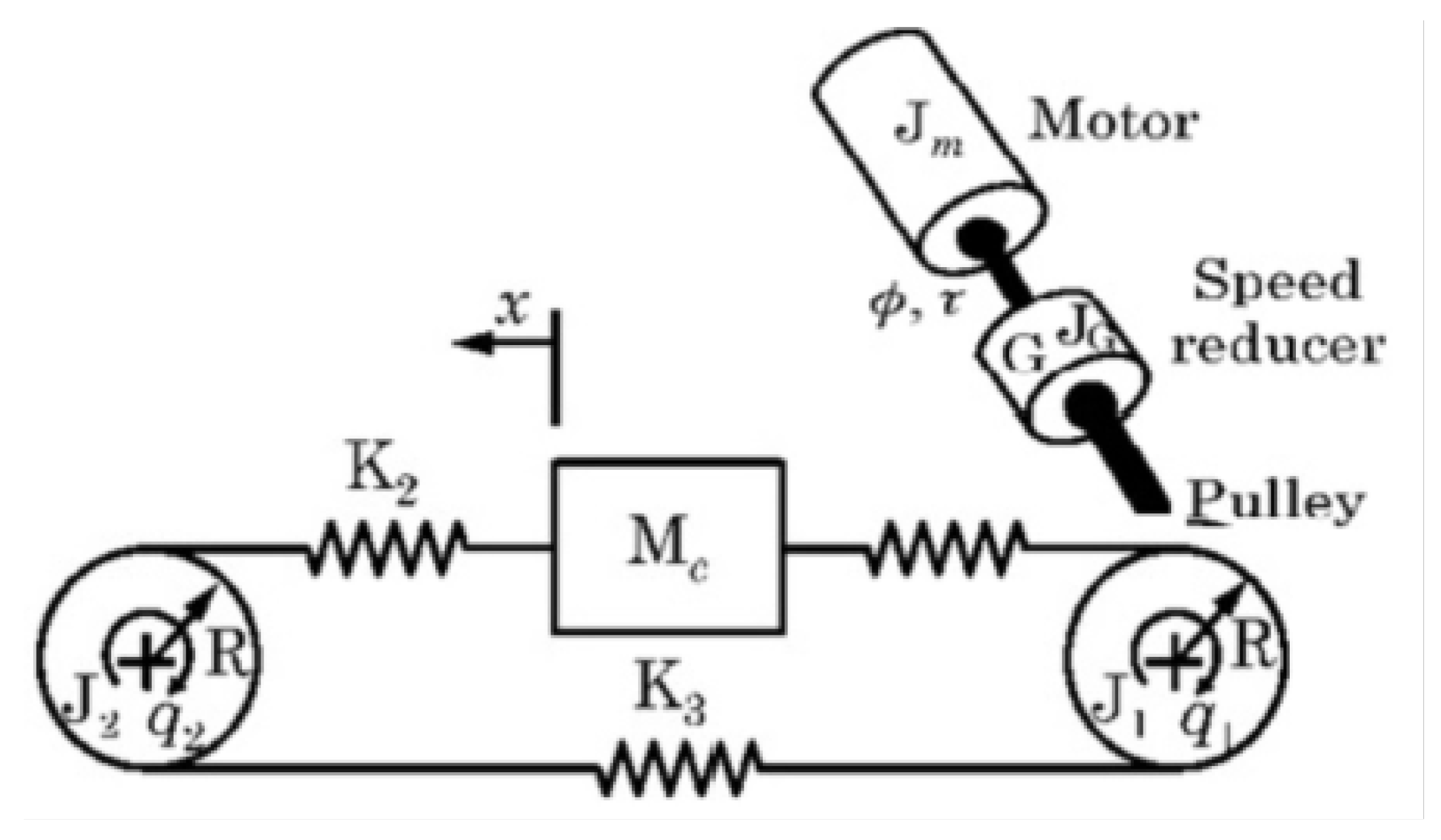
| Reference | Vibration Source | Modeling Technique | Vibrations Control Strategy | Key Findings |
|---|---|---|---|---|
| [6] | Pneumatic tool attached to the end effector | Equivalent robotic model + modal model | Vibration reduction using TVA | Reduced high-frequency vibrations |
| [46] | Cutting head vibrations | Sherman–Morrison formula | Vibration reduction using TVA | Predicted TVA effects on vibrations |
| [47] | End-effector low-frequency vibrations | Input trajectory preshaping | Preshaping control | Reduced vibration settling time |
| [48] | Jerk influence on vibration | Theoretical formulations and experimentation | Jerk-Controlled Movement Law | Motion trajectories influence vibrations |
| [49] | Cutting application vibration | Frequency analysis of TMD | Tuned mass damper (TMD) | Minimized vibration amplitude |
| [50] | Structural vibrations of robot link | Component Mode Synthesis (CMS) | Actuator and controller model | Vibration model validated experimentally |
| Reference | Vibration Phenomenon | Modeling Approach | Influencing Factors | Key Outcomes |
|---|---|---|---|---|
| [29] | Resonance and anti-resonance frequencies | Transfer function analysis | Effective stiffness, cart position | Resonance as function of cart position |
| [51] | Variable belt resonance | Reduced-order observer with high-pass filter | Effective stiffness, cart position | Resonance suppression |
| [52] | Timing belt noise | Multi-body simulations and experiments | Belt wear, fault conditions | Fault diagnosis by vibration analysis |
| [53,54] | Additional robot’s vibrations | Spectrum analysis | Variation in belt tension | High belt tension increases vibrations |
| [56,57] | Friction, impact, and air-induced noise | Analytical noise modeling | Tooth parameters, operating conditions | Identified noise-contributing factors |
| [59,60] | Transversal vibrations of belt drive | Analytical model and FEM solutions | Motion at high acceleration | Analyzed amplitude and frequency of vibrations |
| Reference | Addressed Problem | Control Algorithm | Key Outcomes |
|---|---|---|---|
| [29] | Belt drive’s parametric uncertainties and disturbances. | Centralized motion controller | QFT enhances robustness and accuracy |
| [73] | Belt drive’s nonlinear friction and mechanical complexities | Parametric identification strategy for controller design | Improved position tracking |
| [28] | Position uncertainties due to low-cost belt and elasticity of Cartesian robot | Inner vibration controller and outer VSS-based position controller | Precise positioning and reduced vibrations |
| [25] | Belt elasticity causing vibrations | SMC with extended switching function | Effectively minimizes vibrations |
| [26] | Nonlinear friction and variable belt stiffness of belt drive | SMC with a load and belt stretch manifold | Enhanced position tracking and low vibration |
| [27] | Position error peaks at velocity reversals | SMC with a disturbance observer | Reduces error peaks and improved tracking |
| [74] | Load oscillations of a high-speed gantry robot. | Fuzzy scheduled and SMC | Reduces oscillations effectively |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Mehmood, Y.; Cannella, F.; Cocuzza, S. Analytical Modeling, Virtual Prototyping, and Performance Optimization of Cartesian Robots: A Comprehensive Review. Robotics 2025, 14, 62. https://doi.org/10.3390/robotics14050062
Mehmood Y, Cannella F, Cocuzza S. Analytical Modeling, Virtual Prototyping, and Performance Optimization of Cartesian Robots: A Comprehensive Review. Robotics. 2025; 14(5):62. https://doi.org/10.3390/robotics14050062
Chicago/Turabian StyleMehmood, Yasir, Ferdinando Cannella, and Silvio Cocuzza. 2025. "Analytical Modeling, Virtual Prototyping, and Performance Optimization of Cartesian Robots: A Comprehensive Review" Robotics 14, no. 5: 62. https://doi.org/10.3390/robotics14050062
APA StyleMehmood, Y., Cannella, F., & Cocuzza, S. (2025). Analytical Modeling, Virtual Prototyping, and Performance Optimization of Cartesian Robots: A Comprehensive Review. Robotics, 14(5), 62. https://doi.org/10.3390/robotics14050062








