A Methodology to Characterize an Optimal Robotic Manipulator Using PSO and ML Algorithms for Selective and Site-Specific Spraying Tasks in Vineyards
Abstract
1. Introduction
1.1. Robot Optimization
1.2. Robotic Simulation
1.3. Machine Learning in Robotics
1.4. Agricultural Robotics
2. Methods
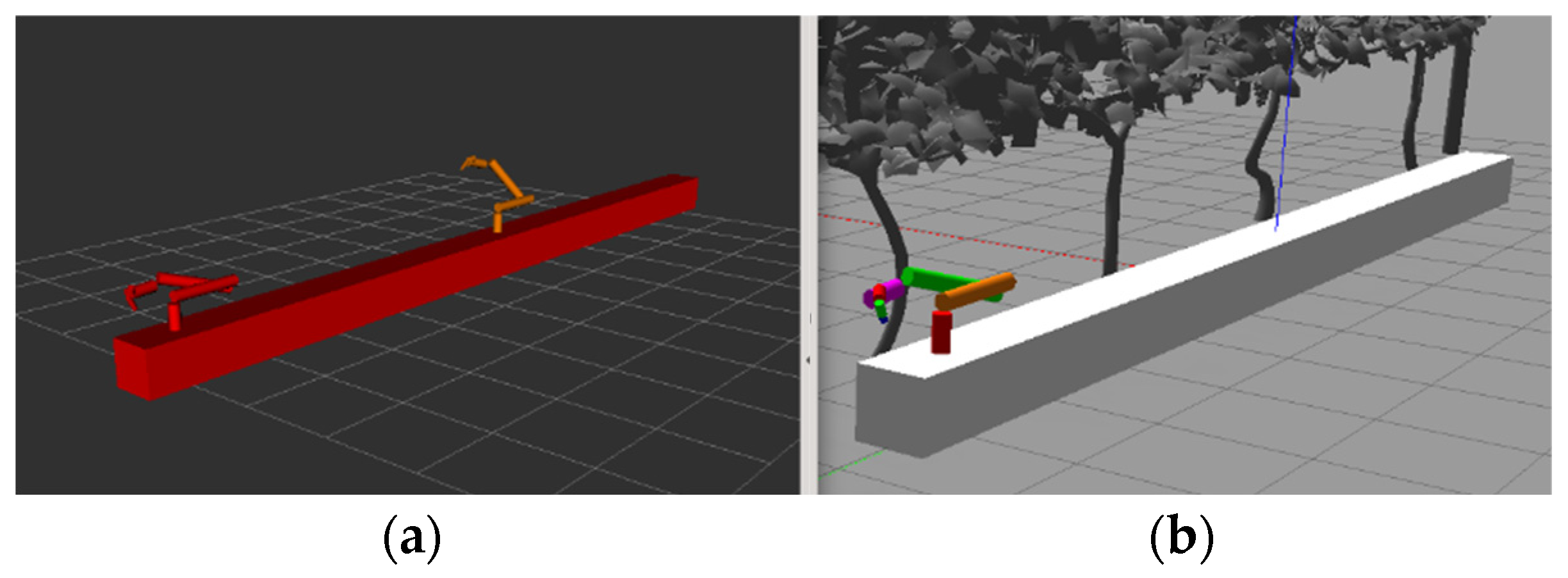
2.1. Robot Manipulator Description
- Joint definition: The joint type, , set the motion type available for each joint. Three types of joints are considered:
- Roll—revolute joint about the Z-axis in the element coordinate system.
- Pitch—revolute joint about the Y-axis in the element coordinate system.
- Prismatic—linear sliding along the Z-axis in the element coordinate system.
- Axis definition: The axis denoted as was used to set a connection between the current coordinate system and the coordinate of the previous element for each joint. Each axis element has an associated coordinate system that is attached to its link such that the Z-axis is along the link.
- Link length definition: Each link is shaped as a cylinder. The radiuses are from UR3 structures of 0.049 m, 0.045 m, 0.04 m, 0.035 m, 0.03 m, and 0.025 m for 1, 2, 3, 4, 5, and 6 DOF, respectively. The variable is the link length, denoted as , for a set of options [0.1, 0.3, 0.5, 0.7 m].
- Joint type:
- Axis:
- Link length:
2.2. The Optimization Problem
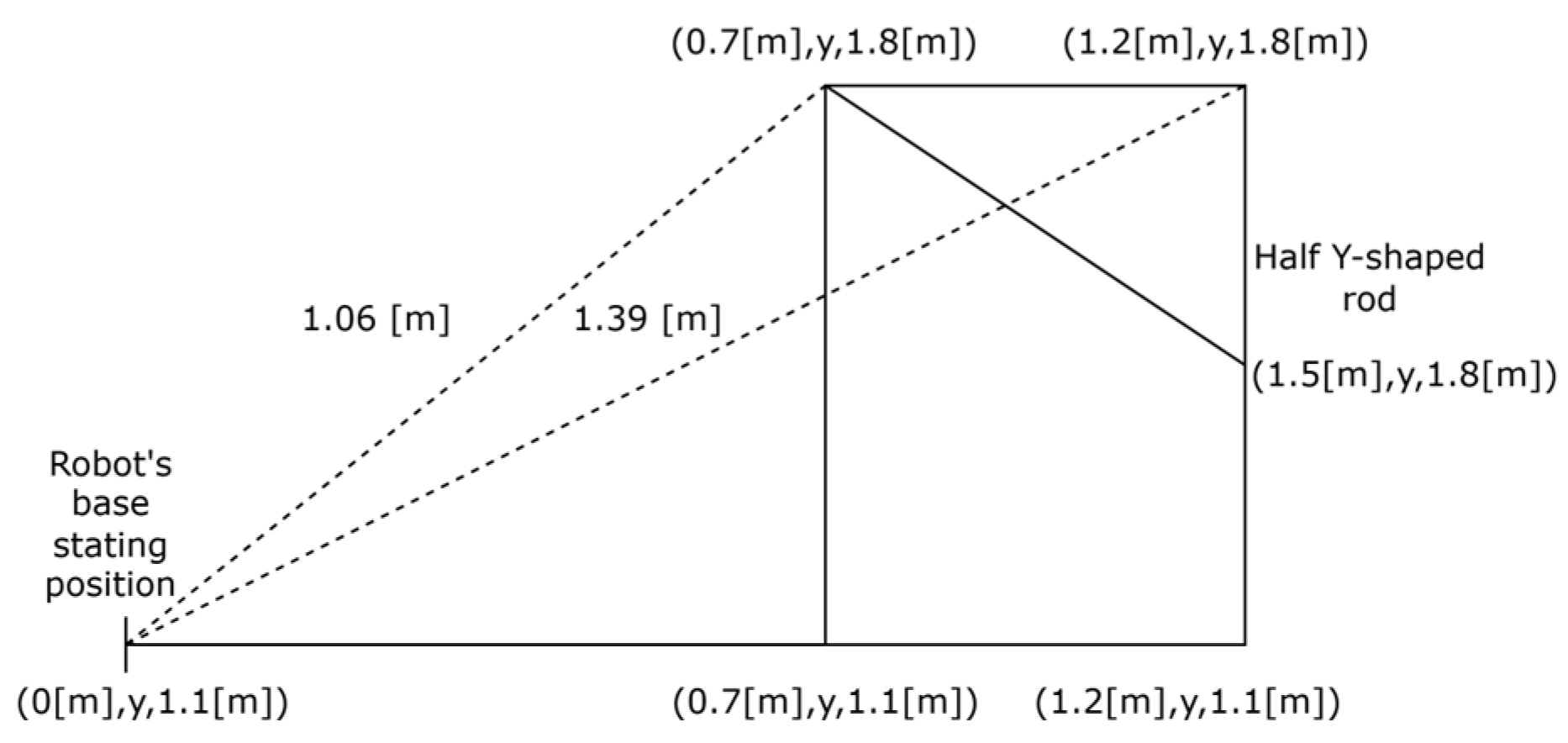
2.3. The Solution Space
- Two adjacent prismatic joints must be perpendiculars to avoid redundancy in motion and control complexity:
- A configuration will have no more than 3 prismatic joints. Prismatic joints provide linear motion rather than rotational, so having too many prismatic joints restricts the manipulator’s dexterity, and the workspace becomes less versatile.
- A Roll joint will not be followed by a Roll\Pitch joint in the Z-axis to avoid redundancy and the loss of manipulability:
- A Roll joint will not be followed by an element axis in the X-axis:
- 5.
- If the current joint is a prismatic Z joint and its previous joint is a Roll joint, the next joint will not be the X-axis:
- The first joint is rotational along the Z-axis:
- The first link length is 0.1 m.
- The total length of all links is in the range of 1.4 m to 2 m:
- Joints limits:
- Links lengths:
2.3.1. The Dataset
- Joint Families: The dataset consists of 6836 joint families. All joint families were selected to be sampled.
- Link Families: For each joint family, 15 link families were randomly selected from a total of 456 available options. The selection of 15 link families per joint family provides a sufficient sample size to capture diversity while maintaining manageable computational complexity.
- Configuration Generation: This random selection process generated a comprehensive set of 102,540 unique manipulator configurations.
2.4. Simulation
URDF Generator
2.5. Optimization Algorithm
2.6. Machine Learning Models
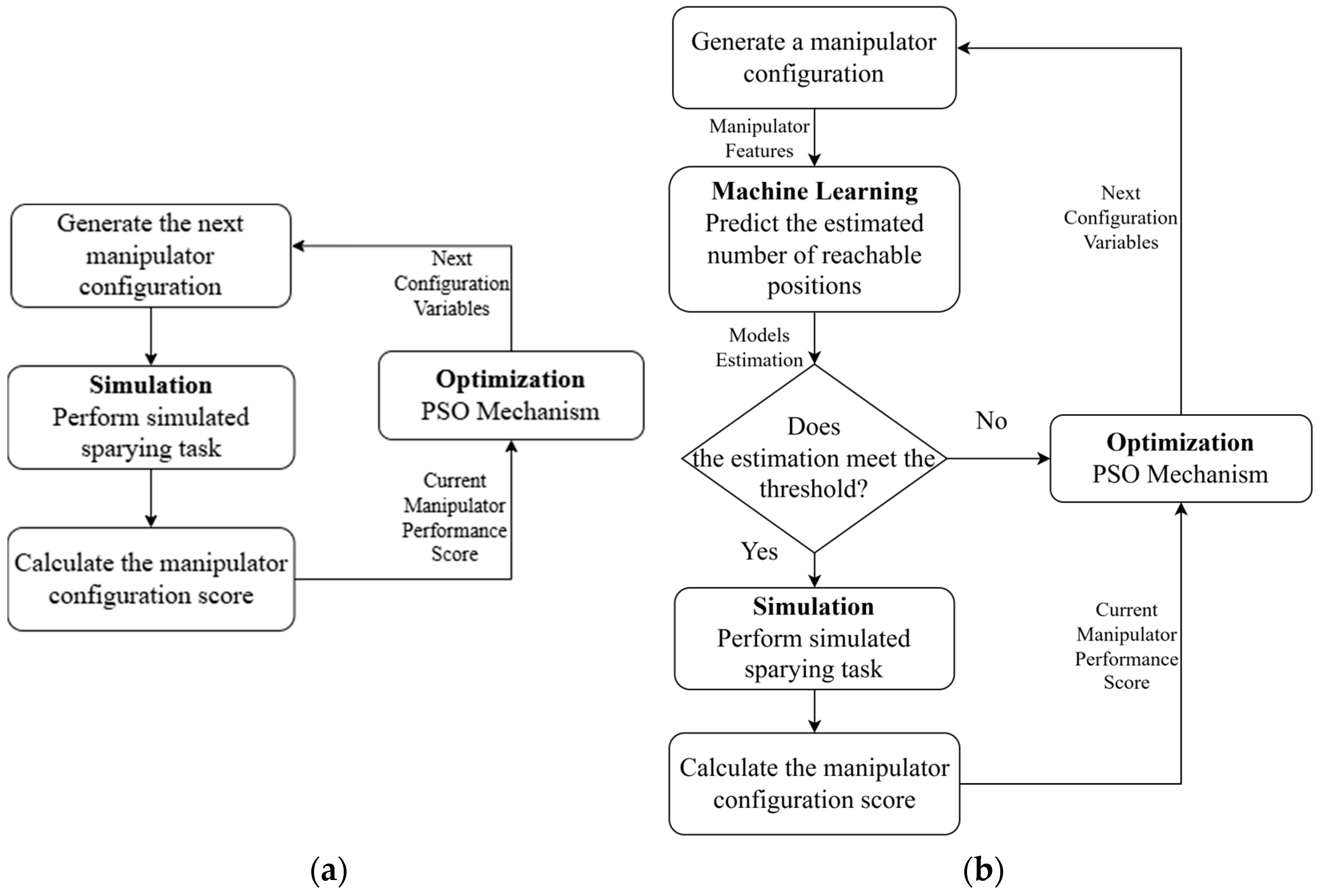
3. Improved Methodology Development
- A robotic manipulator configuration is generated.
- The manipulator directly performs a simulated task.
- Performance indicators are calculated from the simulation.
- These results feed into a PSO mechanism.
- The PSO mechanism then influences the next generation of manipulator configuration.
- A robotic manipulator configuration is generated.
- Trained XGBoost models are loaded to validate the configuration.
- A decision point checks if the manipulator is expected to reach the threshold.
- Only configurations passing this validation proceed to the simulation.
- Performance indicators are calculated only for valid configurations.
- The PSO mechanism optimizes based on these results.
4. Results and Discussions
4.1. PSO Hyperparameter Tuning
- 1.
- Inertia Weight (ω): The inertia weight is a critical parameter influencing the performance of the PSO algorithm. It determines how much of a particle’s previous velocity is retained in its current iteration, effectively controlling the momentum of particles. A higher inertia weight promotes global exploration by encouraging particles to move into new regions of the search space, while a lower value facilitates local exploitation by focusing on refining existing solutions. It was adjusted by using three different strategies: (i) a constant parameter value of 0.795, (ii) a linear function decreasing in time with the set and (iii) a chaotic linear decreasing with the set .
- 2.
- Population Size: The population size represents the number of individual particles or potential solutions maintained simultaneously in the swarm during the PSO algorithm’s execution. Each particle represents a candidate solution to the optimization problem and moves through the search space based on its own experience and the collective knowledge of the swarm. The population size is determined by the specific problem being addressed; however, it is generally not highly sensitive to variations in problem characteristics [31]. The options considered were population sizes of 20 or 50 particles.
- Inertia Weight (ω): Chaotic inertia weight. The fundamental concept of the chaotic inertia weight method involves using a chaotic map to set the inertia weight coefficient. In this method, the Logistic mapping is used to achieve this. The formula for Logistic mapping is as follows:where Logistic mapping occurs as chaotic phenomena.
- 2.
- Population Size: set to 50.
- 3.
- Cognitive Coefficient (c1) and Social Coefficient (c2): Both coefficients were set to 1.49, reflecting a balanced influence between a particle’s personal best position and the swarm’s best-known position.
- 4.
- Generation Number (Iterations): The number of generations was set to 200 due to computational considerations.
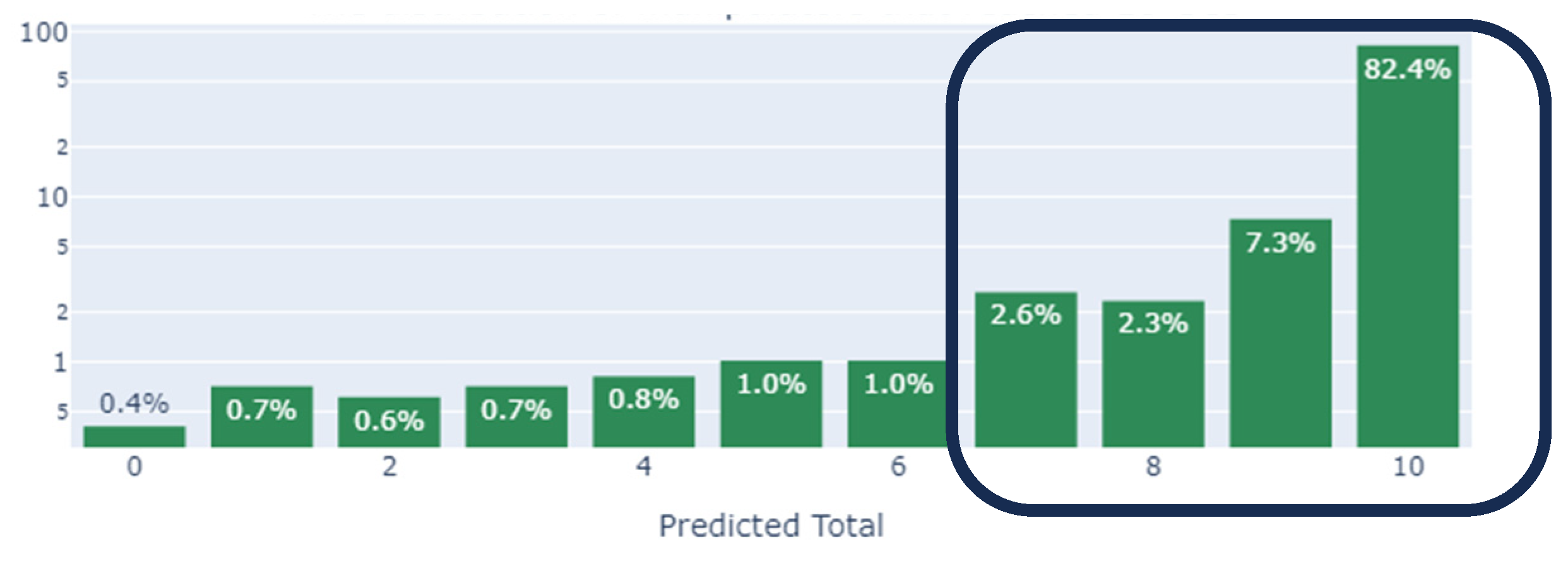
4.2. ML Training Results
4.3. Methodologies Comparison
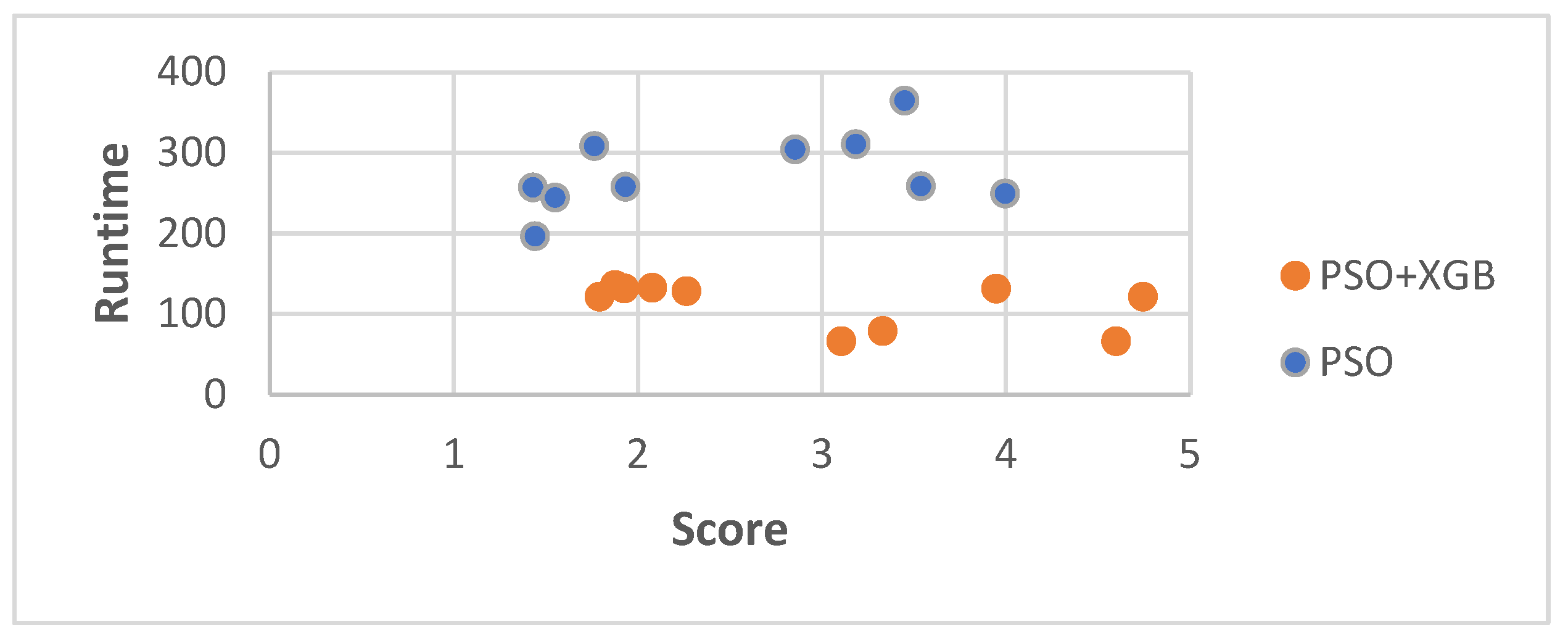
- Runtime: As illustrated in Figure 7, the improved methodology significantly reduced runtime compared to the current methodology. The use of XGBoost reduced the average runtime by 59.06%, demonstrating a substantial increase in computational efficiency. Both methodologies used PSO with 200 iterations.
- Optimization objective score: In the improved methodology, the manipulability index, in six out of the ten runs, achieved higher optimization objective scores, with an average increase of 29.75% in comparison to the current methodology. This indicates that the improved methodology can also potentially achieve higher-quality solutions.
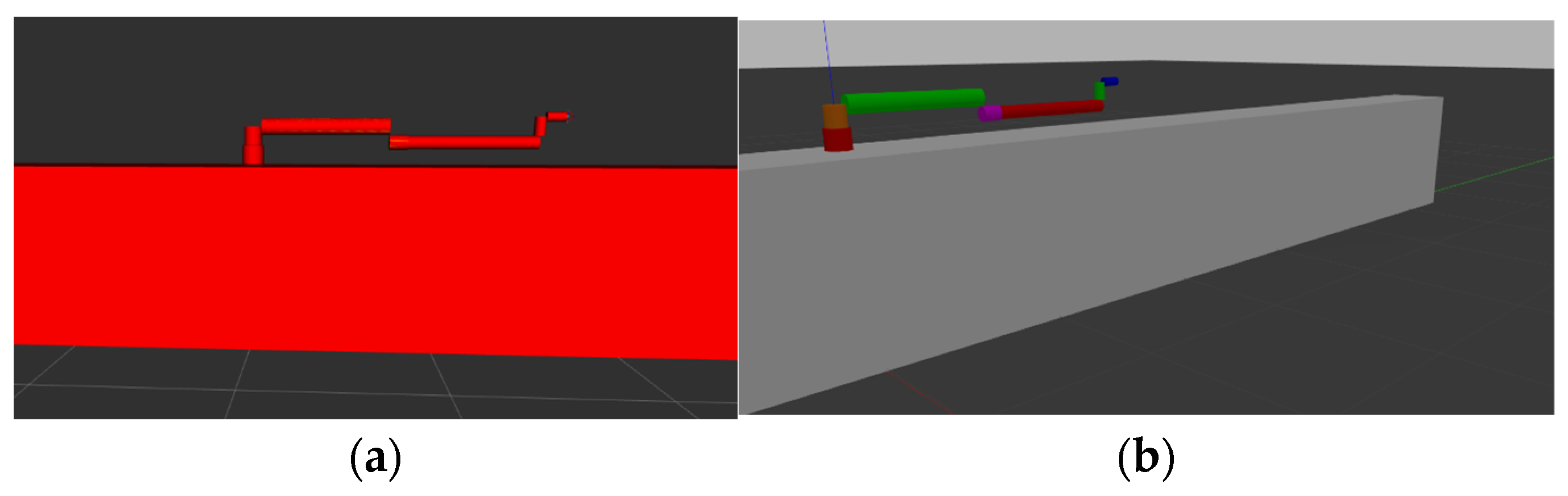
4.4. Optimal Manipulator
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Alrashdi, A.M.A.; Al-Qurashi, A.D.; Awad, M.A.; Mohamed, S.A.; Al-rashdi, A.A. Quality, antioxidant compounds, antioxidant capacity and enzymes activity of ‘El-Bayadi’ table grapes at harvest as affected by preharvest salicylic acid and gibberellic acid spray. Sci. Hortic. 2017, 220, 243–249. [Google Scholar] [CrossRef]
- Berenstein, R.; Shahar, O.B.; Shapiro, A.; Edan, Y. Grape clusters and foliage detection algorithms for autonomous selective vineyard sprayer. Intell. Serv. Robot. 2010, 3, 233–243. [Google Scholar] [CrossRef]
- Danton, A.; Roux, J.C.; Dance, B.; Cariou, C.; Lenain, R. Development of a spraying robot for precision agriculture: An edge following approach. In Proceedings of the CCTA 2020-4th IEEE Conference on Control Technology and Applications, Montreal, QC, Canada, 24–26 August 2020; pp. 267–272. [Google Scholar] [CrossRef]
- Fountas, S.; Mylonas, N.; Malounas, I.; Rodias, E.; Santos, C.H.; Pekkeriet, E. Agricultural robotics for field operations. Sensors 2020, 20, 2672. [Google Scholar] [CrossRef] [PubMed]
- García-Vanegas, A.; García-Bonilla, M.J.; Forero, M.G.; Castillo-García, F.J.; Gonzalez-Rodriguez, A. AgroCableBot: Reconfigurable Cable-Driven Parallel Robot for Greenhouse or Urban Farming Automation. Robotics 2023, 12, 165. [Google Scholar] [CrossRef]
- Wang, D.; Tan, D.; Liu, L. Particle swarm optimization algorithm: An overview. Soft Comput. 2018, 22, 387–408. [Google Scholar] [CrossRef]
- Bechar, A.; Vigneault, C. Agricultural robots for field operations. Part 2: Operations and systems. Biosyst. Eng. 2017, 153, 110–128. [Google Scholar] [CrossRef]
- Zhou, L.; Bai, S. A new approach to design of a lightweight anthropomorphic arm for service applications. J. Mech. Robot. 2015, 7, 031001. [Google Scholar] [CrossRef]
- Xiao, Y.; Fan, Z.; Li, W.; Chen, S.; Zhao, L.; Xie, H. A Manipulator Design Optimization Based on Constrained Multi-objective Evolutionary Algorithms. In Proceedings of the 2016 International Conference on Industrial Informatics-Computing Technology, Intelligent Technology, Industrial Information Integration (ICIICII), Wuhan, China, 3–4 December 2016; pp. 199–205. [Google Scholar] [CrossRef]
- Meir, I.; Bechar, A.; Sintov, A. Kinematic Optimization of a Robotic Arm for Automation Tasks with Human Demonstration. In Proceedings of the 2024 IEEE International Conference on Robotics and Automation (ICRA), Yokohama, Japan, 13–17 May 2024; pp. 7172–7178. [Google Scholar] [CrossRef]
- Shirazi, A.R.; Fakhrabadi, M.M.S.; Ghanbari, A. Optimal design of a 6-DOF parallel manipulator using particle swarm optimization. Adv. Robot. 2012, 26, 1419–1441. [Google Scholar] [CrossRef]
- Farooq, S.S.; Baqai, A.A.; Shah, M.F. Optimal design of tricept parallel manipulator with particle swarm optimization using performance parameters. J. Eng. Res. 2021, 9, 378–395. [Google Scholar] [CrossRef]
- Ore, J.; Detweiler, C.; Elbaum, S. Towards Code-Aware Robotic Simulation Vision Paper. In Proceedings of the 1st International Workshop on Robotics Software Engineering, Gothenburg, Sweden, 28 May 2018; pp. 40–43. [Google Scholar]
- Zhibao, S.; Haojie, Z.; Sen, Z. A robotic simulation system combined USARSim and RCS library. In Proceedings of the 2017 2nd Asia-Pacific Conference on Intelligent Robot Systems (ACIRS), Wuhan, China, 16–19 June 2017; pp. 240–243. [Google Scholar] [CrossRef]
- Wang, H.; Hohimer, C.J.; Bhusal, S.; Karkee, M.; Mo, C.; Miller, J.H. Simulation as A Tool In Designing and Evaluating A Robotic Apple Harvesting System. IFAC-PapersOnLine 2018, 51, 135–140. [Google Scholar] [CrossRef]
- Takaya, K.; Asai, T.; Kroumov, V.; Smarandache, F. Simulation environment for mobile robots testing using ROS and Gazebo. In Proceedings of the 2016 20th International Conference on System Theory, Control and Computing (ICSTCC), Sinaia, Romania, 13–15 October 2016; pp. 96–101. [Google Scholar] [CrossRef]
- Huang, Z.; Li, F.; Xu, L. Modeling and simulation of 6 DOF robotic arm based on gazebo. In Proceedings of the 2020 6th International Conference on Control, Automation and Robotics (ICCAR), Singapore, 20–23 April 2020; pp. 319–323. [Google Scholar] [CrossRef]
- Karoly, A.I.; Galambos, P.; Kuti, J.; Rudas, I.J. Deep Learning in Robotics: Survey on Model Structures and Training Strategies. IEEE Trans. Syst. Man Cybern. Syst. 2021, 51, 266–279. [Google Scholar] [CrossRef]
- Pierson, H.A.; Gashler, M.S. Deep learning in robotics: A review of recent research. Adv. Robot. 2017, 31, 821–835. [Google Scholar] [CrossRef]
- Yue, S.; Shi, Y. Manipulator Smooth Control Method Based on LSTM-XGboost and Its Optimization Model Construction. Appl. Sci. 2023, 13, 8994. [Google Scholar] [CrossRef]
- Lin, X.; Wang, Z.-Q.; Chen, X.-Y. Path Planning with Improved Artificial Potential Field Method Based on Decision Tree. In Proceedings of the 2020 27th Saint Petersburg International Conference on Integrated Navigation Systems (ICINS), Saint Petersburg, Russia, 25–27 May 2020. [Google Scholar] [CrossRef]
- Yoo, J.-H.; Park, Y.-K.; Han, S.-S. Predictive Maintenance System for Wafer Transport Robot Using K-Means Algorithm and Neural Network Model. Electronics 2022, 11, 1324. [Google Scholar] [CrossRef]
- Lenz, I.; Lee, H.; Saxena, A. Deep learning for detecting robotic grasps. Int. J. Robot. Res. 2015, 34, 705–724. [Google Scholar] [CrossRef]
- Wu, J.; Yildirim, I.; Lim, J.J.; Freeman, W.T.; Tenenbaum, J.B. Galileo: Perceiving physical object properties by integrating a physics engine with deep learning. Adv. Neural Inf. Process. Syst. 2015, 28, 127–135. [Google Scholar]
- McArthur, C. Embed to Control: A Locally Linear Latent Dynamics Model for Control from Raw Images. Cine. J. 2008, 47, 147–152. [Google Scholar] [CrossRef]
- Oberti, R.; Marchi, M.; Tirelli, P.; Calcante, A.; Iriti, M.; Tona, E.; Hočevar, M.; Baur, J.; Pfaff, J.; Schütz, C.; et al. Selective spraying of grapevines for disease control using a modular agricultural robot. Biosyst. Eng. 2016, 146, 203–215. [Google Scholar] [CrossRef]
- Wandkar, S.V.; Bhatt, Y.C.; Jain, H.K.; Nalawade, S.M.; Pawar, S.G. Real-Time Variable Rate Spraying in Orchards and Vineyards: A Review. J. Inst. Eng. (India) Ser. A 2018, 99, 385–390. [Google Scholar] [CrossRef]
- Yoshikawa, T. Manipulability of Robotic Mechanisms. Int. J. Robot. Res. 1985, 4, 439–446. [Google Scholar] [CrossRef]
- Qian, W.; Xia, Z.; Xiong, J.; Gan, Y.; Guo, Y.; Weng, S.; Deng, H.; Hu, Y.; Zhang, J. Manipulation task simulation using ROS and Gazebo. In Proceedings of the 2014 IEEE International Conference on Robotics and Biomimetics (ROBIO 2014), Bali, Indonesia, 5–10 December 2014; pp. 2594–2598. [Google Scholar] [CrossRef]
- Eberhart, R.; Kennedy, J. A new optimizer using particle swarm theory. In MHS ’95: Proceedings of the Sixth International Symposium on Micro Machine and Human Science; Nagoya Municipal Industrial Research Institute: Nagoya, Japan, 1995; pp. 39–43. [Google Scholar]
- Ahmed, A.A.W.; Markendahl, J.; Ghanbari, A. Development of An Autonomous Kiwifruit Picking Robot. In Proceedings of the 2009 4th International Conference on Autonomous Robots and Agents, Wellington, New Zealand, 10–12 February 2009; pp. 1–5. Available online: https://ieeexplore.ieee.org/document/4804023/authors#authors (accessed on 18 April 2025).
- Shi, Y.H.; Eberhart, R. Modified particle swarm optimizer. In Proceedings of the 1998 IEEE International Conference on Evolutionary Computation Proceedings (ICEC), Anchorage, AK, USA, 4–9 May 1998; pp. 69–73. [Google Scholar] [CrossRef]
- Yan, K. Student performance prediction using XGBoost method from a macro perspective. In Proceedings of the 2021 2nd International Conference on Computing and Data Science (CDS), Stanford, CA, USA, 28–29 January 2021; pp. 453–459. [Google Scholar] [CrossRef]

| Amount | |
|---|---|
| Number of joint configuration families | 6836 |
| Number of link configuration families | 456 |
| Total manipulator configurations | 3,117,216 |
| Estimated run time on a standard intel i7 computer | 1443.15 days |
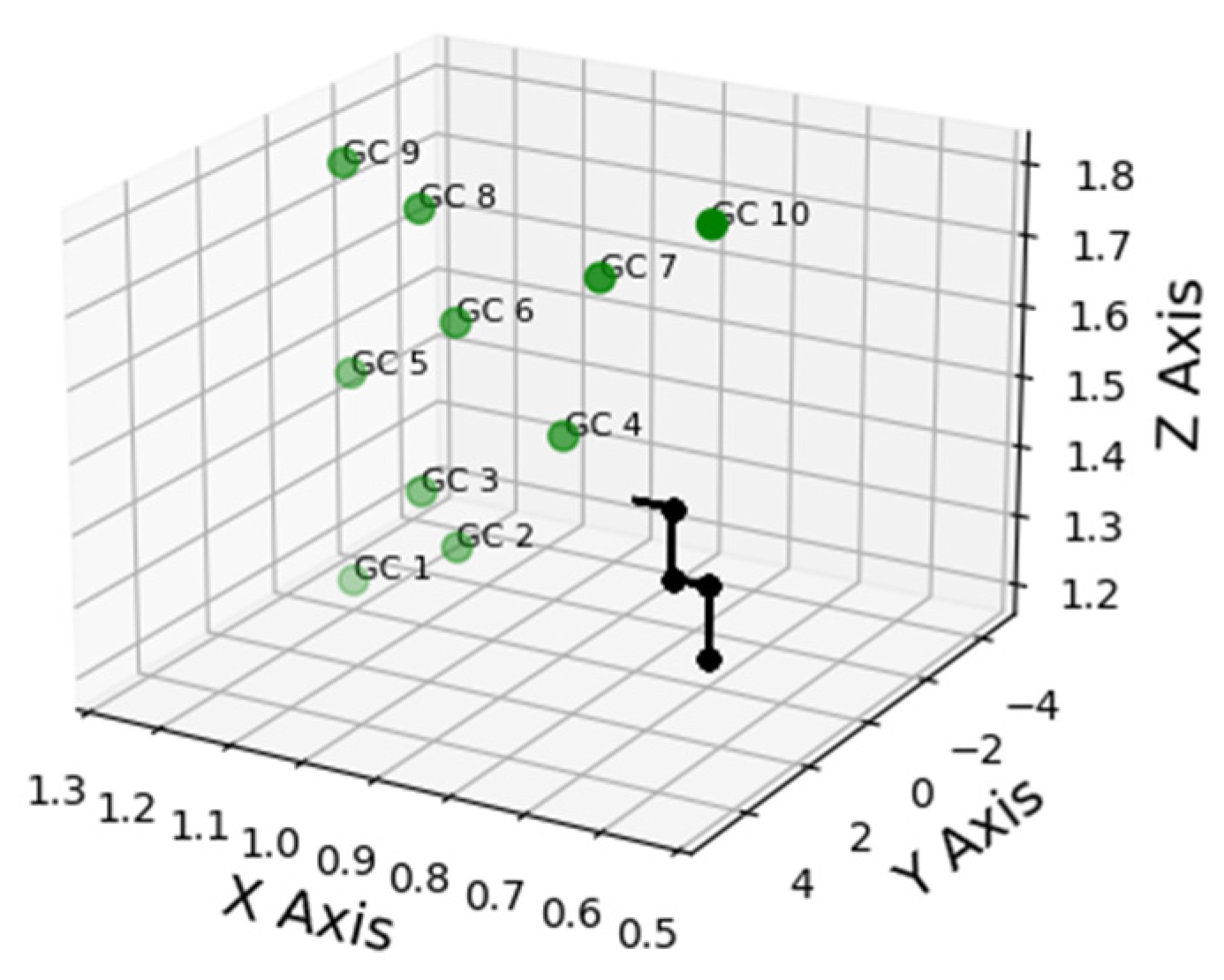
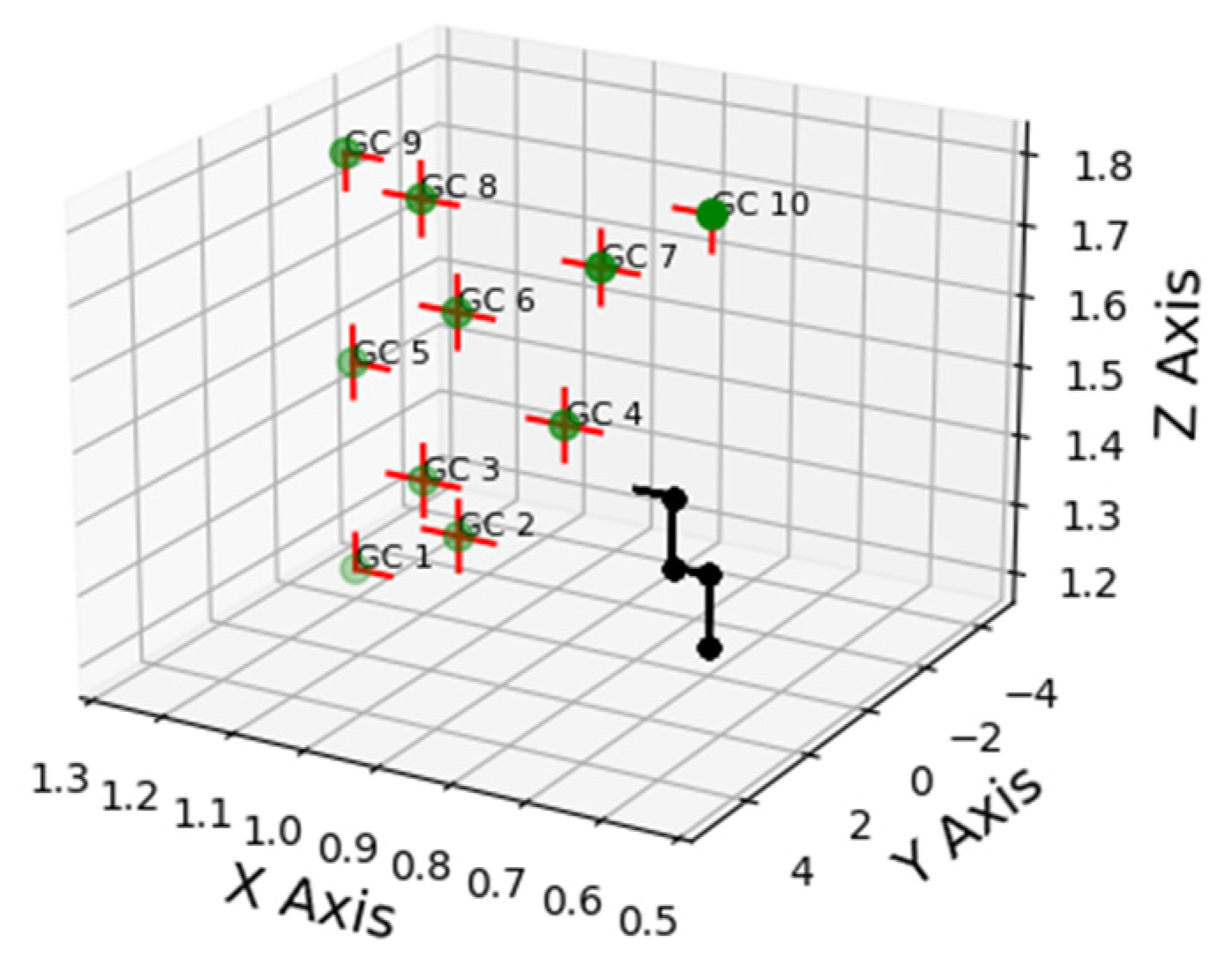
| Position Predicted | NPV | PPV |
|---|---|---|
| GC1 | 0.884 | 0.862 |
| GC2 | 0.865 | 0.856 |
| GC3 | 0.843 | 0.82 |
| GC4 | 0.835 | 0.827 |
| GC5 | 0.85 | 0.833 |
| GC6 | 0.835 | 0.822 |
| GC7 | 0.815 | 0.804 |
| GC8 | 0.819 | 0.803 |
| GC9 | 0.825 | 0.815 |
| GC10 | 0.794 | 0.795 |
| Average | 0.831 | 0.824 |
| Rep. | Performance Score | Optimal Manipulator [Link Family No., Joint Family No.] | Runtime [Mins] | Runtime Difference (%) | Score Difference (%) | |||
|---|---|---|---|---|---|---|---|---|
| PSO | PSO + XGB | PSO | PSO + XGB | PSO | PSO + XGB | |||
| 1 | 1.43 | 1.926 | [334, 3616] | [328, 3854] | 256.98 | 131.37 | −48.88% | 34.69% |
| 2 | 1.763 | 2.078 | [152, 1958] | [118, 1856] | 308.18 | 132.23 | −57.09% | 17.87% |
| 3 | 3.449 | 2.264 | [270, 6787] | [280, 2896] | 364.67 | 127.87 | −64.94% | −34.36% |
| 4 | 2.855 | 4.745 | [268, 6794] | [268, 6787] | 303.85 | 121.02 | −60.17% | 66.20% |
| 5 | 1.4409 | 1.791 | [435, 2794] | [454, 6087] | 196.32 | 121.10 | −38.31% | 24.3% |
| 6 | 3.538 | 3.106 | [270, 289] | [287, 295] | 258.37 | 65.88 | −74.50% | −12.21% |
| 7 | 3.185 | 3.947 | [381, 3152] | [420, 6078] | 310.68 | 131.03 | −57.82% | 23.92% |
| 8 | 1.55 | 4.599 | [199, 4461] | [119, 2691] | 244.05 | 65.97 | −72.97% | 196.71% |
| 9 | 3.996 | 3.33 | [119, 2383] | [119, 1575] | 249.25 | 78.53 | −68.49% | −16.66% |
| 10 | 1.933 | 1.876 | [281, 289] | [251, 3117] | 257.52 | 135.52 | −47.37% | −2.95% |
| Avarage | 2.514 | 2.97 | 275.99 | 111.95 | −59.06% | 29.75% | ||
| Manipulator Configuration [Link Family No., Joint Family No.] | Reachability | Performance Score | Methodology | |
|---|---|---|---|---|
| 1 | [420, 6078] | 43 | 3.702 | PSO + XGB |
| 2 | [381, 3152] | 43 | 3.105 | PSO |
| 3 | [270, 289] | 43 | 2.691 | PSO |
| 4 | [268, 6787] | 43 | 2.301 | PSO + XGB |
| 5 | [287, 295] | 43 | 2.091 | PSO + XGB |
| 6 | [454, 6087] | 43 | 1.697 | PSO + XGB |
| 7 | [435, 2794] | 43 | 1.407 | PSO |
| 8 | [199, 4461] | 43 | 1.403 | PSO |
| 9 | [281, 289] | 43 | 1.36 | PSO |
| 10 | [268, 6794] | 43 | 1.3 | PSO |
| 11 | [251, 3117] | 43 | 1.066 | PSO + XGB |
| 12 | [328, 3854] | 43 | 0.991 | PSO + XGB |
| 13 | [280, 2896] | 43 | 0.513 | PSO + XGB |
| 14 | [334, 3616] | 43 | 0.34 | PSO |
| 15 | [270, 6787] | 9 | 5.098 | PSO |
| 16 | [152, 1958] | 27 | 1.765 | PSO |
| 17 | [118, 1856] | 37 | 1.657 | PSO + XGB |
| 18 | [119, 1575] | 10 | 1.439 | PSO + XGB |
| 19 | [119, 2691] | 39 | 0.826 | PSO + XGB |
| 20 | [119, 2383] | 42 | 0.589 | PSO |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Azriel, R.; Degani, O.; Bechar, A. A Methodology to Characterize an Optimal Robotic Manipulator Using PSO and ML Algorithms for Selective and Site-Specific Spraying Tasks in Vineyards. Robotics 2025, 14, 58. https://doi.org/10.3390/robotics14050058
Azriel R, Degani O, Bechar A. A Methodology to Characterize an Optimal Robotic Manipulator Using PSO and ML Algorithms for Selective and Site-Specific Spraying Tasks in Vineyards. Robotics. 2025; 14(5):58. https://doi.org/10.3390/robotics14050058
Chicago/Turabian StyleAzriel, Roni, Oded Degani, and Avital Bechar. 2025. "A Methodology to Characterize an Optimal Robotic Manipulator Using PSO and ML Algorithms for Selective and Site-Specific Spraying Tasks in Vineyards" Robotics 14, no. 5: 58. https://doi.org/10.3390/robotics14050058
APA StyleAzriel, R., Degani, O., & Bechar, A. (2025). A Methodology to Characterize an Optimal Robotic Manipulator Using PSO and ML Algorithms for Selective and Site-Specific Spraying Tasks in Vineyards. Robotics, 14(5), 58. https://doi.org/10.3390/robotics14050058







