Effectiveness of Unsupervised Training for Applications in Deep Neural Network Robot Navigation

Abstract

Supervised training of neural networks is time consuming, and the scenarios required for obtaining a representative dataset must be carefully considered for each task. Applying an unsupervised training approach can greatly simplify this data collection aspect. This paper explores options for the unsupervised training of a convolutional neural network for the navigation of a mobile robot and compares its benefits with respect to a supervised training approach. A simulated training environment was created, in which the robot, through random motion, gathered the required data needed for training. Two approaches to training were investigated: either selectively choosing the training data from the random set acquired or considering modifying the network output to favor improved navigation. Both methods proved successful at obtaining an optimum value of 80% efficiency of directional travel whilst maintaining a collision avoidance performance of 97.7%. The results proved our approach was comparable in performance with respect to supervised training approaches, whilst it demonstrated superiority in terms of training-data collection.

1. Introduction

Robot navigation is a fundamental challenge in robotics, requiring systems to perceive, interpret, and autonomously move through environments. Traditional approaches based on rule-based logic and sensor fusion have struggled to generalize across dynamic or unstructured environments. Neural networks, leveraging large datasets and advanced computational power, have emerged as a transformative tool in addressing these challenges and have become a cornerstone in developing advanced navigation systems for robots due to their ability to learn from data, generalize across various scenarios, and improve performance through experience.

Convolutional neural networks (CNNs) are extensively used for visual navigation, leveraging their ability to process and interpret visual data. They have proven effective in processing visual data for navigation tasks such as object detection and obstacle avoidance [1,2]. CNNs have been extensively utilized for visual navigation tasks, including feature extraction [3], depth estimation [4], and semantic segmentation [5]. Notable implementations include residual neural networks (ResNets), utilized for feature extraction and scene understanding, and VGG (developed by the Visual Geometry Group at Oxford University), employed for object detection and localization tasks [6].

Supervised learning involves training neural networks on labelled datasets, where input–output pairs are explicitly provided. Supervised learning is a cornerstone of robot navigation research, enabling precise and reliable task performance in structured environments. Early studies by Lecun et al. demonstrated the potential of end-to-end supervised learning for use in off-road navigation, mapping raw sensory inputs to control outputs [7]. This was extended by Bojarski et al., who trained a deep neural network to predict steering angles from monocular camera inputs, achieving robust navigation in structured environments like roads [2]. Tai et al. conducted a study in which they trained a CNN on a large dataset of images labelled with corresponding steering angles. The model learned to predict steering commands based on visual inputs, enabling autonomous navigation in diverse environments [8]. The CNN achieved high accuracy in steering prediction, demonstrating robust performance in both indoor and outdoor settings. This study highlighted the importance of using a diverse training dataset to ensure generalization across different scenarios. Loquercio et al. applied supervised learning to aerial drones, training models on labelled images of terrains to predict flight commands, enabling obstacle avoidance in cluttered spaces [9]. Pashevich et al. introduced multimodal learning, combining visual and textual data to train robots for natural-language-guided navigation [10].

Recent advancements have explored integrating supervised learning with imitation learning. Wigness et al. developed a framework where robots learned navigation strategies from human demonstrations, enabling them to adapt to noisy or sparse data [11]. Cheng et al. introduced a data-efficient supervised learning approach, reducing the dependency on large datasets while maintaining performance [12]. Further developments have leveraged supervised learning for specific applications, such as semantic navigation. Gupta et al. trained models to navigate environments based on semantic understanding, combining scene recognition with goal-driven path planning [13]. Choi et al. extended this by incorporating semantic segmentation into end-to-end navigation systems, enhancing adaptability in indoor environments [14].

While supervised learning excels in controlled settings, its reliance on labelled data remains a significant limitation. This challenge has led to the exploration of unsupervised learning and hybrid paradigms to overcome these constraints. Unsupervised learning is a subfield of machine learning that has become prominent in recent years due to its potential to impart a degree of self-sufficiency to robots, allowing a robot to explore and understand its environment by discerning inherent patterns and relationships in the data it gathers, without the need for explicit human-provided labels. This not only reduces dependence on extensive, manually labelled datasets but also equips robots with adaptability and versatility crucial for navigating in previously unseen and unstructured environments [15].

Zhou et al. introduced a self-supervised framework for visual odometry, training a CNN to predict relative camera motion using photometric consistency [16]. This approach eliminated the need for labelled data while also achieving competitive performance with respect to supervised methods. Godard et al. advanced unsupervised monocular depth estimation by leveraging stereo vision, using left–right consistency in image pairs to train models for depth prediction [17]. Zhan et al. extended this approach by facilitating simultaneous learning of depth and ego-motion from video sequences, improving robustness in dynamic environments [18]. Ma et al. used Variational Autoencoders (VAEs) to extract latent space representations from sensory inputs, which were then employed for path planning and obstacle avoidance [19]. Similarly, Sermanet et al. introduced Time-Contrastive Networks (TCNs), which learned to recognize self-supervised visual representations by predicting temporal proximity between video frames [20]. Dugas et al. applied contrastive loss to train a model on representations capturing spatial and temporal relationships, enabling generalization to unseen environments [21]. Jayaraman and Grauman proposed reinforcement-inspired unsupervised learning, where robots predicted future states of their environments to improve exploration and decision-making [22]. Chen et al. explored integrating unsupervised learning with multimodal data by training models to acquire depth and semantic information simultaneously from video streams, improving understanding of 3D environments [23]. Other studies have combined unsupervised learning with pre-trained models, using transfer learning to fine-tune navigation systems with minimal labelled data [24]. While unsupervised learning significantly reduces dependence on annotations, achieving precision comparable to supervised methods in complex scenarios remains an ongoing challenge.

Whilst not the primary focus of this review, reinforcement learning, transfer learning, and hybrid approaches have also contributed significantly to robot navigation and will be briefly mentioned here. Deep reinforcement learning (DRL) integrates deep learning with reinforcement-learning principles, with models like Deep Q-Networks (DQNs), Proximal Policy Optimization [25], and Asynchronous Advantage Actor–Critic (A3C) excelling in learning optimal policies through environmental interaction [26,27], albeit at a high computational cost.

Transfer learning leverages pre-trained models from related domains, adapting them to new tasks with minimal additional training. Chen et at. utilized a pre-trained ResNets model for feature extraction in indoor navigation tasks [28]. The model was fine-tuned on a small dataset of indoor scenes, significantly reducing the required training time and labelled data. The transfer learning approach achieved high accuracy in navigation tasks, demonstrating effective generalization to new environments. This study highlighted that transfer learning can expedite model development and enhance performance, particularly when labelled data is scarce. Selecting an appropriate pre-trained model is crucial for successful transfer learning.

Hybrid approaches can significantly improve navigation performance, particularly in dynamic environments with moving obstacles. Pfeiffer et al. combined supervised learning with reinforcement learning to develop a hybrid approach for robot navigation [29]. The model was initially trained using supervised learning on a labelled dataset of navigation paths, and then reinforcement learning was employed to fine-tune the model in a simulated environment. Hybrid architectures combining CNNs and recurrent neural networks (RNNs) have further enhanced navigation performance in real-world applications [30] and shown effectiveness in fusing spatial and temporal features. Zhang et al. proposed an integrated architecture for visual navigation, demonstrating superior performance in cluttered and dynamic environments [31]. Autoencoder-based unsupervised models have also been explored for feature learning, enabling efficient data compression and reconstruction for navigation tasks [32,33]. Zhang et al. developed a comprehensive navigation system integrating supervised learning, unsupervised learning, and reinforcement learning [34]. The model was initially trained using supervised learning, followed by self-supervised fine-tuning and reinforcement learning in a simulated environment. The hybrid model exhibited superior adaptability and robustness, efficiently navigating complex and dynamic environments. These studies demonstrated that hybrid approaches can address the limitations of individual methods, resulting in more versatile and effective navigation systems. Balancing the contributions of each learning strategy is key to optimizing performance.

Supervised learning, in which models are trained on labelled datasets, excels in controlled environments where data annotations are readily available. However, these techniques still rely heavily on user input to facilitate good performance, and a significant research gap exists in developing techniques in which robots are left to satisfy their own training needs. Nevertheless, unsupervised learning reduces reliance on labelled data, enabling robots to learn from raw sensory inputs. The integration of these paradigms, along with emerging techniques like self-supervised learning, has the potential to advance the robustness and adaptability of navigation systems.

The problem addressed by this paper is to find a way to circumvent the need for user input for the development of robot navigation controllers. The objective of this work is to devise an approach that allows a robot to train itself to drive on a bearing towards a goal position whilst avoiding objects, with no requirements for user input in terms of training or cost function development. In this work, we employ a differential-drive robot whose motion is constrained to be either straight or a fixed-radius turn to either the left or right. This study assumes the robot is in a cluttered but static environment in which to navigate, with no map available to aid in path planning. We also assume there is a robot positional system that can allow the robot to determine the required bearing with respect to the goal.

The methodology consists of utilizing a simple convolutional neural network architecture that the robot needs to train. This supervised learning approach to navigation, but using an unsupervised training paradigm, is considered appropriate as it allows the user to define the network output but requires no user input in network training. Two training approaches are considered: either the training data is biased, in which case the neural network is trained predominantly based on data resulting from a correct goal bearing heading, or random obstacle avoidance is considered, but the output from the neural network is then biased towards decisions leading to the required goal bearing. In both cases, lidar scans are converted into images, and a convolution neural network is used to determine whether these images should result in the robot moving straight or turning. The performance of these self-trained networks is assessed by comparison with a supervisor trained network.

2. Simulated Environment and Network Design

2.1. Webots Environment

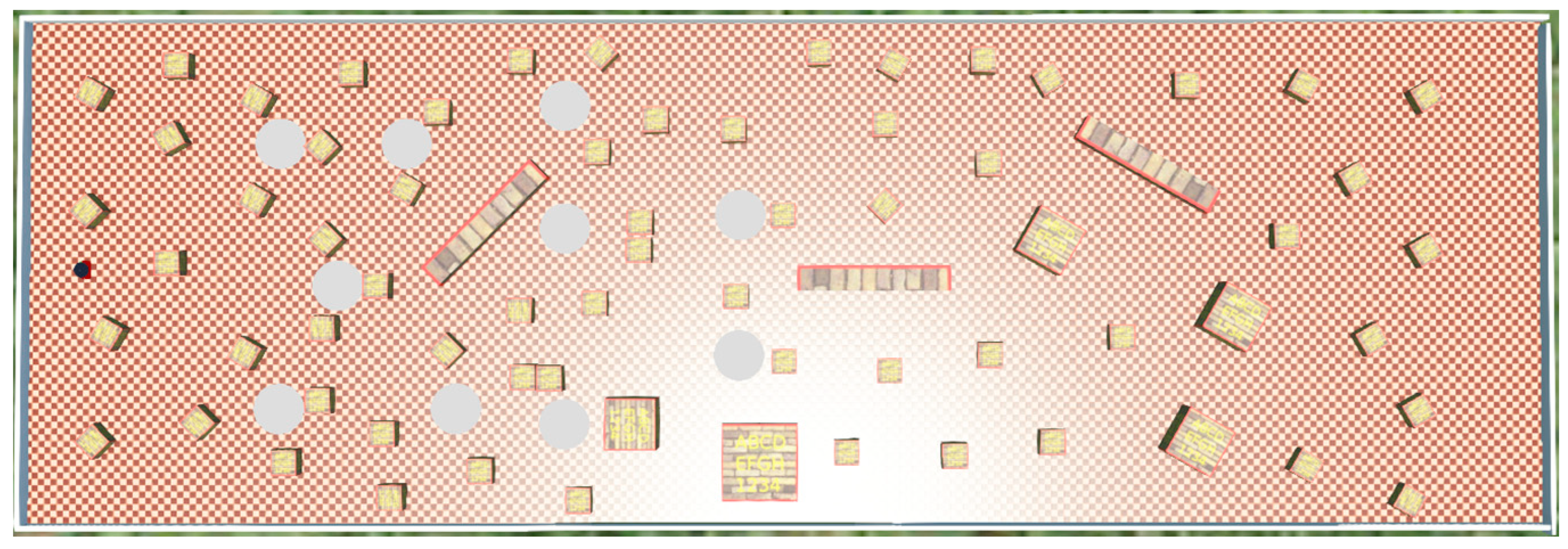
A virtual environment in which to simulate a differential-drive robot and collect training data was created in the robot simulation software Webots 2023a (Cyberbotics Ltd., Lausanne, Switzerland) using a PC with a Xeon Gold 5217 CPU, 192 GB of RAM, and an NVIDIA Quadro RTX A6000 GPU. Matlab R2023a was used as the programming language for controlling the robot and building the neural network. The simulated differential-drive robot, shown in Figure 1, incorporated a magnetometer to allow for determination of heading, a bumper to detect any collisions with objects, and a Hokuyo LiDAR sensor with a range of 5.6 m, a scan angle of ±120 (consisting of 667 points), and a scan time of 100 ms, although as the robot was stopped for each lidar scan, scan time, relative to robot speed, did not influence the range data. The bumper was made sufficiently large so that it was the only part of the robot that could come into contact with any objects.

The simulated environment shown in Figure 1 (with a full overhead view shown in Appendix A, Figure A1) was designed as a spacious, enclosed rectangular area measuring 20 m by 100 m, with the aim for the robot being to travel towards a goal position with a compass bearing of 0° (north) whilst avoiding obstacles. For the simulation, the robot’s position was given by a supervisory controller; in practice, a positioning system such as a GPS or beacons would be used. The bearing towards a virtual goal position of 0° was arbitrarily chosen for the simulation (with the Webots environment preferentially extended in this direction); in practice, the bearing would be specified by the current relationship between the robot’s position and the goal position. As the CNN uses an offset value with respect to the required goal bearing in its analysis rather than the absolute bearing value, the network can be trained using any arbitrary goal bearing. The space is populated with a variety of boxes of various sizes, placed to simulate real-world obstacles in a range of randomized positions. This area features a distinct checkered parquetry floor, with each tile measuring 0.5 m by 0.5 m, allowing for easier observation of the robot’s position during supervised learning. The boxes positioned on this floor space serve as obstacles to challenge the robot’s navigation capabilities. A relatively high density of boxes was used, with no two adjacent boxes being more than 5m apart, to facilitate large variation in the lidar scan data to be collected whilst still allowing a sufficient amount of floor space to allow the robot to maneuver around the boxes. The experimental area was bounded by four walls, effectively constraining the robot’s movement to the interior space. This setup ensured there was a controlled but varied environment where the robot’s decision-making and mobility could be rigorously tested under various obstructive conditions.

The robot initially started from a southerly located central position, as shown in Figure 1; however, ten circular zones were defined and designated as potential new starting positions for the robot if a position reset was required. The zones were labelled as white circles to make matters clear for the user, and robot orientation within the zone was randomized following a reset. A position reset was used when either the robot reached the northerly most point of the area or collided with an object.

In this work, the output of the CNN was broken down into three core decision-making processes for robotic movement: moving forward, turning left, and turning right. Each decision was uniquely defined by the differential wheel speeds. Specifically, when moving forward, both wheels operate at a uniform rotational speed of 1.0 rads⁻¹. For turning left, the controller reduces the left wheel’s speed to 0.5 rads⁻¹ while maintaining the right wheel’s speed at 1.0 rads⁻¹. Conversely, when turning right, the left wheel speed is set at 1.0 rads⁻¹, and the right wheel is slowed to 0.5 rads⁻¹. A critical parameter in this simulation was movement duration, which is quantified as 100 program loops. This corresponds to a distance travelled between decisions of 0.45 m when moving straight and 0.34 m when turning. This was deemed appropriate because of the density of obstacles within the area, giving a reasonable amount of change between lidar scans whilst also giving time for the robot to change direction if required.

2.2. Data Collection

In supervised control mode, the robot, guided by a human operator, avoids obstacles whilst heading in the goal direction (north). The robot moves continually and at incremental points in time. The simulation reads the current input from the operator, saves the metadata, and reacts accordingly. Due to the discrete nature of the motion of the robot, collisions with static objects may occur due to either the inexperience of the operator or cases where the robot has ended up in a situation from which it is impossible to escape. In such circumstances, the robot is reset to one of the 10 randomly chosen starting positions. An experienced human operator usually drives a robot north, with few collisions, so to ensure a comprehensive dataset was acquired for each possible orientation of the robot, the robot’s position was also reset following five decisions of purely northerly travel, regardless of whether a collision occurred. Following such resets, the user would need to turn the robot north again, thereby allowing for data collection in these scenarios. Through this method, data was collected at a rate of approximately 7000 data points per hour.

In contrast, unsupervised control mode entailed allowing the robot to navigate randomly. In each decision stage, the robot randomly decided to embark on one of three possible trajectories and completed the corresponding movement. This randomness naturally led to many collisions, requiring a structured approach to data collection. ‘Good’ data corresponded to a decision that subsequently led to at least five consecutive decisions being implemented (proving that the robot had not decided to drive into a scenario from which escape is impossible). ‘Bad’ data corresponded to a decision that led to a collision within the next five decisions. Following a collision, the robot was moved back to its position after the last good decision point, and another decision was made. For example, if the robot was on its 12th decision that led to a collision, the robot would be moved back to the point of its 7th decision, and another option would be chosen at this point. If subsequent collisions occurred, the robot would be repeatably moved back to this seventh decision point until all decision scenarios were exhausted. If all three decisions led to collisions, the decision was labelled ‘bad,’ and the robot was reset to one of the ten new random starting positions with a random orientation. If the robot made it to the 13th decision, the 7th decision would be regarded as ‘good’. Metadata was saved once the decision was verified as being either good or bad. For this unsupervised control, the simulated world display was not rendered, allowing for a faster simulation, resulting in a data collection rate for good decisions of 4300 data points per hour, with this rate being limited due to the high number of collisions resulting from the random motion.

To ensure there was a comprehensive dataset for every scenario, the data was divided into 12 folders corresponding to one of the three possible decisions made and one of the four current directions of travel. The heading was discretized by considering the amount of turning between each decision; in this case, a left or right decision resulted in a bearing change of 20.4°. Setting a goal (northerly) heading range of ±20° ensured that a single decision could take the robot out of this goal (north) direction zone and would therefore encourage the CNN to turn the robot back into this zone when the next decision was made. Similarly, south was designated as 180° ± 20° to encourage the CNN to turn out of this zone within one decision. The remaining angular ranges were designated for the east- and west-facing zones.

Data files of the 667 lidar points were initially saved containing the metadata regarding whether a collision occurred, the three positional and three magnetometer values (to allow for heading calculation), and the decision at that point. A subsequent MATLAB program then read each data file and, using the contained information, saved the data as a corresponding image file in the appropriate folder. Range data was linearly transformed into pixel data, with a 0 m range corresponding to a pixel intensity of 0 and 5.6 m (or greater) corresponding to a pixel value of 255. As with the heading transformation, the pixel value corresponding to the required goal bearing (north) was set to 255, which linearly decreased to a pixel value of 0 for a pixel corresponding to a bearing in the opposite direction of the goal position (south). Images were made to be only one tenth of the size of the original data to make network computation easier. Examples of the two types of image files created, together with an example of the raw data file, are shown in Figure 2. Images with dimensions of 1 × 67 were created from the ‘good’ data from the lidar scans, and images with dimensions of 2 × 67 were created by representing the offset from the required compass bearing in the first row of the image, with the second image row consisting of lidar data. Conceptually, the robot needed to learn to head towards the white areas (the pixel values closest to 255) of these images.

2.3. Neural Network Design

Thomas et al. [35] utilized a form of Alexnet, a CNN developed for image recognition, to process a view of the environment into an output to control the direction in which the robot was supposed to move. In this work, we utilized a similar principle, with the idea being to convert sensor data into an equivalent image and then utilize a CNN to process this image into an appropriate controller decision. This equivalent image of up to 134 pixels is greatly reduced from the 4800-pixel image processed by the former Alexnet, and we decided to utilize a simpler CNN architecture here. The CNN was developed on the MATLAB Deep Network Designer App and is based on the architecture used for the MATLAB digit recognition CNN example. Its structure is shown in Figure 3, with the details of each layer given in

Table A1. The structure of the CNN, highlighting the parameters used for each layer. Oversized filters allow for modification of the input data without needing to alter the remaining layers of the CNN.

Type	Description
Image Input	imageinput: 1 × 67 × 1 images with ‘zerocenter’ normalization or imageinput: 2 × 67 × 1 images with ‘zerocenter’ normalization
2-D Convolution	conv_1: 8 3 × 3 convolutions with a stride of [1 1] and padding set to ‘same’
Batch Normalization	batchnorm_1
ReLU	relu_1
2-D Max Pooling	maxpool_1: 2 × 2 max pooling with a stride of [2 2] and padding set to ‘same’
2-D Convolution	conv_2: 16 3 × 3 convolutions with a stride of [1 1] and padding set to ‘same’
Batch Normalization	batchnorm_2
ReLU	relu_2
2-D Max Pooling	maxpool_2: 2 × 2 max pooling with a stride of [2 2] and padding set to ‘same’
2-D Convolution	conv_3 32 3 × 3 convolutions with a stride of [1 1] and padding set to ‘same’
Batch Normalization	batchnorm_3
ReLU	relu_3
Fully Connected	fc: 3 fully connected layer
Softmax	Softmax
Classification Output	classoutput

of Appendix A. Utilization of dropout layers was investigated, but their inclusion did not lead to any improvements in network performance, and they were therefore excluded from the final network design.

A total of 60,000 images were utilized for each training cycle (20,000 for each decision). An initial learning rate of 0.0001 was used, the max epochs value was set to 20, and 25% of the data was used for validation. Although the training appeared reasonable, validation always demonstrated poor performance, as shown in Figure A2 of Appendix A. This was attributed to the possibility that each image had more than one control (output) option for successfully navigating the obstacles, and therefore rather than the typical one-to-one correspondence relationship in a CNN, for this problem, there are potentially one-to-many relationships. Therefore, to evaluate the success of the network architecture and training, each CNN controller was run on the Webots simulation to evaluate its performance.

3. Experimental Details

Two experiments were conducted for unsupervised learning. In the first, a specific selection of training data was used to attempt to train the network to preferentially choose the required direction of travel. In the second, a random selection of training data was used, but the output decision was modified to bias the final decision towards the required direction. In both cases, the network was also trained using supervised learning as a benchmark for the results.

Optimum navigation involves getting to the desired location in the quickest amount of time (or with the shortest distance travelled) with a minimum number of incidents. To evaluate performance in each experiment, the following four values were recorded: (a) distance travelled towards the goal (north); (b) total distance covered; (c) number of good decisions made (G), namely, those that do not lead to a collision; and (d) number of bad decisions made (B), namely, those that lead to a collision with an object. From these, two performance parameters were defined: (i) the ratio of the distance travelled towards the goal to the total distance travelled, which indicates the efficiency of moving toward the correct heading, and (ii) the ratio of the number of good decisions made to the total number of decisions made, G/(G + B), which indicates collision avoidance ability. Normalizing the parameters to these two ratios gives a clear indication of the effectiveness of the approach, where values range from 0% (poor) to 100% (optimum).

3.1. Supervised Training

As a benchmark, the robot was driven through the course by an operator. The operator would try to drive the robot in the goal direction (north) whenever possible. A minimum of 20,000 images were required for each decision (with at least 5000 for each current direction of travel). However, after 22 h of driving, it was proving difficult to obtain this minimum number for each possible combination of decision and direction. Therefore, from the available datasets, additional data was artificially created by adding noise to the recorded lidar data. This was achieved by adding a random value from 0 to 9 to any pixel value less than 200, corresponding to slightly increasing lidar measurement values with respect to distance from the objects, effectively moving detected objects further away from the robot. Although this approach limits the representativeness of the possible range of data for the smaller datasets obtained, it is important to note that it does not affect whether a decision is categorized as good.

From this modified dataset, a random selection of 5000 images was taken from each of the 12 folders and used for network training and validation. Once trained, the neural network was deployed on the simulated robot, and the simulation was run. At each decision point, the current data scan (converted to a corresponding image) was input into the neural network, and the highest value output was used to make the next decision. This process continued until 10,000 positions were recorded (9999 decisions made). The performance parameters were then recorded to assess the long-term performance of this supervisor-trained network.

3.2. Unsupervised Training

The approach adopted here for unsupervised training consisted of allowing the robot to move around randomly but only remember, i.e., make, decisions that were classed as good. Inevitably, this resulted in many collisions during the training phase. By using only lidar data, a robot can be taught how to avoid collisions. However, to be useful, a robot needs to head in the required goal direction (north, in this case). For our current set of data from unsupervised training, two training options will be considered.

3.2.1. Biasing the Training Data (Using the 2 × 67 Image Dataset)

To mimic the scenario of supervised training, the dataset used for training may be biased to making decisions leading towards the goal (a northerly trajectory). Thus, the preference would be to choose 1 (head straight) if the robot is facing north, 2 (turn left) if the robot is facing east, 3 (turn right) for a west-facing robot, and either randomly 2 or 3 (turn left or right) for a south-facing robot.

Our biased training dataset contained a selection of data from the four sectors. One might initially think that it would be best to use only data specific to the direction in which the robot needs to travel; for example, if the robot is travelling east, one might think that only the data that involves a left turn should be used. The problem with only using this biased data is that the robot may preferentially decide to turn north regardless of whether a collision is likely to occur. To account for this, the biased data is mixed with a random selection of collision avoidance data. The ratio of biased data to random data was varied from 0:100 (wherein only collision avoidance data is used for training) to 90:10 (where 90% of the data is biased towards the required direction). This combined dataset was used to train the network; the specific ratios for each level of biasing are given in Appendix A,

Table A2. Data training ratios used for biasing the training data.

Movement Decision	Compass Bearing	Number of Images Used in Training (20,000 per Movement Decision)
		0%	10%	30%	50%	70%	90%
Go straight	North	5000	6500	9500	12,500	15,500	18,500
Go straight	East	5000	4500	3500	2500	1500	500
Go straight	South	5000	4500	3500	2500	1500	500
Go straight	West	5000	4500	3500	2500	1500	500
Turn left	North	5000	4500	3500	2500	1500	500
Turn left	East	5000	5833	7500	9167	10,833	12,500
Turn left	South	5000	5167	5500	5833	6167	6500
Turn left	West	5000	4500	3500	2500	1500	500
Turn right	North	5000	4500	3500	2500	1500	500
Turn right	East	5000	4500	3500	2500	1500	500
Turn right	South	5000	5167	5500	5833	6167	6500
Turn right	West	5000	5833	7500	9167	10,833	12,500

. As with supervised training, each decision contained a total of 20,000 datasets (with the required ratio of data taken from each folder). For each trained network, the robot was assessed after making 9999 decisions to assess long-term performance.

3.2.2. Biasing the Output Data (Using the 1 × 67 Image Dataset)

Another option is to simply use the collision avoidance data but then bias the output decisions towards the goal (north) direction. The output from the network shows weightings for the preferred decision, and usually the highest of these values is chosen. However, sometimes, these values may be similar; for example, a similar value is given for moving straight or turning in a particular direction, in which case either decision may be suitable, as neither would result in a collision. In such cases, the preference would be to choose the decision that directs the robot towards the required northerly direction.

To implement this approach, output values for the network were scaled by a value of f(x) in accordance with the direction the robot was facing at a given point in time.

Table 1. The scaling functions used for the CNN output decisions.

Heading	1 (Straight)	2 (Left Turn)	3 (Right Turn)
North	1 + 2x	1 − x	1 − x
East	1	1 + 2x	1 − 2x
South	1 − 2x	1 + x	1 + x
West	1	1−2x	1 + 2x

shows the various adjustment factors used for the network’s output depending on the robot’s current direction of travel. For example, if the robot is facing east, with the output of the neural network being probabilities of 0.45, 0.4, and 0.15 for moving straight, turning left, and turning right, respectively, with a value of x of 0.1 being used, these probabilities, when scaled, become 0.45 × 1 = 0.45, 0.4 × (1 + 0.2) = 0.48, and 0.15 × (1 − 0.2) = 0.12. In this example case, the robot would therefore turn north (preferentially turning left despite the original network output for straight-ahead motion). The value of x was varied from 0.00 (corresponding to completely random motion) to 0.25 (a strong bias towards the required direction). The robot’s performance was assessed over 9999 decisions to assess long-term performance.

4. Results and Discussion

The network performance resulting from biasing the training and output was tested in the Webots environment shown in Figure 1. The corresponding results are given in Figure 4 and Figure 5, respectively (with the corresponding data tables given in Appendix B,

Table A3. Results for the trained neural network resulting from biasing the training data. A total dataset of 60,000 images with dimensions of 2 × 67 were used for training. Data is plotted in Figure 4.

Type of Training	Directional Data (%)	Distance (m)	Distance North (m)	Percentage North (%)	Decisions Good (G)	Decisions Bad (B)	G/(G + B) (%)
Supervised		4049	3414	84.33	9903	96	99.04
Unsupervised	0	3610	1790	49.59	9566	433	95.67
Unsupervised	10	3720	2452	65.92	9490	509	94.91
Unsupervised	30	3822	2947	77.11	9417	582	94.18
Unsupervised	50	3678	2786	75.74	9173	826	91.74
Unsupervised	70	3697	2854	77.19	9102	897	91.03
Unsupervised	90	3653	2791	76.39	8968	1031	89.69

and

Table A4. Results for the trained neural network resulting from biasing the output data. A total dataset of 60,000 images with dimensions of 1 × 67 were used for training. Data is plotted in Figure 5.

Type of Training	Adjustment Factor x	Distance (m)	Distance North (m)	Percentage North (%)	Decisions Good (G)	Decisions Bad (B)	G/(G + B) (%)
Supervised		3734	77	2.07	9997	2	99.98
Unsupervised	0	3791	309	8.16	9967	32	99.68
Unsupervised	0.05	3959	2747	69.38	9943	56	99.44
Unsupervised	0.1	3986	3200	80.28	9772	227	97.73
Unsupervised	0.15	3739	2757	73.73	9350	649	93.51
Unsupervised	0.2	3640	2777	76.29	9083	916	90.84
Unsupervised	0.25	3607	2718	75.36	8969	1030	89.70

).

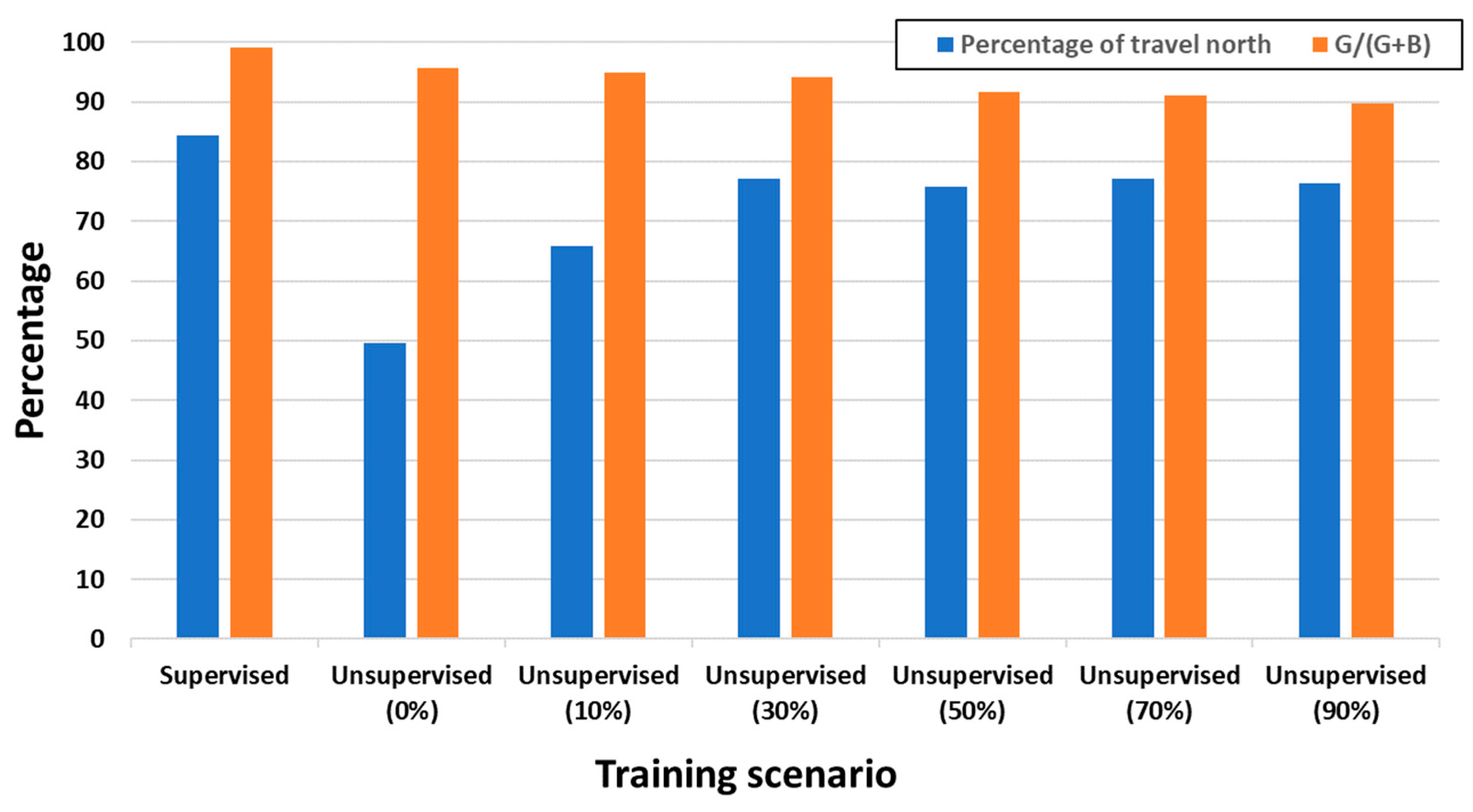
The supervised learning approach gives a benchmark for comparison with both sets of experiments. For the training data containing both lidar and directional information (Figure 4), 84.3% of the total travel time was spent in the goal (northerly) direction, with a 99.0% success rate for avoiding a collision. For the training data containing only lidar readings (Figure 5), collision avoidance success reached 99.98% for supervised training, although very little directional travel to the north was achieved, as would be expected for what is effectively a collision-avoidance-only controller. The unsupervised collision avoidance (with an output bias of x = 0) achieved a similar performance, with good collision avoidance and minimal directional movement.

The unexpected result was observed for directional unsupervised learning (Figure 4), with 0% bias; this essentially means that an equal amount of data is taken for every direction and decision scenario, so an initial expectation would be that the robot would move randomly. However, 49.6% of the motion was biased towards the goal (north). This finding can be attributed to the network looking for gaps (white areas compared to the blocked dark areas) regardless of which sensor is being used, and therefore training the robot to avoid blocked locations indicated by the lidar data inherently resulted in the robot being trained to try to avoid what appear to be blocked areas, as indicated by the dark areas from the compass data. This result can be attributed to the convolution and max-pooling layers of the network, which effectively defocus images during analysis, thereby merging the data from the different sensors, leading to a more generalized sensor interpretation. This demonstrates that such a CNN approach, in which sensor data is merged into a single data image file (as is the case for the biased-input training approach), is suitable for sensor fusion and provides a means of combining information from a multitude of sensors located on the robot, with the convolution and max-pooling matrix sizes dictating the amount of fusion required between the different sensors.

In terms of the performance of the CNN trained via unsupervised training, the preference for moving towards the goal (travelling north) for biased training (Figure 4) improved at 30% bias and above, yielding 76.6% ± 0.7% directional movement. However, the collision avoidance performance of 94.2% drops off more rapidly above this 30% bias point, and therefore a 30% bias in the training data appears to be the optimal scenario for this approach. Biasing the output (Figure 5) resulted in a similar performance for directional movement, 76.4% ± 2.8% for x ≥ 0.1, but with a higher collision avoidance probability of 97.7% at x = 0.1, again dropping off as more directional bias is applied to the result. This drop-off in collision avoidance ability in both methods was expected, as the robot assigns more importance to trying to turn towards the goal in order to avoid collisions. The slight improvement in the performance of the biased-output CNN is attributable to the reduced number of permutations possible in the input image, thereby effectively meaning the training data contains a larger percentage of possible input scenarios. Examples of trajectories from both approaches are given in Figure 6, which demonstrates the robot’s attempts to travel north (towards the goal position) whilst avoiding objects (objects are not shown in the figure).

Supervised training provided slightly better results compared to unsupervised training but proved to be more difficult to set up in terms of collecting training data, as the user had to carefully consider all potential scenarios in which data was required, a situation differing from that for the comprehensive dataset collected from the random motion of the robot during unsupervised training. Also, the unsupervised learning approach required minimal user input, as once the simulation started, no input (and therefore time) is required from the user. The simulation can then be left to run for as long as is required, thus allowing huge savings regarding user time. In addition, this form of learning can go on indefinitely, and thus such robots can be automatically and continually upgraded with networks trained on increasingly larger datasets and static environmental setups, leading to improved performance as time passes.

As a final test, the best-performing unsupervised trained networks were uploaded to an equivalent real robot and tested in the lab; see Figure 7 (30% bias and x = 0.1 assessed). The robot consisted of a Hokuyo URG-04LX-UG01 lidar (Hokuyo Automatic Co., Ltd., Osaka, Japan) and Popolu MinIMU-9 v5 (Pololu Corporation, Las Vegas, NV, USA) which contained an accelerometer, a gyroscope, and a magnetometer with a Marvelmind Robotics beacon system (Marvelmind OÜ, Tallinn, Estonia) used to track motion. A series of under-desk drawers were used as obstacles to be avoided. Figure 7 shows the performance over several runs, with the robot demonstrating good performance in travelling towards the goal position (defined by the location of beacon 5) whilst avoiding obstacles. Once the robot reached this point, as shown in Figure 7e, it effectively adopted an obstacle avoidance strategy, as shown by the blue tracing, due to the proximity of the wall at this point, until it gained enough clearance to resume heading towards the goal, as shown by the purple tracing. This is not unexpected, as the CNN was never trained to react to reaching a final goal position.

Due to the reduced environment size and run time in the real environment compared to the simulated world, fewer collisions were experienced during testing. The collisions that did occur were predominantly the result of the robot just clipping the edges of objects as it navigated through the environment. A larger collision bumper during simulation would help alleviate this issue. However, as shown in the results, navigation is not 100% accurate, and collisions will inevitably occur. Thus, in practice, secondary and more robust collision avoidance algorithms, such as the potential field method [36], need to be included to modify the decision regarding the output of the neural network controller when in proximity to objects. Although not included in this work, the ability to recognize when the goal position has been reached, for example, via positional information or visual recognition, and then act accordingly would need to be included in a full solution.

A practical issue of this experimental work was the finite scan time of the lidar. The robot was stopped for each scan, thereby simplifying the problem for this initial assessment of the technique. In practice, this is impractical, as it significantly slows the robot’s motion. To rectify this issue, time stamping of each lidar point in conjunction with knowing the robot’s position at this time through dead reckoning could be used to transfer all measured lidar points to equivalent measurements at one point in time, namely, the time when the next decision is to be made. This would be equivalent to a stationary measurement at that decision point, subject to any errors in the dead-reckoning positional calculation.

The aim of this work was to minimize human input requirements when training neural-network-controlled robots. The unsupervised training approach for the CNN reported here demonstrates a feasible starting point for such work in robot navigation. Short-term future goals should involve developing the following aspects of this work:

• The discrete nature of each turn needs to be converted into a continuous turning motion allowing for turning radii of any value. This could be accomplished with the use of more output options and/or a function capable of converting these output probabilities into continuous values.
• The proposed network is only suitable for static environments, as no temporal information is considered, unlike, for example, RNNs and their variants, such as Long Short-Term Memory (LSTM) networks [37,38]. An important way of further developing this work would be to apply it to dynamic environments, potentially via the inclusion of neuro-fuzzy approaches, as successfully demonstrated by Marichal et al. [39] and Stavrinidis et al. [40].

• Longer-term goals would be to address the following:

• User input is still required to generate the simulated environment. Automated creation and updating of a digital twin via the robot would allow for continuous training and improvement in a simulated environment without the need for human intervention.
• In this work, we demonstrate a solution approaching optimality through experimenting with trial parameters, whereas in practice, the robot would look to utilize a cost function to optimize the solution for itself, i.e., utilizing deep reinforcement learning approaches to self-assess its performance.
• If the robot is self-assessing, then ultimately it needs to self-improve, so the ultimate goal would be for the robot to modify its own neural network, possibly through the use of genetic algorithms, with the most successful simulated next-generation networks being progressively utilized.

5. Conclusions

The aim of this work was to investigate possible unsupervised training strategies for neural network navigation. Two approaches were investigated: either selectively choosing appropriate training data or considering modifying the CNN output towards a preferential direction. These approaches were compared to an operator-trained CNN.

The supervised training benchmark proved problematic in terms of the user time needed to collect data and the careful thought needed to ensure the captured data comprised a good range of possible input scenarios. In contrast, unsupervised training proved to be an efficient means of collecting the required data. By biasing either the input training data for the neural network or the output decision of an obstacle avoidance network, both approaches demonstrated good performance in the simulator because they allowed successful navigation around obstacles towards the required goal direction. The CNN controller program was then uploaded to a robot in the real world, and it proved to be able to successfully navigate around a lab. Combining sensor data within one image also demonstrated that this is a suitable approach to sensor fusion.

Using discrete rotations was a feasible way to assess the feasibility of this CNN-training approach for navigation, although, ultimately, the robot would require a continuous means by which to turn and acknowledge it has reached its goal. These will be aspects of future development in the short term. Additionally, with an unsupervised learning approach offering a means of continual data collection and retraining, longer-term studies should investigate options allowing the robot to self-assess and then self-improve its controller, giving it scope to operate in a wider variety of environments.