Quadrupedal Locomotion with Passive Ventral Wheels: A Data-Driven Approach to Energy Efficiency Analysis

Abstract

In this paper, a hybrid locomotion approach is proposed and experimentally validated for a quadrupedal robot to enhance energy efficiency on mixed terrains. A mechanical solution was implemented by adding passive wheels on the robot’s abdomen, to allow for gliding on flat portions of the faced terrains. This strategy aims to reduce the use of the legs, decreasing the overall energy consumption. To allow an efficient use of simulations, a data-driven approach was developed to estimate motor power consumption from joint dynamics on the real robot and subsequently applied within the simulation environment. The neural network achieved a coefficient of determination of R² = 0.97, ensuring accurate estimation of energy consumption under both simulated and real conditions. Experimental and simulated results show that the proposed sliding gait reduces the average Cost of Transport from approximately 4.5–6.0 during trotting to 0.8–1.1 during sliding, corresponding to a four–five-fold improvement in energy efficiency. Overall, the results demonstrate that a simple mechanical upgrade of the robot’s body structure can significantly enhance locomotion efficiency and versatility on flat or slightly descending terrains.

1. Introduction

Bio-inspired robotics offers a promising solution to the limitations of traditional robotic systems. By drawing inspiration from principles that nature has refined over millions of years of evolution [1], researchers have developed humanoid and quadrupedal robots that overcome many of the constraints of classical systems such as wheeled platforms. Terrestrial animals, for instance, have evolved diverse locomotion strategies that enable them to adapt to unpredictable terrain conditions. Legged locomotion allows for climbing steep, irregular surfaces and maintaining stability on soft or unsteady ground [2], explaining its evolutionary success. These natural solutions have, in turn, inspired roboticists to replicate similar levels of mobility and adaptability in artificial systems [3].

One of the main advantages of legged robots, especially quadrupeds, lies in their ability to traverse complex and uneven terrain with high adaptability and minimal environmental impact. Notable examples increasingly used in industrial, exploratory, and inspection contexts include MIT’s Mini Cheetah, Boston Dynamics’ Spot, and the Unitree family of robots [4,5,6]. Despite these advances, energy efficiency remains a major challenge, particularly for long-duration autonomous missions.

Previous studies have extensively examined the energetic performance of legged locomotion. Arena et al. [7] analysed bio-inspired control strategies on a Mini Cheetah-based platform, showing that adaptive gait modulation can reduce energy use on irregular terrain. Lei et al. [8] introduced specific resistance, also called Cost of Transport (COT), as a reference index for assessing quadrupedal energy efficiency, while Silva and Machado [9] demonstrated the influence of gait parameters and velocity COT values, typically ranging between 3 and 8. More recently, Zhu et al. [10] tackled the transferability gap between simulated and real-world energy performance through reinforcement learning. Collectively, these works highlight that legged robots remain considerably less efficient than wheeled systems (COT < 1), motivating the exploration of hybrid locomotion approaches combining walking and rolling.

Wheeled robots are characterised by their mechanical simplicity and high efficiency on flat, structured terrain. They are widely used in applications such as warehouse automation, delivery services, and urban inspection. Their main limitation, however, arises in unstructured or uneven environments, where their limited adaptability severely restricts mobility.

Some hybrid approaches, implemented, for instance, in the quadruped ANYmal, tried to enhance energy efficiency by integrating rolling mechanisms at the ends of the legs, thereby combining the advantages of walking and wheeled locomotion [11,12].

Similar strategies appear in other hybrid robots equipped with both legs and wheels, such as Centauro [13], Max [14], Pegasus [15], Cassino Hexapod [16], the hexapods from Brno University of Technology [17], and RoboSimian [18]. These platforms aim to improve mobility on flat terrain without compromising navigation capabilities on rough ground [19].

Such hybrid solutions enable greater efficiency and speed on structured surfaces while retaining adaptability on uneven terrain. However, they often suffer from limitations during transitions between locomotion modes and may compromise performance in traditional gaits by reducing grip during climbing. Moreover, versatile mobility introduces challenges such as complex control requirements, increased mechanical wear, and terrain-specific constraints. For instance, the transition from walking to skating requires sophisticated control to maintain stability and coordination [20].

For example, Chen et al. [21] proposed a quadruped with 4-DoF legs capable of roller-skating gaits such as swizzling, stroking, and trot-like motions. They reported a significant reduction in energy consumption compared with traditional trotting, based on mechanical energy computed from joint torque and velocity. However, their evaluation excluded electrical energy measurements or data-driven estimation, and the additional actuated joint increased mechanical complexity.

Our approach employs passive wheels mounted on the ventral side of the robot, enabling rolling locomotion when the terrain is sufficiently flat and thereby reducing actuator effort.

Accurately estimating the robot’s total energy consumption is essential, since it depends not only on actuator torques but also on various onboard modules and sensors. Reliable data-driven estimation is, therefore, required to ensure consistency between simulation and real experiments.

To address this, an efficient estimator of total energy consumption based on real data is required to ensure the reliability of simulated evaluations. In this work, we propose a neural network-based reverse-engineering approach to energy estimation, designed to enhance the robustness of simulation campaigns.

In this paper, we present three main innovations that distinguish our approach from existing wheeled–legged robots:

• Passive wheels are mounted on the robot’s belly rather than on the feet or tibia joints. This configuration preserves the robot’s natural locomotion abilities (e.g., trotting and crawling) while avoiding additional weight and inertial effects due to more complex limb mechanisms. During skating, redistributing part of the robot’s weight onto the belly-mounted wheels reduces actuator load and smooths transitions between walking and gliding without compromising gait performance.
• A data-driven neural network model was implemented to estimate the robot’s power consumption from joint torques and angular velocities. Trained on real-world data and integrated into the simulation environment, the model accurately predicts electrical current draw, thereby improving the realism of simulated dynamics. This enables the safe and reliable virtual testing of new gait patterns and control strategies, reducing experimental risk and accelerating development through more trustworthy simulations.
• A method is proposed to evaluate the energy efficiency of hybrid gaits in simulation using neural network-based power estimation, ensuring consistency with COT measurements obtained from real-world experiments.

2. Bio-Inspired Locomotion

Sliding-based locomotion is commonly observed in animals living in low-friction environments, where it provides an energy-efficient alternative to conventional walking.

One of the most notable examples is the emperor penguin, which engages in a behaviour known as tobogganing: gliding on its belly while propelling itself forward using its flippers and feet. This technique enables penguins to travel quickly and with reduced energy expenditure over long distances—often exceeding 100 km—between feeding grounds and breeding colonies. Their oil-coated feathers further reduce friction, improving overall gliding efficiency [22].

Otters have also been observed gliding on snow or muddy ground, possibly to conserve muscular energy and move more efficiently across slippery surfaces. Although sometimes interpreted as playful or social behaviour, this action also plays a role in locomotion efficiency under specific environmental conditions [23].

In broader biological studies, animals such as mudskippers and hatchling turtles demonstrate similar strategies that combine active propulsion with partial body–ground interaction. For example, hatchling turtles use their front flippers for thrust while keeping part of their body in contact with the substrate, thereby alternating between active movement and passive gliding [24].

Inspired by these natural strategies, this work aims to replicate comparable advantages in robotic locomotion. The focus lies not only on mimicking the motion patterns but also on adapting them to surfaces with low friction, such as snow or ice. To mimic these conditions, we equipped the robot with passive wheels mounted on its belly, as described in the following section. This biologically inspired approach represents the basis for the development of a gait that reduces actuator load and energy consumption by utilising passive gliding phases on suitable terrains. This natural pattern of alternating active and passive phases also inspired our hybrid gait, which alternates between muscular effort through leg activation and energy-saving sliding, similar to how some animals optimise their endurance during long journeys on certain terrains.

From a mechanical perspective, the design of the ventral wheel system followed an iterative process aimed at ensuring structural compatibility with the existing robot chassis. The wheels were positioned at the four corners of the main body, close to the natural contact line of the abdomen, to provide uniform support and minimise the elevation of the robot’s centre of mass. The initial prototype featured three wheels (two at the rear and one at the front), but stability tests indicated the need for a fourth wheel to achieve balanced load distribution during motion. The vertical placement was adjusted to allow for free leg articulation while maintaining a posture similar to natural crouching, ensuring smooth transitions between walking and sliding gaits. The support structures were modelled on the torso geometry and 3D-printed to achieve a rigid, lightweight, and body-integrated configuration. Commercial castor wheels were selected to enable omnidirectional rolling and in-place turning, enhancing manoeuvrability in confined environments while keeping friction low. This design approach represents a balance between biological inspiration, efficient belly-supported sliding as observed in animals and the mechanical constraints typical of mobile robotic systems.

3. Control Framework

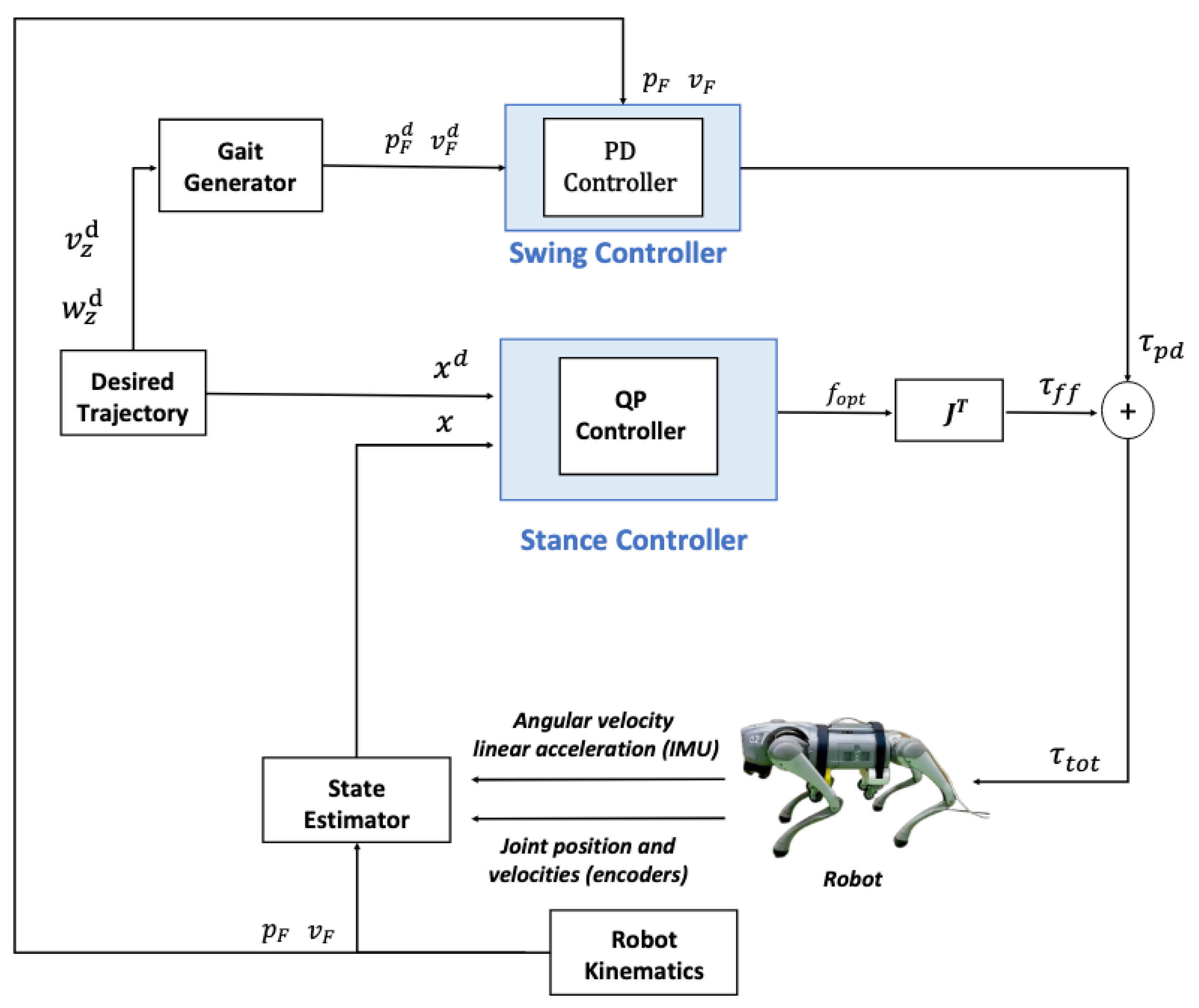
The proposed control architecture is composed of three interdependent modules, each responsible for a specific aspect of locomotion.

• Gait Generator: This module computes the foot contact configuration over time based on the desired linear and angular velocities along the vertical direction, ${v_z}^d$ and ${w_z}^d$, and the height of the centre of mass (COM) of the target body and outputs the desired foot position ${p_F}^d$ and velocity ${v_F}^d$ relative to the gait, as well as the phase delay between foot contacts. It also coordinates the sequence of leg movements by determining the start of the swing and stance phases for each foot and specifying their placement to achieve the commanded movement. In a sliding gait, the legs are synchronised in pairs in a caterpillar-like pattern (i.e. front left with front right and rear left with rear right) to ensure stability and avoid unwanted COM rotations that could be caused by other gaits that lack front-to-back synchrony. This coordination strategy reflects the biological inspiration underlying our hybrid gait: just as penguins and otters use synchronised sliding movements to maintain stability while reducing muscle effort on low-friction surfaces, the robot uses synchronisation of paired legs and passive abdominal support to achieve similar energetic benefits.
• Stance QP Controller: During the stance phase, the joint torques are calculated by solving a Quadratic Program (QP) that optimises the ground reaction forces under physical constraints such as friction cones. The dynamics of the four-legged robot are modelled using a floating-base rigid body abstraction, which takes into account both the effects of the active leg forces and the passive castor reactions. The equations of motion can be expressed as follows:

  $$\mathbf{M} \mathbf{b}=\sum _{i=1}^4{\mathbf{J}}_i^{\top }{\mathbf{f}}_{\mathrm{leg},i}+\sum _{j=1}^4{\mathbf{C}}_j^{\top }{\mathbf{f}}_{\mathrm{castor},j}+{\mathbf{f}}_{ex}$$

  (1)

  where $\mathbf{M}\in {\mathbb{R}}^{6\times 6}$ denotes the mass–inertia matrix of the floating base, ${\mathbf{p}}_{\mathrm{CoM}}\in {\mathbb{R}}^3$ is the position of the centre of mass in the body frame, and $\mathbf{b}={[{\ddot{\mathbf{p}}}_{\mathrm{CoM}}^{\top };{\dot{\omega }}_b^{\top }]}^{\top }\in {\mathbb{R}}^6$ is the generalised acceleration vector, comprising the linear acceleration of the centre of mass ${\ddot{\mathbf{p}}}_{\mathrm{CoM}}\in {\mathbb{R}}^3$ and the angular acceleration of the body ${\dot{\omega }}_b\in {\mathbb{R}}^3$. The matrices ${\mathbf{J}}_i\in {\mathbb{R}}^{6\times 3}$ and ${\mathbf{C}}_j\in {\mathbb{R}}^{6\times 3}$ represent the Jacobians mapping the forces applied at the i-th leg and j-th castor, respectively, to the wrench acting on the body, while ${\mathbf{f}}_{\mathrm{leg},i}\in {\mathbb{R}}^3$ and ${\mathbf{f}}_{\mathrm{castor},j}\in {\mathbb{R}}^3$ denote the contact forces at the legs and the passive castor reactions, and  ${\mathbf{f}}_{ex}=[0 0 -mg 0 0 0]\in {\mathbb{R}}^6$ accounts for the external translational forces and external torques acting on the floating base.
  A QP problem is formulated to achieve an optimal distribution of contact forces that keeps the robot in equilibrium while respecting the contact and friction constraints. This QP explicitly considers the forces on the four legs of the robot, labelled ${\mathbf{f}}_{\mathrm{leg}}$, as well as on the passive ventral wheels, labelled ${\mathbf{f}}_{\mathrm{castor}}$. By transferring part of the robot’s body weight to the wheels, the load on the legs is reduced during locomotion, while the robot can continue to generate the forces required for propulsion.
  The mapping of contact forces to the base wrench is then defined as

  $${\mathbf{A}}_s{\mathbf{f}}_{\mathrm{tot}}={\mathbf{b}}_d,$$

  (2)

  where

  $${\mathbf{A}}_s=\left[\begin{array}{ccc}{\mathbf{I}}_3& \dots & {\mathbf{I}}_3\\ \mathrm{skew}({\mathbf{p}}_1-\mathbf{R}·{\mathbf{p}}_{\mathrm{CoM}})& \dots & \mathrm{skew}({\mathbf{p}}_8-\mathbf{R}·{\mathbf{p}}_{\mathrm{CoM}})\end{array}\right],$$

  (3)

  $${\mathbf{b}}_d=\left[\begin{array}{c}m({\ddot{\mathbf{p}}}_{\mathrm{CoM}}^d-\mathbf{g})\\ {\mathbf{I}}_b{\dot{\omega }}^{\mathrm{d}}\end{array}\right]$$

  (4)

  with ${\mathbf{p}}_i$ denoting the positions of legs ($i=1\dots 4$) and wheels ($i=5\dots 8$) in the world frame, ${\mathbf{A}}_{\mathbf{s}}\in {\mathbb{R}}^{6x24}$, and the skew-symmetric operator $\mathrm{skew}(·)$ converting vectors into matrices to compute torque contributions. The vector ${\mathbf{b}}_d\in {\mathbb{R}}^6$ is the generalised vector of the desired acceleration. The matrix R is the rotation matrix that transforms vectors from the body frame to the global frame.
  The vector of contact forces is structured as follows:

  $${\mathbf{f}}_{\mathrm{tot}}={\left[\begin{array}{cccccccc}{\mathbf{f}}_{\mathrm{leg},1}^T& {\mathbf{f}}_{\mathrm{leg},2}^T& {\mathbf{f}}_{\mathrm{leg},3}^T& {\mathbf{f}}_{\mathrm{leg},4}^T& {\mathbf{f}}_{\mathrm{castor},1}^T& {\mathbf{f}}_{\mathrm{castor},2}^T& {\mathbf{f}}_{\mathrm{castor},3}^T& {\mathbf{f}}_{\mathrm{castor},4}^T\end{array}\right]}^T,$$

  where ${\mathbf{f}}_{\mathrm{leg},i}\in {\mathbb{R}}^3$, with $i=1,\dots ,4$, represents the force at the i-th leg, while ${\mathbf{f}}_{\mathrm{castor},j}\in {\mathbb{R}}^3$, with $j=1,\dots ,4$ corresponds to the passive wheel forces. The passive wheels are included directly in ${\mathbf{f}}_{\mathrm{tot}}$, with constraints enforcing zero horizontal force components and allowing for vertical reaction to support weight.
  The sliding-force control problem is then posed as the following QP:

  $$\begin{array}{cc}\hfill \underset{{\mathbf{f}}_{tot}\in {\mathbb{R}}^{24}}{min} & {\displaystyle \frac{1}{2}}{\mathbf{f}}_{tot}^{\top }{\mathbf{G}}_s{\mathbf{f}}_{tot}+{\mathbf{g}}_{0,s}^{\top }{\mathbf{f}}_{tot}\hfill \\ \hfill \mathrm{s}.\mathrm{t}. & {\mathbf{A}}_s\mathbf{f}={\mathbf{b}}_d,\hfill \\ \hfill & {\mathbf{C}}_E{\mathbf{f}}_{tot}={\mathbf{c}}_E,\hfill \\ \hfill & {\mathbf{C}}_I{\mathbf{f}}_{tot}\le {\mathbf{c}}_I.\hfill \end{array}$$

  (5)
  The cost matrix ${\mathbf{G}}_s\in {\mathbb{R}}^{24\times 24}$ is composed of three terms:

  $${\mathbf{G}}_s={\mathbf{A}}_s^{\top }\mathbf{S}{\mathbf{A}}_s+\alpha \mathbf{W}+\beta \mathbf{U},$$

  (6)

  where $\mathbf{S}\in {\mathbb{R}}^{6\times 6}$ penalises deviations from the desired wrench, $\mathbf{W}\in {\mathbb{R}}^{24\times 24}$ penalises the magnitude of contact forces, and $\mathbf{U}\in {\mathbb{R}}^{24\times 24}$ penalises temporal variations in these forces. The scalar parameters $\alpha$ and $\beta$ act as regularisation coefficients, weighting the respective contributions of force magnitude and smoothness.
  The linear term in the cost function is defined as

  $${\mathbf{g}}_0^{\top }=-{\mathbf{b}}_d^{\top }\mathbf{S}{\mathbf{A}}_{\mathbf{s}}-\beta {\mathbf{f}}_{\mathrm{prev}}^{\top }\mathbf{U}+\Delta {\mathbf{f}}_{\mathrm{res}}^{\top },$$

  (7)

  where ${\mathbf{f}}_{prev}\in {\mathbb{R}}^{24}$ contains the contact forces (legs and castor reactions) from the previous control step, and $\Delta {\mathbf{f}}_{res}\in {\mathbb{R}}^{24}$ represents fictitious resistive forces applied to the legs to compensate for undesired body motion:

  $$\Delta {\mathbf{f}}_{\mathrm{res}}=\left[\begin{array}{c}-\frac{1}{2}{\mathbf{f}}_{\mathrm{res},1}\\ -\frac{1}{2}{\mathbf{f}}_{\mathrm{res},2}\\ -\frac{1}{2}{\mathbf{f}}_{\mathrm{res},3}\\ -\frac{1}{2}{\mathbf{f}}_{\mathrm{res},4}\\ {\mathbf{0}}_{12}\end{array}\right] , {\mathbf{f}}_{\mathrm{res},i}\in {\mathbb{R}}^3, i=1,\dots ,4.$$

  (8)
  The resistive forces acting on the robot base are modelled as a combination of viscous and Coulomb friction. A pure Coulomb model leads to a discontinuity at zero velocity, which is undesirable for both numerical optimisation and simulation. To overcome this problem, a smoothed Coulomb formulation was used in [25], where the discontinuity of the sign function is regulated by the parameter $\epsilon$:

  $${\mathbf{f}}_{\mathrm{res}}=k_{\mathrm{visc}} {\mathbf{v}}_{xy} + k_{\mathrm{coul}} {\displaystyle \frac{{\mathbf{v}}_{xy}}{\sqrt{{\mathbf{v}}_{xy}^{\top }{\mathbf{v}}_{xy}+{\epsilon }^2}}},$$

  (9)

  where ${\mathbf{v}}_{xy}\in {\mathbb{R}}^2$ denotes the horizontal velocity of the robot base, and $k_{\mathrm{visc}}$, $k_{\mathrm{coul}}$, and $\epsilon$ are tunable parameters regulating viscous and smoothed Coulomb friction. The parameter values used in the optimisation problem are summarised in Table 1.
  Table 1. Controller parameters for the sliding gait. The matrices $\mathbf{W}$ and $\mathbf{U}$ used in the optimisation problem are diagonal, with the vectors $W_s$ and $U_s$ being placed on their diagonals. The first 12 entries of $W_s$ and $U_s$ correspond to the leg forces, while the last 12 entries correspond to the castor forces. Formally, we have $\mathbf{W}=\mathrm{diag}\left(W_s\right),\mathbf{U}=\mathrm{diag}\left(U_s\right),W_s,U_s\in {\mathbb{R}}^{24},W_s=[ W_s^{\mathrm{legs}}, W_s^{\mathrm{castor}} ], U_s=[ U_s^{\mathrm{legs}}, U_s^{\mathrm{castor}} ]$.

  Symbol	Control Parameter
  $\mathbf{S}$	$\mathbf{S}=\mathrm{diag}(20, 20, 50, 450, 450, 450)$
  $\alpha$	$0.0001$
  $\beta$	$0.2$
  $k_{\mathrm{visc}}$	$10.0$
  $k_{\mathrm{coul}}$	$500.0$
  $\epsilon$	$0.05$
  $W_s$	$\left[\begin{array}{ccc}{W}_s^{\mathrm{legs}}& :& 10,10,4, 10,10,4, 10,10,4, 10,10,4\\ W_s^{\mathrm{castor}}& :& 0,0,8, 0,0,8, 0,0,8, 0,0,8\end{array}\right]$
  $U_s$	$\left[\begin{array}{ccc}{U}_s^{\mathrm{legs}}& :& 3,3,3, 3,3,3, 3,3,3, 3,3,3\\ U_s^{\mathrm{castor}}& :& 0,0,3, 0,0,3, 0,0,3, 0,0,3\end{array}\right]$

  Table 1. Controller parameters for the sliding gait. The matrices $\mathbf{W}$ and $\mathbf{U}$ used in the optimisation problem are diagonal, with the vectors $W_s$ and $U_s$ being placed on their diagonals. The first 12 entries of $W_s$ and $U_s$ correspond to the leg forces, while the last 12 entries correspond to the castor forces. Formally, we have $\mathbf{W}=\mathrm{diag}\left(W_s\right),\mathbf{U}=\mathrm{diag}\left(U_s\right),W_s,U_s\in {\mathbb{R}}^{24},W_s=[ W_s^{\mathrm{legs}}, W_s^{\mathrm{castor}} ], U_s=[ U_s^{\mathrm{legs}}, U_s^{\mathrm{castor}} ]$.

  Symbol	Control Parameter
  $\mathbf{S}$	$\mathbf{S}=\mathrm{diag}(20, 20, 50, 450, 450, 450)$
  $\alpha$	$0.0001$
  $\beta$	$0.2$
  $k_{\mathrm{visc}}$	$10.0$
  $k_{\mathrm{coul}}$	$500.0$
  $\epsilon$	$0.05$
  $W_s$	$\left[\begin{array}{ccc}{W}_s^{\mathrm{legs}}& :& 10,10,4, 10,10,4, 10,10,4, 10,10,4\\ W_s^{\mathrm{castor}}& :& 0,0,8, 0,0,8, 0,0,8, 0,0,8\end{array}\right]$
  $U_s$	$\left[\begin{array}{ccc}{U}_s^{\mathrm{legs}}& :& 3,3,3, 3,3,3, 3,3,3, 3,3,3\\ U_s^{\mathrm{castor}}& :& 0,0,3, 0,0,3, 0,0,3, 0,0,3\end{array}\right]$

  The standard quadratic programming formulation

  $$\underset{\mathbf{x}}{min}{\displaystyle \frac{1}{2}}{\mathbf{x}}^{\top }H\mathbf{x}+g^{\top }\mathbf{x}+c$$

  (10)

  includes the linear term $g^{\top }\mathbf{x}$, which captures any bias or affine contribution to the cost function, whereas the constant term c does not influence the minimisation process [26,27]. Therefore, any additive term that enters linearly with respect to the decision variables, such as a residual force bias $\Delta {\mathbf{f}}_{res}$, should be included in g. In our formulation, the setting

  $$\mathbf{g}=-{\mathbf{A}}_s^{\top }\mathbf{S}{\mathbf{b}}_d-\beta \mathbf{U}{\mathbf{f}}_{prev}+\Delta {\mathbf{f}}_{res}$$

  (11)

  is thus formally correct and preserves the convexity of the QP.
  The parameters reported in Table 1 were obtained through an iterative optimisation process aimed at minimising oscillations and accurately reproducing the real robot’s dynamic response during sliding locomotion. Specifically, the control gains $\alpha$ and $\beta$ were empirically adjusted to achieve stable locomotion in simulation. The diagonal entries of $W_s$ and $U_s$ are carefully tuned according to the role of each contact: active leg forces are weighted more uniformly to enforce consistent regulation across all legs, while passive castor wheel forces are assigned different weights to reflect their limited actuation, with zero penalties on unconstrained directions. This selection of values ensures that the optimisation produces contact forces that are both physically realistic and temporally smooth, providing stable and reliable performance during sliding locomotion. The viscous and Coulomb friction coefficients ($k_{visc}$, $k_{coul}$) were identified by matching the simulated and measured horizontal forces required to initiate motion, thereby reproducing the resistive behaviour of the real passive wheels. The smoothing term $\epsilon$ was set to a small value ($0.05$) to preserve numerical continuity around zero velocity in the smoothed Coulomb model.
  The equality and inequality constraint matrices, ${\mathbf{C}}_E$ and ${\mathbf{C}}_I$, enforce the physical limits described in Table 2.
  Table 2. Equality (${\mathbf{C}}_E$) and inequality (${\mathbf{C}}_I$) constraints for contact forces.

  Symbol	Constraint	Formulation
  ${\mathbf{C}}_E$	Non-contact legs	${\mathbf{f}}_{leg,i}=0$
  ${\mathbf{C}}_E$	Castors (no horizontal force)	$f_x=0, f_y=0$
  ${\mathbf{C}}_I$	Global vertical force limit	$\sum f_z\le mg$
  ${\mathbf{C}}_I$	Contact feet (friction cone)	${\mathbf{C}}_{\mathrm{fric}} {\mathbf{R}}_{\mathrm{terrain}}^{\top }{\mathbf{f}}_{leg,i}\le 0$

  Table 2. Equality (${\mathbf{C}}_E$) and inequality (${\mathbf{C}}_I$) constraints for contact forces.

  Symbol	Constraint	Formulation
  ${\mathbf{C}}_E$	Non-contact legs	${\mathbf{f}}_{leg,i}=0$
  ${\mathbf{C}}_E$	Castors (no horizontal force)	$f_x=0, f_y=0$
  ${\mathbf{C}}_I$	Global vertical force limit	$\sum f_z\le mg$
  ${\mathbf{C}}_I$	Contact feet (friction cone)	${\mathbf{C}}_{\mathrm{fric}} {\mathbf{R}}_{\mathrm{terrain}}^{\top }{\mathbf{f}}_{leg,i}\le 0$

  This formulation takes into account a slight castor slip during the sliding phases and ensures a robust and realistic interaction between the robot and the terrain. The resulting contact forces are then used to calculate the forward joint torques as follows:

  $${\mathit{\tau }}_{ff}={\mathbf{J}}^{\top }{\mathbf{f}}_{leg}$$

  (12)
• Swing Controller: The trajectories of the swing legs are generated using a cycloid profile that enables smooth acceleration and deceleration phases. The desired foot positions are tracked using inverse kinematics and regulated by a proportional–derivative (PD) controller in the joint space, which enables accurate and stable foot positioning, even during transitions between walking and sliding.

Overall, the commanded torques to be sent to the robot are as follows:

$$\tau ={\tau }_{ff}+k_p·(q^d-q)+k_d·(d{q}^d-dq)$$

(13)

The overall control scheme and robot configuration are shown in Figure 1 and Figure 2. It operates at the constant frequency of 500 Hz, locked by a specifically designed timing logic, which guarantees the performance of the global control loop, similarly to that adopted in [28].

4. Simulation and Experimental Setup

Experiments were conducted both in simulation and on the physical quadrupedal robot (Unitree Go2). This dual approach made it possible to first validate the proposed sliding-based locomotion strategy under controlled and repeatable conditions in simulation and then confirm its effectiveness on real hardware.

Two gaits were analysed in this study: trotting and sliding. Each gait was tested at four target speeds (0.16, 0.22, 0.28, and 0.34 m/s), with four repetitions per condition, resulting in a total of 32 trials. Each trial covered a distance of 10 m, with the duration depending on the commanded speed.

Data were collected entirely onboard the robot by using its internal sensors and control system. The recorded variables included joint positions, velocities, torques, ground reaction forces, and control commands (feedforward, proportional, and derivative terms), as well as battery voltage and current, all sampled at 500 Hz.

Voltage and current were acquired from the robot’s low-level state interface and logged together with the joint and IMU data. Specifically, the Unitree low-level interface provides the pair $(V,I)$ through the fields powerV and powerA (accessible via LowlevelState::getVA()), which were logged at the same sampling rate as the other state variables. Electrical power was computed as $P\left(t\right)=V\left(t\right) I\left(t\right)$. The Cost of Transport (COT) was then derived accordingly. No additional external sensing hardware was employed; data acquisition relied on the robot’s internal sensors and factory calibration, and run-to-run consistency was verified by repeating trials under identical conditions.

In the simulation environment, battery-related measurements such as voltage and current were not available; instead, current was estimated using the neural network model. Apart from this difference, the same logging structure was maintained wherever possible to ensure consistency between simulated and real datasets.

4.1. Simulation Framework

The simulation environment was created using Gazebo Classic and the DART (Dynamic Animation and Robotics Toolkit) physics engine [29], which was chosen for its precise handling of joint dynamics. Although DART does not allow for the fine-tuning of surface friction parameters in the Simulation Description Format (SDF), it provides solid joint-level physics, well-suited for modelling and controlling the robot’s kinematic chain.

The ground–wheel friction coefficient was neither explicitly measured nor tuned in the simulator; the default value provided by the DART physics engine was used. Instead of tuning this parameter, the joint-level friction and damping coefficients were empirically adjusted to reproduce the smooth rolling and sliding behaviour observed in the real robot on a painted concrete surface. This approach ensured that the overall motion dynamics in simulation closely matched the experimental observations, even though the exact ground–wheel friction coefficient was not directly identified.

The simulated robot model was designed to closely resemble the real hardware. However, one notable discrepancy concerned the third joint: in simulation, it was modelled as a directly motorised joint, whereas in the real robot, it is actuated via a transmission system. To account for this difference, a correction factor of 1.4 was applied to the simulated torque of the third joint, which was adjusted experimentally by comparing the simulated and measured torque curves to improve the match with the real behaviour. This adjustment brought the simulated torque much closer to the real behaviour and was used consistently in all experiments with sliding and trotting gaits.

The passive ventral wheels were modelled as castor wheels with a vertical axis of rotation, using continuous joints to allow for free pivoting as in the real wheels. Physical properties such as mass, inertia, and shape were determined based on realistic estimates of the actual components.

The damping and friction of the joints were implemented as numerical coefficients on the joint level (they correspond to the viscous friction forces expressed in $\mathrm{N}·\mathrm{m}·\mathrm{s}/\mathrm{rad}$). Their values (0.015 and 0.01, respectively) were empirically tuned to reproduce the behaviour of the real robot.

4.2. Real Robot Testing

The real experiments took place indoors on a smooth, painted concrete floor, which was very similar to the simulated flat terrain, as shown in Figure 3.

Chassis Modifications

To enable sliding locomotion, two removable support structures were mounted beneath the robot’s belly. These supports held the castor wheels and were carefully designed to integrate seamlessly with the robot’s existing walking capabilities. Their placement and geometry were planned so as not to interfere with leg motion or ground clearance.

The passive wheels were positioned symmetrically at the four corners of the main body, maintaining a balanced centre-of-mass distribution. Thanks to this configuration, the overall weight distribution remains stable during motion.

The additional ventral wheels slightly reduce the robot’s ground clearance but do not compromise its ability to perform standard gaits such as trotting or crawling. The robot retains its full range of motion and can transition smoothly between walking and sliding phases, as shown in Figure 4.

The ventral wheels were designed to integrate seamlessly with the walking capabilities, without affecting ground clearance or leg motion. Commercial castor wheels were selected for their light weight, availability, and omnidirectional motion capability. The rubber coating provides sufficient grip while maintaining low rolling friction for smooth gliding. Each wheel was mounted using a 3D-printed support precisely shaped to fit the robot’s torso, ensuring rigidity and symmetry across the four contact points while remaining easy to attach or remove when required. Further specifications of the ventral wheels are summarised in

Table 3. Physical and geometric properties of the ventral wheels. Mounting height h corresponds to the total vertical distance from the ground to the robot torso during sliding, while abdomen clearance c represents the height of the supporting structure beneath the torso.

Property	Symbol / Unit	Value
Wheel type	–	Castor wheel
Material	–	Rubber
Diameter	D [mm]	50
Width	w [mm]	18
Mass (each)	m [g]	120
Bearing type	–	Ball-bearing swivel joint
Number of wheels	n	4
Torso height from ground (mounting height)	h [mm]	105
Support structure height (abdomen clearance)	c [mm]	51
Longitudinal spacing (front–rear)	$L_{\mathrm{long}}$ [mm]	200
Lateral spacing (left–right)	$L_{\mathrm{lat}}$ [mm]	130

.

4.3. Comparative Analysis

To check how well the simulation matched reality, we compared the torque and speed profiles of the joints. Figure 5 and Figure 6 show typical torque curves for sliding and trotting gaits at a reference forward speed of 0.22 m/s, which prove the good accuracy of the simulation.

The availability of a simulation very close to the real behaviour of the robot is a first step that still requires further effort to estimate the power consumption in the simulated environment for COT analyses. For this purpose, a neural network was trained based on real data to predict the robot’s power consumption, which enabled a consistent assessment of energy consumption in both the simulation and the real experiments.

Figure 7 shows representative foot trajectories in the sagittal plane (X-Z) calculated using forward kinematics from onboard joint measurements. Two gait patterns, sliding and trotting, are compared. While the sliding gait shows smoother and flatter trajectories due to the continuous support from the abdomen, the trotting gait shows more pronounced cycloid movement typical of the periodic lifting of the legs. This contrast reflects the different control settings and body postures. In the trotting gait, the robot performs shorter and faster steps (period $T=0.6$ s, stance ratio = 0.5, leg tip height 0.08 m), resulting in higher, rounder trajectories that help maintain dynamic stability during the alternating foot support phases. The period T refers to the duration of the stride cycle, the stance ratio indicates the proportion of the cycle in which the foot is in contact with the ground, and the leg tip height corresponds to the vertical amplitude of the foot lift.

In contrast, the ventral wheels provide continuous support during sliding, which allows for longer and slower steps (period $T=0.8$ s, stance ratio = 0.6, and leg tip height = 0.03 m), resulting in lower and longer foot travel. The lowered posture during sliding also increases the effective range of leg extension.

See also the supplementary video material (https://youtu.be/1UYCAia5hS8, (accessed on 22 September 2025)), which illustrates the foot trajectories during motion and provides a visual confirmation of the observed differences.

All values have been experimentally tuned to ensure stable and smooth locomotion in both gaits. To closely replicate the real behaviour of the robot, it became necessary to estimate power consumption within the simulated environment to compute the COT.

4.4. Data-Driven Current Estimation Model

To estimate the robot’s power consumption during the simulation, we developed a neural network model that was trained exclusively on experimental data. The decision to use a neural network was driven by the complex and highly nonlinear nature of the robot’s power consumption, which depends on joint torques, velocities, and their dynamic interactions. In addition, many parameters depend on hardware details (e.g. sensors, drivers, circuit boards, and onboard embedded computer) that are difficult to estimate analytically. However, these parameters play a crucial role in COT estimation. Traditional analytical or linear models proved insufficient to capture these features. In contrast, the neural network showed high estimation accuracy and generalisation under all tested conditions.

The neural model takes as input the joint torques and angular velocities of all 12 actuated joints, resulting in 24 input features, and produces a single scalar output representing the estimated total current absorbed by the robot. Figure 8 illustrates the network architecture.

The proposed neural network architecture consists of a fully connected feedforward multilayer perceptron with ReLU activation functions and the Mean Squared Error (MSE) loss function. The final output layer consists of a single linear neuron that produces the continuous prediction. A thorough grid search was performed over multiple hyperparameters, including the number of hidden layers, neurons per layer, learning rates, and batch sizes, to determine the optimal architecture and training configuration, as shown in Figure 9. The results show that both the network depth and the number of neurons per layer strongly influence the performance: models with at least four hidden layers and 32 or more neurons per layer consistently achieved higher $R^2$ values. The batch size also played a role, with medium-to-large values (256–512) giving the best results, while excessively large batch sizes degraded performance. In contrast, the learning rate mainly affected performance at extreme values, with most settings in the $3\times {10}^{-5}$–${10}^{-3}$ range achieving similarly good results. Therefore, the selected network configuration is characterised by four hidden layers, each comprising 256 neurons. Training was performed with the Adam optimiser using a learning rate of $3\times {10}^{-4}$, a batch size of 512, and early stopping based on validation loss.

The dataset used for network training was built from on-board sensor measurements collected over multiple experimental trials. Specifically, 75% of the recorded runs—corresponding to three out of four repetitions for each gait and speed—were used to form the training and validation dataset, resulting in a total of 367,840 samples recorded at 500 Hz across all runs. Within this subset, the data were further divided into 80% for training and 20% for validation through random splitting. The remaining 25% of the runs (one repetition per condition) were kept completely separate and used as an independent test set to evaluate the model’s generalisation capability. No data augmentation or input normalisation was applied, relying on the intrinsic consistency and bounded ranges of the experimental measurements.

The neural model achieves a Mean Squared Error (MSE) of 0.1674, a Mean Absolute Error (MAE) of 0.1684, and a coefficient of determination ($R^2$) of 0.9740 on the independent test set, indicating a strong generalisation ability. These results confirm that the model accurately reproduces the complex nonlinear relationship among joint dynamics, robot hardware, and current consumption. Additional error statistics, including the Mean Absolute Percentage Error (MAPE) and the 95th percentile of the absolute error, are reported in

Table 4. Neural model performance on the independent test set.

Metric	Symbol	Value
Mean Squared Error	MSE	0.1674
Mean Absolute Error [A]	MAE	0.1684
Coefficient of determination	$R^2$	0.974
Mean Absolute Percentage Error [%]	MAPE	6.28
Std. deviation of abs. error [A]	${\sigma }_{\left|e\right|}$	0.357
95th percentile of abs. error [A]	-	0.468

All metrics are computed on the independent test set using measured and predicted total current.

.

These results confirm that the proposed neural model effectively captures the nonlinear relationship between joint dynamics and electrical power consumption. Its low error and high $R^2$ make it suitable for use as a reliable data-driven estimator of the robot’s instantaneous current, enabling accurate COT evaluation in simulation without requiring additional physical measurements.

Figure 10 shows a comparison between the measured current and the current predicted by the neural network over a period of 5 s. The prediction slightly underestimates the peak values but accurately reflects the overall temporal profile.

Figure 11 shows a regression diagram comparing the predicted and measured current values for the test set. The close correspondence of the data points with the diagonal line indicates that the model can accurately capture the magnitude and overall distribution of the real measurements.

4.5. Data Preparation

For each trial, the initial 1.5–2.0 s was discarded to remove start-up transients and compute all quantities under steady-state conditions. In the simulation, log files were parsed, and the torque of the third joint was scaled by a factor of 1.4 to match the real transmission, as detailed before. For the real-robot dataset, missing or null samples were flagged, and outliers were detected using a z-score threshold ($\left|z\right|>4$) on each channel; flagged samples were then linearly interpolated along time (with nearest-neighbour fallback) to preserve continuity. The neural network inputs were constructed by concatenating joint torques and velocities (24 features), and the target was the electrical current, corresponding to the total current measured with the robot’s power interface.

While the training and test data cover the nominal range of 0.16–0.34 m/s, the intrinsic variability and broadband nature of legged locomotion produce a wide spectrum of instantaneous velocities and dynamic conditions, which enrich the dataset with intrinsic noise within this interval. This enables the model to generalise reliably even beyond the trained speed range.

4.6. Sensitivity Analysis

To further interpret the neural model and assess the physical relevance of its predictions, the Pearson correlation coefficient [30] was computed between each input feature (joint torque or angular velocity) and both the measured and predicted total current. As shown in

Table 5. Top 10 input features ranked by absolute Pearson correlation with current.

Feature	Type	${\left|\mathit{r}\right|}_{\mathbf{real}}$	${\left|\mathit{r}\right|}_{\mathbf{pred}}$
T9	Torque	0.491	0.499
T7	Torque	0.456	0.464
T6	Torque	0.441	0.450
T8	Torque	0.426	0.428
T4	Torque	0.363	0.370
T12	Torque	0.357	0.354
T3	Torque	0.324	0.321
T10	Torque	0.307	0.303
T11	Torque	0.259	0.257
T1	Torque	0.232	0.228

Pearson correlation coefficients computed for each input feature with both the measured and predicted total current. The similarity between real and predicted patterns confirms that the neural model preserves the physical relevance of the joint torques.

, the variable importance analysis indicates that joint torques are the primary drivers of current consumption, and that the hind legs are the main contributors during sliding, whereas the fore legs act predominantly for stabilisation. Measured and predicted correlation patterns match closely ($\Delta r<0.01$), confirming that the model successfully captures the relevant physical dependencies.

4.7. Cost of Transport

The main motivation for estimating the motor current was to enable an accurate calculation of the robot’s COT [8], which is defined as follows:

$$\mathrm{COT}={\displaystyle \frac{P_{\mathrm{E}}}{mgv}}$$

(14)

where $P_{\mathrm{E}}$ is the total electrical power consumption, m is the robot’s mass, g is the gravitational acceleration, and v is the average forward velocity. Electrical power was computed as

$$P_{\mathrm{E}}=V_b·I$$

(15)

where I is the electrical current and $V_b$ the battery voltage. On the real robot, both I and $V_b$ were directly measured with onboard sensors. In the simulation, current was estimated through the neural network, while the battery voltage was assumed constant at the nominal voltage of the real system (28.8 V). This assumption was verified through experimental measurements: during real trials, the onboard voltage remained highly stable around its nominal value, with a mean variation of about 0.7 V (±1.0 V standard deviation) and intra-trial fluctuations below 1.3%. Since electrical power is computed as $P_{\mathrm{E}}=V_{b}I$, a voltage change of ±1 V (≈3.5%) would induce a comparable relative variation in the estimated COT. Such an effect is negligible compared with the observed ≈80% difference between gaits, confirming that the constant-voltage approximation introduces only a minor error.

This approach allowed us to compute a realistic and consistent estimate of $P_{\mathrm{E}}$, and consequently of the COT, in both simulations and real experiments.

The Cost of Transport (COT) was computed for both trotting and sliding gaits based on measured and NN-estimated power consumption across different commanded speeds. Figure 12 illustrates the distribution of COT values, while

Table 6. Cost of Transport (mean ± std) for trotting and sliding at four commanded speeds.

Gait	Source	0.16 m/s	0.22 m/s	0.28 m/s	0.34 m/s
Trotting	Real (measured)	6.06 ± 0.03	4.61 ± 0.07	4.15 ± 0.02	3.69 ± 0.03
	Real (NN)	5.96 ± 0.02	4.73 ± 0.05	4.08 ± 0.03	3.64 ± 0.02
	Sim (NN)	6.24 ± 0.03	4.67 ± 0.01	4.07 ± 0.02	3.48 ± 0.04
Sliding	Real (measured)	1.12 ± 0.01	1.00 ± 0.01	0.82 ± 0.01	0.76 ± 0.01
	Real (NN)	1.13 ± 0.01	1.00 ± 0.00	0.83 ± 0.01	0.77 ± 0.01
	Sim (NN)	1.07 ± 0.01	0.97 ± 0.00	0.85 ± 0.01	0.73 ± 0.01

summarises the corresponding numerical results (mean ± std).

As shown in Table 6, the neural model reproduces the experimental trends with remarkable consistency, both across gaits and speeds.

This close correspondence enables straightforward calculation of the power consumption and thus the COT in the simulation. This careful validation was crucial to ensuring that our neural network for estimating motor current works reliably under both simulated and real-world conditions.

The present study already demonstrates that the sliding gait achieves a COT approximately five times lower than that of the trotting gait. To formally assess the significance and consistency of this method, a statistical analysis was performed as described in the following section. Although the addition of wheels slightly increases the total weight of the robot, the corresponding COT remains very close to that of the standard configuration. This is mainly due to the relatively small increase in mass (around 4%), which only has a marginal effect on the overall energy consumption. From Equation (14), it results that the impact of this added mass on the normalised COT is negligible: any small increase in mass produces an equivalent effect on the required power, leading to nearly unchanged COT values.

In addition, the robot exhibits greater stability in the sliding configuration, as it has four points of contact (the passive belly wheels) with the ground. This improved stability, combined with the significantly reduced COT values, makes the sliding gait a promising locomotion strategy on flat or slightly inclined surfaces. Overall, the experiments confirm that the robot maintains an optimal posture and achieves speeds comparable to those of a trot while benefiting from the improved stability and lower energy costs of sliding.

Statistical Validation

Two complementary analyses were conducted: Welch’s unequal-variance t-tests [31], to compare mean COT values between gaits for each speed and data source, and a two-way ANOVA [32], to assess the influence of gait and speed, as well as their interaction.

Welch’s t-tests confirmed that the mean COT of the sliding gait is significantly lower than that of the trotting gait across all speeds and data sources ($p<0.001$), with an average reduction of about 80%. This demonstrates that the observed energy savings are consistent and not due to random variability, as also evidenced by

Table 7. Welch’s t-test results comparing trotting and sliding gaits. Values are reported as mean ± standard deviation. All differences are statistically significant ($p<0.001$).

Source	Speed [m/s]	Trot	Slide	Ratio (T/S)	$\Delta$ [%]
Real (measured)	0.16	6.06 ± 0.03	1.12 ± 0.01	5.4	81.4
	0.22	4.61 ± 0.07	1.00 ± 0.01	4.6	78.4
	0.28	4.15 ± 0.02	0.82 ± 0.01	5.0	80.2
	0.34	3.69 ± 0.03	0.76 ± 0.01	4.9	79.4
Real (NN)	0.16	5.96 ± 0.02	1.13 ± 0.01	5.3	81.0
	0.22	4.73 ± 0.05	1.00 ± 0.00	4.7	78.9
	0.28	4.08 ± 0.03	0.83 ± 0.01	4.9	79.7
	0.34	3.64 ± 0.02	0.77 ± 0.01	4.7	78.8
Sim (NN)	0.16	6.24 ± 0.03	1.07 ± 0.01	5.8	82.8
	0.22	4.67 ± 0.01	0.97 ± 0.00	4.8	79.1
	0.28	4.07 ± 0.02	0.85 ± 0.01	4.8	79.2
	0.34	3.48 ± 0.04	0.73 ± 0.01	4.8	79.0

$\Delta$: Mean percentage reduction in COT for sliding relative to trotting gaits. All pairwise Welch’s t-tests yielded $p<0.001$ and large effect sizes (${\eta }^2>0.99$), confirming that the energy reduction of approximately 80% is highly significant across all conditions.

.

The two-way ANOVA (Gait × Speed) confirmed that both gait and commanded speed have statistically significant effects on the COT, as well as a strong interaction between the two factors (

Table 8. Two-way ANOVA ($\mathrm{Gait}\times \mathrm{Speed}$) results for each data source.

Source	p (Gait)	p (Speed)	p (Interaction)
Real (measured)	5.98 × 10−46	3.45 × 10−31	5.78 × 10−28
Real (NN)	9.84 × 10−48	6.42 × 10−33	1.43 × 10−29
Sim (NN)	4.66 × 10−51	1.68 × 10−37	5.43 × 10−35

Both gait and speed have highly significant effects ($p<{10}^{-30}$), and their interaction confirms that the reduction in COT with sliding is consistent but slightly modulated by velocity.

). This analysis demonstrates that the energy efficiency advantage of sliding remains robust across all tested speeds and datasets.

Overall, these results demonstrate that the sliding gait reduces energy expenditure by approximately 80% while maintaining stable and repeatable performance across speeds and datasets. This confirms the validity of the proposed estimation framework and its suitability for guiding future data-driven gait optimisation.

5. Conclusions

In this work, we presented a novel hybrid locomotion strategy for quadrupedal robots that combines traditional legged gait with sliding assisted by passive wheels mounted on the abdomen. In addition to this mechanical innovation, we have introduced a neural network model that can estimate the motor current directly from the joint dynamics, which enables a consistent calculation of the COT in the simulation.

This reverse-engineering approach allows for extensive use of the simulation environment by compensating for missing information through reliable estimations derived from the real robot. The main advantage is the ability to rely on simulation for testing and validation, thereby reducing mechanical stress on the hardware and limiting the need for time-consuming experimental campaigns.

This limitation in friction control was considered an acceptable trade-off between surface friction and accurate joint dynamics. In our case, the main goal was to reproduce realistic actuator behaviour and controller response, which DART handles reliably. Even with simplified friction modelling, the simulated sliding motion showed good agreement with the real robot, both in its kinematic behaviour and in overall energy trends. If future studies require simulating terrains with very different friction characteristics (for example, ice or soft soil), other physics engines could be used to achieve finer control of surface properties, although this would likely reduce the accuracy of the joint dynamics. Overall, the current setup proved effective: the real and simulated controllers performed consistently, and any small differences could be corrected by tuning the controller parameters.

The results clearly show that the sliding gait achieves significant energy savings, with a COT that is almost five times lower than that of the classic trot. This is particularly remarkable considering that the robot maintains a speed and stability comparable to those of a trot thanks to the continuous ground contact of the ventral wheels.

A neural network was developed to estimate the current consumption for different gaits and speeds. This enables reliable estimation of COT in simulation and paves the way for safer and more realistic gait optimisation before hardware implementation.

It is important to note that the effectiveness of the sliding gait is limited to flat or slightly descending terrain due to the relatively small radius of the wheels and their reduced ability on uneven surfaces. On uneven or obstacle-strewn terrain, the trot is still the preferred gait. However, in indoor or industrial environments, sliding is a very favourable solution to reduce energy consumption without sacrificing performance.

This result is also in line with the biologically inspired foundations of our work. In developing the hybrid gait, we were inspired by animals such as penguins, otters, and turtles, which utilise sliding on low-friction surfaces to reduce muscle effort and improve energy efficiency. Similarly, our robot uses passive ventral wheels to alternate between active locomotion and energy-saving sliding phases. This parallel between biological and robotic locomotion emphasises the effectiveness of sliding as a natural strategy to achieve efficiency and stability on suitable terrain.

This type of locomotion could be particularly useful in semi-structured environments such as industrial plants or tunnels, as these environments are typically characterised by the presence of flat paths, as well as ladder or single stairs. Here, the advantages of our approach are clear; of course, to maximise efficiency, a parallel algorithm able to classify the type of terrain and autonomously switch between sliding and other legged locomotion patterns has to be conveniently used. Regarding this point, in the literature, several efficient solutions are already available.

The sliding conditions, including friction cones, contact constraints, and passive wheel handling, are currently enforced via a QP. In future work, these constraints could be integrated into a reinforcement learning framework by embedding them into the reward function, penalising violations and rewarding compliant actions. Additionally, incorporating the robot’s total electrical power into the reward would promote energy-efficient locomotion, encouraging smoother motions and minimising unnecessary actuator effort while maintaining physically consistent sliding behaviour. Such an approach could further enhance efficiency and adaptability, enabling the policy to optimise gait selection based on terrain and payload, to maximise energetic performance.

In addition, the dynamic applicability of the proposed sliding approach depends on the terrain slope and the robot’s speed. While mild downhill surfaces can further reduce the COT thanks to gravity assistance, steeper slopes would require active braking or specific control strategies to keep the robot stable and manoeuvrable. Therefore, although the sliding gait remains highly efficient under favourable conditions, safe operation in more dynamic scenarios will depend on the implementation of dedicated control mechanisms.