Efficient Parallel Computing Algorithms for Robotic Manipulator Kinematics

Abstract

A method for compiling object schemes is proposed, which allows constructing algorithms for calculating the kinematic parameters of robotic manipulators. Examples of compiling object schemes for calculating the velocities and accelerations of points selected on the links of the robotic manipulator are considered. An analysis of the computational complexity of the obtained algorithms is carried out and a method for increasing their computational efficiency is proposed. An increase in computational efficiency is achieved based on the use of the associativity property due to the reduction of additional and multiplication operations performed by the algorithm. Graphs of computational processes illustrating the developed algorithms are presented. The developed algorithms allow parallel calculations; this will further increase the efficiency of calculations when using multiprocessor computing systems. As a result of the study, based on the object approach, an effective universal method for calculating the kinematic parameters of robotic manipulators has been developed. This will improve the quality of robot control.

1. Introduction

Artificial intelligence technologies and modeling methods have a decisive influence on the development of modern robotic systems [1,2,3]. Modeling robotic manipulators allows studying their characteristics in a virtual mode based on a numerical experiment. Mathematical models used to model robot motion are the basis for developing robot control systems [3,4]. In addition, much attention is currently paid to the problem of controlling several robots of different types working together under changing conditions, which requires the use of scenario control methods, linear programming, and machine learning [5].

When modeling the motion of robots, various kinematic and dynamic problems can be considered. The kinematics of robot manipulators is usually considered in two coordinate systems. Thus, the planning of the trajectories of the working element is performed in Cartesian coordinates, and the control of the robot’s motion is carried out in axial (generalized) coordinates.

The direct kinematics problem consists of determining the kinematic parameters, velocities, and accelerations of the robot’s manipulation system links when it moves along a given trajectory. The inverse kinematics problem is reduced to determining the axial coordinates corresponding to the movement of the robot’s working element along a trajectory given in Cartesian coordinates. The studies presented in this article are devoted to algorithms for solving the direct kinematics problem.

The problems of kinematics and dynamics of robot manipulators have been previously considered by many researchers. Thus, in works [6,7], new methods for solving the inverse kinematics problem for robot manipulators are presented. The study [8] aims to construct a kinematic model of a hexapod leg with two degrees of freedom (2-DOF) for a walking robot. The study [9] is focused on the design of a small-sized robot manipulator with three degrees of freedom (3-DOF) to perform the “pick and move” task using the inverse kinematics method. The study [10] aims to teach robot programming based on a 5-DOF robot manipulator prototype and open-source software.

The paper [11] considers analytical solutions to the direct and inverse kinematics problems for a hybrid 5-DOF robot that consists of a parallel mechanism with three degrees of freedom and a rotating head with two degrees of freedom. The paper [12] considers the features of solving the inverse kinematics problem for serial-parallel manipulators.

The paper [13] presents a detailed review of the methods used in robotic machining of lightweight materials. The paper [14,15] proposes a method for constructing a tool path for a 5-DOF industrial robot during the machining process. The paper [16] considers the calibration problem for a 5-DOF hybrid machining robot. This paper presents a semi-analytical continuous toolpath corner smoothing method for a 5-DOF (degree of freedom) hybrid robot. The paper [17] proposes a criterion for estimating the maximum load on the actuator of a 6-DOF industrial robot when performing a forming process. In study [18], the technology of kinematic calibration of a 5-DOF robot manipulator was investigated. Study [19] proposes a simple inverse kinematics calculation scheme for an industrial serial manipulator. The proposed technique can calculate appropriate values of the joint variables to realize the desired end-effector position and orientation while considering the motion costs of each joint. The article [20] describes fuzzy adaptive compensation control for space manipulators. The works [21] demonstrate algorithms for solving the inverse kinematics problem for a robot manipulator with seven degrees of freedom (7-DOF), and the works [22] use the deep reinforcement learning algorithm for this purpose. The works [23,24] develop efficient algorithms based on topological analysis that are capable of finding the optimal solution to the inverse kinematics problem for robot manipulators with kinematic redundancy. The paper [25] focuses on the theoretical and experimental analysis of a three-axis MEMS gyroscope, implementing an innovative feedforward PI quadrature compensation architecture.

Currently, the study of the problems of kinematics and dynamics of robotic manipulators also remains relevant. A promising direction for the development of applied research in this area is the development of neuromorphic algorithms for modeling and controlling robotic manipulators [26,27].

In our research, we develop the theme of developing parallel algorithms based on an object-oriented approach and borrow part of the material from our previously published article [28] to complete the additionally published material. The previous article described in detail the method for constructing parallel algorithms using the object-oriented approach. The method was illustrated by constructing a parallel algorithm for calculating the dynamic model of a robot manipulator.

The published material of this article examines the application of the method described earlier for compiling algorithms for solving problems of the kinematics of robot manipulators. The object-oriented approach in this case allowed us to modify the mathematical dependencies obtained for calculating the kinematic characteristics of robot manipulators. At the same time, an analysis of the computational complexity of the algorithms was carried out. The main emphasis in the new work is on increasing the efficiency of algorithms for calculating the kinematic parameters of robotic manipulators intended for creating software and mathematical support for robot control systems.

The above review of publications aimed at solving problems in robot manipulator kinematics shows the high relevance of solving these problems in various fields. The method of compiling computational algorithms for solving these problems that we have described allows us to significantly increase their efficiency.

2. Methods of Kinematic Analysis

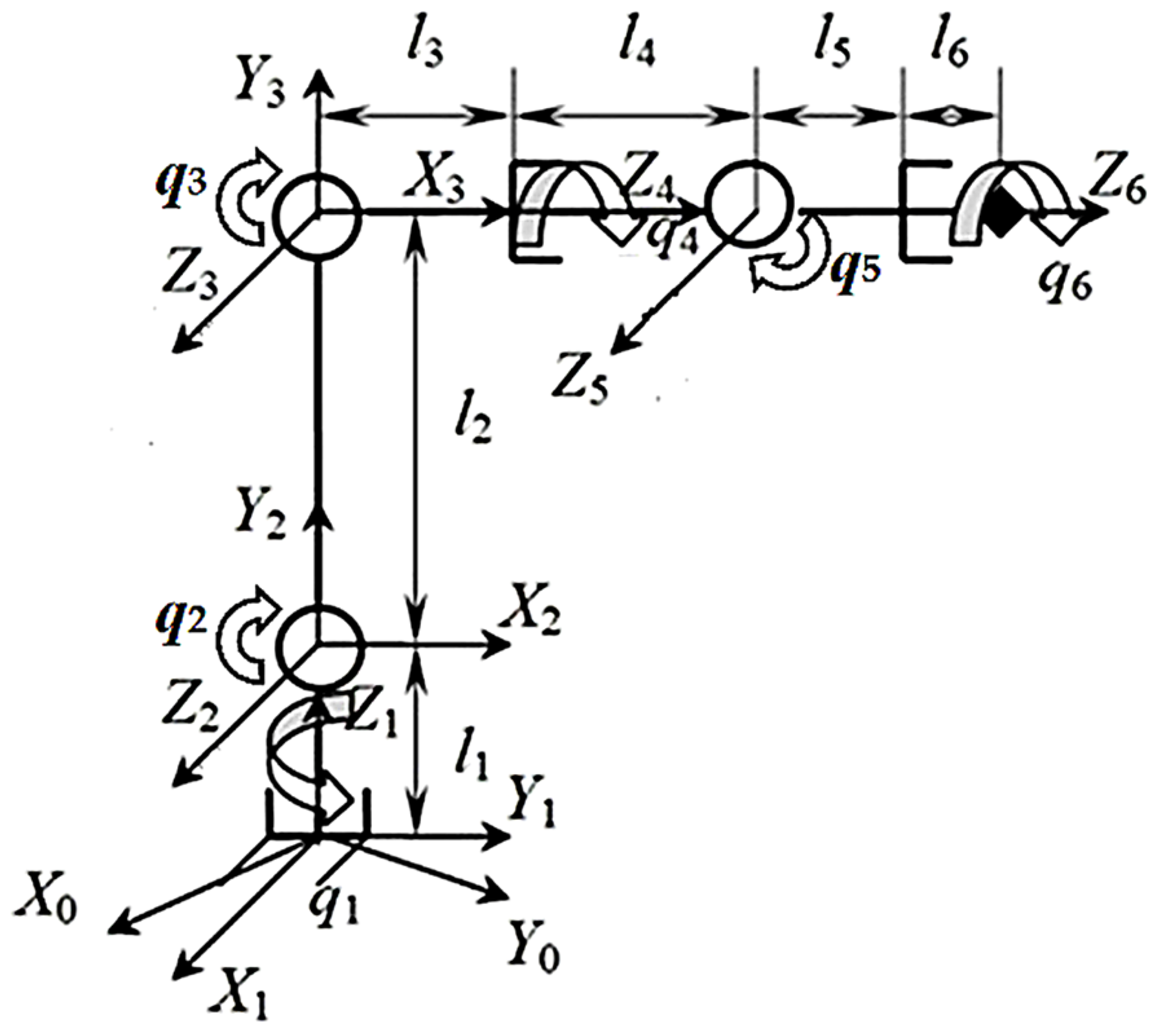
Robot manipulators are multi-link mechanisms with a sequential kinematic structure. Kinematic diagrams of mechanisms are used to describe such structures. Examples of a robot manipulator with six links (6-DOF) and the corresponding kinematic diagram are presented below (see Figure 1 and Figure 2).

On the kinematic diagram of the mechanism in the selected scale, the links are depicted by straight lines. Hinges are depicted at the nodes of the links. The arrangement of the links on the kinematic diagram of the robot manipulator is determined by the lengths of the links l_i and the values of the coordinates of the hinges q_i, i = 1,…,n; n—is the number of links. When the mechanism moves, its image on the kinematic diagram at each moment of time t will be determined by the values of the hinge coordinates, which are functions q_i = q_i(t).

To specify the position of the links in space, it is necessary to associate the Cartesian coordinate system S_i(X_i, Y_i, Z_i) with each link. The movement of the robot manipulator is considered in the coordinate system S₀(X₀, Y₀, Z₀), associated with the fixed base (see Figure 2).

The transformation of the bases of the coordinate systems associated with the links can be performed using the (4 × 4) matrices of the transformation of homogeneous coordinates. The structure of such a matrix for the case of mapping the basis of the system S_i into the system S_(i−1) has the form:

$$A_{(i-1),i}:S_i\to S_{(i-1)}$$

(1)

$$\stackrel{4\times 4}{A_{(i-1),i}}=\left[\begin{array}{cccc}& \stackrel{3\times 3}{R_{(i-1),i}}& & l_{(i-1)}^{3\times 1}\\ 0& 0& 0& 1\end{array}\right],$$

(2)

where A_(i−1),i is a 4 × 4 matrix, that performs the homogeneous coordinate transformation from the S_i, system, corresponding to i-th link, into the S_(i−1) system, corresponding to (i − 1)-th; R_(i−1),i is a 3 × 3 rotation matrix containing the cosines of the angles between the corresponding axes of the S_i and S_(i−1) coordinate systems; $l_{(i-1)}={\left[\begin{array}{ccc}{l}_{x(i-1)}& l_{y(i-1)}& l_{z(i-1)}\end{array}\right]}^T$—link length (i − 1), $\left(l_{x(i-1)},\hspace{0.33em}{l}_{y(i-1)},\hspace{0.33em}{l}_{z(i-1)}\right)$—projections of the (i − 1)-th link onto the axes of the coordinate system S_(i−1).

Since the components of the matrices A_(i−1),i are functions of the hinge (generalized) coordinates: R_(i−1),i = R_(i−1),i(q_i), if the i-th hinge is rotational, l_(i−1)= l_(i−1)(q_i), if it is translational (telescopic), then the matrix A_(i−1),i = A_(i−1)(q_i)_, is also a function of the hinge coordinates.

The set of 4 × 4 homogeneous transformation matrices, defined by the expression:

$$A_{0,k}={\displaystyle \prod _{i=1}^k{A}_{(i-1),i}},\hspace{1em}k=1,\dots ,n,$$

(3)

performs mappings:

$$A_{0,k}:S_k\to S_0,k=1\dots n,$$

(4)

where S_k is a coordinate system corresponding to the k-th link.

Since the matrices A_(i−1),i = A_(i−1)(q_i) are functions of the hinge coordinates, then the matrices A_0,k = A_0,k(q), q = (q₁, q₂, …, q_k), will also be functions of the hinge coordinates.

Then the absolute coordinates of an arbitrary point of the k-th link in the S₀ fixed coordinate system, which are the projections of the radius vector $r^{(0)}={\left[\begin{array}{cccc}{x}^{(0)}& y^{(0)}& z^{(0)}& 1\end{array}\right]}^T$, can be determined from the equation:

$$r^{(0)}=A_{0,k}(q)r^{(k)},$$

(5)

where $r^{(k)}={\left[\begin{array}{cccc}{x}^{(k)}& y^{(k)}& z^{(k)}& 1\end{array}\right]}^T$ is a radius vector that defines the local coordinates of the selected point, given in the S_k, connected with the k-th link; q is the vector of hinge coordinates.

In the future, when writing equations, we will denote matrices with capital letters, and vectors and scalars with small letters. This will simplify the writing of equations and will not lead to confusion, since each vector is pre-defined, and the scalars in the equations will only be indices, time, and hinge coordinates.

To obtain linear kinematic parameters, it is necessary to differentiate function (5) an appropriate number of times. The arbitrary point speed of the k-th link in the S₀ system will have the form:

$$v^{(0)}={\displaystyle \frac{d{r}^{(0)}}{dt}}={\displaystyle \sum _{i=1}^k\frac{\partial A_{0,k}}{\partial q_i}{\dot{q}}_i{r}^{(k)}},$$

(6)

and the acceleration of the same point is

$$a^{(0)}={\displaystyle \frac{d^2{r}^{(0)}}{d{t}^2}}=\left({\displaystyle \sum _{i=1}^k\frac{\partial A_{0,k}}{\partial q_i}{\ddot{q}}_i+{\displaystyle \sum _{i,j=1}^k\frac{{\partial }^2{A}_{0,k}}{\partial q_i\partial q_j}{\dot{q}}_i{\dot{q}}_j}}\right)r^{(k)}.$$

(7)

In expressions (6) and (7) used to calculate the kinematic parameters, it is necessary to calculate the partial derivatives of the transformation matrices of homogeneous coordinates, according to the corresponding generalized coordinates:

$${\displaystyle \frac{\partial A_{0,k}}{\partial q_i}},\hspace{0.33em}{\displaystyle \frac{{\partial }^2{A}_{0,k}}{\partial q_i\partial q_j}},\hspace{0.33em}\mathrm{if}\hspace{0.33em}i=j,\hspace{0.33em}\mathrm{then}{\displaystyle \frac{{\partial }^2{A}_{0,k}}{\partial q_i\partial q_j}}={\displaystyle \frac{{\partial }^2{A}_{0,k}}{\partial q_i^2}}\hspace{0.33em}(i,j,k=1\dots n).$$

(8)

In accordance with (3), we will have

$${\displaystyle \frac{\partial A_{0,k}}{\partial q_i}}=A_{0,1}{A}_{1,2}\dots {\displaystyle \frac{\partial A_{(i-1),i}}{\partial q_i}}\dots A_{(k-1),k},$$

$${\displaystyle \frac{{\partial }^2{A}_{0,k}}{\partial q_i^2}}=A_{0,1}{A}_{1,2}\dots {\displaystyle \frac{{\partial }^2{A}_{(i-1),i}}{\partial q_i^2}}\dots A_{(k-1),k},$$

$${\displaystyle \frac{{\partial }^2{A}_{0,k}}{\partial q_i\partial q_j}}=A_{0,1}{A}_{1,2}\dots {\displaystyle \frac{\partial A_{(i-1),i}}{\partial q_i}}\dots {\displaystyle \frac{\partial A_{(j-1),j}}{\partial q_j}}\dots A_{(k-1),k}.$$

(9)

Calculating the differentiated transformation matrices of homogeneous coordinates (8) and (9) can be performed using intermediary matrices D_i:

$${\displaystyle \frac{\partial A_{(i-1),i}}{\partial q_i}}=A_{(i-1),i}{D}_i, {\displaystyle \frac{\partial A_{0,k}}{\partial q_i}}=A_{0,(i-1)}{A}_{(i-1),i}{D}_i{A}_{i,(i+1)}\dots A_{(k-1),k},$$

$${\displaystyle \frac{{\partial }^2{A}_{0,k}}{\partial q_i\partial q_j}}=A_{0,1}{A}_{1,2}\dots A_{(i-1),i}{D}_i{A}_{i,(i+1)}\dots A_{(j-1),j}{D}_j{A}_{j,(j+1)}\dots A_{(k-1),k}.$$

(10)

Matrices D_i of differentiating transformation matrices of homogeneous coordinates have the form:

$$D_i=\left[\begin{array}{cccc}0& -{\mathrm{\beta }}_i& 0& 0\\ {\mathrm{\beta }}_i& 0& 0& 0\\ 0& 0& 0& 1-{\mathrm{\beta }}_i\\ 0& 0& 0& 0\end{array}\right],$$

(11)

where β_i is the coefficient corresponding to the type of the i-th kinematic pair. β_i = 1, if the i-th kinematic pair is rotational and β_i = 0, if it is translational.

To use the differentiation matrix in the form (11), it is necessary to direct the axes Z_i coordinate systems S_i along the axes of the hinges connecting the links (i − 1) and i. Then the matrix A_(i−1),i(q_i) can be represented as a product of two matrices A_(i−1),i = A_{(i−1),(i−1)*}A_(i−1)*,i(q_i), in this case the matrix A_(i−1)*,i(q_i) will look as follows:

$$A_{{(i-1)}^{*},i}=\left[\begin{array}{cccc}\cos ({\mathrm{\beta }}_i{q}_i)& -\sin ({\mathrm{\beta }}_i{q}_i)& 0& 0\\ \sin ({\mathrm{\beta }}_i{q}_i)& \cos ({\mathrm{\beta }}_i{q}_i)& 0& 0\\ 0& 0& 1& (1-{\mathrm{\beta }}_i)q_i\\ 0& 0& 0& 1\end{array}\right].$$

When multiplying a matrix A_(i−1)*,i both left and right on the matrix D_i, for example, at β_i = 1 we obtain the derivative matrix

$$D_i{A}_{(i-1)*,i}=A_{(i-1)*,i}{D}_i={\displaystyle \frac{\partial A_{(i-1)*,i}}{\partial q_i}}.$$

It is obvious that

$${\displaystyle \frac{\partial A_{(i-1),i}}{\partial q_i}}=A_{(i-1),(i-1)*}{\displaystyle \frac{\partial A_{(i-1)*,i}}{\partial q_i}}=A_{(i-1),(i-1)*}{A}_{(i-1)*,i}{D}_i.$$

Using expressions (10) instead of (9) significantly increases the algorithm efficiency for calculating the kinematic parameters.

3. Object Modeling of Kinematics

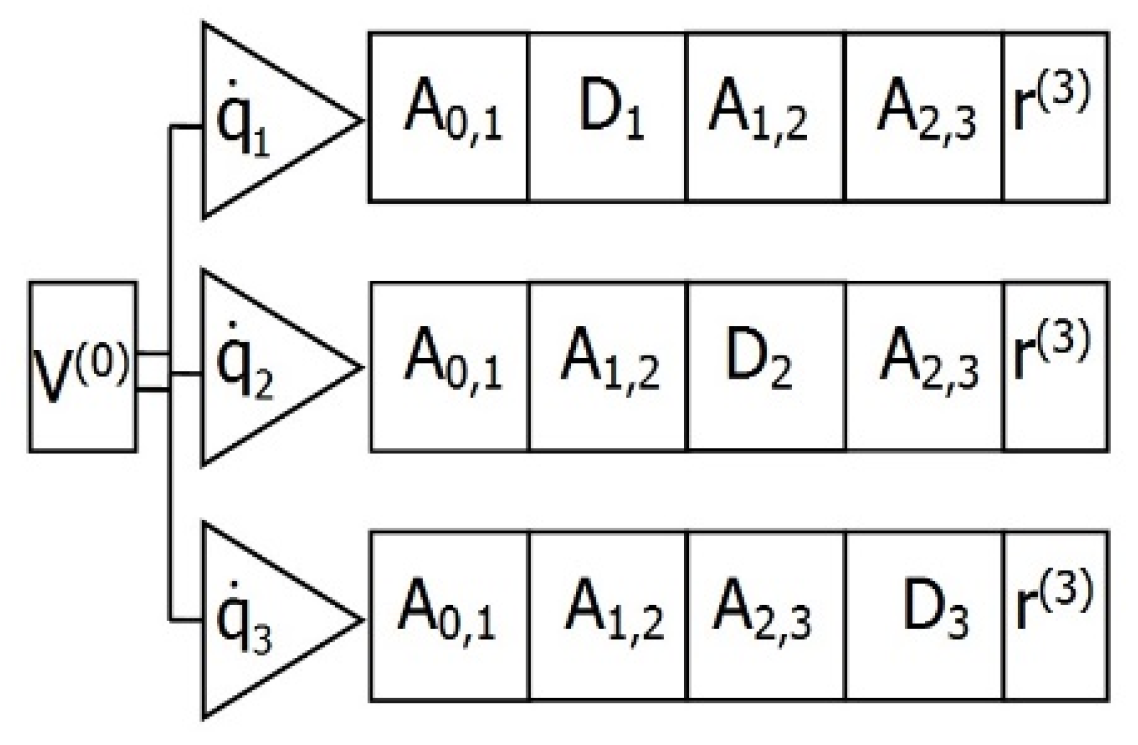
We will consider expression (3) as an integral part of the mathematical model (1)–(5), which determines the relative position of each link of the manipulation robot relative to the fixed coordinate system. Based on the matrices that make up Equation (3), we will create objects of the corresponding classes. These classes inherit the properties of their base Matrix class, which contains the necessary constructors for initializing objects and methods for performing basic operations on matrices.

Figure 3 shows the object scheme of the mathematical model (1)–(5), for the case k = 3, corresponding to a three-link (3-DOF) manipulation robot.

Matrix objects are depicted in the diagram as rectangular elements. The multiplication operation is represented by adding on the right or left of the matrix object another corresponding matrix object. The rules for constructing object diagrams of mathematical models of manipulation robots are considered in [28].

When calculating the kinematic parameters, the operation of differentiating the transformation matrices of homogeneous coordinates is performed. As it has already been noted, this operation can be fulfilled using differentiation matrices (8)–(11). Object schemes for calculating partial derivatives of transformation matrices of homogeneous coordinates when modelling the kinematics of the 6-DoF robot are presented below (see Figure 4, Figure 5 and Figure 6).

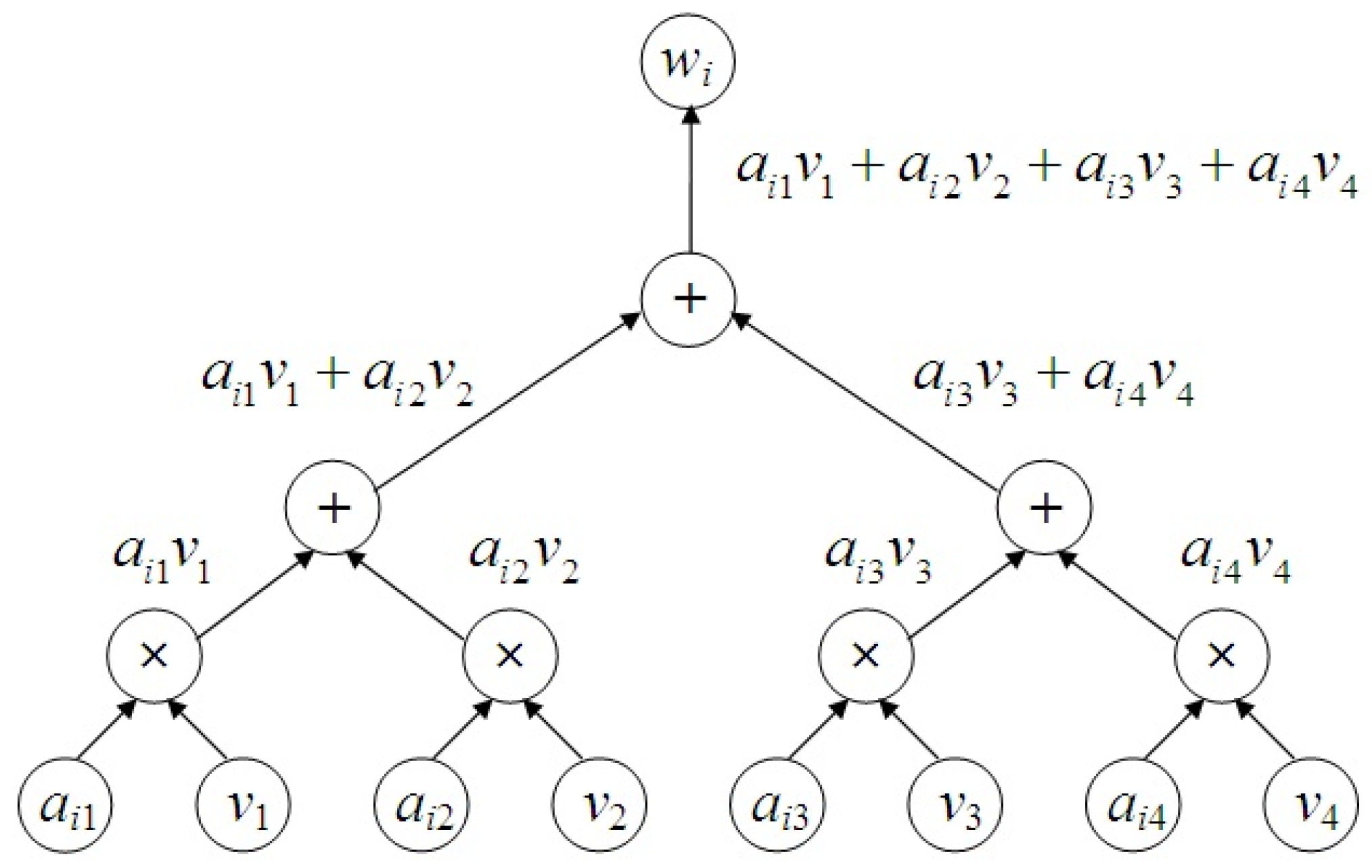
The expression for calculating the speed of a certain point of the third link of the manipulation robot in the S₀ fixed coordinate system, according to (6) for the case k = 3, will have the form

$$v^{(0)}=\left({\displaystyle \frac{\partial A_{0,3}}{\partial q_1}}{\dot{q}}_1+{\displaystyle \frac{\partial A_{0,3}}{\partial q_2}}{\dot{q}}_2+{\displaystyle \frac{\partial A_{0,3}}{\partial q_3}}{\dot{q}}_3\right)\hspace{0.17em}{r}^{(3)}.$$

(12)

Using differentiation matrices (11) allows representing expression (12) in the form

$$v^{(0)}=\left({\dot{q}}_1{A}_{0,1}{D}_1{A}_{1,2}{A}_{2,3}+{\dot{q}}_2{A}_{0,1}{A}_{1,2}{D}_2{A}_{2,3}+q_3{A}_{0,1}{A}_{1,2}{A}_{2,3}{D}_3\right)r^{(3)}.$$

(13)

Thus, the object scheme for calculating the certain point speed of the third link of the manipulation robot in the S₀ fixed coordinate system, given by its radius vector r⁽³⁾ in the S₃ coordinate system, corresponding to expression (13), will have the form (see Figure 7).

On the object scheme (see Figure 7), scalar elements are shown in the form of triangles. The operation of multiplying an object by a scalar is represented by attaching a triangle with one of its vertices to the side of the rectangle representing the object being multiplied by a scalar.

Consider expression (7) for calculating the acceleration of a certain point of the 3rd link of the manipulation robot in the S₀ fixed coordinate system.

$$a^{(0)}=\left(\begin{array}{l}{\displaystyle \frac{\partial A_{0,3}}{\partial q_1}}{\ddot{q}}_1+{\displaystyle \frac{\partial A_{0,3}}{\partial q_2}}{\ddot{q}}_2+{\displaystyle \frac{\partial A_{0,3}}{\partial q_3}}{\ddot{q}}_3+\\ +{\displaystyle \frac{{\partial }^2{A}_{0,3}}{\partial q_1^2}}{\dot{q}}_1^2+{\displaystyle \frac{{\partial }^2{A}_{0,3}}{\partial q_2^2}}{\dot{q}}_2^2+{\displaystyle \frac{{\partial }^2{A}_{0,3}}{\partial q_3^2}}{\dot{q}}_3^2+\\ +2\left({\displaystyle \frac{{\partial }^2{A}_{0,3}}{\partial q_1\partial q_2}}{\dot{q}}_1{\dot{q}}_2+{\displaystyle \frac{{\partial }^2{A}_{0,3}}{\partial q_1\partial q_3}}{\dot{q}}_1{\dot{q}}_3+{\displaystyle \frac{{\partial }^2{A}_{0,3}}{\partial q_2\partial q_3}}{\dot{q}}_2{\dot{q}}_3\right)\end{array}\right)r^{(3)}$$

(14)

Similarly to (13), expression (14) can be represented by the expression

$$a^{(0)}=\left(\begin{array}{l}{\ddot{q}}_1{A}_{0,1}{D}_1{A}_{1,2}{A}_{2,3}+{\ddot{q}}_2{A}_{0,1}{A}_{1,2}{D}_2{A}_{2,3}+{\ddot{q}}_3{A}_{0,1}{A}_{1,2}{A}_{2,3}{D}_3+\\ +{\dot{q}}_1^2{A}_{0,1}{D}_1{D}_1{A}_{1,2}{A}_{2,3}+{\dot{q}}_2^2{A}_{0,1}{A}_{1,2}{D}_2{D}_2{A}_{2,3}+q_3^2{A}_{0,1}{A}_{1,2}{A}_{2,3}{D}_3{D}_3+\\ +2\left({\dot{q}}_1{\dot{q}}_2{A}_{0,1}{D}_1{A}_{1,2}{D}_2{A}_{2,3}+{\dot{q}}_1{\dot{q}}_3{A}_{0,1}{D}_1{A}_{1,2}{A}_{2,3}{D}_3+{\dot{q}}_1{\dot{q}}_3{A}_{0,1}{A}_{1,2}{D}_1{A}_{2,3}{D}_3\right)\end{array}\right)r^{(3)}$$

(15)

the object scheme for a certain point acceleration calculation of the manipulation robot 3rd link in the S₀ fixed coordinate system, given by its radius vector r⁽³⁾ in the S₃ coordinate system, corresponding to expression (15), will look as follows (see Figure 8).

4. Computational Complexity of Algorithms

Let us analyze the computational complexity of the matrix algorithm execution. In this case, we will be based on comparing the number of addition and multiplication operations performed with matrix elements. Let us compare the number of addition (+) and multiplication (×) operations performed when executing matrix expressions with elements of n × n matrices and n × 1 vectors.

When multiplying two n × n matrices, the number of addition operations is K₊ = n²(n − 1), and the number of multiplication operations is K_× = n³. When multiplying an n × n matrix by an n × 1 vector, the number of addition operations is K₊ = n(n − 1), and the number of multiplication operations is K_× = n².

Consider a more general case representing the product of several matrices and a vector

$$\left(\stackrel{(n\times n)}{A_1}\cdot \cdot \cdot \stackrel{(n\times n)}{A_k}\right)\stackrel{(n\times 1)}{V}=\stackrel{(n\times n)}{A_1}\cdot \cdot \cdot \left(\stackrel{(n\times n)}{A_{k-1}}\left(\stackrel{(n\times n)}{A_k}\stackrel{(n\times 1)}{V}\right)\right)$$

(16)

The number of addition operations on the left side of the matrix Equation (16) is K₊^(L) = n²(n − 1)(k − 1) + n(n − 1) = n(n − 1)((k − 1)n + 1), and on the right side it is K₊^(R) = kn(n − 1). The ratio of these coefficients shows

$${\displaystyle \frac{K_{+}^{(L)}}{K_{+}^{(R)}}}={\displaystyle \frac{(k-1)n+1}{k}},\hspace{0.33em}\Rightarrow \mathrm{at} n=4, k=3, {\displaystyle \frac{K_{+}^{(L)}}{K_{+}^{(R)}}}=3.$$

(17)

The number of multiplication operations on the left side of the matrix Equation (16) is K_×^(L) = n²((k − 1)n + 1), and on the right side it is K_×^(R) = kn². The ratio of these coefficients shows

$${\displaystyle \frac{K_{\times }^{(L)}}{K_{\times }^{(R)}}}={\displaystyle \frac{(k-1)n+1}{k}},\hspace{0.33em}\Rightarrow \mathrm{at} n=4, k=3, {\displaystyle \frac{K_{\times }^{(L)}}{K_{\times }^{(R)}}}=3.$$

(18)

Analysing the computational complexity of expression (13) for calculating the point acceleration shows that the number of addition operations when this expression is executed is K₊⁽¹³⁾ = 9n³ − 6n² − n, for n = 4 it equals K₊⁽¹³⁾ = 476, and the number of multiplication operations is K_×⁽¹³⁾ = 9n³ + 4n², for n = 4 it equals K_×⁽¹³⁾ = 640.

Based on results (17) and (18), we can assume that reducing expression (13) to the form

$$v^{(0)}={\dot{q}}_1\left(A_{0,1}\left(D_1\left(A_{1,2}\left(A_{2,3}{r}^{(3)}\right)\right)\right)\right)+{\dot{q}}_2\left(A_{0,1}\left(A_{1,2}\left(D_2\left(A_{2,3}{r}^{(3)}\right)\right)\right)\right)+{\dot{q}}_3\left(A_{0,1}\left(A_{1,2}\left(A_{2,3}\left(D_3{r}^{(3)}\right)\right)\right)\right)$$

(19)

will decrease in the number of addition and multiplication operations performed.

The number of addition operations when executing expression (19) K₊⁽¹⁹⁾ = 2n(6n − 5), for n = 4, equals K₊⁽¹⁹⁾ = 152, and the number of multiplication operations K_×⁽¹⁹⁾ = 15n2, for n = 4, equals K_×⁽¹⁹⁾ = 240.

The ratio of the coefficients obtained for mathematical models (13) and (19) for n = 4 shows

$${\displaystyle \frac{K_{+}^{(13)}}{K_{+}^{(19)}}}=3.13,\hspace{1em}{\displaystyle \frac{K_{\times }^{(13)}}{K_{\times }^{(19)}}}=2.67.$$

(20)

Analysing the computational complexity of expression (15) for calculating the point acceleration shows that the number of addition operations when this expression is executed is K₊⁽¹⁵⁾ = 33n³ − 24n² − n, for n = 4 it equals K₊⁽¹⁵⁾ = 1724, and the number of multiplication operations is K_×⁽¹⁵⁾ = 11n²(3n + 1), for n = 4 it equals K_×⁽¹⁵⁾ = 2288.

Based on results (17) and (18), similarly to the transformations performed for the speed, we transform expression (15) to the form

$$\begin{gathered} a^{(0)}={\ddot{q}}_1\left(A_{0,1}\left(D_1\left(A_{1,2}\left(A_{2,3}\hspace{0.17em}{r}^{(3)}\right)\right)\right)\right)+{\ddot{q}}_2\left(A_{0,1}\left(A_{1,2}\left(D_2\left(A_{2,3}\hspace{0.17em}{r}^{(3)}\right)\right)\right)\right)+{\ddot{q}}_3\left(A_{0,1}\left(A_{1,2}\left(A_{2,3}\left(D_3\hspace{0.17em}{r}^{(3)}\right)\right)\right)\right)+ \\ {\dot{q}}_1^2\left(A_{0,1}\left(D_1\left(D_1\left(A_{1,2}\left(A_{2,3}\hspace{0.17em}{r}^{(3)}\right)\right)\right)\right)\right)+{\dot{q}}_2^2\left(A_{0,1}\left(A_{1,2}\left(D_2\left(D_2\left(A_{2,3}\hspace{0.17em}{r}^{(3)}\right)\right)\right)\right)\right)+q_3^2\left(A_{0,1}\left(A_{1,2}\left(A_{2,3}\left(D_3\left(D_3\hspace{0.17em}{r}^{(3)}\right)\right)\right)\right)\right)+ \\ 2{\dot{q}}_1{\dot{q}}_2\left(A_{0,1}\left(D_1\left(A_{1,2}\left(D_2\left(A_{2,3}\hspace{0.17em}{r}^{(3)}\right)\right)\right)\right)\right)+2{\dot{q}}_1{\dot{q}}_3\left(A_{0,1}\left(D_1\left(A_{1,2}\left(A_{2,3}\left(D_3\hspace{0.17em}{r}^{(3)}\right)\right)\right)\right)\right)+ \\ 2{\dot{q}}_1{\dot{q}}_3\left(A_{0,1}\left(A_{1,2}\left(D_1\left(A_{2,3}\left(D_3\hspace{0.17em}{r}^{(3)}\right)\right)\right)\right)\right). \end{gathered}$$

(21)

The number of addition operations when executing expression (21) K₊⁽²¹⁾ = 2n(21n − 17), for n = 4 equals K₊⁽²¹⁾ = 536, and the number of multiplication operations K_×⁽²¹⁾ = 51n² + 9, for n = 4 equals K_×⁽²¹⁾ = 825.

The ratio of the coefficients obtained for mathematical models (15) and (21) for n = 4 shows

$${\displaystyle \frac{K_{+}^{(15)}}{K_{+}^{(21)}}}=3.22,\hspace{1em}{\displaystyle \frac{K_{\times }^{(15)}}{K_{\times }^{(21)}}}=2.77.$$

(22)

Taking the direction of executing sequential calculations in the rows of object circuits (Figure 8 and Figure 9) from right to left, we obtain that the calculation efficiency is proportional to the calculated values (20) and (22).

An analysis of the computational complexity of matrix expressions (19) and (21) shows that the transformation of matrix expressions based on the associativity property makes it possible to increase the efficiency of algorithms for calculating the kinematic parameters of robotic manipulators by approximately three times.

To test the efficiency of the proposed algorithms, a computational experiment was conducted. The computer program was written in the C programming language. The program contained algorithms for calculating kinematic parameters in accordance with expressions (13), (15), (19), and (21). Special operators were included in the program code [29]:

$$\begin{array}{l}\#\mathit{include}<\mathit{windows}.\mathit{h}>//\mathit{GetTickCount}\left(\right)\\ \mathit{LARGE}\_\mathit{INTEGER\; tu}\_\mathit{freq},\mathit{tu}\_\mathit{start},\mathit{tu}\_\mathit{end};\\ \_\_\mathit{int64\; t}\_\mathit{ns};\\ \dots \\ \mathit{QueryPerformanceFrequency}(\&\mathit{tu}\_\mathit{freq});\\ \mathit{QueryPerformanceCounter}(\&\mathit{tu}\_\mathit{start});\\ \mathit{CalcKinemParam}\left(\right);\\ \mathit{QueryPerformanceCounter}(\&\mathit{tu}\_\mathit{end});\\ \mathit{t}\_\mathit{ns}=1000000000\mathit{ULL}*(\mathit{tu}\_\mathit{end}.\mathit{QuadPart}-\mathit{tu}\_\mathit{start}.\mathit{QuadPart})/\mathit{tu}\_\mathit{freq}.\mathit{QuadPart};\end{array}$$

where CalcKinemParam()—function for calculating kinematic parameters in accordance with expressions (13), (15), (19), (21); t_ns—function execution time.

The computer program provided the determination of the execution time of the CalcKinemParam() function with excess precision measured in nanoseconds. However, the relevance of the experiment is not absolute, since, when executing the computer program, not only the time spent performing arithmetic operations was taken into account, but also the time spent calling functions, transferring data to processor registers, and accessing RAM. Let us attribute these factors to associated errors.

The calculations were carried out under the Windows 11 operating system on a computer equipped with an Intel Celeron central processor, 2 Cores, 1.1–2.8 GHz, 8 GB.

The kinematic structures of robot manipulators from 2-DOF to 6-DOF were studied. The speed calculation results are presented in the diagram (Figure 9). The data shown in the diagram are labeled “Usual” and correspond to algorithm (13), while those labeled “Optimized” correspond to algorithm (19). The numerical values correspond to the calculation time in microseconds (mks).

The results of the computational experiment showed that for different kinematic structures, the ratio of the execution time of the functions corresponding to expressions (13) and (15), as well as (19) and (21), varied in the range from 1.5 to 3. Taking into account the associated errors, the efficiency of algorithms (13) and (19) in comparison with similar algorithms (15) and (21) averaged 2.5–3, or more than twice. Which is in good agreement with the coefficients (20) and (22).

5. Algorithms for Parallel Computing

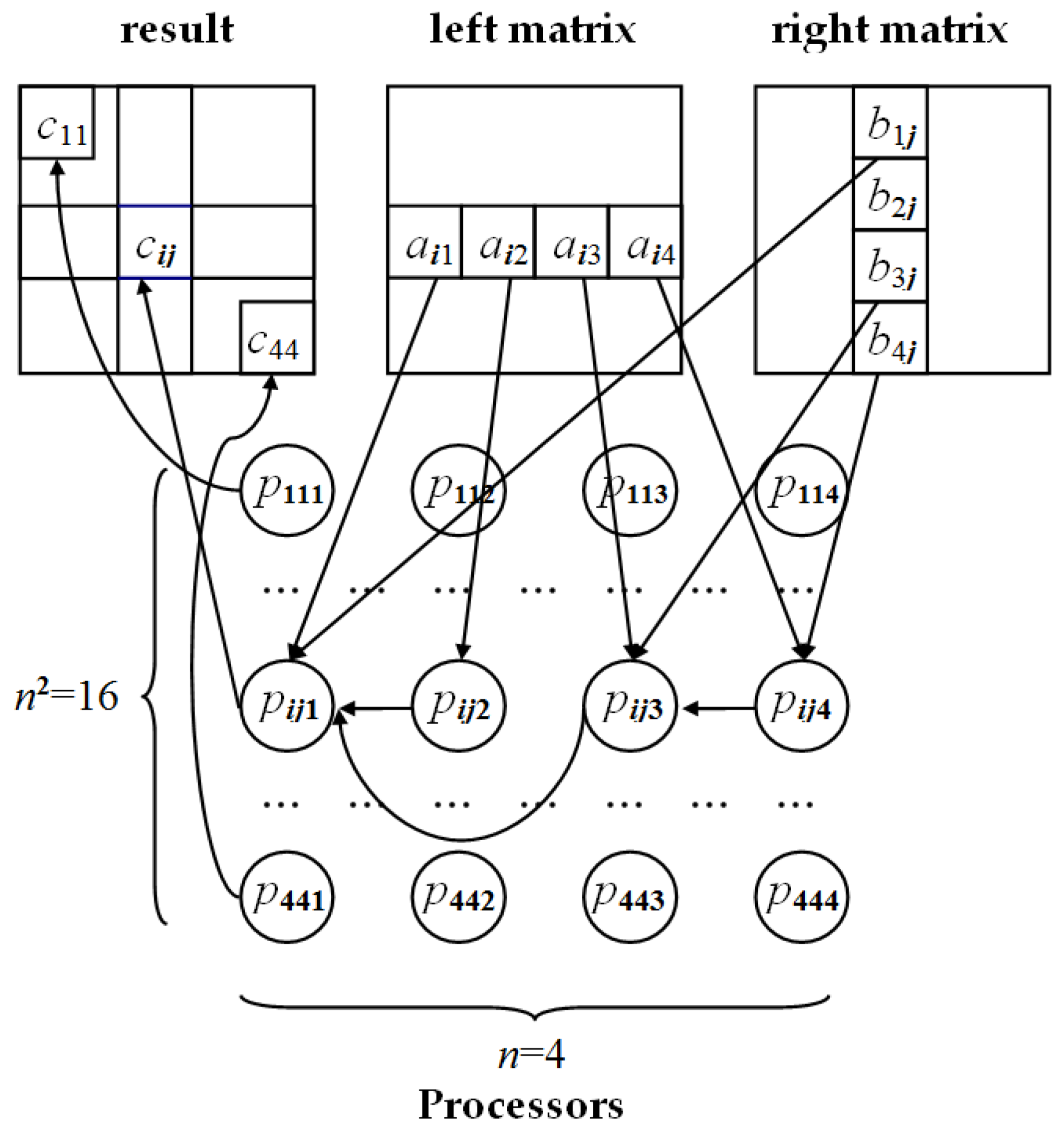
Consider the graph of the computational process of a 4 × 4 matrix product by a 4 × 1 vector (see Figure 10), based on the ratio.

$$w_i={\displaystyle \sum _{j=1}^4{a}_{ij}{v}_j,\hspace{0.33em}i=\left\{1,\dots ,4\right\}}.$$

(23)

When calculating the product of an n × n matrix by the corresponding vector, the number of necessary scalar operations of addition and multiplication can be estimated by the value

$$K=2n^2.$$

(24)

Analysing the graph of the computational process (Figure 11) shows that parallel methods for solving the problem of the matrix product by a vector can be obtained based on applying parallel summation algorithms; in this case, a cascade summation algorithm is used. In addition, the way in which parallel computing is organized will depend on the number of available processors.

It should be noted that the sequences of performed operations of multiplying individual n matrix rows by a vector are independent and can be fulfilled in parallel. The operations of multiplying each row by a vector involve n independent elementwise multiplications and can also be performed in parallel. Thus, the maximum required number of processors is determined by the value:

$$p=n^2.$$

(25)

The execution time of a parallel algorithm, referred to as the execution time of one scalar operation, when using p processors, is determined by the execution time of the multiplication operation and the execution time of the cascade summation algorithm:

$$T_p=1+{\log }_{2}n.$$

(26)

Efficiency indicators of the parallel algorithm are,

$$S_p={\displaystyle \frac{K}{T_p}}={\displaystyle \frac{2n^2}{1+{\log }_{2}n}},$$

(27)

where S_p is the acceleration for p processors obtained by using a parallel algorithm;

$$E_p={\displaystyle \frac{S_p}{p}}={\displaystyle \frac{2}{1+{\log }_{2}n}},$$

(28)

where E_p is the efficient use of processors.

The information graph corresponding to the computational process of multiplying the i-th row of the 4 × 4 matrix by the 4 × 1 vector (Figure 11), built on the basis of 4 processors (see Figure 11).

The problem of multiplying rectangular matrices is defined by the relation:

$$c_{ij}={\displaystyle \sum _{l=1}^k{a}_{il}{b}_{lj},\hspace{0.33em}i=\left\{1,\dots ,n\right\}},\hspace{0.33em}j=\left\{1,\dots ,m\right\}.$$

(29)

In the case of multiplying n × n square matrices, the number of scalar multiplication and addition operations is proportional to n³, and the value can be used to evaluate them.

$$K=2n^3.$$

(30)

The sequences of the performed operations of multiplying individual rows of the first matrix by the corresponding column of the second matrix are independent and can be performed in parallel. An algorithm for parallel computation of matrix multiplication can be built on the basis of the considered computational algorithm for matrix-vector multiplication. Accordingly, the required number of processors for maximum parallelization of the computational algorithm will be determined by the value:

$$p=n^3.$$

(31)

The information graph corresponding to the computational process of the 4 × 4 matrix multiplication, built on the basis of 64 processors (see Figure 12).

The execution time of the parallel algorithm, as before, will be determined by expression (26). The resulting acceleration for p processors will increase:

$$S_p={\displaystyle \frac{K}{T_p}}={\displaystyle \frac{2n^3}{1+{\log }_{2}n}},$$

(32)

and the efficiency of using processors in accordance with (28) will not change.

Reducing the number of processors used will require restructuring the information graph (see Figure 12), which reflects the computational process of matrix multiplication. This will increase the computation time.

Matrices must be calculated first A_(i−1),i (i = 1,…,n) (2). At this stage, the number of independently calculated matrices is proportional to the number n degrees of freedom of the manipulation system. Since the maximum number of processors required for the simultaneous calculation of the 4 × 4 matrices is 64, the required number of processors for implementing parallel computing at the lower level will be:

$$p_1=64n.$$

(33)

At the next stage, the objects corresponding to the matrices A_0,k (k = 1,…,n) (3) and the matrices of their partial derivatives (8)–(10) are calculated. When calculating matrices of partial derivatives, it must be considered that these matrices will vanish under the conditions:

$${\displaystyle \frac{\partial A_{0,k}}{\partial q_s}}=0\mathrm{at} s>k, {\displaystyle \frac{{\partial }^2{A}_{0,k}}{\partial q_i\partial q_j}}=0\mathrm{at}i>k\mathrm{or}j>k$$

Number N₁ of the calculated partial derivative matrices ${\displaystyle \frac{\partial A_{0,k}}{\partial q_s}}$ (k,s = 1,…,n) will be determined by the expression

$$N_1={\displaystyle \frac{n}{2}}\left(n+1\right),$$

(34)

and in accordance with the property, ${\displaystyle \frac{{\partial }^2{A}_{0,k}}{\partial q_i\partial q_j}}={\displaystyle \frac{{\partial }^2{A}_{0,k}}{\partial q_j\partial q_i}}$ number N₂ of the second partial derivative matrices will be determined by the expression

$$N_2={\displaystyle \sum _{k=1}^n\frac{k}{2}}\left(k+1\right).$$

(35)

Accordingly, for implementing parallel computing at level (II), the maximum number of processors will be

$$p_2=64(n+N_1+N_2).$$

(36)

For most manipulative robots, n = 6. The graph of the computational process of the matrix A_0,6 (see Figure 13).

The graph of the computational process of the matrix ${\displaystyle \frac{\partial A_{0,6}}{\partial q_2}}$, using differentiation matrices (10) and (11) (see Figure 14), and matrices ${\displaystyle \frac{{\partial }^2{A}_{0,6}}{\partial q_1\partial q_3}}$ (see Figure 15).

The calculations of the kinematic parameters are completed in accordance with expressions (13) and (15). However, as was shown above, expressions (19) and (21), obtained on the basis of using the associativity property, allow increasing the efficiency of the computational process by three times.

It should be noted that the issues of constructing a methodology and creating high-performance computers with a parallel structure have been considered earlier, for example, in the works [30,31,32].

6. Conclusions

A method for compiling object schemes is proposed, allowing the construction of algorithms for calculating the kinematic parameters of robot manipulators. The method is based on the use of matrices (4 × 4) of the transformation of homogeneous coordinates. Examples of compiling object schemes for calculating the velocities and accelerations of points selected on the links of manipulator robots are considered.

An analysis of the computational complexity of algorithms for calculating the kinematic parameters of robotic manipulators was carried out, and a method was proposed that allows for a significant increase in the efficiency of calculations by reducing the number of addition and multiplication operations performed based on the use of the associativity property.

Information and computational graphs illustrating the developed algorithms are presented. The proposed algorithms allow parallel calculations, which will further an increase in the efficiency of calculations when using multiprocessor computing systems.

Low-code visual programming technology can be implemented on the basis of the proposed object approach. Object schemes created using this technology are assembled from basic elements. Elements are connected to each other in accordance with the type of corresponding mathematical expressions. In this case, the assembly of complex objects is regulated by the compatibility of the simple objects that make them up.

The object approach and the algorithm development methods developed on its basis can be used in robot control systems. The conducted research is designed to automate the process of developing algorithms for calculating the kinematic parameters of robot manipulators. This will allow reconfiguring the model of the controlled object in the mode of dialogue with the human operator. This eliminates the stages associated with the process of creating a special program and the procedure for reprogramming the microcontroller.

The algorithms presented in this article were used in the development of the trajectory planning function for a robotic manipulator in the control system of an automated apple harvesting complex. (Complex for Harvesting Apple Crops) [33].

The methods for increasing the efficiency of computational algorithms substantiated in the article can also be used in control systems for robotic manipulators built on the basis of multiprocessor computing systems.