Experiences Using MediaPipe to Make the Arms of a Humanoid Robot Imitate a Video-Recorded Dancer Performing a Robot Dance
Abstract
1. Introduction
1.1. Dancing Robots
1.2. MediaPipe Framework for Human Body Pose Estimation
1.3. Dancer Pose Estimation Using MediaPipe
1.4. New Contribution
- The evaluation of the MediaPipe BlazePose framework for the offline extraction of the skeletal mesh of the dancer from the video-recorded dance;
- The analysis of the execution time of the MediaPipe BlazePose framework on 1080 × 1920 resolution videos under various configuration settings;
- The development of a virtual model for the humanoid robot and the application of a minimization function to match the skeletal mesh of the dancer and the angles of the arms of the virtual model;
- The extraction of the Euler angles of the servomotors that control the arms of the humanoid robot;
- The appropriate generation of the motion commands to replicate the robot dance with the humanoid robot.
1.5. Paper Structure
2. Materials and Methods
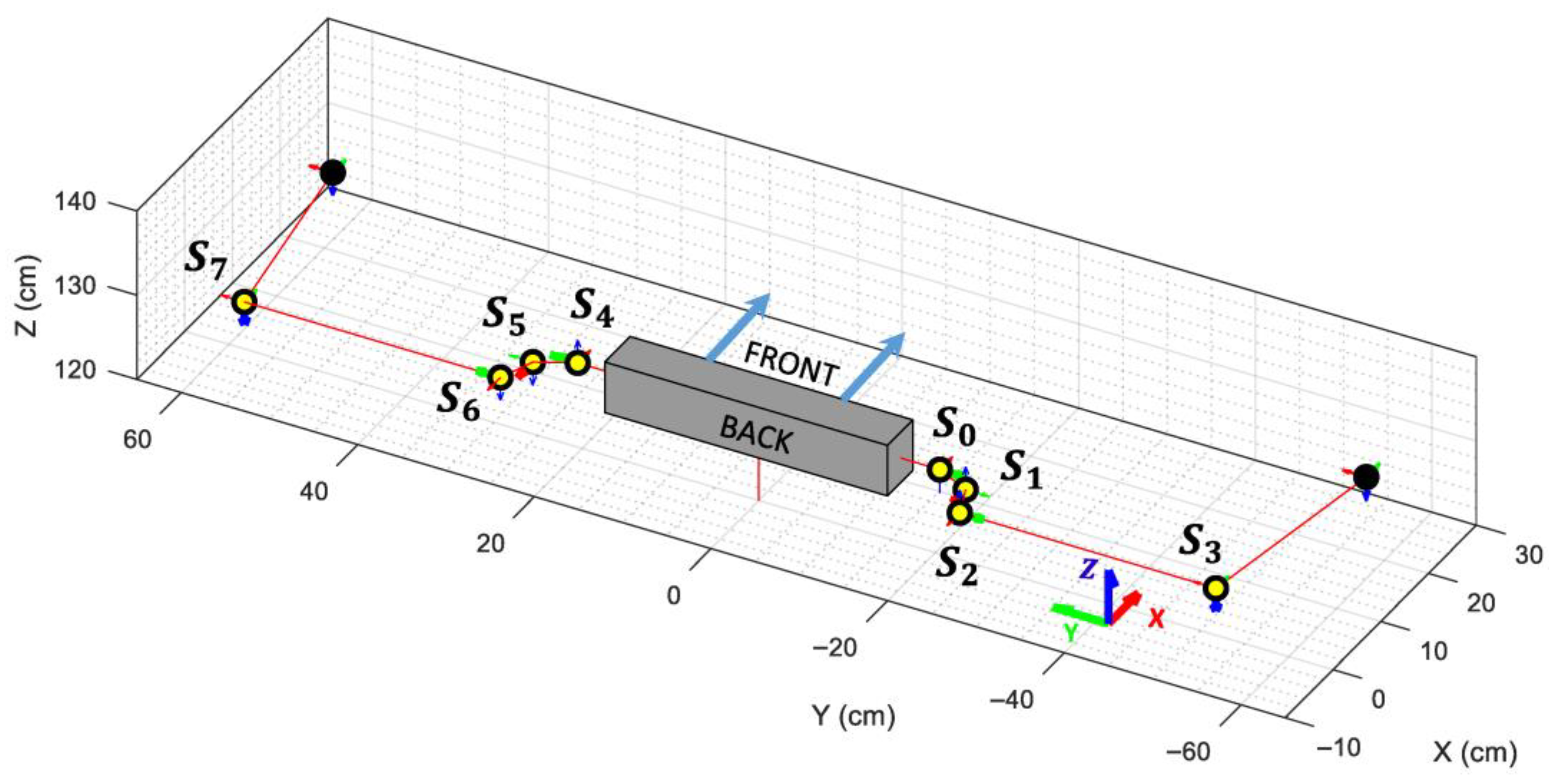
2.1. Humanoid Robot
2.2. MediaPipe BlazePose
2.3. Robot Dance
3. Procedure for Dance Imitation Based on MediaPipe BlazePose
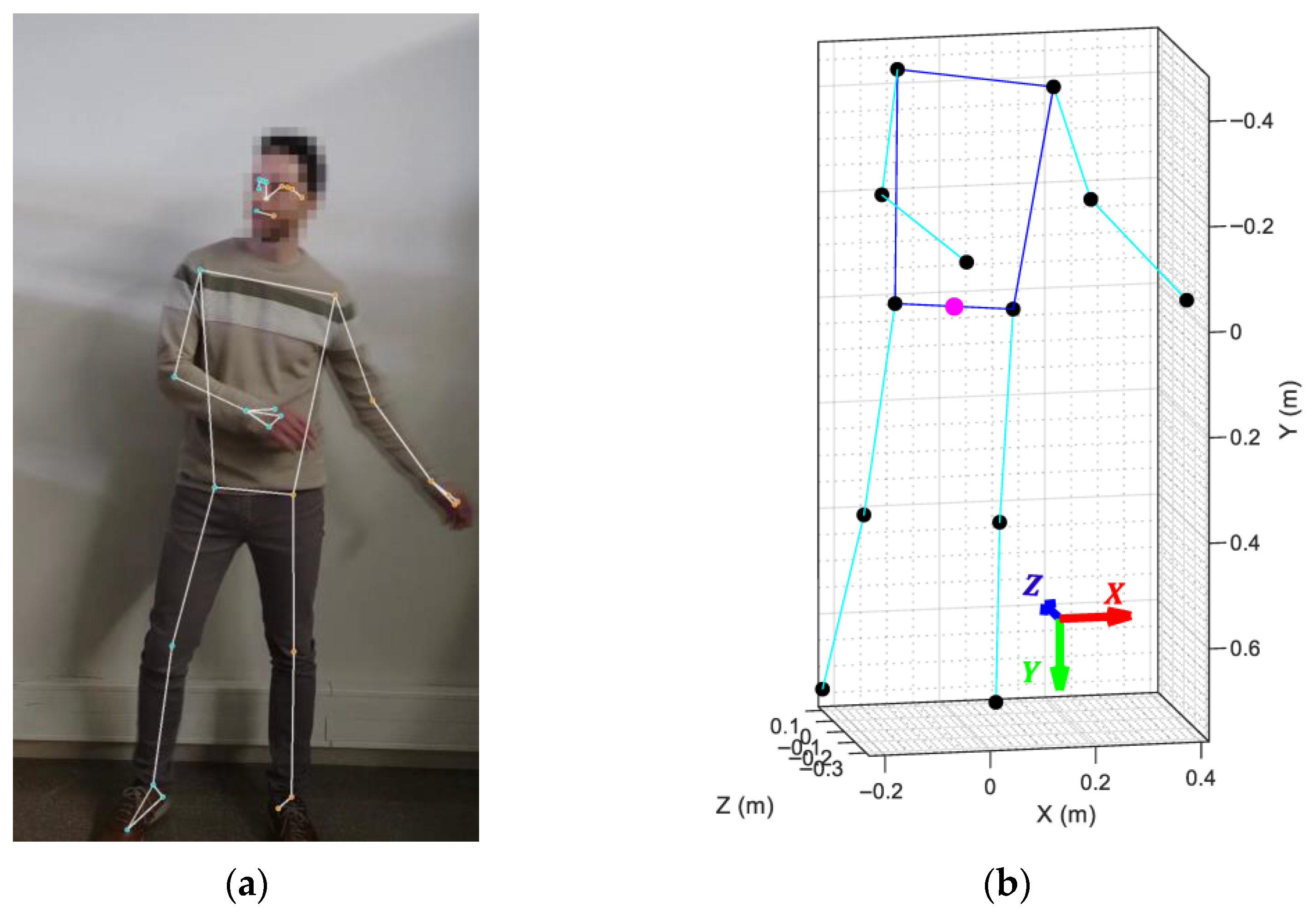
3.1. Skeletal Mesh Post-Processing
3.2. Virtual Robot Model (VRM)
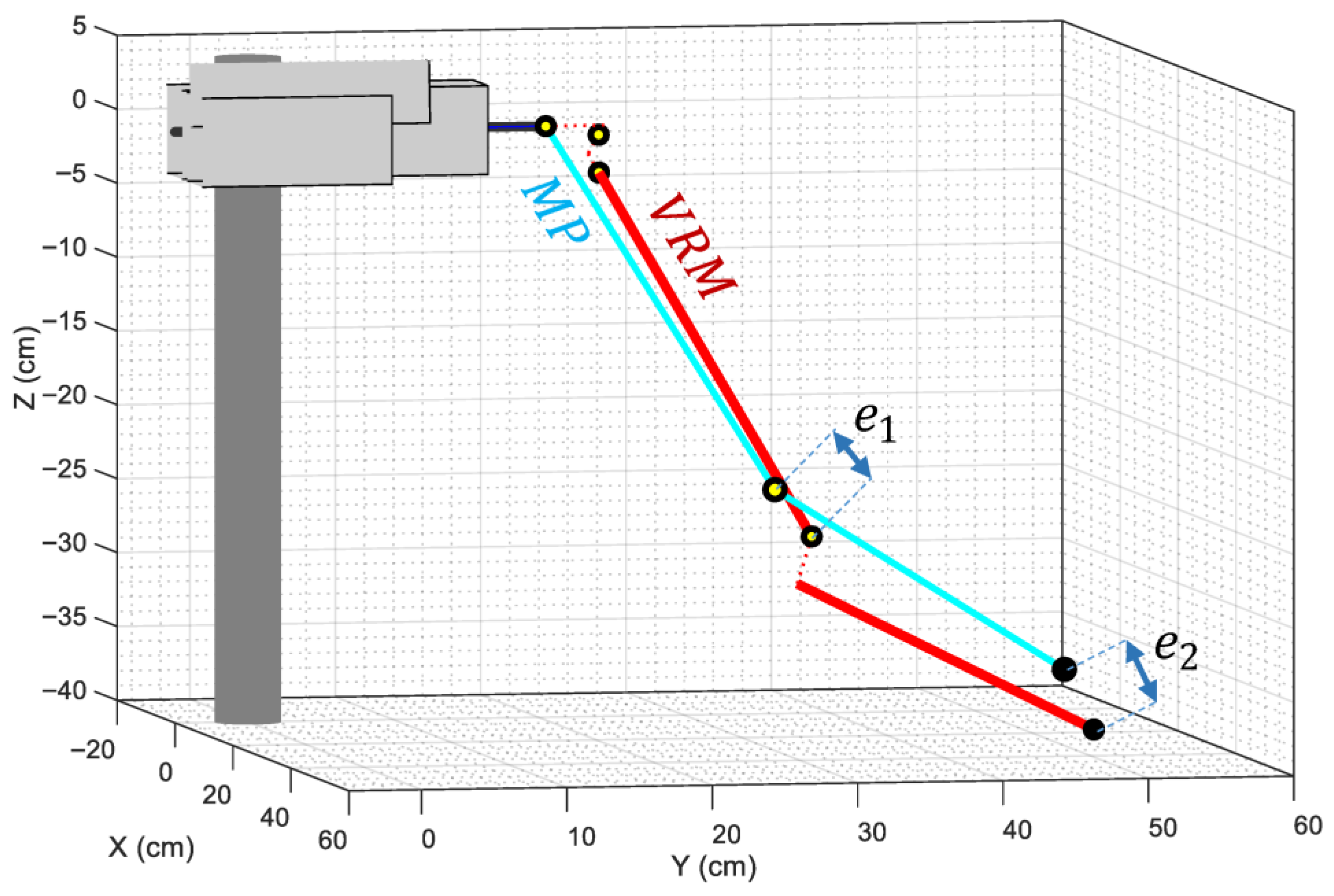
3.3. Person-to-Robot Angle Minimization Function
3.4. Person-to-Robot Angle Conversion Procedure
4. Results
4.1. Pose Detection Results
4.2. Angle Extraction Results
4.3. Robot Pose Results
5. Conclusions
Supplementary Materials
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Minato, T.; Shimada, M.; Ishiguro, H.; Itakura, S. Development of an Android Robot for Studying Human-Robot Interaction. In Proceedings of the Innovations in Applied Artificial Intelligence, Graz, Austria, 9 July 2004; Orchard, B., Yang, C., Ali, M., Eds.; Springer: Berlin, Germany, 2004; pp. 424–434. [Google Scholar]
- Lee, D.; Lee, T.; So, B.-R.; Choi, M.; Shin, E.-C.; Yang, K.; Baek, M.; Kim, H.-S.; Lee, H.-G. Development of an Android for Emotional Expression and Human Interaction. In Proceedings of the 17th World Congress the International Federation of Automatic, Control, Seoul, Republic of Korea, 6 July 2008; pp. 4336–4337. [Google Scholar]
- Lee, K.W.; Kim, H.-R.; Yoon, W.C.; Yoon, Y.-S.; Kwon, D.-S. Designing a Human-Robot Interaction Framework for Home Service Robot. In Proceedings of the 2005 IEEE International Workshop on Robot and Human Interactive Communication, Nashville, TN, USA, 13 August 2005; pp. 286–293. [Google Scholar]
- Muthugala, M.A.V.J.; Jayasekara, A.G.B.P. MIRob: An Intelligent Service Robot That Learns from Interactive Discussions While Handling Uncertain Information in User Instructions. In Proceedings of the 2016 Moratuwa Engineering Research Conference (MERCon), Moratuwa, Sri Lanka, 5 April 2016; pp. 397–402. [Google Scholar]
- Vasquez, H.A.; Vargas, H.S.; Sucar, L.E. Using Gestures to Interact with a Service Robot Using Kinect 2. Res. Comput. Sci. 2015, 96, 85–93. [Google Scholar] [CrossRef]
- Lin, C.-J.; Li, T.-H.S.; Kuo, P.-H.; Wang, Y.-H. Integrated Particle Swarm Optimization Algorithm Based Obstacle Avoidance Control Design for Home Service Robot. Comput. Electr. Eng. 2016, 56, 748–762. [Google Scholar] [CrossRef]
- Palacín, J.; Clotet, E.; Martínez, D.; Martínez, D.; Moreno, J. Extending the Application of an Assistant Personal Robot as a Walk-Helper Tool. Robotics 2019, 8, 27. [Google Scholar] [CrossRef]
- Chaichaowarat, R.; Prakthong, S.; Thitipankul, S. Transformable Wheelchair–Exoskeleton Hybrid Robot for Assisting Human Locomotion. Robotics 2023, 12, 16. [Google Scholar] [CrossRef]
- Shimada, M.; Yoshikawa, Y.; Asada, M.; Saiwaki, N.; Ishiguro, H. Effects of Observing Eye Contact between a Robot and Another Person. Int. J. Soc. Robot. 2011, 3, 143–154. [Google Scholar] [CrossRef]
- Rubies, E.; Palacín, J.; Clotet, E. Enhancing the Sense of Attention from an Assistance Mobile Robot by Improving Eye-Gaze Contact from Its Iconic Face Displayed on a Flat Screen. Sensors 2022, 22, 4282. [Google Scholar] [CrossRef]
- Kondo, Y.; Takemura, K.; Takamatsu, J.; Ogasawara, T. A Gesture-Centric Android System for Multi-Party Human-Robot Interaction. J. Hum.-Robot. Interact. 2013, 2, 133–151. [Google Scholar] [CrossRef]
- Huang, Z.; Ren, F.; Bao, Y. Human-like Facial Expression Imitation for Humanoid Robot Based on Recurrent Neural Network. In Proceedings of the 2016 International Conference on Advanced Robotics and Mechatronics (ICARM), Macau, China, 18 August 2016; pp. 306–311. [Google Scholar]
- Ahn, H.S.; Lee, D.-W.; Choi, D.; Lee, D.Y.; Hur, M.H.; Lee, H.; Shon, W.H. Development of an Android for Singing with Facial Expression. In Proceedings of the IECON 2011—37th Annual Conference of the IEEE Industrial Electronics Society, Melbourne, VIC, Australia, 7 November 2011; pp. 104–109. [Google Scholar]
- Becker-Asano, C.; Ishiguro, H. Evaluating Facial Displays of Emotion for the Android Robot Geminoid F. In Proceedings of the 2011 IEEE Workshop on Affective Computational Intelligence (WACI), Paris, France, 11 April 2011; pp. 1–8. [Google Scholar]
- Oh, K.-G.; Jung, C.-Y.; Lee, Y.-G.; Kim, S.-J. Real-Time Lip Synchronization between Text-to-Speech (TTS) System and Robot Mouth. In Proceedings of the 19th International Symposium in Robot and Human Interactive Communication, Viareggio, Italy, 13 September 2010; pp. 620–625. [Google Scholar]
- Mehrabian, A. Silent Messages: Implicit Communication of Emotions and Attitudes, 2nd ed.; Wadsworth Publishing Company: Belmont, CA, USA, 1981; ISBN 978-0-534-00910-6. [Google Scholar]
- Ekman, P.; Friesen, W.V. Unmasking the Face: A Guide to Recognizing Emotions from Facial Clues; ISHK: Woolooware, NSW, Australia, 2003; ISBN 978-1-883536-36-7. [Google Scholar]
- Mori, M.; MacDorman, K.F.; Kageki, N. The Uncanny Valley [From the Field]. IEEE Robot. Autom. Mag. 2012, 19, 98–100. [Google Scholar] [CrossRef]
- Kwak, S.S.; Kim, Y.; Kim, E.; Shin, C.; Cho, K. What Makes People Empathize with an Emotional Robot?: The Impact of Agency and Physical Embodiment on Human Empathy for a Robot. In Proceedings of the 2013 IEEE RO-MAN, Gyeongju, Republic of Korea, 26 August 2013; pp. 180–185. [Google Scholar]
- Kwon, D.-S.; Kwak, Y.K.; Park, J.C.; Chung, M.J.; Jee, E.-S.; Park, K.-S.; Kim, H.-R.; Kim, Y.-M.; Park, J.-C.; Kim, E.H.; et al. Emotion Interaction System for a Service Robot. In Proceedings of the RO-MAN 2007—The 16th IEEE International Symposium on Robot and Human Interactive Communication, Jeju, Republic of Korea, 26 August 2007; pp. 351–356. [Google Scholar]
- Hyung, H.; Lee, D.; Yoon, H.U.; Choi, D.; Lee, D.; Hur, M. Facial Expression Generation of an Android Robot Based on Probabilistic Model. In Proceedings of the 2018 27th IEEE International Symposium on Robot and Human Interactive Communication (RO-MAN), Nanjing, China, 27 August 2018; pp. 458–460. [Google Scholar]
- Go, D.; Hyung, H.; Lee, D.; Yoon, H.U. Andorid Robot Motion Generation Based on Video-Recorded Human Demonstrations. In Proceedings of the 2018 27th IEEE International Symposium on Robot and Human Interactive Communication (RO-MAN), Nanjing, China, 27 August 2018; pp. 476–478. [Google Scholar]
- Noma, M.; Saiwaki, N.; Itakura, S.; Ishiguro, H. Composition and Evaluation of the Humanlike Motions of an Android. In Proceedings of the 2006 6th IEEE-RAS International Conference on Humanoid Robots, Genova, Italy, 4 December 2006; pp. 163–168. [Google Scholar]
- Lin, C.-Y.; Huang, C.-C.; Cheng, L.-C. A Small Number Actuator Mechanism Design for Anthropomorphic Face Robot. In Proceedings of the 2011 IEEE International Conference on Robotics and Biomimetics, Karon Beach, Thailand, 7 December 2011; pp. 633–638. [Google Scholar]
- Hyung, H.-J.; Yoon, H.U.; Choi, D.; Lee, D.-Y.; Lee, D.-W. Optimizing Android Facial Expressions Using Genetic Algorithms. Appl. Sci. 2019, 9, 3379. [Google Scholar] [CrossRef]
- Ravignani, A.; Cook, P.F. The Evolutionary Biology of Dance without Frills. Curr. Biol. 2016, 26, R878–R879. [Google Scholar] [CrossRef]
- Laland, K.; Wilkins, C.; Clayton, N. The Evolution of Dance. Curr. Biol. 2016, 26, R5–R9. [Google Scholar] [CrossRef]
- Peng, H.; Zhou, C.; Hu, H.; Chao, F.; Li, J. Robotic Dance in Social Robotics—A Taxonomy. IEEE Trans. Hum.-Mach. Syst. 2015, 45, 281–293. [Google Scholar] [CrossRef]
- Michalowski, M.P.; Sabanovic, S.; Kozima, H. A Dancing Robot for Rhythmic Social Interaction. In Proceedings of the HRI ’07: The ACM/IEEE International Conference on Human-Robot Interaction; Association for Computing Machinery, New York, NY, USA, 10 March 2007; pp. 89–96. [Google Scholar]
- Nakaoka, S.; Nakazawa, A.; Kanehiro, F.; Kaneko, K.; Morisawa, M.; Hirukawa, H.; Ikeuchi, K. Learning from Observation Paradigm: Leg Task Models for Enabling a Biped Humanoid Robot to Imitate Human Dances. Int. J. Robot. Res. 2007, 26, 829–844. [Google Scholar] [CrossRef]
- Kaneko, K.; Kanehiro, F.; Kajita, S.; Hirukawa, H.; Kawasaki, T.; Hirata, M.; Akachi, K.; Isozumi, T. Humanoid Robot HRP-2. In Proceedings of the IEEE International Conference on Robotics and Automation, New Orleans, LA, USA, 26 April 2004; Volume 2, pp. 1083–1090. [Google Scholar]
- Xia, G.; Tay, J.; Dannenberg, R.; Veloso, M. Autonomous Robot Dancing Driven by Beats and Emotions of Music. In Proceedings of the AAMAS ’12: The 11th International Conference on Autonomous Agents and Multiagent Systems; International Foundation for Autonomous Agents and Multiagent Systems, Richland, SC, USA, 4 June 2012; pp. 205–212. [Google Scholar]
- Okamoto, T.; Shiratori, T.; Kudoh, S.; Nakaoka, S.; Ikeuchi, K. Toward a Dancing Robot with Listening Capability: Keypose-Based Integration of Lower-, Middle-, and Upper-Body Motions for Varying Music Tempos. IEEE Trans. Robot. 2014, 30, 771–778. [Google Scholar] [CrossRef]
- Ramos, O.E.; Mansard, N.; Stasse, O.; Benazeth, C.; Hak, S.; Saab, L. Dancing Humanoid Robots: Systematic Use of OSID to Compute Dynamically Consistent Movements Following a Motion Capture Pattern. IEEE Robot. Autom. Mag. 2015, 22, 16–26. [Google Scholar] [CrossRef]
- Gkiokas, A.; Katsouros, V. Convolutional Neural Networks for Real-Time Beat Tracking: A Dancing Robot Application. In Proceedings of the 18th International Society for Music Information Retrieval Conference, Suzhou, China, 24 October 2017. [Google Scholar]
- Qin, R.; Zhou, C.; Zhu, H.; Shi, M.; Chao, F.; Li, N. A Music-Driven Dance System of Humanoid Robots. Int. J. Humanoid Robot. 2018, 15, 1850023. [Google Scholar] [CrossRef]
- Güney, G.; Jansen, T.S.; Dill, S.; Schulz, J.B.; Dafotakis, M.; Hoog Antink, C.; Braczynski, A.K. Video-Based Hand Movement Analysis of Parkinson Patients before and after Medication Using High-Frame-Rate Videos and MediaPipe. Sensors 2022, 22, 7992. [Google Scholar] [CrossRef]
- Kim, J.-W.; Choi, J.-Y.; Ha, E.-J.; Choi, J.-H. Human Pose Estimation Using MediaPipe Pose and Optimization Method Based on a Humanoid Model. Appl. Sci. 2023, 13, 2700. [Google Scholar] [CrossRef]
- Zhang, Y.; Notni, G. 3D Geometric Features Based Real-Time American Sign Language Recognition Using PointNet and MLP with MediaPipe Hand Skeleton Detection. Meas. Sens. 2025, 38, 101697. [Google Scholar] [CrossRef]
- Fu, Z.; Zhao, T.Z.; Finn, C. Mobile ALOHA: Learning Bimanual Mobile Manipulation with Low-Cost Whole-Body Teleoperation. arXiv 2024, arXiv:2401.02117. [Google Scholar]
- Yasar, M.S.; Islam, M.M.; Iqbal, T. PoseTron: Enabling Close-Proximity Human-Robot Collaboration Through Multi-Human Motion Prediction. In Proceedings of the 2024 ACM/IEEE International Conference on Human-Robot Interaction, Boulder, CO, USA, 11 March 2024; ACM: Singapore, 2024; pp. 830–839. [Google Scholar]
- Kreiss, S.; Bertoni, L.; Alahi, A. PifPaf: Composite Fields for Human Pose Estimation. In Proceedings of the 2019 IEEE/CVF Conference on Computer Vision and Pattern Recognition (CVPR), Long Beach, CA, USA, 15 June 2019; pp. 11969–11978. [Google Scholar]
- Sun, K.; Xiao, B.; Liu, D.; Wang, J. Deep High-Resolution Representation Learning for Human Pose Estimation. In Proceedings of the 2019 IEEE/CVF Conference on Computer Vision and Pattern Recognition (CVPR), Long Beach, CA, USA, 15 June 2019; pp. 5686–5696. [Google Scholar]
- Bazarevsky, V.; Grishchenko, I.; Raveendran, K.; Zhu, T.; Zhang, F.; Grundmann, M. BlazePose: On-Device Real-Time Body Pose Tracking. arXiv 2020, arXiv:2006.10204. [Google Scholar]
- Lugaresi, C.; Tang, J.; Nash, H.; McClanahan, C.; Uboweja, E.; Hays, M.; Zhang, F.; Chang, C.-L.; Yong, M.; Lee, J.; et al. MediaPipe: A Framework for Perceiving and Processing Reality. In Proceedings of the 2019 IEEE/CVF Conference on Computer Vision and Pattern Recognition (CVPR), Long Beach, CA, USA, 15 June 2019. [Google Scholar]
- Google MediaPipe Solutions Guide. Available online: https://ai.google.dev/edge/mediapipe/solutions/guide (accessed on 29 July 2024).
- Bazarevsky, V.; Zhang, F. On-Device, Real-Time Hand Tracking with MediaPipe. Available online: http://research.google/blog/on-device-real-time-hand-tracking-with-mediapipe/ (accessed on 29 July 2024).
- Jeong, S.; Kook, J. CREBAS: Computer-Based REBA Evaluation System for Wood Manufacturers Using MediaPipe. Appl. Sci. 2023, 13, 938. [Google Scholar] [CrossRef]
- Güney, G.; Jansen, T.S.; Braczynski, A.K.; Rohr, M.; Dill, S.; Antink, C.H. Analyzing the Effect of Age and Gender on the Blink Reflex Using MediaPipe. Curr. Dir. Biomed. Eng. 2023, 9, 423–426. [Google Scholar] [CrossRef]
- Kompoliti, K.; Verhagen, L. (Eds.) Glabellar Reflex. Encyclopedia of Movement Disorders, 1st ed.; Academic Press: New York, NY, USA, 2010; ISBN 978-0-12-374101-1. [Google Scholar]
- Supanich, W.; Kulkarineetham, S.; Sukphokha, P.; Wisarnsart, P. Machine Learning-Based Exercise Posture Recognition System Using MediaPipe Pose Estimation Framework. In Proceedings of the 2023 9th International Conference on Advanced Computing and Communication Systems (ICACCS), Coimbatore, India, 17 March 2023; Volume 1, pp. 2003–2007. [Google Scholar]
- Zhang, W.; Li, Y.; Cai, S.; Wang, Z.; Cheng, X.; Somjit, N.; Sun, D.; Chen, F. Combined MediaPipe and YOLOv5 Range of Motion Assessment System for Spinal Diseases and Frozen Shoulder. Sci. Rep. 2024, 14, 15879. [Google Scholar] [CrossRef] [PubMed]
- Amprimo, G.; Masi, G.; Pettiti, G.; Olmo, G.; Priano, L.; Ferraris, C. Hand Tracking for Clinical Applications: Validation of the Google MediaPipe Hand (GMH) and the Depth-Enhanced GMH-D Frameworks. Biomed. Signal Process. Control 2024, 96, 106508. [Google Scholar] [CrossRef]
- Garg, S.; Saxena, A.; Gupta, R. Yoga Pose Classification: A CNN and MediaPipe Inspired Deep Learning Approach for Real-World Application. J. Ambient Intell. Humaniz. Comput. 2023, 14, 16551–16562. [Google Scholar] [CrossRef]
- Chaudhary, I.; Thoiba Singh, N.; Chaudhary, M.; Yadav, K. Real-Time Yoga Pose Detection Using OpenCV and MediaPipe. In Proceedings of the 2023 4th International Conference for Emerging Technology (INCET), Belgaum, India, 26 May 2023; pp. 1–5. [Google Scholar]
- Bora, J.; Dehingia, S.; Boruah, A.; Chetia, A.A.; Gogoi, D. Real-Time Assamese Sign Language Recognition Using MediaPipe and Deep Learning. Procedia Comput. Sci. 2023, 218, 1384–1393. [Google Scholar] [CrossRef]
- Wang, Y.; Li, R.; Li, G. Sign Language Recognition Using MediaPipe. In Proceedings of the International Conference on Computer Graphics, Artificial Intelligence, and Data Processing (ICCAID 2022), Guangzhou, China, 23 January 2022; SPIE: Washington, DC, USA, 2022; Volume 12604, pp. 807–813. [Google Scholar]
- Zick, L.A.; Martinelli, D.; Schneider de Oliveira, A.; Cremer Kalempa, V. Teleoperation System for Multiple Robots with Intuitive Hand Recognition Interface. Sci. Rep. 2024, 14, 30230. [Google Scholar] [CrossRef]
- Rhee, W.; Kim, Y.G.; Lee, J.H.; Shim, J.W.; Kim, B.S.; Yoon, D.; Cho, M.; Kim, S. Unconstrained Lightweight Control Interface for Robot-Assisted Minimally Invasive Surgery Using MediaPipe Framework and Head-Mounted Display. Virtual Real. 2024, 28, 114. [Google Scholar] [CrossRef]
- Ballantyne, G.H.; Moll, F. The Da Vinci Telerobotic Surgical System: The Virtual Operative Field and Telepresence Surgery. Surg. Clin. 2003, 83, 1293–1304. [Google Scholar] [CrossRef]
- Santos, B.; Gonçalves, G.; Pinto, V.; Ribeiro, F. Using a Dexterous Robotic Hand for Automotive Painting Quality Inspection. In Proceedings of the Thirteenth International Conference on Intelligent Systems and Applications (INTELLI 2024), Athenas, Greece, 10–14 March 2024; pp. 1–6. [Google Scholar]
- Lin, P.-C.; Lin, F.-C. Research on Interaction between Dancers’ Motion Capture and Robotic Arm. In Proceedings of the 2023 International Conference on Consumer Electronics–Taiwan (ICCE-Taiwan), PingTung, Taiwan, 17 July 2023; pp. 117–118. [Google Scholar]
- Solkar, A.; Dhingra, G.; Chavan, K.; Patil, N. Kathak Dance Movement Recognition and Correction Using Google’s Mediapipe. In Proceedings of the 2023 14th International Conference on Computing Communication and Networking Technologies (ICCCNT), Delhi, India, 6 July 2023; pp. 1–6. [Google Scholar]
- Wang, J.; Zhao, Y. Time Series K-Nearest Neighbors Classifier Based on Fast Dynamic Time Warping. In Proceedings of the 2021 IEEE International Conference on Artificial Intelligence and Computer Applications (ICAICA), Dalian, China, 28 June 2021; pp. 751–754. [Google Scholar]
- Aishwarya, V.; Babu, R.D.; Adithya, S.S.; Jebaraj, A.; Vignesh, G.R.; Veezhinathan, M. Identification of Improper Posture in Female Bharatanatyam Dancers—A Computational Approach. In Proceedings of the 2023 International Conference on Inventive Computation Technologies (ICICT), Lalitpur, Nepal, 26 April 2023; pp. 560–566. [Google Scholar]
- Kishore Kumar, A.V.; Emmadisetty, R.; Chandralekha, M.; Saleem, K. Mediapipe-Powered SVM Model for Real-Time Kuchipudi Mudras Recognition. In Proceedings of the 2024 2nd International Conference on Advancement in Computation & Computer Technologies (InCACCT), Gharuan, India, 2 May 2024; pp. 583–588. [Google Scholar]
- Cortes, C.; Vapnik, V. Support-Vector Networks. Mach. Learn. 1995, 20, 273–297. [Google Scholar] [CrossRef]
- Wang, H.; Zhao, C.; Huang, X.; Zhu, Y.; Qu, C.; Guo, W. Emotion Recognition in Dance: A Novel Approach Using Laban Movement Analysis and Artificial Intelligence. In Digital Human Modeling and Applications in Health, Safety, Ergonomics and Risk Management; Duffy, V.G., Ed.; Springer Nature: Cham, Switzerland, 2024; pp. 189–201. [Google Scholar]
- Mccormick, J.; Pyaraka, J.C. Real Robot Dance Challenge: Exploring Live and Online Dance Challenge Videos for Robot Movement. In Proceedings of the 9th International Conference on Movement and Computing, Utrecht, The Netherlands, 30 May 2024; ACM: Singapore, 2024; pp. 1–4. [Google Scholar]
- Costilla Caballero, S. NAO Robot That Imitates Human Movements Using Mediapipe. In Applied Robotics–Digitale Methoden WS2023; Groth, C., Ed.; Hochschule für Angewandte Wissenschaften Hof: Hof, Germany, 2024; pp. 11–14. [Google Scholar]
- Hong, H.; Costa, I.T.D.C.E.; Tanguy, A.; Kheddar, A.; Chen, C.-Y. A Cross-Temporal Robotic Dance Performance: Dancing with a Humanoid Robot and Artificial Life. In Proceedings of the ISEA 2024—29th International Symposium on Electronic Art, Brisbane, Australia, 30 May–2 June 2024. [Google Scholar]
- Clotet, E.; Martínez, D.; Moreno, J.; Tresanchez, M.; Palacín, J. Assistant Personal Robot (APR): Conception and Application of a Tele-Operated Assisted Living Robot. Sensors 2016, 16, 610. [Google Scholar] [CrossRef]
- Bitriá, R.; Palacín, J.; Rubies, E.; Clotet, E. Experience Embedding a Compact eNose in an Indoor Mobile Delivery Robot for the Early Detection of Gas Leaks. Appl. Sci. 2025, 15, 3430. [Google Scholar] [CrossRef]
- Palacín, J.; Rubies, E.; Clotet, E. The Assistant Personal Robot Project: From the APR-01 to the APR-02 Mobile Robot Prototypes. Designs 2022, 6, 66. [Google Scholar] [CrossRef]
- Robot VS Human VS Alien//Incredible Dance Moves Ver.4 “Dance Battle Compilations”. Available online: https://www.youtube.com/watch?v=0zdVRzjkWMU (accessed on 29 July 2024).
- Zhang, L.; Du, H.; Qin, Z.; Zhao, Y.; Yang, G. Real-Time Optimized Inverse Kinematics of Redundant Robots under Inequality Constraints. Sci. Rep. 2024, 14, 29754. [Google Scholar] [CrossRef] [PubMed]
- Ning, Y.; Sang, L.; Wang, H.; Wang, Q.; Vladareanu, L.; Niu, J. Upper Limb Exoskeleton Rehabilitation Robot Inverse Kinematics Modeling and Solution Method Based on Multi-Objective Optimization. Sci. Rep. 2024, 14, 25476. [Google Scholar] [CrossRef]
- Boukheddimi, M.; Harnack, D.; Kumar, S.; Kumar, R.; Vyas, S.; Arriaga, O.; Kirchner, F. Robot Dance Generation with Music Based Trajectory Optimization. In Proceedings of the 2022 IEEE/RSJ International Conference on Intelligent Robots and Systems (IROS), Kyoto, Japan, 23–27 October 2022; pp. 3069–3076. [Google Scholar]
- Latreche, A.; Kelaiaia, R.; Chemori, A.; Kerboua, A. Reliability and Validity Analysis of MediaPipe-Based Measurement System for Some Human Rehabilitation Motions. Measurement 2023, 214, 112826. [Google Scholar] [CrossRef]
- Dewanto, F.M.; Santoso, H.A.; Shidik, G.F. Purwanto Scoping Review of Sign Language Recognition: An Analysis of MediaPipe Framework and Deep Learning Integration. In Proceedings of the 2024 International Seminar on Application for Technology of Information and Communication (iSemantic), Semarang, Indonesia, 21–22 September 2024; pp. 451–458. [Google Scholar]
- Zhuang, F.; Qi, Z.; Duan, K.; Xi, D.; Zhu, Y.; Zhu, H.; Xiong, H.; He, Q. A Comprehensive Survey on Transfer Learning. Proc. IEEE 2021, 109, 43–76. [Google Scholar] [CrossRef]
- Yoshii, K.; Goto, M.; Okuno, H.G. Drum Sound Recognition for Polyphonic Audio Signals by Adaptation and Matching of Spectrogram Templates with Harmonic Structure Suppression. IEEE Trans. Audio Speech Lang. Process. 2007, 15, 333–345. [Google Scholar] [CrossRef]
- Tsunoo, E.; Ono, N.; Sagayama, S. Rhythm Map: Extraction of Unit Rhythmic Patterns and Analysis of Rhythmic Structure from Music Acoustic Signals. In Proceedings of the 2009 IEEE International Conference on Acoustics, Speech and Signal Processing, Taipei, China, 19–24 April 2009; pp. 185–188. [Google Scholar]

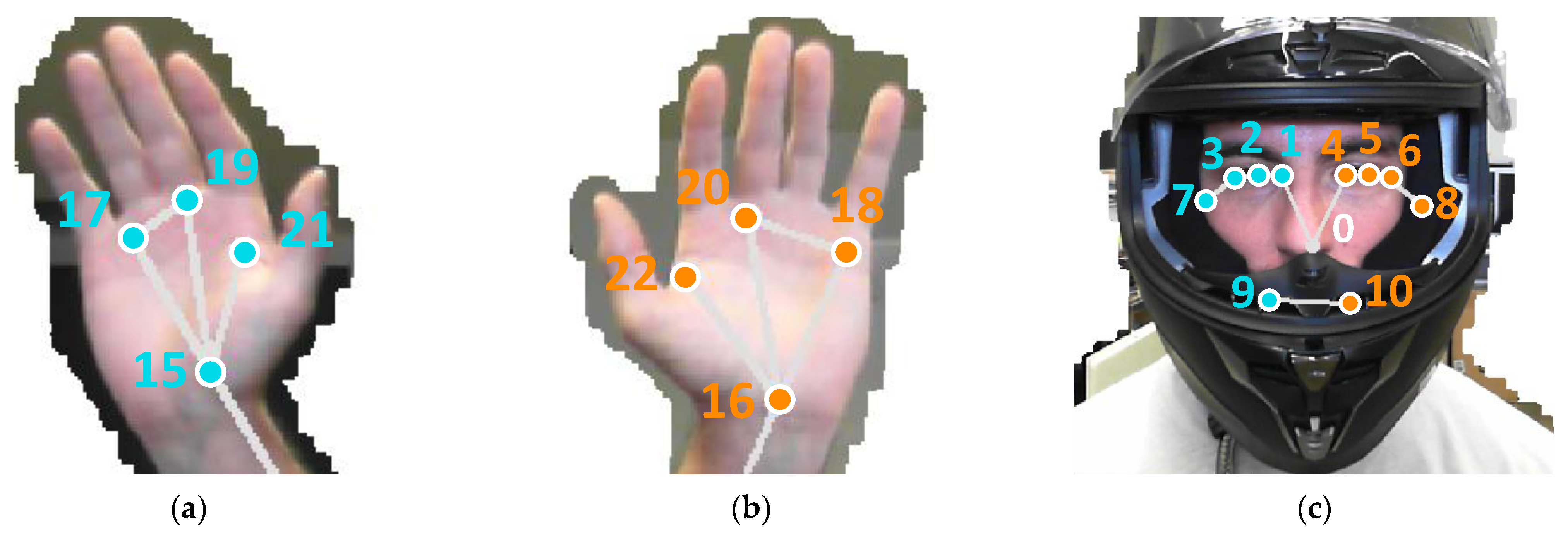







| Head | Body | Left Arm | Right Arm | Left Foot | Right Foot |
|---|---|---|---|---|---|
| 0. Nose | 11. Right Shoulder | 16. Left Wrist | 15. Right Wrist | 28. Left Ankle | 27. Right Ankle |
| 1. Right Eye Inner | 12. Left Shoulder | 18. Pinky Knuckle | 17. Pinky Knuckle | 30. Heel | 29. Heel |
| 2. Right Eye | 13. Right Elbow | 20. Index Knuckle | 19. Index Knuckle | 32. Foot Index | 31. Foot Index |
| 3. Right Eye Outer | 14. Left Elbow | 22. Thumb Knuckle | 21. Thumb Knuckle | ||
| 4. Left Eye Inner | 15. Right Wrist | ||||
| 5. Left Eye | 16. Left Wrist | ||||
| 6. Left Eye Outer | 23. Right Hip | ||||
| 7. Right Ear | 24. Left Hip | ||||
| 8. Left Ear | 25. Right Knee | ||||
| 9. Mouth Right | 26. Left Hip | ||||
| 10. Mouth Left | 27. Right Ankle | ||||
| 28. Left Ankle |
| Link | Position Offset (cm) | Orientation (Rad) | Joint Name | Rotating Axis | ||||
|---|---|---|---|---|---|---|---|---|
| 0 | 0 | 0 | 0 | π | 0 | 0 | Base | None |
| 1 | 0 | 0 | 130 | 0 | 0 | 0 | Neck-shoulder | None |
| 2 | 0 | 20.5 | 0 | 0 | π | 0 | ||
| 3 | −2 | 4 | 0 | 0 | −π | 0 | ||
| 4 | 4 | 1.5 | 0 | 0 | 0 | 0 | ||
| 5 | 0 | 29 | 0 | π | 0 | |||
| 6 | 3.5 | 25 | 0 | 0 | 0 | 0 | Wrist-right | None |
| Link | Position Offset (cm) | Orientation (Rad) | Joint Name | Rotating Axis | ||||
|---|---|---|---|---|---|---|---|---|
| 0 | 0 | 0 | 0 | 0 | 0 | 0 | Base | None |
| 1 | 0 | 0 | 130 | 0 | 0 | 0 | Neck-shoulder | None |
| 2 | 0 | 20.5 | 0 | 0 | 0 | 0 | ||
| 3 | −2 | 4 | 0 | 0 | −π | 0 | ||
| 4 | 4 | 1.5 | 0 | 0 | 0 | 0 | ||
| 5 | 0 | 29 | 0 | 0 | 0 | |||
| 6 | 3.5 | 25 | 0 | 0 | 0 | 0 | Wrist-left | None |
| Parameter | Value |
|---|---|
| Algorithm | Interior-point |
| BarrierParamUpdate | monotone |
| HessianApproximation | bfgs |
| MaxFunctionEvaluations | 3000 |
| MaxIterations | 1000 |
| ObjectiveLimit | −1 × 1020 |
| OptimalityTolerance | 1 × 10−6 |
| ConstraintTolerance | 3 |
| StepTolerance | 1 × 10−3 |
| Model Complexity | Frame | ||||||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 217 | 288 | 289 | 375 | 463 | 481 | 482 | 483 | 535 | 536 | 537 | 538 | 539 | 540 | 541 | 542 | 543 | 291 | Wrong | |
| 0 | ✓ | ✕ | ✕ | ✕ | ✕ | ✕ | ✕ | ✕ | ✕ | ✕ | ✕ | ✕ | ✕ | ✕ | ✕ | ✕ | ✕ | ✕ | 17 |
| 1 | ✕ | ✕ | ✕ | ✓ | ✓ | ✕ | ✕ | ✕ | ✓ | ✓ | ✕ | ✓ | ✓ | ✓ | ✓ | ✓ | ✓ | ✓ | 7 |
| 2 | ✓ | ✕ | ✕ | ✕ | ✓ | ✕ | ✕ | ✓ | ✓ | ✓ | ✓ | ✓ | ✓ | ✓ | ✓ | ✓ | ✕ | ✓ | 6 |
| Model Complexity | Example Frame Sequence | ||||
|---|---|---|---|---|---|
| 480 | 481 | 482 | 483 | 484 | |
| 0 |  |  |  |  |  |
| 1 |  |  |  |  |  |
| 2 |  |  |  |  |  |
| Model Complexity | Frame Time (ms) | Total Time (s) | Total Time Increase | Wrong Frames | ||
|---|---|---|---|---|---|---|
| Min | Max | Mean | ||||
| 0 | 55.5443 | 181.1137 | 63.8294 | 54.0634 | (reference) | 17 |
| 1 | 63.8814 | 176.9082 | 72.0636 | 61.0379 | +12% | 7 |
| 2 | 133.1644 | 478.2957 | 149.7633 | 126.8495 | +133% | 6 |
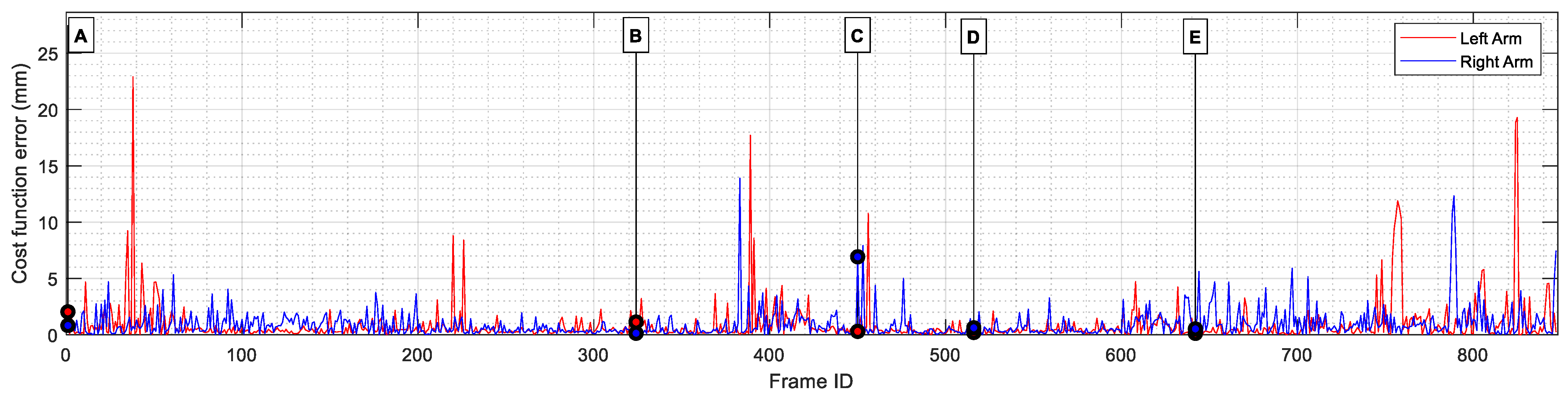
| Side | Elbow Error (mm) | Wrist Error (mm) | Total Error (mm) | ||||||
|---|---|---|---|---|---|---|---|---|---|
| Min | Max | Mean | Min | Max | Mean | Min | Max | Mean | |
| Left | 3.50 × 10−4 | 2.23 | 0.19 | 2.78 × 10−3 | 23.03 | 0.61 | 4.19 × 10−3 | 23.21 | 0.80 |
| Right | 4.19 × 10−3 | 23.21 | 0.23 | 2.70 × 10−3 | 13.91 | 0.60 | 14.86 × 10−3 | 14.23 | 0.83 |
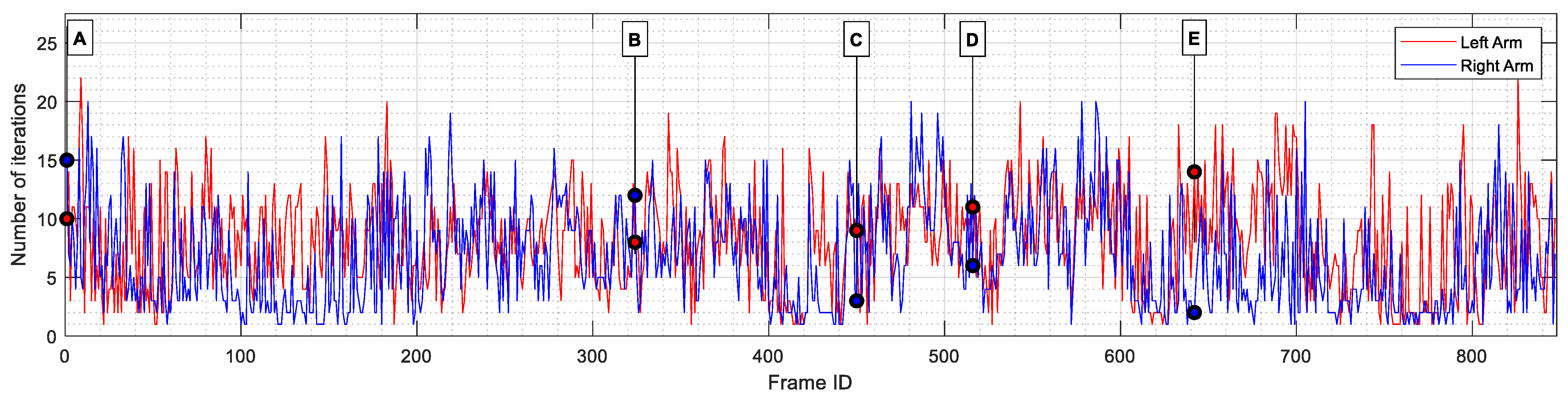
| Side | Number of Iterations | ||
|---|---|---|---|
| Min | Max | Mean | |
| Left | 1 | 22 | 8.16 |
| Right | 1 | 20 | 6.73 |
| Frame (Labels According to Figure 14) | |||||
|---|---|---|---|---|---|
| 1 (A) | 324 (B) | 450 (C) | 516 (D) | 642 (E) | |
| Human dancer |  |  |  |  |  |
| VRM | 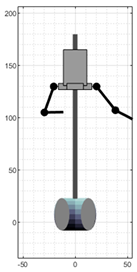 | 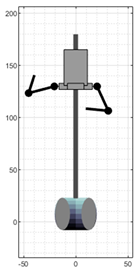 |  | 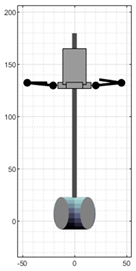 | 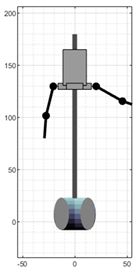 |
| APR robot |  |  |  |  |  |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Clotet, E.; Martínez, D.; Palacín, J. Experiences Using MediaPipe to Make the Arms of a Humanoid Robot Imitate a Video-Recorded Dancer Performing a Robot Dance. Robotics 2025, 14, 153. https://doi.org/10.3390/robotics14110153
Clotet E, Martínez D, Palacín J. Experiences Using MediaPipe to Make the Arms of a Humanoid Robot Imitate a Video-Recorded Dancer Performing a Robot Dance. Robotics. 2025; 14(11):153. https://doi.org/10.3390/robotics14110153
Chicago/Turabian StyleClotet, Eduard, David Martínez, and Jordi Palacín. 2025. "Experiences Using MediaPipe to Make the Arms of a Humanoid Robot Imitate a Video-Recorded Dancer Performing a Robot Dance" Robotics 14, no. 11: 153. https://doi.org/10.3390/robotics14110153
APA StyleClotet, E., Martínez, D., & Palacín, J. (2025). Experiences Using MediaPipe to Make the Arms of a Humanoid Robot Imitate a Video-Recorded Dancer Performing a Robot Dance. Robotics, 14(11), 153. https://doi.org/10.3390/robotics14110153







