Achieving Accurate Turns with LEGO SPIKE Prime Robots

Abstract

LEGO SPIKE Prime robots (The LEGO Group, Billund, Denmark) are widely used in educational settings to foster STEM skills and develop problem-solving competencies. A common task in robotics classes and competitions is moving and controlling wheeled vehicles where precise manoeuvrability, especially turning, is essential for successful navigation. This study aims to provide a comprehensive analysis of the turning mechanisms of LEGO SPIKE Prime robots to facilitate more accurate and effective control. This research combines theoretical analysis with experimental validation. We mathematically derived formulas to relate wheel speeds and steering parameters to the turning radius, and we used regression analysis to refine our models. Additionally, we developed a method where the robot itself collects data on its turning performance, enabling autonomous regression modelling. We found that directly adjusting wheel speeds offers greater precision in turning than using a steering parameter. This finding is supported by the results of the Wilcoxon test, which was performed on a random sample of 30 elements and showed that the effect size is significant (r = 0.7) at a significance level of 0.05. This study provides educators and students with a detailed understanding of turning mechanisms and offers guidance on practical and effective means for achieving the accuracy and consistency needed in educational robotics and robot competitions.

1. Introduction

Rapid technological advances require new learning and teaching methods, and a reform of traditional school curricula, to foster STEM (science, technology, engineering, mathematics) education and the skills required in the 21st century [1,2]. Automation and intelligent devices are becoming increasingly widespread, making robotics and programming essential skills [3]. Educational robotics (ER) is an effective tool for preparing students for the challenges of a technology-driven future. Integrating robotics into education stimulates student interest in science and engineering and motivates them to pursue careers in these fields [4]. Robotics transforms education by providing hands-on and engaging learning experiences beyond traditional classroom methods. Using robots in the classroom positively impacts students’ knowledge, skills, and attitudes [5,6]. ER helps us to understand STEM concepts and is a highly effective tool for promoting STEM awareness, providing opportunities to learn about specific scientific concepts related to mathematics, computer science, and programming [7]. However, robotics is not just about building and coding robots; it also helps in developing fundamental soft skills such as cooperation, creative thinking, and teamwork [8,9,10].

The main tools used in educational robotics are various robotic kits. There are numerous platforms available, ranging from DIY kits to more standardised solutions [11,12,13], and since the COVID-19 pandemic, there has also been considerable interest in virtual robo- tics [14]. When choosing among the various kits available, there are several factors to consider. However, our decision should be primarily based on the educational objective and the learners’ knowledge level [15,16]. Other important considerations include the quality and functionality of the hardware devices (controllers, motors, sensors) in the kit, programming options, expandability, modularity, and, last but not least, purchase costs.

Educational robotic kits are highly versatile tools that can be used in many different ways within educational settings. As tools for STEM learning, they demonstrate the practical application of numerous physical, mechanical, and electronic phenomena; introduce basic programming techniques; and help in developing algorithmic thinking and problem-solving skills. Outside the classroom, these skills can be further developed through participation in robotics clubs, camps, and courses, where students can actively create, experiment, and learn STEM competencies in a playful way [17,18]. The most dedicated and talented students can test their skills in robotics competitions. Participating in robotics competitions not only helps them in developing robotics skills but also positively impacts students’ academic performance, improves communication and cooperation among team members, and boosts their self-confidence [19,20,21,22].

In robotics classes and clubs, students often work with mobile robots, as moving wheeled vehicles or creatures with legs is an exciting and spectacular task that immediately engages most children. Wheel-legged robots are mobile robots designed to move efficiently on flat, smooth surfaces and uneven, complex terrain. These robots have important practical applications, including logistics and warehouse automation, industrial inspection in hazardous environments, and search and rescue in disaster situations. The mechanical design and control systems of wheel-legged robots are highly complex [23,24]. A similarly complex control system is discussed in the case of a snake robot in [25], and another is also discussed in relation to the underwater movement of a beaver-like robot in [26]. Precise robot movement and motion stabilisation are at the forefront of robotics research [27,28].

Robot competitions usually involve mobile robots competing against each other, face-to-face, as in the case of sumo robots, or alone on a track, as in the case of maze navigation [29]. For successful navigation, the programmer must have perfect control of the robot’s movements [30]. The robot’s movements are performed as a series of simple steps, including moving forward or backwards in a straight line, turning, and cornering. The more of these operations the robot performs in succession in autonomous mode, the greater the chance that the robot’s movements will become inaccurate. Students do not tolerate it well when the robot misses the target, so it is important to clarify that educational robots are more like toys than precision instruments. Inaccuracy can be caused by several factors, such as wheels slipping more easily due to excessive speed, low battery, programming errors, or inaccurate initial alignment. Students must be able to identify what causes the robot’s inaccuracy and, if possible, improve its reliability.

Turning is one of the critical operations for mobile robots, and several factors must be considered to ensure its accurate execution. The robot’s mechanical structure primarily determines how it turns, but the degree of the turning arc depends on the robot’s geometry. Generally, we also need to consider the wheels’ size and the track distance. We can control the motors that drive the wheels or the steering mechanism during programming. However, the relationship between the parameters specified in the code and the manner of turning is not always immediately apparent. Therefore, students often use the trial-and-error method, changing the parameters until the robot produces an acceptable result. With enough patience, this strategy will succeed, especially if we only need to find the best setting for one parameter at a time. The process becomes more complicated if multiple parameters must be handled simultaneously or if the values are too diverse. The trial-and-error method is often time-consuming and can even damage the robot. We may find a working solution, but it may not be the best in terms of time or overall efficiency. In contrast, we are more likely to find the optimal solution if we examine a problem using a systematic and scientific approach. From an educational point of view, it is also more useful to thoroughly explore the background of the problem, as students learn a lot during the process, broadening their horizons and developing their creativity. If we solve a given problem in general, our robot can cope more easily with new situations. Noting the effectiveness of the scientific method, students also recognise that it is more useful to study control problems theoretically than to search for one-off solutions using trial and error.

This paper will empirically and theoretically examine the problem of turning mobile robots built from a popular robotic kit. The examination covers programming options, correct parameter settings, and accuracy limits. The experiments presented can be repeated in robotics clubs, and by processing the test results, participants can gain helpful information about controlling their own robots. Thus, this article has two objectives: on the one hand, we would like to explain the exact role of the parameters used for robot turning, and on the other hand, we would like to guide robot trainers in STEM education on this specific topic.

This study is structured as follows: Section 2 presents the LEGO robot models used in this research and describes the research methodology and problems. Section 3 presents the turning control capabilities of LEGO Spike Prime robots. We then discuss the relationships between the parameters used in turning programming and the turning radius, which we derived using mathematical methods. Here we also present the results of experiments conducted with test robots. Section 4 discusses the results achieved, comparing the applicability and limitations of different turning methods. Finally, Section 5 contains some concluding remarks.

2. Materials and Methods

The main findings of this article relate to LEGO SPIKE Prime robots. LEGO SPIKE Prime robotic kits are primarily designed for educational purposes, mainly for high school students. However, the sets can also be adapted for slightly younger learners or university students. Like the other sets in the MINDSTORMS series (NXT, EV3, Robot Inventor), SPIKE Prime kits combine the well-known creativity associated with LEGO bricks with motors, sensors, and a programmable hub, allowing users to design, build, and control robots. Playing with LEGO is a familiar environment for most children, eager to try out programmable versions. LEGO robot kits are becoming increasingly popular in educational institutions and robotics clubs and are being developed to support STEM education and the development of 21st-century skills [31,32]. Using LEGO robots can change attitudes towards science and scientists [33,34] and can also help children with disabilities in terms of their development [35,36].

Since its commercial release in 2020, the SPIKE Prime kit has been chosen by an increasing number of teams to compete in robotics competitions. Participation in major international robotics competitions, such as FLL or WRO, not only helps participants in developing their engineering and scientific knowledge but also strengthens their communication, cooperation, social, and cultural skills [37,38]. A fundamental requirement for successful participation in robot competitions is that the robot must be able to navigate safely on the track and between obstacles, which also includes the precise execution of turning [39].

The values in the code that control the robot’s curved motion are often referred to as steering parameters. In the case of LEGO NXT robots, the relationship between the turning arc and the steering parameters is described in [40,41]. In his books for robotics competition participants, Trobaugh devotes a separate chapter to consistent turning for NXT and EV3 robots [42,43]. In [44], the problem of turning was examined using EV3 robots in Grades 4–7 classrooms, and the mathematical concepts that arose during the process were also discussed. To our knowledge, no one has yet conducted a deeper investigation of the steering parameters of robot models built from the new LEGO SPIKE Prime kits. As SPIKE Prime robots become more widespread and popular in robotics classes and robot competitions, it is time to provide a comprehensive overview of their turning characteristics. The SPIKE Prime programming application’s features allow us to explore turning options that did not exist in previous versions or were more difficult to implement. Recognising a gap identified in previous research, we also provide practical guidance on how the measurement results can be used to explore relationships between parameters that control turning.

In this article, we provide an overview of the curved movements performed by LEGO SPIKE Prime robots. We examine the commands related to robot turning and provide guidance on parameterising them correctly. The tests and experiments introduced in this paper were performed with SPIKE Prime robot models. However, this does not mean that the results cannot be applied to other types of mobile robots. We describe the methodology of the experiments in detail and the conclusions drawn from them so that we can perform the tests with other robots and establish the desired correlations.

2.1. Turning with Differentially Steered Drive System

In the case of wheeled robots, there are basically two main ways to turn. The more complex solution involves the steering drive system, which most cars use, where a separate motor rotates the wheels while another motor controls the turning. Many LEGO Technic models have a steering drive system, and a similar mechanism can also be built from the components of LEGO robot kits. The construction and control of a steering drive system are certainly instructive from a mechanical point of view. However, due to the complexity of these tasks, they are not suitable for those just getting acquainted with robotics. At first, it is advisable to build simpler robots that use a differentially steered drive system for turning. This method of steering changes the speed or direction of rotation of the drive wheels on opposite sides of the vehicle. The basic concept is that the vehicle has two independent drive mechanisms, one on each side, as in tanks or electric wheelchairs [45]. Instead of having a separate steering mechanism that turns the wheels, the robot has two separate motors which drive the wheels independently. In addition to its simplicity, this solution has the advantage that the robot can manoeuvre in very tight spaces, as it can turn around its axis.

2.2. The Test Robots Used in the Experiments

Our tests mainly used the Driving Base (DB) and Advanced Driving Base (ADB) models recommended in LEGO Education SPIKE App v. 3.5.1. For a broader generalisation, we also used a third robot model in the experiment to compare the turning methods. The building instructions for the DB and ADB models can be found in the Build menu of the SPIKE Prime app. The SPIKE PRIME Expansion set is also required to build the advanced model. Both models are equipped with two wheels of the same size on both sides of the robot, driven by separate motors, so they can turn by rotating the wheels at different speeds (differentially steered drive system). One or two roller balls ensure the robot’s balance, which rotate passively as the robot turns. We chose these two models because they are the ones most SPIKE Prime users encounter. On the other hand, the robots’ structures are quite different, so we can also demonstrate the effect of wheel size and wheelbase on turning. We built the two models following the building instructions, with minor additions. Both robot models are equipped with a force sensor at the front, which stops the robot if it encounters an obstacle. We also made minor modifications to the rear of the base models in order to adjust the starting position more accurately when aligning it with the wall of the test table. In addition, we built a simple workbench on which the robots could be placed so that the wheels could rotate freely. This solution allowed us to obtain data on the rotation angle of the wheels using the built-in rotation sensor without having to move the robot on the ground or the table (see Figure 1).

2.3. Methodology

The results obtained during the study of robot turning were achieved theoretically, through mathematical reasoning, and practically, through experiments conducted with the test robots. There are two options for controlling turning for SPIKE Prime robots with a differentially steered drive system. Either we specify the speed of the two wheels directly or specify a steering parameter, and the hub itself distributes the drive force to the wheels as appropriate. In the first case, it is possible to determine what happens when two specific values are entered for the speed of the wheels based purely on mathematical considerations. Using the results of the mathematical derivation, we can also determine the meaning of the steering parameter, assuming that there is a linear relationship between the steering parameter and the ratio of wheel speeds. We tested this assumption experimentally using one of the test robots. Similarly, we empirically examined the steering parameters’ behaviour to verify the theoretical results. We recommend that students and teachers of this topic consider the theoretical model only as a starting point and determine the specific relationships applicable to their robots through experimentation. To this end, we provide an example in the next section where the robot collects and processes the experimental results by calculating the coefficients of the proposed regression model.

2.4. Research Problems

LEGO SPIKE Prime robots using a differentially steered drive system can control turning in two basic ways. One option for turning is to directly specify the speed of the wheels, while the other method involves specifying a steering parameter. In both cases, we investigate two problems:

(P1)

How do the parameters (wheel speed or steering value) affect the turning radius?

(P2)

How should the parameters be specified to achieve a given turning radius?

In the next section, we will examine the types of possible curved movements and the tools available to control turning when programming SPIKE Prime robots. Using theoretical and experimental approaches, we will derive formulas that give the relationships between the turning radius and the parameters of the code controlling the robot.

3. Results

This section introduces the SPIKE programming application’s control options for turning on SPIKE robots. Based on a mathematical analysis of the movement and experiments with test robots, we provide the basic relationships between the steering parameters and the radius of the turning arc.

3.1. Curved Motion with LEGO SPIKE Prime Robots

When students perform activities with mobile robots, they must first learn how to control the robots’ movements. This includes moving forward and backwards in a straight line or curved path. Later, after becoming familiar with the sensors, they can move on to line following, obstacle avoidance, and other more complex forms of movement. Turning and moving along curved paths often pose a challenge for beginners, as the relationship between the parameters in the code and robot movement is not always easy to understand. Compared to straight movement, the situation is further complicated because the robot’s geometry greatly influences its turning behaviour, so values that worked well for one model will not necessarily work for another robot. Of course, the main problem is determining which mechanism we want to use to solve the turning problem. In most cases, the robot’s wheels are driven by separate motors, allowing the wheels to rotate at different speeds, i.e., to move along a non-linear path.

3.2. SPIKE Prime Programming App

LEGO SPIKE Prime robots can be programmed using the LEGO SPIKE Prime app, which offers two main programming modes: Word Blocks, a Scratch-based programming environment, and MicroPython. The first option is best suited for beginners in programming, while Python is recommended for advanced users who require greater control and flexibility. Word Blocks users work on a drag-and-drop interface with colourful blocks. Each block represents a command or action, and the blocks are organised into different categories, such as “Motors,” “Sound,” “Events,” and “Sensors”. These blocks must be parameterised and linked together in sequences, loops, and conditional statements to control the robot’s behaviour.

In the SPIKE Prime programming app, three categories contain blocks to directly control the robot’s movement: Motors, Movement, and More Movement. The blocks in the Motors group provide the independent control of the motors. For example, if a single motor drives a lifting mechanism, the Motors group contains blocks that can be used to control lifting and lowering. If a vehicle’s wheels are driven by independent motors, we can control the robot’s movement by controlling these motors in parallel, but we must be very careful to ensure that the motors start and stop at the same time. In this case, it is simpler and more convenient to use one of the Movement blocks, which allows for the synchronised operation of two motors. For example, the Move for Duration block moves the robot forward or backwards for a specified distance or time, at a speed adjusted with the Set Movement Speed block.

The Movement group also contains two blocks that cause the robot to turn: Move with Steering for Duration and Start Moving with Steering. The difference between the two options is that the effect of the first block lasts for a particular duration, while the second lasts forever, so in this case, we need to provide a stopping criterion, which is usually the fulfilment of a condition detected by a sensor. For both blocks, a steering parameter must be specified, which determines the degree of turning by controlling the ratio between the speeds of the two motors. Unfortunately, this relationship is not documented, so we can only find the parameter that leads to the desired turning radius through experimentation and experience. First, it is worth studying the third block, which can be used for turning, to gain a thorough understanding of the steering parameter. It is the Start Moving at Speed block, which can be found in the More Movement category.

3.3. The Start Moving at Speed Block

In the LEGO Education SPIKE programming app, the apparent option to choose to control the differentially steered drive system is the Start Moving at Speed block. It is a synchronised block that controls the two motors simultaneously. Two values must be specified, one for the speed of the left motor and the other for the right motor. Both values must be integers in the range [−100,100]. Let us assume that the first parameter controls the power of the left motor, while the second parameter controls the power of the right motor. The order depends on how we initially set the motors with the Set Movement Motors block. The Start Moving at Speed block does not have any other parameters; therefore, the code must ensure in some other way that the process stops when a specific condition is met. The stop criterion may be the occurrence of an event detected by one of the sensors or the expiry of the time set on the timer.

3.4. Types of Curved Movement

Next, we will examine the robot’s movement when we enter different parameter pairs in the Start Moving at Speed block. Let us denote the two speed values by $s_{left}$ and $s_{right}$.

• $s_{left}=s_{right}$: If the motors have the same power and we enter two identical numbers as the speed values, then both wheels will travel the same distance in a given time so that the robot will move straight ahead. The direction of movement will be forward if both parameters are positive and backwards if we enter two identical negative numbers.
• $s_{left}=-s_{right}$: If one wheel rotates forward at the same speed as the other wheel rotates backwards, the robot performs a spin turn, i.e., it turns around its axis while remaining in place.
• $s_{left}=0$ or $s_{right}=0$: If one wheel is halted and only the other wheel is turning, the robot will turn around using the stationary wheel as its pivot point. This type of turn is often referred to as a pivot turn.
• When $s_{left}$ and $s_{right}$ have the same sign, are not 0, and are different from each other, the robot turns in a curved path towards the slower wheel. This is the case of a smooth turn, which allows the robot to make wider turns. The robot rotates around a pivot point outside of the robot.
• When $s_{left}$ and $s_{right}$ are different nonzero numbers with different signs, the robot performs a tighter turn, where the centre of rotation is between the drive wheels. We will call this point turning.

3.5. Determining the Turning Radius

Except for some special parameter pairs, we do not know precisely at what radius the robot will turn if we enter two values in the Start Moving at Speed block. We show that this turning radius can be determined if we know the track, i.e., the distance between the wheels. Suppose that the robot performs a right turn, where the centre of rotation is denoted by P, and the distances between P and the wheels are $r_{left}$ and $r_{right}$, respectively. The distance between the centrelines of the two wheels is called the track width or simply the track of the robot and is denoted by t in Figure 2.

After $\Delta t$ time, the robot performed an arc of a $\Delta \alpha$ angle. If this angle is measured in radians, the lengths of the arcs traversed by the wheels can be expressed by $r_{left}\Delta \alpha$ and $r_{right}\Delta \alpha$. On the other hand, in $\Delta t$ time, the left wheel rotates $s_{left}\Delta t$ degrees and travels the distance ${\displaystyle \frac{s_{left}\Delta t}{360}}·K$, where K denotes the perimeter of the wheel. Similarly, the distance travelled by the right wheel is ${\displaystyle \frac{s_{right}\Delta t}{360}}·K$. We obtained the following equations:

$$\begin{array}{cc}\hfill r_{left}\Delta \alpha & ={\displaystyle \frac{s_{left}\Delta t}{360}}·K\hfill \end{array}$$

(1)

$$\begin{array}{cc}\hfill r_{right}\Delta \alpha & ={\displaystyle \frac{s_{right}\Delta t}{360}}·K.\hfill \end{array}$$

(2)

Dividing (1) by (2), we have

$${\displaystyle \frac{r_{left}}{r_{right}}}={\displaystyle \frac{s_{left}}{s_{right}}}=q.$$

(3)

In the case of point turns, the ratio q is considered to be negative, as the wheels are rotated in opposite directions, which can be achieved by setting the speed parameters to values of opposite signs. This means that in this case, the sign of $r_{right}$ can be considered negative. This agreement is useful because it allows us to describe the track distance t for smooth and point turns using the same formula: $t=r_{left}-r_{right}$. This implies

$$q={\displaystyle \frac{r_{left}}{r_{right}}}={\displaystyle \frac{r_{right}+t}{r_{right}}}=1+{\displaystyle \frac{t}{r_{right}}}⟹q-1={\displaystyle \frac{t}{r_{right}}}⟹r_{right}={\displaystyle \frac{t}{q-1}}.$$

(4)

Similarly,

$${\displaystyle \frac{1}{q}}={\displaystyle \frac{r_{right}}{r_{left}}}={\displaystyle \frac{r_{left}-t}{r_{left}}}=1-{\displaystyle \frac{t}{r_{left}}}⟹{\displaystyle \frac{t}{r_{left}}}=1-{\displaystyle \frac{1}{q}}={\displaystyle \frac{q-1}{q}}⟹r_{left}={\displaystyle \frac{tq}{q-1}}.$$

(5)

So, the radius of the circle that the robot’s hypothetical centre travels around is

$$r_{centre}={\displaystyle \frac{r_{left}+r_{right}}{2}}={\displaystyle \frac{t(q+1)}{2(q-1)}}.$$

(6)

This means that the turning radius of the robot is independent of the wheel size; it depends only on the track width and the ratio of the speed of the wheels. Substituting these values into Equation (6), we can easily calculate the radius of the circle along which the centre of the robot moves. However, if we want the robot to stop after completing a full circle or a specific section of the arc, we also need to know the size of the robot’s wheels. This problem usually arises when the robot has to move along a predetermined circular path. Let us assume that the robot faces an obstacle that it must avoid and return to its starting point. To conduct this, the robot must describe a complete circle with a sufficiently large radius. First of all, we need the inverse of Formula (6), where q is expressed by $r_{centre}$:

$$q={\displaystyle \frac{2r_{centre}+t}{2r_{centre}-t}}.$$

(7)

For example, if we want the centre of the Driving Base to make a complete circle with a radius of 20, then we first compute the ratio of the wheel’s speed:

$$q={\displaystyle \frac{40+11.2}{40-11.2}}={\displaystyle \frac{51.2}{28.8}}=1.7778,$$

(8)

where we used the track width value $t=11.2$. We need to find two integers between 0 and 100 whose quotient is approximately equal to the fraction 1.7778. Fortunately, the fraction is exactly ${\displaystyle \frac{16}{9}}$, and we have six choices for specifying the speeds, as shown in

Table 1. Options for specifying the speed pairs required to turn the Driving Base in a 20 cm radius arc ($s_{left}$: speed of the left motor; $s_{right}$: speed of the right motor.)

$s_{left}$	16	32	48	64	80	96
$s_{right}$	9	18	27	36	45	54

.

If the hypothetical centre of the robot describes a complete circle with a radius of 20 cm, then its inner (right) wheel describes a circle with a radius of $20-{\displaystyle \frac{t}{2}}=14.4$ cm. The distance travelled by the inner wheel is $14.4\pi$ cm. The diameter of the wheel is 5.6 cm, and its circumference is $5.6\pi$ cm, so ${\displaystyle \frac{14.4\pi }{5.6\pi }}={\displaystyle \frac{18}{7}}$ revolutions are required to complete the circle. This means that the robot must be stopped when the rotation angle measured on the right wheel reaches $360·{\displaystyle \frac{18}{7}}\approx 926$ degrees.

3.6. Steering Parameter Analysis

After exploring the relationship between the speed parameters specified in the Start Moving at Speed block and the robot’s turning radius, we can examine the steering parameter we use in the Movement group blocks. The Move with Steering for Duration and Start Moving with Steering blocks allow an integer between −100 and 100 to be used as a steering parameter. If the steering value is 0, the robot moves straight ahead; if the value is positive, it turns right; otherwise it turns left. In addition to the value 0, there are four more values when we know exactly how the robot works: a steering value of 50 or −50 results in a pivot turn, while a value of 100 or −100 causes the robot to perform a spin turn. For the sake of simplicity, we will only examine the case of turning right, since the same thing happens when turning left, only the roles of the motors are reversed. If we have previously set the speed of the motors in the program (if not, the default 50% applies), then when turning right, the left motor will rotate at this speed. The steering parameter is responsible for controlling the speed of the other motor. There are three cases where we know the relationship between the speeds of the motors, as shown in

Table 2. The relationship between the speed of the motors at particular steering values ($s_{left}$: speed of the left motor; $s_{right}$: speed of the right motor).

Steering Parameter	0	50	100
	$s_{right}=s_{left}$	$s_{right}=0$	$s_{right}=-s_{left}$

.

The problem now concerns how the speed of the right motor changes relative to the left motor at intermediate values. We assumed that it changes linearly. To investigate this, we conducted the following experiment. We started the robot 11 times in a row, increasing the steering parameter value by 10 units each time, with the starting value set to 0. The initial motor speed was set to the default 50%, and the left motor operated at this power throughout. The speed of the motors was measured using the built-in rotation sensor, which indicates how many degrees the motor rotated from start to stop. The rotation sensor of the motor has a resolution of 360 counts per revolution and an accuracy of less than or equal to $\pm 3$ degrees. Since the robot operated for 1 s in each case, the angle rotation obtained is equal to the angular velocity value. The results are summarised in

Table 3. The proportion of the motor speeds as a function of the steering parameter at movement speed 50%. Negative numbers indicate that the direction of rotation is the opposite.

Steering Parameter	${\mathit{s}}_{\mathit{left}}$$\left(\frac{\mathbf{degree}}{\mathbf{sec}}\right)$	${\mathit{s}}_{\mathit{right}}$$\left(\frac{\mathbf{degree}}{\mathbf{sec}}\right)$	${\displaystyle \frac{{\mathit{s}}_{\mathit{right}}}{{\mathit{s}}_{\mathit{left}}}}$
0	447	447	1
10	451	357	0.7916
20	456	271	0.5943
30	459	181	0.3943
40	457	90	0.1969
50	459	0	0
60	459	−89	−0.1939
70	459	−180	−0.3922
80	453	−267	−0.5894
90	452	−358	−0.7920
100	447	−446	−0.9978

.

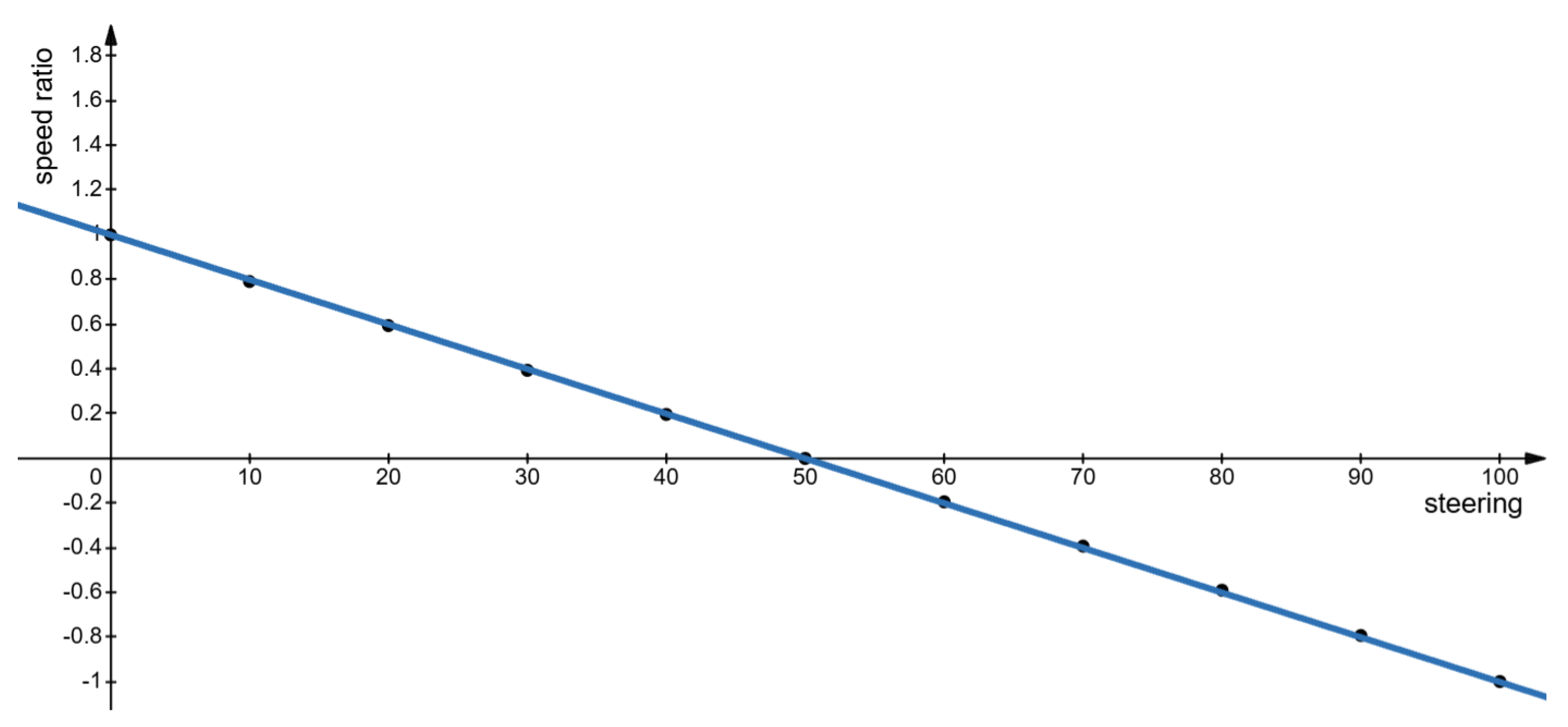
We use a linear regression model to describe the relationship between the speed ratio and steering parameter. The equation of the best-fitting linear function is as follows:

$$y=-0.0199x+0.9937.$$

(9)

For the sake of simplicity, we will use Equation (9) with rounded coefficients in the form

$${\displaystyle \frac{s_{right}}{s_{left}}}=-0.02x+1,$$

(10)

where x denotes the steering parameter. The coefficient of determination for function (10) is $R^2=0.9999$, which indicates a close linear relationship between the data. Figure 3 shows the linear function (10).

This relationship and the previous result regarding the speed ratio and the turning radius help us to understand the steering parameter. Indeed, from Equation (3) we have

$${\displaystyle \frac{s_{right}}{s_{left}}}={\displaystyle \frac{1}{q}}.$$

(11)

Introducing the variable ${\displaystyle \frac{1}{q}}$ into Equation (6) and using (10), we obtain

$$r_{centre}={\displaystyle \frac{t(1+\frac{1}{q})}{2(1-\frac{1}{q})}}={\displaystyle \frac{t(1-0.02x+1)}{2(1-(-0.02x+1\left)\right)}}={\displaystyle \frac{t(2-0.02x)}{0.04x}}={\displaystyle \frac{50t}{x}}-{\displaystyle \frac{t}{2}}.$$

(12)

This means that the turning radius can be determined as the product of the track width and a rational function of the steering parameter. Taking into account that the track value is 11.2 for the Driving Base and 14.4 for the Advanced Driving Base, we obtain the following theoretical functions for our test robots:

$$r_{DB}\left(x\right)={\displaystyle \frac{560}{x}}-5.6\mathrm{and}{r}_{ADB}\left(x\right)={\displaystyle \frac{770}{x}}-7.7,$$

(13)

where $r_{DB}\left(x\right)$ gives the radius of the arc along which the centre of the Driving Base robot moves when the steering parameter is x, and $r_{ADB}\left(x\right)$ indicates the same for the Advanced Driving Base.

3.7. Experimental Verification of Formula (12)

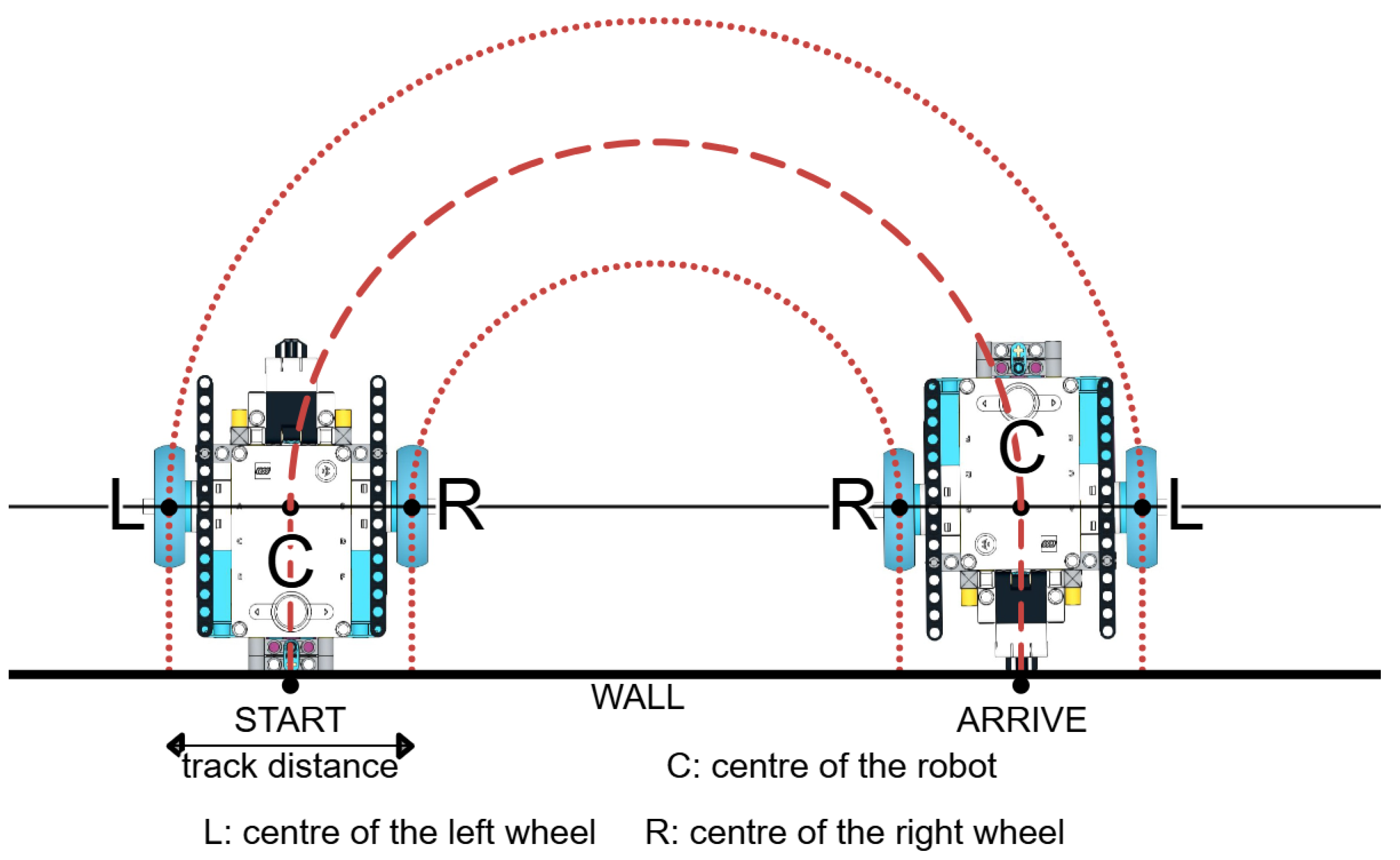
We experimented to examine the steering parameters using our test robots. We tested the robot models on an official FLL competition table. Its wall-to-wall playing area dimensions are approximately 93 inches × 45 inches (2362 mm × 1143 mm), with border walls. The table surface is painted plywood, providing a smooth but non-slip surface. The coefficient of friction is approximately 0.35. During the experiments, we also had to ensure the wheels were clean, as dusty, dirty wheels make the robot’s movement unpredictable. The robots started by aligning with the wall of the table and stopped automatically after half a lap. To conduct this, we fitted a force sensor to the front of the robots, which pushes in and stops the robot when it reaches the wall, so we could measure the diameter of the arc the robots have moved around. This method is mainly suitable for measuring the arc of smooth turns, because in the case of tighter turns, the force sensor cannot precisely detect when the turn is finished. This is why the robots were tested only with steering values not greater than 50.

The experiments were always carried out under identical conditions and with fully charged batteries. The robots started from the same position in each round, aligned their back to the wall of the table (Figure 4). In the first round, we started the robots with a steering value of 50, then reduced the parameter value by 5 until it reached 10. The last test round, corresponding to a steering value of 5, was performed on the floor because the table was too small to complete a semicircle. After the force sensor stopped the robots, we measured the distance between the START and ARRIVE points (see Figure 4). The measurement was performed using a standard Class II measuring tape, i.e., the maximum permissible error is 0.5 mm per 1000 mm. Half of the measured values are listed in

Table 4. Steering parameters and the turning radii of the test robots: $r_{DB}=$ turning radius of the Driving Base model; $r_{ADB}=$ turning radius of the Advanced Driving Base model.

Steering Value	50	45	40	35	30	25	20	15	10	5
$r_{DB}$ (cm)	5.4	6.6	8.3	10.4	13.1	16.9	22.5	31.7	50.9	107.1
$r_{ADB}$ (cm)	7	8.9	10.8	13.4	16.8	21.4	29.2	40.9	64.7	138.2

as the turning radii of the Driving Base models.

We fit a regression model representing the relationship between the steering values and the turning radii of the robots. Using our previous observation that the turning radius is theoretically a rational function of the steering parameter, we consider a rational regression function in the form

$$r\left(x\right)={\displaystyle \frac{a}{x}}+b,$$

(14)

where a and b are real parameters. We use the least squares method to find the best-fitting function by minimising the sum of the squared differences between the given data and the predicted values [46]. The coefficients a and b can be calculated from the normal equation

$$A^{T}A\left[\begin{array}{c}a\\ b\end{array}\right]=A^{T}y,$$

(15)

where the vector y contains the measured data, and the matrix A consists of two columns, containing the coefficients of a and b in Formula (14) evaluated for the steering values. For the Driving Base,

$$\begin{array}{cc}\hfill y^T& =\left[\begin{array}{cccccccccc}5.4& 6.6& 8.3& 10.4& 13.1& 16.9& 22.5& 31.7& 50.9& 107.1\end{array}\right]\hfill \end{array}$$

(16)

$$\begin{array}{cc}\hfill A^T& =\left[\begin{array}{cccccccccc}{\displaystyle \frac{1}{50}}& {\displaystyle \frac{1}{45}}& {\displaystyle \frac{1}{40}}& {\displaystyle \frac{1}{35}}& {\displaystyle \frac{1}{30}}& {\displaystyle \frac{1}{25}}& {\displaystyle \frac{1}{20}}& {\displaystyle \frac{1}{15}}& {\displaystyle \frac{1}{10}}& {\displaystyle \frac{1}{5}}\\ 1& 1& 1& 1& 1& 1& 1& 1& 1& 1\end{array}\right].\hfill \end{array}$$

After calculating the elements of the products $A^{T}A$ and $A^{T}y$, we obtain the normal equation

$$\left[\begin{array}{cc}0.0620& 0.5858\\ 0.5858& 10.0000\end{array}\right]\left[\begin{array}{c}a\\ b\end{array}\right]=\left[\begin{array}{c}31.6203\\ 272.9000\end{array}\right].$$

(17)

Its solution is $a=564.9083$ and $b=-5.8020$, implying the rational regression function for the Driving Base model:

$$r_{DB}^{regr}\left(x\right)={\displaystyle \frac{564.9083}{x}}-5.8020.$$

(18)

The theoretical function describing the relationship between the steering parameter and the turning radius is given in Equation (13). Its coefficients are 560 and −5.6, which do not differ significantly from the coefficients of the regression function. Indeed, if we evaluate the regression and theoretical functions for all integers between 5 and 50, the maximum deviation is 0.78, which occurred at $x=5$. This means that the theoretical function

$$r_{DB}\left(x\right)={\displaystyle \frac{560}{x}}-5.6$$

(19)

gives an acceptable estimate of the turning radius of the Driving Base model.

Using the second data series in Table 4, we also calculated the regression function for the Advanced Driving Base, with the following result:

$$r_{ADB}^{regr}\left(x\right)={\displaystyle \frac{727.1603}{x}}-7.4666.$$

(20)

In this case, the theoretical function given in Equation (13) is not very good at estimating the turning radius, at least for small steering parameters. For example, when evaluating the theoretical function $r_{ADB}\left(x\right)$ and the regression function $r_{ADB}^{regr}\left(x\right)$ for x = 5, the difference is more than 8 cm. In the case of our Advanced Driving Base model, it is therefore advisable to use the regression function based on measurement data to estimate the turning radius. This observation is supported by the method presented in the following subsection, in which the robot provides measurement results and processes this data.

3.8. An Alternative Way of Creating a Regression Model for the Steering Parameter

In the experiment detailed in the previous section, we measured the diameters of the semicircles travelled by the robots and used these data to create a regression model. Human intervention (and thus measurement errors caused by measuring tapes) can be eliminated from the measurement process by entrusting the calculation of the turning radius to the robot. Using the built-in rotation sensor, the robot measures the angular rotations of the motors. These data give information about the distance travelled by the wheels, from which we can calculate the radius of the turning arc. To collect data, we repeated the experiment described in Section 3.7 with both test robots. The robots started with different steering parameters, and after completing a semicircle, the force sensor stopped them. Instead of physically measuring the distances between the starting and arrival points, the robot computed the average of the angular rotations measured on the left and right motors. This number shows how many degrees a fictitious wheel mounted in the centre of the robot would rotate. This wheel can be considered the same size as the other two real wheels, so we can use its circumference and the number of turns it has made to determine how far the robot’s centre has travelled. This distance is equal to the circumference of the semicircle created by the robot, so we can also calculate its radius using the formula of the circle’s perimeter.

To formalise the calculation, we introduce the variables $d_{left}$ and $d_{right}$, representing the angular rotations of each wheel in degrees. In addition, we denote the diameter of the wheels by $d_w$ and let r be the radius of the semicircle along which the centre of the robot moves. The distance travelled by the fictitious wheel in the robot’s centre equals the product of its revolutions and circumference, and this product gives the perimeter of the semicircle. This means

$${\displaystyle \frac{\frac{1}{2}\left(d_{left}+d_{right}\right)}{360}}·d_w\pi ={\displaystyle \frac{2r\pi }{2}}$$

(21)

implying

$$r={\displaystyle \frac{d_w}{720}}\left(d_{left}+d_{d_{right}}\right).$$

(22)

The values $d_{left}$ and $d_{right}$ are provided by the rotation sensors of the motors, so after specifying the wheel size $d_w$, the turning radius r can be determined. The calculations required in (22) can be carried out in the SPIKE Prime app; moreover, the results of different launches can be stored in a list. So, we can create a program that automatically provides the desired data with minimal human interaction. The robots have to start from the START position of the competition table with a given steering value, and after it stops, the robot calculates the turning radius. Then the process is repeated with a different steering value. It is worth organising a loop, where the setting of the steering values and the evaluations of the results are automated. We need time after each step to move the robot to the START position again. It is recommended that this be conducted by hand because precise alignment is needed for every launch.

Moreover, the coefficients of the regression model can also be obtained by working only with operations available in the app. Indeed, suppose that we design an experiment with the same ten steering parameters as in Section 3.7. After completing the ten launches, the computed turning radii are saved in a list y. To calculate the coefficients a and b of the rational regression function $r\left(x\right)={\displaystyle \frac{a}{x}}+b$, we need to solve the normal Equation (15) using the vector y. Note that the left-hand side of the normal equation contains the same coefficients as in (17), because the product $A^{T}A$ depends only on the choice of the input steering values. On the right-hand side of the normal equation, we have to compute the two components of the vector $A^{T}y$, which can be easily solved with two summing variables in a loop. If we know the six coefficients of a two-variable linear system consisting of two equations, the unknowns can be determined using simple algebraic operations in the SPIKE Prime application.

Figure 5 shows the result of such a program for our Advanced Driving Base model. The elements of the list y are the turning radii calculated by the robot for the steering parameters 50, 45, …, 5. These values are roughly equivalent to our measurement data in the second row of Table 4. Using this data, the robot solved the normal equation, i.e., it determined the regression coefficients, producing the rational regression function

$$r_{ADB}^{regr\ast }\left(x\right)={\displaystyle \frac{719.6679}{x}}-7.519233.$$

(23)

In terms of its coefficients, this function is closer to the $r_{ADB}^{regr}\left(x\right)$ function derived from the measurement data than to the theoretical function $r_{ADB}\left(x\right)$ given in Equation (13), confirming our assumption that the theoretical model is less accurate in this case. Thus, if we are looking for a function with simple coefficients that fits the measurement data well, the following could be a good choice:

$$r\left(x\right)={\displaystyle \frac{725}{x}}-7.5.$$

(24)

The maximum deviation of the $r\left(x\right)$ function from the $r_{ADB}^{regr}\left(x\right)$ function in the interval [5, 50] is 0.4655 cm, while that from the $r_{ADB}^{regr\ast }\left(x\right)$ function is 1.0857 cm. Since it is close to both regression functions based on measurement data, the function $r\left(x\right)$ can be reliably used to predict the turning radius of the Advanced Driving Base robot.

3.9. Statistical Analysis of Turning Methods

We discussed two basic methods for turning: turning by setting the wheel speeds and turning using the steering parameter. In this section, we test and compare the accuracy of the turning methods. We used a new robot model to verify the applicability of the methods on a model with a configuration different from that of previous test models and to provide guidance on using these methods to robotics teachers and students. We used the competition robot (without attachments) shown in Figure 6 during the tests.

The team competing with this robot won the robot game award in the Hungarian National Finals of the 2023/2024 FLL season. The robot has two normal-sized wheels driven by medium motors, rests on a caster ball at the rear, and has a track distance shorter than that of the Driving Base models. For the tests, we mounted a force sensor on the front of the robot so that it would stop on the test table after completing a semicircle.

First, we generated the target turning radii of 30 random integers ranging from 0 to 100 cm. These radii are listed in the first column of

Table 5. The experimental results for statistical analysis. The first column labelled “Radius” contains the target turning radii. $s_{left}$ and $s_{right}$ are the values set in the wheel speed method, $r_1$ is the measured result with these settings, and $d_1$ is the deviation from the target value. The column labelled “Steering” contains the setting required for the steering parameter method, $r_2$ is the measured result with this setting, and $d_2$ is the deviation from the target value.

Radius	${\mathit{s}}_{\mathit{left}}$	${\mathit{s}}_{\mathit{right}}$	${\mathit{r}}_1$	${\mathit{d}}_1$	Steering	${\mathit{r}}_2$	${\mathit{d}}_2$
8	80	20	8.4	0.4	38	7.9	0.1
9	69	21	9	0	35	9.2	0.2
12	56	24	12.3	0.3	29	12.1	0.1
15	66	34	15.2	0.2	25	14.6	0.4
17	54	30	16.9	0.1	22	17.3	0.3
18	57	33	18.3	0.3	21	18.3	0.3
21	43	27	21.1	0.1	19	20.9	0.1
23	46	30	23.2	0.2	18	21.9	1.1
26	77	53	26.1	0.1	16	25.4	0.6
27	53	37	27.3	0.3	15	27.3	0.3
28	41	29	28.1	0.1	15	27.3	0.7
33	63	47	33.5	0.5	13	32.5	0.5
35	40	30	34.2	0.8	12	35.3	0.3
41	38	30	41.3	0.3	11	39.1	1.9
43	50	40	43.8	0.8	10	43.7	0.7
46	37	30	47	1.0	10	43.7	2.3
55	37	31	54.6	0.4	8	55.8	0.8
58	59	50	59.6	1.6	8	55.8	2.2
60	54	46	60.5	0.5	8	55.8	4.2
65	58	50	65.5	0.5	7	63.2	1.8
68	45	39	67.3	0.7	7	63.2	4.8
70	47	41	70.5	0.5	7	63.2	6.8
73	48	42	72.1	0.9	6	75.5	2.5
76	50	44	75.4	0.6	6	75.5	0.5
78	69	61	78.8	0.8	6	75.5	2.5
79	43	38	79.1	0.1	6	75.5	3.5
85	47	42	86.8	1.8	5	92.9	7.9
88	58	52	88.3	0.3	5	92.9	4.9
91	60	54	91.5	0.5	5	92.9	1.9
94	62	56	94.7	0.7	5	92.9	1.1

. The values were limited to 100 cm to fit the size of the competition table where the experiments were conducted. In the case of the wheel speed method, for each radius, a pair of reasonable speeds was selected so that Equation (7) is fulfilled. Let us look at two examples of this process. For the radius $r=18$ cm, the speed proportion should be $q={\displaystyle \frac{2·18+9.6}{2·18-9.6}}={\displaystyle \frac{43}{27}}$ (the track distance is $t=9.6$ cm for the competition robot). Choosing wheel speeds 43 and 27, the robot is expected to turn in a radius of 18 cm. For the radius of 85 cm, the fraction $q={\displaystyle \frac{2·85+9.6}{2·85-9.6}}={\displaystyle \frac{449}{401}}$ is not suitable to directly provide the speed values. This is why we must seek a fraction with approximately the same value as ${\displaystyle \frac{449}{401}}$ with allowed numbers as the numerator and denominator. We chose ${\displaystyle \frac{47}{42}}=1.1190$, because it only slightly differs from ${\displaystyle \frac{449}{401}}=1.1197$. The calculated speed pairs are listed in the second and third columns of Table 5. After determining a suitable pair of speeds for each radius, we experimented. The robot started from the start position on the competition table with the actual speed settings, and after completing a semicircle, its force sensor stopped it. Then we measured the diameter of the semicircle, and half of it was written in column $r_1$ of the table. The expected and measured radius deviations are shown in column $d_1$.

The steering parameter method required some precalculations because we first had to create a suitable regression function that described the relationship between the steering parameter and the turning radius. We repeated the experiment described in Section 3.7 three times with the competition robot, obtaining three measured radii for the ten steering parameters 50, 45, …, 5. To increase the stability of the data, we used the average of the measured values and listed them in

Table 6. Steering parameters and the average turning radii for the competition robot.

Steering value	50	45	40	35	30	25	20	15	10	5
$r_{average}$ (cm)	4.57	6.08	7.35	9.07	11.40	14.72	19.47	27.40	43.92	92.93

.

The regression function was searched in the form $y={\displaystyle \frac{a}{x}}+b$, and the calculated coefficients are $a=489.20$ and $b=-4.97$. For simplicity, we rounded off these factors and used the function and its inverse in the following form:

$$r\left(s\right)={\displaystyle \frac{490}{s}}-5\mathrm{and}s\left(r\right)={\displaystyle \frac{490}{r+5}}.$$

(25)

Note that the theoretical regression function given in (6) would be $r\left(s\right)={\displaystyle \frac{480}{s}}-4.8$. The inverse regression function in (25) provides us with the appropriate steering parameter to adjust for a given turning radius. For example, for the first radius $r=8$, we compute $s={\displaystyle \frac{490}{8+5}}=37.69$ and set the closest integer (38) as a steering parameter. The calculated values are listed in the Steering column of Table 5. The next column, $r_2$, gives the turning radii measured on the test table after the robot completed the semicircle with the actual steering parameter. Finally, the last column of the table contains the expected and measured radius deviations ($d_2$). We determine the methods’ accuracy by statistically comparing the deviations $d_1$ and $d_2$.

The statistical calculator DATAtab (DATAtab e.U., Graz, Austria) was used for data analysis. The descriptive statistics are presented in

Table 7. Descriptive statistics for $d_1$ and $d_2$.

	${\mathit{d}}_1$	${\mathit{d}}_2$
N	30	30
Mean (M)	0.51	1.84
Median	0.45	0.95
Mode	0.1	0.3
Standard Deviation (SD)	0.41	2.02
Minimum	0	0.1
Maximum	1.8	7.9
Median Absolute Deviation (MAD)	0.25	0.85

.

Hypothesis testing was used to determine whether there is a statistically significant difference between the values of $d_1$ and $d_2$. The following hypotheses were formulated:

• Null hypothesis: The variable $d_2$ has smaller or equal values than the variable $d_1$.
• Alternative hypothesis: The variable $d_2$ has larger values than the variable $d_1$.

We checked whether the normality condition was met. We used four different statistical tests to check the normality, and the results are shown in

Table 8. Different statistical tests to check the normality.

	${\mathit{d}}_1$		${\mathit{d}}_2$
	Statistics	p	Statistics	p
Kolmogorov–Smirnov	0.18	0.257	0.21	0.129
Kolmogorov–Smirnov (Lilliefors)	0.18	0.015	0.21	0.002
Shapiro–Wilk	0.86	0.001	0.8	<0.001
Anderson–Darling	1.16	0.004	2.11	<0.001

.

Low p-values, less than 0.05, indicate that the data differ significantly from a normal distribution. In our case, three out of four tests show that the data differ significantly from the normal distribution. Therefore, we should proceed with a statistical method for hypothesis testing that does not assume the normality of the data. Due to the failure of normality assumptions, we used the Wilcoxon test to compare $d_1$ and $d_2$. The Wilcoxon test is designed for paired data, which is relevant in our case. This test accounts for the individual paired differences, providing a robust analysis even in the presence of outliers [47].

Table 9. Wilcoxon signed-rank test results for $d_1$ and $d_2$.

	W	z	p	r
$d_1$, $d_2$	24	−3.85	<0.001	0.7

presents a detailed statistical analysis of the results. The Wilcoxon test statistic (W) is 24, representing the sum of the ranks of the positive differences. The standardised z-score of −3.85 reinforces the significance of the results, while the p-value of less than 0.001 confirms that the changes in scores are statistically significant, leading us to reject the null hypothesis. The effect size (r) of 0.7 reflects a large effect according to [48]. The null hypothesis is thus rejected.

4. Discussion

The research problems examined in this study focused on the relationship between the parameters used to control the turning of LEGO SPIKE Prime robots and the actual turning radius of the robot. We established that turning can be achieved using two basic programming methods. In both cases, we specified the mutual relationships between the turning radius and the corresponding parameters.

4.1. Turning by Setting the Wheel Speeds

If we conduct turning by controlling the speed of the two wheels separately, then based purely on geometric and mathematical considerations, we obtain Formula (6), from which the turning radius of the centre of the robot can be calculated. This theoretical relationship is independent of wheel size, but it includes track width as a parameter. However, we must accept that this formula is only valid under ideal conditions and, in practice, only provides an approximate value for the radius. LEGO robots are not precision machines, and many factors, such as motor wear, battery charge level, and the cleanliness of the wheels or ground, influence their operation. Using Equation (7), which is the inverse of Formula (6), we can answer problem (P2), often giving several possible answers, since the equation only gives the ratio of the speeds (see Table 1). If the ratio can be expressed in several ways as a quotient of two integers between −100 and 100, it is advisable to choose a pair in which neither speed is too small or too large; values between 25 and 75 are considered the best choice. If we cannot express the ratio in the problem as a quotient of appropriate integers, this again affects accuracy, as our input parameters will also be rounded values.

In summary, if the robot turns by adjusting the wheel speeds, Equations (6) and (7) answer research problems P1 and P2. However, it should be noted that for travelling on a circle of a given radius, Formula (7) only specifies the ratio of the wheel speeds. This means that the same result can be achieved with several different speed pairs, and the appropriate one must be selected. However, it often happens that the desired ratio can only be achieved approximately with the permissible speed values, which results in the inaccuracy of the turning radius.

4.2. Turning by Setting the Steering Parameter

Turning with the steering parameter may seem more straightforward, as only one parameter must be specified in this case. However, the effect of this parameter is more challenging to examine from a purely theoretical point of view, as we do not know precisely how the SPIKE hub distributes the wheel speeds when it receives the steering parameter. Our experimental analysis showed a linear relationship between the steering parameter and the ratio of wheel speeds. Combining this observation with our previous results, we established the theoretical relationship between the steering parameter and the turning radius in Equation (12). If, due to the inaccuracy of the robot, this theoretical formula does not provide results that are accurate enough for our needs, we can create a more accurate functional relationship between the variables using a customised regression model. For this, we need empirical data, which we obtain by determining the robot’s turning radius as accurately as possible at different steering values. Data can be collected by direct measurement with a tape, but we can also use the motor’s rotation sensor. In the latter case, we can entrust the data processing entirely to the robot, as SPIKE software can perform the operations necessary to calculate the regression coefficients. Once we have created the regression function, we can use its inverse to determine the steering parameter required to achieve a given turning radius. However, this is where the biggest shortcoming of the steering parameter method becomes apparent. The steering parameter can only be an integer, and the smaller the number, the greater the turning radius, and the greater the differences between the turning radii corresponding to adjacent steering values. For the Driving Base model, we found that function (19) estimates the turning radius well. With this function, a steering value of 5 corresponds to a turning radius of approximately 106 cm, while a value of 4 corresponds to a turning radius of approximately 134 cm. Let us assume that we want to move the robot in a circle with a radius of 120 cm. The inverse of function (19) is

$$x\left(r\right)={\displaystyle \frac{560}{r+5.6}}.$$

(26)

Evaluating this function at $r=120$, we have a value of around 4.5. We can start the robot with a steering value of 4 or 5, but unfortunately, in both cases, there will be an error of 14 cm in the result. In contrast, we can achieve better results by adjusting the speed of the wheels. Indeed, applying Formula (7), we have

$$q={\displaystyle \frac{2·120+11.2}{2·120-11.2}}={\displaystyle \frac{251.2}{228.8}}=1.0979.$$

(27)

Therefore, the speed of one wheel should be approximately 1.1 times that of the other, so setting the speeds to 33 and 30 or 44 and 40 would be a good choice. Calculated with a ratio of $q=1.1$, Equation (6) gives a result of $r=117.6$ cm for the expected turning radius. This result still has a deviation of 2.4 cm from the target radius, but it is more acceptable than the result obtained with the steering parameter.

In summary, we established the theoretical function (12), which gives the turning radius for a given steering value when the robot turns using the steering parameter. Suppose we find this formula insufficiently accurate for a given robot. In this case, we can create a regression function based on our own measurement results or measurements performed by the robot, which will better match the values seen in practice. This regression function provides the answer to problem P1. However, the inverse of the function can only provide a limited answer to problem P2, as there are turning radii that can only be achieved with a huge error using an integer steering parameter. In such cases, it is advisable to choose the first method for turning, as more accurate results can be achieved by adjusting the wheel speeds separately.

In general, in the case of problem P2, it is more practical to use separate wheel speed settings for turning instead of the steering parameter. This finding also follows from the fact that the steering parameter can only be an integer between −100 and 100, meaning that this method can cover a total of 201 turning situations. However, by adjusting the speed of the wheels individually, many more combinations are possible, so this method offers a better chance of achieving a given turning radius with acceptable accuracy. The experiment conducted in Section 3.9 and its statistical analysis also confirm the greater accuracy of the wheel speed method. However, the experimental results also show that, in the case of smaller radii, the robot can turn in the desired arc by adjusting the steering parameters. For example, the robot in the experiment turned with an acceptable error up to a turning radius of 40 cm. In the case of larger radii, it performed well when the radius value was close to the value corresponding to a permissible steering parameter. The following recommendation can be made regarding the practical application of turning methods. The wheel speed method is more generally applicable, but good results can be achieved by adjusting the steering parameters if the turning radius is not too large. To determine the maximum radius for which the method can be used safely, a regression model of the robot’s steering parameters can be created based on manual measurements or as described in Section 3.8. A table of turning radii can also be created for each steering parameter. The difference between the radii corresponding to adjacent steering values increases. If this difference exceeds the error limit we consider acceptable, it is not worth applying the steering parameter method to such radii, unless the desired radius is included in the table.

4.3. Comparison of Existing Research with Current Study

In this section, we compare the results presented in this article with findings related to the turning characteristics of the predecessors of SPIKE Prime robots. Both NXT and EV3 offer the option of independently adjusting wheel speed, and there is also a turning option controlled by steering parameters.

The most comprehensive study on the turning of NXT robots was conducted by Alamisis et al. [41], where both turning methods were examined. It was proven that the turning radius is independent of wheel size and depends only on the track distance and wheel speed. We also obtained this result using a different derivation in Equation (6). Similarly to our approach, the effect of the steering parameter was examined experimentally in [41]. A pen was attached to the robot, and the robot was started with different steering parameters, and then the radius of the drawn circle was measured. The data was plotted, and the graph shows that the turning radius is a rational function of the steering parameter, but the specific function relationship formula is missing. This procedure corresponds to the experiment presented in this article, where we measured the turning radii corresponding to different steering parameters on the test table. From these data, we constructed regression models and derived formulas that describe the dependence of the turning radius on the steering parameter.

The most detailed description of EV3 robot turning can be found in Trobaugh’s book [42]. The author focuses primarily on pivot and point turns, and the mathematical background is also limited to these cases. The book mentions both turning methods but does not provide formula-based guidance on the behaviour of the parameters. There is a list of the effects of special steering parameters, but for the other values, the author recommends using the trial-and-error method.

Without rigorous justification for their conclusion, both sources agree that it is better to solve the turning problem by adjusting wheel speeds rather than using steering parameters. This finding is consistent with our opinion, and the example presented at the end of the previous section also shows that, for specific turning radii, turning with the steering parameter is less accurate. We also supported this conclusion with the statistical analysis in Section 3.9.

5. Conclusions and Future Plans

Using educational robotics in STEM fields helps in developing student competencies, especially key competencies for solving problems [49]. LEGO robot kits have become popular educational tools in schools because they encourage students’ interest in science in a playful way and help in developing their scientific and technical creativity. A common task in robotics classes is moving and controlling wheeled vehicles and overcoming obstacles. The precise execution of these manoeuvres is also a decisive factor in the success of robot competitions. Programming a robot model to turn and move along a curved path is a basic operation in robot control. The method of turning is determined primarily by the design. The most commonly used solution is to move the robot’s wheels independently of each other and control the turning by adjusting the wheel speeds. In the case of LEGO robots, the wheel speeds can be coded in several ways, but the parameters do not clearly indicate how the robot will move. Therefore, students often code using trial and error, fine-tuning the robot’s operation step by step. Although this method can also lead to the desired result, the problem of turning parameters can also be approached theoretically, and this process has many lessons to offer.

In [40,41,42,43,44], the authors presented the turning characteristics of LEGO’s previous robot kits, the NXT and EV3 models, and recommended some coding solutions for controlling turns. In this article, our goal was to provide a more general and in-depth approach to exploring the turning mechanisms of LEGO SPIKE Prime robots than previous descriptions. To this end, we used mathematical methods to derive formulas that theoretically give the relationships between the parameters used for turning and the actual turning radius. We also provided a method for experimentally testing the steering parameter in case the desired accuracy cannot be achieved with the theoretical formulas, for example, due to motor wear. Particularly noteworthy is the experiment presented in Section 3.8, in which the robot collects and processes the information necessary to perform autonomous regression modelling. Another important finding of this study is that turning with the steering parameter allows for a much smaller range of turning radii than when setting the wheel speeds separately. This fact also implies that the robot generally operates more accurately when programmed using the wheel speed adjustment method. We verified this by performing a statistical analysis of the accuracy of the methods.

Although we attempted to provide a comprehensive overview of the turning characteristics of LEGO SPIKE Prime robots, there are some areas that we did not examine but that may be worthy of future research. We answered problem P1 about the method of setting wheel speeds using only a theoretically derived formula. An interesting question is whether it is possible and worthwhile in this case to create an experimentally obtained formula, similarly to the steering parameter method. Developing a procedure that selects the optimal speed pair from among the possible speed pairs when applying the wheel speed method would also be useful. Environmental parameters and the physical condition of the engines also influence turning performance, and a description of these relationships would merit a separate study.

Since LEGO robots are not industrial robots, perfect accuracy cannot be expected during their operation. However, we must strive for the greatest possible accuracy and consistency in certain situations, such as robot competitions. We hope the methods and results described in our article will contribute to achieving this goal.