TGPSO: An Adaptive Gait Optimization Algorithm for Hexapod Robots in Multi-Terrain Environments

Abstract

To address the limited adaptability of traditional fixed-parameter strategies for hexapod robots operating in multi-material terrain environments, this study proposes a terrain-aware gait optimization method based on an improved particle swarm optimization algorithm that incorporates foot-end sinking perception. This method establishes a ground sinking detection mechanism based on foot-end position sensors, constructs a dynamic weight allocation strategy based on ground bearing capacity, and develops a Terrain-aware Ground Particle Swarm Optimization algorithm (TGPSO) that integrates Latin hypercube sampling, linearly decreasing inertia weights, and stagnation exploration mechanisms. Furthermore, it establishes a unified terrain-based reward function framework to achieve dynamic adjustment of weights for velocity, stability, and transportation efficiency. Simulink simulation verification demonstrates that TGPSO achieves superior optimization performance compared to traditional strategies across three typical terrain types, while exhibiting faster convergence speed and enhanced stability. The research findings provide theoretical foundations and technical support for intelligent motion control of hexapod robots across varying material properties, achieving targeted optimization of locomotion performance under diverse terrain conditions.

1. Introduction

The hexapod robot has proven invaluable in challenging environmental scenarios, including disaster response [1,2], military reconnaissance [3,4], planetary exploration [5,6], and so on. Its hexapod structure allows for stable operation across diverse material surfaces challenging for conventional wheeled or tracked robots. Consequently, the hexapod robot has emerged as a significant research focus in robotics due to its exceptional stability and terrain adaptability in complex environmental contexts [7]. Notable research platforms such as the LAURON series, which has demonstrated successful hexapod locomotion across multiple generations of development, have established strong foundations for advancing hexapod robot technology [8]. Yet, as application scenarios diversify, the constraints of conventional fixed-parameter strategies on unstructured terrain become more apparent. Consequently, current research emphasizes gait planning and optimization techniques utilizing intelligent algorithms to enable terrain-aware motion control of robots across varying environmental conditions [9,10,11,12].

Historically, hexapod robot gait planning predominantly employed fixed-parameter approaches. Liu and Sun extensively examined the kinematics of triangular gait [13,14], whereas Wang and Luneckas systematically investigated the dynamics of wave gait [15,16]. While these methodologies are theoretically robust, their practical adaptability is notably limited when confronted with varying terrain conditions, posing challenges in fulfilling the mobility needs across heterogeneous material surfaces. For example, a fixed gait optimized for rigid rock surfaces with parameters emphasizing stability (low step Frequency, moderate step height) would result in inefficient locomotion when transitioning to sand terrain, where higher step frequency could achieve better speed without stability penalties. Conversely, aggressive gait parameters optimized for sand (high step frequency, large step size) would cause excessive impact forces and potential instability on rock surfaces. Additionally, fixed parameters optimized for load-bearing surfaces fail catastrophically in clay environments where foot sinkage occurs, as they lack mechanisms to detect and adapt to substrate deformation, potentially leading to entrapment scenarios.

To address the limitations of conventional gait planning approaches, terrain-aware methods utilizing intelligent optimization algorithms have been proposed. Luneckas pioneered the application of the Red Fox Optimization (RFO) algorithm [16], inspired by nature, for selecting gait parameters in a hexapod robot. Their objective was to minimize transportation cost (COT) while intelligently transitioning between triangular and wave gaits. Genetic algorithm, a classical method for global optimization, demonstrates robust search capabilities in optimizing hexapod robot gaits. Genetic algorithm theory framework serves as a crucial foundation for coding and optimizing gait parameter [11,17,18]. Additionally, The Particle Swarm Optimization (PSO) algorithm, known for its simplicity and rapid convergence, has been widely adopted for robot gait control. The standard PSO algorithm developed by Kennedy and Eberhart offers a novel solution to this challenge [19]. Building upon this work, Chen and Tao successfully extended the PSO algorithm to optimize gait parameters with significant outcomes [20,21].

Despite the notable achievements of intelligent optimization algorithms in theoretical and laboratory settings, their practical implementation across diverse material properties poses significant challenges. The efficiency of legged robots’ gaits is closely linked to the characteristics of the terrain they traverse [22]. Brooks introduced a ground classification approach based on foot subsidence, offering a novel perspective on terrain identification [23]. The successful deployment of the RHex robot has validated the applicability of this method across various terrains such as rocks, soil, and sand in robotic studies [24]. Recent advancements in reinforcement learning have introduced a parametric model for granular mediums, enabling the comprehensive representation of ground surfaces ranging from soft beach sands to rigid asphalt [25]. This model serves as a valuable framework for testing and refining adaptive motion control algorithms. Building upon this foundation, researchers have proposed terrain recognition techniques leveraging visual perception and force feedback [26,27], significantly enhancing robots’ environmental awareness and adaptability.

Although existing research has achieved significant progress in robotic gait optimization, three critical challenges remain in practical applications that directly relate to the complexity of terrain-robot interactions:

• Terrain-induced sinkage risks: Foot penetration into soft substrates creates entrapment scenarios where traditional extraction methods prove inadequate, yet current approaches lack sinkage-aware control mechanisms.
• Substrate-dependent parameter optimization: Different ground materials (rock, sand, clay) require distinct combinations of step size, height, and frequency due to varying stiffness, damping, and friction properties, but existing methods employ fixed-weight objective functions that cannot adapt to these material-specific requirements.
• Limited global search capability: Traditional PSO algorithms demonstrate poor convergence when handling the multimodal optimization landscapes created by terrain heterogeneity, frequently becoming trapped in local optima that correspond to suboptimal gait configurations.

To address these challenges, this study proposes a terrain-aware gait optimization method with real-time parameter selection that considers ground subsidence. Three typical ground materials—rock ground, sand ground, and clay ground—are selected as research subjects. These three materials represent the fundamental modes of robot foot–ground interaction: rock ground provides a rigid contact interface, sand ground exhibits the compressible characteristics of granular media, and clay ground demonstrates semi-fluid deformable contact, covering the fundamental spectrum of material contact properties in robotic locomotion research.

The paper is organized as follows: Section 2 establishes the problem model, details the construction methods for velocity, stability, and efficiency objective functions, TGPSO algorithm design, and gait optimization process; Section 3 validates the effectiveness of the proposed method through simulation and experiments; Section 4 analyzes performance comparison results under different ground conditions; Section 5 summarizes the research findings and outlines future research directions.

2. Materials and Methods

2.1. Problem Modeling

2.1.1. Problem Description and Definition

The terrain-adaptive gait optimization problem for hexapod robots stems from the adaptive limitations of traditional fixed-parameter strategies across varying material properties. Different terrains exhibit distinct foot–ground interaction characteristics: rock ground provides rigid contact but involves impact loads, sand ground offers good load-bearing capacity, and clay ground is prone to foot subsidence. The core challenge of this problem lies in how to achieve coordinated unification of the triple objectives of velocity, stability, and transportation cost through real-time perception of ground characteristics and dynamic adjustment of gait parameters. Specific technical challenges include:

• Real-time terrain identification based on foot subsidence.
• Dynamic allocation of multi-objective weights under different terrains.
• Global optimization solving under strongly coupled gait parameter conditions.

This research problem is formulated as follows: The terrain-aware gait optimization for hexapod robots is formulated as a constrained multi-objective optimization problem. Given terrain characteristics T identified through foot sinkage δ, the objective is to determine the optimal gait parameter vector θ = [L, H, f] that maximizes the comprehensive performance index.

Decision Variables: L: Step Size (m); H: Step Height (m); f: Step Frequency (Hz).

$$\max \mathrm{F}(\mathrm{\theta },\mathrm{T})={\mathrm{\lambda }}_1\mathrm{Speed}(\mathrm{\theta },\mathrm{T})+{\mathrm{\lambda }}_2\mathrm{Stability}(\mathrm{\theta },\mathrm{T})+{\mathrm{\lambda }}_3\mathrm{Efficiency}(\mathrm{\theta },\mathrm{T})$$

(1)

In the equation, X ∈ Ω represents the gait  parameter constraint space; T denotes the terrain type; and λ is the weight  coefficient dynamically adjusted according to terrain characteristics.

Based on the aforementioned robot dimensional  limitations and findings from the model parameter adjustment process during  simulation, the following constraint conditions are established:

• Step Size ∈  [0, 0.3] m; Stpheight ∈ [0, 0.2] m; StepFrequency ∈ [0.5, 2] Hz;
• Stability constraints: center of mass fluctuation < 0.05 m;
• Energy consumption constraints: joint torque shall not exceed the  rated torque of the motor;
• Terrain adaptability constraints: foot-end sinkage < 0.5 m.

2.1.2. Hexapod Robot System Modeling

The mechanical structure of the simulated robot in  this study adopts a circumferential arrangement of the body and legs, where the  six legs are uniformly distributed around the main structure at various angles,  forming a stable and highly flexible configuration. The robot body measures 660  mm in length, 676 mm in width, and 145 mm in height, with a total weight of  121.2 kg. In the Simulink of MatlabR2023b simulation environment, the robot can  achieve a forward speed of 0.5 m/s and a lateral speed of 0.5 m/s on hard  surfaces. Each leg of the robot has 3 degrees of freedom, with leg segment  lengths as follows: coxa: 165 mm, femur: 240 mm, and tibia: 510 mm. The  three-dimensional model diagram of the hexapod simulation robot is shown in the  Figure 1.

Hexapod robots, with their multi-leg structure, can  achieve stable locomotion through coordinated leg movement. The gait patterns  of legged robots focus on determining the swing and support sequences of each  leg after establishing the foot trajectory. Triangular, quadrupedal, and wave  gaits are common locomotion patterns for hexapod robots. Subsequently, using  the simulated hexapod robot designed in the previous section as a prototype,  this paper focuses on the straight-line triangular gait, which exhibits both  high speed and excellent stability, as the primary research object.

The triangular gait of hexapod robots refers to a  gait planning pattern in which three legs continuously support the body while  the other three legs remain in the swing phase during locomotion. This gait is  termed “triangular” because the supporting legs form a triangular  configuration. Derived from crab locomotion patterns, this gait possesses  characteristics of stable movement, high speed, and low energy consumption,  making it the most commonly employed gait in hexapod robot control. In the  triangular gait, the six legs are divided into two groups, with legs within  each group maintaining synchronized movement states.

Taking forward locomotion as an example, the six  legs are numbered 1–6 in a counterclockwise direction starting from the left  front leg, divided into two groups: 1, 3, 5 and 2, 4, 6, The key characteristic  of triangular gait is that the two groups alternate between swing and stance  phases, ensuring continuous body support and propulsion. Initially, all six  legs are in the support state as shown in Figure 2a. During the first half-cycle,  legs 1, 3, and 5 lift into the swing state and move forward, while legs 2, 4,  and 6 simultaneously remain in stance phase and actively propel the body  forward as depicted in Figure 2b. During the second half-cycle, legs 2, 4,  and 6 lift into swing motion, while legs 1, 3, and 5 simultaneously transition  to stance phase and propel the body forward as illustrated in Figure 2c.  Finally, legs 2, 4, and 6 land, and the robot returns to the initial  configuration as shown in Figure 2d, completing one complete gait cycle. This  alternating pattern ensures that three legs always maintain ground contact for  stability while the other three advance for forward progression.

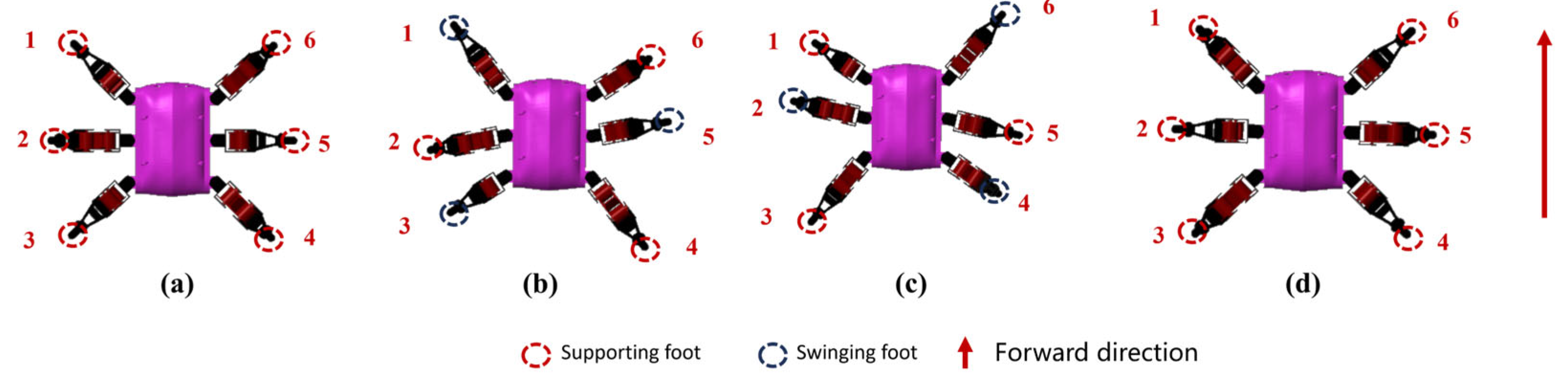
2.1.3. System Architecture and Methodology Overview

The proposed terrain-adaptive gait optimization system integrates three core functional modules to address the challenges of hexapod robot locomotion across varying material surfaces, as illustrated in Figure 3.

Terrain Analysis Module: This module employs real-time foot-end position sensors to detect ground subsidence and classify terrain characteristics. The terrain classifier utilizes contact force feedback, dynamic friction measurements, and sinkage depth data to distinguish between rock ground (rigid contact), sand ground (compressible granular medium), and clay ground (deformable semi-fluid contact). The measured parameters feed into a terrain identification algorithm that outputs terrain type classifications.

Algorithmic Framework Module: The core optimization engine implements the Terrain-aware Ground Particle Swarm Optimization (TGPSO) algorithm with integrated Latin hypercube sampling for particle initialization. The framework incorporates adaptive parameter adjustment mechanisms including linearly decreasing inertia weights and dynamic learning factor modification. A unified reward function dynamically weights speed, stability, and efficiency objectives based on terrain characteristics identified by the terrain analysis module.

Action Generation Module: This module serves as the critical interface between optimization results and physical robot implementation, integrating multiple sensor subsystems for comprehensive motion control and performance monitoring. The module translates optimized gait parameters (Step Size, Step Height, Step Frequency) into executable robot commands through a multi-layered control architecture.

Inertial Measurement Unit (IMU): Mounted on the robot’s central body, the IMU provides continuous monitoring of body orientation, angular velocity, and linear acceleration. This sensor enables real-time calculation of velocity indicators for the speed objective function and detects body inclination changes that affect stability margins during locomotion across uneven terrain.

Foot-end Sinkage Perception Module: Each leg terminus integrates position sensors and force sensors to detect foot penetration depth and contact force magnitude. The sinkage perception system continuously monitors vertical displacement relative to initial ground contact, enabling real-time detection of substrate deformation and potential entrapment scenarios. This data directly feeds into the terrain classification algorithm and provides critical input for the efficiency objective function calculations.

Stability Margin Assessment Module: This subsystem combines IMU data with foot force measurements to calculate real-time stability indicators including center of mass position relative to the support polygon, force distribution among supporting legs, and dynamic stability margins. The module computes the distance from the center of gravity projection to the support polygon boundaries, providing essential feedback for the stability objective function.

The proposed system is implemented and validated in Simulink of MatlabR2023b simulation environment using the following configuration: The simulation employs ODE45 variable-step solver with maximum Step Size set to 1 × 10⁻³ s (equivalent to 1000 Hz baseline resolution). The integrated sensor modules from Simulink library are configured as follows:

• Position and velocity measurements: Transformer sensor modules sample at 1 kHz simulation time.
• IMU data acquisition: Three-axis accelerometer and AHRS (Attitude and Heading Reference System) modules provide orientation and angular velocity data at 1 kHz simulation rate.
• Contact force sensors: Integrated within the foot–ground contact model, updating at the solver’s variable step rate.

The contact force calculation (Equation (2)) is computed at each solver step, with computational complexity of O(n) per leg contact. In the Simulink of MatlabR2023b environment, the complete hexapod dynamics simulation including all six legs runs at approximately 0.1–0.3× real-time speed on standard workstation hardware, indicating the computational feasibility for real-time implementation on dedicated control hardware.

For practical robot implementation, these simulation parameters translate to achievable real-time performance: typical embedded control systems can execute the contact model calculations within 100–200 μs per leg, supporting control frequencies of 500–1000 Hz commonly used in legged robotics applications.

2.1.4. Mechanical Modeling of Foot–Ground Interaction

The subsidence phenomenon occurring when hexapod robot feet contact the ground can be described using elastic mechanics models. A foot–ground contact model is established based on Hertz contact theory:

$${\mathrm{F}}_{\mathrm{n}}={\mathrm{k}}_{\mathrm{p}}\mathrm{x}+{\mathrm{k}}_{\mathrm{d}}\stackrel{·}{\mathrm{x}}$$

(2)

where ${\mathrm{F}}_{\mathrm{n}}$ represents the normal contact force; x denotes the foot subsidence depth; and ${\mathrm{k}}_{\mathrm{p}},{\mathrm{k}}_{\mathrm{d}}$ represent the stiffness coefficient and damping coefficient, respectively.

The Hertz contact model is applicable across all three terrain types with appropriate parameter adjustments: For rock ground, the high stiffness coefficient (3 × 10⁹ N/m) captures the rigid contact characteristics with minimal deformation. For sand ground, the moderate stiffness (9.1 × 10⁶ N/m) represents the compressible nature of granular media where particles rearrange under loading. For clay ground, the lower stiffness (1.7 × 10⁶ N/m) models the semi-fluid deformable properties where significant subsidence can occur. The damping coefficients are correspondingly adjusted to represent the energy dissipation characteristics of each terrain type during foot–ground interaction.

Based on Simulink of MatlabR2023b simulation, this study employs a foot–ground contact model that incorporates spherical geometry embedded within the robot foot coordinate system, with a rigid body simulating the ground substrate (dimensions: 100 m × 100 m × 1 m). Real-time calculation and transmission of normal and tangential contact forces during foot–ground interaction are achieved through a contact force calculation module. To acquire foot subsidence characteristic data, the simulation model integrates position sensors, force sensors, and an IMU, which are respectively used for real-time monitoring of foot vertical displacement relative to the ground, contact force components at the foot–ground contact interface, and foot motion velocity. The ground subsidence detection mechanism operates by establishing a reference ground height when each foot initially contacts the surface, followed by continuous monitoring of the foot’s vertical position using position sensors. The subsidence depth is calculated as the difference between the initial contact height and the current foot position, with average subsidence values computed across all supporting legs to ensure robust terrain identification. These sensor data will provide critical inputs for subsequent ground mechanical parameter identification and gait optimization. It should be noted that while force sensors provide contact state information for stability calculations, the contact model parameters kp and kd in Equation (2) are predetermined from material property databases rather than identified from real-time force measurements, ensuring computational efficiency for online optimization.

Due to the special characteristics of the operating environment for hexapod crab-inspired robots, ground conditions are complex, and different ground materials impose varying gait requirements on the robot. Therefore, this study configures different parameters for robot–ground contact to maximally reproduce the effects of various ground materials on robot locomotion. Figure 4 shows three typical terrains where the hexapod robot introduced in this article comes into contact with the ground.

The formula for calculating the contact stiffness between robot foot and ground surface is as follows [28].

$${\mathrm{k}}_{\mathrm{p}}={\displaystyle \frac{4\mathrm{G}\mathrm{r}}{1-\mathrm{\nu }}}$$

(3)

where G represents the shear modulus (Pa); ν denotes Poisson’s ratio; r represents the contact radius; and the damping coefficient is calculated using the following formula [29].

$${\mathrm{k}}_{\mathrm{d}}=2\mathrm{\zeta }\sqrt{{\mathrm{k}}_{\mathrm{p}}\times \mathrm{m}}$$

(4)

where ζ represents the damping ratio; ${\mathrm{k}}_{\mathrm{p}}$ denotes the contact  stiffness (N/m); and m represents the equivalent mass.

Based on the above calculation formulas and considering the characteristics of different ground materials combined with Simulink of MatlabR2023b simulation properties, the corresponding simulation parameters are configured as shown in the following

Table 1. Mechanical parameters of three types of ground material [30].

Ground Type	Stiffness (N/m)	Damping (N/(m/s))	Dynamic Friction	Static Friction	Density (kg/m3)
Rock Ground	$3\times {10}^9$	$1.8\times {10}^5$	0.52	0.55	1800
Sand Ground	$9.1\times {10}^6$	9000	0.6	0.65	1700
Clay Ground	$1.7\times {10}^6$	3900	0.5	0.55	1600

.

2.2. Algorithm Design

2.2.1. Multi-Objective Optimization Problem Modeling

In unstructured ground environments, motion optimization of hexapod robots based on triangular gait faces multiple constraints and challenges. The unstructured characteristics of ground environments result in high uncertainty in robot–ground contact states, necessitating the pursuit of optimal balance among speed, stability, and transportation cost. For hexapod crab-inspired robots employing triangular gait forward locomotion, during the motion process, objective functions for speed, stability, and Cost of Transport (COT) are defined and normalized through measurements of hexapod robot velocity, center of mass fluctuation and stability margin, and energy consumption of individual robot joints [31].

Speed Objective Function:

$$\mathrm{Speed}(\mathrm{X},\mathrm{T})={\displaystyle \frac{\mathrm{v}-{\mathrm{v}}_{\min }}{{\mathrm{v}}_{\max }-{\mathrm{v}}_{\min }}}$$

(5)

where v represents the robot’s vector velocity, and the velocity of the hexapod robot during operation ranges from [0, 0.5] m/s.

Stability Objective Function:

$$\mathrm{Stability}(\mathrm{X},\mathrm{T})={\mathrm{\omega }}_1\times {\mathrm{e}}^{{\displaystyle \frac{-\mathrm{\sigma }\mathrm{Z}}{\mathrm{\sigma }\mathrm{Max}}}}+{\mathrm{\omega }}_2\times {\mathrm{D}(\mathrm{P}}_{\mathrm{c}},\mathrm{\partial }\mathrm{p})\times (1-\min ({\displaystyle \frac{\mathrm{\epsilon }}{\mathrm{\mu }}},0.5))$$

(6)

where ${\mathrm{\sigma }}_z$ represents the standard deviation of the robot’s center of mass in the vertical direction during operation, ${\mathrm{\sigma }}_{\mathrm{Max}}$ represents the maximum tolerable fluctuation, and an exponential decay approach is designed to achieve the effect that larger fluctuations result in lower scores; ${\mathrm{D}(\mathrm{P}}_{\mathrm{c}},\mathrm{\partial }\mathrm{p})$ represents the distance calculation formula, computing the distance from the center of gravity projection point ${\mathrm{\partial }}_{\mathrm{p}}$ to the support polygon ${\mathrm{p}}_{\mathrm{c}}$; $1-\min ({\displaystyle \frac{\mathrm{\epsilon }}{\mathrm{\mu }}},0.5)$ represents the force balance correction factor, where ε denotes the standard deviation of contact forces and μ represents the mean of contact forces.

Cost of Transport (COT) Function:

$$\begin{array}{c}\mathrm{Effiency}=1-{\displaystyle \frac{{\left(\mathrm{W}/\mathrm{mg}\mathrm{s}\right)}_{\mathrm{i}}-{\left(\mathrm{W}/\mathrm{mg}\mathrm{s}\right)}_{\min }}{{\left(\mathrm{W}/\mathrm{mg}\mathrm{s}\right)}_{\max }-{\left(\mathrm{W}/\mathrm{mg}\mathrm{s}\right)}_{\min }}}\\ \mathrm{W}={\displaystyle \sum _0^{18}{\displaystyle \int \left|\mathrm{\omega }\times \mathrm{\tau }\right|}dt}\end{array}$$

(7)

where ω (rad/s) represents  the joint angular velocity, and τ represents the joint torque.

2.2.2. PSO Algorithm

The PSO algorithm is an optimization algorithm that simulates the foraging behavior of bird flocks, treating potential solutions as points in the search space, referred to as particles. Each particle’s fitness value is defined as, its individual optimum is defined as $c_1$, and the global optimum of the population is $c_2$, where i and g represent the number of particles, and the dimension is denoted as D. During each iteration process, particles optimize their velocity and position through individual and global optima, with the mathematical expressions and iterative formulas as follows:

$${\mathrm{V}}_{\mathrm{ij}}^{\mathrm{t}+1}=\mathrm{w}\times {\mathrm{V}}_{\mathrm{ij}}^{\mathrm{t}}+{\mathrm{c}}_1\times \mathrm{rand}()\times ({\mathrm{P}}_{\mathrm{ij}}-{\mathrm{X}}_{\mathrm{ij}}^{\mathrm{t}})+{\mathrm{c}}_2\times \mathrm{rand}()\times ({\mathrm{P}}_{\mathrm{gj}}-{\mathrm{X}}_{\mathrm{ij}}^{\mathrm{t}})$$

(8)

$${\mathrm{X}}_{\mathrm{ij}}^{\mathrm{t}+1}={\mathrm{X}}_{\mathrm{ij}}^{\mathrm{t}}+{\mathrm{V}}_{\mathrm{ij}}^{\mathrm{t}+1}$$

(9)

where rand () represents a random number varying within the range (0, 1); ${\mathrm{c}}_1$ and ${\mathrm{c}}_2$ are positive real numbers called learning factors; and w represents the inertia weight.

Through the introduction of the particle swarm optimization algorithm, θ = {$L_1,H_2,f_3$} represent Step Size, Step Height, and Step Frequency, respectively. The fitness function value ${\mathrm{V}}_{\mathrm{ij}}=\mathrm{Fitness}$ is constructed through simulation data collection, and through continuous iteration, the optimal step length, step height, and step frequency are optimized according to different ground conditions.

However, due to the random initialization strategy of traditional PSO algorithms, particle distribution becomes non-uniform, failing to achieve global search, which leads to the particle swarm algorithm easily falling into local optima and being unable to effectively select optimal gait parameters. Additionally, the single initialization and reward function do not consider the influence of different ground environments on optimization objective weights, resulting in lower efficiency.

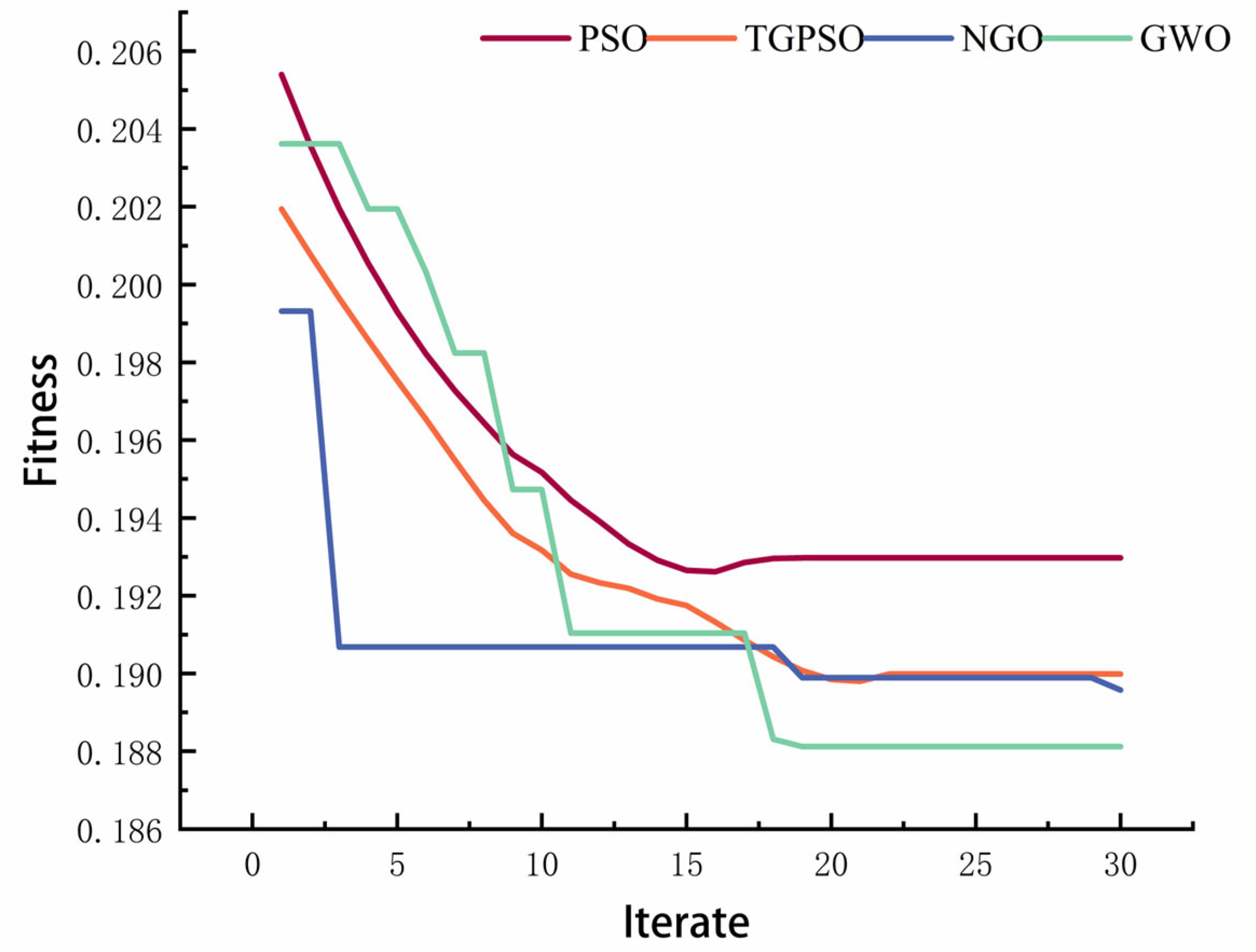
2.2.3. TGPSO Algorithm Design

To ensure global search implementation, Latin hypercube sampling is employed during particle initialization to guarantee uniform distribution of particles in the parameter space, with the formula as follows:

$${\mathrm{x}}_{\mathrm{i}}^{\mathrm{j}}=\mathrm{L}{\mathrm{B}}_{\mathrm{j}}+{\displaystyle \frac{\mathrm{U}{\mathrm{B}}_{\mathrm{j}}-\mathrm{L}{\mathrm{B}}_{\mathrm{j}}}{\mathrm{N}}}\times ({\mathrm{\pi }}_{\mathrm{i}}+{\mathrm{u}}_{\mathrm{i}})$$

(10)

where $x_i^j$ represents the initial position of the i-th particle in the j-th dimension; ${\Pi }_i$ represents a random permutation of {1, 2, 3, …, N}; ${\mathrm{u}}_{\mathrm{i}}$ denotes a uniformly distributed random number in (0, 1); and $\mathrm{L}{\mathrm{B}}_{\mathrm{j}},\mathrm{U}{\mathrm{B}}_{\mathrm{j}}$ represent the parameter boundaries.

Simultaneously employing linearly decreasing inertia weight and dynamically adjusting adaptive learning factors to achieve smooth transition from global search to local optimization:

$$\mathrm{w}(\mathrm{t})={\mathrm{w}}_{\max }-{\displaystyle \frac{{\mathrm{w}}_{\max }-{\mathrm{w}}_{\min }}{{\mathrm{T}}_{\max }}}\times \mathrm{t}$$

(11)

$$\begin{array}{c}{\mathrm{c}}_1(\mathrm{t})=({\mathrm{c}}_1,\mathrm{init}-0.5)\times (1-{\displaystyle \frac{\mathrm{t}}{\mathrm{T}\max }})+{\mathrm{\partial }}_1\\ {\mathrm{c}}_2(t)=({\mathrm{c}}_2,\mathrm{init}-0.5)\times {\displaystyle \frac{\mathrm{t}}{\mathrm{T}\max }}+{\mathrm{\partial }}_2\end{array}$$

(12)

where $\mathrm{w}(\mathrm{t})$ represents the inertia weight at the current moment; ${\mathrm{c}}_1(\mathrm{t})$ represents the individual learning factor; ${\mathrm{c}}_2\left(\mathrm{t}\right)$ represents the social learning factor; and ${\mathrm{\partial }}_1,{\mathrm{\partial }}_2$ takes the value of 0.5 in the formula.

A stagnation exploration mechanism is simultaneously employed to continuously monitor the global optimal solution. When the global optimal solution shows no improvement for N consecutive iterations, the 30% worst-performing particles are reinitialized to ensure optimality of the convergence value.

$$\begin{array}{l}\mathrm{if}|{\mathrm{f}}_{\mathrm{gbest}}(\mathrm{t})-{\mathrm{f}}_{\mathrm{gbest}}(\mathrm{t}-{\mathrm{N}}_{\mathrm{stag}})<\mathrm{\epsilon }\\ \mathrm{then}{\mathrm{X}}_{\mathrm{worst}30\%}^{\mathrm{new}}=\mathrm{LHS}(0.3\mathrm{N},\mathrm{D},\mathrm{L}\mathrm{B},\mathrm{U}\mathrm{B})\end{array}$$

(13)

Compared to standard PSO, the improved algorithm significantly enhances optimization performance and convergence stability under the same computational complexity through intelligent parameter adjustment and diversity maintenance mechanisms. The algorithm flowchart is shown in Figure 1.

Through the aforementioned improvement strategies, this algorithm can adaptively adjust optimization strategies according to terrain characteristics, effectively balancing the requirements for speed, stability, and transportation cost of hexapod robots in complex environments, providing theoretical foundation and technical support for intelligent motion control of hexapod working robots.

2.2.4. Terrain-Aware Reward Function Framework with Dynamic Weight Allocation

Based on the ground adaptive recognition mechanism utilizing foot subsidence measurements, this study proposes a unified reward function framework that adapts to different terrain characteristics through dynamic adjustment of weight coefficients. According to the problem description section presented earlier, the reward function defined in this paper is:

$$\left\{\begin{array}{c}\mathrm{F}(\mathrm{\theta },\mathrm{T})={\mathrm{\lambda }}_1\mathrm{Speed}(\mathrm{\theta },\mathrm{T})+{\mathrm{\lambda }}_2\mathrm{Stability}(\mathrm{\theta },\mathrm{T})+{\mathrm{\lambda }}_3\mathrm{Efficiency}(\mathrm{\theta },\mathrm{T})\\ {\mathrm{\lambda }}_1+{\mathrm{\lambda }}_2+{\mathrm{\lambda }}_3=1\end{array}\right.$$

(14)

Meanwhile, to achieve convergence in the algorithmic process, the convergence function in the PSO algorithm is defined as:

$$\mathrm{Fitness}={\mathrm{e}}^{-\mathrm{\alpha }{\mathrm{W}}_{\mathrm{i}}}$$

(15)

where α represents the convergence constant, with a value of 2.5.

Based on real-time perception of terrain physical characteristics, this paper proposes a dynamic adjustment approach for motion control optimization objectives, establishing a low-medium-high weight allocation mechanism for speed, stability, and efficiency. Moreover, this weight configuration satisfies the normalization constraint, ensuring targeted optimization of robot motion performance under different terrain conditions and mathematical rationality of parameter settings. According to the weight setting principles in multi-objective optimization, combined with the actual requirement hierarchy of robot motion control, this simulation experiment sets the primary objective weight at 0.5, with secondary objective weights decreasing progressively as shown below:

$$\left[\begin{array}{ccc}{\mathrm{\lambda }}_1& {\mathrm{\lambda }}_2& {\mathrm{\lambda }}_3\end{array}\right]=\left\{\begin{array}{c}\left[\begin{array}{ccc}0.2& 0.5& 0.3\end{array}\right]\\ \left[\begin{array}{ccc}0.5& 0.2& 0.3\end{array}\right]\\ \left[\begin{array}{ccc}0.3& 0.2& 0.5\end{array}\right]\end{array}\right.\begin{array}{c}\mathrm{\delta }<0.05\\ 0.05\le \mathrm{\delta }\le 0.1\\ \mathrm{\delta }\ge 0.1\end{array}$$

(16)

where δ represents the foot subsidence in the robot foot–ground contact model.

In rock ground, due to the rigid surface with irregular protrusions and crevices, the system prioritizes stability through conservative gait strategies, employing a reward function construction method with high weight for stability, medium weight for efficiency, and low weight for speed to reduce imbalance risks. Under sand ground conditions, where the surface has certain load-bearing capacity, the robot can adopt faster step frequencies and larger step lengths, implementing a strategy with high weight for speed, medium weight for efficiency, and low weight for stability, maintaining dynamic balance and achieving efficient propulsion through rapid continuous gait transitions. In clay ground, where surface load-bearing capacity is weak and prone to foot subsidence, the system prioritizes energy efficiency maximization and postural stability, adopting anti-sinking strategies for effective escape. Therefore, a reward function construction with high weight for efficiency, medium weight for speed, and low weight for stability is employed. Through this unified adaptive control framework, the robot can continuously monitor ground characteristic changes and adjust gait parameters and motion strategies in real-time, thereby achieving targeted parameter optimization in dynamic and complex environments.

3. Results

3.1. Simulation Environment Setup

To validate the effectiveness of the proposed algorithm, this study established a high-fidelity hexapod crab-inspired robot systematic platform based on the Simulink of MatlabR2023b simulation experimental platform, completely reproducing its dynamic characteristics. Utilizing the system characteristics of Simulink of MatlabR2023b, through modular and low-code approaches, inverse kinematics methods are employed to calculate the joint angles of each leg via triangular gait patterns, analyze the robot’s kinematic capabilities, and collect relevant data for verification. The detailed videos of the robot locomotion are as follows, This video is intended to demonstrate the walking performance of the hexapod robot in the simulation system:

https://www.bilibili.com/video/BV1QWtzz7EVz/?spm_id_from=333.1387.homepage.video_card.click&vd_source=20dab27a722882d32e15353a60854dc0 (accessed on 20 August 2025) [M1].

The hexapod robot Simulink model is shown in the following Figure 5.

3.2. Gait Simulation Parameter Design and Results

This simulation experiment is conducted based on hexapod robots, verifying the gait parameter optimization effects through establishing different terrain physical models. Considering the differences in terrain mechanical characteristics, differentiated parameter search strategies and multi-objective weight allocation methods are employed.

This study adopts improved particle swarm optimization with 20 particles and a maximum of 30 iterations. The inertia weight ω decreases linearly from 0.9 to 0.4 to balance global search and local exploitation, while learning factors c₁ decreases from 2.5 to 0.5 and c₂ increases from 0.5 to 2.5, achieving dynamic transition from individual learning to social learning in the algorithm. The optimization results using the TGPSO algorithm for different ground materials are shown in the following Figure 6.

The combined visualization displays parameter space exploration for (a) rock ground, (b) sand ground, and (c) clay ground. The 3D scatter plots show the evolution of particle positions in parameter space, with color gradients representing performance values and marking global optimal values. The convergence curves demonstrate the optimization progress across iterations, comparing convergence speed and best performance achieved to date. The optimization convergence performance of TGPSO is detailed in Section 4, where convergence curves are presented for rock ground, sand ground, and clay ground, demonstrating its superior convergence speed and stability compared to traditional strategies.

The parameters for different ground surfaces optimized based on the TGPSO algorithm are shown in

Table 2. Optimization results for different ground parameters.

Ground Type	Step Size (m)	Step Height (m)	Step Frequency (Hz)	v (m/s)	Standard Deviation (mm)	COT	Reward
Rock Ground	0.153	0.076	0.64	0.21	0.4	6.8	0.66
Sand Ground	0.30	0.143	2.00	0.41	1.3	39.1	0.73
Clay Ground	0.117	0.01	0.84	0.31	2.6	21.7	0.71

.

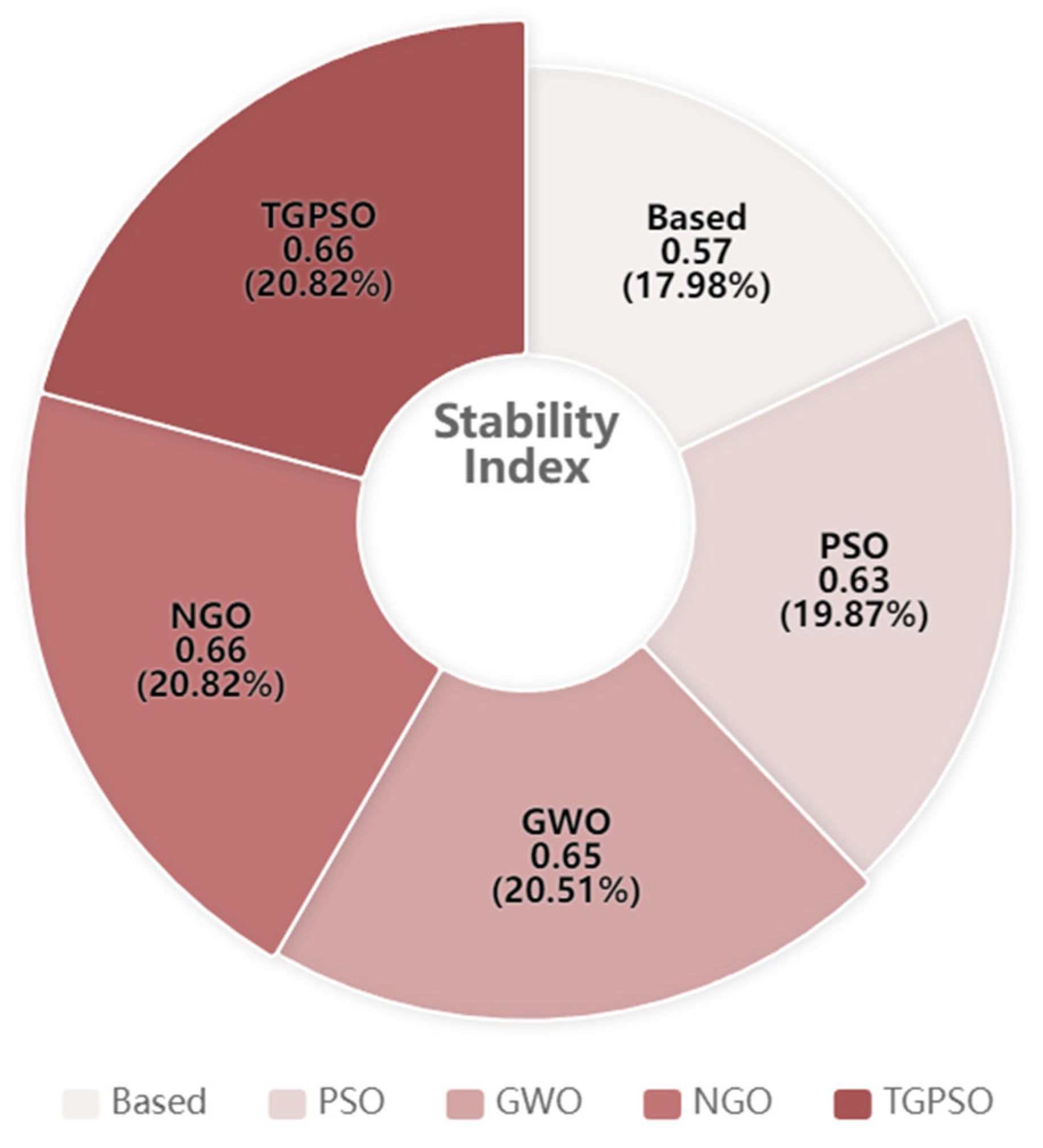
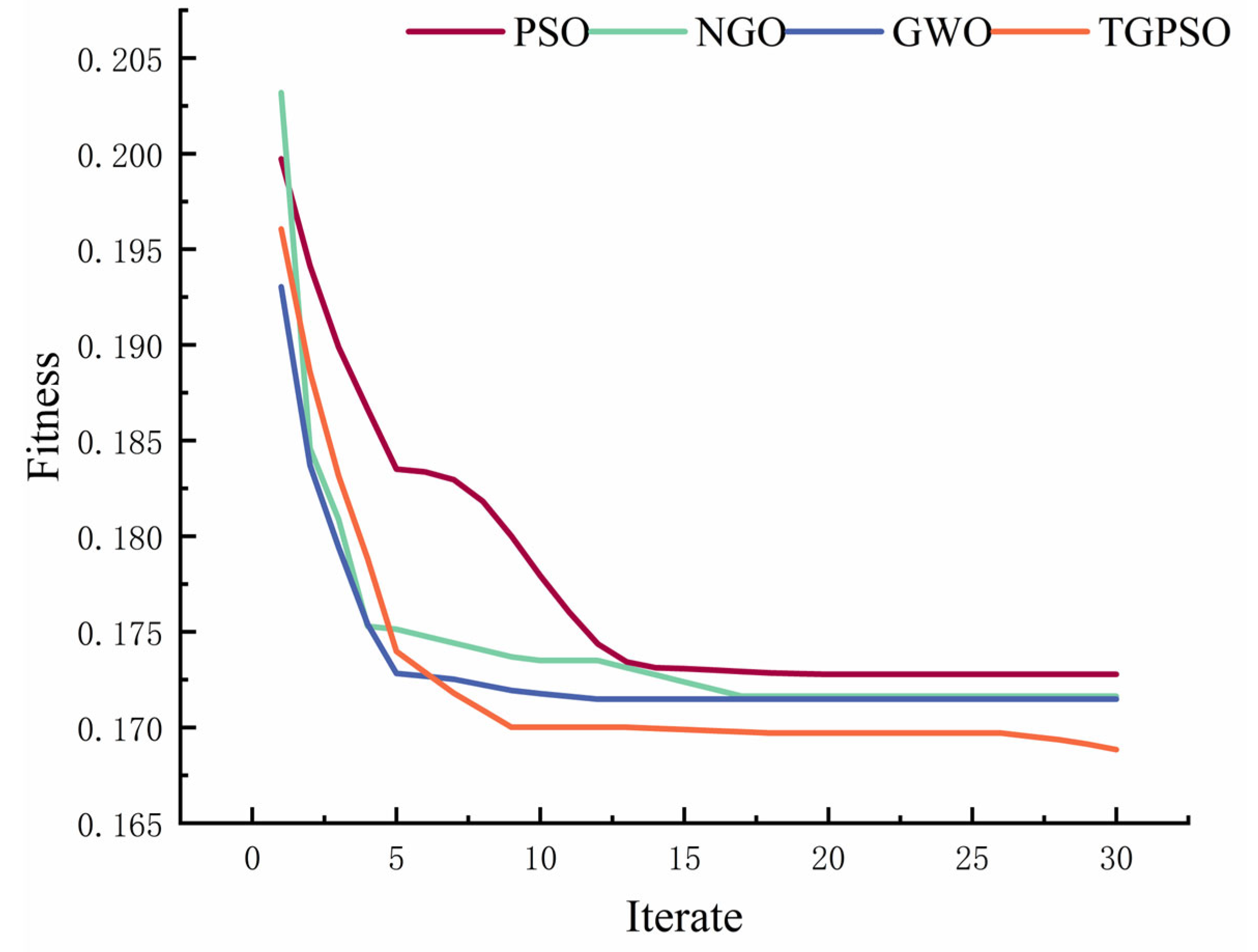
4. Discussion

To verify the effectiveness of gait parameters optimized by the TGPSO algorithm, this study designed a comparative experimental scheme. The experiment selected three ground types (rock ground, sand ground, and clay ground), with five sets of gait parameters configured for performance comparison on each terrain: (1) TGPSO optimized parameter group, representing the optimal gait parameters obtained through the proposed algorithm; (2) Traditional fixed parameter group, employing empirical gait parameters commonly used for hexapod robots in literature, combined with the dimensions of the simulation robot [32,33]. (3) Standard PSO optimized parameter group, representing optimal gait parameters obtained using traditional PSO algorithms [19]; (4) Grey Wolf Algorithm (GWO) optimized parameter group [34]; and (5) Northern Goshawk Optimization (NGO) optimized parameter group [35]. Through the Simulink of MatlabR2023b simulation platform, quantitative evaluation of the motion performance of the five parameter groups under corresponding terrain conditions was conducted, with focused analysis on three key performance indicators: robot forward speed, stability, and cost of transport consumption, to verify the effectiveness and superiority of the proposed optimization method in enhancing hexapod robot adaptability to unstructured terrain. The experimental results are shown in Figure 7 below.

The simulation results demonstrate that TGPSO exhibits superior optimization performance across optimization tasks for all three ground types, achieving optimal reward values in each case. The detailed optimization indicators for each algorithm are shown in the following

Table 3. Different optimization parameters for various ground algorithms.

Ground Type	Algorithm Type	Step Size (m)	Step Height (m)	Step Frequency (Hz)	Reward
Rock Ground	Based	0.18	0.07	1	0.6
	PSO	0.073	0.037	1.1	0.65
	GWO	0.097	0.048	0.77	0.66
	NGO	0.086	0.043	0.76	0.66
	TGPSO	0.153	0.076	0.63	0.66
Sand Ground	Based	0.18	0.07	1	0.62
	PSO	0.3	0.148	2.0	0.71
	GWO	0.29	0.144	1.98	0.72
	NGO	0.3	0.145	1.88	0.70
	TGPSO	0.3	0.143	2.00	0.73
Clay Ground	Based	0.18	0.07	1	0.58
	PSO	0.115	0.031	0.65	0.70
	GWO	0.136	0.01	0.5	0.70
	NGO	0.132	0.04	0.57	0.70
	TGPSO	0.117	0.01	0.84	0.71

.

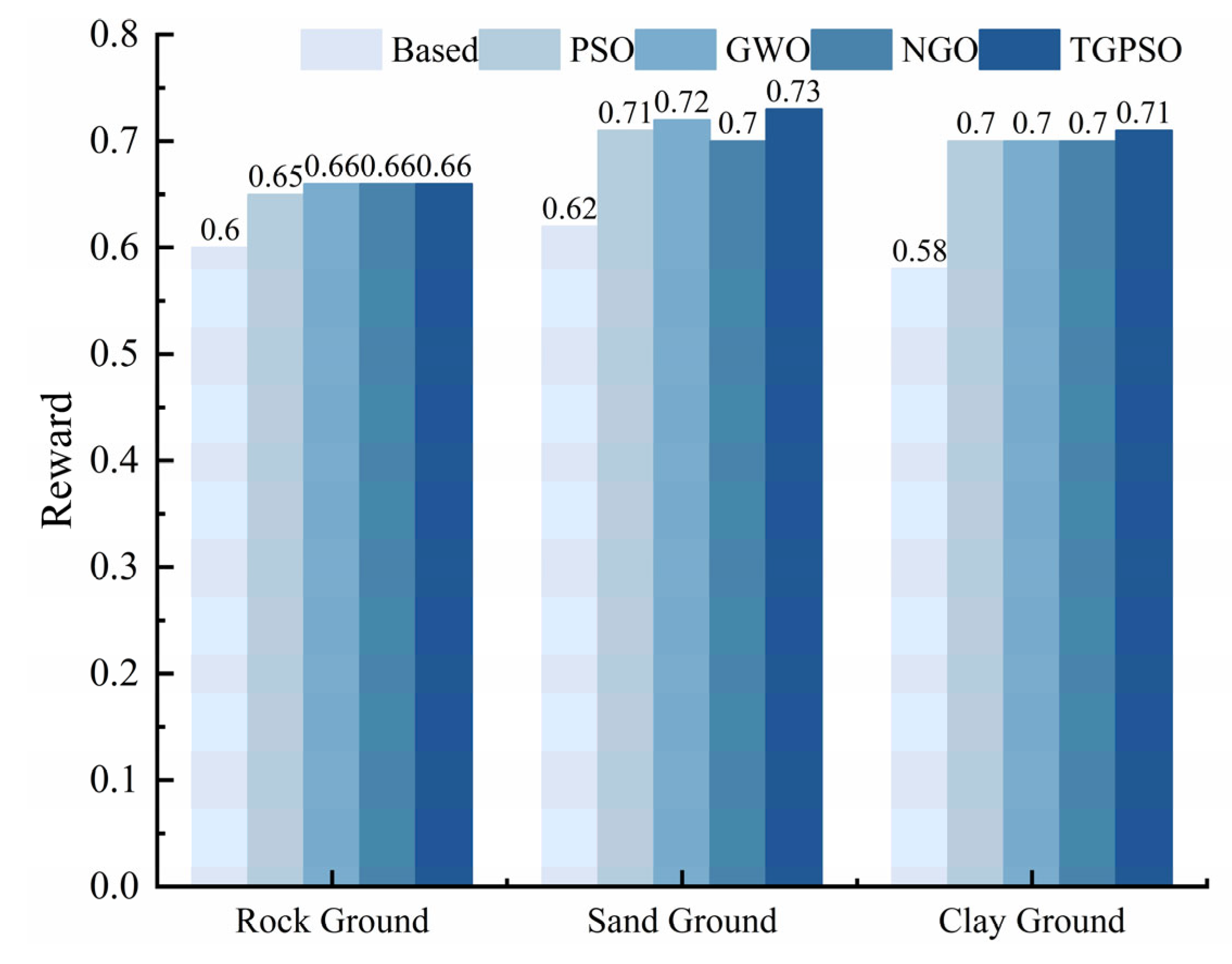
4.1. Rock Ground

Rock ground, as a typical rigid contact interface, possesses mechanical characteristics of high stiffness and low damping, presenting severe challenges to hexapod robot stability control. Based on these terrain characteristics, this study employs a reward function construction strategy with high weighting for stability. The stability indicators optimized by each algorithm are extracted and shown in the following Figure 8.

The simulation results demonstrate that, as shown in Figure 8, the TGPSO algorithm achieves optimal stability indicators in rock ground environments. In terms of stability optimization, the TGPSO algorithm obtained an optimal stability indicator of 0.66, tied for best with NGO, representing a 4.7% improvement over traditional PSO algorithms and a 1% improvement compared to the GWO algorithm. Regarding comprehensive performance, as illustrated in Figure 7, the TGPSO algorithm achieved an optimal reward value of 0.66, tied for best with GWO and NGO algorithms, showing a 10% improvement over traditional fixed parameter strategies and a 1.5% improvement compared to standard PSO algorithms. From the parameter configuration perspective, the algorithm intelligently selected larger step length (0.153 m) and step height (0.076 m) to ensure obstacle-crossing capability, while employing lower step frequency (0.63 Hz) to reduce impact loading, reflecting accurate understanding of the stability-priority strategy for hard ground surfaces. The convergence curves for each algorithm on rock ground are shown in the following Figure 9.

In terms of convergence characteristics, the TGPSO algorithm demonstrates excellent comprehensive performance across multiple aspects. From an optimization accuracy perspective, TGPSO converges to a fitness value of 0.190, significantly outperforming standard PSO’s 0.193 and ranking second among the four algorithms, only after GWO’s 0.188. Regarding convergence curves, TGPSO exhibits a steady and gradual convergence process, reaching stability at iterations 14–16. While its convergence speed is not as rapid as NGO’s jump-style fast convergence, it avoids the potential algorithmic instability and local optimum risks that such abrupt convergence may introduce. Compared to GWO, which has similar convergence timing, TGPSO demonstrates a smoother convergence trajectory with reduced oscillation phenomena during the search process. Relative to standard PSO, TGPSO not only achieves significant improvement in final optimization accuracy but also shows certain enhancement in convergence speed. Overall, TGPSO maintains stable and reliable convergence characteristics while ensuring high optimization accuracy.

4.2. Sand Ground

Sand ground as a typical granular medium terrain, exhibits mechanical characteristics of compressibility combined with good load-bearing capacity. Its cushioning properties and inter-particle friction provide conditions for robots to adopt aggressive motion parameters. Targeting these terrain characteristics, this study constructed an optimization objective system with high weight for speed, medium weight for efficiency, and low weight for stability. Therefore, the comparison of speed indicators optimized by the five experimental groups in this environment is shown in the following Figure 10.

The simulation results demonstrate that the TGPSO algorithm exhibits excellent performance in speed optimization for sand environments, achieving an optimal speed indicator of 0.41, tied for first place with the NGO algorithm. This represents a significant 141% improvement compared to the baseline fixed parameter method, while achieving 20.6% and 13.9% improvements over traditional PSO and GWO algorithms, respectively. Moreover, in the comprehensive reward comparison shown in Figure 6, it obtained the highest reward value in sand environments, showing a 17.7% improvement over traditional fixed parameter strategies (0.62), a 2.8% improvement over standard PSO algorithms (0.71), and a 1.4% improvement over GWO algorithms (0.72), performing optimally among all comparative algorithms. This fully demonstrates that the TGPSO algorithm, through its adaptive parameter adjustment mechanism, can precisely identify the compressibility and good load-bearing characteristics of sand ground. By selecting aggressive motion parameter configurations with maximum step length (0.30 m) and highest step frequency (2.00 Hz), it maximally utilizes the dynamic advantages of this terrain type, achieving optimal results in both individual speed indicators and comprehensive performance trade-offs. The convergence curves for each algorithm on sand ground are shown in the following Figure 11.

From a convergence performance perspective, the TGPSO algorithm achieves stable convergence within 18 iterations, representing a 28% improvement in convergence speed compared to the standard PSO algorithm (25 iterations), with the entire optimization process being smooth and monotonic, successfully avoiding the local optimum trap that PSO encounters during iterations 3–10. Compared to other advanced algorithms, TGPSO demonstrates a more stable descent trajectory than NGO in terms of convergence stability, avoiding the severe fluctuations that NGO experiences in the initial phase, while maintaining convergence smoothness comparable to GWO. From the perspective of final optimization accuracy, TGPSO converges to the optimal value, significantly outperforming PSO, GWO, and NGO, indicating that TGPSO achieves an effective balance between convergence efficiency and algorithmic stability while ensuring optimal solution quality.

4.3. Clay Ground

Clay ground represents the most challenging terrain environment, characterized by semi-fluid deformable contact properties. The surface bearing capacity is significantly weaker than the previous two terrain types and prone to severe foot sinkage phenomena, necessitating that robots adopt transportation cost-priority strategies centered on anti-entrapment and extrication capabilities. Based on the stringent constraints imposed by this terrain, this study designed a reward function architecture with high efficiency weighting, medium speed weighting, and low stability weighting. The comparison of Cost of Transport (COT) metrics optimized for five experimental groups under these environmental conditions is illustrated in the following Figure 12.

The simulation results comprehensively validate the technical advantages of the TGPSO algorithm under complex constrained environments. TGPSO achieved the lowest transportation cost and obtained an optimal reward value of 0.71 in comprehensive evaluation, representing a significant 22.4% improvement over traditional fixed parameter strategies (0.58) and a 1.4% enhancement compared to standard PSO, GWO, and NGO algorithms (all achieving 0.70). The algorithm demonstrates exceptionally refined anti-entrapment optimization capabilities, optimizing step height to an extremely low value of 0.01 m to maximize sinkage risk reduction, while selecting moderate step length (0.135 m) and minimum step frequency (0.51 Hz) to ensure stable locomotion on soft terrain surfaces. This reflects the algorithm’s profound understanding and precise adaptation to complex terrain constraints. The convergence curves of all algorithms on clay ground are shown in Figure 13.

In terms of convergence efficiency, TGPSO achieves stable convergence within approximately 10–12 iterations, significantly improving convergence speed compared to standard PSO’s 15–20 iterations, demonstrating excellent search efficiency. From the algorithm stability perspective, TGPSO exhibits ideal smooth progressive convergence characteristics with stable and controllable optimization processes, avoiding the premature convergence issues that may arise from the rapid convergence patterns of NGO and GWO algorithms (which experience sharp decline within the first 5–8 iterations), thereby ensuring comprehensive exploration of the solution space. Regarding optimization accuracy, TGPSO ultimately converges to a fitness value of approximately 0.169, markedly superior to the values around 0.173 achieved by the other three algorithms, reflecting stronger global optimization capabilities. In summary, TGPSO successfully achieves an optimal balance among convergence speed, algorithm stability, and optimization accuracy, obtaining superior solution quality while ensuring comprehensive search thoroughness.

5. Conclusions

This study focuses on hexapod robots and addresses the requirements for efficient locomotion across multi-material terrain environments by designing an adaptive gait optimization method that incorporates foot-terrain sinkage models. The significance of this research lies in providing theoretical foundations and technical support for bottom-dwelling hexapod robots operating in complex environments, offering important reference for subsequent research in intelligent robot motion control and environmental adaptability. The specific contributions include:

• Proposed the TGPSO optimization algorithm, which integrates foot sinkage detection mechanisms and dynamic weight adjustment strategies. Through Latin hypercube sampling, linearly decreasing inertia weights, and stagnation exploration mechanisms, it effectively addresses the local optima entrapment issues inherent in traditional PSO algorithms, significantly enhancing global search capabilities and convergence stability.
• Established a unified terrain-adaptive reward function framework that dynamically adjusts the weighting coefficients for speed, stability, and transportation cost based on foot sinkage measurements. For three typical terrain types— rock ground, sand ground, and clay ground—adaptive adjustment of optimization objectives was achieved.
• Validation through the Simulink of MatlabR2023b simulation platform demonstrated that the TGPSO algorithm achieved superior locomotion performance across all terrain conditions, while exhibiting excellent performance in center-of-mass fluctuation control, fully demonstrating the algorithm’s technical advantages in multi-material surface motion control.

While this study demonstrates the effectiveness of the TGPSO algorithm in simulation environments, we acknowledge that inherent differences exist between computational modeling and real-world implementation. In future work, we will focus on extending the algorithm’s applicability to geometrically complex terrain scenarios including slopes, obstacles, and irregular surfaces; conducting validation experiments on physical robot platforms to evaluate the algorithm’s robustness and practicality in real environments; and integrating online path planning methods to combine gait optimization with dynamic path planning, enhancing the algorithm’s real-time path adaptation capabilities and complex environment navigation performance, thereby providing more comprehensive technical solutions for the engineering applications of hexapod robots.