Research on Energy Consumption Optimization Strategies of Robot Joints Based on NSGA-II and Energy Consumption Mapping
Abstract
1. Introduction
2. Kinematics and Dynamics Modeling
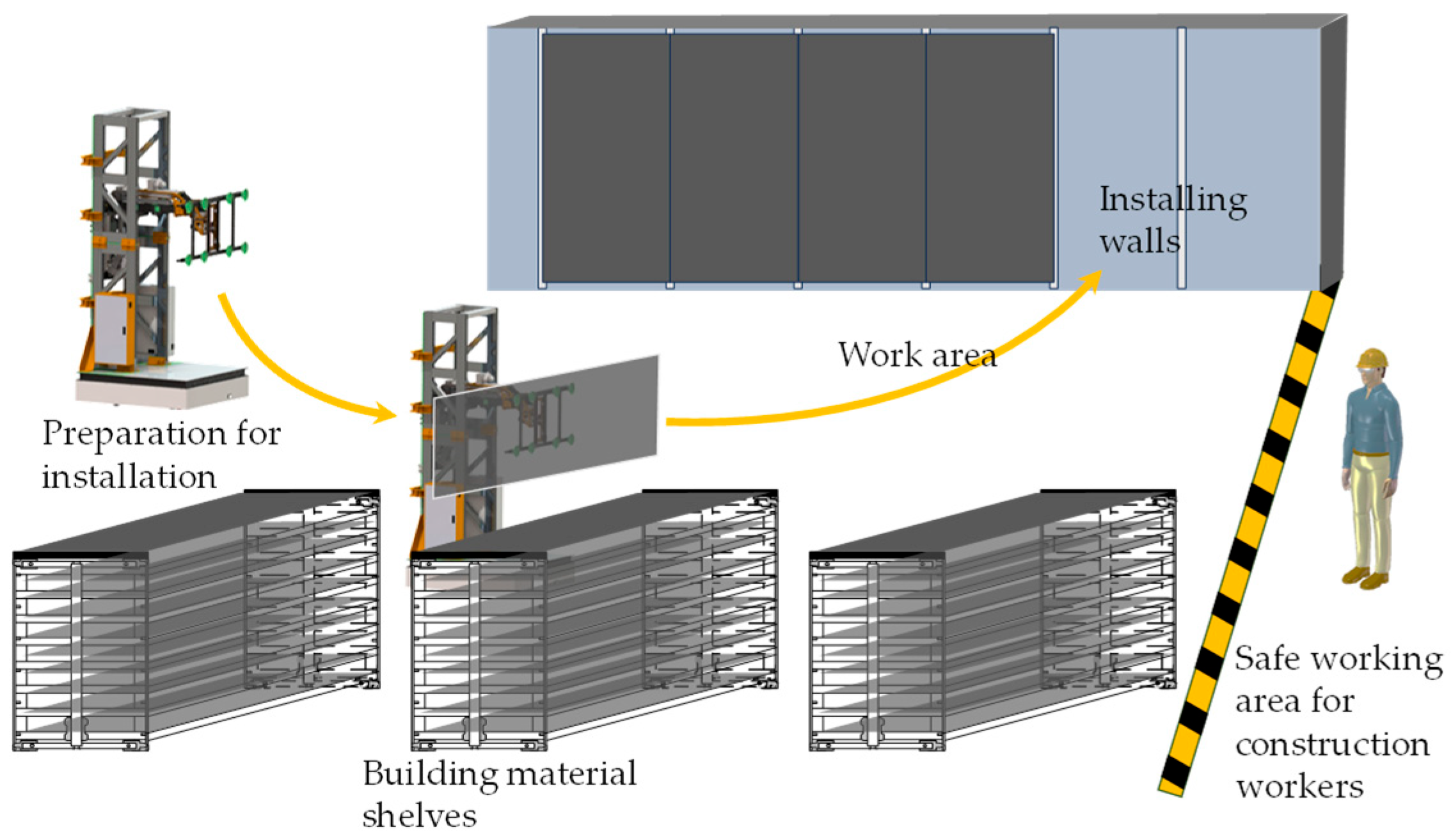
2.1. Kinematics Analysis of the Building Slabstone-Installing Robot
2.2. Dynamic Analysis of the Building Slabstone-Installing Robot
3. Robot Energy Consumption Optimization Strategy
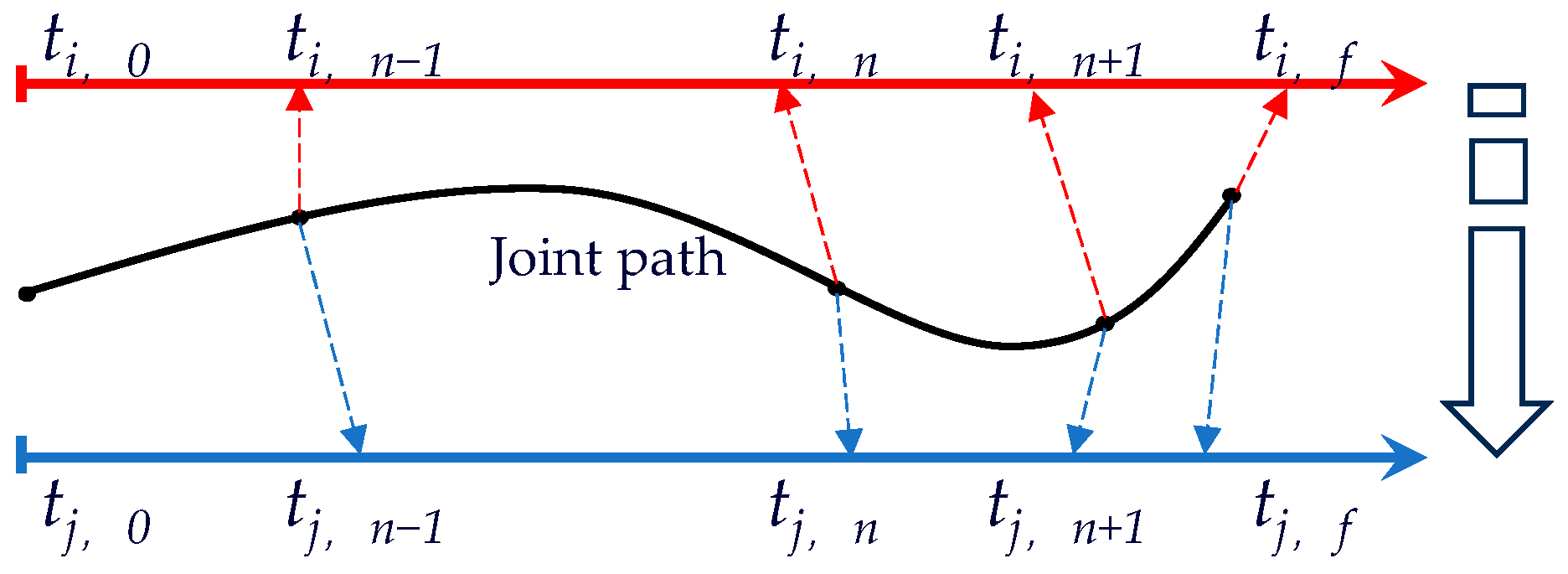
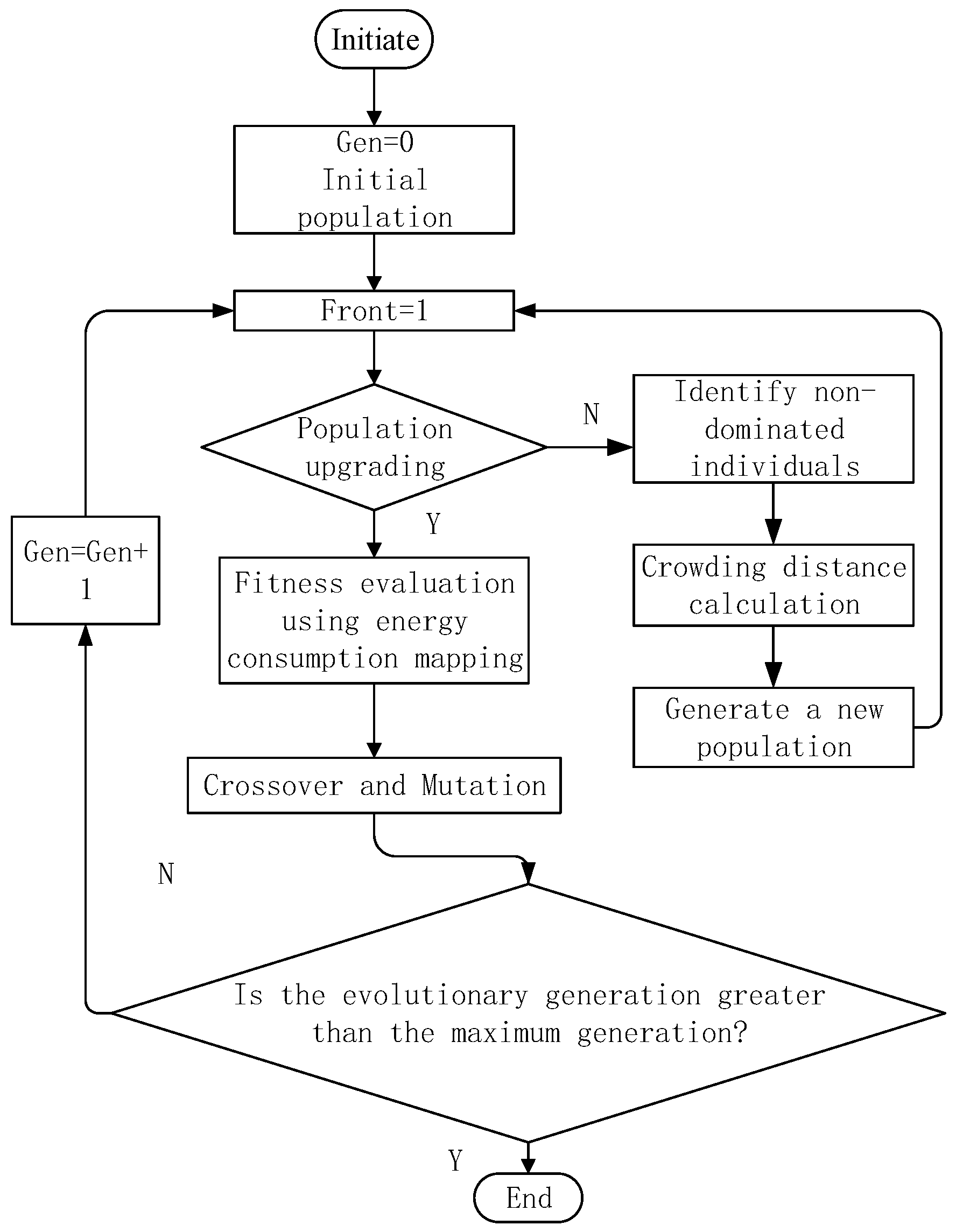
3.1. Multi-Objective Optimization Algorithm
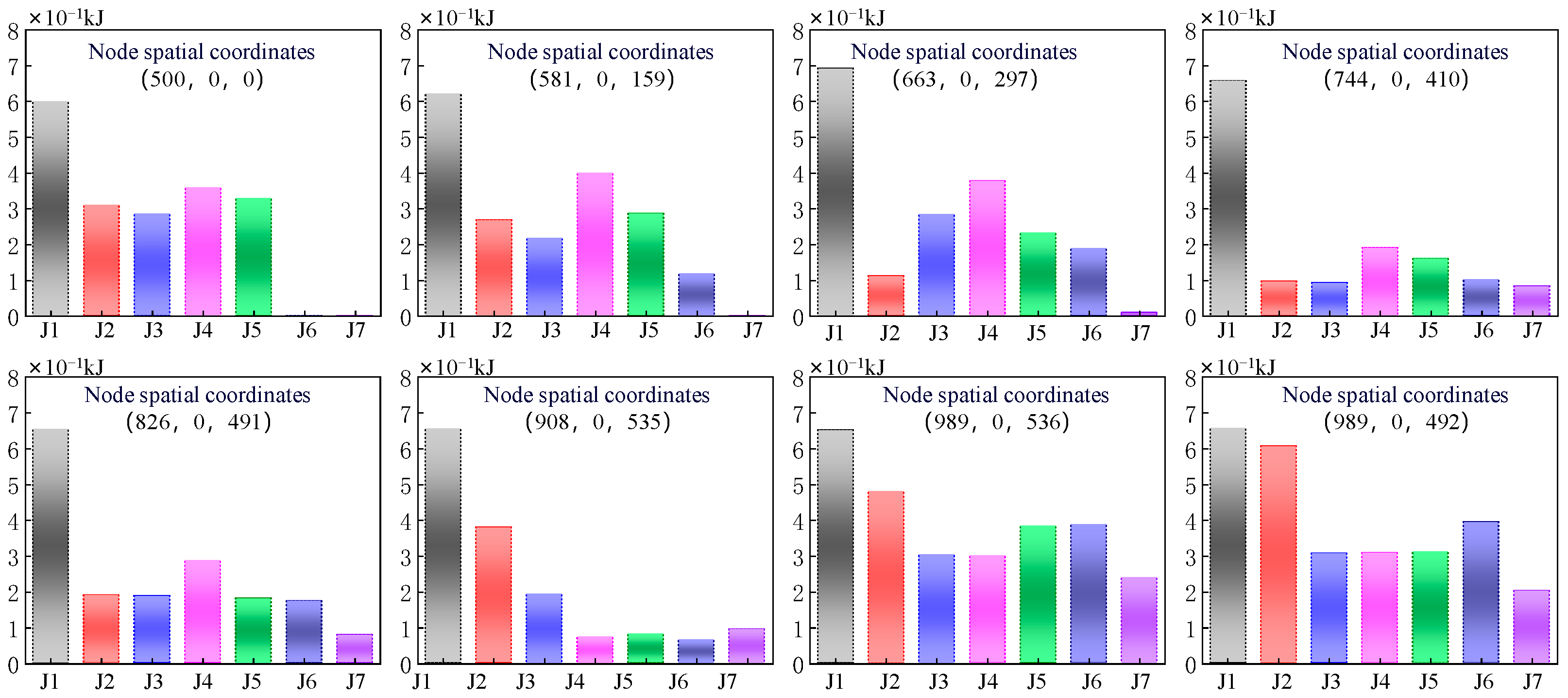
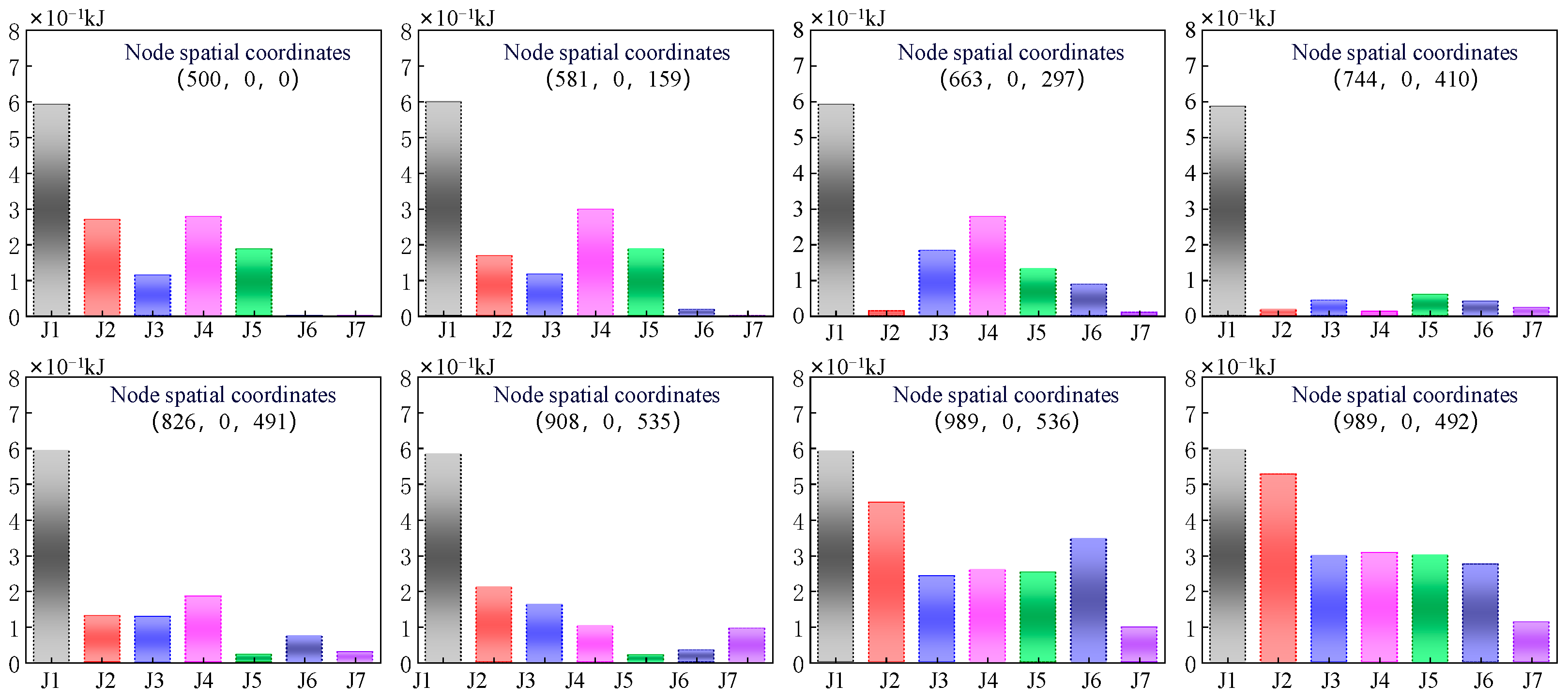
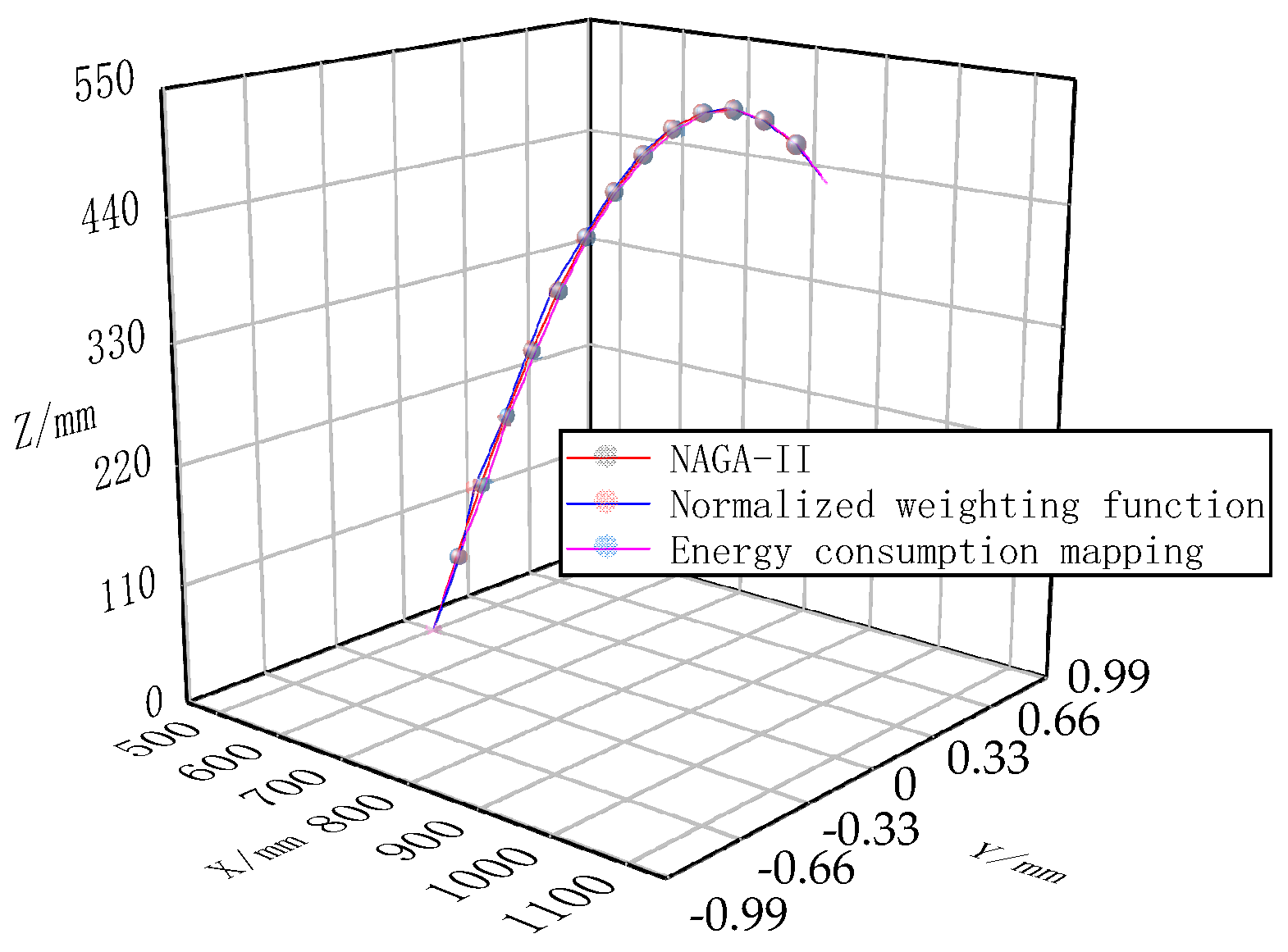
3.2. Dynamic Optimization Result
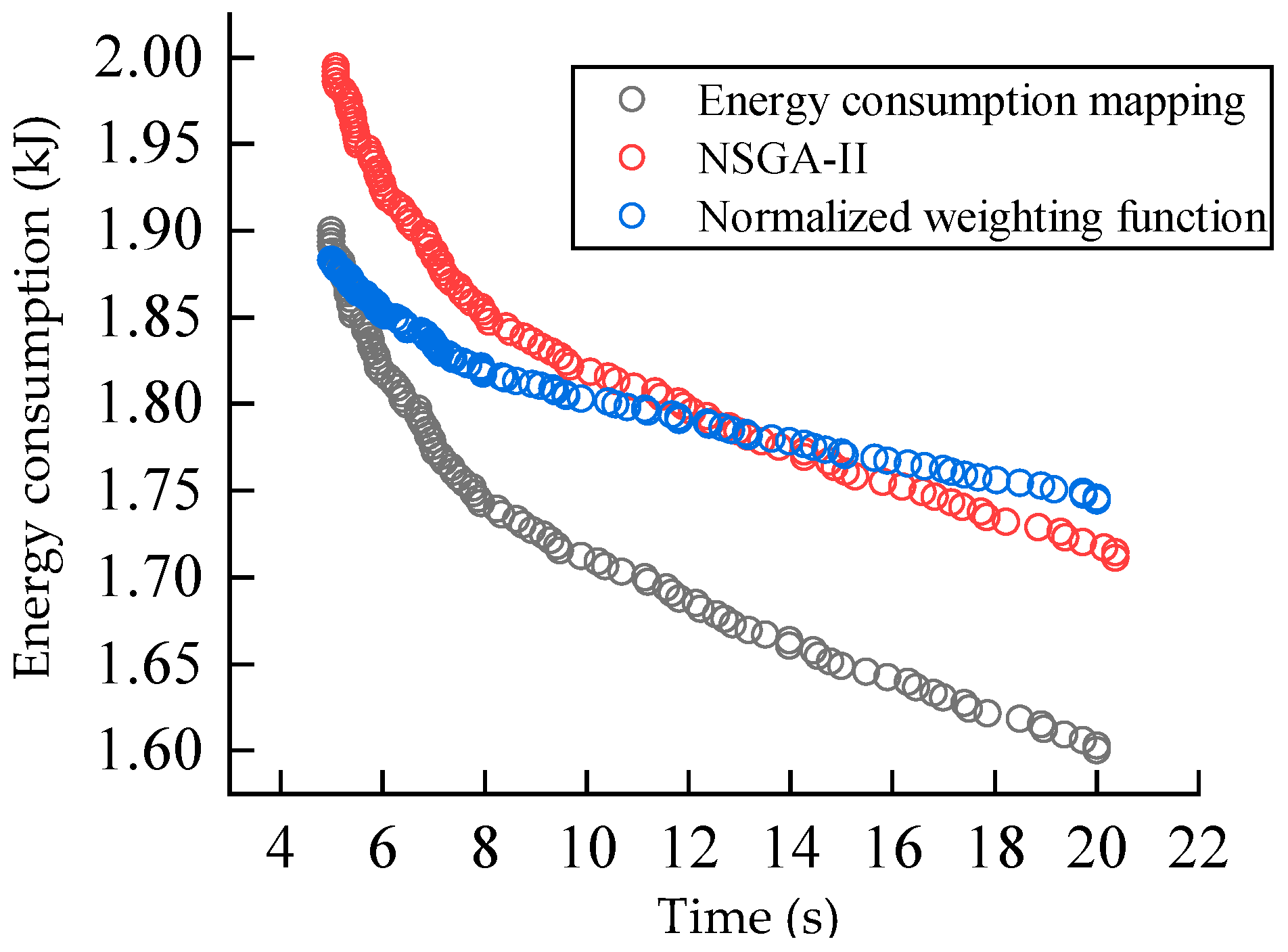
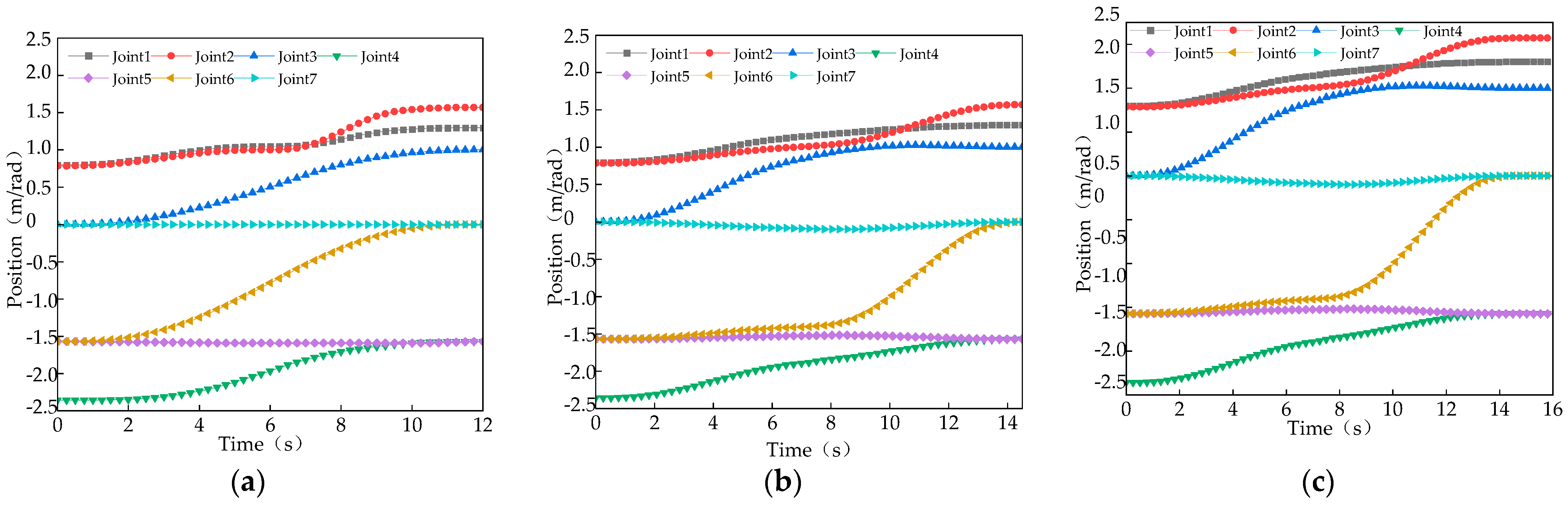
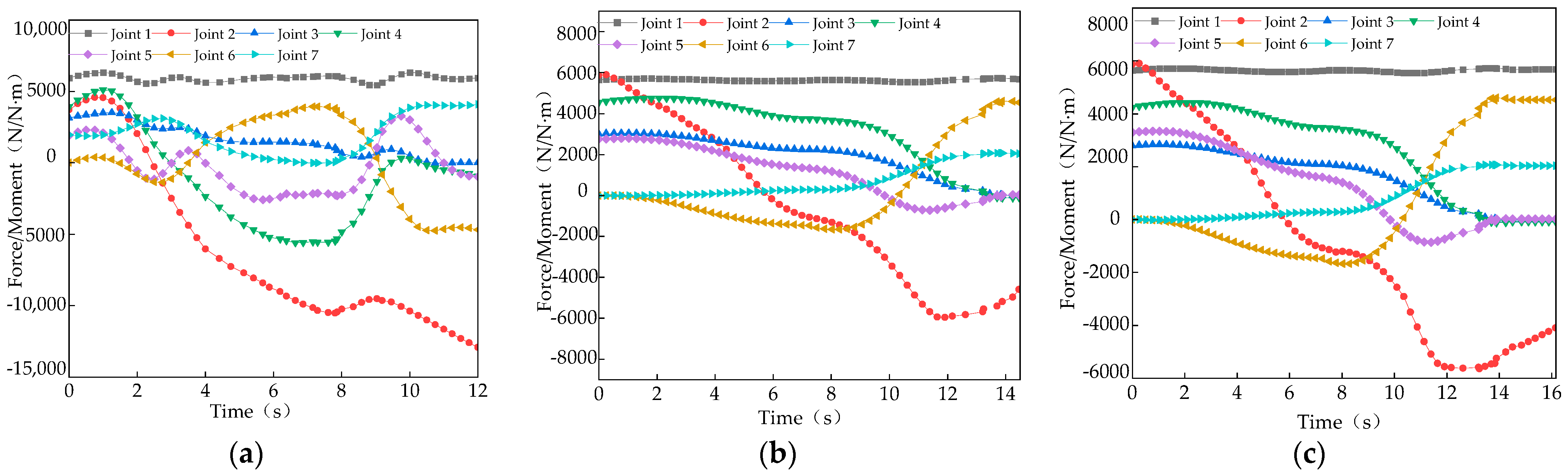
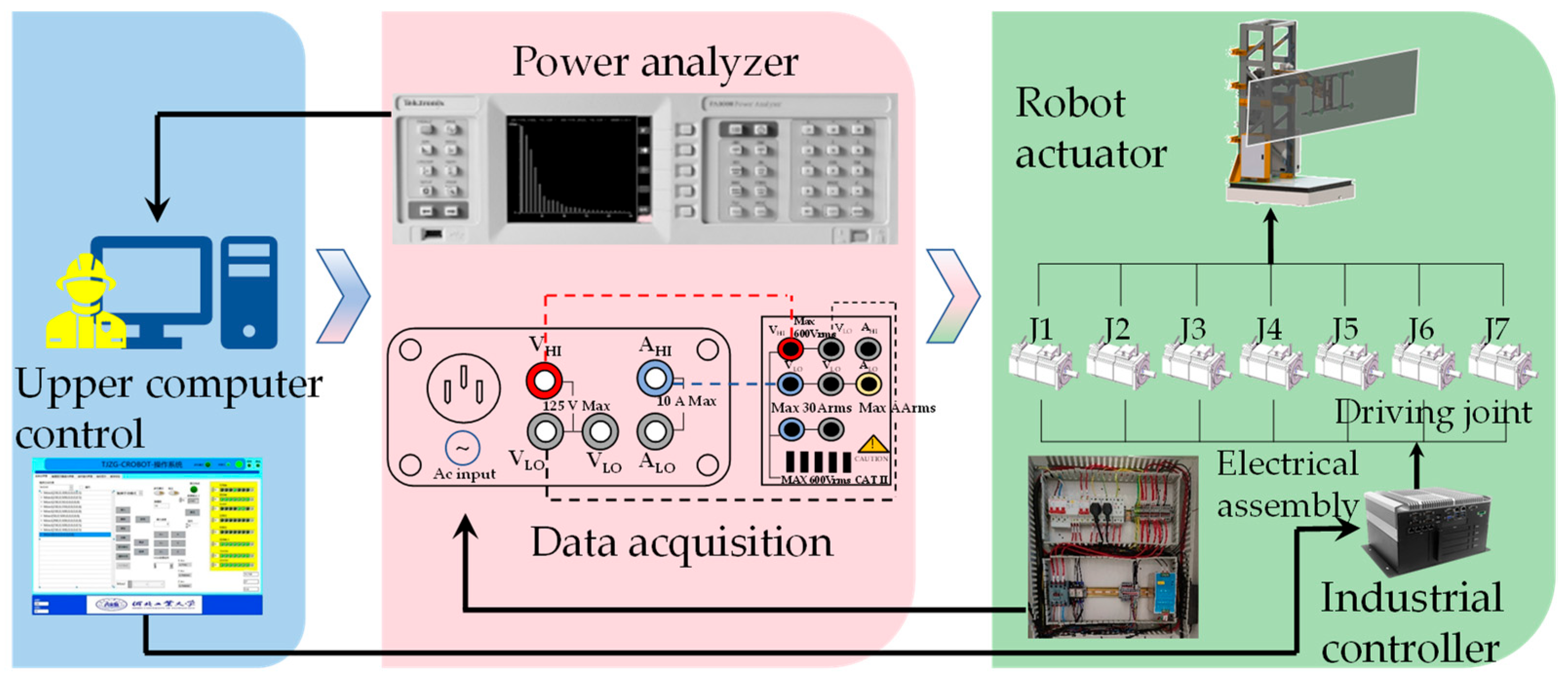
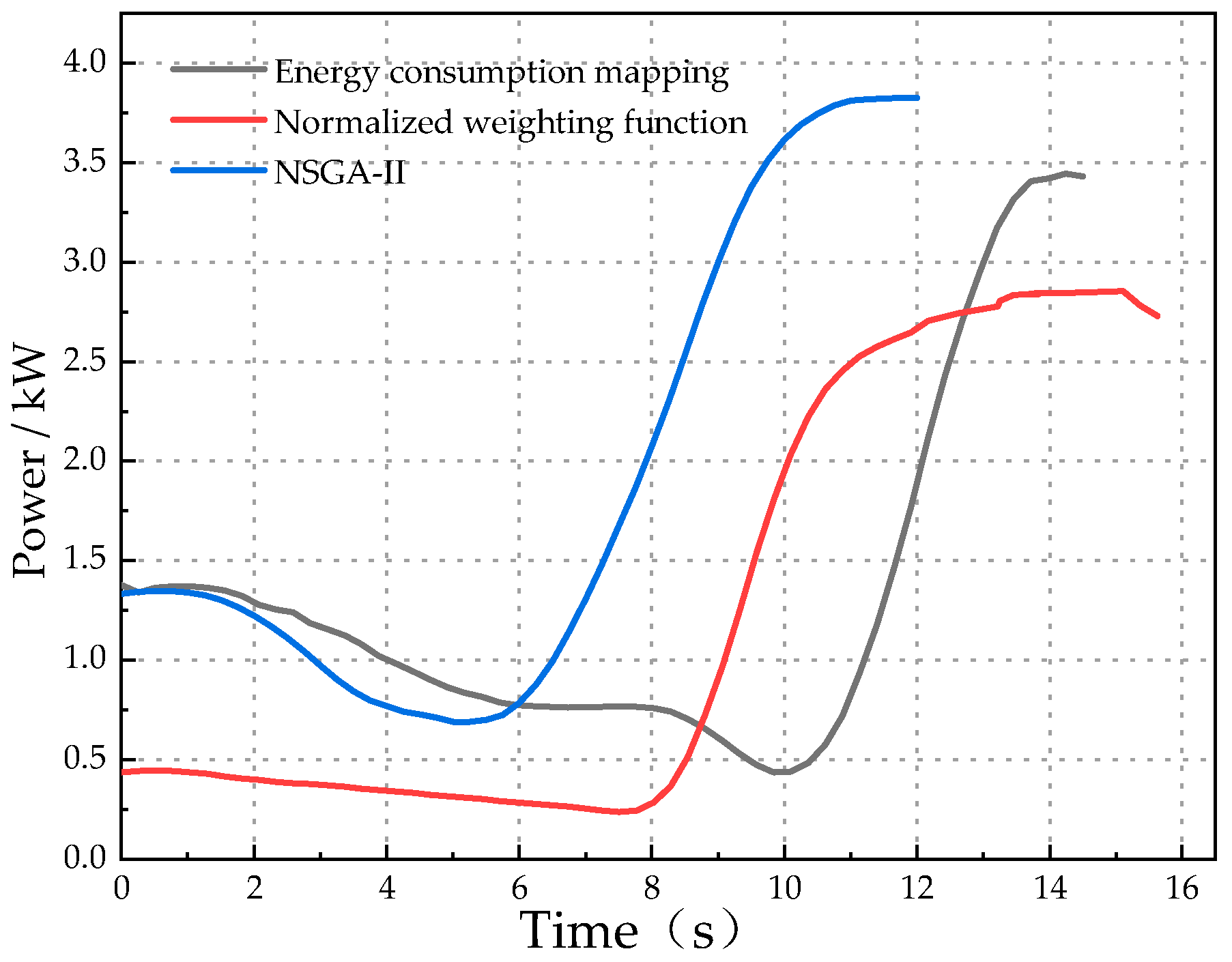
4. Experimental Conditions and Results
5. Conclusions
- (1).
- The introduction of energy consumption mapping: The energy consumption distribution model of the workspace is constructed to provide guidance for the identification of low-energy-consumption areas in the optimization process, which is of great significance for improving the energy efficiency of the robot.
- (2).
- Multi-objective optimization combined with the NSGA-II: Through the NSGA-II, we aim to achieve a balance between minimizing energy consumption and time and generate a Pareto-optimal solution set. This provides an effective solution for multi-objective optimization, especially for applications in complex task environments.
- (3).
- Dynamic feedback mechanism: In the optimization process, relying on energy consumption mapping, the population distribution is adjusted in real time, thus improving the convergence of the algorithm and enhancing the uniformity of the solution set.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Soori, M.; Arezoo, B.; Dastres, R. Optimization of energy consumption in industrial robots, a review. Cogn. Robot. 2023, 3, 142–157. [Google Scholar] [CrossRef]
- Bugmann, G.; Siegel, M.; Burcin, R. A role for robotics in sustainable development? In Proceedings of the IEEE Africon ’11, Victoria Falls, Zambia, 13–15 September 2011; pp. 1–4. [Google Scholar]
- Bouaziz, N.E.I.; Mechali, O.; Besseghieur, K.L.; Achour, N. Trajectory Planning for Autonomous Formation of Wheeled Mobile Robots via Modified Artificial Potential Field and Improved PSO Algorithm. Unmanned Syst. 2024, 12, 1085–1104. [Google Scholar] [CrossRef]
- Pellicciari, M.; Berselli, G.; Leali, F.; Vergnano, A. A method for reducing the energy consumption of pick-and-place industrial robots. Mechatronics 2013, 23, 326–334. [Google Scholar] [CrossRef]
- Mohammed, A.; Schmidt, B.; Wang, L.; Gao, L. Minimizing energy consumption for robot arm movement. Procedia CIRP 2014, 25, 400–405. [Google Scholar] [CrossRef]
- Van Oosterwyck, N.; Vanbecelaere, F.; Knaepkens, F.; Monte, M.; Stockman, K.; Cuyt, A.; Derammelaere, S. Energy optimal point-to-point motion profile optimization. Mech. Based Des. Struct. Mach. 2024, 52, 239–256. [Google Scholar] [CrossRef]
- Nonoyama, K.; Liu, Z.; Fujiwara, T.; Alam, M.M.; Nishi, T. Energy-efficient robot configuration and motion planning using genetic algorithm and particle swarm optimization. Energies 2022, 15, 2074. [Google Scholar] [CrossRef]
- He, Y.; Mei, J.; Fang, Z.; Zhao, Y. Minimum Energy Trajectory Optimization for Driving Systems of Palletizing Robot Joints. Math. Probl. Eng. 2018, 2018, 7247093. [Google Scholar] [CrossRef]
- Qie, X.; Kang, C.; Zong, G.; Chen, S. Trajectory Planning and Simulation Study of Redundant Robotic Arm for Upper Limb Rehabilitation Based on Back Propagation Neural Network and Genetic Algorithm. Sensors 2022, 22, 4071. [Google Scholar] [CrossRef]
- Benghezal, A.; Nemra, A.; Bouaziz, N.E.I.; Tadjine, M. New robust backstepping attitude control approach applied to quanser 3 DOF hover quadrotor in the case of actuators faults. Unmanned Syst. 2024, 12, 3–17. [Google Scholar] [CrossRef]
- Cui, Y.; Geng, Z.; Zhu, Q.; Han, Y. Multi-objective optimization methods and application in energy saving. Energy 2017, 125, 681–704. [Google Scholar] [CrossRef]
- Serralheiro, W.; Maruyama, N.; Saggin, F. Self-Tuning Time-Energy Optimization for the Trajectory Planning of a Wheeled Mobile Robot. J. Intell. Robot. Syst. 2019, 95, 987–997. [Google Scholar] [CrossRef]
- Ma, H.P.; Zhang, Y.J.; Sun, S.Y.; Liu, T.; Shan, Y. A comprehensive survey on NSGA-II for multi-objective optimization and applications. Artif. Intell. Rev. 2023, 56, 15217–15270. [Google Scholar] [CrossRef]
- Holzmann, P.; Pfefferkorn, M.; Peters, J.; Findeisen, R. Learning Energy-Efficient Trajectory Planning for Robotic Manipulators Using Bayesian Optimization. In Proceedings of the 2024 European Control Conference, Stockholm, Sweden, 25–28 June 2024; pp. 1374–1379. [Google Scholar]
- Paryanto; Brossog, M.; Bornschlegl, M.; Franke, J. Reducing the energy consumption of industrial robots in manufacturing systems. Int. J. Adv. Manuf. Technol. 2015, 78, 1315–1328. [Google Scholar] [CrossRef]
- Quann, M.; Ojeda, L.; Smith, W.; Rizzo, D.; Castanier, M.; Barton, K. Off-road ground robot path energy cost prediction through probabilistic spatial map. J. Field Robot. 2020, 37, 421–439. [Google Scholar] [CrossRef]
- Tipary, B.; Kovács, A.; Erdős, F.G. Planning and optimization of robotic pick-and-place operations in highly constrained industrial environments. Assem. Autom. 2021, 41, 626–639. [Google Scholar] [CrossRef]
- Bilal, H.; Yin, B.; Kumar, A.; Ali, M.; Zhang, J.; Yao, J. Jerk-bounded trajectory planning for rotary flexible joint manipulator: An experimental approach. Soft Comput. 2023, 27, 4029–4039. [Google Scholar] [CrossRef]
- Bonello, A.; Refalo, P.; Francalanza, E. The Impacts of Industrial Safety on Environmental Sustainability in Human-Robot-Collaboration within Industry 5.0. Procedia CIRP 2024, 122, 282–287. [Google Scholar] [CrossRef]
- Kong, M.X.; Chen, L.; Du, Z.; Sun, L. Multi-objective Optimization on Dynamic Performance for a Planar Parallel Mechanism with NSGA-II Algorithm. Robot 2010, 32, 271–277. [Google Scholar] [CrossRef]
- Llopis-Albert, C.; Rubio, F.; Valero, F. Improving productivity using a multi-objective optimization of robotic trajectory planning. J. Bus. Res. 2015, 68, 1429–1431. [Google Scholar] [CrossRef]
- Zhang, P.; Yao, Z.; Du, Z. Global performance index system for kinematic optimization of robotic mechanism. J. Mech. Des. 2014, 136, 031001. [Google Scholar] [CrossRef]
- Yang, C.; Ye, W.; Li, Q. Review of the performance optimization of parallel manipulators. Mech. Mach. Theory 2022, 170, 104725. [Google Scholar] [CrossRef]
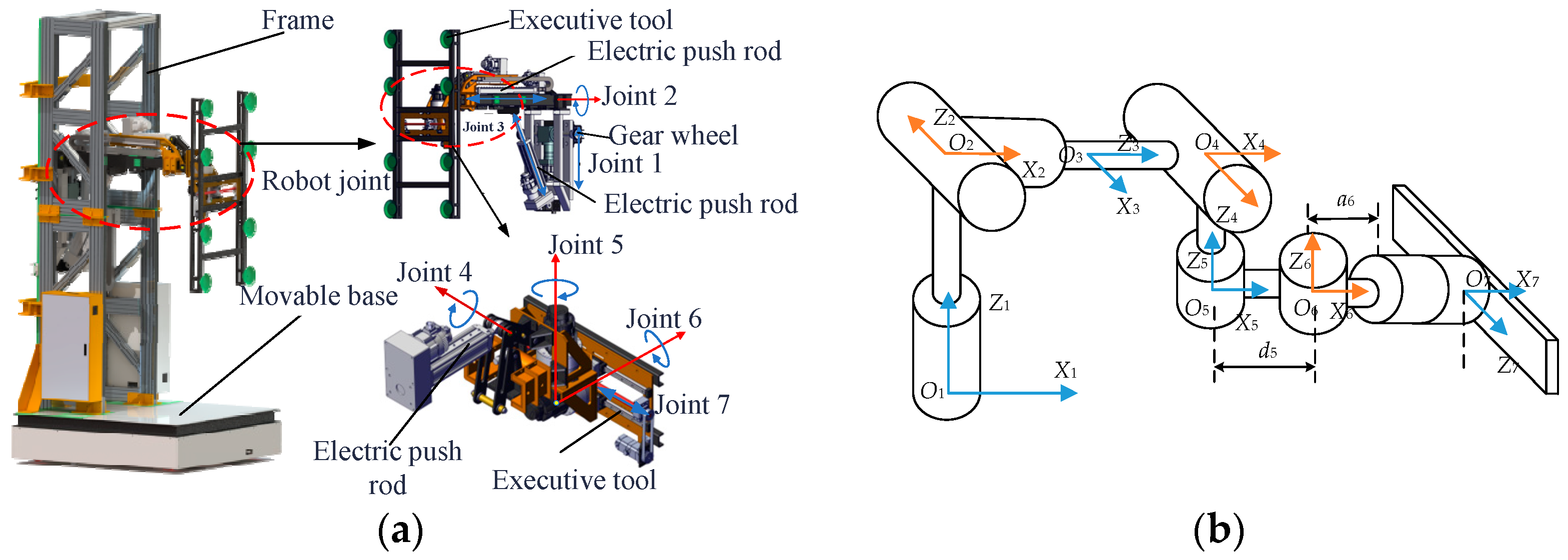

| Joint i | Joint 1 | Joint 2 | Joint 3 | Joint 4 | Joint 5 | Joint 6 | Joint 7 |
|---|---|---|---|---|---|---|---|
| 0 | 0 | 0 | |||||
| [0,2] | 0 | [0,1] | 0 | −0.234 | 0 | [0,0.511] | |
| 0 | 0 | 0 | 0 | 0 | 0.158 | 0 | |
| 0 |
| Joint i | Speed (m/s) | Acceleration (rad/s) | Joint i | Angular Velocity (m/s2) | Angular Acceleration (rad/s2) |
|---|---|---|---|---|---|
| Joint 1 | 0.113 | 3.54 | Joint 2 | 1.298 | 1.5 |
| Joint 3 | 0.0625 | 5.85 | Joint 4 | 1.298 | 1.5 |
| Joint 7 | 0.0625 | 3 | Joint 5 | 1.298 | 1.39 |
| Joint 6 | 1.298 | 1.5 |
| Link | Quality | The Centroid of the Link | Moment of Inertia (kg × mm2) | |||||
|---|---|---|---|---|---|---|---|---|
| i | mi (kg) | Pci (m) | ||||||
| 1 | 61.789 | [0,0,2] | 292.555 | 289.489 | 3.74 | 0.003 | 5.615 | 0.042 |
| 2 | 89.005 | [0.319,0,2] | 503.141 | 520.203 | 19.36 | 0.003 | 69.689 | 0.014 |
| 3 | 136 | [0.644,0,2] | 987.691 | 1065.702 | 89.428 | 4.662 | 230.985 | 33.607 |
| 4 | 45.071 | [0.982,0,2] | 418.916 | 473.879 | 55.372 | 0.311 | 146.069 | 0.568 |
| 5 | 29.761 | [1.6,0,1.7] | 191.376 | 269.935 | 78.856 | 0.319 | 122.493 | 0.217 |
| 6 | 28.402 | [1.6,0,1.7] | 152.392 | 231.974 | 79.808 | 0.136 | 110.012 | 0.189 |
| 7 | 16.032 | [1.9,0,1.7] | 84.97 | 138.695 | 54.17 | 0.597 | 67.293 | 0.668 |
| Parameters and Names | Value |
|---|---|
| Population size N | 200 |
| Competition scale St | 2 |
| Crossover probability Pc | 0.5 |
| Mutation probability Pm | 0.9 |
| Maximum generation G | 500 |
| Argument | |||||
|---|---|---|---|---|---|
| Value | 0.2 | 0.2 | 0.6 | 0.5 | 0.5 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Yang, D.; Wei, X.; Han, M. Research on Energy Consumption Optimization Strategies of Robot Joints Based on NSGA-II and Energy Consumption Mapping. Robotics 2025, 14, 138. https://doi.org/10.3390/robotics14100138
Yang D, Wei X, Han M. Research on Energy Consumption Optimization Strategies of Robot Joints Based on NSGA-II and Energy Consumption Mapping. Robotics. 2025; 14(10):138. https://doi.org/10.3390/robotics14100138
Chicago/Turabian StyleYang, Dong, Xin Wei, and Ming Han. 2025. "Research on Energy Consumption Optimization Strategies of Robot Joints Based on NSGA-II and Energy Consumption Mapping" Robotics 14, no. 10: 138. https://doi.org/10.3390/robotics14100138
APA StyleYang, D., Wei, X., & Han, M. (2025). Research on Energy Consumption Optimization Strategies of Robot Joints Based on NSGA-II and Energy Consumption Mapping. Robotics, 14(10), 138. https://doi.org/10.3390/robotics14100138





