Enhanced Design of an Adaptive Anthropomorphic Finger through Integration of Modular Soft Actuators and Kinematic Modeling †
Abstract
1. Introduction
2. Methods
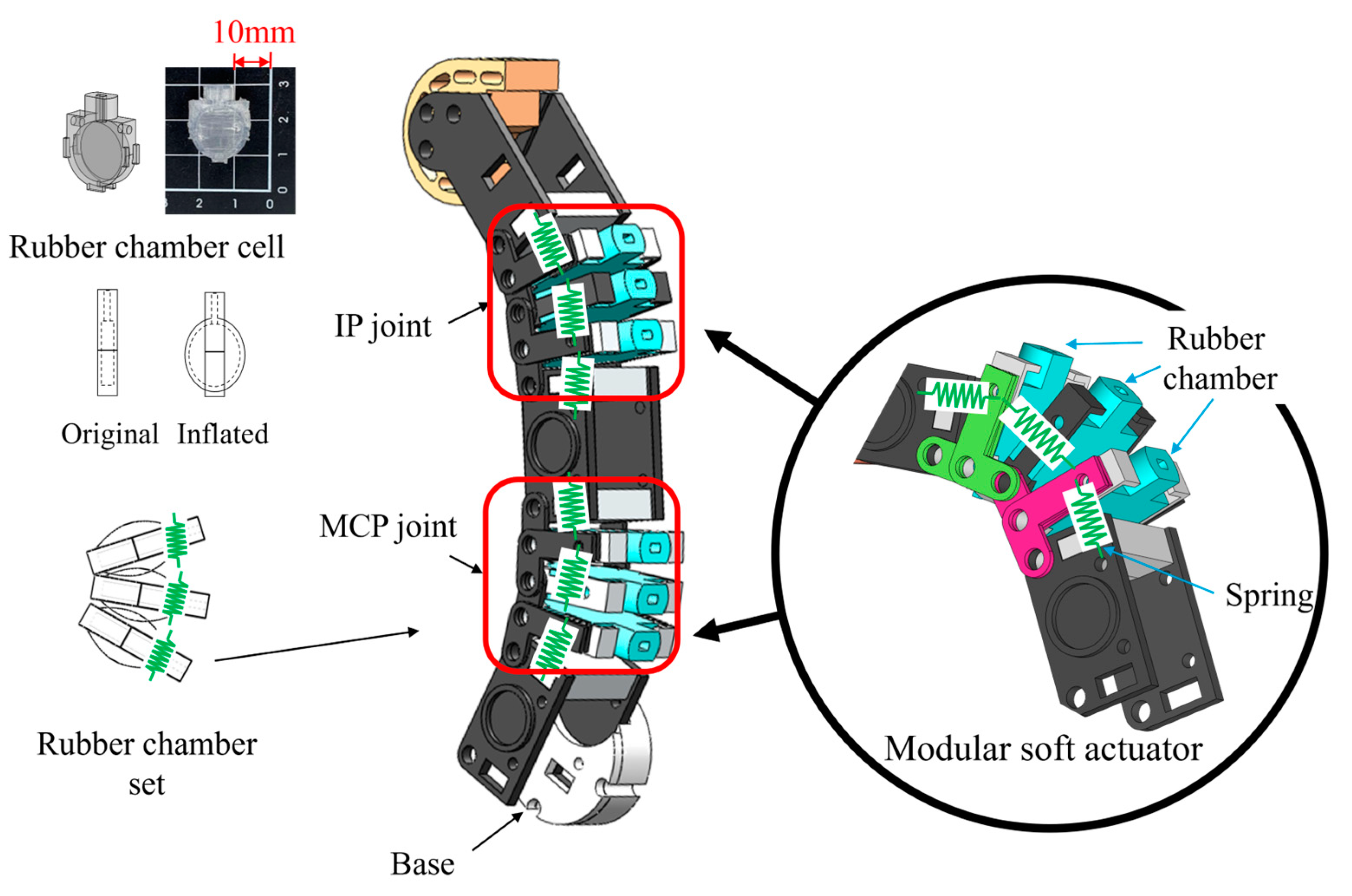
2.1. Modular Soft Actuator (MSA)
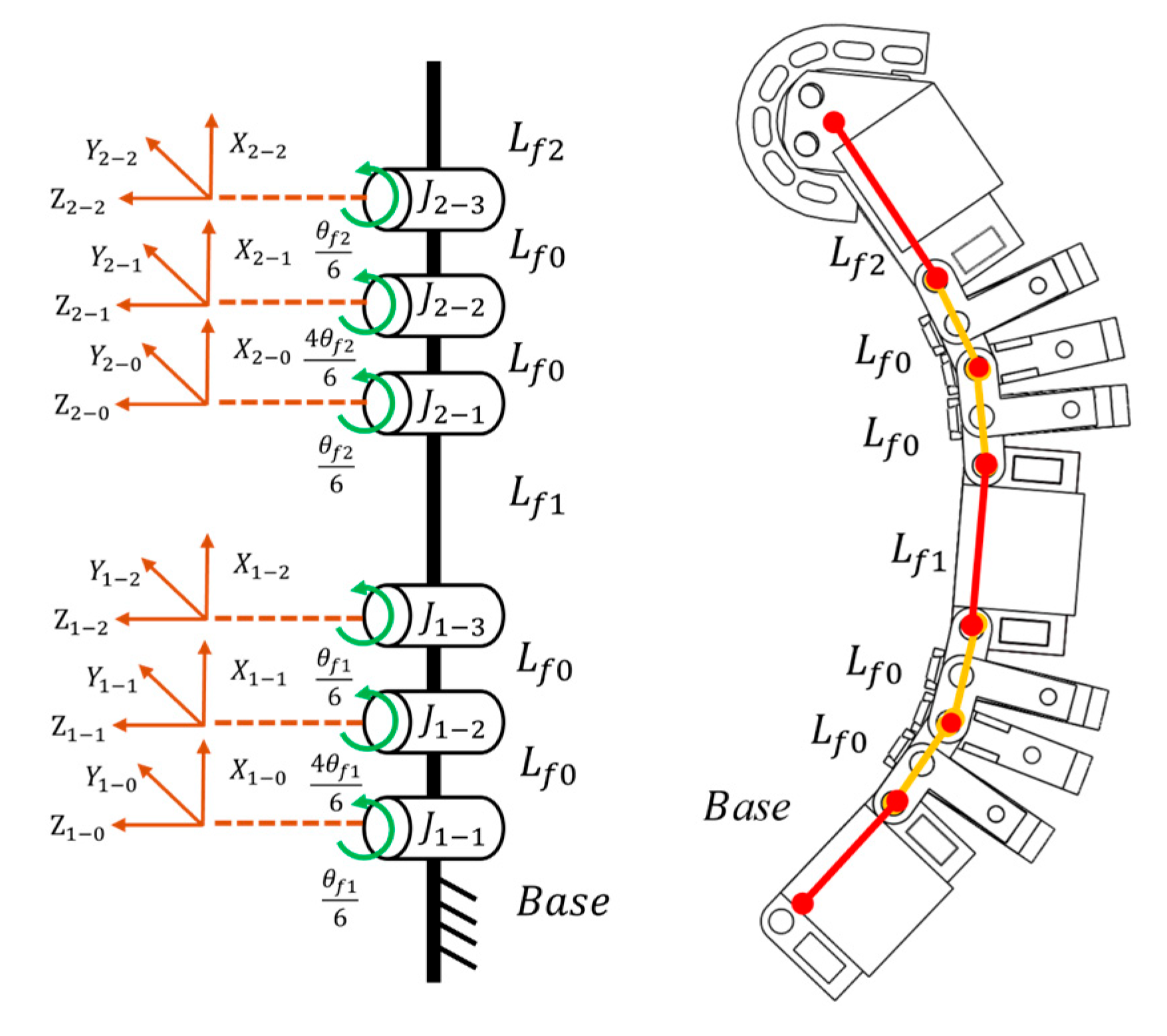
2.2. Kinematics
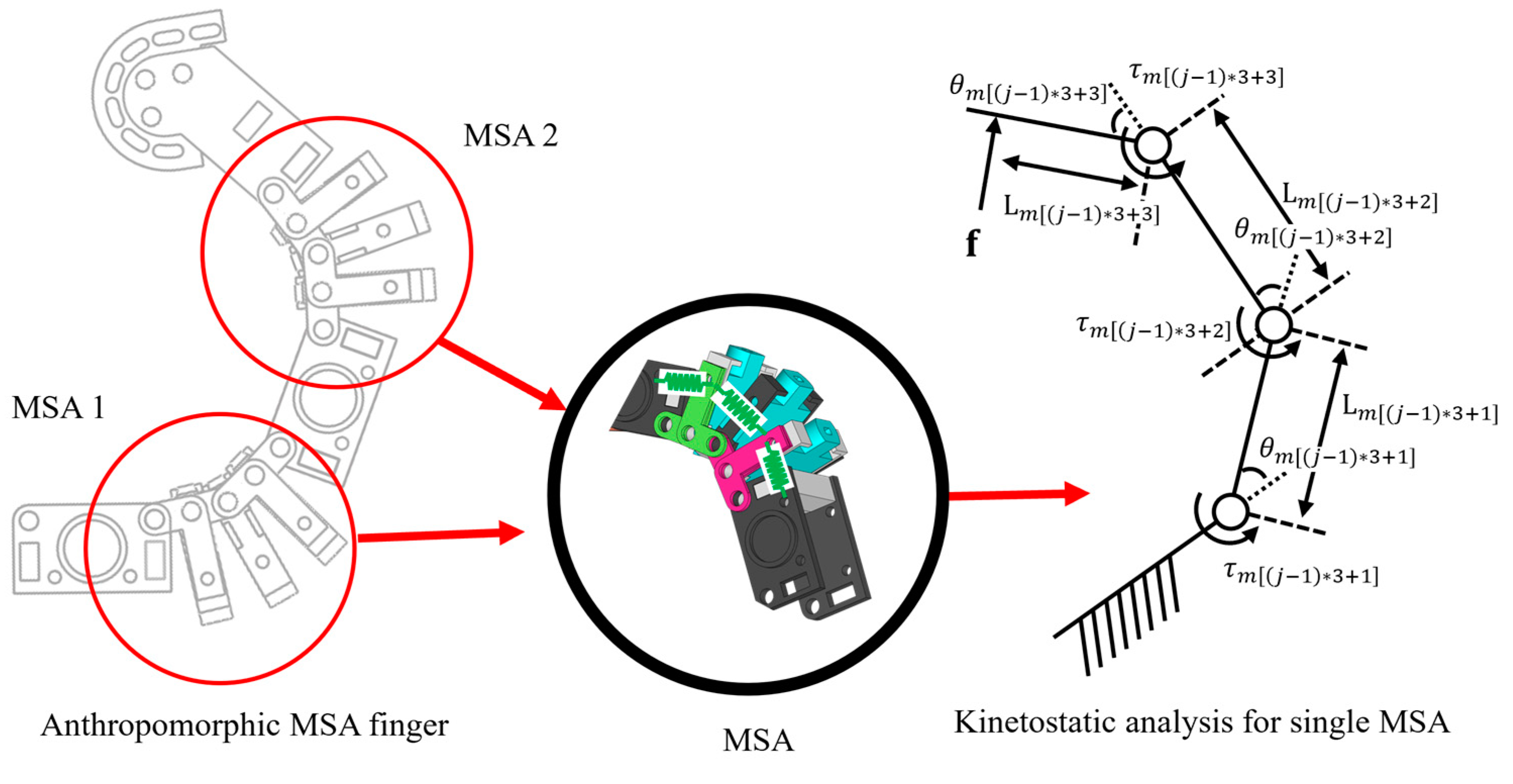
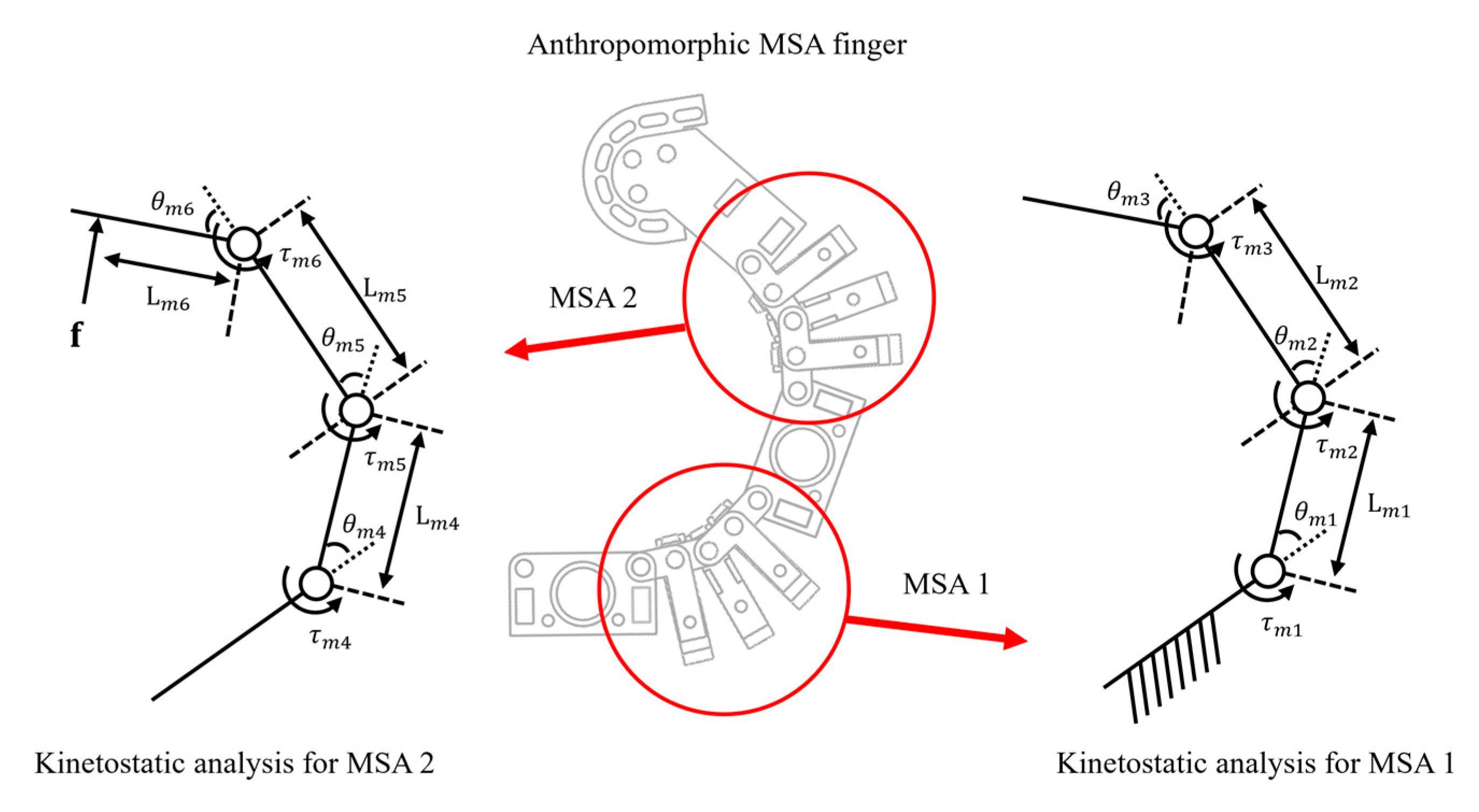
2.3. Kinetostatic
2.4. Experiment
3. Results and Discussion
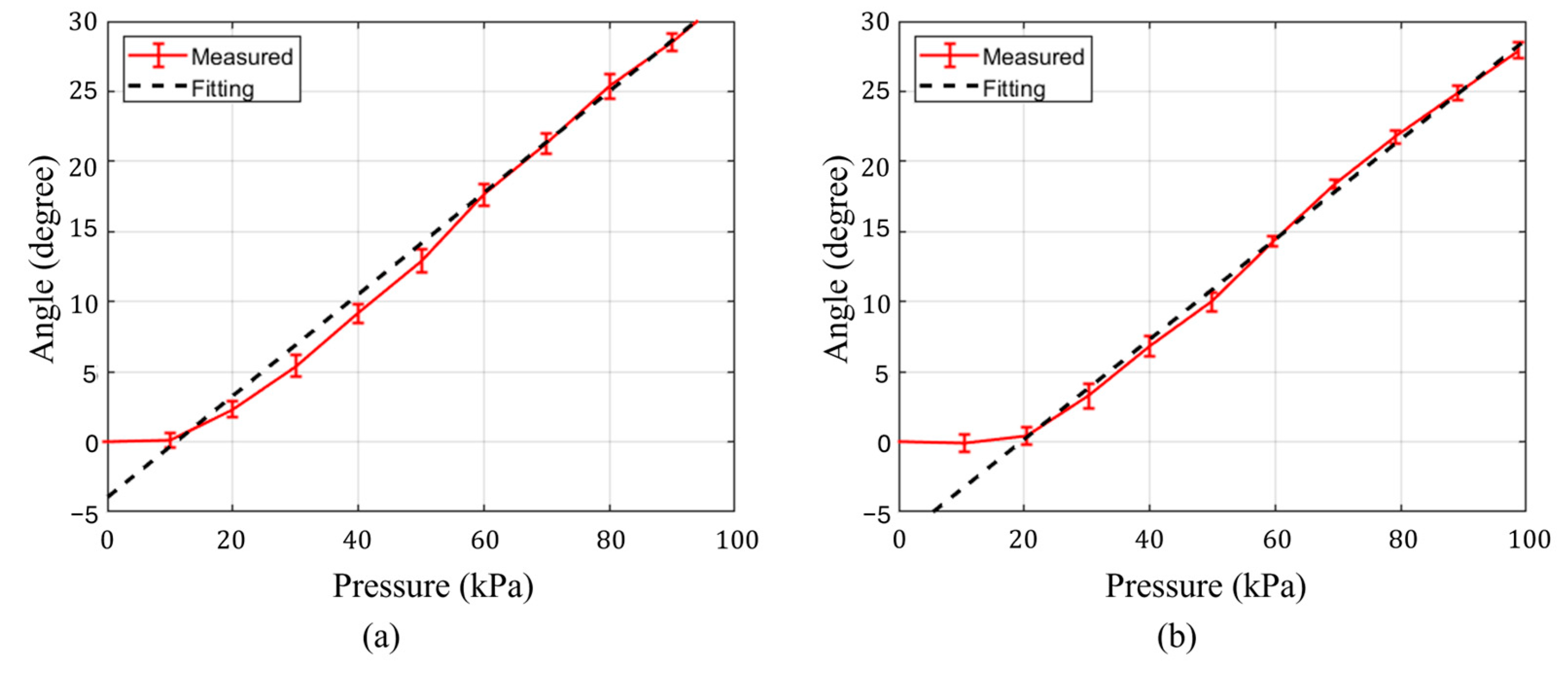
3.1. Adaptive Capabilities
3.2. Lateral Force Comparison
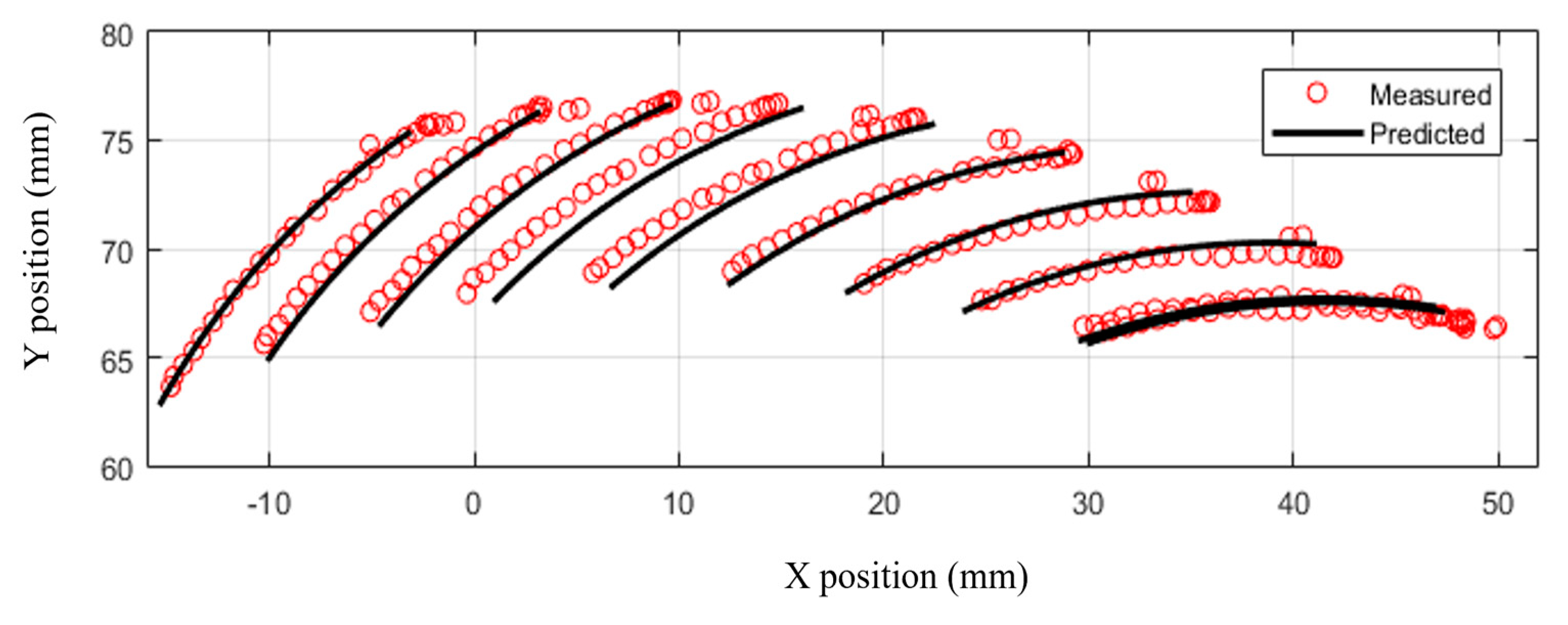
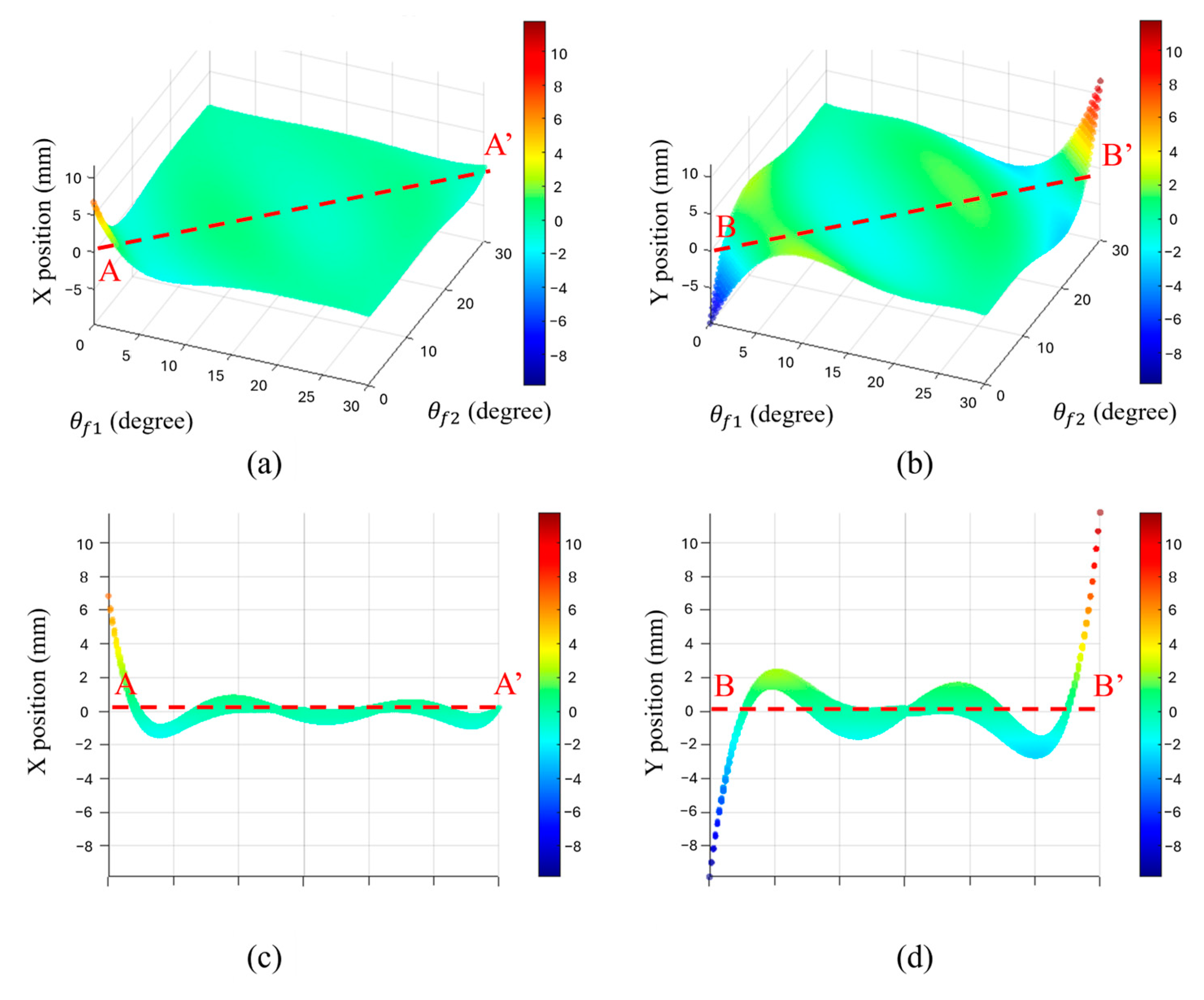
3.3. Motion-Trajectories Analysis
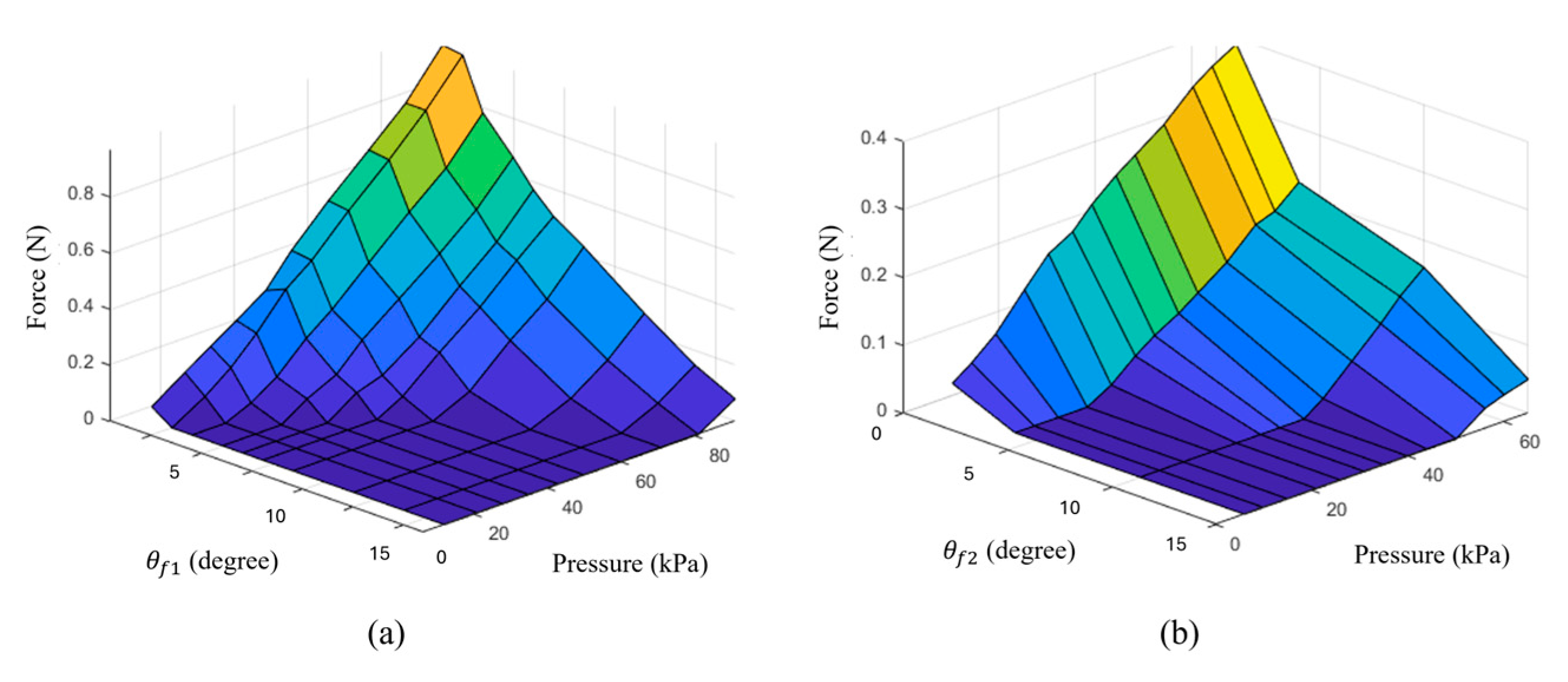
3.4. Force Output Analysis
4. Conclusions
Supplementary Materials
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Li, M.; Pal, A.; Aghakhani, A.; Pena-Francesch, A.; Sitti, M. Soft actuators for real-world applications. Nat. Rev. Mater. 2022, 7, 235–249. [Google Scholar] [CrossRef] [PubMed]
- Cheng, L.-W.; Liu, S.-W.; Chang, J.-Y. Design of an eye-in-hand smart gripper for visual and mechanical adaptation in grasping. Appl. Sci. 2022, 12, 5024. [Google Scholar] [CrossRef]
- Backus, S.B.; Dollar, A.M. An adaptive three-fingered prismatic gripper with passive rotational joints. IEEE Robot. Autom. Lett. 2016, 1, 668–675. [Google Scholar] [CrossRef]
- Birglen, L. Enhancing versatility and safety of industrial grippers with adaptive robotic fingers. In Proceedings of the 2015 IEEE/RSJ International Conference on Intelligent Robots and Systems (IROS), Hamburg, Germany, 28 September–2 October 2015. [Google Scholar]
- Xu, W.; Zhang, H.; Yuan, H.; Liang, B. A compliant adaptive gripper and its intrinsic force sensing method. IEEE Trans. Robot. 2021, 37, 1584–1603. [Google Scholar] [CrossRef]
- Petković, D.; Pavlović, N.D.; Shamshirband, S.; Anuar, N.B. Development of a new type of passively adaptive compliant gripper. Ind. Robot. Int. J. 2013, 40, 610–623. [Google Scholar] [CrossRef]
- Mosadegh, B.; Polygerinos, P.; Keplinger, C.; Wennstedt, S.; Shepherd, R.; Gupta, U.; Shim, J.; Bertoldi, K.; Walsh, C.J.; Whitesides, G.M. Pneumatic networks for soft robotics that actuate rapidly. Adv. Funct. Mater. 2014, 24, 2163–2170. [Google Scholar] [CrossRef]
- Deimel, R.; Brock, O. A novel type of compliant and underactuated robotic hand for dexterous grasping. Int. J. Robot. Res. 2016, 35, 161–185. [Google Scholar] [CrossRef]
- Till, J.; Aloi, V.; Rucker, C. Real-time dynamics of soft and continuum robots based on Cosserat rod models. Int. J. Robot. Res. 2019, 38, 723–746. [Google Scholar] [CrossRef]
- Jeong, J.; Mitra, A.; Lee, J.B.J. Atomized Liquid Metal Droplet-enabled Enhancement of Sensing Range and Stability for Ultrasensitive Crack-based Sensor. In Proceedings of the 2022 IEEE Sensors, Dallas, TX, USA, 30 October–2 November 2022. [Google Scholar]
- El-Atab, N.; Mishra, R.B.; Al-Modaf, F.; Joharji, L.; Alsharif, A.A.; Alamoudi, H.; Diaz, M.; Qaiser, N.; Hussain, M.M. Soft actuators for soft robotic applications: A review. Adv. Intell. Syst. 2020, 2, 2000128. [Google Scholar] [CrossRef]
- Xu, Q.; Liu, J. Effective enhanced model for a large deformable soft pneumatic actuator. Acta Mech. Sin. 2020, 36, 245–255. [Google Scholar] [CrossRef]
- Zhou, J.; Chen, X.; Chang, U.; Lu, J.-T.; Leung, C.C.Y.; Chen, Y.; Hu, Y.; Wang, Z. A Soft-Robotic Approach to Anthropomorphic Robotic Hand Dexterity. IEEE Access 2019, 7, 101483–101495. [Google Scholar] [CrossRef]
- Zhang, Z.; Han, T.; Pan, J.; Wang, Z. Design of Anthropomorphic Fingers with Biomimetic Actuation Mechanism. IEEE Robot. Autom. Lett. 2019, 4, 3465–3472. [Google Scholar] [CrossRef]
- Li, C.S.; Gu, X.; Xiao, X.; Zhu, G.; Prituja, A.V.; Ren, H. Transcend Anthropomorphic Robotic Grasping with Modular Antagonistic Mechanisms and Adhesive Soft Modulations. IEEE Robot. Autom. Lett. 2019, 4, 2463–2470. [Google Scholar] [CrossRef]
- Correll, N.; Kriegman, D.; Otto, S.; Watson, J. A Versatile Robotic Hand with 3D Perception, Force Sensing for Autonomous Manipulation. arXiv 2024, arXiv:2402.06018. [Google Scholar]
- Almassri, A.M.; Hasan, W.Z.W.; Ahmad, S.A.; Ishak, A.J.; Ghazali, A.M.; Talib, D.N.; Wada, C. Pressure sensor: State of the art, design, and application for robotic hand. J. Sens. 2015, 2015, 846487. [Google Scholar] [CrossRef]
- Mutlu, R.; Alici, G.; Panhuis, M.I.H.; Spinks, G.M. 3D Printed Flexure Hinges for Soft Monolithic Prosthetic Fingers. Soft Robot. 2016, 3, 120–133. [Google Scholar] [CrossRef]
- Wang, T.; Ge, L.; Gu, G. Programmable design of soft pneu-net actuators with oblique chambers can generate coupled bending and twisting motions. Sens. Actuators A Phys. 2018, 271, 131–138. [Google Scholar] [CrossRef]
- Yu, Y.; Fu, T. Design and Experimental Study of Cavity Structure of Pneumatic Soft Actuator. Actuators 2023, 12, 314. [Google Scholar] [CrossRef]
- Liu, Z.; Wang, F.; Liu, S.; Tian, Y.; Zhang, D. Modeling and analysis of soft pneumatic network bending actuators. IEEE/ASME Trans. Mechatron. 2020, 26, 2195–2203. [Google Scholar] [CrossRef]
- Yang, W.-T.; Kurkcu, B.; Tomizuka, M. Optimized Design of a Soft Actuator Considering Force/Torque, Bendability, and Controllability via an Approximated Structure. J. Mech. Des. 2024, 146, 123301. [Google Scholar] [CrossRef]
- Zhang, Z.; Calderon, A.D.; Huang, X.; Wu, G.; Liang, C. Design and Driving Performance Study of Soft Actuators for Hand Rehabilitation Training. Med. Devices 2024, 17, 237. [Google Scholar] [CrossRef]
- Wang, J.B.; Fei, Y.Q.; Pang, W. Design, Modeling, and Testing of a Soft Pneumatic Glove with Segmented PneuNets Bending Actuators. IEEE/ASME Trans. Mechatron. 2019, 24, 990–1001. [Google Scholar] [CrossRef]
- Zhang, C.; Zhu, P.; Lin, Y.; Jiao, Z.; Zou, J. Modular soft robotics: Modular units, connection mechanisms, and applications. Adv. Intell. Syst. 2020, 2, 1900166. [Google Scholar] [CrossRef]
- Zhang, X.; Yu, S.; Dai, J.; Oseyemi, A.E.; Liu, L.; Du, N.; Lv, F. A modular soft gripper with combined Pneu-Net actuators. Actuators 2023, 12, 172. [Google Scholar] [CrossRef]
- Zhang, N.; Ge, L.; Xu, H.; Zhu, X.; Gu, G. 3D printed, modularized rigid-flexible integrated soft finger actuators for anthropomorphic hands. Sens. Actuators A Phys. 2020, 312, 112090. [Google Scholar] [CrossRef]
- Lin, S.-G.; Chang, J.-Y. Design of an Adaptive Anthropomorphic Finger with Modular Soft Actuators. In IFToMM World Congress on Mechanism and Machine Science, Proceedings of the 16th IFToMM World Congress 2023, Tokyo, Japan, 5–10 November 2023; Springer: Berlin/Heidelberg, Germany, 2023. [Google Scholar]
- Galloway, K.C.; Polygerinos, P.; Walsh, C.J.; Wood, R.J. Mechanically programmable bend radius for fiber-reinforced soft actuators. In Proceedings of the 2013 16th International Conference on Advanced Robotics (ICAR), Montevideo, Uruguay, 25–29 November 2013. [Google Scholar]
- Denavit, J.; Hartenberg, R.S. A kinematic notation for lower-pair mechanisms based on matrices. J. Appl. Mech. 1955, 22, 215–221. [Google Scholar] [CrossRef]
- Olson, E. AprilTag: A robust and flexible visual fiducial system. In Proceedings of the 2011 IEEE International Conference on Robotics and Automation, Shanghai, China, 9–13 May 2011. [Google Scholar]







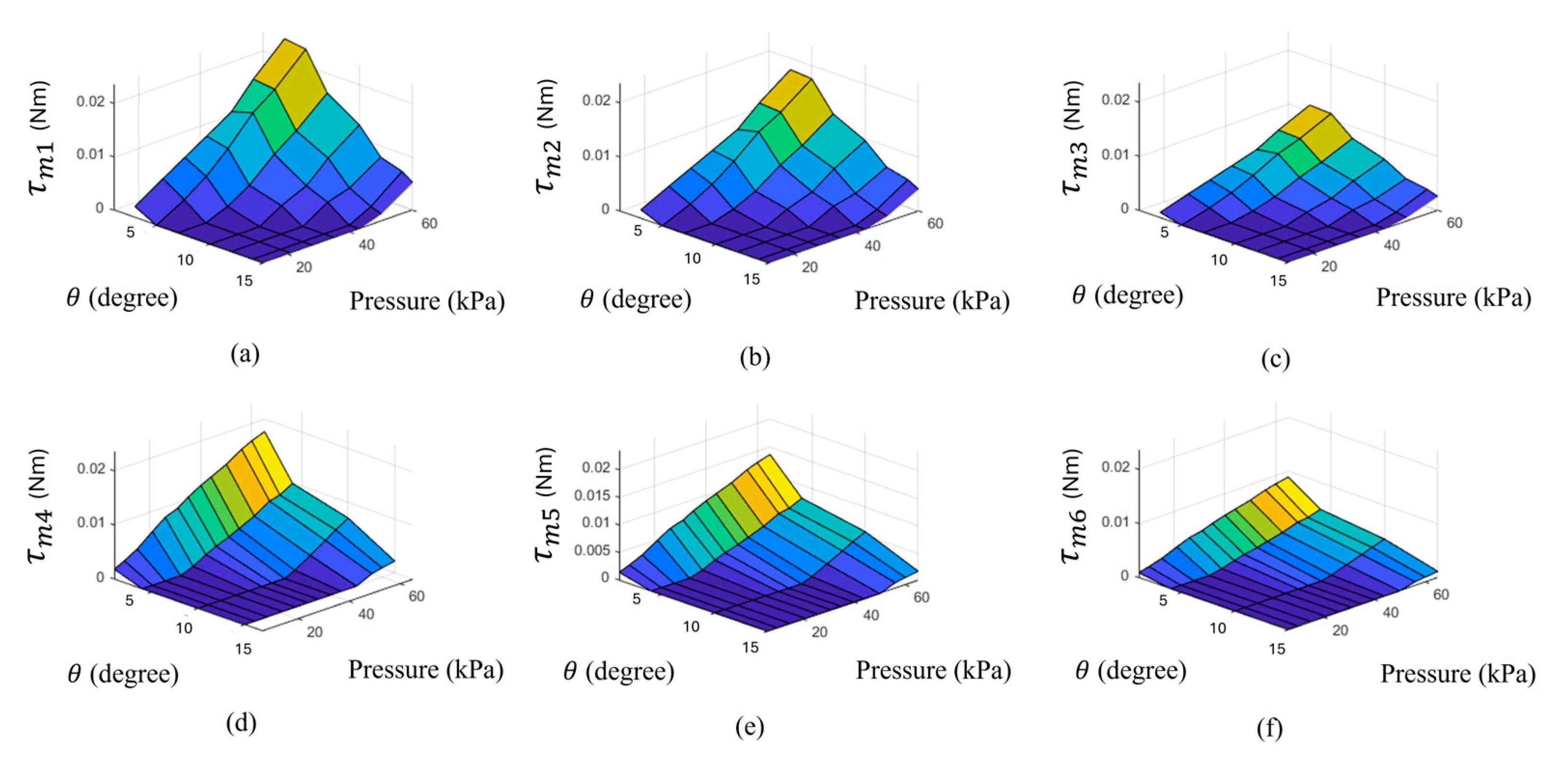

| Polynomial Degree | for X | for Y |
|---|---|---|
| 1 | 0.50469 | 0.60865 |
| 2 | 0.78918 | 0.95795 |
| 3 | 0.99277 | 0.97985 |
| 4 | 0. 99649 | 0.99969 |
| 5 | 0.99997 | 0.99986 |
| 4th-Degree Coefficient for X | Value | 4th-Degree Coefficient for Y | Value | 5th-Degree Coefficient for X | Value | 5th-Degree Coefficient for Y | Value |
|---|---|---|---|---|---|---|---|
| a00 | −24.63 | b10 | −28.25 | a00 | −24.63 | b00 | 2.507 |
| a10 | −0.2333 | b01 | −8.256 | a10 | 2.122 | b10 | −29.22 |
| a01 | 23.76 | b20 | 0.9165 | a01 | 26.29 | b01 | −8.952 |
| a20 | 13.43 | b11 | 22.65 | a20 | 13.43 | b20 | 0.9165 |
| a11 | 7.809 | b02 | 10.97 | a11 | 7.809 | b11 | 22.65 |
| a02 | 3.067 | b30 | 3.311 | a02 | 3.067 | b02 | 10.97 |
| a30 | 0.5845 | b21 | 2.62 | a30 | −0.4762 | b30 | 4.102 |
| a21 | −7.224 | b12 | 2.006 | a21 | −10.56 | b21 | 3.628 |
| a12 | −7.081 | b03 | 0.5056 | a12 | −10.37 | b12 | 2.89 |
| a03 | −1.946 | b40 | 0.111 | a03 | −3.293 | b03 | 0.8489 |
| a40 | −0.7709 | b31 | −2.3 | a40 | −0.7709 | b40 | 0.111 |
| a31 | −0.8341 | b22 | −3.507 | a31 | −0.8341 | b31 | −2.3 |
| a22 | −0.9935 | b13 | −2.178 | a22 | −0.9935 | b22 | −3.507 |
| a13 | −0.5658 | b04 | −0.4432 | a13 | −0.5658 | b13 | −2.178 |
| a04 | −0.1092 | b00 | 2.507 | a04 | −0.1092 | b04 | −0.4432 |
| a50 | −0.01672 | b50 | −0.1425 | ||||
| a41 | 0.5408 | b41 | −0.1961 | ||||
| a32 | 1.117 | b32 | −0.3163 | ||||
| a23 | 1.079 | b23 | −0.2802 | ||||
| a14 | 0.496 | b14 | −0.1222 | ||||
| a05 | 0.08045 | b05 | −0.01896 |
| kPa1 (kPa) | kPa2 (kPa) | Predicted Force |
|---|---|---|
| 32 | 31 | 0.10 |
| 44 | 40 | 0.15 |
| 51 | 51 | 0.20 |
| 57 | 59 | 0.25 |
| 60 | 66 | 0.30 |
| 65 | 72 | 0.35 |
| 69 | 71 | 0.40 |
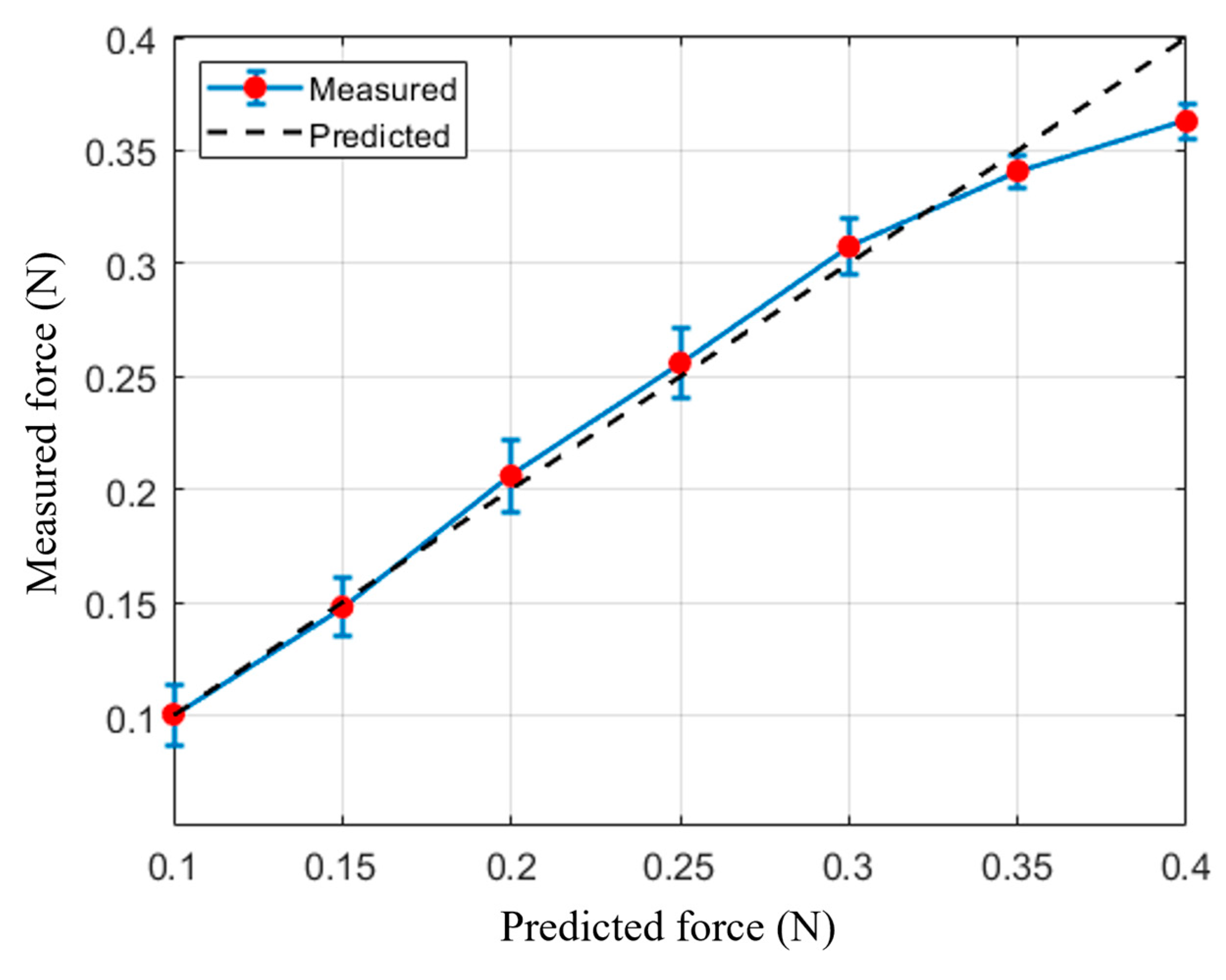
| Force (N) | Mean Measured Value (N) | Error (N) | Standard Deviation |
|---|---|---|---|
| 0.1 | 0.10050 | 0.00050 | 0.0134 |
| 0.15 | 0.14800 | 0.00200 | 0.0132 |
| 0.2 | 0.20600 | 0.00600 | 0.0158 |
| 0.25 | 0.25600 | 0.00600 | 0.0151 |
| 0.3 | 0.30750 | 0.00750 | 0.0121 |
| 0.35 | 0.34100 | 0.00900 | 0.0074 |
| 0.4 | 0.36300 | 0.03700 | 0.0079 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Lin, S.-G.; Chang, J.-Y. Enhanced Design of an Adaptive Anthropomorphic Finger through Integration of Modular Soft Actuators and Kinematic Modeling. Robotics 2024, 13, 116. https://doi.org/10.3390/robotics13080116
Lin S-G, Chang J-Y. Enhanced Design of an Adaptive Anthropomorphic Finger through Integration of Modular Soft Actuators and Kinematic Modeling. Robotics. 2024; 13(8):116. https://doi.org/10.3390/robotics13080116
Chicago/Turabian StyleLin, Sheng-Guan, and Jen-Yuan (James) Chang. 2024. "Enhanced Design of an Adaptive Anthropomorphic Finger through Integration of Modular Soft Actuators and Kinematic Modeling" Robotics 13, no. 8: 116. https://doi.org/10.3390/robotics13080116
APA StyleLin, S.-G., & Chang, J.-Y. (2024). Enhanced Design of an Adaptive Anthropomorphic Finger through Integration of Modular Soft Actuators and Kinematic Modeling. Robotics, 13(8), 116. https://doi.org/10.3390/robotics13080116





_Chang.jpg)

