Abstract
In many Unmanned Aerial Vehicle (UAV) operations, accurately estimating the UAV’s position and orientation over time is crucial for controlling its trajectory. This is especially important when considering the landing maneuver, where a ground-based camera system can estimate the UAV’s 3D position and orientation. A Red, Green, and Blue (RGB) ground-based monocular approach can be used for this purpose, allowing for more complex algorithms and higher processing power. The proposed method uses a hybrid Artificial Neural Network (ANN) model, incorporating a Kohonen Neural Network (KNN) or Self-Organizing Map (SOM) to identify feature points representing a cluster obtained from a binary image containing the UAV. A Deep Neural Network (DNN) architecture is then used to estimate the actual UAV pose based on a single frame, including translation and orientation. Utilizing the UAV Computer-Aided Design (CAD) model, the network structure can be easily trained using a synthetic dataset, and then fine-tuning can be done to perform transfer learning to deal with real data. The experimental results demonstrate that the system achieves high accuracy, characterized by low errors in UAV pose estimation. This implementation paves the way for automating operational tasks like autonomous landing, which is especially hazardous and prone to failure.
1. Introduction
The research on Unmanned Aerial Vehicles (UAVs) are very popular nowadays [1], being used for several applications, such as surveillance [2,3], Search And Rescue (SAR) [4,5], remote sensing [6,7], military Intelligence, Surveillance and Reconnaissance (ISR) operations [8,9], sea pollution monitoring and control [10,11], among many others. Performing UAV autonomous control is essential since it can decrease human intervention [12,13], increasing the system’s operational capabilities and reliability [14]. In typical UAV operations, the most dangerous stages are usually the take-off and landing [15,16], and the automation of these stages is essential to increase the safety of personnel and material, thus increasing the overall system reliability.
A rotary-wing UAV, due to its operational capabilities, can easily perform Vertical Take-Off and Landing (VTOL) [17]. Still, the same thing does not usually happen in the fixed-wing UAV case [18,19]. However, some fixed-wing currently present VTOL capability [20,21]. They are only suitable for certain operations where the platform may be stationary for a specific time period, and the landing’s site weather conditions allow a successful landing [22]. Using a ground-based Red, Green, and Blue (RGB) vision system to estimate the pose of a fixed-wing UAV can help adjust its trajectory during flight and perform guidance during a landing maneuver [23]. In real-life operations, all the possible incorporation of data in the control loop [12] should be considered since it will facilitate the operator’s operational procedures, decreasing the accident probability.
The standard UAV mission profile commonly consists of three stages, as illustrated in Figure 1. It typically includes a climb, a mission envelope, and the descent to perform landing, usually following a well-defined trajectory state machine [24]. In a typical landing trajectory state machine, the UAV performs loiters around the landing site’s predefined position until the detection is performed. After detection, the approach and the respective landing are performed. During the landing operation, as illustrated in Figure 1, it is essential also to consider two distinct cases: (i) when the approach is at a No Return state where the landing maneuver cannot be aborted even if needed, and (ii) when a Go Around maneuver is possible, and the landing maneuver can be canceled due to external reasons, e.g., camera data acquisition failure.
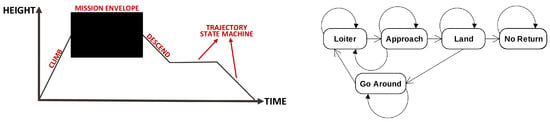
Figure 1.
Standard mission profile (left) and typical trajectory state machine (right) [24].
Many vision-based approaches have been developed for UAV pose estimation using Computer Vision (CV), and they are mainly divided into ground-based and UAV-based approaches [23]. The ground-based approaches typically use stereoscopic [25] or monocular vision [26,27] to detect the UAV in the frame and retrieve information used in the guidance process, and the UAV-based typically use its camera to detect landmarks [28,29,30] that can be used in the UAV guidance. The limited processing power available in most UAVs makes it preferable to use a ground-based approach since it allows access to more processing power [18,31]. The proposed system approach will use a RGB monocular ground-based system.
The proposed system, as illustrated in Figure 2, captures a single RGB frame and processes it into a binary image utilizing a Background Subtraction (BS) algorithm to represent the UAV. Subsequently, a Self-Organizing Map (SOM) [32,33,34] is used to identify the cluster in the image that represents the UAV. The resulting cluster is represented by 2D weights corresponding to the output space, which can be interpreted as the UAV’s pixel position cluster representation since the cluster maintains the input space topology. These weights are used as feature points for retrieving pose information using a Deep Neural Network (DNN) structure to estimate the UAV’s pose, including translation and orientation. Access to the UAV Computer-Aided Design (CAD) model allows the creation of a synthetic dataset for training the proposed networks. It also allows for pre-training the networks and fine-tuning using real data to perform transfer learning.

Figure 2.
Simplified system architecture.
The primary objective is to build upon the work presented in [26,27] for RGB single frame fixed-wing UAV pose estimation. This involves implementing an alternative pose estimation framework that can estimate the UAV pose by combining techniques not commonly used together in this field. Subsequently, a comparison with [26,27] is conducted using similarly generated synthetic data and appropriate performance metrics to evaluate the advantages and disadvantages of adopting different components, including state-of-the-art components such as DNNs. Our focus is not on the BS algorithm [35,36], but rather on using the SOM output for pose estimation using DNNs and comparing the results with those obtained previously.
This article is structured as follows: Section 2 provides a brief overview of related work in the field of study. Section 3 presents the problem formulation and describes the methodologies used. Section 4 details the experimental results obtained, analyzing the system performance using appropriate metrics. Finally, Section 5 presents the conclusions and explores additional ideas for further developments in the field.
2. Related Work
This section will briefly describe some related work in the field, which is essential to understand better the article’s contribution and state-of-the-art. Section 2.1 will describe some of the UAV characteristics and operational details, Section 2.2 will explain some of the existing BS algorithms, Section 2.3 will describe the SOM algorithm and some of its applications, Section 2.4 will briefly explain some of the current state-of-the-art DNNs in the UAV field, and Section 2.5 will perform a resume of the section providing essential insights for the system implementation and analysis.
2.1. Unmanned Aerial Vehicles (UAVs)
UAVs can be classified based on various characteristics such as weight, type, propulsion, or mission profile [37,38,39]. The typical requirement for implementing guidance algorithms on a UAV is the existence of a simple controller that can perform trajectories given by a Ground Control Station (GCS) [40]. When choosing a UAV for a specific task, it is essential to consider all these characteristics since the mission success should be a priority. In regular UAV operations, the most critical stages are take-off and landing [19,27], being essential to automating these stages to ensure safety and reliability. Most accidents occur during the landing stage, mainly due to human factors [41,42]. Some UAV systems use a combination of Global Positioning System (GPS), Inertial Navigation System (INS), and CV data to perform autonomous landing [43]. Using CV allows operations in jamming environments [44,45,46].
2.2. Background Subtraction (BS)
Some CV systems use BS algorithms [47] to be able to detect objects in the image, using, e.g., a Gaussian Mixture Model (GMM) [48,49], a DNN [50,51], among many other methods. The CV applications are vast, ranging from human-computer interface [52], background substitution [53], visual surveillance [54], and fire detection [55], among others. Independently of the adopted methods, the objective is to perform BS and obtain an image representing only the objects or some desired regions of interest. Depending on the intended application, this pre-processing stage can be very important since it removes unnecessary information from the captured frame that can worsen the results or require more complex algorithms to obtain the same results [56,57]. The BS operation presents several challenges, such as dynamic backgrounds that continuously change, illumination variations typical of outdoor environments, and moving cameras that prevent the background from being static, among others [35,58]. Outdoor environments present a complex and challenging setting, and the current state-of-the-art methods include DNNs to learn more generalized features and effectively handle the variety existing in outdoor environments [59,60]. As described in Section 1, the main article focus will not be on the BS algorithm and methods but instead on using this data to perform single frame monocular RGB pose estimation combining a SOM with DNNs.
2.3. Self-Organizing Maps (SOMs)
SOMs are a type of Artificial Neural Network (ANN) based on unsupervised competitive learning that can produce a low dimensional discretized map giving training samples as input [32,33,34]. This map represents the data clusters as output space, usually used for pattern classification since it preserves the data topology given as input space [61,62,63,64]. A SOM can have several applications, such as in meteorology and oceanography [65], finance [66], intrusion detection [67], electricity demand daily load profiling [62], health [68], and handwriting digit recognition [69], among many others. The applications regarding CV pose estimation using RGB data are much less common. Some existing applications combine SOMs with a Time-of-Flight (TOF) camera to estimate human pose [70] or with isomaps for a non-linear dimensionality reduction [71,72]. Our application is intended to maximize the SOM advantages since it can obtain a representation of the UAV projection in the captured frame, a cluster of pixels using a matrix of weights. Those weights directly relate to the pixel’s location since the cluster representation (SOM output) maintains its topology.
2.4. Deep Neural Networks (DNNs)
Regarding DNNs, human [73,74,75] and object [76,77] pose estimation has been a highly researched topic over the past years. Some navigation and localization UAV methods predict latitude and longitude from aerial images using Convolutional Neural Networks (CNNs) [78], employ transfer learning from indoor to outdoor environments combined with Deep Learning (DL) to classify navigation actions and perform autonomous navigation [79], among others. The UAV field, particularly its pose estimation using DNNs, is a topic that has yet to be fully developed. Still, by its importance, it is essential to make proper contributions to the field since the UAV applications are increasingly daily [80,81,82]. Some applications use DNNs for UAV pose estimation using a ground system combining sensor data with CV [83] or a UAV-based fully onboard approach using CV [84]. Despite the great interest and development in the UAV field in the past years, the vast majority of the study problems are not yet fully solved and must be constantly improved, as must happen with the UAV pose estimation task [26,27]. Concerning UAV pose estimation using a CV ground-based system but combining different methods that are not purely based in DNNs, we currently have some applications that combine a pre-trained dataset of UAV poses with a Particle Filter (PF) [26,27] or use the Graphics Processing Unit (GPU) combined with an optimization algorithm [85].
2.5. General Analysis
Independently of the chosen method, ensuring a low pose estimation error and, if possible, real-time or near real-time pose estimation is essential. As described before, since a small size UAV usually has low processing power available onboard, the most obvious solution for the processing step is to perform it using a ground-based system and then transmit it to the UAV onboard controller by Radio Frequency (RF) at appropriate time intervals to ensure smooth trajectory guidance. Performing single-frame pose estimation is difficult, mainly when relying only on a single RGB frame without any other sensor or data fusion. Using only CV for pose estimation allows us to perform operations and estimations even in jamming environments where GPS data becomes unavailable. Still, it is a significant problem without an easy solution. As will be described, combining methods can help develop a system that can be used for single-frame pose estimation with acceptable accuracy for guidance purposes.
3. Problem Formulation & Methodologies
A monocular RGB ground-based pose estimation system can be helpful to ensure that we can estimate the UAV pose to be able to perform its trajectory guidance when needed. The proposed system assumes that we previously know the used UAV model and have its CAD model available, allowing the training of the proposed networks using synthetic data. The main focus will not be on the BS algorithm and methods [35,36], as initially described in Section 1, but on the use of a SOM combined with DNNs to estimate the UAV pose from a single frame without relying on any additional information. Other different approaches, architectures, and combinations of algorithms could be explored. Still, testing and exploring all the existing applications is impossible, so retrieving as much information as possible from the proposed architecture is essential.
When we capture a camera frame at time t, our goal is to preprocess it to remove the background and estimate the cluster representing the UAV using a predefined set of weights obtained from a SOM. These weights will serve as inputs for two different DNNs: one for translation estimation, , and the other for orientation estimation using quaternion representation, . Here, represents the real part, and represents the imaginary part of the quaternion representation, allowing us to estimate the UAV’s pose. The system architecture, along with the variables used, is illustrated in Figure 3.

Figure 3.
System architecture with a representation of the used variables.
This section will formulate the problem and explain the adopted methodologies. Section 3.1 will describe the synthetic data generation process used during the training and performance measurement tests, Section 3.2 will briefly describe the SOM and its use in the problem at hand, and Section 3.3 will describe the proposed DNNs used for pose estimation.
3.1. Synthetic Data Generation
As initially described before, to generate synthetic data, it is essential to have the UAV CAD model available, i.e., we must know what we want to detect and estimate previously. Nowadays, accessing the UAV CAD model is easy and does not present any significant issues in the system development and application. Since we are using a ground-based monocular RGB vision system [19,23], the intended application should be a small size UAV with a simple controller onboard, as illustrated in Figure 4. A CAD model in .obj format is typically constituted by vertices representing points in space, vertices normals representing normal vectors at each vertice for lighting calculations, and faces defining polygons made up of vertices that define the object surface.

Figure 4.
Used UAV CAD model illustration.
For the UAV CAD model projection, we are using the pinhole camera model [86,87] that is a commonly used model for mapping a 3D point in the real world into a 2D point in the image plane (frame). It is possible to perform rotation and translation to the given points representing the model vertices using the extrinsic matrix, while the camera parameters are represented by the intrinsic matrix. This relationship can be represented as [88,89,90]:
where represents a 3D point, represents the 2D coordinates of a point in the image plane. The parameters define the horizontal and vertical focal lengths, and represent the optical center in the image. The matrices and correspond to the rotation and translation, respectively, and are known as extrinsic parameters. The skew coefficient is considered to be zero. The camera and UAV reference frames are depicted in Figure 5.
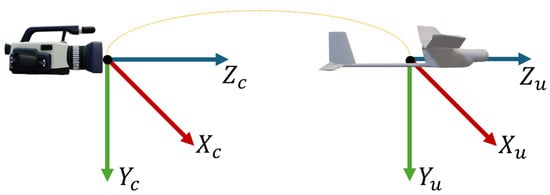
Figure 5.
Camera and UAV reference frames.
Both the chosen image size of 1280 width and 720 height () and the intrinsic matrix parameters are consistent with those used in [26,27] for the purpose of performance comparison. By utilizing Equation (1), it becomes simple to create synthetic data for training algorithms and analyzing performance. Figure 6 illustrates two examples of binary images created using synthetic rendering. These binary images will be used as SOM input, as illustrated in Figure 3.
Figure 6.
Example of generated UAV binary images.
When capturing real-world images, considering the possibility of additional noise in the image when performing BS is important since a pre-processing step must ensure that it is minimized, not significantly influencing the SOM cluster detection. One way of performing this simple pre-processing is to use the Z-score [91,92]. Z-score is a statistical measure useful to quantify the distance between a data point and the mean of the provided dataset. The Z-score calculation can be obtained by [91,92]:
where represent the obtained Z-scores for a specific frame at time instant t, describe the pixel coordinates that contain a binary value of 1 from the pre-processed binary image, denotes the mean of the pixel coordinates containing a binary value of 1, and represents the Standard Deviation (SD) of the pixel coordinates containing a binary value of 1. Since we are dealing with points in the image plane (frame) that represent pixels, we can compute the Euclidean distance from the origin to each point to be able to analyze each one using a single value. When the calculated distance for a certain point is below a predefined threshold , we can consider that point as part of our cluster. This technique, or another equivalent, has the primary objective of only selecting and using the pixels that belong to the UAV in the presence of noise, decreasing the obtained error, and obtaining a SOM input with lower error.
Each implementation case must be analyzed independently since, as expected, more errors usually result in a worse estimation. Therefore, it is essential to employ pre-processing with adequate complexity to deal with this kind of case. Most daily implementations have real-time processing requirements, and optimizing the system architecture to achieve them is essential.
3.2. Clustering Using a Self-Organizing Map (SOM)
A SOM allows the mapping of patterns known as input space onto a n-dimensional map of neurons known as output space [32,33,34,93]. In the intended application, the input space at time instant t will be the pixel coordinates that contain a binary value of 1 from the pre-processed binary image. The binary image containing the UAV is represented by , as illustrated in Figure 6, and has a size of . The output space will be a 2-dimensional map represented by a set of a predefined number of weights given by , that preserves the topological relations of the input space, as illustrated in Figure 3. The implemented SOM adapted to the problem at hand with all the proper descriptions of the definitions and notations is described in Algorithm 1.
| Algorithm 1 Self-Organizing Map (SOM) [32,33,93] |
|
In Figure 7 and Figure 8, it is illustrated three different cases of the SOM output space after training epochs (iterations) with an initial learning rate of and a final learning rate of for two different examples. After analyzing the figures, it is possible to see a relationship between the output space given by the neuron positions represented by the dots and the topology of the input space in green. After analyzing Figure 7right, it is also possible to state that a higher number of neurons in the grid does not always represent our cluster or UAV better since, e.g., in the grid case, we have neurons located outside the considered input space that is represented using green color.
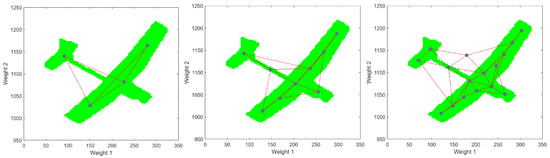
Figure 7.
Example I of obtained clustering maps using SOM after 250 iterations: grid (left), grid (center) and grid (right). The dots represent the neuron positions according to their weights (output space).
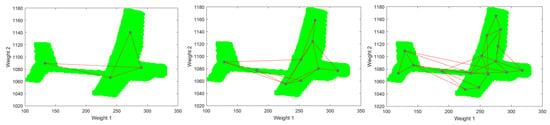
Figure 8.
Example II of obtained clustering maps using SOM after 250 iterations: grid (left), grid (center) and grid (right). The dots represent the neuron positions according to their weights (output space).
In Figure 9, it is illustrated the sample hit histogram and the neighbor distances map for the neuron grid (output space) shown in Figure 7 center. The sample hit histogram demonstrates the number of input vectors classified for each neuron, providing insight into the data distribution. The neighbor distances map illustrates the variance between adjacent neurons. The blue hexagons represent the neurons, the red lines depict the connections between neighboring neurons, and the colors indicate the distances, with darker colors representing larger distances and lighter colors representing smaller distances. Observing this data makes it possible to see that we have a cluster representation of the input space using a SOM, as needed and expected to be able to perform the pose estimation task.
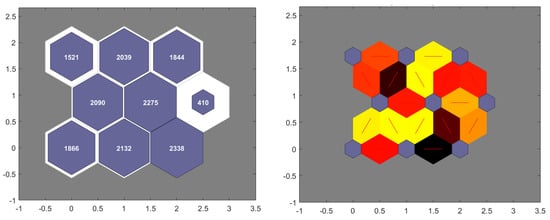
Figure 9.
Example of the obtained sample hits (left), where the numbers indicate the number of input vectors, and neighbor distances (right), where the red lines depict the connections between neighboring neurons for the grid shown in Figure 7 center. The colors indicate the distances, with darker colors representing larger distances and lighter colors representing smaller distances.
It is possible to try to estimate the original UAV pose directly from the output space representing the input space topology, but it is not an easy task. It resembles trying to estimate an object’s pose considering a series of feature points with the advantage of being positioned according to the input space topology. Given the vast amount of possible UAV poses using, e.g., a pre-computed codebook [94] to try to estimate the UAV poses in a specific frame is impractical due to its dimension and can lead to a high error rate causing this estimate to have so much error that it cannot be used reliably.
3.3. Pose Estimation Using Deep Neural Networks (DNNs)
Using the SOM output space, it is possible to try to estimate the UAV pose using data obtained from a single frame. As briefly described before, and given the vast amount of possible UAV poses, using a pre-computed codebook of known poses is impractical [94]. DNNs are highly used nowadays in our daily lives and present a good capacity to solve complex and non-linear problems that generally will be unsolvable or need highly complex algorithm design. It is impractical to test all the possible network architectures, particularly since they are practically infinite without a parameter size limit. Since the output space of the SOM are weights that represent the topology of the input space, they can be considered as 2D feature points representing the input space.
To be able to use different loss functions, we have used almost the same network structure for translation and orientation but divided it into two different networks. Since we are dealing with weights that we have considered similar to 2D feature points, we have used Self-Attention (SA) layers [95,96], as described in Section 3.3.1, to consider the entire input and not a local neighborhood as usually considered in the standard convolutional layers. Also, when dealing with rotations and especially due to the quaternion representation, it was used a Quaternion Activation Function (QReLU) [97,98], as described in Section 3.3.3.
Section 3.3.1 will provide some notes about the common architecture layers used for translation and orientation estimation, Section 3.3.2 will describe the specific loss function and architecture used for the translation estimation, and finally, Section 3.3.3 will also describe the loss function and architecture used for the orientation estimation. Both used architectures are similar, with some adaptations to the task’s specificity.
3.3.1. General Description
SA layers were used in the adopted DNNs architectures to capture relations between the elements in the input sequence [95,96]. If we consider an input tensor with shape , where H is the height, W is the width, and C is the number of channels, the SA mechanism allows the model to attend to different parts of the input while considering their interdependencies (relationships). This approach is highly valuable when dealing with tasks that require capturing long-range dependencies or relationships between distant elements. The model can concentrate on relevant information and efficiently extract important features from the input data by calculating query and value tensors and implementing attention mechanisms. This enhances the model’s capacity to learn intricate patterns and relationships within the input sequence. The implemented SA layer is described in Algorithm 2.
| Algorithm 2 Self-Attention Layer [95,96] |
|
Both architectures for translation and orientation estimation share the same main architecture, only differing in the used loss functions and activation function since the orientation DNN use the QReLU activation function [97,98] near the output and performs quaternion normalization to ensure that the orientation estimation is valid, as will be explored in the next sections.
3.3.2. Translation Estimation
The translation estimation DNN is intended to estimate the vector at each instant t with low error. Given the SOM output, and taking into account the relations between the elements in the input sequence using SA layers, it was possible to create a DNN structure to perform this estimation, as illustrated in Figure 10. The details of each layer, its output shape, the number of parameters, and notes are described in Appendix A.

Figure 10.
Used translation estimation DNN structure.
As illustrated in Figure 10, the proposed architecture primarily consists of 2D convolutions (Conv), SA layers (Attn), dropout to prevent overfitting (Dout), batch normalization to normalize the activations - neuron outputs (BN), and fully connected layers (FC). Since we want to estimate translations in meters, the implemented loss function was the Mean Square Error (MSE) between the labels (true value) and the obtained predictions. Although the structure seems complex, only the 2D convolution, the batch normalization, and the fully connected layers present trainable parameters, as described in Table A1.
3.3.3. Orientation Estimation
The orientation estimation DNN is intended to estimate the vector at each instant t with low error. Given the SOM output, and taking into account the relations between the elements in the input sequence using SA layers, it was possible to create a DNN structure to perform estimation, as illustrated in Figure 11. The details of each layer, its output shape, the number of parameters, and notes are described in Appendix B.

Figure 11.
Used orientation estimation DNN structure.
As illustrated in Figure 11, the proposed architecture primarily consists of 2D convolutions (Conv), SA layers (Attn), dropout to prevent overfitting (Dout), batch normalization to normalize the activations—neuron outputs (BN), fully connected layers (FC), and a layer that obtains the quaternion normalization as the network output. Since we want to estimate orientation using a quaternion near the output, it was implemented the QReLU [97,98] activation function. The traditional Rectified Linear Unit (ReLU) activation function can lead to the dying ReLU problem, where neurons stop learning due to consistently negative inputs. QReLU addresses this issue by applying ReLU only to the real part of the quaternion, enhancing the robustness and performance of the neural network in the orientation estimation. Given a quaternion , where represent the real part and the imaginary part, the QReLU can be defined as [97,98]:
The adopted loss function was the quaternion loss [99,100]. Given the true quaternion (label) and the predicted quaternion , it can be defined as [99,100]:
where and the dot product is given by:
By analyzing Equation (4), it is possible to state that it ensures the normalization of quaternions and computes the symmetric quaternion loss based on the dot product of normalized quaternions, averaged over all samples N. This is especially useful when we use batches during training. As described before, although the structure seems complex, only the 2D convolution, the batch normalization, and the fully connected layers present trainable parameters, as described in Table A2.
4. Experimental Results
This section presents experimental results to evaluate the performance of the developed architecture. Section 4.1 describes the used datasets, the network training process, and the parameters used. Section 4.2 explains the performance metrics adopted to quantify the results. Section 4.3 details the translation and orientation errors obtained, compares them with current state-of-the-art methods in RGB monocular UAV pose estimation using a single frame, and explores the system’s robustness in the presence of noise typical of real-world applications. Section 4.4 includes ablation studies to analyze the performance based on the adopted network structure. Section 4.5 provides some insights and analysis about applying the current system architecture to the real world. Finally, Section 4.6 presents a comprehensive overall analysis and discussion of the primary results achieved.
4.1. Datasets, Network Training & Parameters
Since there is no publicly available dataset with ground truth data and we have not been able to acquire an actual image dataset, we used a realistic synthetic dataset [101,102]. The system can then be applied to real data using transfer learning or by performing fine-tuning with the acquired real data. The training dataset contains 60,000 labeled inputs and was created using synthetically generated data, containing images with a size of . The synthetic data is created by rendering the UAV CAD model directly at the desired pose. This method ensures that the training dataset includes a wide range of scenarios and orientations. The ability to render the UAV in a wide range of poses and orientations using synthetic data enables the training of a robust and dependable model. The rendered poses vary in the following intervals: m, and guaranteeing that the UAV is rendered on the generated frame. The synthetically generated pose orientations vary within the interval of degrees around each Euler angle, as illustrated in Figure 5. In real captured frames, the obtained BS error could be decreased and ideally removed using the Z-score approach, as described in Section 3.1.
The considered SOM output space consisted of 9 neurons arranged in a grid, which were trained over 250 iterations, as detailed in Section 3.2. Our main goal was to estimate the UAV pose using 9 feature points ( neuron grid) obtained from the SOMs output (output space). This number of feature points is reasonable considering the number of pixels available for clustering connected to the UAV distance to the camera.
During the training of the DNNs, the MSE was used as a loss function for translation estimation, and quaternion loss was utilized as a loss function for orientation estimation, as described in Section 3.3. 80% of the dataset was used for training and 20% for validation over 50,000 iterations using the Adaptive Moment Estimation (ADAM) optimizer and a batch size of 256 images. As expected, the loss decreased during training, with a significant reduction observed during the initial iterations, as described in Section 4.4. Minor adjustments were performed during the remainder of the training to optimize the trainable parameter values and minimize errors. The pose estimation performance analysis used three different datasets of 850 poses at and 10, with X and Y varying within the intervals of m and Euler angles within the interval of degrees.
4.2. Performance Metrics
The algorithms were implemented on a 3.70 GHz Intel i7-8700K Central Processing Unit (CPU) and NVIDIA Quadro P5000 with a bandwidth of 288.5 GB/s and a pixel rate of 110.9 GPixel/s. The obtained processing time was not a performance metric since we used a ground-based system without power limitations and easy access to high processing capabilities. Although this is not a design restriction, a simple system was developed to allow the system implementation without requiring high computational resources.
The translation error between the estimated poses and the ground truth labels was determined using the Euclidean distance. In contrast, the quaternion error was calculated as follows:
where ⊗ represents the unit quaternion multiplication, represents the ground truth, and represents the conjugate of the predicted quaternion (estimate). The angular distance in radians corresponding to the orientation error is obtained by:
where is them converted into degrees to be analyzed. Both translation and orientation errors were analyzed using Median, Mean Absolute Error (MAE), SD, and Root Mean Square Error (RMSE) [103].
4.3. Pose Estimation Error
Given three different datasets of 850 poses, as described in Section 4.1, the pose estimation error was analyzed at different camera distances using the performance metrics described in Section 4.2. Estimating the UAV pose with low error is essential to automate important operational tasks such as autonomous landing.
When analyzing Table 1, it is clear that the translation error increases as the distance from the camera increases. The greatest error occurs in the Z coordinate since the scale factor is difficult to estimate. However, the performance is still satisfactory, with a low error of around 0.33 m as indicated by the obtained MAE at distances of 5 and 7.5 m.

Table 1.
Obtained translation error in meters.
By analyzing Table 2, it is evident that the orientation error also increases with the camera distance but at a lower rate than the observed for the translation. A MAE of approximately 29 degrees at distances of 5 and 7.5 m was obtained. The maximum error is observed near 180 degrees, primarily due to the UAV’s symmetry. It makes it difficult to differentiate between symmetric poses because the rendered pixels present almost the same topology, as illustrated in Figure 12.

Table 2.
Obtained orientation error in degrees.

Figure 12.
Example of a similar topology shown by a UAV symmetric pose.
The translation error boxplot is illustrated in Figure 13, where we can see the existence of some outliers. Still, most of the translation estimations are near the median, as described before. On the other hand, when analyzing the orientation error histogram, as illustrated in Figure 14, we can see that the vast majority of the error is near zero degrees, as expected.
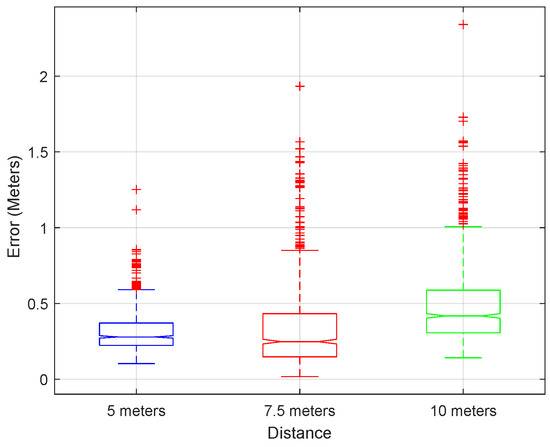
Figure 13.
Translation error boxplot in meters.
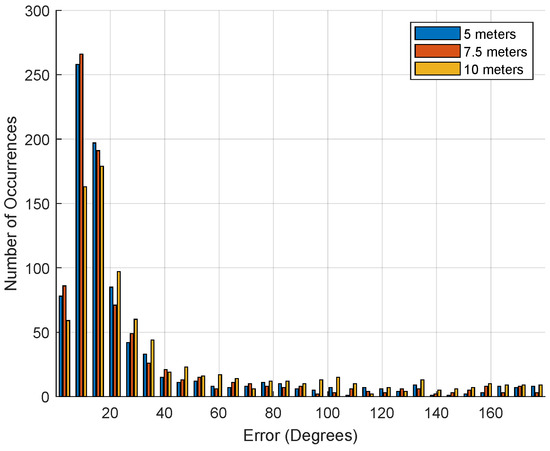
Figure 14.
Orientation error histogram in degrees.
Some examples of pose estimation using the proposed architecture are illustrated in Figure 15, demonstrating the good orientation performance obtained by the proposed method. As described earlier and illustrated in Figure 14, some bad estimations and outliers will exist, but they can be reduced using temporal filtering [23].
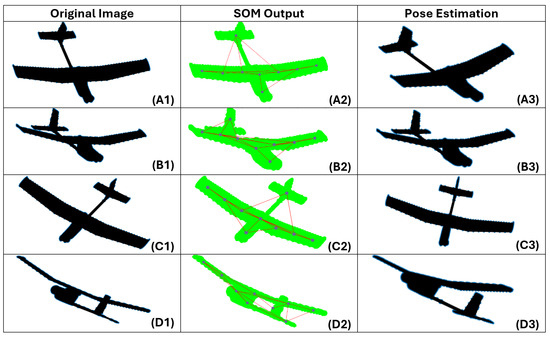
Figure 15.
Examples of pose estimation using the proposed architecture—Original image (left), SOM output (center), and pose estimation (right). The orientation error for (A3) was 30.6 degrees, for (B3) 3.3 degrees, for (C3) 22.2 degrees, and for (D3) 14.4 degrees.
4.3.1. Comparison with Other Methods
It is possible to compare the proposed system with other state-of-the-art RGB ground-based UAV pose estimation systems. In [26], a PF based approach using 100 particles is employed, enhanced by optimization steps using a Genetic Algorithm based Framework (GAbF). In [27], three pose optimization techniques are explored under different conditions from those in [26], namely Particle Filter Optimization (PFO), a modified Particle Swarm Optimization (PSO) version, and the GAbF again. These applications do not perform pose estimation in a single shot, relying on pose optimization steps using the obtained frame.
When we compare the translation error achieved by the current state-of-the-art ground-based UAV UAV pose estimation systems using RGB data, as outlined in Table 3, it becomes apparent that the used optimization algorithms in [26,27] result in more accurate translation estimates. This is primarily attributed to optimizing the estimate using multiple filter iterations on the same frame, which allows for a better scale factor adjustment and consequently provides a more accurate translation estimation. However, it should be noted that we are discussing very small errors that are suitable for most trajectory guidance applications [23].

Table 3.
Translation error comparison in meters with current state-of-the-art applications at 5 m.
The main advantage is verified in orientation estimation, as shown in Table 4, where the obtained MAE is, on average, 2.72 times smaller than that achieved by the state-of-the-art methods. It is important to note that these results are obtained in a single shot without any post-processing or optimization, unlike the considered algorithms that rely on a local optimization stage. The obtained results can be further improved using temporal filtering, as multiple frame information can enhance the current pose estimation [19].

Table 4.
Orientation error comparison in degrees with current state-of-the-art applications at 5 m.
As far as we know, no other publicly available implementations of single-frame RGB monocular pose estimation exist for a proper comparative analysis. Therefore, we chose these methods for comparison.
4.3.2. Noise Robustness
In real-world applications, it is typical to have noise present that can affect the estimate. As described before, the main focus of this article is not on the BS algorithm and methods but rather on using this data to perform single-frame monocular RGB pose estimation by combining a SOM with DNNs. To analyze the performance of the DNN in the presence of noise, a Gaussian distribution with mean zero () and different values of SD () was added to the obtained weights (SOM output), and the resulting error was analyzed. Adding noise to the output space of the SOM is equivalent to adding noise to the original image since the final product of this noise will be a direct error in the cluster topology represented by the weights. Given the three different datasets of 850 poses, as described in Section 4.1, the pose estimation error was analyzed at different camera distances and with the addition of Gaussian noise using the performance metrics described in Section 4.2.
By analyzing Table 5, it is clear that there is a direct relationship between the obtained error and the added Gaussian noise SD, as the error increases with the increase in the SD value. The RMSE increases by approximately 47.1%, the MAE increases by approximately 28.1%, and the maximum obtained error increases by approximately 161.2% when varying the noise SD from one to 50. Additionally, the network demonstrates remarkable robustness to noise, as adding Gaussian noise with a significantly changes the weights’ positions. However, the DNN can still interpret and retrieve scale information from them.

Table 5.
Translation error at 5 m when varying the Gaussian noise SD (meters).
After analyzing Table 6, it is evident that the orientation estimation is highly affected by the weights’ topology (SOM output space), as expected. The RMSE increases by approximately 55.6%, and the MAE increases by approximately 85.6% when varying the noise SD from one to 15. The topology is randomly changed when Gaussian noise is added to the weights, and the orientation estimation error increases. However, the error remains acceptable even without temporal filtering [23] and relying solely on single-frame information since the considered sigmas provide a significant random change in the weight values. Figure 16 illustrates the orientation error histogram obtained when changing the SD. It is evident that as the SD increases, the orientation error also increases, resulting in more non-zero error values.

Table 6.
Orientation error at 5 m when varying the Gaussian noise SD (degrees).
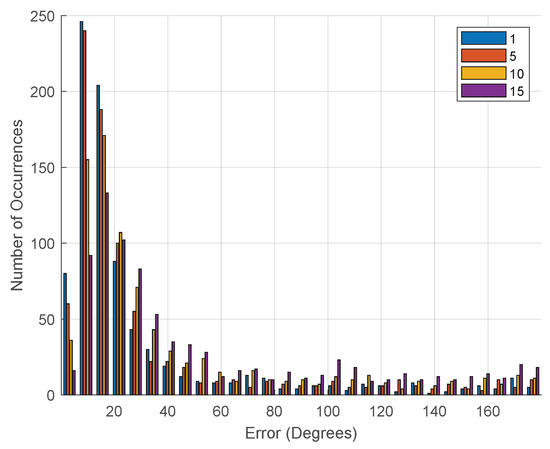
Figure 16.
Orientation error histogram at 5 m when varying the Gaussian noise SD (degrees).
4.4. Ablation Studies: Network Structure
In this section, we conducted ablation studies to evaluate the impact of each layer in the network structure on the training process. We analyzed how each layer influenced the network learning during training. We systematically removed layers from the proposed architecture during the ablation studies to understand their contribution during training. The network was trained for 2500 iterations using the dataset containing 60,000 labeled inputs described in Section 4.1.
For the translation DNN analysis, the network layers were removed according to the described in Table 7. From the analysis of Figure 17, it is possible to state that the training loss obtained by the MSE is slightly affected when using DNN-T2 and DNN-T3. Still, when removing the batch normalization layers DNN-T4, the network cannot learn from its inputs, justifying its use in the proposed structure.

Table 7.
Summary of DNN models for translation estimation used for ablation studies.
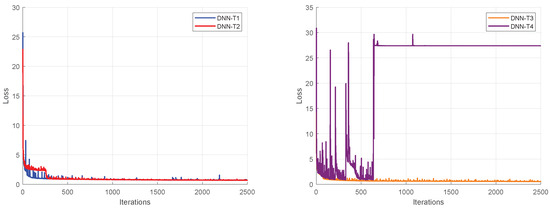
Figure 17.
Obtained loss during the translation DNN training when removing network layers, as described in Table 7.
The network layers were removed according to the description in Table 8 for the orientation DNN analysis. Analysis of Figure 18 indicates that training is significantly affected by removing network components. The importance of the SA block is evident, as it allows for better capture of the relationship between input elements, which is particularly important for orientation estimation. Since the loss is determined by the quaternion loss, seemingly minor differences in the obtained values represent major differences obtained during training and, consequently, during the estimation process.

Table 8.
Summary of DNN models for orientation estimation used for ablation studies.
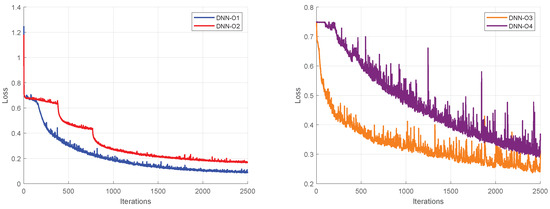
Figure 18.
Obtained loss during the orientation DNN training when removing network layers, as described in Table 8.
4.5. Qualitative Analysis of Real Data
Due to the absence of ground-truth real data, only a simple qualitative analysis was possible. Figure 19 shows the original captured frame and the result of implementing a BS algorithm. It is easily perceptible that the UAV in the captured frame is located at a higher distance than those used in the synthetic dataset generated for training our DNN.

Figure 19.
Qualitative analysis example: Real captured frame (left) and BS obtained frame (right).
A qualitative comparison of the obtained result with the original frame is also possible. From the analysis of Figure 20, some pose error is evident. Still, the orientation error is acceptable and can be minimized by training the DNNs with more samples at higher distances and performing fine-tuning with a real captured dataset. It is important to note that we are not implementing any algorithm to fine-tune the obtained pose estimation. Instead, we consider the SOM output space as 9 feature points and use only that information to perform pose estimation. Due to the considered UAV distance to the camera, the number of used feature points was considered fixed at 9 ( grid). For higher distances, the need to use fewer points should be analyzed as the pixel image information becomes too low, and more points do not bring any additional information.
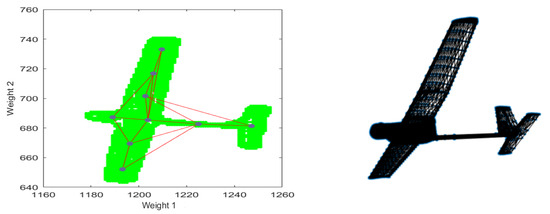
Figure 20.
Real captured frames obtained clustering maps using SOM with 9 neurons ( grid) after 250 iterations (left) and obtained estimation pose rendering using the network trained after 50,000 iterations (right).
It is important to state that the system can be trained using synthetic data to obtain better performances in real-world scenarios and then fine-tuned using real data to ensure high pose estimation accuracy.
4.6. Overall Analysis & Discussion
We have implemented an architecture that performs single-frame RGB monocular pose estimation without relying on additional data or information. The proposed system demonstrates comparable performance and superior orientation estimation accuracy compared with other state-of-the-art methods [26,27]. As described in Section 4.3.2, and as expected, the addition of noise increases the pose estimation error since the pose estimation is dependent on the SOM output space topology. However, the system demonstrates overall good performance and acceptable robustness to noise. As described in Section 3, testing all possible network structures and implementations is impractical due to the almost infinite possibilities. The system was developed as a small network with limited trainable parameters, allowing it to be implemented on devices with low processing power capabilities if needed while maintaining high accuracy. For example, in fixed-wing autonomous landing operations in net-based retention systems [16,23], the typical landing area is about m, and the developed system’s accuracy is sufficient to meet this requirement. Including a temporal filtering architecture [8,18] that relies on information from multiple frames using temporal filtering can improve results, as the physical change in UAV pose between successive frames is limited.
5. Conclusions
A new architecture for single RGB frame UAV pose estimation has been developed based on a hybrid ANN model, enabling essential estimates to automate mission tasks such as autonomous landing. High accuracy is achieved by combining a SOM with DNNs, and the results can be further improved by incorporating temporal filtering in the estimation process. This work fixed the SOM grid at , representing its output space and DNNs input. Future research could adapt the grid size to the UAV’s distance from the camera and combine multiple SOM output grids for better pose estimation, investigating the impact of different grid sizes and configurations to optimize computational efficiency and accuracy. Additionally, incorporating temporal filtering to utilize information between frames can smooth out estimation noise and enhance robustness. Integrating additional sensor data, such as Light Detection And Ranging (LIDAR), Infrared Radiation (IR) cameras, or Inertial Measurement Units (IMUs), could provide a more comprehensive understanding of the UAV’s environment and further enhance accuracy. However, this was not explored here since one of the objectives was to maintain robustness against jamming actions using only CV. The architecture’s application can extend beyond autonomous landing to tasks such as obstacle avoidance, navigation in GPS-denied environments, and precise maneuvering in complex terrains. Continuous development and testing in diverse real-world scenarios is essential to validate the system’s robustness and versatility. In conclusion, the proposed hybrid ANN model for single RGB frame UAV pose estimation represents a significant advancement in the field, with the potential to greatly improve the reliability of UAV operations.
Funding
The research carried out by Nuno Pessanha Santos was supported by national funds through Fundação para a Ciência e a Tecnologia (FCT) under the projects—LA/P/0083/2020, UIDP/50009/2020 and UIDB/50009/2020—Laboratory of Robotics and Engineering Systems (LARSyS).
Data Availability Statement
The manuscript contains all the data and materials supporting the presented conclusions. For further inquiries, please get in touch with the corresponding author.
Conflicts of Interest
The author declares no conflict of interest.
Appendix A. Deep Neural Network (DNN)—Translation: Additional Information
Table A1 presents a detailed description of the DNN architecture used for translation estimation. The Layer (type) describes the type of layer, Output Shape indicates the size of the layer’s output, Parameters shows the number of trainable parameters, Notes provides additional information about each layer, and Label refers to the names used to represent the layers in Figure 10. As performed in both cases - translation and orientation, the DNN input was considered a grid of neurons, totaling 9, because the SOM output space adopted this configuration. The weights were considered similar to 2D feature points to capture spatial relations between the neurons, with a topology representing the UAV pose for estimation. If needed, the network can be easily adapted to deal with different inputs, changing the SOM output space and continuing to perform the pose estimation correctly.

Table A1.
DNN model used for the translation estimation summary.
Table A1.
DNN model used for the translation estimation summary.
| Layer (Type) | Output Shape | Parameters | Notes | Label |
|---|---|---|---|---|
| Input | (3, 3, 2) | - | - | Input |
| 2D Convolution | (3, 3, 64) | 1216 | - | Conv1 |
| Batch Normalization | (3, 3, 64) | 256 | - | BN1 |
| Activation (ReLU) | (3, 3, 64) | - | - | ReLU1 |
| Self Attention | (3, 3, 64) | 4689 | - | Attn1 |
| 2D Convolution | (3, 3, 64) | 36,928 | - | Conv2 |
| Batch Normalization | (3, 3, 64) | 256 | - | BN2 |
| Activation (ReLU) | (3, 3, 64) | - | - | ReLU2 |
| Self Attention | (3, 3, 64) | 4689 | - | Attn2 |
| 2D Convolution | (3, 3, 64) | 36,928 | - | Conv3 |
| Batch Normalization | (3, 3, 64) | 256 | - | BN3 |
| Activation (ReLU) | (3, 3, 64) | - | - | ReLU3 |
| Self Attention | (3, 3, 64) | 4689 | - | Attn3 |
| Dropout | (3, 3, 64) | - | 0.5 | Dout1 |
| Self Attention | (3, 3, 64) | 4689 | - | Attn4 |
| 2D Convolution | (3, 3, 128) | 73,856 | - | Conv4 |
| Batch Normalization | (3, 3, 128) | 512 | - | BN4 |
| Activation (ReLU) | (3, 3, 128) | - | - | ReLU4 |
| Self Attention | (3, 3, 128) | 18,593 | - | Attn5 |
| 2D Convolution | (3, 3, 128) | 147,584 | - | Conv5 |
| Batch Normalization | (3, 3, 128) | 512 | - | BN5 |
| Activation (ReLU) | (3, 3, 128) | - | - | ReLU5 |
| Self Attention | (3, 3, 128) | 18,593 | - | Attn6 |
| Dropout | (3, 3, 128) | - | 0.5 | Dout2 |
| 2D Convolution | (3, 3, 256) | 295,168 | - | Conv6 |
| Batch Normalization | (3, 3, 256) | 1024 | - | BN6 |
| Activation (ReLU) | (3, 3, 256) | - | - | ReLU6 |
| 2D Convolution | (3, 3, 256) | 590,080 | - | Conv7 |
| Batch Normalization | (3, 3, 256) | 1024 | - | BN7 |
| Activation (ReLU) | (3, 3, 256) | - | - | ReLU7 |
| 2D Convolution | (3, 3, 256) | 590,080 | - | Conv8 |
| Batch Normalization | (3, 3, 256) | 1024 | - | BN8 |
| Activation (ReLU) | (3, 3, 256) | - | - | ReLU8 |
| Dropout | (3, 3, 256) | - | 0.5 | Dout3 |
| Flatten | 2304 | - | - | Flatten |
| Fully Connected | 512 | 1,180,160 | ReLU, L2 () | FC1 |
| Dropout | 512 | - | 0.5 | Dout4 |
| Fully Connected | 256 | 131,328 | ReLU, L2 () | FC2 |
| Dropout | 256 | - | 0.5 | Dout5 |
| Fully Connected | 3 | 771 | Linear | Output |
Appendix B. Deep Neural Network (DNN)—Orientation: Additional Information
Table A2 presents a detailed description of the DNN architecture used for orientation estimation. The Layer (type) describes the type of layer, Output Shape indicates the size of the layer’s output, Parameters shows the number of trainable parameters, Notes provides additional information about each layer, and Label refers to the names used to represent the layers in Figure 11. The DNNs architectures are very similar between the translation and orientation, with the main differences in the QReLU activation function, the normalization layer, and the loss functions used during training. As described before, and for both cases—translation and orientation, the DNN input was considered a grid of neurons, totaling 9, because the SOM output space adopted this configuration. The weights were considered similar to 2D feature points to capture spatial relations between the neurons, with a topology representing the UAV pose for estimation. If needed, the network can be easily adapted to deal with different inputs, changing the SOM output space and continuing to perform the pose estimation correctly.

Table A2.
DNN model used for the orientation estimation summary.
Table A2.
DNN model used for the orientation estimation summary.
| Layer (Type) | Output Shape | Parameters | Notes | Label |
|---|---|---|---|---|
| Input | (3, 3, 2) | - | - | Input |
| 2D Convolution | (3, 3, 64) | 1216 | - | Conv1 |
| Batch Normalization | (3, 3, 64) | 256 | - | BN1 |
| Activation (ReLU) | (3, 3, 64) | - | - | ReLU1 |
| Self Attention | (3, 3, 64) | 4689 | - | Attn1 |
| 2D Convolution | (3, 3, 64) | 36,928 | - | Conv2 |
| Batch Normalization | (3, 3, 64) | 256 | - | BN2 |
| Activation (ReLU) | (3, 3, 64) | - | - | ReLU2 |
| Self Attention | (3, 3, 64) | 4689 | - | Attn2 |
| 2D Convolution | (3, 3, 64) | 36,928 | - | Conv3 |
| Batch Normalization | (3, 3, 64) | 256 | - | BN3 |
| Activation (ReLU) | (3, 3, 64) | - | - | ReLU3 |
| Self Attention | (3, 3, 64) | 4689 | - | Attn3 |
| Dropout | (3, 3, 64) | - | 0.5 | Dout1 |
| 2D Convolution | (3, 3, 128) | 73,856 | - | Conv4 |
| Batch Normalization | (3, 3, 128) | 512 | - | BN4 |
| Activation (ReLU) | (3, 3, 128) | - | - | ReLU4 |
| Self Attention | (3, 3, 128) | 18,593 | - | Attn4 |
| 2D Convolution | (3, 3, 128) | 147,584 | - | Conv5 |
| Batch Normalization | (3, 3, 128) | 512 | - | BN5 |
| Activation (ReLU) | (3, 3, 128) | - | - | ReLU5 |
| Self Attention | (3, 3, 128) | 18,593 | - | Attn5 |
| Dropout | (3, 3, 128) | - | 0.5 | Dout2 |
| 2D Convolution | (3, 3, 256) | 295,168 | - | Conv6 |
| Batch Normalization | (3, 3, 256) | 1024 | - | BN6 |
| Activation (ReLU) | (3, 3, 256) | - | - | ReLU6 |
| 2D Convolution | (3, 3, 256) | 590,080 | - | Conv7 |
| Batch Normalization | (3, 3, 256) | 1024 | - | BN7 |
| Activation (ReLU) | (3, 3, 256) | - | - | ReLU7 |
| 2D Convolution | (3, 3, 256) | 590,080 | - | Conv8 |
| Batch Normalization | (3, 3, 256) | 1024 | - | BN8 |
| Activation (ReLU) | (3, 3, 256) | - | - | ReLU8 |
| Dropout | (3, 3, 256) | - | 0.5 | Dout3 |
| Flatten | 2304 | - | - | Flatten |
| Fully Connected | 512 | 1,180,160 | - | FC1 |
| Activation (QReLU) | 512 | - | - | QReLU1 |
| Dropout | 512 | - | 0.5 | Dout4 |
| Fully Connected | 256 | 131,328 | - | FC2 |
| Activation (QReLU) | 256 | - | - | QReLU2 |
| Dropout | 256 | - | 0.5 | Dout5 |
| Fully Connected | 4 | 1028 | - | - |
| Normalization | 4 | - | Quaternion Normalization | Output |
References
- Chaurasia, R.; Mohindru, V. Unmanned aerial vehicle (UAV): A comprehensive survey. In Unmanned Aerial Vehicles for Internet of Things (IoT) Concepts, Techniques, and Applications; Wiley: Hoboken, NJ, USA, 2021; pp. 1–27. [Google Scholar]
- Do, H.T.; Truong, L.H.; Nguyen, M.T.; Chien, C.F.; Tran, H.T.; Hua, H.T.; Nguyen, C.V.; Nguyen, H.T.; Nguyen, N.T. Energy-efficient unmanned aerial vehicle (UAV) surveillance utilizing artificial intelligence (AI). Wirel. Commun. Mob. Comput. 2021, 2021, 8615367. [Google Scholar] [CrossRef]
- Ramachandran, A.; Sangaiah, A.K. A review on object detection in unmanned aerial vehicle surveillance. Int. J. Cogn. Comput. Eng. 2021, 2, 215–228. [Google Scholar] [CrossRef]
- Martinez-Alpiste, I.; Golcarenarenji, G.; Wang, Q.; Alcaraz-Calero, J.M. Search and rescue operation using UAVs: A case study. Expert Syst. Appl. 2021, 178, 114937. [Google Scholar] [CrossRef]
- Lyu, M.; Zhao, Y.; Huang, C.; Huang, H. Unmanned Aerial Vehicles for Search and Rescue: A Survey. Remote Sens. 2023, 15, 3266. [Google Scholar] [CrossRef]
- Osco, L.P.; Junior, J.M.; Ramos, A.P.M.; de Castro Jorge, L.A.; Fatholahi, S.N.; de Andrade Silva, J.; Matsubara, E.T.; Pistori, H.; Gonçalves, W.N.; Li, J. A review on deep learning in UAV remote sensing. Int. J. Appl. Earth Obs. Geoinf. 2021, 102, 102456. [Google Scholar] [CrossRef]
- Zhang, Z.; Zhu, L. A Review on Unmanned Aerial Vehicle Remote Sensing: Platforms, Sensors, Data Processing Methods, and Applications. Drones 2023, 7, 398. [Google Scholar] [CrossRef]
- Pessanha Santos, N.; Rodrigues, V.B.; Pinto, A.B.; Damas, B. Automatic Detection of Civilian and Military Personnel in Reconnaissance Missions using a UAV. In Proceedings of the 2023 IEEE International Conference on Autonomous Robot Systems and Competitions (ICARSC), Tomar, Portugal, 26–27 April 2023; pp. 157–162. [Google Scholar] [CrossRef]
- Wang, H.; Cheng, H.; Hao, H. The Use of Unmanned Aerial Vehicle in Military Operations. In Proceedings of the Man-Machine-Environment System Engineering, Zhengzhou, China, 24–26 October 2020; Long, S., Dhillon, B.S., Eds.; Springer: Singapore, 2020; pp. 939–945. [Google Scholar] [CrossRef]
- Antunes, T.L.; Pessanha Santos, N.; Moura, R.P.; Lobo, V. Sea Pollution: Analysis and Monitoring using Unmanned Vehicles. In Proceedings of the 2023 IEEE Underwater Technology (UT), Tokyo, Japan, 6–9 March 2023; pp. 1–8. [Google Scholar] [CrossRef]
- Yuan, S.; Li, Y.; Bao, F.; Xu, H.; Yang, Y.; Yan, Q.; Zhong, S.; Yin, H.; Xu, J.; Huang, Z.; et al. Marine environmental monitoring with unmanned vehicle platforms: Present applications and future prospects. Sci. Total Environ. 2023, 858, 159741. [Google Scholar] [CrossRef] [PubMed]
- Chen, H.; Wang, X.m.; Li, Y. A survey of autonomous control for UAV. In Proceedings of the 2009 International Conference on Artificial Intelligence and Computational Intelligence, Shanghai, China, 7–8 November 2009; Volume 2, pp. 267–271. [Google Scholar] [CrossRef]
- Han, P.; Yang, X.; Zhao, Y.; Guan, X.; Wang, S. Quantitative Ground Risk Assessment for Urban Logistical Unmanned Aerial Vehicle (UAV) Based on Bayesian Network. Sustainability 2022, 14, 5733. [Google Scholar] [CrossRef]
- Oncu, M.; Yildiz, S. An Analysis of Human Causal Factors in Unmanned Aerial Vehicle (UAV) Accidents. Master’s Thesis, Naval Postgraduate School, Monterey, CA, USA, 2014. [Google Scholar]
- Lee, H.; Jung, S.; Shim, D.H. Vision-based UAV landing on the moving vehicle. In Proceedings of the 2016 International Conference on Unmanned Aircraft Systems (ICUAS), Arlington, VA, USA, 7–10 June 2016; pp. 1–7. [Google Scholar] [CrossRef]
- Pessanha Santos, N.; Lobo, V.; Bernardino, A. Unscented particle filters with refinement steps for uav pose tracking. J. Intell. Robot. Syst. 2021, 102, 52. [Google Scholar] [CrossRef]
- Hadi, G.S.; Kusnaedi, M.R.; Dewi, P.; Budiyarto, A.; Budiyono, A. Design of avionics system and control scenario of small hybrid vertical take-off and landing (VTOL) UAV. J. Instrum. Autom. Syst. 2016, 2, 66–71. [Google Scholar] [CrossRef]
- Pessanha Santos, N.; Lobo, V.; Bernardino, A. Directional statistics for 3D model-based UAV tracking. IEEE Access 2020, 8, 33884–33897. [Google Scholar] [CrossRef]
- Pessanha Santos, N.; Lobo, V.; Bernardino, A. Fixed-wing unmanned aerial vehicle 3D-model-based tracking for autonomous landing. Drones 2023, 7, 243. [Google Scholar] [CrossRef]
- Yuksek, B.; Vuruskan, A.; Ozdemir, U.; Yukselen, M.; Inalhan, G. Transition flight modeling of a fixed-wing VTOL UAV. J. Intell. Robot. Syst. 2016, 84, 83–105. [Google Scholar] [CrossRef]
- Aktas, Y.O.; Ozdemir, U.; Dereli, Y.; Tarhan, A.F.; Cetin, A.; Vuruskan, A.; Yuksek, B.; Cengiz, H.; Basdemir, S.; Ucar, M.; et al. Rapid prototyping of a fixed-wing VTOL UAV for design testing. J. Intell. Robot. Syst. 2016, 84, 639–664. [Google Scholar] [CrossRef]
- Zhou, M.; Zhou, Z.; Liu, L.; Huang, J.; Lyu, Z. Review of vertical take-off and landing fixed-wing UAV and its application prospect in precision agriculture. Int. J. Precis. Agric. Aviat. 2020, 3, 8–17. [Google Scholar] [CrossRef]
- Santos, N.P.; Lobo, V.; Bernardino, A. Autoland project: Fixed-wing UAV landing on a fast patrol boat using computer vision. In Proceedings of the OCEANS 2019 MTS/IEEE, Seattle, WA, USA, 27–31 October 2019; pp. 1–5. [Google Scholar] [CrossRef]
- Pessanha Santos, N. Fixed-Wing UAV Tracking in Outdoor Scenarios for Autonomous Landing. Ph.D. Thesis, University of Lisbon—Instituto Superior Técnico (IST), Lisbon, Portugal, 2021. [Google Scholar]
- Tang, D.; Hu, T.; Shen, L.; Zhang, D.; Kong, W.; Low, K.H. Ground stereo vision-based navigation for autonomous take-off and landing of uavs: A chan-vese model approach. Int. J. Adv. Robot. Syst. 2016, 13, 67. [Google Scholar] [CrossRef]
- Pessanha Santos, N.; Melício, F.; Lobo, V.; Bernardino, A. A ground-based vision system for uav pose estimation. Int. J. Robot. Mechatronics 2014, 1, 138–144. [Google Scholar] [CrossRef]
- Pessanha Santos, N.; Lobo, V.; Bernardino, A. Two-stage 3D model-based UAV pose estimation: A comparison of methods for optimization. J. Field Robot. 2020, 37, 580–605. [Google Scholar] [CrossRef]
- Zhigui, Y.; ChuanJun, L. Review on vision-based pose estimation of UAV based on landmark. In Proceedings of the 2017 2nd International Conference on Frontiers of Sensors Technologies (ICFST), Shenzhen, China, 14–16 April 2017; pp. 453–457. [Google Scholar] [CrossRef]
- Li, F.; Tang, D.q.; Shen, N. Vision-based pose estimation of UAV from line correspondences. Procedia Eng. 2011, 15, 578–584. [Google Scholar] [CrossRef][Green Version]
- Ali, B.; Sadekov, R.; Tsodokova, V. A Review of Navigation Algorithms for Unmanned Aerial Vehicles Based on Computer Vision Systems. Gyroscopy Navig. 2022, 13, 241–252. [Google Scholar] [CrossRef]
- Cazzato, D.; Cimarelli, C.; Sanchez-Lopez, J.L.; Voos, H.; Leo, M. A Survey of Computer Vision Methods for 2D Object Detection from Unmanned Aerial Vehicles. J. Imaging 2020, 6, 78. [Google Scholar] [CrossRef] [PubMed]
- Kohonen, T. The self-organizing map. Proc. IEEE 1990, 78, 1464–1480. [Google Scholar] [CrossRef]
- Kohonen, T. The self-organizing map. Neurocomputing 1998, 21, 1464–1480. [Google Scholar] [CrossRef]
- Kohonen, T. Essentials of the self-organizing map. Neural Netw. 2013, 37, 52–65. [Google Scholar] [CrossRef] [PubMed]
- Kalsotra, R.; Arora, S. Background subtraction for moving object detection: Explorations of recent developments and challenges. Vis. Comput. 2022, 38, 4151–4178. [Google Scholar] [CrossRef]
- Ghedia, N.S.; Vithalani, C. Outdoor object detection for surveillance based on modified GMM and adaptive thresholding. Int. J. Inf. Technol. 2021, 13, 185–193. [Google Scholar] [CrossRef]
- Hassanalian, M.; Abdelkefi, A. Classifications, applications, and design challenges of drones: A review. Prog. Aerosp. Sci. 2017, 91, 99–131. [Google Scholar] [CrossRef]
- Amici, C.; Ceresoli, F.; Pasetti, M.; Saponi, M.; Tiboni, M.; Zanoni, S. Review of propulsion system design strategies for unmanned aerial vehicles. Appl. Sci. 2021, 11, 5209. [Google Scholar] [CrossRef]
- Sabour, M.; Jafary, P.; Nematiyan, S. Applications and classifications of unmanned aerial vehicles: A literature review with focus on multi-rotors. Aeronaut. J. 2023, 127, 466–490. [Google Scholar] [CrossRef]
- Invernizzi, D.; Giurato, M.; Gattazzo, P.; Lovera, M. Comparison of Control Methods for Trajectory Tracking in Fully Actuated Unmanned Aerial Vehicles. IEEE Trans. Control Syst. Technol. 2021, 29, 1147–1160. [Google Scholar] [CrossRef]
- Sharma, S.; Chakravarti, D. UAV operations: An analysis of incidents and accidents with human factors and crew resource management perspective. Indian J. Aerosp. Med. 2005, 49, 29–36. [Google Scholar]
- Balestrieri, E.; Daponte, P.; De Vito, L.; Picariello, F.; Tudosa, I. Sensors and measurements for UAV safety: An overview. Sensors 2021, 21, 8253. [Google Scholar] [CrossRef] [PubMed]
- Xu, G.; Zhang, Y.; Ji, S.; Cheng, Y.; Tian, Y. Research on computer vision-based for UAV autonomous landing on a ship. Pattern Recognit. Lett. 2009, 30, 600–605. [Google Scholar] [CrossRef]
- Hu, H.; Wei, N. A study of GPS jamming and anti-jamming. In Proceedings of the 2009 2nd International Conference on Power Electronics and Intelligent Transportation System (PEITS), Shenzhen, China, 19–20 December 2009; Volume 1, pp. 388–391. [Google Scholar] [CrossRef]
- Ferreira, R.; Gaspar, J.; Sebastiao, P.; Souto, N. Effective GPS jamming techniques for UAVs using low-cost SDR platforms. Wirel. Pers. Commun. 2020, 115, 2705–2727. [Google Scholar] [CrossRef]
- Alrefaei, F.; Alzahrani, A.; Song, H.; Alrefaei, S. A Survey on the Jamming and Spoofing attacks on the Unmanned Aerial Vehicle Networks. In Proceedings of the 2022 IEEE International IOT, Electronics and Mechatronics Conference (IEMTRONICS), Toronto, ON, USA, 1–4 June 2022; pp. 1–7. [Google Scholar] [CrossRef]
- Piccardi, M. Background subtraction techniques: A review. In Proceedings of the 2004 IEEE International Conference on Systems, Man and Cybernetics (IEEE Cat. No. 04CH37583), The Hague, The Netherlands, 10–13 October 2004; Volume 4, pp. 3099–3104. [Google Scholar] [CrossRef]
- Lu, X.; Xu, C.; Wang, L.; Teng, L. Improved background subtraction method for detecting moving objects based on GMM. IEEJ Trans. Electr. Electron. Eng. 2018, 13, 1540–1550. [Google Scholar] [CrossRef]
- Goyal, K.; Singhai, J. Review of background subtraction methods using Gaussian mixture model for video surveillance systems. Artif. Intell. Rev. 2018, 50, 241–259. [Google Scholar] [CrossRef]
- Minematsu, T.; Shimada, A.; Uchiyama, H.; Taniguchi, R.i. Analytics of deep neural network-based background subtraction. J. Imaging 2018, 4, 78. [Google Scholar] [CrossRef]
- Bouwmans, T.; Javed, S.; Sultana, M.; Jung, S.K. Deep neural network concepts for background subtraction: A systematic review and comparative evaluation. Neural Netw. 2019, 117, 8–66. [Google Scholar] [CrossRef] [PubMed]
- Stergiopoulou, E.; Sgouropoulos, K.; Nikolaou, N.; Papamarkos, N.; Mitianoudis, N. Real time hand detection in a complex background. Eng. Appl. Artif. Intell. 2014, 35, 54–70. [Google Scholar] [CrossRef]
- Huang, H.; Fang, X.; Ye, Y.; Zhang, S.; Rosin, P.L. Practical automatic background substitution for live video. Comput. Vis. Media 2017, 3, 273–284. [Google Scholar] [CrossRef]
- Maddalena, L.; Petrosino, A. A Self-Organizing Approach to Background Subtraction for Visual Surveillance Applications. IEEE Trans. Image Process. 2008, 17, 1168–1177. [Google Scholar] [CrossRef] [PubMed]
- Töreyin, B.U.; Dedeoğlu, Y.; Güdükbay, U.; Çetin, A.E. Computer vision based method for real-time fire and flame detection. Pattern Recognit. Lett. 2006, 27, 49–58. [Google Scholar] [CrossRef]
- abd el Azeem Marzouk, M. Modified background subtraction algorithm for motion detection in surveillance systems. J. Am. Arab. Acad. Sci. Technol. 2010, 1, 112–123. [Google Scholar]
- Garcia-Garcia, B.; Bouwmans, T.; Silva, A.J.R. Background subtraction in real applications: Challenges, current models and future directions. Comput. Sci. Rev. 2020, 35, 100204. [Google Scholar] [CrossRef]
- Chapel, M.N.; Bouwmans, T. Moving objects detection with a moving camera: A comprehensive review. Comput. Sci. Rev. 2020, 38, 100310. [Google Scholar] [CrossRef]
- Yang, Y.; Xia, T.; Li, D.; Zhang, Z.; Xie, G. A multi-scale feature fusion spatial–channel attention model for background subtraction. Multimed. Syst. 2023, 29, 3609–3623. [Google Scholar] [CrossRef]
- Tezcan, M.O.; Ishwar, P.; Konrad, J. BSUV-Net 2.0: Spatio-Temporal Data Augmentations for Video-Agnostic Supervised Background Subtraction. IEEE Access 2021, 9, 53849–53860. [Google Scholar] [CrossRef]
- Astel, A.; Tsakovski, S.; Barbieri, P.; Simeonov, V. Comparison of self-organizing maps classification approach with cluster and principal components analysis for large environmental data sets. Water Res. 2007, 41, 4566–4578. [Google Scholar] [CrossRef] [PubMed]
- Santos, R.; Moura, R.; Lobo, V. Application of Kohonen Maps in Predicting and Characterizing VAT Fraud in a Sub-Saharan African Country. In Proceedings of the International Workshop on Self-Organizing Maps, Prague, Czechia, 6–7 July 2022; pp. 74–86. [Google Scholar] [CrossRef]
- Bação, F.; Lobo, V.; Painho, M. The self-organizing map, the Geo-SOM, and relevant variants for geosciences. Comput. Geosci. 2005, 31, 155–163. [Google Scholar] [CrossRef]
- Bação, F.; Lobo, V.; Painho, M. Geo-Self-Organizing Map (Geo-SOM) for Building and Exploring Homogeneous Regions. In Proceedings of the Geographic Information Science, Adelphi, MD, USA, 20–23 October 2004; Egenhofer, M.J., Freksa, C., Miller, H.J., Eds.; Springer: Berlin/Heidelberg, Germany, 2004; pp. 22–37. [Google Scholar] [CrossRef]
- Liu, Y.; Weisberg, R.H. A review of self-organizing map applications in meteorology and oceanography. Self-Organ. Maps Appl. Nov. Algorithm Des. 2011, 1, 253–272. [Google Scholar]
- Deboeck, G.J. Financial applications of self-organizing maps. Neural Netw. World 1998, 8, 213–241. [Google Scholar]
- Qu, X.; Yang, L.; Guo, K.; Ma, L.; Sun, M.; Ke, M.; Li, M. A survey on the development of self-organizing maps for unsupervised intrusion detection. Mob. Netw. Appl. 2021, 26, 808–829. [Google Scholar] [CrossRef]
- Jaiswal, A.; Kumar, R. Breast cancer diagnosis using stochastic self-organizing map and enlarge C4. 5. Multimed. Tools Appl. 2023, 82, 18059–18076. [Google Scholar] [CrossRef]
- Aly, S.; Almotairi, S. Deep Convolutional Self-Organizing Map Network for Robust Handwritten Digit Recognition. IEEE Access 2020, 8, 107035–107045. [Google Scholar] [CrossRef]
- Haker, M.; Böhme, M.; Martinetz, T.; Barth, E. Self-organizing maps for pose estimation with a time-of-flight camera. In Proceedings of the Dynamic 3D Imaging: DAGM 2009 Workshop, Dyn3D 2009, Jena, Germany, 9 September 2009; pp. 142–153. [Google Scholar]
- Guan, H.; Feris, R.S.; Turk, M. The isometric self-organizing map for 3D hand pose estimation. In Proceedings of the 7th International Conference on Automatic Face and Gesture Recognition (FGR06), Southampton, UK, 10–12 April 2006; pp. 263–268. [Google Scholar] [CrossRef]
- Balasubramanian, M.; Schwartz, E.L. The isomap algorithm and topological stability. Science 2002, 295, 7. [Google Scholar] [CrossRef] [PubMed]
- Toshev, A.; Szegedy, C. Deeppose: Human pose estimation via deep neural networks. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Columbus, OH, USA, 23–28 June 2014; pp. 1653–1660. [Google Scholar]
- Khan, N.U.; Wan, W. A review of human pose estimation from single image. In Proceedings of the 2018 International Conference on Audio, Language and Image Processing (ICALIP), Shanghai, China, 16–17 July 2018; pp. 230–236. [Google Scholar] [CrossRef]
- Crescitelli, V.; Kosuge, A.; Oshima, T. POISON: Human pose estimation in insufficient lighting conditions using sensor fusion. IEEE Trans. Instrum. Meas. 2020, 70, 1–8. [Google Scholar] [CrossRef]
- Lin, C.M.; Tsai, C.Y.; Lai, Y.C.; Li, S.A.; Wong, C.C. Visual object recognition and pose estimation based on a deep semantic segmentation network. IEEE Sens. J. 2018, 18, 9370–9381. [Google Scholar] [CrossRef]
- Hoque, S.; Arafat, M.Y.; Xu, S.; Maiti, A.; Wei, Y. A comprehensive review on 3D object detection and 6D pose estimation with deep learning. IEEE Access 2021, 9, 143746–143770. [Google Scholar] [CrossRef]
- Harvey, W.; Rainwater, C.; Cothren, J. Direct Aerial Visual Geolocalization Using Deep Neural Networks. Remote Sens. 2021, 13, 4017. [Google Scholar] [CrossRef]
- Shah, H.; Rana, K. A Deep Learning Approach for Autonomous Navigation of UAV. In Proceedings of the Futuristic Trends in Network and Communication Technologies, Ahmedabad, India, 10–11 December 2021; Singh, P.K., Veselov, G., Pljonkin, A., Kumar, Y., Paprzycki, M., Zachinyaev, Y., Eds.; Springer: Singapore, 2021; pp. 253–263. [Google Scholar] [CrossRef]
- Yao, H.; Qin, R.; Chen, X. Unmanned aerial vehicle for remote sensing applications—A review. Remote Sens. 2019, 11, 1443. [Google Scholar] [CrossRef]
- Radoglou-Grammatikis, P.; Sarigiannidis, P.; Lagkas, T.; Moscholios, I. A compilation of UAV applications for precision agriculture. Comput. Netw. 2020, 172, 107148. [Google Scholar] [CrossRef]
- Muchiri, G.; Kimathi, S. A review of applications and potential applications of UAV. In Proceedings of the Sustainable Research and Innovation Conference, Pretoria, South Africa, 20–24 June 2022; pp. 280–283. [Google Scholar]
- Baldini, F.; Anandkumar, A.; Murray, R.M. Learning Pose Estimation for UAV Autonomous Navigation and Landing Using Visual-Inertial Sensor Data. In Proceedings of the 2020 American Control Conference (ACC), Denver, CO, USA, 1–3 July 2020; pp. 2961–2966. [Google Scholar] [CrossRef]
- Palossi, D.; Zimmerman, N.; Burrello, A.; Conti, F.; Müller, H.; Gambardella, L.M.; Benini, L.; Giusti, A.; Guzzi, J. Fully Onboard AI-Powered Human-Drone Pose Estimation on Ultralow-Power Autonomous Flying Nano-UAVs. Proc. IEEE Internet Things J. 2022, 9, 1913–1929. [Google Scholar] [CrossRef]
- Pessanha Santos, N.; Lobo, V.; Bernardino, A. 3D Model-Based UAV Pose Estimation using GPU. In Proceedings of the OCEANS 2019 MTS/IEEE, Seattle, WA, USA, 27–31 October 2019; pp. 1–6. [Google Scholar] [CrossRef]
- Jähne, B.; Haussecker, H.; Geissler, P. Handbook of Computer Vision and Applications; Citeseer: Princeton, NJ, USA, 1999; Volume 2. [Google Scholar]
- Hartley, R.; Zisserman, A. Multiple View Geometry in Computer Vision; Cambridge University Press: Cambridge, UK, 2003. [Google Scholar]
- Leorna, S.; Brinkman, T.; Fullman, T. Estimating animal size or distance in camera trap images: Photogrammetry using the pinhole camera model. Methods Ecol. Evol. 2022, 13, 1707–1718. [Google Scholar] [CrossRef]
- Dawson-Howe, K.M.; Vernon, D. Simple pinhole camera calibration. Int. J. Imaging Syst. Technol. 1994, 5, 1–6. [Google Scholar] [CrossRef]
- Martins, H.; Birk, J.; Kelley, R. Camera models based on data from two calibration planes. Comput. Graph. Image Process. 1981, 17, 173–180. [Google Scholar] [CrossRef]
- Altman, E.I.; Iwanicz-Drozdowska, M.; Laitinen, E.K.; Suvas, A. Financial distress prediction in an international context: A review and empirical analysis of Altman’s Z-score model. J. Int. Financ. Manag. Account. 2017, 28, 131–171. [Google Scholar] [CrossRef]
- Henderi, H.; Wahyuningsih, T.; Rahwanto, E. Comparison of Min-Max normalization and Z-Score Normalization in the K-nearest neighbor (kNN) Algorithm to Test the Accuracy of Types of Breast Cancer. Int. J. Inform. Inf. Syst. 2021, 4, 13–20. [Google Scholar] [CrossRef]
- Bação, F.; Lobo, V.; Painho, M. Self-organizing maps as substitutes for k-means clustering. In Proceedings of the Computational Science—ICCS 2005: 5th International Conference, Atlanta, GA, USA, 22–25 May 2005; Proceedings, Part III 5. Springer: Berlin/Heidelberg, Germany, 2005; pp. 476–483. [Google Scholar]
- Ferreira, T.; Bernardino, A.; Damas, B. 6D UAV pose estimation for ship landing guidance. In Proceedings of the OCEANS 2021: San Diego—Porto, San Diego, CA, USA, 20–23 September 2021; pp. 1–10. [Google Scholar] [CrossRef]
- Vaswani, A.; Shazeer, N.; Parmar, N.; Uszkoreit, J.; Jones, L.; Gomez, A.N.; Kaiser, Ł.; Polosukhin, I. Attention is all you need. Adv. Neural Inf. Process. Syst. 2017, 30, 13756489. [Google Scholar] [CrossRef]
- Shaw, P.; Uszkoreit, J.; Vaswani, A. Self-attention with relative position representations. arXiv 2018, arXiv:1803.02155. [Google Scholar]
- Parisi, L.; Neagu, D.; Ma, R.; Campean, F. QReLU and m-QReLU: Two novel quantum activation functions to aid medical diagnostics. arXiv 2020, arXiv:2010.08031. [Google Scholar]
- Parcollet, T.; Ravanelli, M.; Morchid, M.; Linarès, G.; Trabelsi, C.; De Mori, R.; Bengio, Y. Quaternion recurrent neural networks. arXiv 2018, arXiv:1806.04418. [Google Scholar]
- Wang, Y.; Solomon, J.M. 6D Object Pose Regression via Supervised Learning on Point Clouds. arXiv 2020, arXiv:2001.08942. [Google Scholar]
- Hong, Y.; Liu, J.; Jahangir, Z.; He, S.; Zhang, Q. Estimation of 6D Object Pose Using a 2D Bounding Box. Sensors 2021, 21, 2939. [Google Scholar] [CrossRef] [PubMed]
- de Melo, C.M.; Torralba, A.; Guibas, L.; DiCarlo, J.; Chellappa, R.; Hodgins, J. Next-generation deep learning based on simulators and synthetic data. Trends Cogn. Sci. 2022, 26, 174–187. [Google Scholar] [CrossRef]
- Nikolenko, S.I. Synthetic Data for Deep Learning; Springer: Berlin/Heidelberg, Germany, 2021; Volume 174. [Google Scholar]
- Willmott, C.J.; Matsuura, K. Advantages of the mean absolute error (MAE) over the root mean square error (RMSE) in assessing average model performance. Clim. Res. 2005, 30, 79–82. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).