Abstract
This paper provides a structured and practical roadmap for practitioners to integrate learning from demonstration (LfD) into manufacturing tasks, with a specific focus on industrial manipulators. Motivated by the paradigm shift from mass production to mass customization, it is crucial to have an easy-to-follow roadmap for practitioners with moderate expertise, to transform existing robotic processes to customizable LfD-based solutions. To realize this transformation, we devise the key questions of “What to Demonstrate”, “How to Demonstrate”, “How to Learn”, and “How to Refine”. To follow through these questions, our comprehensive guide offers a questionnaire-style approach, highlighting key steps from problem definition to solution refinement. This paper equips both researchers and industry professionals with actionable insights to deploy LfD-based solutions effectively. By tailoring the refinement criteria to manufacturing settings, this paper addresses related challenges and strategies for enhancing LfD performance in manufacturing contexts.
1. Introduction
In the context of robotics, learning from demonstration (LfD) refers to “the paradigm in which robots acquire new skills by learning to imitate an expert” [1], i.e., a robot learns to perform a task by watching a human’s actions rather than being explicitly programmed. LfD allows robots to acquire new skills or refine existing ones while reducing the need for manual programming of robot behaviors, ultimately eliminating the requirement for a robotic expert [1].
LfD offers a distinct approach to programming robots compared to traditional manual programming methods. Traditional manual programming involves writing code or scripts to explicitly define the sequence of actions and movements for the robot to perform a task. It requires expertise in robot programming languages, kinematics, and dynamics. Moreover, writing code for complex tasks can be time-consuming, and any changes in the environment or task requirements demand extra reprogramming effort [2]. On another paradigm, optimization-based programming involves formulating the robot’s task as an optimization problem, where the objective is to minimize or maximize a certain objective [3]. While this method optimizes the task execution based on various environments and task requirements and does not need reprogramming, it still requires a high level of robotic expertise to carefully formulate the task as an optimization problem and mathematically model the task and the environment in order to efficiently solve for the best solution.
LfD surpasses these limitations by allowing nonexperts to teach the robot without mathematical formulation or any robotic knowledge. Also, the LfD algorithm learns and generalizes the task flexibly according to the environment and task requirements. Teaching a new task or refining a task takes significantly less effort, does not require robotic expertise, and can have the robotic system up and running in a relatively quicker manner. These benefits have been found to be useful in the industry, where efficiency and agility gain importance when using robots for industrial tasks [4,5].
Several notable reviews and surveys focus on LfD from different points of view and consider various aspects. The work in [1] gives a general review of LfD and provides an updated taxonomy of the recent advances in the field. In [6] the authors survey LfD for robotic manipulation, discussing the main conceptual paradigms in the LfD process. In [7], the focus is on the applications of LfD in smart manufacturing. They introduce and compare the leading technologies developed to enhance the learning algorithms and discuss them in various industrial application cases. In [8] the focus of the survey is on robotic assembly. Specifically, they discuss various approaches to demonstrate assembly behaviors and how to extract features to enhance LfD performance in assembly. They also analyze and discuss various methods and metrics to evaluate LfD performance. Authors in [9] survey LfD advances with respect to human–robot collaborative tasks in manufacturing settings, dedicating their work to collaborative scenarios. They provide detailed insights into the role of various human interactions in different LfD methods. The technical nature of the survey makes it suitable for active researchers in LfD to seek new directions in making the LfD algorithms more collaborative. The authors in [10] conduct a thorough survey of all assembly tasks implemented by LfD, categorizing state-of-the-art LfD approaches in assembly and highlighting opportunities in academia. The work in [11] explores trajectory generation via LfD in technical depth, analyzing the performance of various learning methods. The authors in [12] provide an in-depth algorithmic perspective on learning approaches for robot manipulation, detailing learning methods, their representations, and limitations. The work in [13] focuses on interactive learning, a paradigm we later introduce in Section 5. The work in [14] is dedicated to LfD for path planning, with a focus on obstacle avoidance. The authors in [15] concentrate on LfD for contact tasks, offering detailed insights into this niche area.
While the existing studies provide valuable insights into various aspects of LfD, they often lack a comprehensive roadmap or practical guidance for practitioners. They mostly focus on presenting the state of the art without providing a clear roadmap for practitioners to implement LfD in their robotic tasks. Moreover, the technical depth of most of the studies requires a strong background in LfD, making it inaccessible to nonacademic practitioners or researchers who are new to the field. Therefore, there is a need for a new study that not only consolidates existing knowledge but also bridges the gap between research and practice.
From a practical point of view, the recent advancements in the manufacturing industry create an increasing need for adaptable manufacturing robotic systems to perform flexibly with the variant demands of the market. The production schemes are shifting from mass production, where a fixed line of manufacturing is used to create products on a mass scale, to mass customization, where production is in smaller batches of different products according to the market need [16,17]. To retain the efficiency and cost-effectiveness of mass production schemes, robotic systems have to quickly adapt to new tasks and manufacturing requirements [18,19]. Such transition and requirements have led to a significant application of LfD as a suitable solution in the manufacturing industry. It means that the existing robotic tasks in the mass production scheme need to be transformed via LfD to meet the new requirements of mass customization, which is why it is necessary to provide guidance for industry practitioners to start deploying state-of-the-art LfD solutions in existing robotic tasks. Notably, among all the robotic systems, industrial manipulators are the most popular and versatile robot types widely used in manufacturing and production lines. Therefore, while the application of robotic systems is not limited to manipulators, it is beneficial to have the focus of this paper narrowed down to industrial manipulators, due to their critical role in the automation of manufacturing and production lines.
Motivated by the aforementioned considerations and in contrast to existing reviews, our work aims to offer a practical and structured approach to implementing LfD in manufacturing tasks. Unlike other reviews, our review takes the form of a comprehensive questionnaire-style guide, providing practitioners with a clear roadmap to integrate LfD-based robot manipulation. Tailored for moderate expertise requirements, this tutorial-style taxonomy offers step-by-step instructions, enabling both researchers and professionals to develop application-based LfD solutions. This review provides the readers with the main steps to define the problem and devise an LfD solution, as well as giving main research directions for refining the performance of the LfD. The refinement criteria are also tailored based on the practical application of LfD. Moreover, our work aims to connect all these elements and map them to the requirements of practitioners. By offering a high-level roadmap, practitioners can identify the challenges they face and refer to the associated literature for deeper insights.
The application scenarios for robots in manufacturing are varied and unique, covering tasks like welding, painting, pick-and-place operations, machining, assembly, inspection, material handling, and packaging. Despite significant advancements in LfD for tasks such as peg insertion, gluing, interlocking, pick-and-place, sewing, wiring, stacking, screwing, hammering, and bolting, it remains impractical to comprehensively address all manufacturing tasks due to their diversity and the unique challenges they pose [10], especially in unstructured environments. Therefore, our proposed roadmap offers a comprehensive guideline to assist practitioners in navigating these challenges by identifying key decision points and providing practical implications, advantages, disadvantages, limitations, and recommendations. This roadmap is intended to be used iteratively to enhance the implementation of LfD.
In summary, the original contributions of our paper are as follows:
- Comprehensive roadmap. We provide a structured and practical roadmap for implementing LfD in diverse manufacturing tasks, guiding practitioners through key decision points and offering practical recommendations.
- Tutorial-style taxonomy. Our review includes a step-by-step tutorial designed for practitioners with moderate expertise, enabling the development of application-based LfD solutions.
- Mapping of existing research. We connect various elements from existing in-depth reviews and surveys, offering a high-level guide that helps practitioners identify specific challenges and access detailed insights for deeper understanding.
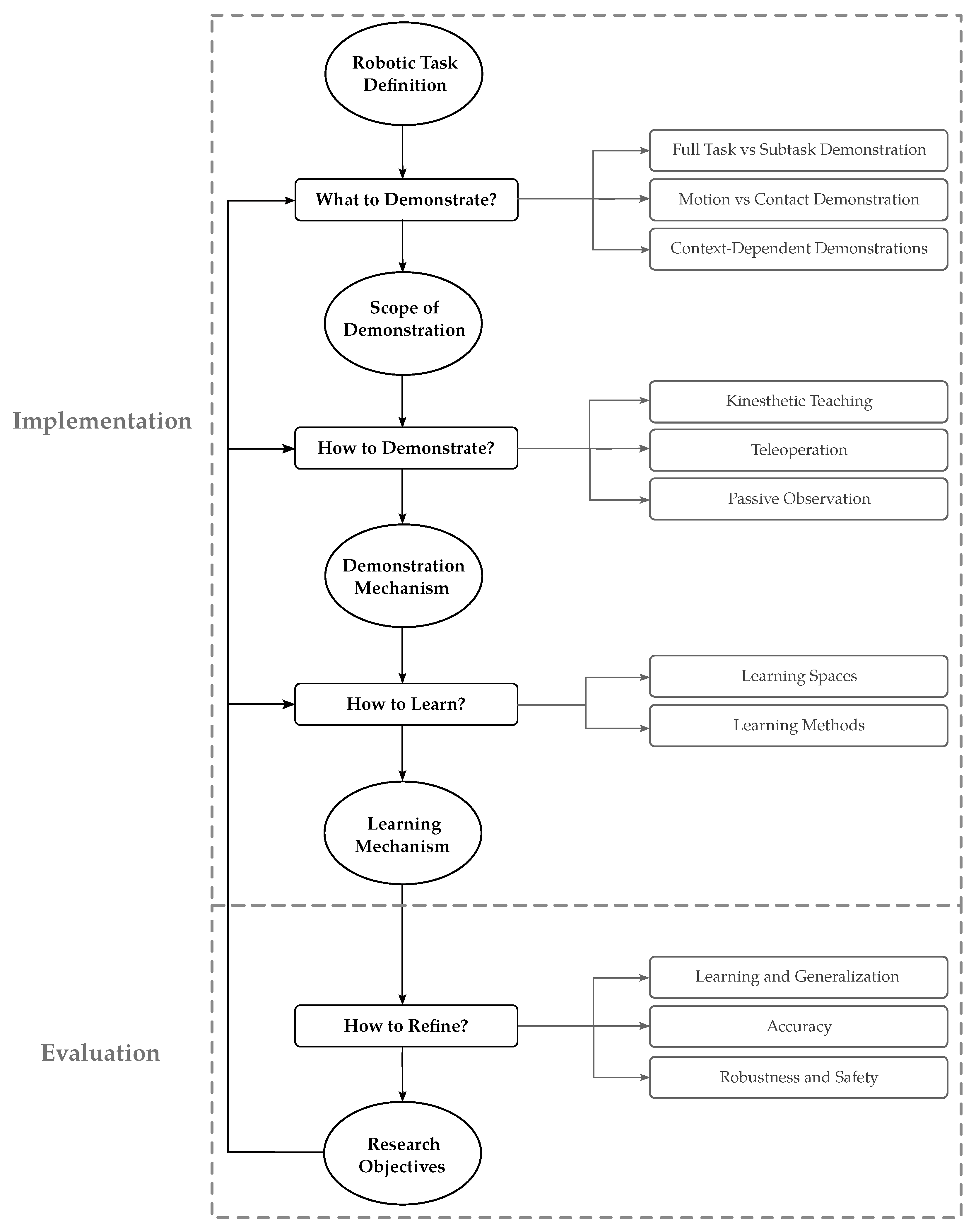
For this purpose, this paper explores how to integrate LfD into the robotization process using manipulators for manufacturing tasks, depicted in Figure 1. First, the practitioner addresses the question of “What to demonstrate” to define the “Scope of demonstration”. Subsequently, the practitioner needs to answer the question of “How to demonstrate” in order to devise a “Demonstration mechanism”. Accordingly, the question of “How to learn” equips the robotic manipulator with the proper “Learning mechanism”. Even though the LfD process implementation is accomplished at this stage, the evaluation of LfD performance leads to the question of “How to refine”, which provides the research objectives and directions in which the performance of the LfD process can be further improved. Taking these points into account, the rest of the paper is structured as follows:
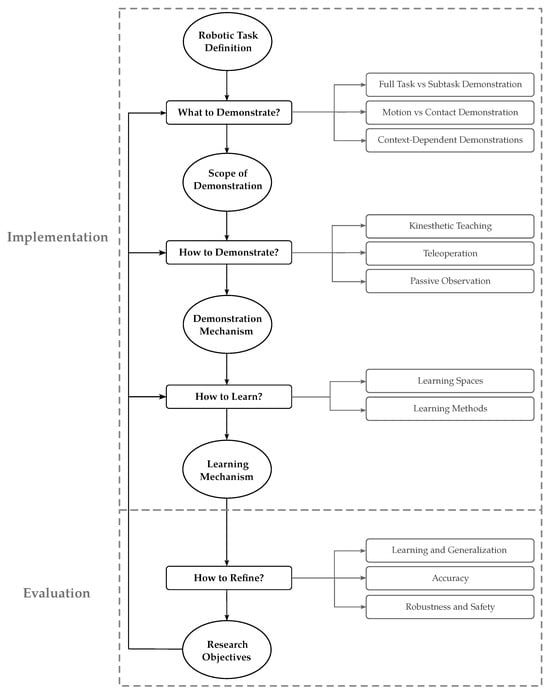
Figure 1.
Overview of our proposed roadmap for LfD implementation.
- What to demonstrate? (Section 2): This section explores how to carefully define the task and identify certain features and characteristics that influence the design of the process.
- How to demonstrate? (Section 3): Building upon the scope of demonstration, this section explores effective demonstration methods, considering task characteristics and their impact on robot learning.
- How to learn? (Section 4): In this section, the focus shifts to implementing learning methods, enabling autonomous task execution based on human demonstrations.
- How to refine? (Section 5): Concluding the structured approach, this section addresses refining LfD processes to meet industrial manufacturing requirements, outlining challenges and strategies for enhancing LfD solutions in manufacturing settings.
2. What to Demonstrate
This section focuses on the first step in developing an LfD solution, i.e., extracting the scope of the demonstration from the desired task. In this step, with a specific robotic task as the input, we explore how to determine the knowledge or skills a human teacher needs to demonstrate to the robot. The scope of demonstration establishes clear boundaries for what the robot should be able to accomplish after learning. Defining the scope is crucial because it sets the foundation for the entire LfD process. A well-defined scope ensures that the provided demonstrations comprehensively and accurately capture the desired robot behavior. Conversely, a poorly defined scope can lead to incomplete or inaccurate demonstrations, ultimately limiting the effectiveness of the LfD solution.
To determine “What to demonstrate”, three different aspects of the robotic task will be investigated as follows.
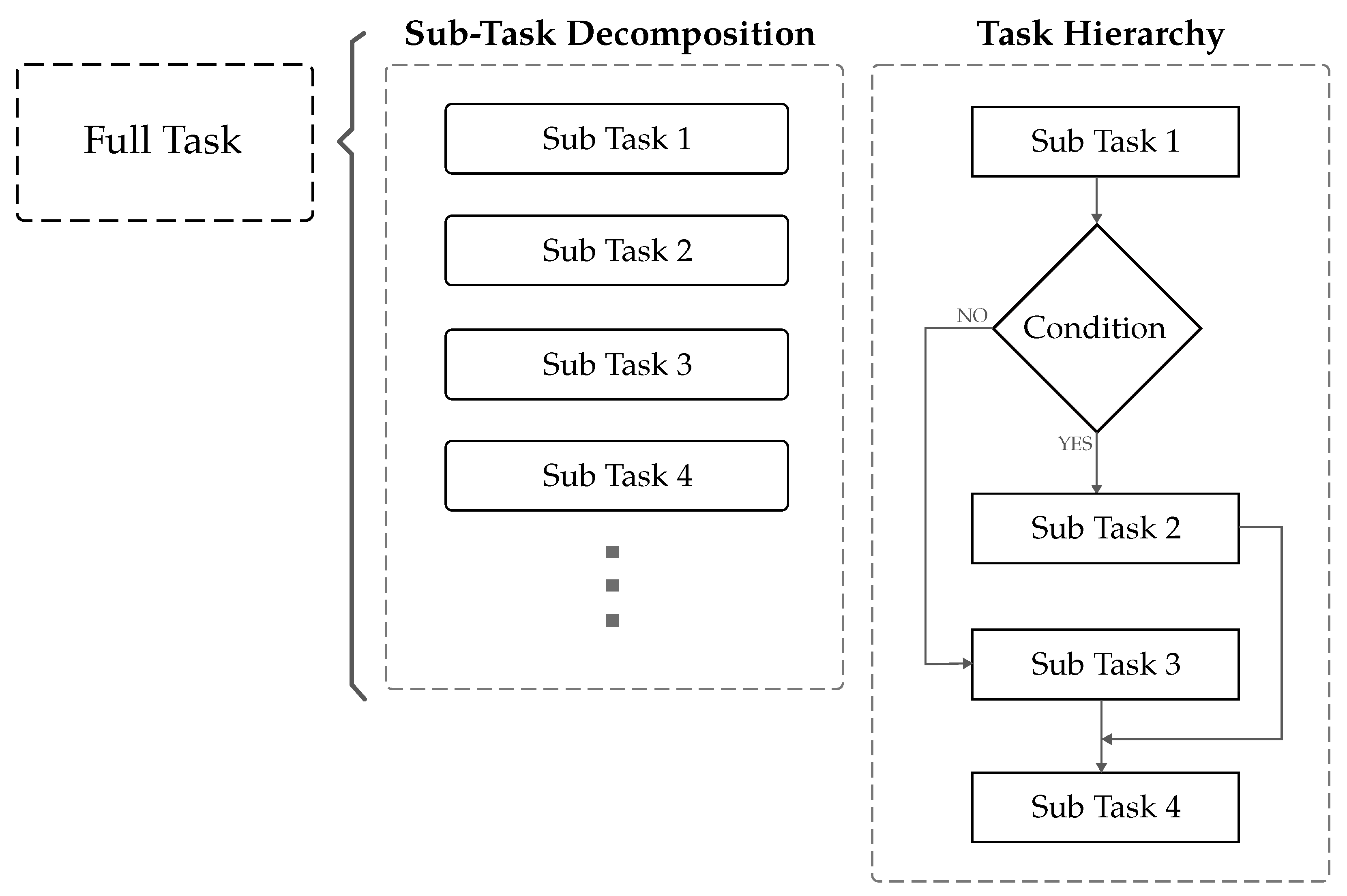
2.1. Full Task versus Subtask Demonstration
A full robotic task can be decomposed into smaller steps called subtasks, along with their associated task hierarchy or their logical sequence (Figure 2). In a full-task demonstration, the human teacher demonstrates the entire process, including all subtasks in their logical order. In contrast, subtask demonstration focuses on teaching each subtask of the robotic task one at a time. Here, we explore whether to demonstrate the full robotic task at once, or aim to demonstrate subtasks separately.
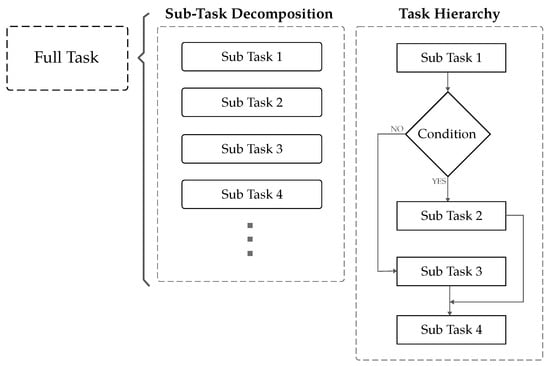
Figure 2.
Illustration of how subtasks and task hierarchy comprise a full task.
What happens when learning full task: In the case of full-task demonstration, the LfD algorithm is required first to segment the task into smaller subtasks and learn them separately [20,21,22,23,24,25,26,27,28,29,30]. Otherwise, training a single model on the entire task can lead to information loss and poor performance [31]. Beyond identifying subtasks, a full robotic task involves the logical order in which they should be executed—the task hierarchy. The LfD algorithm is required to extract these relationships between subtasks to build the overall task logic [20,22,23,24,28,29]. This segmentation is achieved through spatial and temporal reasoning on demonstration data [21,23,25,26,27,28,30,32,33,34,35,36]. Spatial features help identify subtasks, while temporal features reveal the high-level structure and sequence.
For instance, consider demonstrating a pick-and-place task as a full task. The LfD algorithm can easily segment the demonstration into “reaching”, “moving”, and “placing” the object, along with their sequential task hierarchy. Because these subtasks involve clearly defined motions and follow a straightforward, linear order, the LfD algorithm can reliably extract the complete logic required to perform the entire pick-and-place task. On the other hand, consider a pick-and-insert task with tight tolerances. Precise insertion is challenging to demonstrate and requires retry attempts as recovery behavior. This creates a conditional task hierarchy. The successful insertion depends on achieving tight tolerances, and if the initial attempt fails, the LfD system needs to learn the recovery behavior of repositioning the object and attempting insertion again. Consequently, LfD’s reliance on automatic segmentation to extract the detailed task logic in such cases becomes less reliable. However, background information on the task characteristic can be provided as metadata by the human teacher and leveraged by the learning algorithm to improve the segmentation method in semantic terms [26,37].
What happens when learning subtask: When subtasks are demonstrated individually, the human teacher manually breaks down the full task and provides separate demonstrations for each one, along with the associated task hierarchy. This isolates the LfD algorithm’s learning process, allowing it to focus on learning one specific subtask at a time [38,39,40,41,42,43,44]. It is evident that this approach requires extra effort from the teacher compared to full-task demonstration.
For complex or intricate tasks such as pick-and-insert with tight tolerances, the teacher can individually provide “reaching”, “moving”, and “inserting” subtasks along with recovery behaviors. While this requires the teacher to separately define the task hierarchy and provide demonstrations for each subtask, it yields several benefits. First, the teacher can focus on providing clear and accurate demonstrations for each isolated step. Second, it allows for a reliable demonstration of the conditional hierarchy involved in complex tasks [45,46].
When to demonstrate full task versus subtask: One of the significant differences between full-task and subtask demonstrations emerges in conditional behaviors, especially when recovery behaviors need to be demonstrated and implemented. For instance, in an assembly process with a stationary vision system, the vision system must detect a part for the robot to grasp. If the grasping fails, the robot should attempt the grasp again by first moving its arm outside the vision system’s field of view, allowing the object to be redetected before retrying. With full-task demonstration, it is impossible to showcase both the primary and recovery behaviors completely and in one pass. Therefore, subtask demonstration becomes necessary, either for the recovery behavior alone or for the entire task.
To further illustrate the difference, consider a welding task. Welding requires high precision and is dependent on the geometry of the object being welded. Making the learning method geometry-aware can enhance its generalization accuracy. In full-task demonstration, the practitioner needs to encode the entire geometry into the learning method and rely on the segmentation algorithm’s efficiency to correctly segment the full demonstration and the geometric information. Conversely, subtask demonstration allows the practitioner to manually segment the full task based on their knowledge of the object’s geometry. This approach provides better control over the welding performance, isolates the learning of subtasks, and facilitates the encoding of geometric information. In contrast, for tasks such as painting or stacking, full-task segmentation can be reliably achieved through spatial and temporal reasoning and can be left to the learning method. Manually dividing these tasks into subtasks would result in a large number of subtasks, making the demonstration process cumbersome and time-consuming.
Overall, demonstrating the entire robotic task at once can be efficient for teaching simple, sequential tasks, as the algorithm can segment and learn reliably. However, for complex tasks with conditional logic or unstructured environments, this approach struggles. Breaking the task into subtasks and demonstrating them individually is more effective in these cases. This removes the burden of segmentation from the learning algorithm and allows for better performance, especially when dealing with conditional situations. By teaching subtasks first, and then layering the task hierarchy on top, robots can handle more complex tasks and learn them more efficiently. In essence, full-task demonstration is recommended for simple behaviors with linear task logic, while complex tasks are recommended to be decomposed into subtasks and demonstrated separately. As a general example, full-task demonstration is recommended for tasks such as painting, material handling, stacking, and packaging, as the complexity of such tasks is limited, and at the same time, division of the task into subtasks will result in numerous subtasks, which increases the effort of task implementation. On the other hand, subtask demonstration is recommended for tasks such as welding, interlocking, screwing, and bolting, since such tasks are more precise and complex, and require more reliability to ensure high-quality demonstration. Nonetheless, these examples only serve as an intuitive guideline, and the actual choice depends on the detailed and various situations of the desired task.
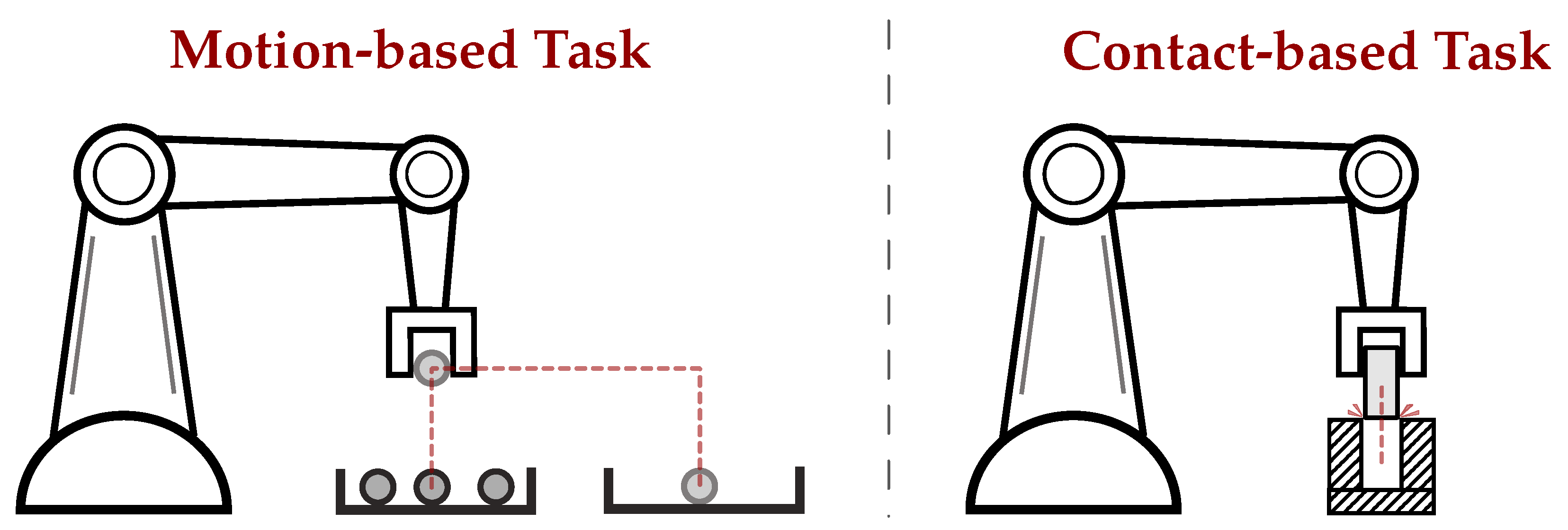
2.2. Motion-Based versus Contact-Based Demonstration
Robot task demonstrations can be categorized into two main types: motion-based and contact-based. Motion-based tasks, like pick-and-place [42,43,44], focus on teaching the robot’s movement patterns. The key information for success is captured in the robot’s trajectory and kinematics, with limited and controlled contact with the environment [42,43,44,47,48,49,50,51,52,53,54]. Conversely, contact-based tasks, such as insertion [39,55,56,57,58,59,60,61,62,63,64,65,66], require the robot to understand how to interact with objects. Here, task success also relies on understanding forces and contact points [66]. Simply replicating the motion does not suffice, and the robot needs to learn to apply appropriate force or adapt to tight tolerances to avoid failure. This highlights the importance of contact-based demonstrations for tasks where interaction with the environment is crucial. The comparison of motion-based and contact-based tasks is illustrated in Figure 3. For deeper insights, the works in [14,15] dive deeper into motion-based and contact-based tasks, respectively.
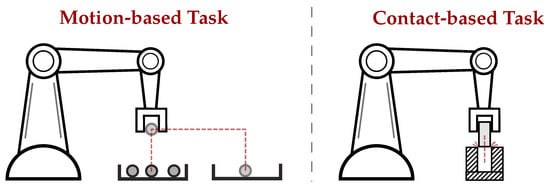
Figure 3.
Comparison of motion-based versus contact-based task. On the left, the pick-and-place task has a structured and predictable interaction with the environment, while the insertion task on the right needs to deal with the contact resulting from tight tolerances to successfully perform the task. The red lines indicate the motion of the robot’s end effector.
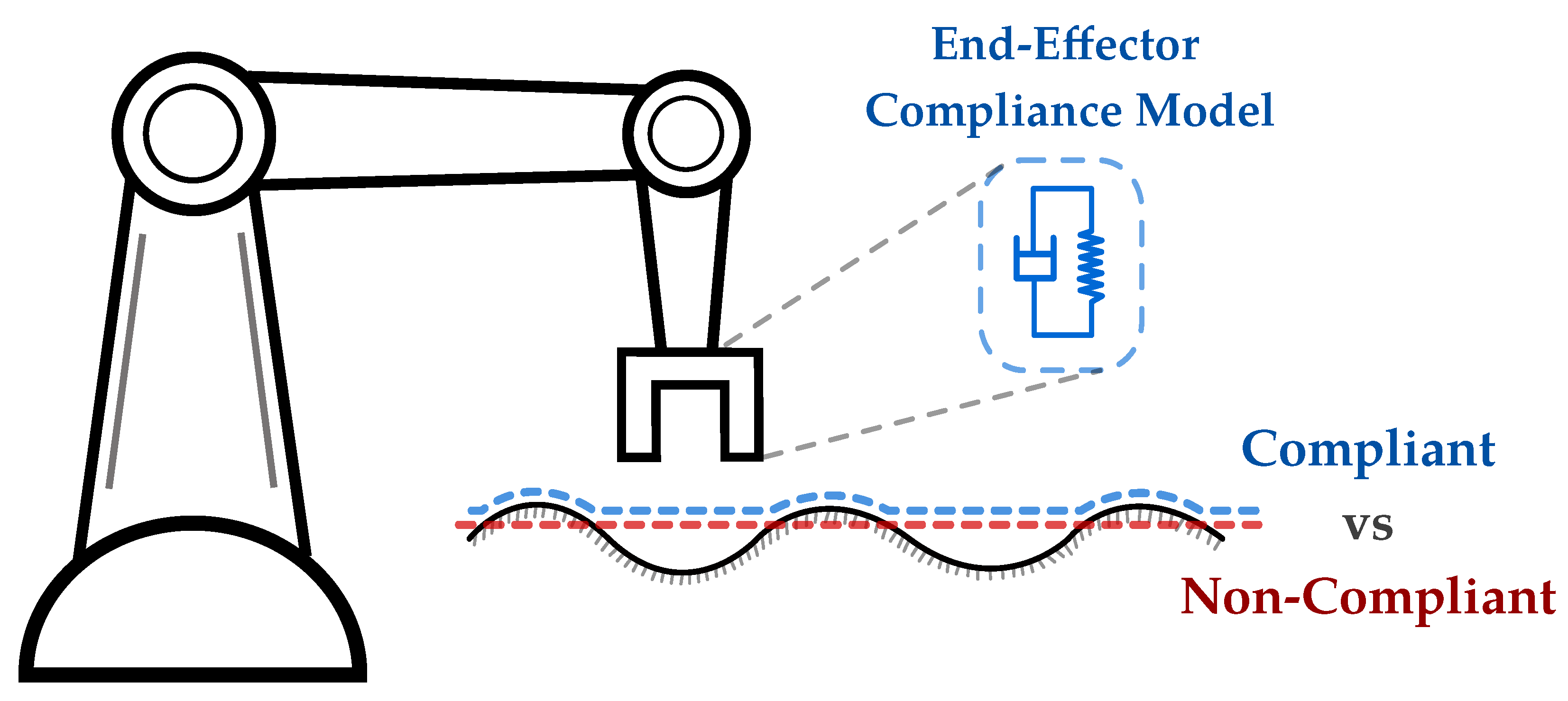
Notion of compliance: To understand whether a task is motion-based or contact-based, it is necessary to understand the notion of compliance. Compliance in robotics refers to the capacity of a robotic system to yield or adjust its movements in response to external forces, ensuring a more adaptable and versatile interaction with its environment [67]. This adaptability is typically achieved via impedance controllers, where the end effector of the robot is modeled as a spring-damper system to represent compliance (Figure 4) [68,69]. In motion-based tasks, the robot prioritizes following a planned path with minimal adjustment (low compliance), i.e., external forces cannot alter the robot’s behavior, while contact-based tasks allow for more adaptation (high compliance) to better interact with the environment. It is important not to confuse compliance with collision avoidance. Collision avoidance involves actively preventing contact with the environment by adapting the behavior on the kinematic level, while compliance relates to the robot’s ability to adjust its behavior in response to external forces.
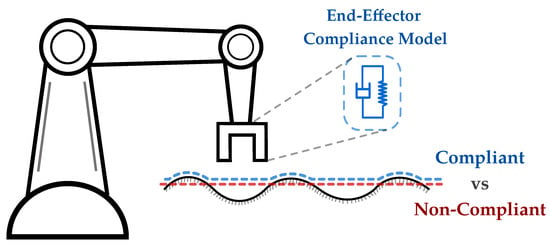
Figure 4.
Illustration of compliant versus noncompliant behavior against the environment. The black line represents the environment surface, the red path represents a noncompliant behavior, and the blue path represents the compliant behavior against the environment surface. In impedance control, the end-effector is modeled as a spring-damper system.
What is learned and when to teach: With motion-based demonstration, the LfD algorithm learns under the assumption of zero compliance and replicates the behavior on a kinematic level, i.e., strict motion. On the other hand, contact-based teaching enables the LfD algorithm to learn how to react when compliance is high; therefore, it learns the skills on how to interact with the working environment.
One critical factor in selecting between motion-based and contact-based demonstration is the analysis of the desired task through the lens of its dependence on compliance. For example, in an insertion task with tight tolerances, if there are slight inaccuracies in measurements and the peg lands with a slight offset to the hole, compliance can be helpful to react skillfully to this misalignment and attempt to find the right insertion direction. Conversely, a pick-and-place task typically does not require compliance in the case when the grasping mechanism is simple and structured.
Practical implications: From the point of view of practical implementation, the trade-off between motion and contact during the task execution is a key design factor to implement the task successfully [21,39,65,66,70,71,72]. For example, in tasks such as rolling dough [66], board wiping [39], and grinding [21], hybrid motion and force profile are learned as both are crucial for successful task execution, i.e., a force profile is needed to be tracked alongside the motion. As mentioned, this factor is best encoded via impedance control, where at each point of task execution, it can be determined whether position or force requirements are in priority [56,73]. However, this method requires torque-controlled compliant robots and cannot be applied to many industrial robots, which are position-controlled and stiff [58]. For such robots, the alternative to impedance control is admittance control, which operates with an external force sensor and can be implemented on stiff industrial robots [74].
As a general example, tasks such as inspection, welding, and packaging can rely mainly on motion demonstration, as environment interaction is either very limited or nonexistent. On the other hand, tasks such as peg insertion, interlocking, and bolting depend mainly on contact demonstration. Finally, the motion–contact trade-off plays a major role in tasks such as painting, screwing, and hammering, since both motion and contact demonstration should be respected to successfully complete the task. Again, the final design choice can vary depending on the requirements of the desired task and through iteratively finding the best scope of demonstration.
2.3. Context-Dependent Demonstrations
In addition to the choice of scope between full task versus subtask and motion versus contact demonstration, the operation of the robot is influenced by various specific contexts. Such contextual settings are highly dependent on the requirements of the task and often need to be custom-designed and tailored for the task. Nonetheless, here, we discuss several common contexts alongside the considerations required for each.
2.3.1. Collaborative Tasks
Tasks that involve collaborating with humans or other robots typically provide interaction through an observation or interaction interface, which serves as a channel for information exchange between the robot and its collaborators [43,75,76,77,78,79]. These interfaces can take various forms, such as physical interaction mechanisms or dedicated communication protocols [78,80,81,82], and are specifically designed and tailored to facilitate the collaborative task. Consequently, when providing demonstrations for such tasks, careful consideration must be given to ensure alignment with the interaction interface.
A typical example of a collaborative task is collaborative object transportation, where one side of the object is held by the robot and the other part is held by the human [76]. In this case, the interaction interface is physical human–robot interaction (pHRI), where not only is the motion important, but also the compliance becomes relevant. Another aspect to consider in collaborative tasks is safety and collision avoidance since the robot’s operating environment is closely shared with the human collaborator [43]. It means that the human teacher needs to further teach safety strategies to the robot. Moreover, collaborative tasks have a more complicated task logic since the execution can depend on the collaborator’s actions, which adds more conditions and more branching in the logic of the task. It also requires the robot to predict the intention of the human in order to follow the task hierarchy [80]. For a deeper insight into LfD for collaborative tasks, refer to [9].
2.3.2. Bi-Manual Tasks
Bi-manual tasks involve the coordinated use of both robot arms to manipulate objects or perform activities that require dual-handed dexterity [33,47,70,83,84,85]. Teaching a robot to perform bi-manual tasks through LfD should emphasize synchronization and coordination between the robot’s multiple arms. For instance, in tasks like assembling components or handling complex objects, the robot needs to learn how to distribute the workload efficiently between its arms. Also, in dual-arm assembly, the coordination of both arms plays a crucial role in achieving the desired precision [70,84,86].
Moreover, bi-manual tasks often require specialized grasping strategies if both arms are simultaneously used for manipulating items [85,87]. Given the proximity of both arms in bi-manual tasks, safety considerations become of great importance. The teaching should emphasize safe practices, including collision avoidance strategies and safety-aware learning.
2.3.3. Via Points
In certain contexts, teaching robot-specific via points within a task can be a highly effective way to convey nuanced information and refine the robot’s execution [63,88,89]. Via points serve as intermediate locations or configurations within a task trajectory, guiding the robot through critical phases or ensuring precise execution. One notable scenario where demonstrating via points can enhance the learning process is in assembly processes [90]. For complex machinery assembly, instructors can guide the robot through specific via points to ensure proper component alignment or correct part insertion. Additionally, via points serve as an excellent measure of accuracy to optimize the robot motion and tool manipulation while ensuring successful task execution as long as the via point is passed throughout the path. Those enable the learning algorithm to understand optimal trajectories, adapt to changing conditions, and enhance its overall versatility.
2.3.4. Task Parameters
Some contexts require explicitly teaching a robot specific task parameters to enhance its understanding and performance in specialized scenarios. These task parameters go beyond the general actions and involve teaching the robot how to adapt to specific conditions or requirements. Here, the focus is on tailoring the robot’s learning to handle variations in the environment, object properties, or operational constraints [78,89,91,92,93].
Teaching the robot about variations in object properties is essential for tasks where the characteristics of objects significantly impact the manipulation process. For instance, in material handling tasks, the robot needs to learn how to handle objects of different shapes, sizes, weights, and materials [91,94]. Demonstrations can be designed to showcase the manipulation of diverse objects, allowing the robot to generalize its learning across a range of scenarios. Additionally, robots operating in manufacturing settings often encounter specific operational constraints that influence task execution. Teaching the robot about these constraints ensures that it can adapt its actions accordingly. Examples of operational constraints include limited workspace, restricted joint movements, or specific safety protocols [95].
3. How to Demonstrate
The next step after answering the question of “What to demonstrate” and defining the scope of demonstration is to realize how to provide demonstrations to transfer the required knowledge and skills from the human teacher to the robot, i.e., the channel through which the information intended by the teacher could be efficiently mapped to the LfD algorithm on the robot. According to [1], demonstration methods can be classified into three main categories: kinesthetic demonstration, teleoperation, and passive observation. In this section, we discuss these categories and analyze their advantages and disadvantages with respect to the scope of demonstration, with a summary provided in Table 1.

Table 1.
Summary of the comparison of demonstration mechanisms.
3.1. Kinesthetic Teaching
Kinesthetic teaching is a method wherein a human guides a robot through a desired motion within the robot’s configuration space. In this approach, a human physically guides the robot to perform a task, and the robot records the demonstration using its joint sensors (Figure 5a) [21,38,42,43,56,58,62,64,77,96,97,98,99]. The key aspect is the direct interaction between the human teacher and the robot in the robot’s configuration space.

Figure 5.
Illustrative examples of the main demonstration approaches.
What Setup is Required: Kinesthetic teaching offers a straightforward setup, requiring only the robot itself. This simplicity contributes to ease of implementation and reduces the complexity of the teaching process, as well as minimizing the associated costs. This makes kinesthetic teaching an affordable and cost-effective option for training robots. Moreover, the interaction with the robot is intuitive for the teacher, making it easier to convey complex tasks and subtle details.
However, the suitability of kinesthetic teaching can be limited by the physical demands it requires, particularly with larger or heavier robots. Safety concerns also arise, especially in scenarios involving rapid movements or the handling of hazardous materials. This limitation can affect the scalability of kinesthetic demonstrations in diverse manufacturing contexts.
How demonstration data are obtained: Through kinesthetic teaching, the robot records the demonstration using its joint sensors. The recorded data form the basis for training the robot, allowing it to learn and replicate the demonstrated motion. The mapping of training data into the learning algorithm is straightforward, which enhances the reliability of the demonstration framework. However, the recorded demonstration data contain noise, as they depends on the physical interaction between the human and the robot. This noise can affect the smoothness of the training data and require additional processing to improve the learning algorithm’s performance [100]. Additionally, since the training data depend on the robot hardware, the scalability of the training data to another setup will be limited.
Recommendations: Kinesthetic teaching is effective for instructing both full-task hierarchies and low-level subtasks, especially excelling in demonstrating complex and detailed subtasks with its precise physical guidance of the robot. However, for full-task demonstrations, additional post-processing of training data is advised to enhance segmentation and eliminate noise. While kinesthetic teaching offers precise control for motion demonstrations, the recorded data often suffer from noise and lack smoothness due to the physical interaction between human and robot. However, it becomes limiting for contact-based demonstrations because unreliable torque readings from joint sensors prevent teaching the desired force profile to the robot, as the human guides its movements.
3.2. Teleoperation
Teleoperation refers to the process in which the human teacher remotely controls the movements and actions of the robot (Figure 5b). This control can be facilitated through different methods including joysticks, haptic interfaces, or other input devices, enabling the operator to teach the robot from a distance [39,66,101,102,103,104,105]. This method differs from kinesthetic teaching as it allows for remote teaching to the robot.
What setup is required: Setting up teleoperation involves equipping the robotic manipulator with necessary sensors like cameras and force/torque sensors to relay feedback about the robot and its surroundings. On the human side, a well-designed control interface is required for intuitive and accurate control of the robot’s movements. A robust communication system, whether wired or wireless, is necessary for real-time transmission of control signals and feedback. Safety measures, including emergency stop mechanisms, are essential to prevent unexpected behaviors, especially since the robot is operated remotely and immediate access to the robot is not possible in case of a malfunction.
The teleoperation setup is inherently well suited for the tasks being operated in dangerous or hard-to-reach environments. Moreover, the design of the teleoperation interface can be versatile according to the target task, to provide the operator with a teaching interface closest to human-like dexterity. On the downside, teleoperation requires a more sophisticated setup compared to kinesthetic teaching, and it requires further designing the control and the communication interface according to the task. While it can promote intuitive teaching, it often requires extra training for the operator on how to use the setup for their teaching and demonstration. The remote nature of teleoperation can also raise concerns over the communication latency of the setup and how it affects the task demonstration depending on the task.
How demonstration data are obtained: Through teleoperation, the acquisition of the training data can be flexibly designed based on what information is required for learning. The training data can be obtained by joint sensor readings, force/torque sensors on the joints or the end effector, haptic feedback, etc. It is the decision of the robotic expert how to map the raw teaching data to processed and annotated training data suitable for the LfD algorithm. One main advantage of teleoperation is that it is possible to isolate the teaching to a certain aspect of the task. For example, in [42], a joystick is used as the teleoperation device, where certain buttons only adjust the velocity of the robot, and other buttons directly affect the end-effector position and leave the execution velocity untouched. This benefit can enable better-tailored teaching or iterative feedback to increase the efficiency of the learning process.
Recommendations: Teleoperation is a suitable approach for demonstrating contact-rich tasks, since there is no physical interaction, and the joint torque sensors or the end effector force sensor on the robot can reliably record the contact-based demonstration as training data. It is also well suited for tasks demanding real-time adjustments. One of the most common combinations of demonstration approaches is to use kinesthetic demonstration for motion demonstration, and use teleoperation for iterative refinements or providing contact-based demonstrations [106].
3.3. Passive Observation
Passive observation refers to the process of a robot learning by observing and analyzing the actions performed by a human or another source without direct interaction or explicit guidance, i.e., the teaching happens with the robot outside the loop while passively observing via various sensors (Figure 5c) [27,70,84,107,108,109,110]. During passive observation, the robot captures and analyzes the relevant data, such as the movements, sequences, and patterns involved in a particular task. The features and characteristics of the task are extracted from the observation and fed into the LfD algorithm as training data for learning and generalization.
What setup is required: Setting up the teaching framework for passive observation involves various sensors such as 2D/3D cameras, motion capture systems, etc., to enable the LfD algorithm to observe the environment and the actions performed by the human teacher. The information from raw observation is then processed by sophisticated machine learning and computer vision algorithms to extract key features of the demonstration and track them throughout the teaching. In this setup, humans often teach the task in their own configuration space (i.e., with their own hands and arms), which makes the teaching easy and highly intuitive for the humans. However, the setup is complicated and expensive due to the requirement of various sensory systems.
When it comes to the scalability of demonstration across numerous tasks and transferability from one robotic platform to another, passive observation stands out as a suitable option for large-scale collections of demonstration datasets for various tasks, making it preferable when extensive datasets are needed for training purposes. This is why kinesthetic teaching and teleoperation mainly rely on a specific robotic platform and often cannot be scaled across tasks or robots.
How demonstration data are obtained: Acquisition of training data through passive observation mainly relies on the extraction of the key features, as the learning performance critically depends on how well the features represent the desired behavior of the robot on the task. This forms a bottleneck in learning, since the more complex the task, the less efficient the feature extraction. Consequently, passive observation can suffer from learning and performance issues when it comes to complex and detailed demonstrations. Overall, as the demonstration setup is complex for this approach and the correspondence problem limits the possibility of demonstrating complex tasks, this approach is not common for manufacturing use cases.
Recommendations Nonetheless, passive observation has been used for demonstrating high-level full-task hierarchies. It is a suitable approach in scenarios where a diverse range of demonstrations across various tasks needs to be captured. For instance, in [70], human demonstrations are observed via a Kinect motion tracker, and then a motion segmentation is applied to build the overall task logic. In terms of scalability, passive observation stands out as a fit option for large-scale data collection, making it particularly suitable when extensive datasets are needed for training purposes.
3.4. Summary of Limitations, Efficiency, and Robustness
In addressing the limitations, efficiency, and robustness of the proposed demonstration methods for robot learning in manufacturing scenarios, several key insights emerge. Kinesthetic teaching, while straightforward and cost-effective, faces challenges due to its physical demands and safety concerns, particularly with larger robots or hazardous materials. The method’s reliance on direct human–robot interaction introduces noise in demonstration data, requiring additional processing to ensure smooth learning and replication by the robot. Teleoperation offers flexibility in data acquisition and enhances safety in hazardous environments, yet it requires sophisticated setups and operator training, potentially introducing communication delays that affect task demonstration efficiency. Passive observation stands out for its scalability in collecting extensive datasets across various tasks but is restricted by complex setup requirements and limitations in extracting detailed features necessary for complex task demonstrations.
In terms of efficiency, kinesthetic teaching excels in its ease of implementation and intuitive interaction, enabling precise control and effective transfer of complex tasks. Teleoperation provides efficient teaching by isolating specific task aspects and supporting real-time adjustments, making it suitable for contact-rich tasks despite its setup complexities. Passive observation proves efficient in large-scale data collection for training purposes but struggles with the efficient extraction of features crucial for complex task demonstrations. Robustness across these methods varies: kinesthetic teaching is robust for both hierarchical tasks and subtasks but constrained by physical limitations; teleoperation robustly handles contact tasks and real-time adjustments but faces setup complexities and latency issues; passive observation is robust in data scalability but limited by setup intricacies and feature extraction efficiency. These insights underscore the need for careful method selection based on specific manufacturing requirements to ensure optimal robot learning and deployment effectiveness.
To provide general examples, kinesthetic teaching is recommended for tasks such as pick-and-place operations, inspection, and packaging. Kinesthetic teaching also proves effective for tasks requiring precise motion control and manipulation, such as welding. Teleoperation is recommended for tasks such as screwing, painting, and gluing. This is because teleoperation enables remote and safe demonstration for tasks such as gluing or painting, as well as allowing for haptic feedback to facilitate contact demonstration in tasks such as screwing and painting. Finally, passive observation, although less common in manufacturing due to its setup complexity, can be applied effectively in tasks like inspection and material handling. In material handling and packaging, passive observation enables robots to learn diverse grasping techniques and packaging sequences by analyzing human operators’ actions from video feeds or motion capture data, enhancing versatility and scalability across different products and packaging formats. These examples serve as a guideline to better design the demonstration mechanism, while the final choice depends on the settings of individual manufacturing tasks in their own specific context.
3.5. Remarks
There are alternative approaches to provide demonstrations tailored to a specific context or situation. For example, in [111], the demonstration is in the form of comparison between trajectories, i.e., the robot produces a set of candidate trajectories, while the human provides preferences and comparison among them to imply which robot behavior is more suitable. In [112], the human feedback has the form of a corrective binary signal in the action domain of the LfD algorithm during robot execution. The binary feedback signifies an increase or decrease in the current action magnitude.
4. How to Learn
This section focuses on the development of the LfD algorithm itself, after determining the scope of demonstration and the demonstration mechanism. The aim of this section is to consider how to design and develop a learning mechanism to meet the requirements of our desired task. We first discuss the possible learning spaces in which the robot can learn, and then we explore the most common learning methods used as the core of the LfD algorithm.
4.1. Learning Spaces
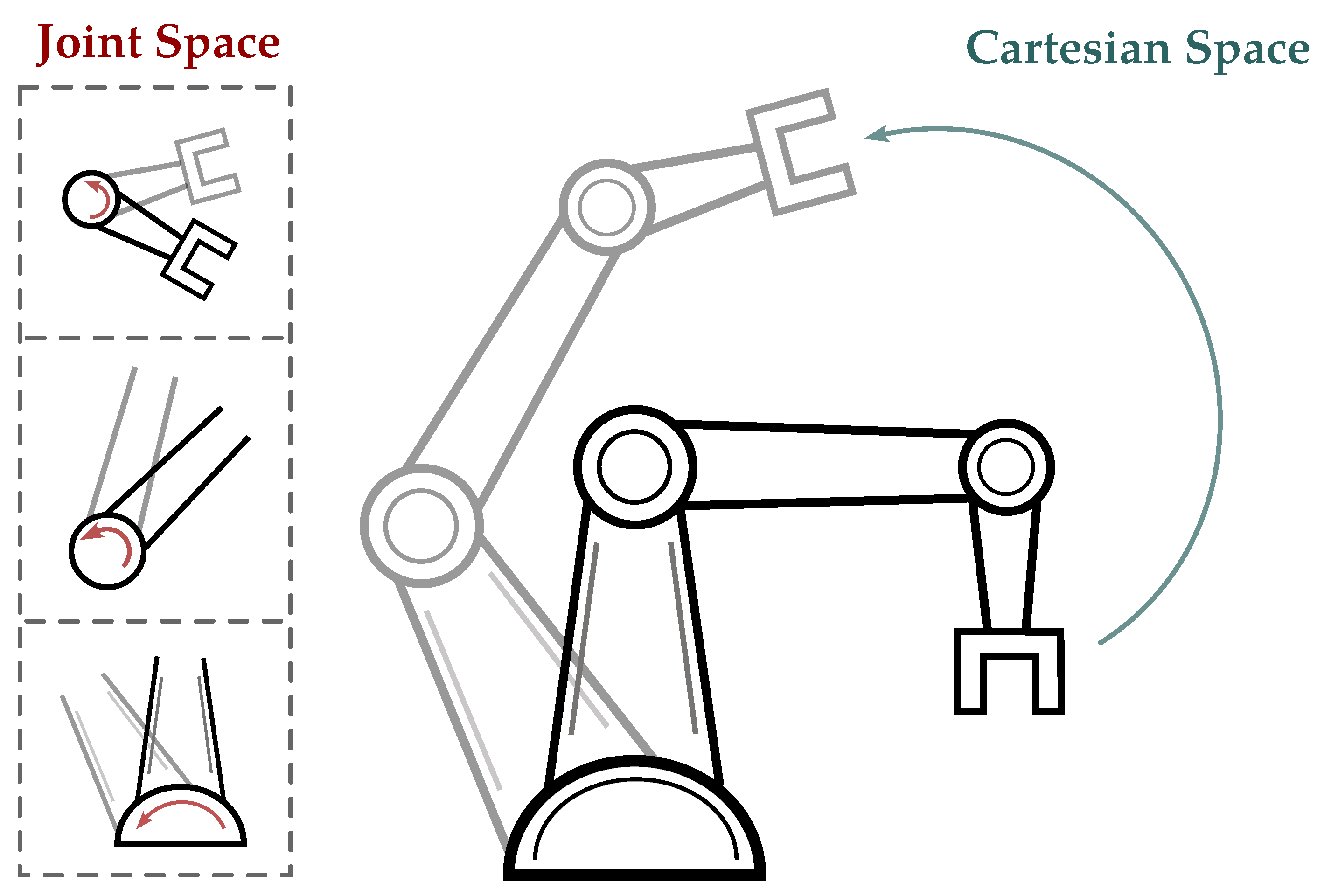
Here, we discuss the concept of learning spaces when representing demonstration data. The learning space not only encompasses where the training data from demonstrations are represented but also serves as the environment where the learning algorithm operates and generalizes the learned behavior. The choice of learning space is important as it provides background knowledge to the algorithm, thereby facilitating better learning and generalization within that designated space. While there are several possibilities for learning spaces, here, we focus on two main choices commonly used for robotic manipulators (Figure 6).
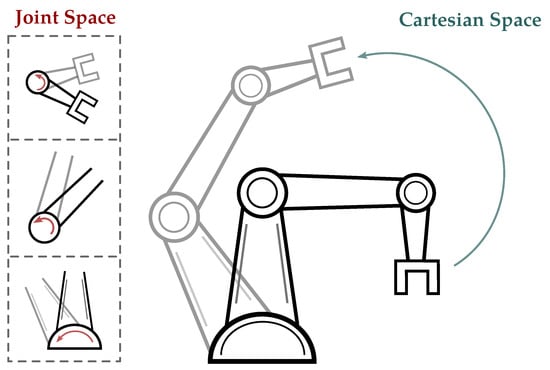
Figure 6.
Illustrative comparison of joint space and Cartesian space. The red arrows represent the joint space motion, while the blue arrow show the same motion via the end effector in the Cartesian space.
4.1.1. Joint Space
The joint space of a robot is a comprehensive representation of its individual joint configurations. This space serves as the primary language of motor commands which offers a low-level and precise representation of the possible configuration of each joint [38,100,113,114].
Learning in joint space: Learning in joint space offers several advantages for LfD algorithms. Existing in Euclidean space makes the underlying math and data processing more efficient and straightforward. Additionally, since joint space directly corresponds to the robot’s control layer, learned behaviors can be seamlessly integrated into the controller, which further simplifies the process.
However, a potential downside of learning in joint space is the risk of overfitting to specific demonstrations, which limits the robot’s generalizability. Furthermore, focusing on joint space learning fails to capture higher-level contextual information which relates to the semantics of the task. Finally, joint space learning is sensitive to hardware variations, making it difficult when it comes to scalability and transferring skills between different robots.
Demonstrating in joint space: One notable advantage of demonstrating in joint space is the richness of the information obtained during the demonstration process, including the precise configuration of each individual joint. This level of detail is particularly advantageous for kinematically redundant manipulators, which can optimize null-space motion and obstacle avoidance.
However, a drawback lies in the intuitiveness of the learning process for human teachers. While joint space offers rich data for the robot to learn from, understanding how the learning algorithm learns and generalizes from these data is not intuitive for humans. The complexity involved in translating joint configurations into meaningful task representations can pose challenges for human teachers in understanding the learning process and predicting how the robot generalizes its learned skills.
In terms of acquiring demonstration data, kinesthetic teaching and teleoperation are straightforward methods for obtaining joint space data since joint states can be directly recorded. However, passive observation requires an additional step to convert raw information into joint space data, making it less practical to operate directly in joint space for this approach. In such cases, adding unnecessary transformations to obtain joint data is not justified, as it complicates the demonstration process.
4.1.2. Cartesian Space
This section introduces Cartesian space, a mathematical representation of three-dimensional physical space using orthogonal axes. In robotics, Cartesian space is commonly employed to describe the position and orientation of a robot’s end-effector. LfD in Cartesian space involves training robots to imitate demonstrated tasks or movements by utilizing the coordinates of the end-effector [40,42,56,57,58,59,60,65,71,115].
Learning in Cartesian Space: Cartesian space offers a natural representation for tasks involving end-effector movements and positioning, simplifying the learning process by directly addressing the space where tasks are being operated and executed. This choice is particularly advantageous for applications requiring precise end-effector control and potentially leads to better generalization in new situations. The consistency in representation allows for more effective generalization across different robotic systems and tasks.
One significant advantage of Cartesian space is the consistency of the dimension of the end-effector pose state across various robot platforms, regardless of their joint configurations. This standardized representation facilitates a more uniform approach to learning compared to joint space, which can vary in dimensionality from one robot to another. However, challenges arise when dealing with rotations within Cartesian coordinates, as rotation resides in a different manifold. It is required to utilize the calculus in a non-Euclidean space. This can increase the computational complexity of learning algorithms compared to those in the straightforward calculations of joint space.
Furthermore, the outcome of learning in Cartesian space cannot be directly integrated into the robot’s controller. A transformation step is required to convert the learned information into joint space, adding an extra layer of complexity to ensure seamless integration into the robot’s control system.
Demonstrating in Cartesian space: Cartesian space is an intuitive space for the human teacher, which facilitates a better understanding of how the learning process happens. Additionally, this intuitiveness enables easier inclusion of task parameters and better iterative feedback to the LfD outcome, allowing the instructor to refine and optimize the robot’s performance over successive teaching sessions.
However, a limitation arises in the encoding of end-effector behavior exclusively. In redundant manipulators, the representation in Cartesian space does not directly consider null-space motion. The null space, which represents additional degrees of freedom beyond the end-effector behavior, is not explicitly encoded in Cartesian space. This limitation restricts the teacher’s ability to convey and refine complex motions involving redundant manipulators, potentially overlooking certain aspects of the robot’s capabilities.
Finally, acquiring training data in Cartesian space via kinesthetic teaching requires having the kinematic model of the robot including the end effector hand or tool, and applying forward kinematic to the raw joint readings. The approach is similar in teleoperation, although it depends on the design of the teleoperation interface. Passive observation, however, demands the development of a mapping between the human hand or held tool and the robot’s end effector. Leveraging pattern recognition and feature extraction techniques, the movements of the human hands are interpreted and translated into end-effector movements, serving as valuable Cartesian-space training data.
4.1.3. Remarks
While joint space and Cartesian space are the most common and fundamental spaces to represent a task, there are a variety of choices that can be particularly designed and developed for the designated task. For example, in [39], the pixel space of the camera was used as a measure of distance between the peg and hole. End-to-end training on visual images was used in [96]. Also, in [21], while the task is learned in Cartesian space, the Cartesian frame changes at each time step in such a way that the z-axis always points towards the direction in which the force has to be applied.
When choosing approaches where a cost or reward function is involved, the design of such functions depends on the choice of latent/feature space, i.e., the space that the reward or cost function has to represent. In [111], the reward function is learned from demonstration, to represent as latent space of the training data. Later, the reward function is used by reinforcement learning to learn a suitable policy. Likewise, in [116], a cost function is learned via inverse optimal control, which represents the task’s requirement for successful execution.
4.2. Learning Methods
Here, we provide a comparative analysis of the most common learning methods used for LfD. For each method, we discuss their learning concept and their training procedure, as well as their characteristics, strengths, and weaknesses. Moreover, in Table 2, we present a summary of our comparative analysis. The table evaluates the learning methods across several key metrics to provide insight into their respective practical strengths and weaknesses in the manufacturing context. The metrics assessed include the implementation effort, explainability, generalization capability, training data efficiency, and safety and robustness. Implementation effort helps evaluate the practicality and resource requirements of integrating a particular learning method into manufacturing processes. Explainability assesses how well the reasoning behind the learned behaviors can be easily understood and interpreted by operators. Generalization capability indicates the extent to which a learning method can adapt to new or unseen situations, enhancing its versatility and applicability. The efficiency of training data usage highlights how effectively a method can learn from limited datasets, optimizing resource utilization and reducing data acquisition costs. Finally, safety and robustness metrics assess the reliability and resilience of learned behaviors in the face of uncertainties.

Table 2.
Comparison of learning methods in manufacturing contexts.
4.2.1. Movement Primitive (MP)
Learning concept: A movement primitive (MP) encapsulates a low-level robot behavior defined by a trajectory generator and an exit condition. The trajectory generator specifies the desired robot motion, while the exit condition determines when the movement should stop [56,57,114,117]. For instance, a typical MP involves moving a robot until contact with a surface, where the trajectory generator guides the robot until a predefined force threshold is reached, signaling the exit condition. MPs do not require demonstration at the subtask level. They are manually designed and optimized by robotic experts. Instead, LfD focuses on the task hierarchy, where the sequence in which to execute these predefined MPs is demonstrated to achieve a full task. Tasks composed of MPs can be structured using various methods such as state machines or task graphs. The essence of MPs is to offer a structured and optimized way to encode low-level robot behaviors that can be combined to achieve more complex tasks.
Training procedure: The design, implementation, and optimization of MPs is performed by the robotic expert, while the human teacher demonstrates the task hierarchy composed of MPs. In this way, subtasks are structured and tailored to specific tasks, resulting in efficient, reliable, and predictable behavior, while the demonstration effort is minimized. However, the manual design and tuning of MPs by robotic experts limit flexibility and control over lower-level behaviors for teachers. While MPs enhance learning performance by constraining the learning space to predefined combinations, their effectiveness depends on expert tuning, making them less adaptable to new behaviors, especially at the subtask level. MPs restrict generalization at the subtask level, demanding expert intervention to encode, tune, and integrate new behaviors into the MPs.
4.2.2. Dynamic Movement Primitive (DMP)
Learning concept: The dynamic movement primitive (DMP) combines a spring-damper dynamical system, known as an attractor model, with a nonlinear function to achieve a desired goal configuration [118,119]. The attractor model ensures convergence to the goal configuration, with its attractor point serving as the target goal. Without the nonlinear function, the model asymptotically converges to the goal. The role of the nonlinear function is to encode a certain behavior represented via the demonstration. By superposition of the nonlinear function and the attractor model, DMP replicates the demonstrated behavior. Essentially, the nonlinear function guides the attractor system towards the desired behavior, while eventually vanishing as the system reaches the goal [21,58,66,73,82,120,121,122,123,124].
Training procedure: To effectively train a DMP, the training data should primarily exhibit temporal dependence, with time progression as the independent variable (x-axis) and the dependent variable (y-axis) representing aspects such as position, force, or stiffness. Subtask learning involves collecting training data by creating trajectories from joint readings, force sensors, or stiffness profiles. For whole task sequences, teaching data must first be segmented into subtasks, with each subtask fitted with its own DMP. While DMPs are more suited for learning subtasks, approaches exist where multiple DMPs can be integrated into a single model to represent entire task sequences [125]. Motion-based and contact-based learning are feasible via DMPs, utilizing position trajectories [58,122], force trajectories [126], or stiffness profiles [127,128] as training data. Notably, DMPs offer the advantage of requiring only a single demonstration to generate a training set and train the model, although multiple demonstrations can be utilized for a more comprehensive training set [126,129]. Moreover, DMPs have been employed in context-dependent learning scenarios for collaborative tasks via points or task parameters [76,130].
This training procedure involves representing time as a phase variable to make DMP systems autonomous from direct time dependence. Training data, along with their derivatives, are input into the DMP equation to generate target values for approximating the nonlinear term. Locally weighted regression (LWR) [131] is a typical choice for the nonlinear function approximator. The learned outcome is a nonlinear function mapping the phase variable to scalar values. The attractor model of DMP is designed to ensure critical damping, facilitating convergence to the goal without oscillation. The core idea of DMP lies in representing behavior as a deterministic system augmented by forcing terms, enabling learning at a higher level. While DMPs offer simplicity and reliability in implementation and generalization, their generalization mechanism is limited to a region around the original demonstration’s configurations. Hyperparameters, although manually tuned, can be applied across various demonstrations without retuning. DMPs can be trained in joint space or Cartesian space, with multiple DMPs synchronized via the phase equation for joint space training, and a modified version for rotational values in Cartesian space represented using quaternions.
4.2.3. Reinforcement Learning (RL)
Learning concept: The reinforcement learning (RL) in the context of LfD involves training robots to execute tasks by interacting with their environment, receiving feedback in the form of rewards or penalties, and adjusting their actions to maximize cumulative rewards [59,60,63,111,115,132,133,134,135]. At its core, RL involves an agent (the robot) learning optimal actions to achieve a predefined objective within a given environment. This learning process hinges on the development of a policy, a strategy that guides the agent’s actions based on the current state of the environment. The policy is refined through the optimization of a value function, which estimates the expected cumulative reward for specific actions in particular states. Rewards serve as feedback, reinforcing desirable actions and discouraging undesired behavior, thereby shaping the agent’s learning trajectory. RL algorithms balance exploration and exploitation, enabling the robot to discover effective strategies while leveraging known successful actions. However, RL alone does not suffice for successful LfD without an accurate reward function encapsulating the task requirements.
The inverse reinforcement learning (IRL) acts as a bridge between RL and LfD. Via human demonstrations, IRL seeks the underlying implicit reward structure that guides those actions. The fundamental idea is to reverse engineer the decision-making process of the human teacher. Capturing the latent reward function enables the robot to replicate and generalize learned behavior to achieve similar goals in diverse contexts [136,137,138].
Training procedure: To train an LfD algorithm via RL-based methods, two key components are essential: a reward function and a policy function. The reward function encapsulates the task’s definition, requirements, and success metrics, essentially encoding all the information provided by the teacher. Meanwhile, the policy function serves as the brain of the robot, dictating its behavior to execute the task. Training proceeds in two stages: first, designing or learning an appropriate reward function that accurately represents the desired task features and requirements, and second, training an RL algorithm to learn a policy function based on this reward function through interaction with the environment.
During the first stage, the focus lies on devising a reward function that encapsulates the teacher’s instructions regarding the task. While this function can be manually designed, a more comprehensive LfD solution involves learning the reward function from human demonstrations [59,62,111,139]. The effectiveness of the LfD solution is directly linked to how well the reward function encapsulates the task’s key aspects. In the second stage, assuming a reward function is already established, an RL algorithm learns a policy function by iteratively refining its behavior based on feedback from the environment and rewards obtained from the reward function.
Training via RL-based approaches offers flexibility in encoding information and learning skills, with training data ranging from raw images to robot trajectories. However, it requires careful engineering of the reward function and task analysis by robotic experts. Additionally, RL-based learning requires a dataset, not just a single demonstration, and involves modeling the environment, adding complexity to the implementation of LfD algorithms in this manner. Tuning hyperparameters associated with the policy and reward functions, as well as potentially modifying the environment model for each task, are the steps that require robotic experts to ensure successful and efficient learning.
4.2.4. Gaussian Process (GP)
Learning concept: The Gaussian process (GP) is a probabilistic modeling approach in machine learning, capturing entire functions through mean and covariance functions known as kernel functions. The kernel function in GPs determines the similarity between function values at different points. This allows GPs to capture intricate patterns and relationships in data, while also estimating the uncertainty in those predictions. GPs are nonparametric, which means they are capable of learning from limited data points while being able to adjust their complexity with more data. Predictions from GPs include both anticipated function values and associated uncertainty, particularly useful in scenarios with sparse or noisy data [40,42,88,89].
The conceptual advantage of learning methods like GP is their ability to quantify uncertainty, which is important for understanding the model’s confidence in its predictions. This feature enhances human comprehension of the learning process and can serve as a safety mechanism for robots, where uncertain policies could lead to errors or damages. By monitoring the model’s uncertainty and providing feedback, human teachers can refine the GP’s behavior and adjust uncertainty bounds accordingly, ensuring safer and more robust execution.
Training procedure: The training process for GP models involves learning from input–output pairs, where the independent variable can be any sequential variable, such as time or the position of the end effector. However, it is important to maintain the sequential nature of the data, e.g., restricting scenarios where the end effector revisits a location. GPs excel at learning subtasks with limited demonstration data, even one-shot demonstration input. To improve the generalization capability, it is advisable to train GPs in Cartesian space. This is because small changes in joint values can result in significant changes in the end effector in joint space. Moreover, training in joint space makes the uncertainty measures less interpretable.
GPs are not particularly demanding in terms of implementation and hyperparameter tuning. The robot expert needs to design a kernel function in the formulation of a GP, as well as very few hyperparameters. Moreover, GPs are flexible across various tasks, i.e., they do not often require significant hyperparameter tuning or design alterations when transitioning from one task to another.
4.2.5. Gaussian Mixture Model (GMM)
Learning concept: The Gaussian mixture model (GMM) offers a probabilistic method similar to GPs for modeling functions, representing them as a mixture of multiple Gaussian distributions. Each Gaussian component within a GMM represents a cluster in the dataset. In the context of LfD, GMMs can be used to model the underlying structure of human demonstrations. Due to their multimodal nature, GMMs can capture complex behaviors while being flexible in terms of the number of learning variables [39,111,140]. They can also encode variability in demonstrations, giving a measure of accuracy at each point, similar to GPs. Additionally, GMMs can be updated locally with new data without affecting other segments of the learned behavior. This allows GMMs to naturally cluster data and learn complex behaviors from human demonstrations.
Training procedure: GMMs allow for flexible training variable dimensions through multivariate Gaussian distributions, enabling each distribution to represent and train on different aspects of a task or subtask. Unlike GPs, which can learn from single demonstration, GMMs require multiple demonstrations to capture the statistics and effectively learn the task. Additionally, GMMs are typically more intuitive when learned in Cartesian space rather than joint space, similar to GPs.
4.2.6. Probabilistic Movement Primitive (ProMP)
Learning concept: probabilistic movement primitive (ProMP) is a learning approach developed for LfD which employs Gaussian basis functions to model demonstrated behavior [141]. The parameters of ProMP are typically weights associated with the basis functions. ProMP introduces a probabilistic aspect into learning, similar to GP and GMM, allowing the model to accommodate uncertainty in learned movements and generalize them to different conditions or contexts [38,43,91,142].
Training procedure: The training procedure for ProMPs involves representing training data as time-series trajectories, with each trajectory corresponding to a specific demonstration of the task. These trajectories are often normalized or preprocessed to ensure consistency across different demonstrations. Through an optimization process, the model seeks to find the parameters that best fit the observed trajectories from demonstrations, constructing a probabilistic model capturing the distribution of trajectories and their likelihood at each point in time. However, ProMPs generally require a larger training dataset compared to other probability-based LfD methods.
4.2.7. Remarks
In addition to the mentioned methods, various other learning approaches serve as the core of the LfD algorithm, with customization based on task-specific requirements. For example, hidden Markov models (HMMs) are commonly utilized for learning behaviors, as used in [65]. Additionally, methods based on optimal control are also employed, which are conceptually similar to RL. For example, in [116], inverse optimal control (IOC) is used to learn the cost function of the task, similar to IRL. This function is later used to find an optimal policy to generalize the desired task. For deeper insights, the work in [12] provides technical analysis into learning methods used in LfD.
4.3. Summary of Limitations, Efficiency, and Robustness
In joint space learning, challenges such as the risk of overfitting to specific demonstrations, hardware sensitivity across different robot configurations, and the omission of higher-level contextual information underscore potential limitations. These factors can constrain the generalizability and adaptability of learned behaviors, impacting performance in diverse manufacturing tasks requiring contextual understanding. Conversely, Cartesian space learning introduces computational complexities due to non-Euclidean rotations and requires additional transformation steps for integration into robot controllers. Issues like null-space motion constraints further affect the capabilities of redundant manipulators. Meanwhile, learning methods such as MPs, DMPs, and RL each present distinct challenges related to effectiveness, adaptability, and computational resource requirements. MPs and DMPs offer efficiency advantages with minimal training data but may lack flexibility for novel tasks, while RL demands extensive data and expert intervention for environment modeling and parameter tuning.
Efficiency considerations highlight methods like DMPs and GPs for their ability to optimize resource utilization and reduce data acquisition costs, crucial for practical deployment in manufacturing settings. However, the varying implementation efforts across these methods underscore the need for careful consideration of computational demands and expertise required for effective application. In terms of robustness and safety, probabilistic models like GPs and GMMs provide inherent uncertainty quantification, enhancing decision making and safety in dynamic and uncertain manufacturing environments. These factors collectively emphasize the importance of addressing these limitations and efficiency concerns through ongoing research to enhance the applicability and reliability of these methods in future robotic manufacturing applications.
To provide general examples, tasks such as welding and painting benefit from learning in Cartesian space, since their performance is dependent on the geometry of a surface, which is naturally encoded in Euclidean space. Learning in Cartesian space can enhance the learning and generalization performance of such tasks. On the other hand, tasks such as pick-and-place operations, assembly behaviors, material handling, and packaging can efficiently learn and generalize in joint space as well, maintaining the performance while keeping the learning complexity minimal. The choice of learning method is highly dependent on the available resources and the specifics of the desired task. For example, if one-shot demonstration is a priority to minimize implementation effort for tasks such as pick-and-place or packaging, GPs and DMPs are recommended. If multiple demonstrations are available, probabilistic approaches can be utilized. For instance, the geometry of the surface can be incorporated as a task parameter to enhance the reliability of welding. Such requirements are numerous and the practitioners should consider their available context to implement the suitable learning mechanism.
5. How to Refine
The final step after completing the design and development of an LfD process is to analyze and evaluate their performance, which guides the question of “How to refine”. This section dives into the main key trends and directions within the state of the art that aim to refine LfD algorithms across various aspects. For each trend, we will explore how it can improve LfD performance and identify potential areas for further research. The goal is to provide insights into possible research objectives for evaluation and improvement. This analysis will provide a refined perspective on the previously discussed aspects, ultimately contributing to an iterative loop of improvement for the entire LfD process.
5.1. Learning and Generalization Performance
Although current LfD approaches can learn from human teachings and generalize the behavior to new situations, it is still far from the idea of learning behavior that can be seen from humans. If human learning capabilities are considered the ideal case, LfD approaches are not even close to cognitive learning capabilities. Therefore, it is a crucial line of refinement on the LfD approaches to bring them closer to the cognitive learning power of human beings. The performance of learning and generalization refers to how well the algorithm can capture the essence of the desired behavior from human demonstration, and how intelligently the algorithm generates essentially the same behavior but adapts to the new environment or situation or context condition. Learning and generalization are two entangled factors that directly affect each other. A better learning performance subsequently leads to a better generalization, and improving generalization essentially means that learning performance has been improved. While using typical state-of-the-art LfD approaches already performs well in learning and generalization, they operate under assumptions, and actually cannot generalize to every possible case or situation. That is why it is necessary to improve the LfD approach based on what we require for our task and what is missing in the current LfD approaches. Improving learning performance means improving how the human demonstrations are processed by the learning algorithm, as well as modifying the core algorithm of learning to better capture different aspects of the behavior from the demonstrations. One trend is the approach of incremental learning [38,40,52,58,96]. Incremental learning refers to the ability of a robot to continuously acquire and refine its knowledge and skills over time as it interacts with its environment or receives additional demonstrations from a human operator. In [40], a GP is learned via one demonstration, but more demonstrations are provided through the operation of the robot to further refine GP training and improve its learned behavior. As another example, authors in [52] focused on continual learning for teaching letters in the alphabet incrementally without the algorithm forgetting the previously learned letters. The algorithm was able to write “Hello World” at the end, with the accumulated knowledge.
Building upon incremental learning, the concept of interactive learning emerges [13,38,66,91]. Interactive learning refers to a learning paradigm in which the robot actively engages with the human teacher or the learning environment to acquire knowledge or skills. Unlike passive learning methods where information is simply presented to the learner, interactive learning involves two-way communication and dynamic interaction between the learner and the learning material. In [112], authors provide an interactive learning framework through which nonexpert human teachers can advise the learner in their state-action domain. In [38], the human teacher kinesthetically corrects the robot’s trajectory during execution to teach the robot to perform the task accurately. A joint probability distribution of the trajectories and the task context is built from interactive human corrections. This distribution is updated over time, and it is used to generalize to the best possible trajectory given a new context.
Another technique is active querying [40,91,111]. In this technique, the learner dynamically decides which data points or demonstrations are most informative for the learning or decision-making process and requests the corresponding information from the teacher. This approach is particularly helpful for improving performance in an efficient way and acquiring the most relevant information. In [91], they focused on the demonstration distribution when training ProMPs, and the fact that it is not trivial determining how to add a good demonstration in terms of improving generalization capabilities. Thus, they learn a GMM over the demonstrations distribution and use epistemic uncertainty to quantify where a new demonstration query is required. Their proposed active learning method iteratively improves its generalization capabilities by querying useful and good demonstrations to maximize the information gain. In a similar way, the uncertainty measure of GPs is used in [40] to trigger a new demonstration request.
In addition to the mentioned learning paradigms, it is often required to modify learning algorithms based on the application use case or the context in which the LfD algorithm is employed. For example, there are several works to improve the performance of LfD with respect to contact-rich tasks [56,57,66,97]. In [57], they proposed an approach to reduce the learning time of insertion tasks with tolerances of up to submillimeters, with application in manufacturing use cases. In [56], a novel task similarity metric was introduced, and it was used to generalize the already-learned insertion skills to novel insertion tasks without depending on domain expertise. In another context, Ref. [55] considered the assembly use cases and explored the idea that skillful assembly is best represented as dynamic sequences of manipulation primitives, and that such sequences can be automatically discovered by reinforcement learning. The authors in [94] extended DMPs to manipulating deformable objects such as ropes or thin films, to account for the uncertainty and variability from the model parameters of the deformable object. Another important aspect of learning is to learn factors which are in non-Euclidean spaces. In [124], the formulation of DMP was modified to become geometry-aware, so that the new formulation could be adapted to the geometric constraints of Reimanian manifold.
Finally, for certain contexts, some works attempt to design and develop control schemes to be learned in order to better learn and execute the behavior. The work in [21] focused on the fact that some tasks such as grinding, sanding, polishing, or wiping require a hybrid control strategy in order to accurately follow the motion and the force profile required for successful task execution. To enhance the learning process of these tasks, they proposed some preprogrammed control strategies with parameters to tune via nonexpert demonstrations. Such parameters are extracted from one-shot demonstrations and learn the motion-force task more efficiently.
In addition to the context, several works have attempted to provide improvements on the learning performance of a certain algorithm. Such algorithm-based improvements are dedicated to resolve the performance issues inherent in a learning method. In [123], they proposed a new formulation for DMPs in order to make them reversible in both directions and make them more generalizable. The authors in [58] introduced constant speed Cartesian DMPs, which completely decouples the spatial and temporal components of the task, contributing to a more efficient learning. In their LfD approach based on IOC, the authors of [116] proposed an ensemble method which allowed for more rapid learning of a powerful model by aggregating several simpler IOC models. The work in [40] combined GPs with DMPs, as GPs do not guarantee convergence to an arbitrary goal. Therefore, a DMP was learned on the GP output to ensure that any arbitrary goal is reached. With respect to deep-learning-based approaches, Ref. [60] focused on reducing the sample complexity by introducing self-supervised methods. For RL-based approaches, the authors in [62] developed a method to use demonstrations for improving learning sparse-reward problems. Both demonstrations and interactions are used to enhance the performance of learning.
5.2. Accuracy
While accuracy and precision can be mainly improved by improving the learning performance, it is not necessarily sufficient to achieve the desired accuracy by focusing generally only on the learning performance. While improving learning can enhance the overall generalization performance of the algorithm in the case of new scenarios, it is not a guarantee that the generalization outcome is accurate in terms of the desired task’s metrics. Not only does the teaching process influence the accuracy of the outcome, but the execution strategy of the LfD is also the final stage that plays a major role in the outcome.
The notion of accuracy has a subjective nature, i.e., it can be defined differently from task to task. Therefore, there is no unified definition to describe the metric of accuracy across arbitrary tasks. However, several factors can be associated generally with the metrics of accuracy, to measure how accurate the LfD algorithm is, to some extent, with respect to the outcome. One of these factors is the success rate. Over various execution of the task via LfD policy, the success rate of the task to achieve a desired goal can be a simple yet effective measure of how accurately a task is executed. If the accuracy requirements are not satisfied until a threshold, the task will not succeed at the end. Hence, success rate can be a measurable factor to describe the accuracy of a task, and a tangible metric to work towards improving by enhancing accuracy.
In addition to focusing on the learning algorithm’s performance, there are more dedicated approaches and trends to improve the accuracy of an LfD algorithm. One direction is to focus on the question of how to modify the teaching and demonstration method to enable human teachers to teach the task more accurately [38,42,64,70,76]. For example, in [76], they separated the demonstration of the shape of the trajectory from the timing of the trajectory. While it is cognitively demanding to demonstrate a motion with high accuracy and a high velocity at the same time, the ability to independently demonstrate the path enables the teachers to solely focus on teaching and refining the robot path and define the behavior in a more precise way. Moreover, in [64], they combined incremental learning with variable stiffness of the robot during kinesthetic feedback. They used the variability of the already-captured demonstrations to adjust the stiffness of the robot. When there is low variation in a region, i.e., higher accuracy, the robot is more stiff, allowing the teacher to provide smaller adjustments, while regions with higher variability have lower stiffness, allowing the teacher to move the robot more freely.
Another approach is to focus on how the LfD output plan is executed finally with the robot. Here, the focus is on execution strategies with the goal of improving the success rate of a task [57,63,71]. In [71], they considered a small-parts assembly scenario, where the tolerances are comparatively low, which leads to more sensitivity to errors in misalignments due to tight tolerances. They proposed an impedance control strategy to drive the robot along the assembly trajectory generated by LfD, but also record and track a required wrench profile so that tolerance misalignments can be resolved with the compliance of the contact, and in this way increasing the success rate of the task and avoiding failures when there is contact due to tolerance errors. In [63], the authors claimed that LfD output performed well in generalization but failed to maintain the required accuracy for a new context. Hence, they used the LfD output as an initial guess for an RL algorithm designed according to the task’s model, and refined the LfD output to find the optimal policy for the specific task.
5.3. Robustness and Safety
The general LfD process is mainly concerned with successfully learning and executing a desired task with a specific accuracy, while it is crucial to consider how the process lifecycle is aligned with safety requirements and how well the system can handle unexpected scenarios. This is of extra importance in manufacturing cases where the robot shares an industrial environment alongside humans, with more potential dangers. Although LfD can generalize to new scenarios, there is no guarantee that the devised task policy is aligned with safety requirements or passes through the safety region. It is also not guaranteed that in the case of unforeseen situations during the task execution, the robot makes a safe decision to accommodate the new situation. Therefore, it is important to equip the LfD processes with proper mechanisms to ensure robustness and safety in the robot’s operational environment.
The concept of robustness gains meaning when there is a possibility of a fault, disturbance, or error throughout the process that might mislead the learning process or cause the system to end up in an unknown state. In this case, a robust LfD system is capable of reliably recovering from the imposed state and successfully finishing the task whatsoever. Alongside robustness, the concept of safety ensures that the robot’s operations and decisions do not cause any harm to the humans working alongside, especially during the teachings and interactions. It also ensures that the operations remain in a safe region to prevent damage to the working environment, work objects, and the robot itself. It is evident that robustness and safety are essential components of LfD systems that must be carefully addressed to enable their effective deployment in real-world applications.
One main aspect of robustness and safety in LfD processes is related to the human–robot interaction (HRI). Since LfD lifecycle is mainly concerned with interaction with humans, it is evident that focusing on HRI robustness and safety becomes a major trend in enhancing the reliability of LfD systems [143].
One main trend of improving safety and robustness is focused on HRI [42,76,80,115,133]. This includes the teaching and demonstration as well as any other form of interaction throughout the process. With respect to robustness, in [133], to efficiently learn from suboptimal demonstrations, the paper proposed an RL-based optimization where the demonstrations serve as the constraints of the optimization framework. The objective was to outperform the suboptimal demonstrations and find the optimal trajectory in terms of length and smoothness. The authors of [115] proposed an interactive learning approach where, instead of depending on perfect human demonstrations to proceed with learning, the human can interactively and incrementally provide evaluative as well as corrective feedback to enhance the robustness of learning against imperfect demonstrations. In terms of safety, in [42], kinesthetic teaching was replaced with teleoperation to enhance safety while providing local corrections to the robot. This is because kinesthetic teaching can become more dangerous with increased robot’s velocity of execution. Moreover, in many works such as, [76,80], the control scheme is based on impedance control to guarantee compliant interactions with humans, avoid sudden unexpected motions, and improve HRI safety.
Another trend for improving robustness is focused on the robustness against various disturbances and errors through out the LfD cycle [39,60,77]. The work in [77] focused on the fact that while LfD can allow nonexperts to teach new tasks in industrial manufacturing settings, exerts are still required to program fault recovery behaviors. They proposed a framework where robots autonomously detect an anomaly in execution and learn how to tackle that anomaly by collaborating with a human. They represented a task via task graphs, where a task is executed from start to end. If the robot detects an anomaly, it waits and asks humans whether to demonstrate a recovery behavior or refine the current execution behavior. In case of learning a new recovery behavior from the teacher, a conditional state is added to the graph at the point of anomaly, and the next time, the robot checks for the condition to see if it should continue the normal execution or switch to the recovery behavior. Similarly, the authors in [39] proposed a Bayesian GMM to quantify the uncertainty of the imitated policy at each state. They fused the learned imitation policy with various conservative policies in order to make the final policy robust to perturbations, errors, and unseen states. For example, in a board wiping task, the imitation policy learned the force profile required to wipe the board, while the conservative policy ensured circular motion on the board. Together, they make the board wiping policy robust so that the motion is desirable while applied force is enough to actually wipe the board.
Lastly, there are several works focusing on robustness and safety considering the limitations in the robot’s operating environment [121,122]. In [121], the problem of collision avoidance was considered. They proposed a modified formulation of DMP, where they incorporated a zeroing barrier function in the formulation and solved a nonconvex optimization in order to find a collision-free path through their constrained DMP. From another perspective, the work in [122] addressed the issue that there is no guarantee that an LfD outcome will respect kinematic constraints when generalizing, so they formed a QP optimization problem that enforces the kinematic constraints and finds the DMP weights where the optimal trajectory is closest to the original DMP trajectory while respecting the constraints.
5.4. Remarks
In addition to the mentioned trends and directions, the future application of LfD is set to undergo substantial evolution driven by technological advancements and shifting industrial paradigms. Key areas of development include the integration of large language models (LLMs) such as GPT-4, which promise enhanced communication between human operators and robots through natural language processing. LLMs also enable intelligent data analysis, helping to identify patterns and suggest process improvements in manufacturing. Moreover, by facilitating interactive learning and troubleshooting, LfD with LLM integration allows robots to engage in real-time dialogue, enhancing their performance continuously [144].
Furthermore, the adoption of LfD within the framework of Industry 5.0 emphasizes collaboration between humans and machines in manufacturing [145,146]. This approach enhances personalized assistance for operators, improves workplace safety through robot training in hazardous tasks, and supports adaptive manufacturing processes that respond dynamically to changes. Emerging paradigms like edge computing and Internet of Things (IoT) integration bring real-time data processing capabilities to LfD, enabling quicker decision-making and data-driven insights [147,148,149]. Additionally, digital twins provide a virtual environment for testing and optimizing LfD algorithms, while augmented reality (AR) and virtual reality (VR) enhance the training and demonstration phases by providing immersive learning experiences [150,151,152,153].
6. Conclusions
This paper presented a structured approach to integrating LfD into the roboticization process using manipulators for manufacturing tasks. It addressed key questions of “What to demonstrate”, “How to demonstrate”, “How to learn”, and “How to refine”, providing practitioners with a clear roadmap to implement LfD-based robot manipulation. First, we identified the scope of demonstration based on the desired task’s characteristics and determined the knowledge and skill required to be demonstrated to the robot. Then, based on the scope of demonstration, we explored demonstration methods and how human teachers can provide demonstrations for the robot, providing insights to extract the demonstration mechanism. Next, we focused on the learning approaches to enable efficient task learning and execution from the provided demonstrations. We first explored the possible learning spaces, followed by the common learning methods along with their pros and cons. Finally, we provided trends and insights to evaluate and improve the LfD process from a practical point of view, giving research directions and objectives for building upon the state of the art.
The final stage of the roadmap involves analyzing and evaluating its effectiveness across various dimensions. Key trends in LfD refinement focus on enhancing learning and generalization performance, accuracy, and robustness/safety. Improving learning and generalization performance aims to bring LfD algorithms closer to human cognitive learning capabilities. This involves strategies like incremental learning, where robots continuously refine skills over time through additional demonstrations or interactions. Interactive learning further engages humans in the teaching process, enabling dynamic feedback and correction during task execution. Active querying methods enhance learning efficiency by strategically requesting informative demonstrations, thereby optimizing the learning process. Accuracy in LfD refers to how precisely and reliably robots execute tasks based on learned behaviors. Strategies to enhance accuracy include modifying teaching methods to allow more precise demonstrations and refining execution strategies to align closely with task requirements. Techniques such as impedance control and reinforcement learning integration help achieve and maintain desired task accuracies. Robustness and safety are critical for deploying LfD systems in real-world environments, especially in industrial settings where robots interact closely with humans.
The future perspective for LfD in mass customization can be evolved by integration of LLMs to enhance human–robot interaction through natural language processing and intelligent data analysis for manufacturing process optimization. LfD with LLM integration facilitates real-time dialogue and interactive learning, continuously improving robot performance. In the context of Industry 5.0, LfD fosters collaboration between humans and robots, supporting personalized assistance, enhanced workplace safety through robotic training in hazardous tasks, and adaptive manufacturing processes responsive to dynamic changes. Emerging technologies such as edge computing and IoT enable rapid data processing, enhancing decision-making and operational insights, while digital twins, AR, and VR provide immersive environments for refining and optimizing LfD algorithms across various industrial applications. With the current roadmap, we established a map from the high-level problem to deeper technical challenges, where the practitioners can follow to the detailed technical depth via the introduced research papers throughout each section.
It is noteworthy to mention that the application scenarios of robots in the manufacturing field are diverse and distinctive. While the state of the art in LfD has advanced significantly in a number of tasks, it is impractical to cover all manufacturing tasks comprehensively due to their diverse nature and the unique challenges each task presents, particularly in unstructured environments. For instance, the complexity integration of LfD into small-part assembly is higher than that of large-part assembly due to the precision required and the greater impact of environmental uncertainties. In unstructured scenarios, which are common in mass customization, the variations are numerous and depend on specific task requirements. These include the scale of objects, the level of uncertainty in the perception system, calibration reliability between the perception system and the robot coordinates, the available setup at the production site such as the programmable logic controller (PLC) and sensory system alongside the robot, the robot hardware and its capabilities, the available grippers, the need for gripper changes during manufacturing, and many other factors.
Given the vast array of possible variations, addressing each scenario individually is impractical. Therefore, our proposed roadmap serves as a comprehensive guideline to help practitioners navigate these challenges by identifying the main key decision points at each step and providing practical implications, advantages, disadvantages, limitations, and recommendations. The roadmap is meant to be used through iterative attempts to improve the implementation of LfD. For example, in small-part assembly, the initial choice for the scope of demonstration might be motion-based demonstration, typically suitable for large-part assembly. Throughout the implementation, if the uncertainty of the vision system violates the tolerance thresholds, the practitioner can include contact-based demonstration suggested by the roadmap to address this uncertainty. Similarly, for kinesthetic demonstration, if gravity compensation mode of the available robot is admittance-based and complicates accurate motion demonstration, the practitioner can refer to the roadmap and consider teleoperation to enhance the process. Regarding the learning mechanism, the practitioner might start with joint space and DMP. If DMP’s generalization capability proves insufficient, the roadmap advises switching to Cartesian space learning or using another learning method such as GP for their probabilistic benefits. Finally, if the execution speed is low, affecting production efficiency, the roadmap guides the practitioner to explore incremental learning to refine robot behavior and increase speed.
This example is an illustration of how the roadmap is meant to be applied in the operation process and in order to facilitate the transformation from mass production to mass customization, and since variations in the task requirements are numerous, the roadmap does not aim to list every possible scenario but provides a toolkit to equip practitioners with the knowledge to address any arising challenges. It helps them identify decision points, leverage the state of the art, or define new research problems systematically. By doing so, the roadmap ensures a robust framework for handling the diverse and unstructured scenarios in manufacturing, enabling practitioners to iteratively and effectively implement LfD in various tasks.
By providing a detailed and structured analysis into determining the scope of demonstration, devising demonstration mechanisms, implementing learning algorithms, and refining LfD processes, our review enables both researchers and industry professionals to develop application-based LfD solutions tailored for manufacturing tasks. This paper offers a practical and structured guide, making LfD accessible to practitioners with moderate expertise requirements. Through comprehensive questionnaire-style guidance, we provide step-by-step instructions and main research directions for refining LfD performance in manufacturing settings, thus bridging the gap between research and practice in the field of robotic automation.
Author Contributions
Conceptualization, A.B.; methodology A.B. and H.H.; formal analysis, A.B. and H.H.; investigation, A.B. and H.H.; resources, H.V.; writing—original draft preparation, A.B.; writing—review and editing, A.B., H.H. and H.V.; supervision, H.V.; project administration, H.V.; funding acquisition, A.B. and H.V. All authors have read and agreed to the published version of the manuscript.
Funding
This research was funded in whole, or in part, by the Luxembourg National Research Fund (FNR), ML-COBOTS Project, ref. 15882013. For the purpose of open access, and in fulfillment of the obligations arising from the grant agreement, the authors have applied a Creative Commons Attribution 4.0 International (CC BY 4.0) license to any author-accepted manuscript version arising from this submission.
Data Availability Statement
Data sharing is not applicable.
Conflicts of Interest
The authors declare no conflicts of interest.
References
- Ravichandar, H.; Polydoros, A.S.; Chernova, S.; Billard, A. Recent advances in robot learning from demonstration. Annu. Rev. Control Robot. Auton. Syst. 2020, 3, 297–330. [Google Scholar] [CrossRef]
- Heimann, O.; Guhl, J. Industrial robot programming methods: A scoping review. In Proceedings of the 2020 25th IEEE International Conference on Emerging Technologies and Factory Automation (ETFA), Vienna, Austria, 8–11 September 2020; IEEE: Piscataway, NJ, USA, 2020; Volume 1, pp. 696–703. [Google Scholar]
- Léger, J.; Angeles, J. Off-line programming of six-axis robots for optimum five-dimensional tasks. Mech. Mach. Theory 2016, 100, 155–169. [Google Scholar] [CrossRef]
- Dean-Leon, E.; Ramirez-Amaro, K.; Bergner, F.; Dianov, I.; Lanillos, P.; Cheng, G. Robotic technologies for fast deployment of industrial robot systems. In Proceedings of the IECON 2016—42nd Annual Conference of the IEEE Industrial Electronics Society, Florence, Italy, 23–26 October 2016; IEEE: Piscataway, NJ, USA, 2016; pp. 6900–6907. [Google Scholar]
- Sanneman, L.; Fourie, C.; Shah, J.A. The State of Industrial Robotics: Emerging Technologies, Challenges, and Key Research Directions; Foundations Trends® in Robotics: Hanover, MA, USA, 2021; Volume 8, pp. 225–306. [Google Scholar]
- Fang, B.; Jia, S.; Guo, D.; Xu, M.; Wen, S.; Sun, F. Survey of imitation learning for robotic manipulation. Int. J. Intell. Robot. Appl. 2019, 3, 362–369. [Google Scholar] [CrossRef]
- Liu, Z.; Liu, Q.; Xu, W.; Wang, L.; Zhou, Z. Robot learning towards smart robotic manufacturing: A review. Robot. Comput.-Integr. Manuf. 2022, 77, 102360. [Google Scholar] [CrossRef]
- Zhu, Z.; Hu, H. Robot learning from demonstration in robotic assembly: A survey. Robotics 2018, 7, 17. [Google Scholar] [CrossRef]
- Sosa-Ceron, A.D.; Gonzalez-Hernandez, H.G.; Reyes-Avendaño, J.A. Learning from Demonstrations in Human–Robot Collaborative Scenarios: A Survey. Robotics 2022, 11, 126. [Google Scholar] [CrossRef]
- Moreno, V.H.; Jansing, S.; Polikarpov, M.; Carmichael, M.G.; Deuse, J. Obstacles and opportunities for learning from demonstration in practical industrial assembly: A systematic literature review. Robot. Comput.-Integr. Manuf. 2024, 86, 102658. [Google Scholar] [CrossRef]
- Li, W.; Wang, Y.; Liang, Y.; Pham, D.T. Learning from demonstration for autonomous generation of robotic trajectory: Status quo and forward-looking overview. Adv. Eng. Inform. 2024, 62, 102625. [Google Scholar] [CrossRef]
- Kroemer, O.; Niekum, S.; Konidaris, G. A review of robot learning for manipulation: Challenges, representations, and algorithms. J. Mach. Learn. Res. 2021, 22, 1395–1476. [Google Scholar]
- Celemin, C.; Pérez-Dattari, R.; Chisari, E.; Franzese, G.; de Souza Rosa, L.; Prakash, R.; Ajanović, Z.; Ferraz, M.; Valada, A.; Kober, J.; et al. Interactive Imitation Learning in Robotics: A Survey; Foundations Trends® in Robotics: Hanover, MA, USA, 2022; Volume 10, pp. 1–197. [Google Scholar]
- Xie, Z.; Zhang, Q.; Jiang, Z.; Liu, H. Robot learning from demonstration for path planning: A review. Sci. China Technol. Sci. 2020, 63, 1325–1334. [Google Scholar] [CrossRef]
- Beltran-Hernandez, C.C.; Petit, D.; Ramirez-Alpizar, I.G.; Harada, K. Accelerating Robot Learning of Contact-Rich Manipulations: A Curriculum Learning Study. arXiv 2022, arXiv:2204.12844. [Google Scholar]
- Pedersen, M.R.; Nalpantidis, L.; Andersen, R.S.; Schou, C.; Bøgh, S.; Krüger, V.; Madsen, O. Robot skills for manufacturing: From concept to industrial deployment. Robot. Comput. Integr. Manuf. 2016, 37, 282–291. [Google Scholar] [CrossRef]
- Cohen, Y.; Naseraldin, H.; Chaudhuri, A.; Pilati, F. Assembly systems in Industry 4.0 era: A road map to understand Assembly 4.0. Int. J. Adv. Manuf. Technol. 2019, 105, 4037–4054. [Google Scholar] [CrossRef]
- Wind, J.; Rangaswamy, A. Customerization: The next revolution in mass customization. J. Interact. Mark. 2001, 15, 13–32. [Google Scholar] [CrossRef]
- Gašpar, T.; Deniša, M.; Radanovič, P.; Ridge, B.; Savarimuthu, T.R.; Kramberger, A.; Priggemeyer, M.; Roßmann, J.; Wörgötter, F.; Ivanovska, T.; et al. Smart hardware integration with advanced robot programming technologies for efficient reconfiguration of robot workcells. Robot. Comput.-Integr. Manuf. 2020, 66, 101979. [Google Scholar] [CrossRef]
- Ekvall, S.; Kragic, D. Robot learning from demonstration: A task-level planning approach. Int. J. Adv. Robot. Syst. 2008, 5, 33. [Google Scholar] [CrossRef]
- Origanti, V.K.; Eiband, T.; Lee, D. Automatic parameterization of motion and force controlled robot skills. In Proceedings of the International Conference on Robot Intelligence Technology and Applications, Daejeon, Republic of Korea, 16–17 December 2021; Springer: Berlin/Heidelberg, Germany, 2021; pp. 66–78. [Google Scholar]
- Niekum, S.; Osentoski, S.; Konidaris, G.; Chitta, S.; Marthi, B.; Barto, A.G. Learning grounded finite-state representations from unstructured demonstrations. Int. J. Robot. Res. 2015, 34, 131–157. [Google Scholar] [CrossRef]
- Steinmetz, F.; Nitsch, V.; Stulp, F. Intuitive task-level programming by demonstration through semantic skill recognition. IEEE Robot. Autom. Lett. 2019, 4, 3742–3749. [Google Scholar] [CrossRef]
- Iovino, M.; Styrud, J.; Falco, P.; Smith, C. A Framework for Learning Behavior Trees in Collaborative Robotic Applications. In Proceedings of the 2023 IEEE 19th International Conference on Automation Science and Engineering (CASE), Auckland, New Zealand, 26–30 August 2023; IEEE: Piscataway, NJ, USA, 2023; pp. 1–8. [Google Scholar]
- French, K.D.; Kim, J.H.; Du, Y.; Goeddel, E.M.; Zeng, Z.; Jenkins, O.C. Super Intendo: Semantic Robot Programming from Multiple Demonstrations for taskable robots. Robot. Auton. Syst. 2023, 166, 104397. [Google Scholar] [CrossRef]
- Willibald, C.; Lee, D. Multi-level task learning based on intention and constraint inference for autonomous robotic manipulation. In Proceedings of the 2022 IEEE/RSJ International Conference on Intelligent Robots and Systems (IROS), Kyoto, Japan, 23–27 October 2022; IEEE: Piscataway, NJ, USA, 2022; pp. 7688–7695. [Google Scholar]
- Mayershofer, L.; Lehner, P.; Leidner, D.; Albu-Schaeffer, A. Task-Level Programming by Demonstration for Mobile Robotic Manipulators through Human Demonstrations based on Semantic Skill Recognition. In Proceedings of the ISR Europe 2023; 56th International Symposium on Robotics, Stuttgart, Germany, 26–27 September 2023; VDE: Frankfurt am Main, Germany, 2023; pp. 22–29. [Google Scholar]
- Gugliermo, S.; Schaffernicht, E.; Koniaris, C.; Pecora, F. Learning behavior trees from planning experts using decision tree and logic factorization. IEEE Robot. Autom. Lett. 2023, 8, 3534–3541. [Google Scholar] [CrossRef]
- Scherf, L.; Fröhlich, K.; Koert, D. Learning Action Conditions for Automatic Behavior Tree Generation from Human Demonstrations. In Proceedings of the Companion of the 2024 ACM/IEEE International Conference on Human-Robot Interaction, Boulder, CO, USA, 11–15 March 2024; pp. 950–954. [Google Scholar]
- Eiband, T.; Liebl, J.; Willibald, C.; Lee, D. Online task segmentation by merging symbolic and data-driven skill recognition during kinesthetic teaching. Robot. Auton. Syst. 2023, 162, 104367. [Google Scholar] [CrossRef]
- Lin, J.F.S.; Karg, M.; Kulić, D. Movement primitive segmentation for human motion modeling: A framework for analysis. IEEE Trans. Hum.-Mach. Syst. 2016, 46, 325–339. [Google Scholar] [CrossRef]
- Sørensen, S.L.B.; Savarimuthu, T.R.; Iturrate, I. Robot Task Primitive Segmentation from Demonstrations Using Only Built-in Kinematic State and Force-Torque Sensor Data. In Proceedings of the 2023 IEEE 19th International Conference on Automation Science and Engineering (CASE), Auckland, New Zealand, 26–30 August 2023; IEEE: Piscataway, NJ, USA, 2023; pp. 1–7. [Google Scholar]
- Dreher, C.R.; Asfour, T. Learning temporal task models from human bimanual demonstrations. In Proceedings of the 2022 IEEE/RSJ International Conference on Intelligent Robots and Systems (IROS), Kyoto, Japan, 23–27 October 2022; IEEE: Piscataway, NJ, USA, 2022; pp. 7664–7671. [Google Scholar]
- Zhou, F.; De la Torre, F.; Hodgins, J.K. Hierarchical aligned cluster analysis for temporal clustering of human motion. IEEE Trans. Pattern Anal. Mach. Intell. 2012, 35, 582–596. [Google Scholar] [CrossRef] [PubMed]
- Xiong, C.; Shukla, N.; Xiong, W.; Zhu, S.C. Robot learning with a spatial, temporal, and causal and-or graph. In Proceedings of the 2016 IEEE International Conference on Robotics and Automation (ICRA), Stockholm, Sweden, 16–21 May 2016; IEEE: Piscataway, NJ, USA, 2016; pp. 2144–2151. [Google Scholar]
- Carpio, E.; Clark-Turner, M.; Begum, M. Learning sequential human-robot interaction tasks from demonstrations: The role of temporal reasoning. In Proceedings of the 2019 28th IEEE International Conference on Robot and Human Interactive Communication (RO-MAN), New Delhi, India, 14–18 October 2019; IEEE: Piscataway, NJ, USA, 2019; pp. 1–8. [Google Scholar]
- Gustavsson, O.; Iovino, M.; Styrud, J.; Smith, C. Combining context awareness and planning to learn behavior trees from demonstration. In Proceedings of the 2022 31st IEEE International Conference on Robot and Human Interactive Communication (RO-MAN), Napoli, Italy, 29 August–2 September 2022; IEEE: Piscataway, NJ, USA, 2022; pp. 1153–1160. [Google Scholar]
- Ewerton, M.; Maeda, G.; Kollegger, G.; Wiemeyer, J.; Peters, J. Incremental imitation learning of context-dependent motor skills. In Proceedings of the 2016 IEEE-RAS 16th International Conference on Humanoid Robots (Humanoids), Cancun, Mexico, 15–17 November 2016; IEEE: Piscataway, NJ, USA, 2016; pp. 351–358. [Google Scholar]
- Pignat, E.; Calinon, S. Bayesian Gaussian mixture model for robotic policy imitation. IEEE Robot. Autom. Lett. 2019, 4, 4452–4458. [Google Scholar] [CrossRef]
- Maeda, G.; Ewerton, M.; Osa, T.; Busch, B.; Peters, J. Active incremental learning of robot movement primitives. In Proceedings of the Conference on Robot Learning, PMLR, Mountain View, CA, USA, 13–15 November 2017; pp. 37–46. [Google Scholar]
- Wang, K.; Fan, Y.; Sakuma, I. Robot Grasp Planning: A Learning from Demonstration-Based Approach. Sensors 2024, 24, 618. [Google Scholar] [CrossRef] [PubMed]
- Mészáros, A.; Franzese, G.; Kober, J. Learning to Pick at Non-Zero-Velocity From Interactive Demonstrations. IEEE Robot. Autom. Lett. 2022, 7, 6052–6059. [Google Scholar] [CrossRef]
- Koert, D.; Pajarinen, J.; Schotschneider, A.; Trick, S.; Rothkopf, C.; Peters, J. Learning intention aware online adaptation of movement primitives. IEEE Robot. Autom. Lett. 2019, 4, 3719–3726. [Google Scholar] [CrossRef]
- Raiola, G.; Lamy, X.; Stulp, F. Co-manipulation with multiple probabilistic virtual guides. In Proceedings of the 2015 IEEE/RSJ international conference on intelligent robots and systems (IROS), Hamburg, Germany, 28 September–2 October 2015; IEEE: Piscataway, NJ, USA, 2015; pp. 7–13. [Google Scholar]
- Mohseni-Kabir, A.; Li, C.; Wu, V.; Miller, D.; Hylak, B.; Chernova, S.; Berenson, D.; Sidner, C.; Rich, C. Simultaneous learning of hierarchy and primitives for complex robot tasks. Auton. Robot. 2019, 43, 859–874. [Google Scholar] [CrossRef]
- Bobu, A.; Peng, A.; Agrawal, P.; Shah, J.A.; Dragan, A.D. Aligning Human and Robot Representations. In Proceedings of the 2024 ACM/IEEE International Conference on Human-Robot Interaction, Boulder, CO, USA, 11–15 March 2024; pp. 42–54. [Google Scholar]
- Dong, Z.; Li, Z.; Yan, Y.; Calinon, S.; Chen, F. Passive bimanual skills learning from demonstration with motion graph attention networks. IEEE Robot. Autom. Lett. 2022, 7, 4917–4923. [Google Scholar] [CrossRef]
- Liu, D.; Lu, B.; Cong, M.; Yu, H.; Zou, Q.; Du, Y. Robotic manipulation skill acquisition via demonstration policy learning. IEEE Trans. Cogn. Dev. Syst. 2021, 14, 1054–1065. [Google Scholar] [CrossRef]
- Mo, Y.; Sasaki, H.; Matsubara, T.; Yamazaki, K. Multi-step motion learning by combining learning-from-demonstration and policy-search. Adv. Robot. 2023, 37, 560–575. [Google Scholar] [CrossRef]
- Frank, F.; Paraschos, A.; van der Smagt, P.; Cseke, B. Constrained probabilistic movement primitives for robot trajectory adaptation. IEEE Trans. Robot. 2021, 38, 2276–2294. [Google Scholar] [CrossRef]
- Zhai, D.H.; Xia, Z.; Wu, H.; Xia, Y. A motion planning method for robots based on DMPS and modified obstacle-avoiding algorithm. IEEE Trans. Autom. Sci. Eng. 2022, 20, 2678–2688. [Google Scholar] [CrossRef]
- Auddy, S.; Hollenstein, J.; Saveriano, M.; Rodríguez-Sánchez, A.; Piater, J. Continual learning from demonstration of robotics skills. Robot. Auton. Syst. 2023, 165, 104427. [Google Scholar] [CrossRef]
- Ruan, S.; Liu, W.; Wang, X.; Meng, X.; Chirikjian, G.S. PRIMP: PRobabilistically-Informed Motion Primitives for Efficient Affordance Learning from Demonstration. IEEE Trans. Robot. 2024, 40, 2868–2887. [Google Scholar] [CrossRef]
- Biagiotti, L.; Meattini, R.; Chiaravalli, D.; Palli, G.; Melchiorri, C. Robot Programming by Demonstration: Trajectory Learning Enhanced by sEMG-Based User Hand Stiffness Estimation. IEEE Trans. Robot. 2023, 39, 3259–3278. [Google Scholar] [CrossRef]
- Vuong, N.; Pham, H.; Pham, Q.C. Learning sequences of manipulation primitives for robotic assembly. In Proceedings of the 2021 IEEE International Conference on Robotics and Automation (ICRA), Xi’an, China, 30 May–5 June 2021; IEEE: Piscataway, NJ, USA, 2021; pp. 4086–4092. [Google Scholar]
- Wu, Z.; Lian, W.; Wang, C.; Li, M.; Schaal, S.; Tomizuka, M. Prim-lafd: A framework to learn and adapt primitive-based skills from demonstrations for insertion tasks. IFAC-PapersOnLine 2023, 56, 4120–4125. [Google Scholar] [CrossRef]
- Johannsmeier, L.; Gerchow, M.; Haddadin, S. A framework for robot manipulation: Skill formalism, meta learning and adaptive control. In Proceedings of the 2019 International Conference on Robotics and Automation (ICRA), Montreal, QC, Canada, 20–24 May 2019; IEEE: Piscataway, NJ, USA, 2019; pp. 5844–5850. [Google Scholar]
- Simonič, M.; Petrič, T.; Ude, A.; Nemec, B. Analysis of methods for incremental policy refinement by kinesthetic guidance. J. Intell. Robot. Syst. 2021, 102, 5. [Google Scholar] [CrossRef]
- Wu, Z.; Lian, W.; Unhelkar, V.; Tomizuka, M.; Schaal, S. Learning dense rewards for contact-rich manipulation tasks. In Proceedings of the 2021 IEEE International Conference on Robotics and Automation (ICRA), Xi’an, China, 30 May–5 June 2021; IEEE: Piscataway, NJ, USA, 2021; pp. 6214–6221. [Google Scholar]
- Lee, M.A.; Zhu, Y.; Srinivasan, K.; Shah, P.; Savarese, S.; Fei-Fei, L.; Garg, A.; Bohg, J. Making sense of vision and touch: Self-supervised learning of multimodal representations for contact-rich tasks. In Proceedings of the 2019 International Conference on Robotics and Automation (ICRA), Montreal, QC, Canada, 20–24 May 2019; IEEE: Piscataway, NJ, USA, 2019; pp. 8943–8950. [Google Scholar]
- Davchev, T.; Luck, K.S.; Burke, M.; Meier, F.; Schaal, S.; Ramamoorthy, S. Residual learning from demonstration: Adapting dmps for contact-rich manipulation. IEEE Robot. Autom. Lett. 2022, 7, 4488–4495. [Google Scholar] [CrossRef]
- Vecerik, M.; Hester, T.; Scholz, J.; Wang, F.; Pietquin, O.; Piot, B.; Heess, N.; Rothörl, T.; Lampe, T.; Riedmiller, M. Leveraging demonstrations for deep reinforcement learning on robotics problems with sparse rewards. arXiv 2017, arXiv:1707.08817. [Google Scholar]
- Vidaković, J.; Jerbić, B.; Šekoranja, B.; Švaco, M.; Šuligoj, F. Accelerating robot trajectory learning for stochastic tasks. IEEE Access 2020, 8, 71993–72006. [Google Scholar] [CrossRef]
- Perico, C.A.V.; De Schutter, J.; Aertbeliën, E. Combining imitation learning with constraint-based task specification and control. IEEE Robot. Autom. Lett. 2019, 4, 1892–1899. [Google Scholar] [CrossRef]
- Roveda, L.; Magni, M.; Cantoni, M.; Piga, D.; Bucca, G. Assembly task learning and optimization through human’s demonstration and machine learning. In Proceedings of the 2020 IEEE International Conference on Systems, Man, and Cybernetics (SMC), Toronto, ON, Canada, 11–14 October 2020; IEEE: Piscataway, NJ, USA, 2020; pp. 1852–1859. [Google Scholar]
- Si, W.; Guan, Y.; Wang, N. Adaptive compliant skill learning for contact-rich manipulation with human in the loop. IEEE Robot. Autom. Lett. 2022, 7, 5834–5841. [Google Scholar] [CrossRef]
- Wang, W.; Loh, R.N.; Gu, E.Y. Passive compliance versus active compliance in robot-based automated assembly systems. Ind. Robot. Int. J. 1998, 25, 48–57. [Google Scholar] [CrossRef]
- Song, P.; Yu, Y.; Zhang, X. A tutorial survey and comparison of impedance control on robotic manipulation. Robotica 2019, 37, 801–836. [Google Scholar] [CrossRef]
- Hogan, N. Impedance control of industrial robots. Robot. Comput.-Integr. Manuf. 1984, 1, 97–113. [Google Scholar] [CrossRef]
- Nemec, B.; Žlajpah, L.; Šlajpa, S.; Piškur, J.; Ude, A. An efficient pbd framework for fast deployment of bi-manual assembly tasks. In Proceedings of the 2018 IEEE-RAS 18th International Conference on Humanoid Robots (Humanoids), Beijing, China, 6–9 November 2018; IEEE: Piscataway, NJ, USA, 2018; pp. 166–173. [Google Scholar]
- Hu, H.; Yang, X.; Lou, Y. A robot learning from demonstration framework for skillful small parts assembly. Int. J. Adv. Manuf. Technol. 2022, 119, 6775–6787. [Google Scholar] [CrossRef]
- Seo, J.; Prakash, N.P.; Zhang, X.; Wang, C.; Choi, J.; Tomizuka, M.; Horowitz, R. Contact-rich SE (3)-Equivariant Robot Manipulation Task Learning via Geometric Impedance Control. IEEE Robot. Autom. Lett. 2023, 9, 1508–1515. [Google Scholar] [CrossRef]
- Kastritsi, T.; Dimeas, F.; Doulgeri, Z. Progressive automation with dmp synchronization and variable stiffness control. IEEE Robot. Autom. Lett. 2018, 3, 3789–3796. [Google Scholar] [CrossRef]
- Yang, S.; Gao, X.; Feng, Z.; Xiao, X. Learning Pose Dynamical System for Contact Tasks under Human Interaction. Actuators 2023, 12, 179. [Google Scholar] [CrossRef]
- Wang, W.; Li, R.; Chen, Y.; Diekel, Z.M.; Jia, Y. Facilitating human–robot collaborative tasks by teaching-learning-collaboration from human demonstrations. IEEE Trans. Autom. Sci. Eng. 2018, 16, 640–653. [Google Scholar] [CrossRef]
- Nemec, B.; Likar, N.; Gams, A.; Ude, A. Human robot cooperation with compliance adaptation along the motion trajectory. Auton. Robot. 2018, 42, 1023–1035. [Google Scholar] [CrossRef]
- Eiband, T.; Willibald, C.; Tannert, I.; Weber, B.; Lee, D. Collaborative programming of robotic task decisions and recovery behaviors. Auton. Robot. 2023, 47, 229–247. [Google Scholar] [CrossRef]
- Rozo, L.; Calinon, S.; Caldwell, D.G.; Jimenez, P.; Torras, C. Learning physical collaborative robot behaviors from human demonstrations. IEEE Trans. Robot. 2016, 32, 513–527. [Google Scholar] [CrossRef]
- Jha, D.K.; Jain, S.; Romeres, D.; Yerazunis, W.; Nikovski, D. Generalizable human-robot collaborative assembly using imitation learning and force control. In Proceedings of the 2023 European Control Conference (ECC), Bucharest, Romania, 13–16 June 2023; IEEE: Piscataway, NJ, USA, 2023; pp. 1–8. [Google Scholar]
- Khoramshahi, M.; Billard, A. A dynamical system approach to task-adaptation in physical human–robot interaction. Auton. Robot. 2019, 43, 927–946. [Google Scholar] [CrossRef]
- Jahanmahin, R.; Masoud, S.; Rickli, J.; Djuric, A. Human-robot interactions in manufacturing: A survey of human behavior modeling. Robot. Comput.-Integr. Manuf. 2022, 78, 102404. [Google Scholar] [CrossRef]
- Xing, X.; Maqsood, K.; Zeng, C.; Yang, C.; Yuan, S.; Li, Y. Dynamic Motion Primitives-based Trajectory Learning for Physical Human-Robot Interaction Force Control. IEEE Trans. Ind. Inform. 2023, 20, 1675–1686. [Google Scholar] [CrossRef]
- Franzese, G.; de Souza Rosa, L.; Verburg, T.; Peternel, L.; Kober, J. Interactive imitation learning of bimanual movement primitives. IEEE/ASME Trans. Mechatron. 2023; early access. [Google Scholar] [CrossRef]
- Krebs, F.; Meixner, A.; Patzer, I.; Asfour, T. The kit bimanual manipulation dataset. In Proceedings of the 2020 IEEE-RAS 20th International Conference on Humanoid Robots (Humanoids), Munich, Germany, 19–21 July 2021; IEEE: Piscataway, NJ, USA, 2021; pp. 499–506. [Google Scholar]
- Stepputtis, S.; Bandari, M.; Schaal, S.; Amor, H.B. A system for imitation learning of contact-rich bimanual manipulation policies. In Proceedings of the 2022 IEEE/RSJ International Conference on Intelligent Robots and Systems (IROS), Kyoto, Japan, 23–27 October 2022; IEEE: Piscataway, NJ, USA, 2022; pp. 11810–11817. [Google Scholar]
- Liu, J.; Sim, H.; Li, C.; Tan, K.C.; Chen, F. Birp: Learning robot generalized bimanual coordination using relative parameterization method on human demonstration. In Proceedings of the 2023 62nd IEEE Conference on Decision and Control (CDC), Singapore, 13–15 December 2023; IEEE: Piscataway, NJ, USA, 2023; pp. 8300–8305. [Google Scholar]
- Mao, X.; Xu, Y.; Wen, R.; Kasaei, M.; Yu, W.; Psomopoulou, E.; Lepora, N.F.; Li, Z. Learning fine pinch-grasp skills using tactile sensing from real demonstration data. arXiv 2023, arXiv:2307.04619. [Google Scholar]
- Jaquier, N.; Ginsbourger, D.; Calinon, S. Learning from demonstration with model-based Gaussian process. In Proceedings of the Conference on Robot Learning, PMLR, Virtual, 16–18 November 2020; pp. 247–257. [Google Scholar]
- Arduengo, M.; Colomé, A.; Lobo-Prat, J.; Sentis, L.; Torras, C. Gaussian-process-based robot learning from demonstration. J. Ambient. Intell. Humaniz. Comput. 2023, 1–14. [Google Scholar] [CrossRef]
- Ding, G.; Liu, Y.; Zang, X.; Zhang, X.; Liu, G.; Zhao, J. A task-learning strategy for robotic assembly tasks from human demonstrations. Sensors 2020, 20, 5505. [Google Scholar] [CrossRef] [PubMed]
- Kulak, T.; Girgin, H.; Odobez, J.M.; Calinon, S. Active learning of Bayesian probabilistic movement primitives. IEEE Robot. Autom. Lett. 2021, 6, 2163–2170. [Google Scholar] [CrossRef]
- Prados, A.; Garrido, S.; Barber, R. Learning and generalization of task-parameterized skills through few human demonstrations. Eng. Appl. Artif. Intell. 2024, 133, 108310. [Google Scholar] [CrossRef]
- Zappa, I.; Fracassi, G.; Zanchettin, A.M.; Rocco, P. Parameterization of Robotic Welding Trajectories from Demonstration. In Proceedings of the 2023 11th International Conference on Control, Mechatronics and Automation (ICCMA), Grimstad, Norway, 1–3 November 2023; IEEE: Piscataway, NJ, USA, 2023; pp. 146–151. [Google Scholar]
- Cui, Z.; Ma, W.; Lai, J.; Chu, H.K.; Guo, Y. Coupled multiple dynamic movement primitives generalization for deformable object manipulation. IEEE Robot. Autom. Lett. 2022, 7, 5381–5388. [Google Scholar] [CrossRef]
- Li, X.; Brock, O. Learning from demonstration based on environmental constraints. IEEE Robot. Autom. Lett. 2022, 7, 10938–10945. [Google Scholar] [CrossRef]
- Johns, E. Coarse-to-fine imitation learning: Robot manipulation from a single demonstration. In Proceedings of the 2021 IEEE international conference on robotics and automation (ICRA), Xi’an, China, 30 May–5 June 2021; IEEE: Piscataway, NJ, USA, 2021; pp. 4613–4619. [Google Scholar]
- Shi, Y.; Chen, Z.; Wu, Y.; Henkel, D.; Riedel, S.; Liu, H.; Feng, Q.; Zhang, J. Combining learning from demonstration with learning by exploration to facilitate contact-rich tasks. In Proceedings of the 2021 IEEE/RSJ International Conference on Intelligent Robots and Systems (IROS), Prague, Czech Republic, 27 September–October 2021; IEEE: Piscataway, NJ, USA, 2021; pp. 1062–1069. [Google Scholar]
- Wohlgemuth, F.; Mizutani, I.; Eichelberger, L.; Mayer, S. Electromyography-based Kinesthetic Teaching of Industrial Collaborative Robots. In Proceedings of the Companion of the 2024 ACM/IEEE International Conference on Human-Robot Interaction, Boulder, CO, USA, 11–15 March 2024; pp. 1124–1128. [Google Scholar]
- Prados, A.; Mora, A.; López, B.; Muñoz, J.; Garrido, S.; Barber, R. Kinesthetic learning based on fast marching square method for manipulation. Appl. Sci. 2023, 13, 2028. [Google Scholar] [CrossRef]
- Barekatain, A.; Habibi, H.; Voos, H. DFL-TORO: A One-Shot Demonstration Framework for Learning Time-Optimal Robotic Manufacturing Tasks. arXiv 2023, arXiv:2309.09802. [Google Scholar]
- Si, W.; Wang, N.; Yang, C. A review on manipulation skill acquisition through teleoperation-based learning from demonstration. Cogn. Comput. Syst. 2021, 3, 1–16. [Google Scholar] [CrossRef]
- Rigter, M.; Lacerda, B.; Hawes, N. A framework for learning from demonstration with minimal human effort. IEEE Robot. Autom. Lett. 2020, 5, 2023–2030. [Google Scholar] [CrossRef]
- Tung, A.; Wong, J.; Mandlekar, A.; Martín-Martín, R.; Zhu, Y.; Fei-Fei, L.; Savarese, S. Learning multi-arm manipulation through collaborative teleoperation. In Proceedings of the 2021 IEEE International Conference on Robotics and Automation (ICRA), Xi’an, China, 30 May–5 June 2021; IEEE: Piscataway, NJ, USA, 2021; pp. 9212–9219. [Google Scholar]
- Luo, J.; Liu, W.; Qi, W.; Hu, J.; Chen, J.; Yang, C. A vision-based virtual fixture with robot learning for teleoperation. Robot. Auton. Syst. 2023, 164, 104414. [Google Scholar] [CrossRef]
- Güleçyüz, B.; von Büren, V.; Xu, X.; Steinbach, E. NetLfD: Network-Aware Learning from Demonstration for In-Contact Skills via Teleoperation. IEEE Robot. Autom. Lett. 2023, 8, 6995–7002. [Google Scholar] [CrossRef]
- Franzese, G.; Mészáros, A.; Peternel, L.; Kober, J. ILoSA: Interactive learning of stiffness and attractors. In Proceedings of the 2021 IEEE/RSJ International Conference on Intelligent Robots and Systems (IROS), Prague, Czech Republic, 27 September–1 October 2021; IEEE: Piscataway, NJ, USA, 2021; pp. 7778–7785. [Google Scholar]
- Yin, C.; Zhang, Q. A multi-modal framework for robots to learn manipulation tasks from human demonstrations. J. Intell. Robot. Syst. 2023, 107, 56. [Google Scholar] [CrossRef]
- Zhu, X.; Ke, J.; Xu, Z.; Sun, Z.; Bai, B.; Lv, J.; Liu, Q.; Zeng, Y.; Ye, Q.; Lu, C.; et al. Diff-lfd: Contact-aware model-based learning from visual demonstration for robotic manipulation via differentiable physics-based simulation and rendering. In Proceedings of the Conference on Robot Learning, PMLR, Atlanta, GA, USA, 6–9 November 2023; pp. 499–512. [Google Scholar]
- Yang, S.; Zhang, W.; Song, R.; Cheng, J.; Wang, H.; Li, Y. Watch and act: Learning robotic manipulation from visual demonstration. IEEE Trans. Syst. Man Cybern. Syst. 2023, 53, 4404–4416. [Google Scholar] [CrossRef]
- Xu, X.; You, M.; Zhou, H.; Qian, Z.; He, B. Robot imitation learning from image-only observation without real-world interaction. IEEE/ASME Trans. Mechatron. 2022, 28, 1234–1244. [Google Scholar] [CrossRef]
- Bıyık, E.; Huynh, N.; Kochenderfer, M.J.; Sadigh, D. Active preference-based Gaussian process regression for reward learning and optimization. Int. J. Robot. Res. 2024, 43, 665–684. [Google Scholar] [CrossRef]
- Celemin, C.; Ruiz-del Solar, J. An interactive framework for learning continuous actions policies based on corrective feedback. J. Intell. Robot. Syst. 2019, 95, 77–97. [Google Scholar] [CrossRef]
- Pastor, P.; Hoffmann, H.; Asfour, T.; Schaal, S. Learning and generalization of motor skills by learning from demonstration. In Proceedings of the 2009 IEEE International Conference on Robotics and Automation, Kobe, Japan, 12–17 May 2009; IEEE: Piscataway, NJ, USA, 2009; pp. 763–768. [Google Scholar]
- Tavassoli, M.; Katyara, S.; Pozzi, M.; Deshpande, N.; Caldwell, D.G.; Prattichizzo, D. Learning skills from demonstrations: A trend from motion primitives to experience abstraction. IEEE Trans. Cogn. Dev. Syst. 2024, 16, 57–74. [Google Scholar] [CrossRef]
- Chisari, E.; Welschehold, T.; Boedecker, J.; Burgard, W.; Valada, A. Correct me if i am wrong: Interactive learning for robotic manipulation. IEEE Robot. Autom. Lett. 2022, 7, 3695–3702. [Google Scholar] [CrossRef]
- Yin, H.; Melo, F.S.; Paiva, A.; Billard, A. An ensemble inverse optimal control approach for robotic task learning and adaptation. Auton. Robot. 2019, 43, 875–896. [Google Scholar] [CrossRef]
- Zhou, Y.; Gao, J.; Asfour, T. Movement primitive learning and generalization: Using mixture density networks. IEEE Robot. Autom. Mag. 2020, 27, 22–32. [Google Scholar] [CrossRef]
- Ijspeert, A.J.; Nakanishi, J.; Hoffmann, H.; Pastor, P.; Schaal, S. Dynamical movement primitives: Learning attractor models for motor behaviors. Neural Comput. 2013, 25, 328–373. [Google Scholar] [CrossRef]
- Saveriano, M.; Abu-Dakka, F.J.; Kramberger, A.; Peternel, L. Dynamic movement primitives in robotics: A tutorial survey. Int. J. Robot. Res. 2023, 42, 1133–1184. [Google Scholar] [CrossRef]
- Nemec, B.; Gams, A.; Ude, A. Velocity adaptation for self-improvement of skills learned from user demonstrations. In Proceedings of the 2013 13th IEEE-RAS International Conference on Humanoid Robots (Humanoids), Atlanta, GA, USA, 15–17 October 2013; IEEE: Piscataway, NJ, USA, 2013; pp. 423–428. [Google Scholar]
- Shaw, S.; Jha, D.K.; Raghunathan, A.; Corcodel, R.; Romeres, D.; Konidaris, G.; Nikovski, D. Constrained dynamic movement primitives for safe learning of motor skills. arXiv 2022, arXiv:2209.14461. [Google Scholar]
- Sidiropoulos, A.; Papageorgiou, D.; Doulgeri, Z. A novel framework for generalizing dynamic movement primitives under kinematic constraints. Auton. Robot. 2023, 47, 37–50. [Google Scholar] [CrossRef]
- Sidiropoulos, A.; Doulgeri, Z. A reversible dynamic movement primitive formulation. In Proceedings of the 2021 IEEE International Conference on Robotics and Automation (ICRA), Xi’an, China, 30 May–5 June 2021; IEEE: Piscataway, NJ, USA, 2021; pp. 3147–3153. [Google Scholar]
- Abu-Dakka, F.J.; Saveriano, M.; Kyrki, V. A Unified Formulation of Geometry-aware Dynamic Movement Primitives. arXiv 2022, arXiv:2203.03374. [Google Scholar] [CrossRef]
- Saveriano, M.; Franzel, F.; Lee, D. Merging position and orientation motion primitives. In Proceedings of the 2019 International Conference on Robotics and Automation (ICRA), Montreal, QC, Canada, 20–24 May 2019; IEEE: Piscataway, NJ, USA, 2019; pp. 7041–7047. [Google Scholar]
- Han, L.; Yuan, H.; Xu, W.; Huang, Y. Modified dynamic movement primitives: Robot trajectory planning and force control under curved surface constraints. IEEE Trans. Cybern. 2022, 53, 4245–4258. [Google Scholar] [CrossRef]
- Chang, C.; Haninger, K.; Shi, Y.; Yuan, C.; Chen, Z.; Zhang, J. Impedance adaptation by reinforcement learning with contact dynamic movement primitives. In Proceedings of the 2022 IEEE/ASME International Conference on Advanced Intelligent Mechatronics (AIM), Sapporo, Japan, 11–15 July 2022; IEEE: Piscataway, NJ, USA, 2022; pp. 1185–1191. [Google Scholar]
- Liao, Z.; Jiang, G.; Zhao, F.; Wu, Y.; Yue, Y.; Mei, X. Dynamic skill learning from human demonstration based on the human arm stiffness estimation model and Riemannian DMP. IEEE/ASME Trans. Mechatron. 2022, 28, 1149–1160. [Google Scholar] [CrossRef]
- Ugur, E.; Girgin, H. Compliant parametric dynamic movement primitives. Robotica 2020, 38, 457–474. [Google Scholar] [CrossRef]
- Sidiropoulos, A.; Doulgeri, Z. Dynamic via-points and improved spatial generalization for online trajectory planning with Dynamic Movement Primitives. arXiv 2022, arXiv:2212.13473. [Google Scholar]
- Cleveland, W.S.; Devlin, S.J. Locally weighted regression: An approach to regression analysis by local fitting. J. Am. Stat. Assoc. 1988, 83, 596–610. [Google Scholar] [CrossRef]
- Peters, J.; Mülling, K.; Kober, J.; Nguyen-Tuong, D.; Krömer, O. Towards motor skill learning for robotics. In Proceedings of the Robotics Research: The 14th International Symposium ISRR, Lucerne, Switzerland, 31 August–3 September 2009; Springer: Berlin/Heidelberg, Germany, 2011; pp. 469–482. [Google Scholar]
- Tsai, Y.Y.; Xiao, B.; Johns, E.; Yang, G.Z. Constrained-space optimization and reinforcement learning for complex tasks. IEEE Robot. Autom. Lett. 2020, 5, 683–690. [Google Scholar] [CrossRef]
- Wang, K.; Zhao, Y.; Sakuma, I. Learning robotic insertion tasks from human demonstration. IEEE Robot. Autom. Lett. 2023, 8, 5815–5822. [Google Scholar] [CrossRef]
- Ma, Y.; Xu, D.; Qin, F. Efficient insertion control for precision assembly based on demonstration learning and reinforcement learning. IEEE Trans. Ind. Inform. 2020, 17, 4492–4502. [Google Scholar] [CrossRef]
- Das, N.; Bechtle, S.; Davchev, T.; Jayaraman, D.; Rai, A.; Meier, F. Model-based inverse reinforcement learning from visual demonstrations. In Proceedings of the Conference on Robot Learning, PMLR, London, UK, 8–11 November 2021; pp. 1930–1942. [Google Scholar]
- Alakuijala, M.; Dulac-Arnold, G.; Mairal, J.; Ponce, J.; Schmid, C. Learning reward functions for robotic manipulation by observing humans. In Proceedings of the 2023 IEEE International Conference on Robotics and Automation (ICRA), London, UK, 29 May–2 June 2023; IEEE: Piscataway, NJ, USA, 2023; pp. 5006–5012. [Google Scholar]
- Trinh, T.; Chen, H.; Brown, D.S. Autonomous assessment of demonstration sufficiency via bayesian inverse reinforcement learning. In Proceedings of the 2024 ACM/IEEE International Conference on Human-Robot Interaction, Boulder, CO, USA, 11–15 March 2024; pp. 725–733. [Google Scholar]
- Escontrela, A.; Adeniji, A.; Yan, W.; Jain, A.; Peng, X.B.; Goldberg, K.; Lee, Y.; Hafner, D.; Abbeel, P. Video prediction models as rewards for reinforcement learning. In Proceedings of the Advances in Neural Information Processing Systems; Curran Associates Inc.: Red Hook, NY, USA, 2024; Volume 36. [Google Scholar]
- Zhu, J.; Gienger, M.; Kober, J. Learning task-parameterized skills from few demonstrations. IEEE Robot. Autom. Lett. 2022, 7, 4063–4070. [Google Scholar] [CrossRef]
- Paraschos, A.; Daniel, C.; Peters, J.R.; Neumann, G. Probabilistic movement primitives. In Proceedings of the Advances in Neural Information Processing Systems, Llake Tahoe, NV, USA, 5–10 December 2013; Volume 26. [Google Scholar]
- Yue, C.; Gao, T.; Lu, L.; Lin, T.; Wu, Y. Probabilistic movement primitives based multi-task learning framework. Comput. Ind. Eng. 2024, 191, 110144. [Google Scholar] [CrossRef]
- Yang, Y.; Chen, L.; Zaidi, Z.; van Waveren, S.; Krishna, A.; Gombolay, M. Enhancing Safety in Learning from Demonstration Algorithms via Control Barrier Function Shielding. In Proceedings of the 2024 ACM/IEEE International Conference on Human-Robot Interaction, Boulder, CO, USA, 11–15 March 2024; pp. 820–829. [Google Scholar]
- Wang, J.; Wu, Z.; Li, Y.; Jiang, H.; Shu, P.; Shi, E.; Hu, H.; Ma, C.; Liu, Y.; Wang, X.; et al. Large language models for robotics: Opportunities, challenges, and perspectives. arXiv 2024, arXiv:2401.04334. [Google Scholar]
- Zhang, C.; Wang, Z.; Zhou, G.; Chang, F.; Ma, D.; Jing, Y.; Cheng, W.; Ding, K.; Zhao, D. Towards new-generation human-centric smart manufacturing in Industry 5.0: A systematic review. Adv. Eng. Inform. 2023, 57, 102121. [Google Scholar] [CrossRef]
- Lou, S.; Hu, Z.; Zhang, Y.; Feng, Y.; Zhou, M.; Lv, C. Human-Cyber-Physical System for Industry 5.0: A Review From a Human-Centric Perspective. IEEE Trans. Autom. Sci. Eng. 2024, 1–18. [Google Scholar] [CrossRef]
- Liu, Y.; Zhang, W.; Pan, S.; Li, Y.; Chen, Y. Analyzing the robotic behavior in a smart city with deep enforcement and imitation learning using IoRT. Comput. Commun. 2020, 150, 346–356. [Google Scholar] [CrossRef]
- Romeo, L.; Petitti, A.; Marani, R.; Milella, A. Internet of robotic things in smart domains: Applications and challenges. Sensors 2020, 20, 3355. [Google Scholar] [CrossRef]
- Groshev, M.; Baldoni, G.; Cominardi, L.; de la Oliva, A.; Gazda, R. Edge robotics: Are we ready? An experimental evaluation of current vision and future directions. Digit. Commun. Netw. 2023, 9, 166–174. [Google Scholar] [CrossRef]
- Liu, C.; Tang, D.; Zhu, H.; Nie, Q.; Chen, W.; Zhao, Z. An augmented reality-assisted interaction approach using deep reinforcement learning and cloud-edge orchestration for user-friendly robot teaching. Robot. Comput.-Integr. Manuf. 2024, 85, 102638. [Google Scholar] [CrossRef]
- Wang, X.V.; Wang, L. Augmented reality enabled human–robot collaboration. In Advanced Human-Robot Collaboration in Manufacturing; Springer: Berlin/Heidelberg, Germany, 2021; pp. 395–411. [Google Scholar]
- Hamon, L. Virtual reality and programming by demonstration: Teaching a robot to grasp a dynamic object by the generalization of human demonstrations. Presence 2011, 20, 241–253. [Google Scholar] [CrossRef]
- Dyrstad, J.S.; Mathiassen, J.R. Grasping virtual fish: A step towards robotic deep learning from demonstration in virtual reality. In Proceedings of the 2017 IEEE International Conference on Robotics and Biomimetics (ROBIO), Macau, Macao, 5–8 December 2017; IEEE: Piscataway, NJ, USA, 2017; pp. 1181–1187. [Google Scholar]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).