Autonomous Alignment and Docking Control for a Self-Reconfigurable Modular Mobile Robotic System

Abstract

This paper presents the path planning and motion control of a self-reconfigurable mobile robot system, focusing on module-to-module autonomous docking and alignment tasks. STORM, which stands for Self-configurable and Transformable Omni-Directional Robotic Modules, features a unique mode-switching ability and novel docking mechanism design. This enables the modules that make up STORM to dock with each other and form a variety configurations in or to perform a large array of tasks. The path planning and motion control presented here consists of two parallel schemes. A Lyapunov function-based precision controller is proposed to align the target docking mechanisms in a small range of the target position. Then, an optimization-based path planning algorithm is proposed to help find the fastest path and determine when to switch its locomotion mode in a much larger range. Both numerical simulations and real-world experiments were carried out to validate these proposed controllers.

1. Introduction

Over the past decades, numerous multi-robot architectures [1,2,3,4,5] have been created and examined to fulfill diverse missions. These multi-robot systems were designed to leverage the collective capabilities of multiple robots, allowing them to undertake tasks that surpass the inherent limitations of a single robot. The objective is to enhance overall system performance, efficiency, and task accomplishment in comparison to individual robotic agents. While multi-robot systems offer these advantages, there are instances where they fall short. A single robot such as Matilda [6], Packbot [7], TAROS [8], TALON [9], SherpaTT [10], and Ralter [11], may have diverse manipulation capabilities and additional functions provided by an extensive configuration, but such capabilities often necessitate a larger structure.

In order to bridge the gap between small multi-robot systems and large single-robot systems to better respond to the challenges of complex tasks and environments, modular robots with reconfigurable capabilities have been proposed. Various modular reconfigurable robot systems have been designed and studied with primary interests in robotic mobility, docking interfaces [12,13,14], and reconfiguration strategies [15,16].

A novel modular robotic system with a self-reconfiguration capability that offers greater versatility and better functionalities over the traditional fixed-structure robots or the typical multiple mobile robot systems is proposed in this paper. During the reconfiguration process, the target coupling mechanism of a multi-directional locomotion module with switching dynamics is required to align with the docking mechanism of another robot module, called the load carrier. Therefore, a well-defined controller that can maneuver the locomotion module of the STORM (Self-configurable and Transformable Omni-Directional Robotic Module) system to the desired pose is required for this process.

The locomotion module is considered a nonholonomic system that is drift-free, under-actuated, and nonlinear. According to Brockett’s theory [17], these systems cannot be stabilized to a desired configuration using a time-invariant state feedback law, which makes it more challenging to develop a motion controller of the locomotion module for the autonomous alignment task. Previously, researchers developed both smooth and nonsmooth time-varying controllers for these systems. In general, the nonsmooth controller behaves better because it achieves an exponential rate of convergence. However, its convergence rate critically depends on the available gains. The oscillatory behavior of the mobile robots during the approach to the goal, which makes the motion rather erratic, is an intrinsic characteristic of time-varying control laws [18]. The polar coordinate transformation-based controller in [19] converges fast and generates smooth paths with a weak dependence on the choice of the control gain parameters. However, it is based on a unicycle model and cannot be generalized to more complicated robot models. The dynamic feedback linearization method [20] also has a fast convergence rate and is able to generate natural curves. However, the parameter tuning process requires a very large feasible set of PD gains to choose from. In this study, a Lyapunov function-based [21,22,23,24,25,26] pose stabilization controller was developed for the locomotion module to accomplish the autonomous alignment task.

In order to bring the robot module close enough to the target module to perform the aforementioned autonomous alignment tasks, a novel path optimization method is also proposed. The new path planning method takes the special mode switch capability (track or wheel) of the locomotion module into consideration and uses numerical methods to find the optimal path.

Therefore, the complete robot module control consists of two stages: the trajectory optimization stage and the motion control stage. The trajectory optimization stage aims to find an optimal path for the robot module when the robot module is away from its target module and the motion control stage aims to perform the module-to-module autonomous docking and alignment tasks when the robot module moves close enough to its target module.

The main contributions of this work are summarized as follows: (1) the development and initial validation of a pose stabilization controller for a novel self-reconfigurable modular mobile robot to achieve autonomous alignment and docking and (2) the development of a direct collocation-based trajectory optimization method to account for the switching mechanism of the locomotion module and thus improve the autonomous docking process.

The rest of this paper is organized as follows. Section 2 introduces the STORM robotic system and analyzes its functionalities in simulations. Section 3 presents the pose stabilization controller for the autonomous alignment and docking processes. Section 4 presents the direct collocation-based path planning algorithm for the improvement of the autonomous alignment control. Section 5 concludes the research and presents future work.

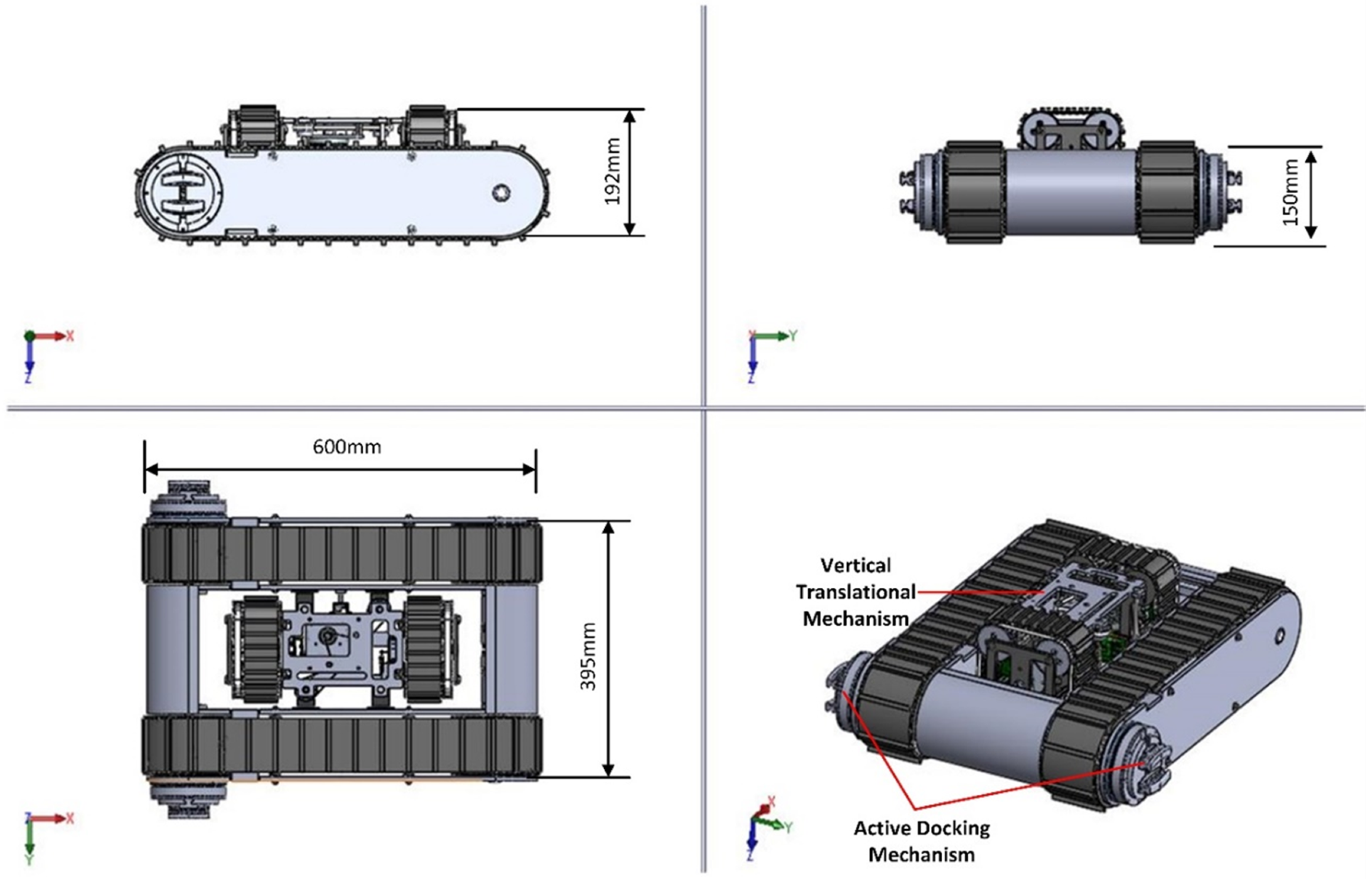
2. Overview of the STORM Robotic System

The proposed robotic system mainly consists of two major types of robotic modules—the load carrier module and the locomotion module—as shown in Figure 1. Each module is capable of navigating through and interacting with the environment independently. In addition, the robotic system is proposed to be able to reassemble autonomously into various configurations, including a humanoid setup, facilitating the system’s ability to traverse obstacles such as ditches. For the autonomous reassembly process, a non-backdrivable active docking mechanism with two Degrees of Freedom (DOFs) was developed to integrate into the tracked units of the robot modules. The quantity and placement of the docking mechanism are flexible, allowing for customization to meet diverse mission and environmental requirements.

The load carrier was designed for carrying and transporting packages. It incorporates four passive docking points and four cameras strategically positioned onboard to facilitate autonomous docking.

The locomotion module (Figure 2) consists of two longitudinal tracked units, two lateral tracked units, and a Vertical Translational Mechanism (VTM) that switches between the two modes of locomotion. An alternative setup for lateral motion involves replacing the tracks with wheels. In the mechanical design of the locomotion module, special attention was given to achieving multi-directional mobility, enhancing spatial alignment capabilities for autonomous docking functionality.

The active docking mechanism is essential for enabling the reconfigurability of the STORM system. The version of this docking mechanism implemented on the locomotion module was updated from those previously developed and discussed in [27]. Figure 3 demonstrates the worm gear assembly drives for the relative rotation between the docking mechanism and the stationary robot frame. The worm drive was chosen for its high torque capability and non-backdriveable nature, allowing the safe rotation of the locomotion module for different configurations. A symmetric translation of the clamping profiles is achieved with a constant lead cam, selected for its compact design and non-backdriveable feature.

Simulations of the STORM System

To evaluate the overall functionalities and feasibility of the STORM system, simulations were conducted using the CoppeliaSim robot simulator [28]. The test environment included a variety of terrain types such as muddy terrain, ditches, rocky terrain, high hills, and narrow corridors. A load carrier module and two locomotion modules were used in the simulations to evaluate the performances of the robot modules in different configurations.

Preliminary tests involving three different configurations on diverse terrains were conducted, demonstrating that the proposed robotic modules successfully navigated through these terrains with distinct configurations. Ongoing tests will further analyze the robots’ performance and limitations. Figure 4 illustrates various configurations designed for different terrain types. The robots adopted a diagonal line configuration to navigate rocky terrain, enhancing balance and preventing unforeseen issues like rollovers or getting stuck on large rocks (Figure 4a). For crossing a ditch, the robot module assumed a crab-like shape to maximize length, ensuring that the center of gravity (COG) falls on the side of the two locomotion modules to prevent rollover (Figure 4b). In the simulation of muddy terrain with a low coefficient of friction, a closed-form configuration was selected to evenly distribute traction and reduce slipping (Figure 4c). A triangular configuration was employed for ascending and descending hills to enhance stability and traction (Figure 4d). The large configuration was decoupled and oriented toward the narrow corridor, as shown in Figure 4). To enhance autonomy and prevent collisions, a local planner [29] based on reinforcement learning was developed.

3. Motion Control of the STORM Module toward Self-Reconfiguration

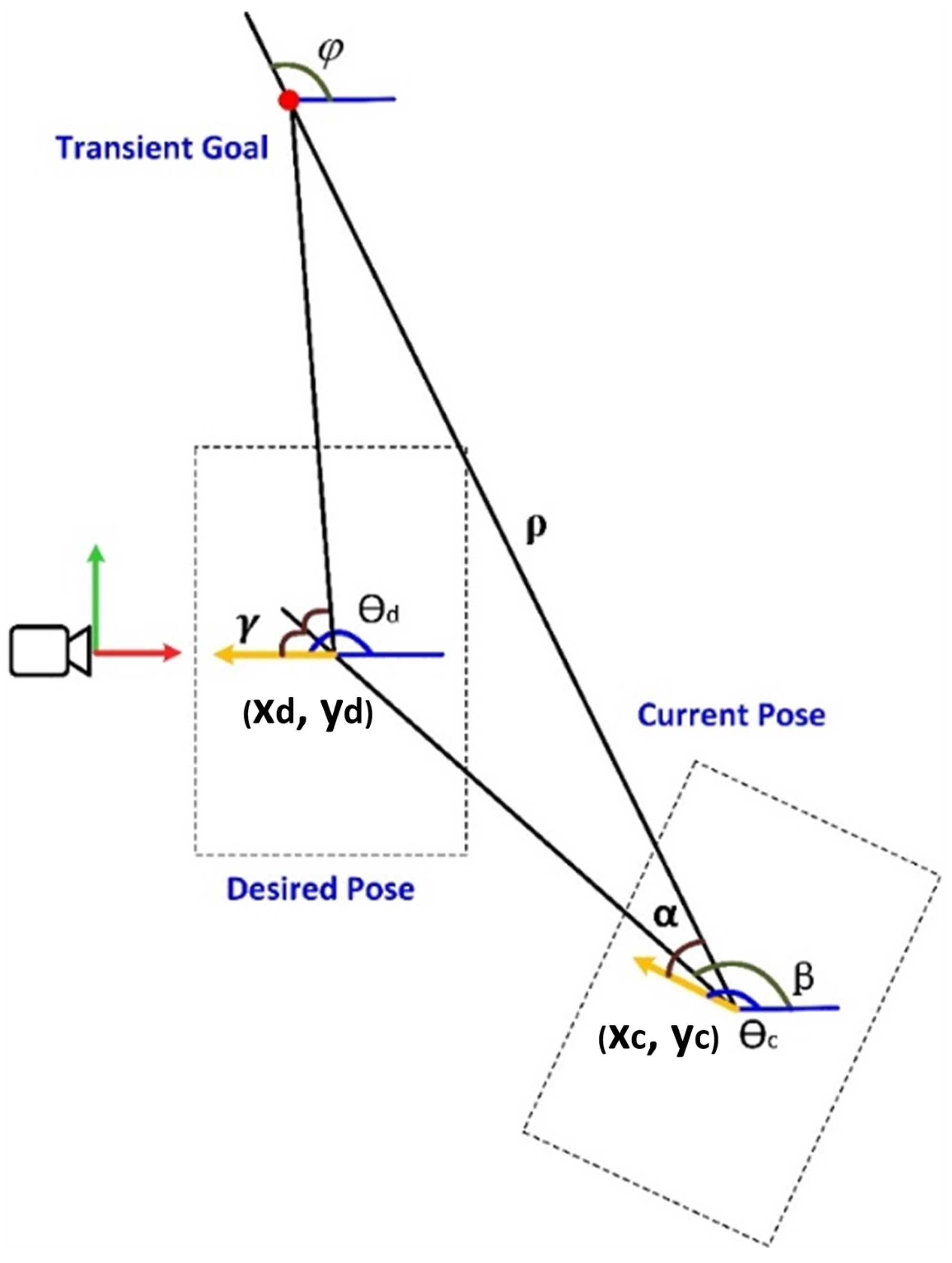
3.1. Problem Statement

To achieve autonomous docking, it is essential to develop efficient algorithms and controllers for the locomotion module. These systems must enable the module to approach the final pose while adapting to the unique characteristics of multi-directional locomotion and accommodating specific task requirements.

It is assumed that the load carrier will be stationary during the docking process. One of the locomotion modules in the lateral tracked mode should gradually approach the desired pose to align the two docking mechanisms. As shown in Figure 5, the determination of a desired pose for the locomotion module was based on the pose of the load carrier, ensuring that the two docking mechanisms align and couple together after the locomotion module reaches the target position. This task is formulated as a pose stabilization problem: the proposed controller takes the differences in pose between the current position and the desired position of the locomotion module as input and generates appropriate velocity commands for the module.

3.2. Controller Design

Addressing the complexity of minimizing the error between an initial pose and the desired pose, which includes orientation, is challenging when dealing with a target system characterized as nonlinear, nonholonomic, and under-actuated. Finding a smooth, time-invariant controller capable of globally asymptotically stabilizing the system under these conditions proves to be difficult [18,30]. In response to this challenge, we propose a solution: a Lyapunov function-based controller with a transit goal generator.

Studying robot kinematics is essential to establish the connection between the velocities of the robot and the speed of each track, facilitating the translation of commands from high-level controllers to low-level controllers. The load carrier shares the same kinematics as the locomotion module in the longitudinal tracked mode, as expressed by the following equation:

$$\dot{\mathbf{x}}=\left[\begin{array}{c}\dot{x}\\ \dot{y}\\ \dot{\theta }\end{array}\right]=\left[\begin{array}{cc}cos\theta & 0\\ sin\theta & 0\\ 0& 1\end{array}\right]\left[\begin{array}{c}v\\ \omega \end{array}\right]=\left[\begin{array}{cc}cos\theta & 0\\ sin\theta & 0\\ 0& 1\end{array}\right]\mathbf{u},$$

(1)

where v and $\omega$ are the linear and angular velocities of the locomotion module, respectively. $(x,y)$ is the current position of the robot (defined at the center of the robot) with respect to the world coordinate frame. $\theta$ is the angle between the heading of the robot and the x-axis of the world frame. $\mathbf{x}={\left[xy\theta \right]}^T$ is the state vector, and $\mathbf{u}={\left[v\omega \right]}^T$ is the control input vector. Therefore, the primary objective of the controller is to find a control input $\mathbf{u}\left(t\right)$ that makes $\underset{t\to \infty }{lim}\mathbf{x}\left(t\right)={\mathbf{x}}_d$, where ${\mathbf{x}}_d$ is the desired pose.

To prevent the scenario where the robot directly reaches the goal position without considering its heading orientation, a transient goal is generated for the robot. The transient goal generator provides alternative target positions until the robot can navigate to the goal position with the desired orientation. The overall control process is shown in Figure 6.

The transient goal generator creates a temporary goal according to the desired state ${\mathbf{x}}_d={\left[\begin{array}{ccc}{x}_d& y_d& {\theta }_d\end{array}\right]}^T$ and the current pose ${\mathbf{x}}_c={\left[\begin{array}{ccc}{x}_c& y_c& {\theta }_c\end{array}\right]}^T$ of the robot following the equation below:

$$\mathbf{G}=\left[\begin{array}{c}{x}_g\\ y_g\end{array}\right]=\left[\begin{array}{c}{x}_d\\ y_d\end{array}\right]+∥{\mathbf{e}}_1∥·\left[\begin{array}{c}cos\left(\beta +\gamma \right)\\ sin\left(\beta +\gamma \right)\end{array}\right],$$

(2)

where ${\mathbf{e}}_1={[x_d-x_c{y}_d-y_c]}^T$, $\beta ={tan}^{-1}\left(\frac{y_d-y_c}{x_d-x_c}\right)$, and $\gamma =\beta -{\theta }_d$. Figure 7 shows the location of the transient goal; as the robot gets closer to the desired position, the transient goal tends to coincide with the desired position. Throughout this process, the locomotion module operates in lateral tracked mode, and the robot’s heading is denoted by the yellow arrow in the figure. This heading has a 90-degree offset compared to the longitudinal tracked mode. The difference between the coordinates of the transient goal and the current position of the robot, ${\mathbf{e}}_2={\left[\begin{array}{cc}{x}_g-x_c& y_g-y_c\end{array}\right]}^{\mathrm{T}}$, as well as the heading angle ${\theta }_c$ of the robot, will be fed to a coordinate converter that aims to represent the robot poses in the Polar coordinate system as $\rho =∥e_2∥$ and $\alpha =\phi -{\theta }_c$, where $\phi ={tan}^{-1}\left(\frac{y_g-y_c}{x_g-x_c}\right)$. The outputs $\rho$ and $\alpha$ are the inputs to the Lyapunov function-based controller. The kinematics of the robot are first converted into polar coordinates to develop the control laws:

$$\left\{\begin{array}{c}\dot{\rho }=-vcos\alpha \\ \dot{\phi }=v\frac{sin\alpha }{\rho }\\ {\dot{\theta }}_c=\omega \end{array}\right.$$

(3)

Then, the control laws are designed to be

$$\begin{array}{c}v=k_1\rho cos\alpha \hfill \\ \omega =k_{1}sin\alpha cos\alpha +k_2\alpha \hfill \end{array},$$

(4)

where $k_1$ and $k_2$ are the gains to be analyzed and tuned to obtain a stable system. The control laws come from a positive definite quadratic form of the Lyapunov function: $\mathrm{V}={\mathrm{V}}_1+{\mathrm{V}}_2=\frac{1}{2}{\rho }^2+\frac{1}{2}{\alpha }^2$. The time derivative can be calculated as follows:

$$\dot{V}={\dot{V}}_1+{\dot{V}}_2=\rho \dot{\rho }+\alpha \dot{\alpha }=\rho (-vcos\alpha )+\alpha (v\frac{sin\alpha }{\rho }-\omega )$$

(5)

If a continuous function $V:\mathbf{U}\subseteq {\mathbb{R}}^n\to \mathbb{R}$ is positive definite such that $V\left(x\right)\to \infty$ as $∥x∥\to \infty$ and its derivative $-\dot{V}$ is positive definite, then the origin of the system is globally asymptotically stable. In order to obtain a stable system, $-\dot{V}$ must be positive definite. Let $V_1=-k_1{\rho }^2{cos}^2\alpha$ and $v=k_1\rho cos\alpha$, where $k_1>0$. Substitute v into Equation (5) and obtain ${\dot{V}}_2=\alpha (k_{1}cos\alpha sin\alpha -\omega )$, where $\omega =k_{1}sin\alpha cos\alpha +k_2\alpha$ and $k_2>0$. Therefore, the system is proved to be globally asymptotically stable at the origin.

After receiving the linear velocity v and angular velocity $\omega$ from the controller, a skid-steer robot model calculates the velocities of the right and left tracks by estimating the Instantaneous Center of Rotation (ICR) for the left and the right units [31,32], $C_2=(x_{c2},y_{c2})$ and $C_3=(x_{c3},y_{c3})$, as shown in Figure 8. Then, the velocities of the left and right tracks $v_L$ and $v_R$ can be calculated as follows:

$$\begin{array}{c}{v}_L=-\left|x_{c2}\right|\omega +v\hfill \\ v_R=\left|x_{c3}\right|\omega +v\hfill \end{array}.$$

(6)

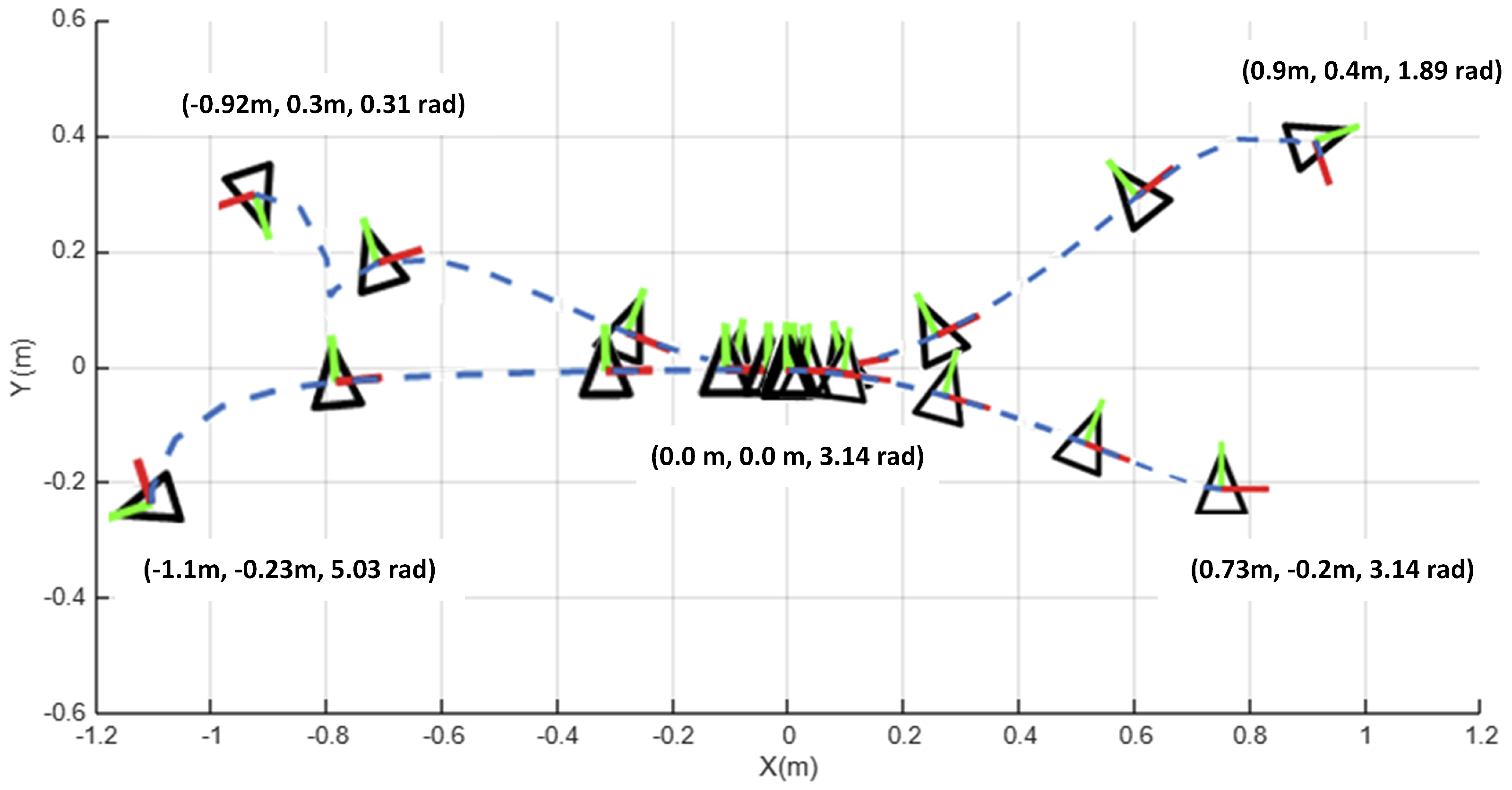
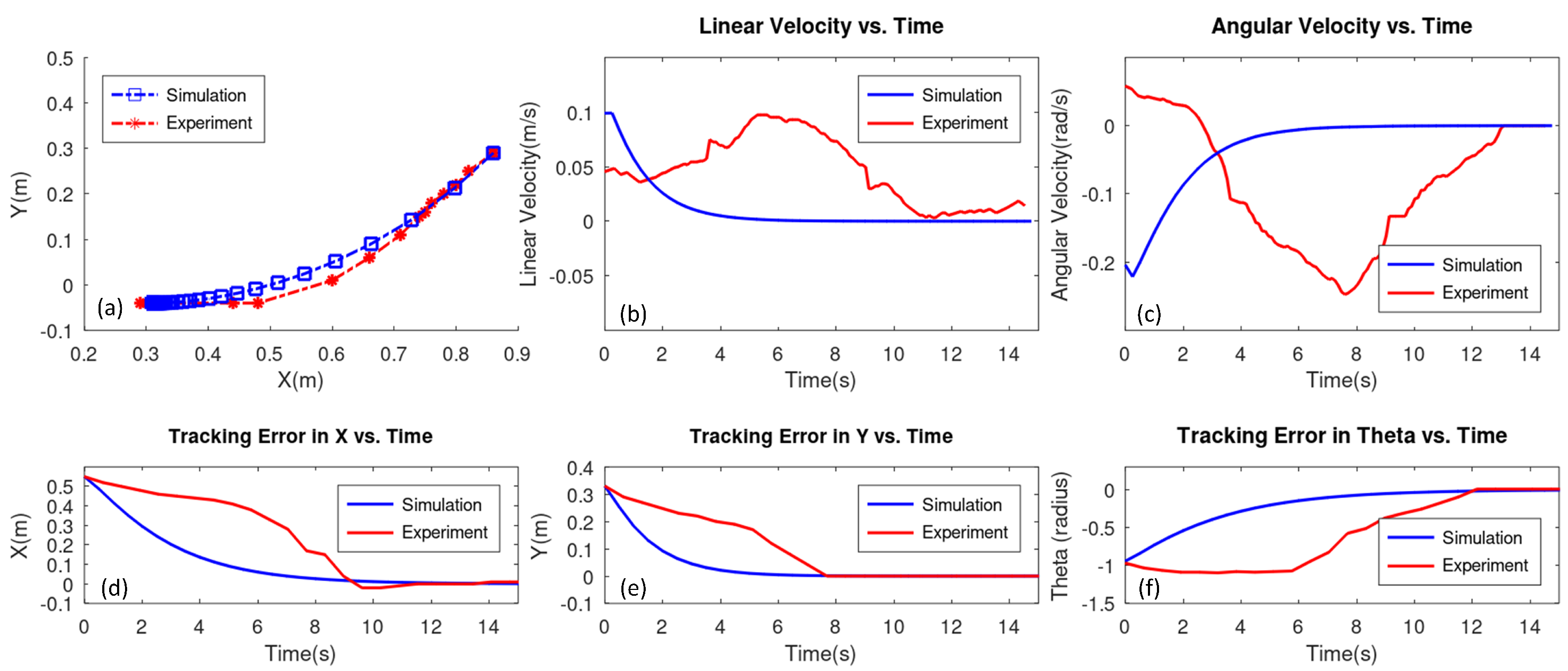
3.3. Simulation Validation

The pose stabilization controller was implemented using Simulink in MATLAB to test the feasibility and tune the parameters of the controller. The Simulink module is presented in Figure 9. The simulation’s stop time was configured to 30 s, with a time step of 0.1.

Four trajectories of the robot are plotted and presented in Figure 10 to demonstrate the performance of the controller. The desired position is set at the origin of the world frame. Four random initial positions, selected from different quadrants within 1.5 m of the target, were used to evaluate the controller. The time intervals between adjacent triangle marks on the trajectories are uniform. The results demonstrate that the robot successfully reaches the desired pose in each run. The desired position is located at the origin of the world frame. Four random initial positions were selected from different quadrants within 1.2 m of the target. It should be pointed out that the controller aims to steer the robot to a transient goal until the robot’s heading is the same as the desired pose. Since the robot allows backward motion, the desired heading of the robot should be determined according to the initial position of the robot. From the results, the robot successfully achieved the desired pose in each run.

3.4. Real-World Validation

A real-world experiment was carried out to validate the feasibility of the proposed controller and the docking process. The essential requirement for this autonomous alignment is a dependable sensing system used to accurately track the poses of the locomotion module. Apriltags [33] were utilized for localizing the locomotion module during the experiment. As shown in Figure 11, an Apriltag was positioned on the track frame of a prototype locomotion module, and a USB camera was configured to track the tag.

The experiment was designed to align the passive docking mechanism on the locomotion module with the active docking mechanism next to the camera. Subsequently, it sought to demonstrate that the docking mechanism could securely hold and rotate the locomotion module to fulfill various task requirements (Figure 11).

The ROS package $apriltag\_ros$ was utilized to publish transformations between the camera frame and the tag frame. To facilitate kinematic analysis, the output relative pose was converted from the camera frame’s relative pose to the local frame of the locomotion module. In ensuring continuous visibility, the Apriltag should remain within the camera’s field of view during autonomous alignment. Upon reaching the desired position, the Vertical Translational Mechanism (VTM) adjusted the height of the passive docking mechanism for alignment along the z-axis. Subsequently, the clamps of the active docking mechanism closed, and the locomotion module rotated 180 degrees. Following the rotation of the locomotion module by 180 degrees through the active docking mechanism, as depicted in Figure 12e, the subsequent Figure 12f shows the module positioned upside down. Given the symmetrical structure of the locomotion module, its vertical translational mechanism can adjust the lateral wheels’ position to ensure that the longitudinal tracked units maintain contact with the ground, thereby enabling longitudinal motions. While the frame remains consistent, the control commands are recalculated to take into account the information from the IMU. The robot then departed following the release of the clamps. However, it is worth noting that this study did not address the motion control problem after the docking mechanism was released. This post-releasing control will be the focus of our future work, particularly concerning aspects such as formation control.

The recorded trajectory of the autonomous alignment process was compared with that of simulation results, as shown in Figure 12. The experimental and simulation findings emphasize the controller’s proficiency in minimizing error between the current and desired pose, encompassing both position and orientation. Discrepancies between simulation and real-world outcomes can be ascribed to various factors acting as disturbances. Despite facing challenges like localization measurement errors, robot slippage, and response delay, the real-world experiment showcased the controller’s effective disturbance rejection performance. This underscores the controller’s ability to navigate unforeseen disruptions while maintaining precise pose control.

4. Trajectory Optimization and Tracking of the STORM Module to Improve the Autonomous Alignment Process

The pose stabilization controller presented in the previous section successfully maneuvered the locomotion module to the desired pose with allowable misalignments for completing the reconfiguration task. However, the prerequisite of this controller is that the locomotion module has already been at a close point to the final destination and is on the wheeled/lateral locomotion mode to perform the autonomous alignment task. Therefore, decisions on how to reach this close point and when to switch from the tracked mode to the wheeled mode are still required for the autonomous alignment task. This section presents the solution to making these decisions.

Similar to other path planning algorithms, the direct collocation method was used to find the fastest path in this study. However, the uniqueness of the solution here is that it takes the special mode-switching ability of the locomotion module into consideration and plans not only the fastest path but also the optimal switching time, which is essentially a numerical solution for the time-optimal problem of a switching system [34].

4.1. Problem Statement

In our cases, the hybrid tracked-wheeled feature of the locomotion module introduces discontinuous system dynamics. For example, the longitudinal locomotion mode, lateral locomotion mode, and the motion of the VTM are intrinsically discrete. Therefore, previous motion planning for the autonomous docking task could be divided into several sub-tasks as follows:

1.

Rough navigation to the desired position using tracks;

2.

Fine adjustment of the robot poses in lateral locomotion mode;

3.

Fine adjustment of the height of the VTM to align the docking mechanism in the Z direction;

4.

Fine adjustment of the clamps’ positions.

To find an optimal solution for the locomotion module to approach the target and choose the best position to switch the dynamics, the problem can be defined as a switched optimal control problem, and a direct collocation-based optimization method is proposed to solve this problem. To apply the direct collocation method, the continuous-time problem is converted into a nonlinear program by discretizing the trajectory into collocation points. The system dynamics are then converted into a set of constraints that apply to the state and control at the collocation points. In this way, both the state and the control variables become a finite set of decision variables.

The proposed trajectory optimization methods should plan an optimal path from the initial pose to the desired pose and determine the position for the locomotion module to switch the dynamics simultaneously. The locomotion module approaches the desired position for reconfiguration in the longitudinal tracked mode. After it arrives at the point determined by the proposed direct collocation-based path planner, the VTM will lower down the lateral tracked unit to change the locomotion mode.

Two different approaches were proposed to determine the position to switch the dynamics. When optimizing the trajectories, the mobile robot is considered an ideal agent moving on flat ground, and there is no slippage between the robot and the ground. The robot dynamics are fully described by the following two dynamics, which correspond to the track and wheel modes. The disturbances from uneven terrain and the robot’s slipperiness are taken into consideration when tracking the trajectory.

4.2. Problem Formulation

The trajectory optimization aims to discover an optimal path according to an objective function that mathematically describes what the best solution should be. In general, an objective function can be defined in Bolza form:

$$J(t_0,t_f,\mathbf{x}\left(t\right),\mathbf{u}\left(t\right))={\int }_{t_0}^{t_f}l(t,\mathbf{x}\left(t\right),\mathbf{u}\left(t\right))dt+g(t_0,t_f,\mathbf{x}\left(t_0\right),\mathbf{x}\left(t_f\right)),$$

(7)

where the state $\mathbf{x}\in {\mathbb{R}}^n$, control $\mathbf{u}\in {\mathbb{R}}^m$, and the initial and final time points $(t_0,t_f)$ are considered the decision variables. The integral of $l:\mathbb{R}\times {\mathbb{R}}^n\times {\mathbb{R}}^m\to \mathbb{R}$ defines the running cost, and the function $g:\mathbb{R}\times \mathbb{R}\times {\mathbb{R}}^n\times {\mathbb{R}}^n\to \mathbb{R}$ defines the boundary objective. If $l\equiv 0$, the problem is said to be in Mayer form. If $g\equiv 0$, it becomes a Lagrange problem. In our case, the best solution is defined as the fastest path from the initial point to the final position, and the objective function is in Lagrange form:

$$J={\int }_{t_0}^{t_f}1dt,$$

(8)

The locomotion module is a hybrid system with discontinuous dynamics. Generally, these control systems have two types of switching behaviors [34,35]. One is the autonomous or uncontrolled switch without the influence from a separate switching mechanism. The second type of switch can be controlled directly, as the switch between the longitudinal tracked mode and vertical tracked mode through the VTM of the locomotion module. In our case, the switch of the system will happen only once during the entire autonomous alignment process. The state variables for the hybrid system are $\mathbf{x}={\left[xy\theta \right]}^T$, where x and y represent the position of the locomotion module in the $\left\{XOY\right\}$ plane, and $\theta$ is the direction of the heading of the locomotion module. The control inputs are $\mathbf{u}={\left[v\omega \right]}^T$, where v and $\omega$ are the linear and angular speeds of the locomotion module, respectively. Before switching, the system dynamics of the locomotion module in the longitudinal tracked mode can be formulated as follows:

$$f_1=\dot{\mathbf{x}}=\left[\begin{array}{c}\dot{x}\\ \dot{y}\\ \dot{\theta }\end{array}\right]=\left[\begin{array}{cc}cos\theta & 0\\ sin\theta & 0\\ 0& 1\end{array}\right]\left[\begin{array}{c}v\\ \omega \end{array}\right]$$

(9)

After switching, the system dynamics of the locomotion module in the lateral tracked mode become

$$f_2=\dot{\mathbf{x}}=\left[\begin{array}{c}\dot{x}\\ \dot{y}\\ \dot{\theta }\end{array}\right]=\left[\begin{array}{cc}cos(\theta +\frac{\pi }{2})& 0\\ sin(\theta +\frac{\pi }{2})& 0\\ 0& 1\end{array}\right]\left[\begin{array}{c}v\\ \omega \end{array}\right].$$

(10)

Then, the problem can be formulated as follows:

$$\begin{array}{c}\mathrm{minimize}J\hfill \\ \mathrm{subject}\mathrm{to}:\hfill \\ \mathrm{dynamics}:\dot{\mathbf{x}}\left(t\right)=\left\{\begin{array}{ccc}{f}_1(\mathbf{x}\left(t\right),\mathbf{u}\left(t\right))& & t⩽t_s\\ f_2(\mathbf{x}\left(t\right),\mathbf{u}\left(t\right))& & t>t_s\end{array}\right.\hfill \\ \mathrm{boundary}\mathrm{constraints}:\mathbf{x}\left(0\right)={\mathbf{x}}_0,\mathbf{x}\left(t_f\right)={\mathbf{x}}_f\hfill \\ \mathrm{path}\mathrm{constraints}:-{\mathbf{x}}_{max}⩽\mathbf{x}⩽{\mathbf{x}}_{max},-{\mathbf{u}}_{max}⩽\mathbf{u}⩽{\mathbf{u}}_{max}\hfill \end{array}$$

(11)

4.3. Proposed Solution

The first step to solve the optimization problem is to define the collocation points by discretizing the trajectory into a finite set of decision variables according to the following steps:

1.

Partition the time interval T into M+N subintervals to compute a piecewise constant control sequence $\{{\mathbf{u}}_{1,1},{\mathbf{u}}_{1,2},\cdots ,{\mathbf{u}}_{1,M}\}$ and $\{{\mathbf{u}}_{2,M+1},{\mathbf{u}}_{2,M+2},\cdots ,{\mathbf{u}}_{2,M+N}\}$; then, the corresponding states at the collocation points are defined as $\{{\mathbf{x}}_1,{\mathbf{x}}_2,\cdots ,{\mathbf{x}}_{M+N}\}$.

2.

Convert the system dynamics into collocation constraints, as follows:

(a)

The dynamics can be constructed in integral form:

$$\left\{\begin{array}{ccc}{\int }_{t_k}^{t_{k+1}}\dot{\mathbf{x}}dt={\int }_{t_k}^{t_{k+1}}{f}_{1}dt& & k=\{1,2,\cdots ,M-1\}\\ {\int }_{t_k}^{t_{k+1}}\dot{\mathbf{x}}dt={\int }_{t_k}^{t_{k+1}}{f}_{2}dt& & k=\{M,\cdots ,M+N-1\}\end{array}\right.,$$

(12)

(b)

Then, the discretized system dynamics can be approximated using trapezoidal quadrature. The approximation is applied between every pair of collocation points as follows:

$$\left\{\begin{array}{ccc}{\mathbf{x}}_{k+1}-{\mathbf{x}}_k=\frac{1}{2}{h}_k(f_{1,k+1}+f_{1,k})& & k=\{1,2,\cdots ,M-1\}\\ {\mathbf{x}}_{k+1}-{\mathbf{x}}_k=\frac{1}{2}{h}_k(f_{2,k+1}+f_{2,k})& & k=\{M,\cdots ,M+N-1\}\end{array}\right.,$$

(13)

where $h_k=t_{k+1}-t_k$ and $t_k$ is the time at collocation point k. Then, the system dynamics at each collocation point become

$$\left\{\begin{array}{ccc}{f}_{1,k}=f_1(t_k,{\mathbf{x}}_k,{\mathbf{u}}_k)& & k=\{1,2,\cdots ,M\}\\ f_{2,k}=f_2(t_k,{\mathbf{x}}_k,{\mathbf{u}}_k)& & k=\{M+1,\cdots M+N\}\end{array}\right.,$$

(14)

where $t_k$, $x_k$, and $u_k$ are the decision variables in the nonlinear program.

3.

Enforce the path constrains at each collocation point—${-\mathbf{x}}_{max}⩽{\mathbf{x}}_k⩽{\mathbf{x}}_{max},{-\mathbf{u}}_{max}⩽{\mathbf{u}}_k⩽{\mathbf{u}}_{max}$—and the boundary constraints should be enforced at the first and the last collocation points.

4.

Find the approximate objective function using the trapezoid rule as follows:

$${\int }_{t_0}^{t_f}l(t,\mathbf{x}\left(t\right),\mathbf{u}\left(t\right))\approx \sum _0^{M+N-1}\frac{1}{2}{h}_k(l_k+l_{k+1})$$

(15)

where $l_k$ and $l_{k+1}$ are the costs at points k and $k+1$. In following the procedures above, the switching dynamics are enforced at the specific collocation point M. However, a further analysis of the timing to change the dynamics is required. Two different methods were utilized to determine the switching point. In the first method, a fixed time interval is set, the switching point at different collocation points is gradually chosen, and the nonlinear program with different switching points to obtain $M+N-1$ paths is solved. Then, the fastest path is selected as the final solution. For convenience, this approach is referred to as the “discrete method” in the following discussion since it mainly optimizes on the discrete collocation points. The second method is to define different time intervals $\Delta t_1$ and $\Delta t_2$ for the two different dynamics. This approach enables us to determine the optimal timing of the switching point by solving the nonlinear programming only once. This method is referred to as the “continuous method” since it mainly optimizes on the continuous time variable. In this method, the objective function becomes

$${\int }_{t_0}^{t_f}l(t,\mathbf{x}\left(t\right),\mathbf{u}\left(t\right))\approx \sum _0^{M-1}\frac{1}{2}\Delta t_1(l_i+l_{i+1})+\sum _M^{M+N-1}\frac{1}{2}\Delta t_2(l_j+l_{j+1})$$

(16)

where $M\in \mathbb{Z}:0⩽M⩽N-2$, and $N\in \mathbb{Z}:N⩾M+1$ are predefined constant values. $l_i$ and $l_{i+1}$ represent the costs at point i and $i+1$ for the longitudinal tracked mode, while $l_j$ and $l_{j+1}$ denote the costs at point j and $j+1$ for the lateral locomotion mode.

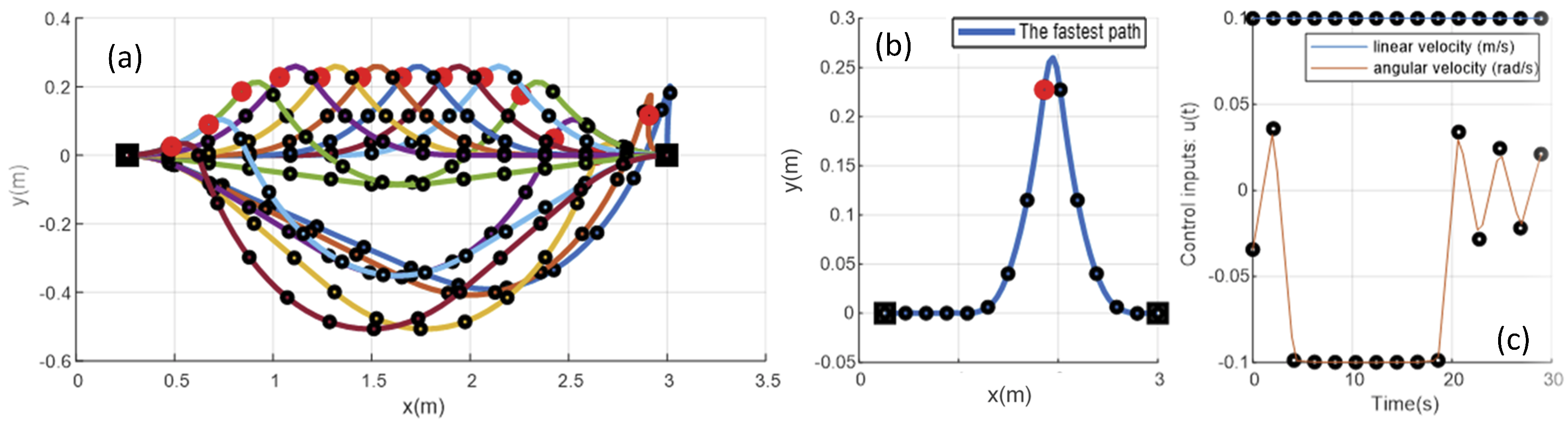
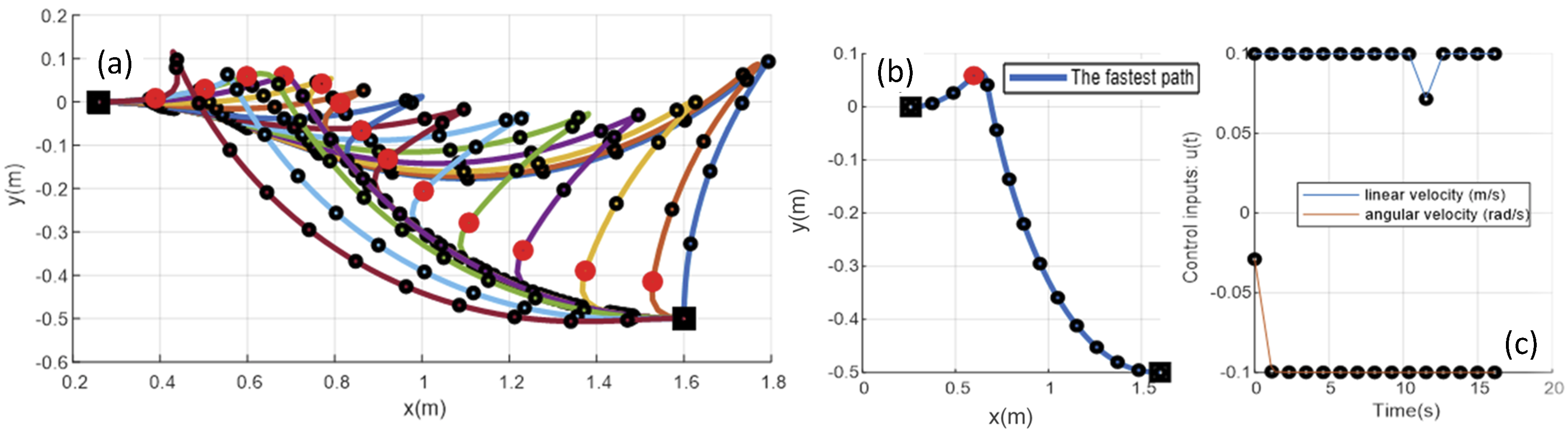
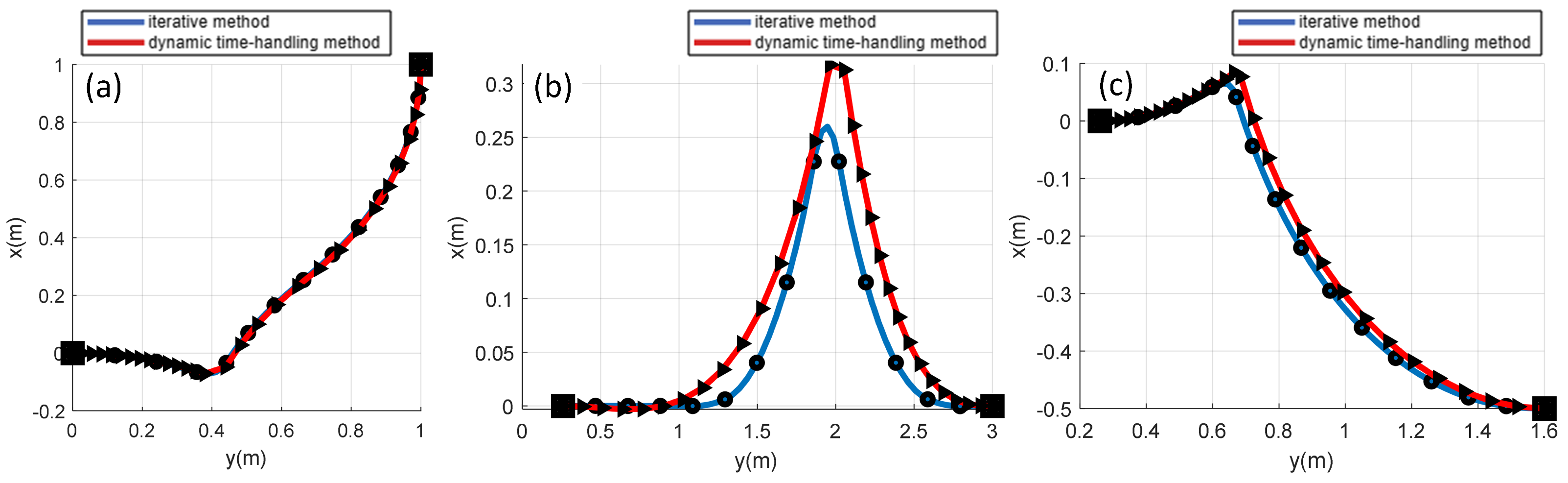
4.4. Numerical Results

The proposed direct collocation-based method for solving an optimal path with a proper switching position was implemented in Matlab using the fmincon solver. As mentioned in Section 4.3, two different approaches were developed to solve the problems. Figure 13, Figure 14 and Figure 15 show the results from the first iterative method (the “discrete method”) in which fifteen collocation points were defined and the switching point was enforced at the first collocation point to the fourteenth points successively. This was to ensure that the robot module will be in the lateral tracked mode in the end.

Different sets of boundary and path constraints were chosen to assess the proposed method. In Figure 13a, all optimal paths are presented under uniform boundary conditions: ${\mathbf{x}}_{\mathbf{0}}$ = (0 m, 0 m, 0 rad) and ${\mathbf{x}}_{\mathbf{f}}$ = (1 m, 1 m, 0 rad), control constraints ${\mathbf{u}}_{\mathbf{max}}$ = (0.5 m/s, 0.5 rad/s), and consistent dynamic constraints. The switching points are marked with red dots. Figure 13b illustrates the fastest path, while Figure 13c demonstrates the control signals required for achieving the optimal trajectory. Similarly, Figure 14 displays results with the initial position set to ${\mathbf{x}}_{\mathbf{0}}$ = (3 m, 0 m, $\pi$ rad), final pose at ${\mathbf{x}}_{\mathbf{f}}$ = (1 m, 1 m, 0 rad), and boundary control inputs ${\mathbf{u}}_{\mathbf{max}}$ = (0.1 m/s, 0.1 rad/s). The boundary conditions for the results shown in Figure 15 are ${\mathbf{x}}_{\mathbf{0}}$ = (1.6 m, −0.5 m, $\pi$ rad), ${\mathbf{x}}_{\mathbf{f}}$ = (0.26 m, 0 m, 0.5$\pi$ rad), and ${\mathbf{u}}_{\mathbf{max}}$ = (0.1 m/s, 0.1 rad/s). In summary, this study shows that the proposed method effectively handles different boundary and path constraints for trajectory optimization.

Additionally, this study evaluated the results obtained from the second method (the “continuous method”), as described in Section 4.3, which formulates the objective function using different time intervals for the two dynamic constraints, under the same boundary conditions as those utilized in the first method. The outcomes from each method were compared, as illustrated in Figure 16. Despite slight variations, the comparison reveals that the optimal trajectories from different methods largely align. In conclusion, the findings across all tests successfully identify the optimal trajectory that satisfies all constraints, including a switching point to adapt dynamics. This underscores the practicality and efficiency of the proposed direct collocation-based optimization approach for path planning in hybrid systems. Moreover, the novel trajectory optimization method demonstrated its feasibility in planning a time-optimal path and determining the optimal timing for switching robot dynamics. Future real-world tests will be conducted to further analyze the effectiveness of the planner.

It is worth noting that the control inputs obtained from both methods show bang-bang control characteristics, which are commonly found in optimal control problems, especially in minimum time problems (or shortest path problems with a bounded speed range). One similar example is the classic Dubins shortest path problem [36,37] wherein the optimal path is found to consist of line segments and arcs (which are generated by saturating its steering control, i.e., fully steering to the left or the right).

5. Conclusion and Future Work

This paper introduced autonomous alignment and docking control for a self-reconfigurable modular robotic system. An overview of the proposed robotic system is provided, and simulations in CoppeliaSim validated its adaptability to various terrains through reconfiguration. A Lyapunov function-based pose stabilization controller was developed and verified in MATLAB simulations for autonomous alignment. Experimental validation was conducted, showcasing the locomotion module’s ability to locate, dock, flip, and drive away from a standalone docking mechanism.

In taking into account the unique mode-switching ability of the modular mobile robot, an optimization approach was introduced to assist the locomotion module in determining the optimal position for switching dynamics and achieving an optimal trajectory for autonomous alignment.

Future work will focus on further analysis and validation. Mechanical design improvements, such as enhanced packaging space, smooth operation, and the increased durability of the active docking mechanism, are envisioned. Prototypes will be manufactured for testing. On the software side, algorithms and controllers will be extended for multiple-robot architectures and implemented on prototype robot modules for real-world experiments.

The current locomotion module can adjust its pose during autonomous alignment, but there are limitations in roll direction adjustments. Experiments assumed reconfiguration on relatively flat terrain within allowable misalignment limits. Future improvements may involve designing a Vertical Translational Mechanism (VTM) capable of rotating tracks to adjust the roll, enhancing the reconfiguration capabilities for challenging terrains.