Real-Time 3D Map Building in a Mobile Robot System with Low-Bandwidth Communication
Abstract
:1. Introduction
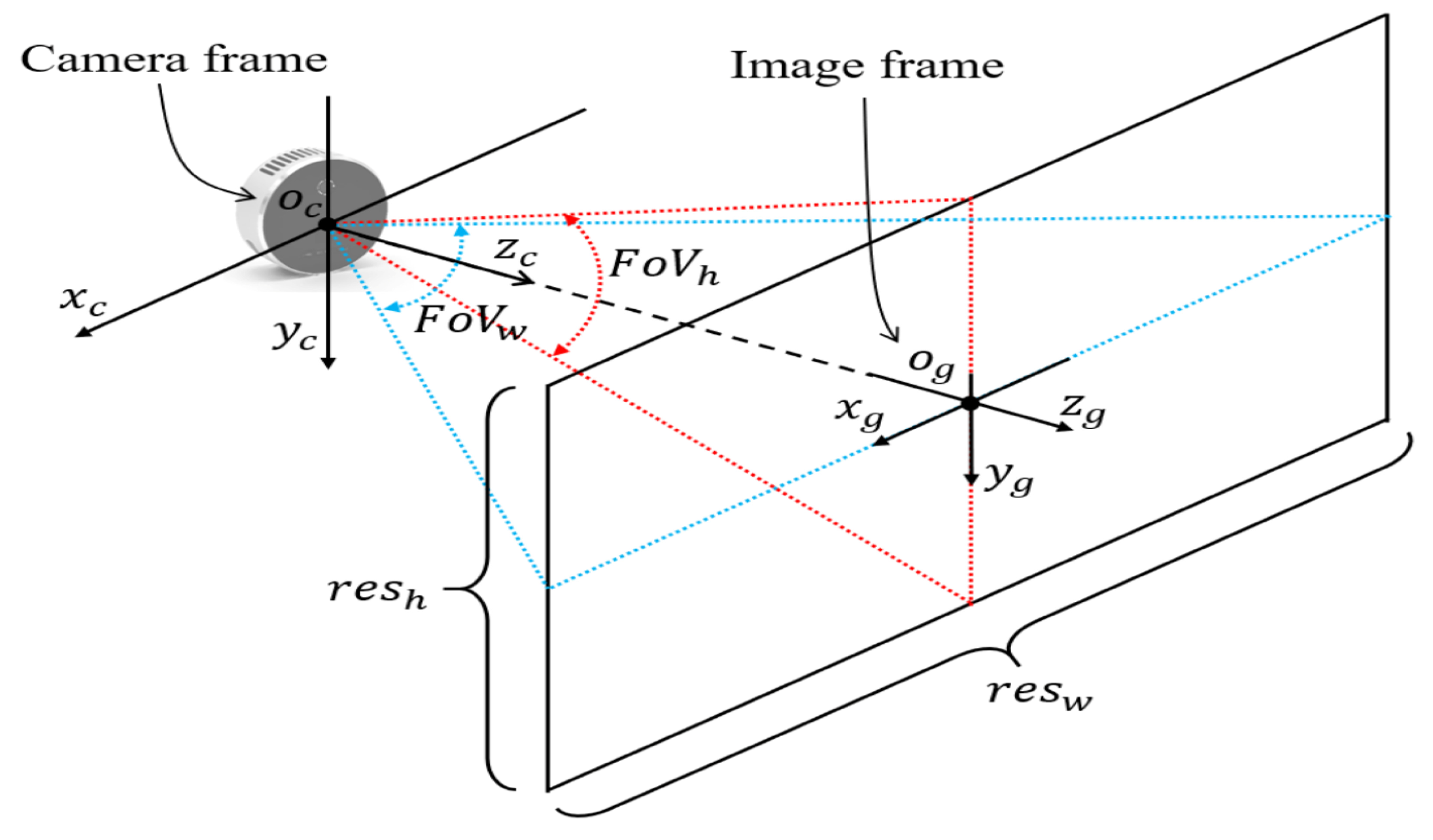
2. System Configuration
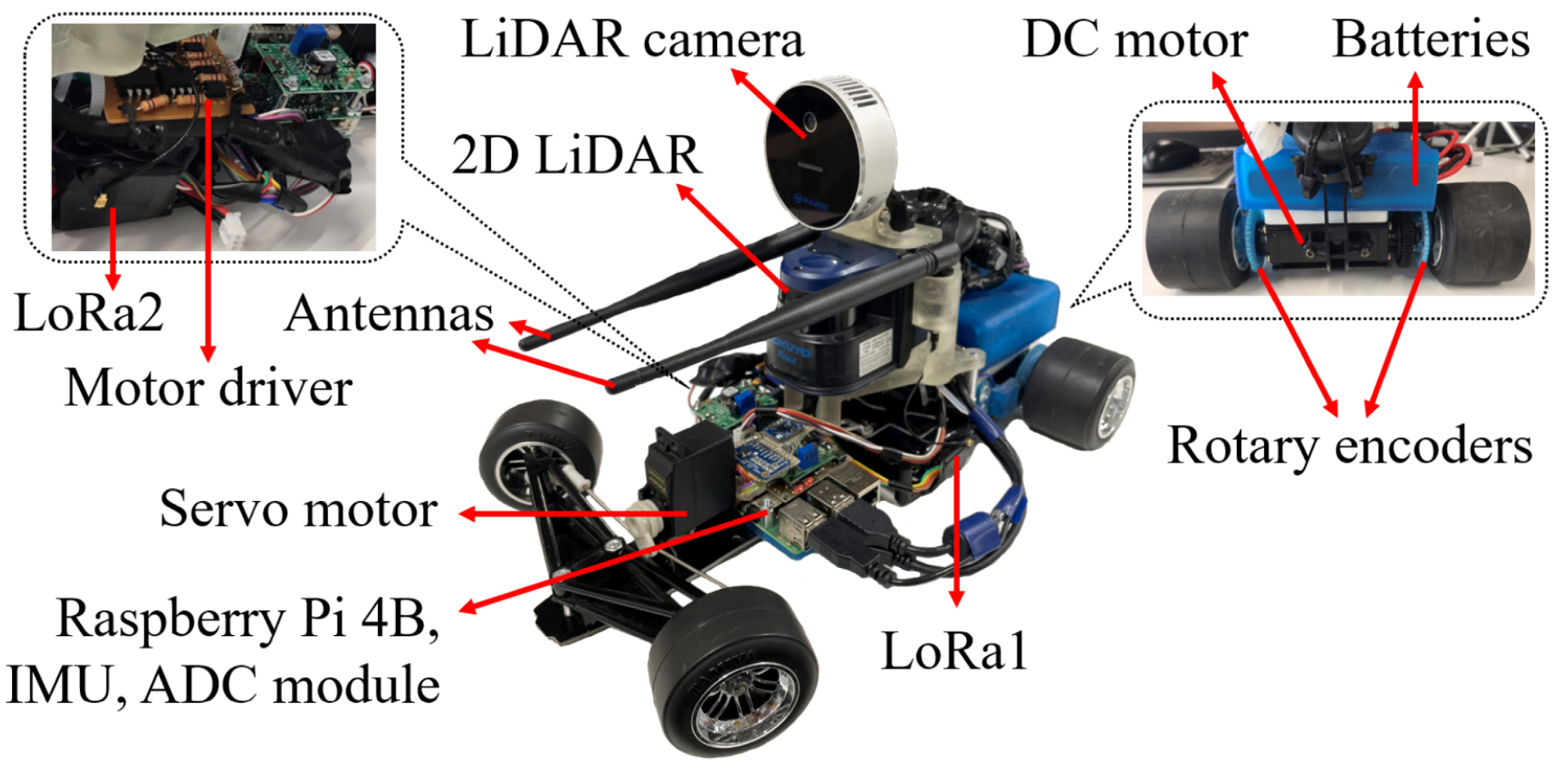
2.1. Hardware Design
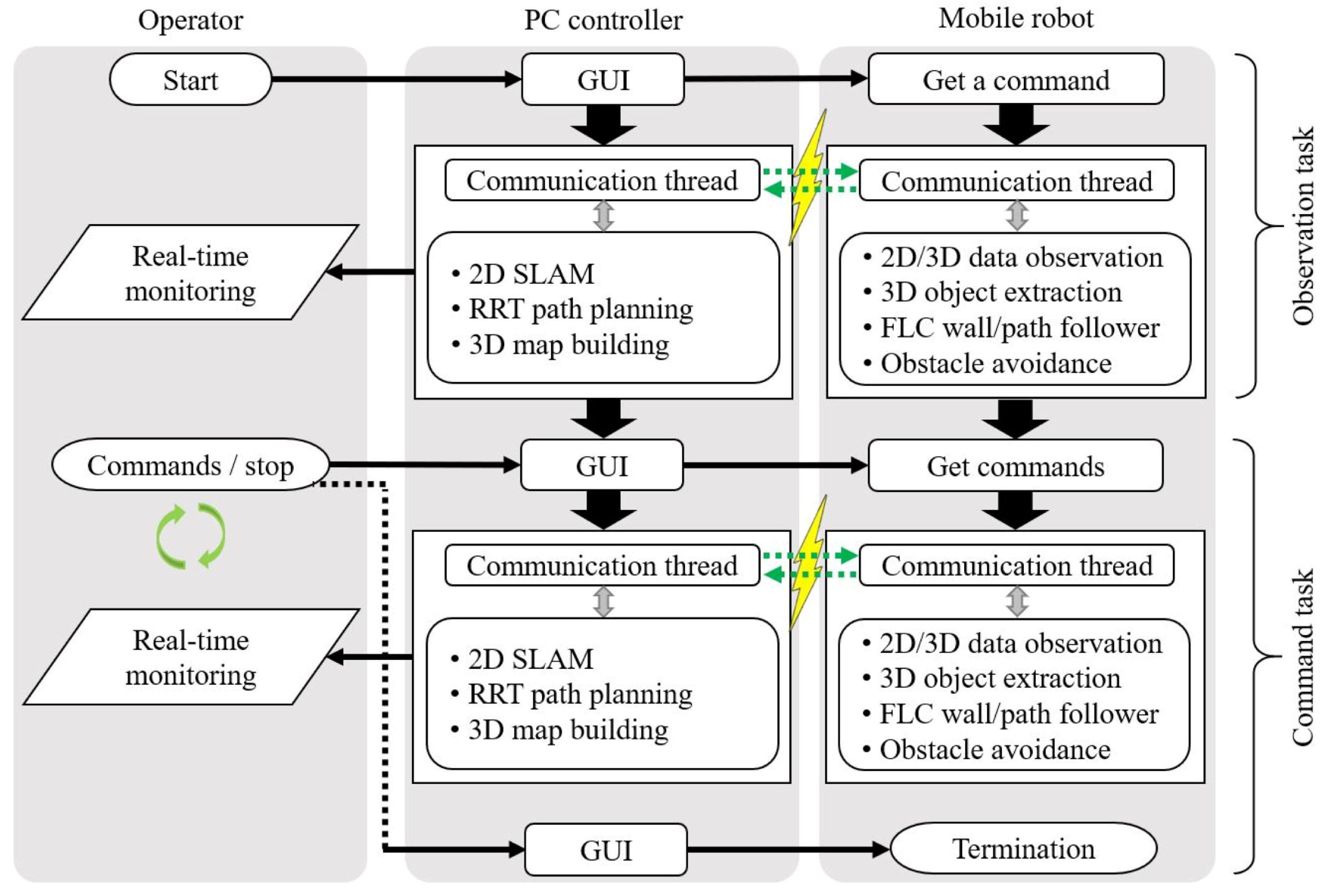
2.2. Software Design
2.3. Experimental Environment
3. Proposed Approach
3.1. 2D Simultaneous Localization and Mapping (SLAM)
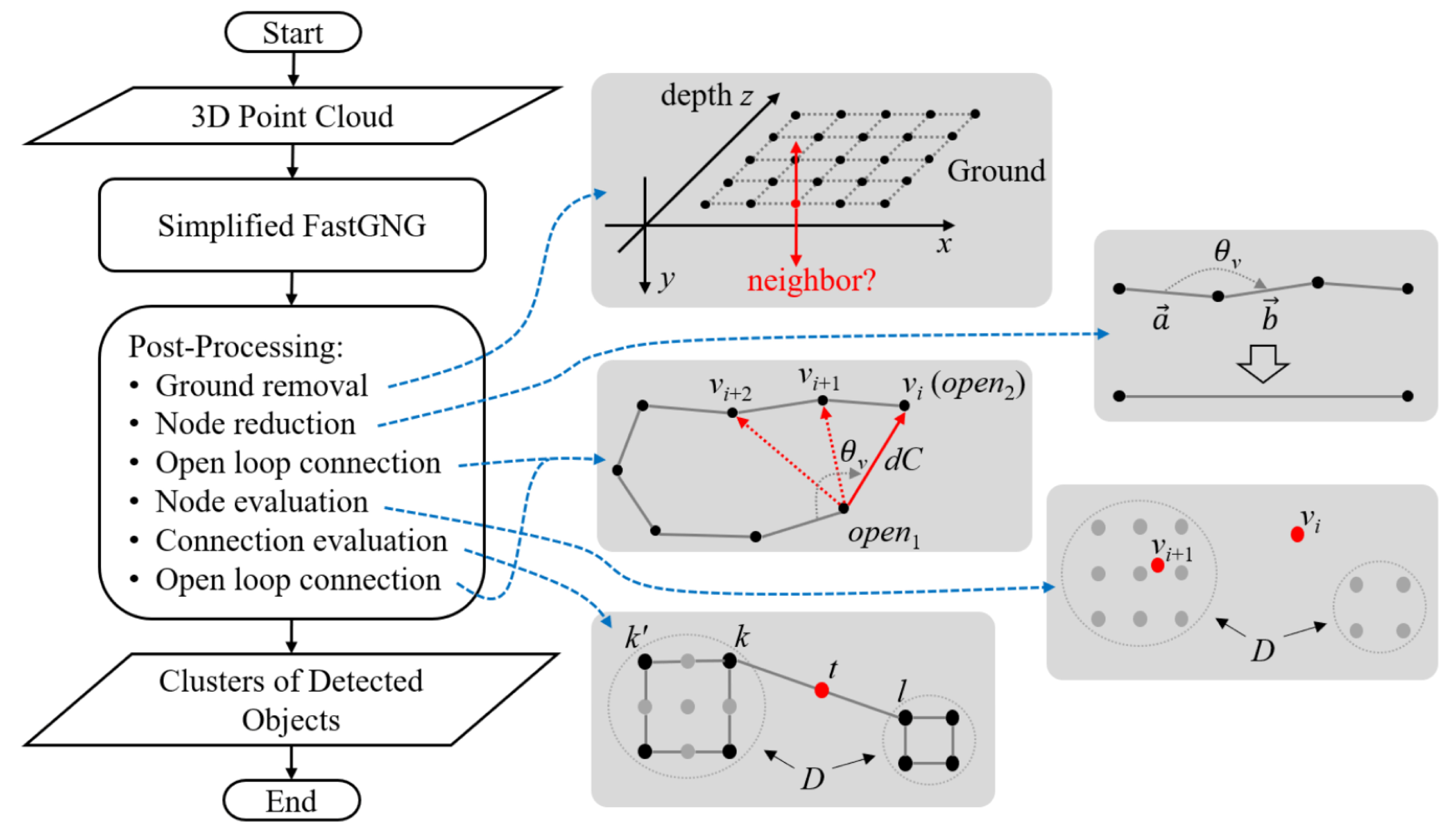
3.2. 3D Object Extraction
- : a set of 3D point cloud data (input);
- : a set of sample nodes;
- : a 3D vector of i-th node;
- : a connection between i-th and j-th node;
- : an internal loop parameter of the algorithm;
- : parameters to set the minimum and maximum connection length;
- : the probability of a sample v is the edge, v is a 3D vector;
- : the probability of adding a sample v to the network.
- Step 1.
- Generate a set of sample nodes using . This generates edge nodes of the depth input to simplify the learning process. The left, right, top, and bottom node of v should be known. is a constant. The higher the value, the higher the difference in value between the edge node and the non-edge node. Hence, making it easier to extract the edge nodes.
- Step 2.
- Generate two nodes using and connect them. Initially, set and to any proper value with a constant , where a higher value results in a higher probability value. Then, initialize the phase level iP to 1.
- Step 3.
- Initialize the internal loop counter iL to 0 and calculate the , , and L.where , , and (i = {1, 2, 3}) are constants for , , and L, respectively. We set higher values of , , and lower values of for a lower phase. Thus, and values are the opposite of the phase level iP. This will speed up the learning process in the first phase, and be slower but more detailed in the higher phases. #A is the number of sample nodes.
- Step 4.
- Generate a new node v using (12) and increase the loop counter iL. Then, calculate the nearest node (13) and the second nearest node .
- Step 5.
- Add the new node v (step 4) to the network with a new index r, and update the connection c. Skip the connection if it already exists. Go to step 4 if iL is less than L.
- Step 6.
- If there are nodes having more than two connections, remove the longest connection. Repeat the removal process until all nodes have a maximum of two connections.
- Step 7.
- As a result of the connection deletion in step 6, remove the nodes having no connection at all, and increase the phase level iP. Stop the process when the stopping criteria are satisfied or iP is more than the max_phase parameter. Otherwise, return to step 3.
3.2.1. Ground Removal
3.2.2. Node Reduction
3.2.3. Open Loop Connection
3.2.4. Node Evaluation
3.2.5. Connection Evaluation
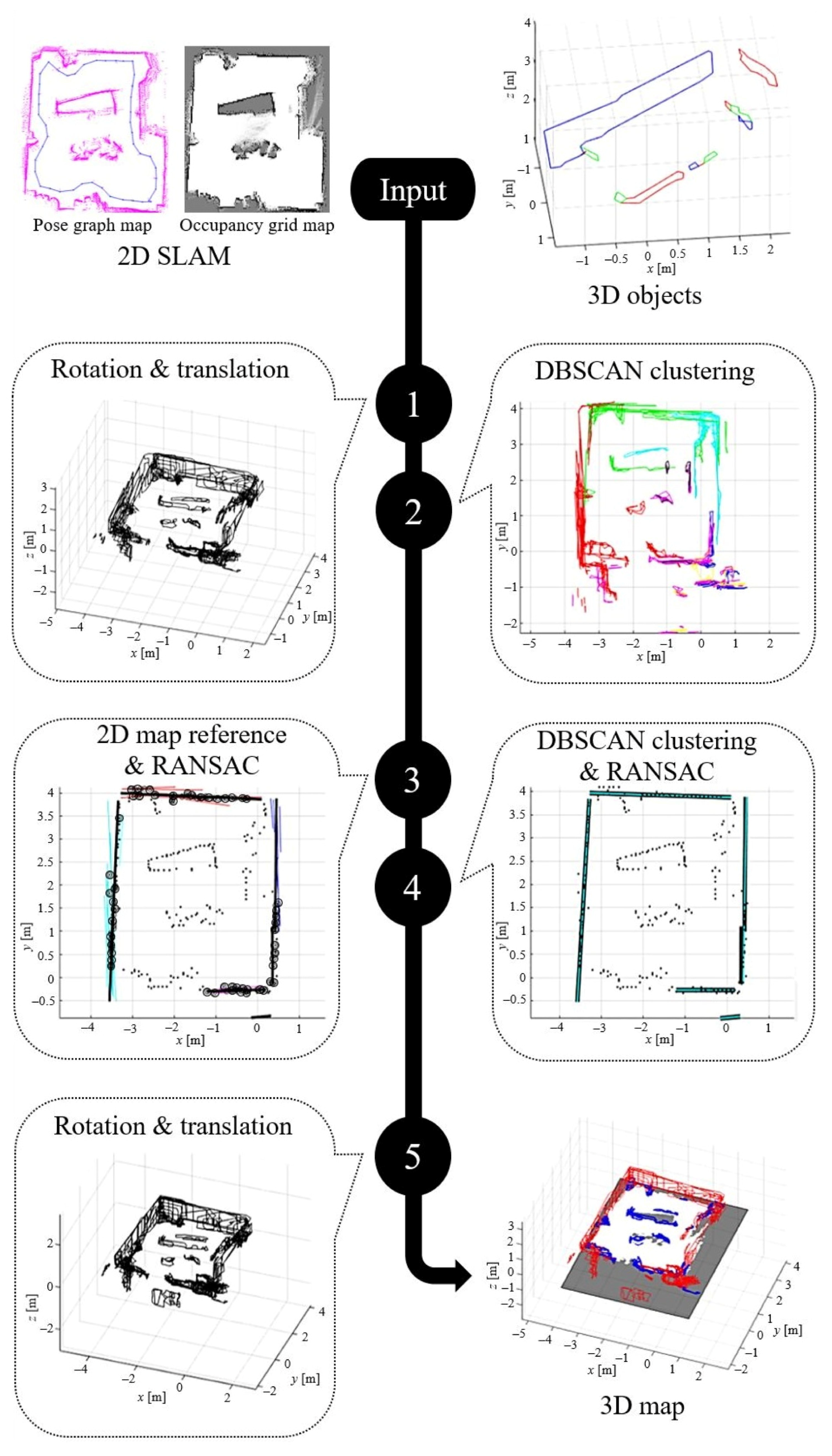
3.3. 2D–3D Combination
- Step 1.
- The pose graph map of 2D SLAM generates the orientations () and 2D position (txi, tyi) that are used for the input references of the rotation (34) and translation (35), respectively. tzi are always zero as the mobile robot only moves on a 2D slat surface.In the equation, x, y, and z are the node coordinates of 3D objects. Meanwhile, the double-apostrophe values are the results of this step. The rotation is completed first, and then followed by the translation.
- Step 2.
- A density-based spatial clustering of application with noise (DBSCAN) is performed to make a correction of the first rotation and translation results. From the top point of view, a single 3D object may have an L-shape or a non-linear shape. Therefore, a density-based clustering algorithm is needed, and DBSCAN is a pioneer of density-based clustering algorithms [48]. DBSCAN is still being adopted in modern techniques due to its simplicity and compactness for topological clustering applications [49]. The DBSCAN clustering is explained in Algorithm 1. In this method, we convert every 3D object into a 2D line from the top point of view. It simplifies the clustering method since the z values are always correct. The mobile robot never moves on the z-axes. Thus, only x and y values need to be corrected. There are several parameters used in the DBSCAN clustering, such as minObj for a minimum number of objects, dEps for minimum search radius, and thetaTh for rotation threshold. The object rotation angle is calculated using its gradient value (36), and the distance between objects is calculated using the Euclidean distance (37).where P1 and P2 are two points in a single object as an xy-line. The output of this step is the clusterObj (colored lines in Figure 11 step 2) that will be used in the next step, and noiseObj (black lines in Figure 11 step 2) that is removed from the map result.
- Step 3.
- The pose graph map of 2D SLAM only generates orientations and positions of the individual map displacements. In other words, they are the mobile robot orientations and positions when scanning the environment or capturing the data. Therefore, to generate a 2D map reference, the occupancy grid map from 2D SLAM is used, as shown in Figure 12. It is generated based on the values of the occupancy grid map, where empty space is represented by low values (near 0), occupied space has high values (near 1), and untraveled space is between 0 and 1 (0.5 initially). We set 0.750 as the threshold to generate the 2D map reference. All nodes of the 2D map reference are then compared to the DBSCAN clustering result. By using a specific threshold, i.e., the Euclidean distance, these nodes can all be known to which DBSCAN cluster they belong. They are shown as black circles in Figure 11 step 3.
Algorithm 1: DBSCAN Clustering Input:sampleObj, thetaTh, dEps, minObj Output:clusterObj, noiseObj clusterObj ← Null noiseObj ← Null while True do temp_clust ← random(sampleObj) isUpdate ← True; l_start ← 1; l_stop ← 1 while isUpdate do isUpdate ← False for i ← l_start to l_stop do core ← temp_clusti for j ← 1 to numOf(sampleObj) do if |sampleObjj.θ – core.θ| ≤ thetaTh and distEuc(sampleObjj, core.xy) ≤ dEps then temp_clust.add(sampleObjj) isUpdate ← True end if end for end for l_start ← l_stop + 1 l_stop ← numOf(temp_clust) end while if numOf(temp_clust) ≥ minObj then clusterObj.add(temp_clust) else if numOf(temp_clust) = 1 then noiseObj.add(temp_clust) else clusterObj.add(temp_clust) end if end if if numOf(noiseObj) + numOf(clusterObj) = numOf(sampleObj) then break end if end while return clusterObj, noiseObj Random sample consensus (RANSAC) [50] is then performed to generate 2D reference lines (black lines in Figure 11 step 3) based on the 2D map reference and the cluster. The line equations used in the RANSAC are as follows;The slope is calculated using the gradient value of two sample points, (x1, y1) and (x2, y2). Then, its y-intercept can be known from the sample point (), and its angle can be known from the value. This process is also explained in Algorithm 2. - Step 4.
- In this step, DBSCAN clustering is performed to the RANSAC results of step 3. It generates new clusters for the 2D map reference nodes as a correction of the previous results. Next, RANSAC is applied to the new clusters to generate new 2D reference lines (light blue lines in Figure 11 step 4). These 2D reference lines are used as the final references to rotate and translate all 3D objects in the last step.
- Step 5.
- All 3D objects are re-rotated and re-translated using the last references from step 4. It is a correction of the rotation and translation in the first step. Finally, ground information from the occupancy grid map of 2D SLAM is combined with the result of this step. This is the final rendering result of 3D surface reconstruction, as shown in Figure 11.
3.4. Communication System
| Algorithm 2: RANSAC |
| Input:sampleData, maxIteration, inliersTh |
| Output:bestM, bestB, bestTheta |
| maxInliers ← –1 |
| fori ← 1 to maxIteration do |
| rand1 ← random(sampleData) |
| rand2 ← random(sampleData) |
| while rand1 = rand2 do |
| rand2 ← random(sampleData) |
| end while |
| mrsc ← |
| brsc ← rand1.y – mrsc rand1.x |
| θrsc ← |
| countInliers ← 0 |
| for j ← 1 to length(sampleData) do |
| if |θrsc| ≤ 45.0 then |
| newX ← sampleDataj.x |
| newY ← mrsc newX + brsc |
| else |
| newY ← sampleDataj.y |
| newX ← |
| end if |
| dist ← distEuc(new.XY, sampleDataj) |
| if dist ≤ inliersTh then |
| countInliers ← countInliers + 1 |
| end if |
| end for |
| if countInliers > maxInliers then |
| maxInliers ← countInliers |
| bestM ← mrsc |
| bestB ← brsc |
| bestTheta ← θrsc |
| end if |
| end for |
| return bestM, bestB, bestTheta |
| Algorithm 3: Connection Manager |
| Input:IPaddr, tcpPort, tcpTimeout, comPort, serBaud, serTimeout |
| Output:cFlag |
| connTCP ← tcpconfig(IPaddr, tcpPort, tcpTimeout) |
| connSer ← serconfig(comPort, serBaud, serTimeout) |
| cFlag ← 1 |
| while True do |
| if cFlag = 1 then |
| try |
| funcTxRx(connTCP) |
| catch |
| cFlag ← 0 |
| end try |
| else |
| funcTxRx(connSer) |
| end if |
| end while |
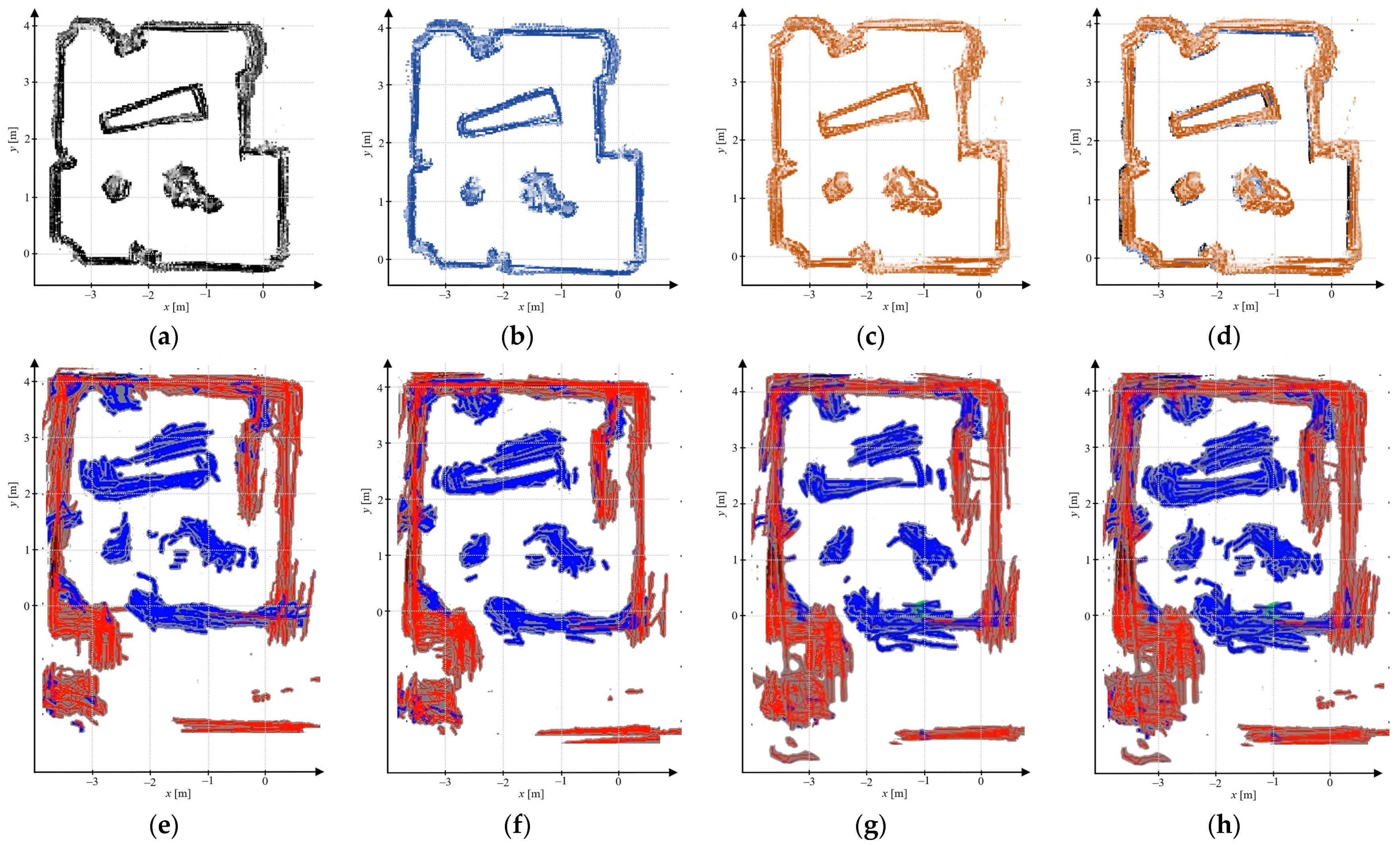
4. Results and Discussion
4.1. 3D Object Extraction Evaluation
4.2. Real-Time Experimental Results
4.3. Discussion
5. Conclusions
Supplementary Materials
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Guo, B.; Dai, H.; Li, Z.; Huang, W. Efficient planar surface-based 3D mapping method for mobile robots using stereo vision. IEEE Access 2019, 7, 73593–73601. [Google Scholar] [CrossRef]
- Schwarz, M.; Rodehutskors, T.; Droeschel, D.; Beul, M.; Schreiber, M.; Araslanov, N.; Ivanov, I.; Lenz, C.; Razlaw, J.; Schuller, S.; et al. NimbRo rescue: Solving disaster-response tasks with the mobile manipulation robot momaro. J. Field Robot. 2016, 34, 400–425. [Google Scholar] [CrossRef]
- Tian, Y.; Liu, K.; Ok, K.; Tran, L.; Allen, D.; Roy, N.; How, J.P. Search and rescue under the forest canopy using multiple UAVs. Int. J. Robot. Res. 2020, 39, 1201–1221. [Google Scholar] [CrossRef]
- Okada, K.; Kagami, S.; Inaba, M.; Inoue, H. Plane segment finder: Algorithm, implementation and applications. IEEE Int. Conf. Robot. Autom. 2001, 2, 2120–2125. [Google Scholar]
- Geromichalos, D.; Azkarate, M.; Tsardoulias, E.; Gerdes, L.; Petrou, L.; Pulgar, C.P.D. SLAM for autonomous planetary rovers with global localization. J. Field Robot. 2019, 37, 830–847. [Google Scholar] [CrossRef]
- Yin, H.; Wang, Y.; Tang, L.; Ding, X.; Huang, S.; Xiong, R. 3D LiDAR map compression for efficient localization on resource constrained vehicles. IEEE Trans. Intell. Transp. Syst. 2021, 22, 837–852. [Google Scholar] [CrossRef]
- Inaba, M.; Kagami, S.; Kanehiro, F.; Hoshino, Y.; Inoue, H. A platform for robotics research based on the remote-brained robot approach. Int. J. Robot. Res. 2000, 19, 933–954. [Google Scholar] [CrossRef]
- Ding, L.; Nagatani, K.; Sato, K.; Mora, A.; Yoshida, K.; Gao, H.; Deng, Z. Terramechanics-based high-fidelity dynamics simulation for wheeled mobile robot on deformable rough terrain. In Proceedings of the 2010 IEEE International Conference on Robotics and Automation, Anchorage, AK, USA, 3–7 May 2010; pp. 4922–4927. [Google Scholar]
- Li, W.; Ding, L.; Gao, H.; Tavakoli, M. Haptic tele-driving of wheeled mobile robots under nonideal wheel rolling, kinematic control and communication time delay. IEEE Trans. Syst. Man Cybern. Syst. 2020, 50, 336–347. [Google Scholar] [CrossRef]
- Li, Y.; Li, M.; Zhu, H.; Hu, E.; Tang, C.; Li, P.; You, S. Development and applications of rescue robots for explosion accidents in coal mines. J. Field Robot. 2019, 37, 466–489. [Google Scholar] [CrossRef]
- Takemori, T.; Miyake, M.; Hirai, T.; Wang, X.; Fukao, Y.; Adachi, M.; Yamaguchi, K.; Tanishige, S.; Nomura, Y.; Matsuno, F.; et al. Development of the multifunctional rescue robot FUHGA2 and evaluation at the world summit 2018. Adv. Robot. 2019, 34, 119–131. [Google Scholar] [CrossRef]
- Jeong, I.B.; Ko, W.R.; Park, G.M.; Kim, D.H.; Yoo, Y.H.; Kim, J.H. Task intelligence of robots: Neural model-based mechanism of thought and online motion planning. IEEE Trans. Emerg. Topics Comput. Intell. 2017, 1, 41–50. [Google Scholar] [CrossRef]
- Kamarudin, K.; Shakaff, A.Y.M.; Bennetts, V.H.; Mamduh, S.M.; Zakaria, A.; Visvanathan, R.; Yeon, A.S.A.; Kamarudin, L.M. Integrating SLAM and gas distribution mapping (SLAM-GDM) for real-time gas source localization. Adv. Robot. 2018, 17, 903–917. [Google Scholar] [CrossRef]
- Aguiar, A.S.; Santos, F.N.d.; Cunha, J.B.; Sobreira, H.; Sousa, A.J. Localization and mapping for robots in agriculture and forestry: A survey. Robotics 2020, 9, 97. [Google Scholar] [CrossRef]
- Iqbal, J.; Xu, R.; Sun, S.; Li, C. Simulation of an autonomous mobile robot for LiDAR-based in-field phenotyping and navigation. Robotics 2020, 9, 46. [Google Scholar] [CrossRef]
- Balta, H.; Bedkowski, J.; Govindaraj, S.; Majek, K.; Musialik, P.; Serrano, D.; Alexis, K.; Siegwart, R.; Cubber, G.D. Integrated data management for a fleet of search-and-rescue robots. J. Field Robot. 2016, 33, 539–582. [Google Scholar] [CrossRef]
- Brooks, R.A. A robust layered control system for a mobile robot. IEEE J. Robot. Autom. 1986, 2, 14–23. [Google Scholar] [CrossRef]
- Jiang, C.; Ni, Z.; Guo, Y.; He, H. Pedestrian flow optimization to reduce the risk of crowd disasters through human-robot interaction. IEEE Trans. Emerg. Topics Comput. Intell. 2020, 4, 298–311. [Google Scholar] [CrossRef]
- Whyte, H.D.; Bailey, T. Simultaneous localization and mapping (SLAM): Part I the essential algorithms. IEEE Robot. Autom. Mag. 2006, 13, 99–110. [Google Scholar] [CrossRef]
- Tsubouchi, T. Introduction to simultaneous localization and mapping. J. Robot. Mechatron. 2019, 31, 367–374. [Google Scholar] [CrossRef]
- Huang, J.; Junginger, S.; Liu, H.; Thurow, K. Indoor positioning systems of mobile robots: A review. Robotics 2023, 12, 47. [Google Scholar] [CrossRef]
- Li, M.; Zhu, H.; You, S.; Wang, L.; Tang, C. Efficient laser-based 3D SLAM for coal mine rescue robots. IEEE Access 2018, 7, 14124–14138. [Google Scholar] [CrossRef]
- Memon, E.A.A.; Jafri, S.R.U.N.; Ali, S.M.U. A rover team based 3D map building using low cost 2D laser scanners. IEEE Access 2021, 10, 1790–1801. [Google Scholar] [CrossRef]
- Xie, Y.; Zhang, Y.; Chen, L.; Cheng, H.; Tu, W.; Cao, D.; Li, Q. RDC-SLAM: A real-time distributed cooperative SLAM system based on 3D LiDAR. IEEE Trans. Intell. Transp. Syst. 2022, 23, 14721–14730. [Google Scholar] [CrossRef]
- Ding, X.; Wang, Y.; Li, D.; Tang, L.; Yin, H.; Xiong, R. Laser map aided visual inertial localization in changing environment. In Proceedings of the 2018 IEEE/RSJ International Conference on Intelligent Robots and Systems (IROS), Madrid, Spain, 1–5 October 2018; pp. 4794–4801. [Google Scholar]
- Mu, L.; Yao, P.; Zheng, Y.; Chen, K.; Wang, F.; Qi, N. Research on SLAM algorithm of mobile robot based on the fusion of 2D LiDAR and depth camera. IEEE Access 2020, 8, 157628–157642. [Google Scholar] [CrossRef]
- Jin, Z.; Shao, Y.; So, M.; Sable, C.; Shlayan, N.; Luchtenburg, D.M. A multisensor data fusion approach for simultaneous localization and mapping. In Proceedings of the 2019 IEEE Intelligent Transportation Systems Conference (ITSC), Auckland, New Zealand, 27–30 October 2019; pp. 1317–1322. [Google Scholar]
- Maset, E.; Scalera, L.; Beinat, A.; Visintini, D.; Gasparetto, A. Performance investigation and repeatability assessment of a mobile robotic system for 3D mapping. Robotics 2022, 11, 54. [Google Scholar] [CrossRef]
- Artal, R.M.; Montiel, J.M.M.; Tardos, J.D. ORB-SLAM: A versatile and accurate monocular SLAM system. IEEE Trans. Robot. 2015, 31, 1147–1163. [Google Scholar] [CrossRef]
- Artal, R.M.; Tardos, J.D. ORB-SLAM2: An open-source SLAM system for monocular, stereo and RGB-D cameras. IEEE Trans. Robot. 2017, 33, 1255–1262. [Google Scholar] [CrossRef]
- Campos, C.; Elvira, R.; Rodriguez, J.J.G.; Montiel, J.M.M.; Tardos, J.D. ORB-SLAM3: An accurate open-source library for visual, visual-inertial and multi-map SLAM. IEEE Trans. Robot. 2021, 37, 1874–1890. [Google Scholar] [CrossRef]
- Silveira, O.C.B.; de Melo, J.G.O.C.; Moreira, L.A.S.; Pinto, J.B.N.G.; Rodrigues, L.R.L.; Rosa, P.F.F. Evaluating a visual simultaneous localization and mapping solution on embedded platforms. In Proceedings of the 2020 IEEE 29th International Symposium on Industrial Electronics (ISIE), Delft, The Netherlands, 17–19 June 2020; pp. 530–535. [Google Scholar]
- Peng, T.; Zhang, D.; Hettiarachchi, D.L.N.; Loomis, J. An evaluation of embedded GPU systems for visual SLAM algorithms. Intl. Symp. Electron. Imaging 2020, 2020, 325-1. [Google Scholar] [CrossRef]
- Sallum, E.; Pereira, N.; Alves, M.; Santos, M. Improving quality-of-service in LoRa low-power wide-area networks through optimized radio resource management. J. Sens. Actuator Netw. 2020, 9, 10. [Google Scholar] [CrossRef]
- Zhou, Q.; Zheng, K.; Hou, L.; Xing, J.; Xu, R. Design and implementation of open LoRa for IoT. IEEE Access 2019, 7, 100649–100657. [Google Scholar] [CrossRef]
- Mahmood, A.; Sisinni, E.; Guntupalli, L.; Rondon, R.; Hassan, S.A.; Gidlund, M. Scalability analysis of a LoRa network under imperfect orthogonality. IEEE Trans. Ind. Informat. 2019, 15, 1425–1436. [Google Scholar] [CrossRef]
- Lewis, J.; Lima, P.U.; Basiri, M. Collaborative 3D scene reconstruction in large outdoor environments using a fleet of mobile ground robots. Sensors 2023, 23, 375. [Google Scholar] [CrossRef]
- Kagawa, T.; Ono, F.; Shan, L.; Miura, R.; Nakadai, K.; Hoshiba, K.; Kumon, M.; Okuno, H.G.; Kato, S.; Kojima, F. Multi-hop wireless command and telemetry communication system for remote operation of robots with extending operation area beyond line-of-sight using 920 MHz/169 MHz. Adv. Robot. 2020, 34, 756–766. [Google Scholar] [CrossRef]
- Mascarich, F.; Nguyen, H.; Dang, T.; Khattak, S.; Papachristos, C.; Alexis, K. A self-deployed multi-channel wireless communications system for subterranean robots. In Proceedings of the 2020 IEEE Aerospace Conference, Big Sky, MT, USA, 7–14 March 2020; pp. 1–8. [Google Scholar]
- Junaedy, A.; Masuta, H.; Sawai, K.; Motoyoshi, T.; Takagi, N. LPWAN-based real-time 2D SLAM and object localization for teleoperation robot control. J. Robot. Mechatron. 2021, 33, 1326–1337. [Google Scholar] [CrossRef]
- Hess, W.; Kohler, D.; Rapp, H.; Andor, D. Real-time loop closure in 2D LiDAR SLAM. In Proceedings of the 2016 IEEE International Conference on Robotics and Automation (ICRA), Stockholm, Sweden, 16–21 May 2016; pp. 1271–1278. [Google Scholar]
- Kaess, M.; Williams, S.; Indelman, V.; Roberts, R.; Leonardo, J.J.; Dellaert, F. Concurrent filtering and smoothing. In Proceedings of the 2012 15th International Conference on Information Fusion, Singapore, 9–12 July 2012; pp. 1300–1307. [Google Scholar]
- Grisetti, G.; Kummerle, R.; Stachniss, C.; Burgard, W. A tutorial on graph-based SLAM. IEEE Intell. Transp. Syst. Mag. 2010, 2, 31–43. [Google Scholar] [CrossRef]
- Junaedy, A.; Masuta, H.; Kubota, N.; Sawai, K.; Motoyoshi, T.; Takagi, N. Object extraction method for mobile robots using fast growing neural gas. In Proceedings of the 2022 IEEE Symposium Series on Computational Intelligence (SSCI), Singapore, 4–7 December 2022; pp. 962–969. [Google Scholar]
- Fritzke, B. A growing neural gas network learns topologies. Intl. Conf. Neural Informat. Process. Syst. 1995, 7, 625–632. [Google Scholar]
- Kubota, N. Multiscopic topological twin in robotics. In Proceedings of the 28th International Conference on Neural Information Processing, Bali, Indonesia, 8–12 December 2021. [Google Scholar]
- Iwasa, M.; Kubota, N.; Toda, Y. Multi-scale batch-learning growing neural gas for topological feature extraction in navigation of mobility support robot. In Proceedings of the 7th International Workshop on Advanced Computational Intelligence and Intelligent Informatics (IWACIII 2021), Beijing, China, 31 October–3 November 2021. [Google Scholar] [CrossRef]
- Ester, M.; Kriegel, H.P.; Sander, J.; Xu, X. A density-based algorithm for discovering clusters in large spatial databases with noise. In Proceedings of the Second International Conference on Knowledge Discovery and Data Mining (KDD-96), Portland, OR, USA, 2–4 August 1996; pp. 226–231. [Google Scholar]
- Wang, W.; Zhang, Y.; Ge, G.; Yang, H.; Wang, Y. A new approach toward corner detection for use in point cloud registration. Remote Sens. 2023, 15, 3375. [Google Scholar] [CrossRef]
- Fischler, M.A.; Bolles, R.C. Random sample consensus: A paradigm for model fitting with applications to image analysis and automated cartography. Commun. ACM 1981, 24, 381–395. [Google Scholar] [CrossRef]
- Junaedy, A.; Masuta, H.; Sawai, K.; Motoyoshi, T.; Takagi, N. A plane extraction method for embedded computers in mobile robots. In Proceedings of the 2021 IEEE Symposium Series on Computational Intelligence (SSCI), Orlando, FL, USA, 5–7 December 2021; pp. 1–8. [Google Scholar]
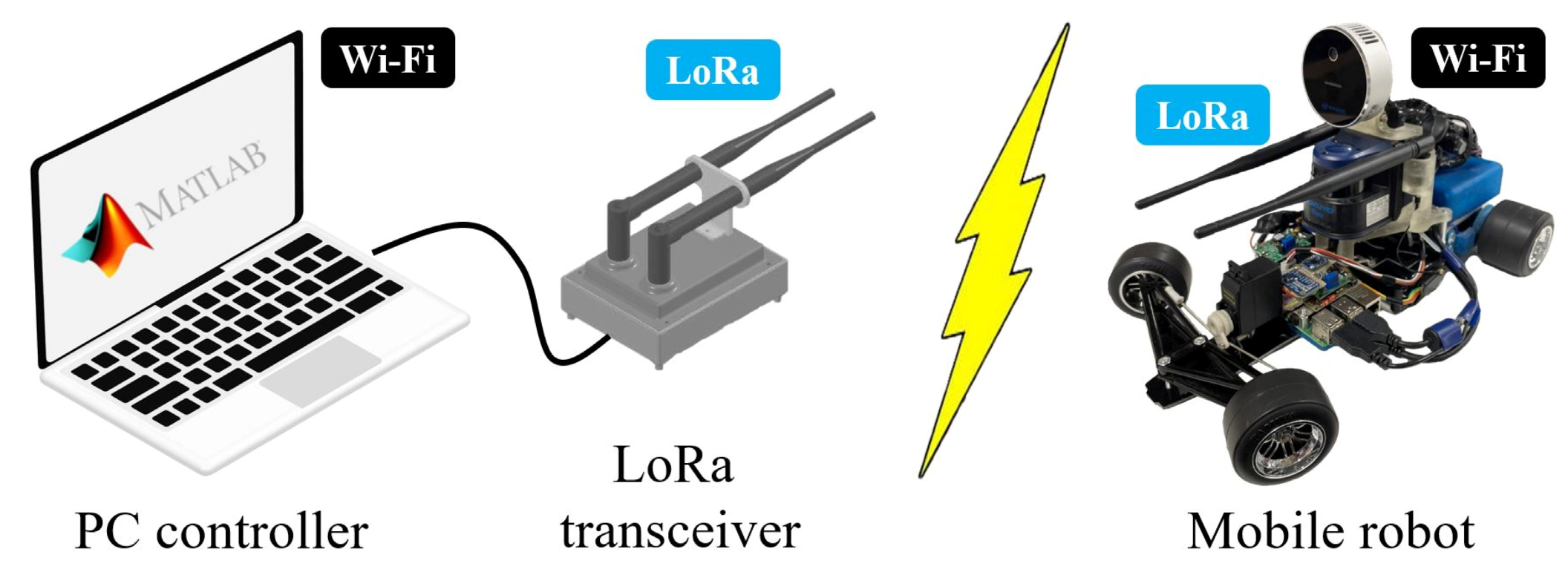


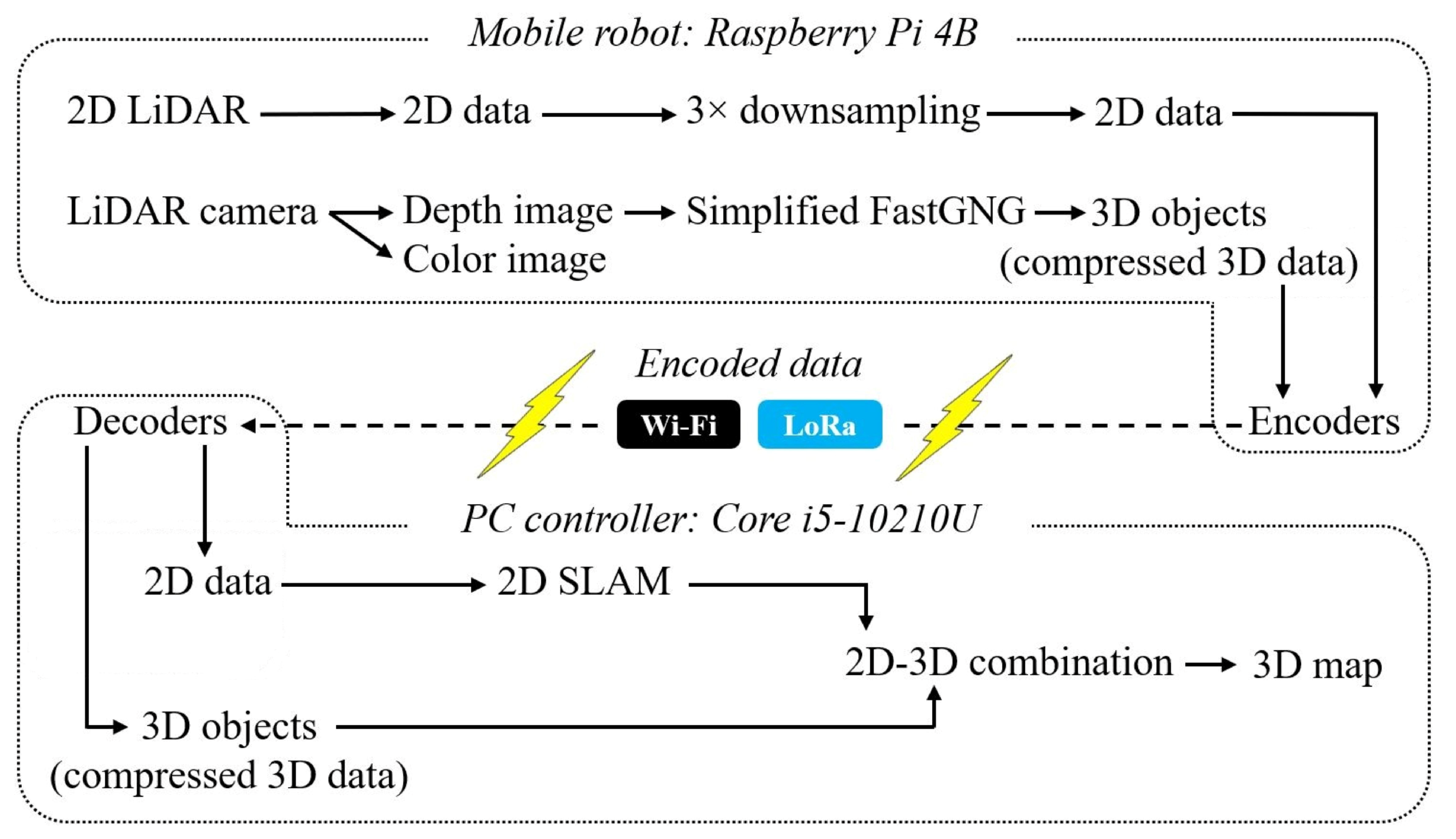








| PC Controller | Core i5-10210U CPU 8 GB RAM; IEEE 802.11ac (353 kbps–9 Mbps) |
| LoRa Transceiver | ES920LR 920.6-928.0 MHz ×2 (6.01 kbps–22 kbps); ES920ANT ×2 Arduino Mega 2560 |
| Mobile Robot | Dimension: 350 mm × 200 mm × 200 mm Rear-drive brushed DC motor Servo motor with Ackermann steering Li-Fe battery 6.6 V/1450 mAh ×3 H-bridge MOSFET motor driver Raspberry Pi 4B 4 GB RAM; IEEE 802.11ac (353 kbps–9 Mbps) IMU module LSM9DS1 (3-DoF accel-gyro-magneto) @100 Hz Rotary encoder SG2A174 ×2 (80 ppr, 200 μs rates) @5 kHz A/D converter module ADS1115 @860 Hz ES920LR 920.6-928.0 MHz ×2 (6.01 kbps–22 kbps); ES920ANT ×2 Hokuyo 2D LiDAR UBG-04LX-F01 (240° scan angle, 0.06–4 m) @25 fps Intel RealSense LiDAR camera L515 (depth: 640 × 480 0.5–9 m, color: 1920 × 1080) @30 fps |
| Standard GNG | |||||
|---|---|---|---|---|---|
| No. | No. of Nodes | No. of Connections | Iteration/Phase | Time [ms] | Mean Time [ms] |
| 1 | 150 | 159 | 3700 | 58.3 | 67.9 |
| 2 | 150 | 165 | 3780 | 61.8 | |
| 3 | 150 | 171 | 4120 | 85.7 | |
| 4 | 150 | 164 | 4070 | 68.3 | |
| 5 | 150 | 166 | 3840 | 65.4 | |
| FastGNG | |||||
| 1 | 148 | 278 | 3 | 22.5 | 22.2 |
| 2 | 149 | 269 | 3 | 23.2 | |
| 3 | 152 | 297 | 3 | 21.2 | |
| 4 | 151 | 278 | 3 | 21.5 | |
| 5 | 150 | 285 | 3 | 22.8 | |
| Simplified FastGNG | |||||
| 1 | 155 | 146 | 3 | 13.6 | 16.2 |
| 2 | 144 | 132 | 3 | 18.2 | |
| 3 | 158 | 143 | 3 | 17.3 | |
| 4 | 152 | 137 | 3 | 16.0 | |
| 5 | 145 | 130 | 3 | 15.8 | |
| Parameter | Value | Definition |
|---|---|---|
| 3.9 | Constant for generating a set of sample nodes A | |
| 1.55 | ||
| Minimum length of a connection in the network for each phase level iP | ||
| Maximum length of a connection in the network for each phase level iP | ||
| Internal loop parameter for mini-batch learning | ||
| Thresholds for ground removal | ||
| Thresholds for open loop connection | ||
| Thresholds for node evaluation | ||
| Thresholds for connection evaluation |
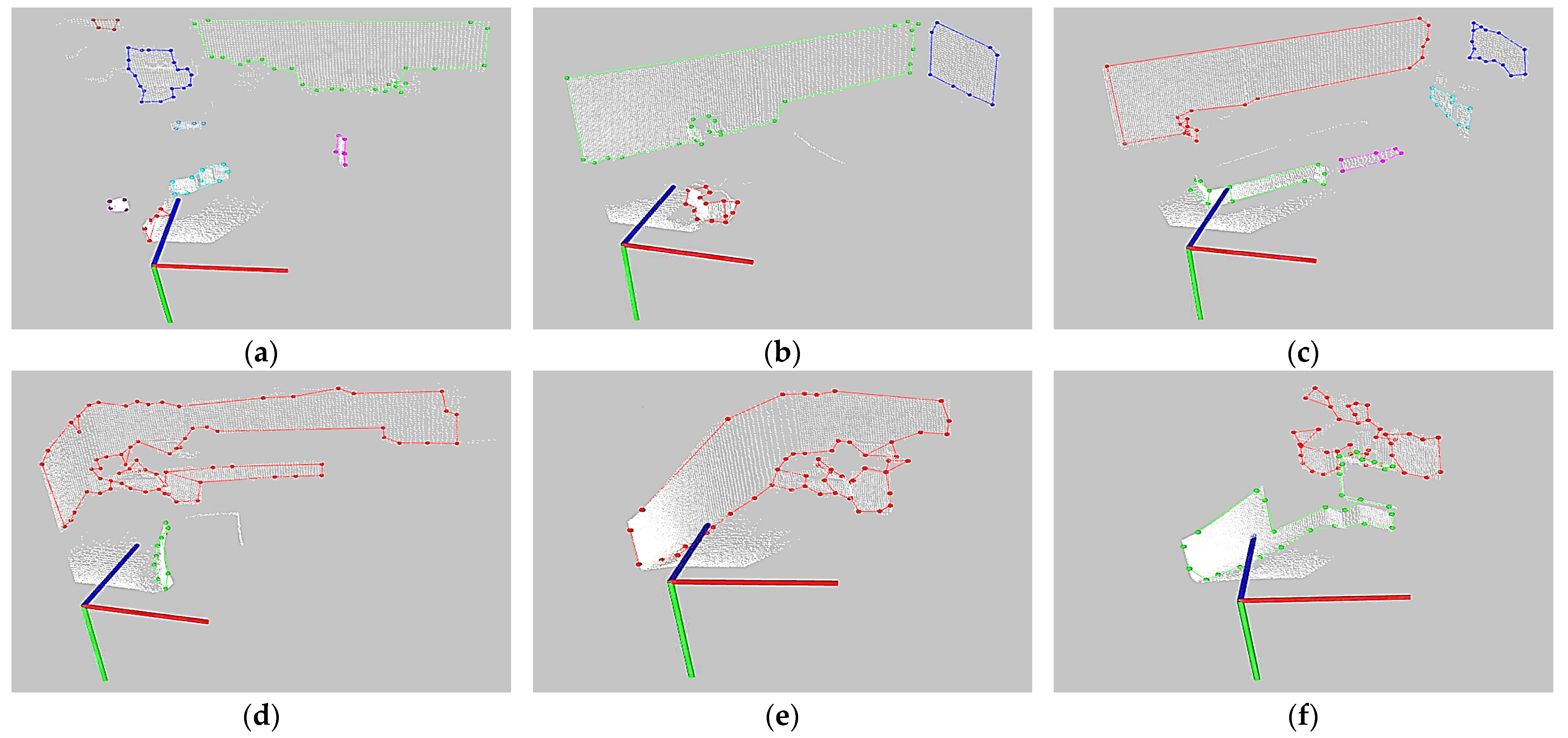
| No. | Input Image | No. of Points in Point Cloud | No. of Nodes | No. of Connections | No. of Clusters | Min Distance between Nodes | Max Distance between Nodes | Time [ms] |
|---|---|---|---|---|---|---|---|---|
| 1 | Figure 14a | 8586 | 77 | 80 | 8 | 0.100 m | 2.430 m | 32.7 |
| 2 | Figure 14b | 11,647 | 48 | 49 | 3 | 0.100 m | 3.210 m | 27.6 |
| 3 | Figure 14c | 10,455 | 61 | 67 | 5 | 0.100 m | 3.180 m | 34.6 |
| 4 | Figure 14d | 10,802 | 80 | 86 | 2 | 0.102 m | 1.575 m | 35.6 |
| 5 | Figure 14e | 13,948 | 54 | 60 | 1 | 0.102 m | 1.217 m | 32.1 |
| 6 | Figure 14f | 14,094 | 70 | 76 | 2 | 0.100 m | 0.560 m | 30.0 |
| Frame Rate: | Mean = = 31.15 fps; Min = = 28.09 fps; Max = = 36.23 fps | |||||||
| Parameter | Value | Definition |
|---|---|---|
| thetaTh | 10° | DBSCAN clustering rotation threshold |
| dEps | 0.10 m (step 2) 0.15 m (step 4) | DBSCAN clustering minimum search radius |
| minObj | 2 | DBSCAN clustering minimum number of objects |
| maxIteration | 1.5 n | RANSAC maximum iteration. n is the number of sample data |
| inliersTh | 0.10 m (step 3, 4) | RANSAC inlier threshold |
| PC Controller | |||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| No. | Network | Data Transmission Time [ms] Mean of 50+ Data | Mean [ms] | 2D SLAM and 2D–3D Combination [ms] Mean of 50+ Data | Mean [ms] | Data Size [KB] Mean of 50+ Data | Mean [KB] | ||||
| 1 | Wi-Fi to LoRa | 273 | 274 | 93 | 98 | 0.727 | 0.734 | ||||
| 2 | 266 | 92 | 0.740 | ||||||||
| 3 | 277 | 106 | 0.735 | ||||||||
| 4 | 272 | 96 | 0.718 | ||||||||
| 5 | 280 | 106 | 0.752 | ||||||||
| 6 | LoRa | 570 | 625 | 89 | 99 | 0.463 | 0.471 | ||||
| 7 | 703 | 106 | 0.472 | ||||||||
| 8 | 618 | 102 | 0.474 | ||||||||
| 9 | 577 | 98 | 0.471 | ||||||||
| 10 | 659 | 103 | 0.475 | ||||||||
| 11 | Wi-Fi | 17 | 18 | 109 | 112 | 0.926 | 0.932 | ||||
| 12 | 23 | 108 | 0.928 | ||||||||
| 13 | 16 | 116 | 0.936 | ||||||||
| 14 | 17 | 109 | 0.914 | ||||||||
| 15 | 18 | 118 | 0.936 | ||||||||
| Mobile Robot | |||||||||||
| Hardware | Sampling Rate | Algorithm | Encoding | Total | |||||||
| 2D Data | 2D LiDAR | 25 fps (40 ms) | 3× Downsampling: 10 ms | 5 ms | 55 ms | ||||||
| 3D Data | LiDAR Camera | 30 fps (33 ms) | Simplified FastGNG: 32.1 ms (mean) | 10 ms | 75.1 ms | ||||||
| Total Computational Cost | |||||||||||
| Wi-Fi to LoRa | 274 ms + 98 ms + 75.1 ms = 447.1 ms (2.24 Hz) | ||||||||||
| LoRa | 625 ms + 99 ms + 75.1 ms = 799.1 ms (1.25 Hz) (main target) | ||||||||||
| Wi-Fi | 18 ms + 112 ms + 75.1 ms = 205.1 ms (4.88 Hz) | ||||||||||
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Junaedy, A.; Masuta, H.; Sawai, K.; Motoyoshi, T.; Takagi, N. Real-Time 3D Map Building in a Mobile Robot System with Low-Bandwidth Communication. Robotics 2023, 12, 157. https://doi.org/10.3390/robotics12060157
Junaedy A, Masuta H, Sawai K, Motoyoshi T, Takagi N. Real-Time 3D Map Building in a Mobile Robot System with Low-Bandwidth Communication. Robotics. 2023; 12(6):157. https://doi.org/10.3390/robotics12060157
Chicago/Turabian StyleJunaedy, Alfin, Hiroyuki Masuta, Kei Sawai, Tatsuo Motoyoshi, and Noboru Takagi. 2023. "Real-Time 3D Map Building in a Mobile Robot System with Low-Bandwidth Communication" Robotics 12, no. 6: 157. https://doi.org/10.3390/robotics12060157
APA StyleJunaedy, A., Masuta, H., Sawai, K., Motoyoshi, T., & Takagi, N. (2023). Real-Time 3D Map Building in a Mobile Robot System with Low-Bandwidth Communication. Robotics, 12(6), 157. https://doi.org/10.3390/robotics12060157











