FABRIKx: Tackling the Inverse Kinematics Problem of Continuum Robots with Variable Curvature
Abstract
1. Introduction
2. Forward Kinematics
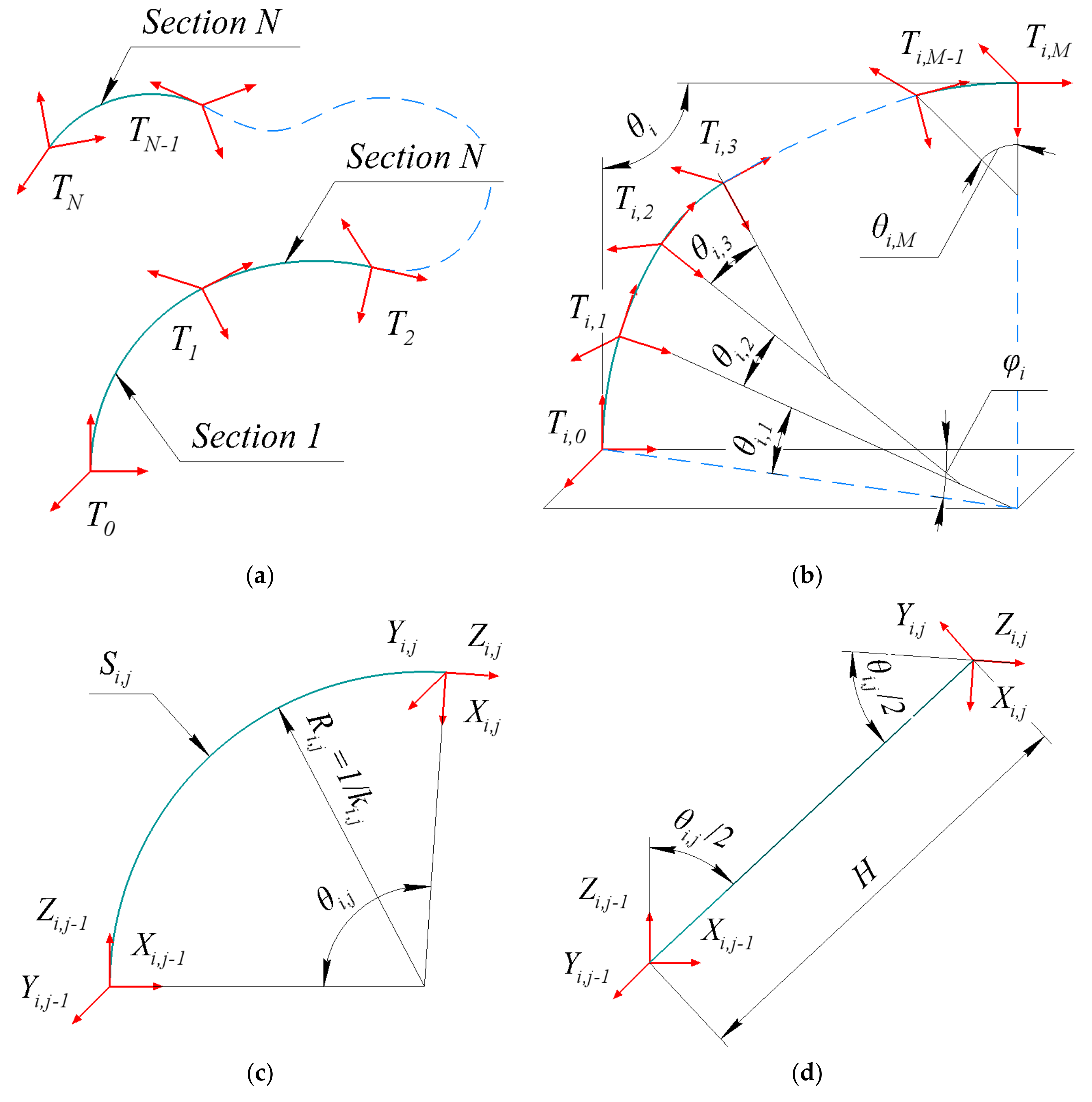
- Continuum robots consist of independent, consecutive sections (Figure 2a). Two bending sections have the same tangent vector at the point of their connection.
- Each section can be divided into subsections (Figure 2b). All subsections bend simultaneously when the section bends. The angle between the first and the last tangent is the bending angle of the section. Two subsections have the same tangent vector at the point of their connection. The robot design excludes section torsion.
3. Inverse Kinematics
3.1. Single-Section Inverse Kinematics
3.1.1. FABRIKc-Based Method
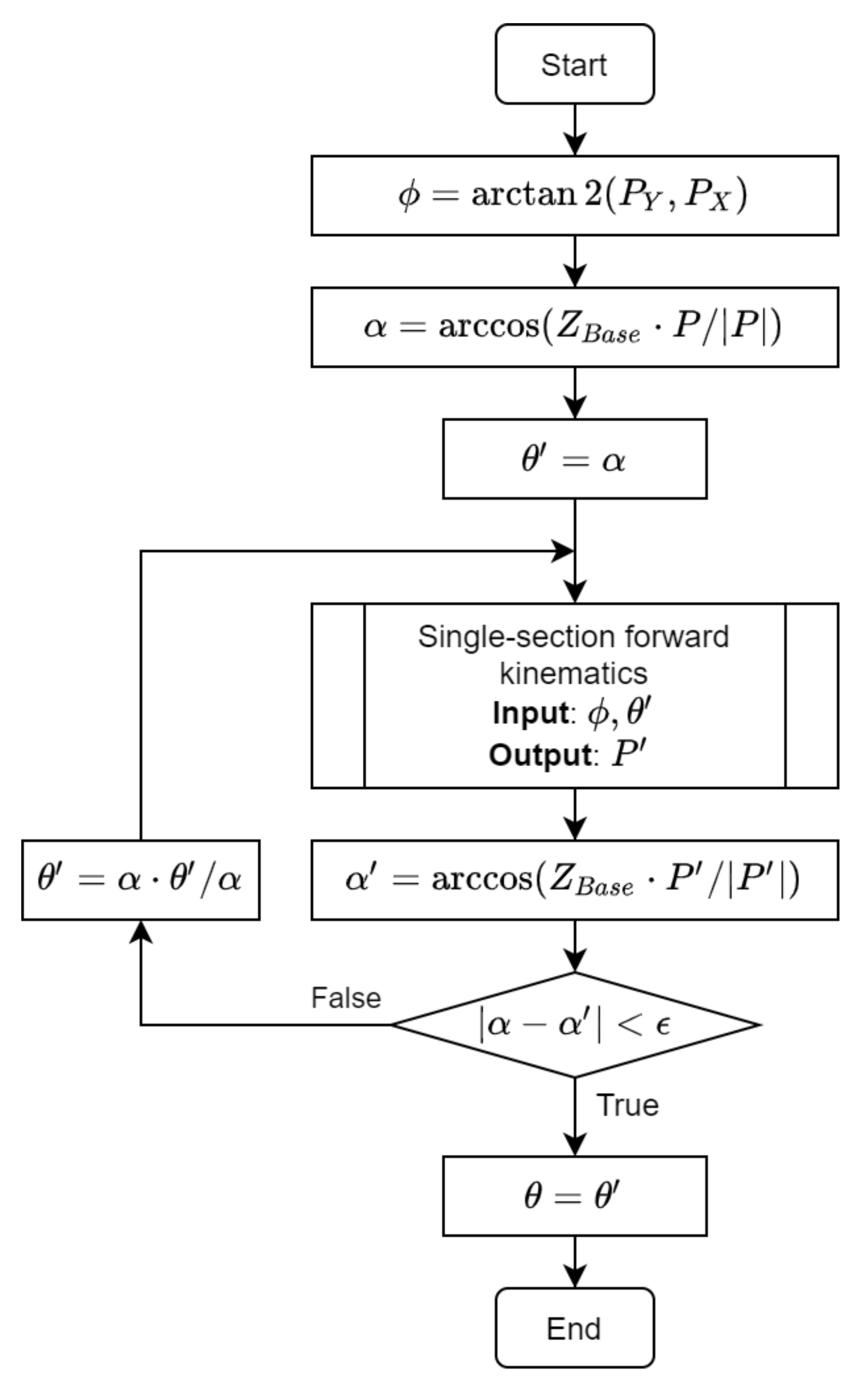
3.1.2. Iterative Method
- Define chord angle :
- Assume that bending angle is equal to chord angle :
- Define section endpoint using forward kinematics (1)–(3) for bending angle and rotation angle .
- Define chord angle for point by (8).
- If the difference between angles and is lower than the tolerance , then is a solution. Otherwise, redefine as follows:
3.1.3. Approximation
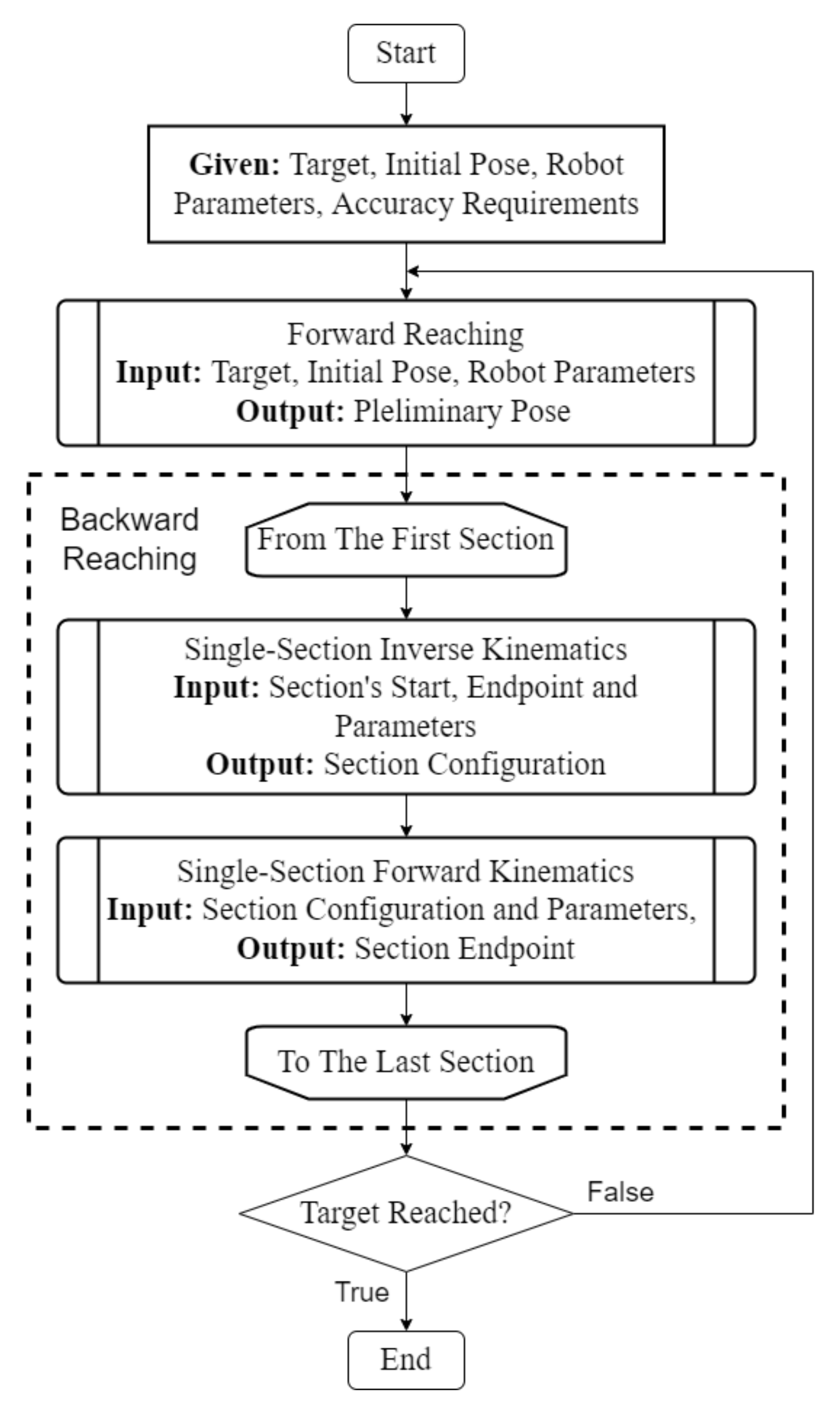
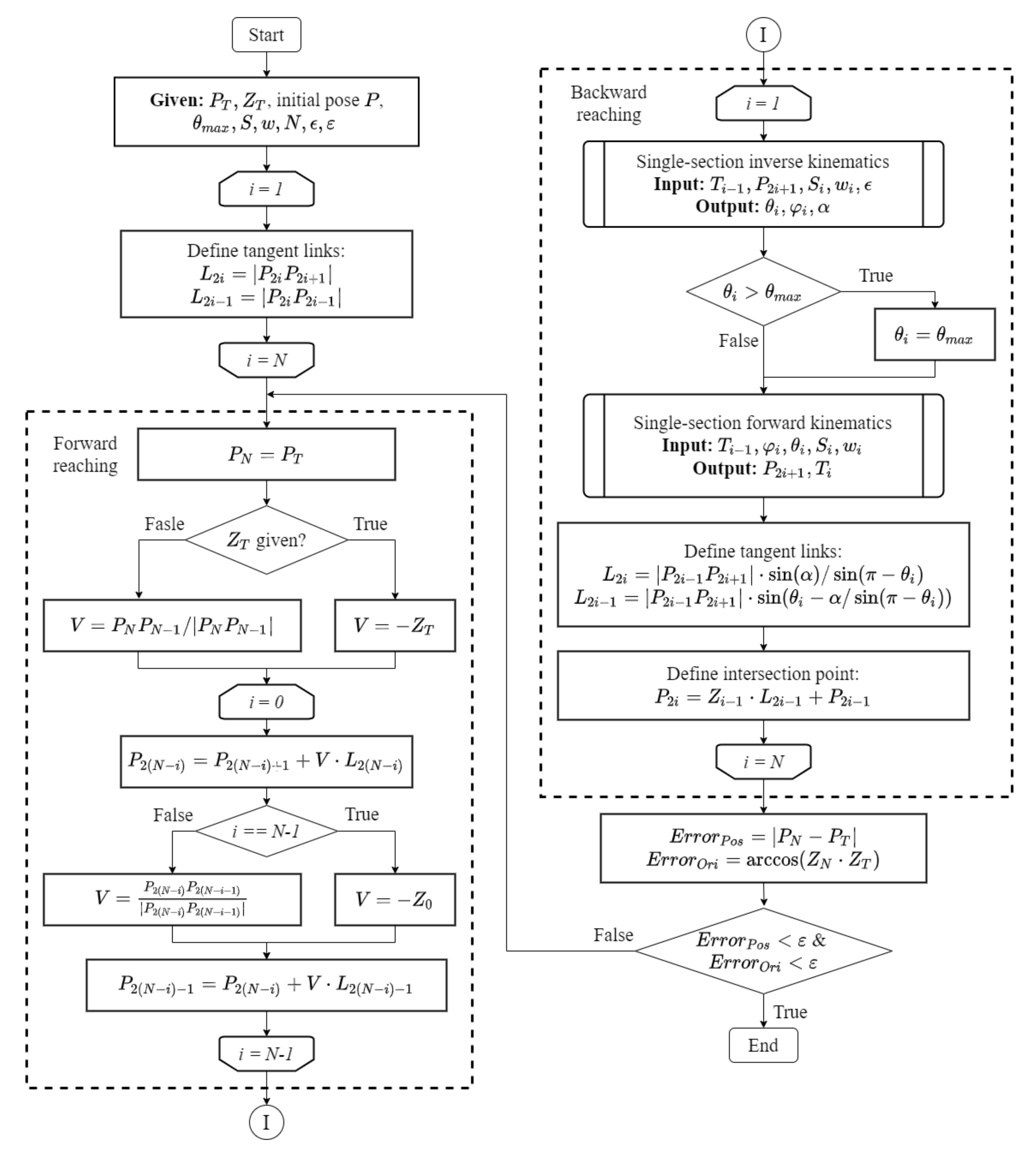
3.2. Multisection Inverse Kinematics
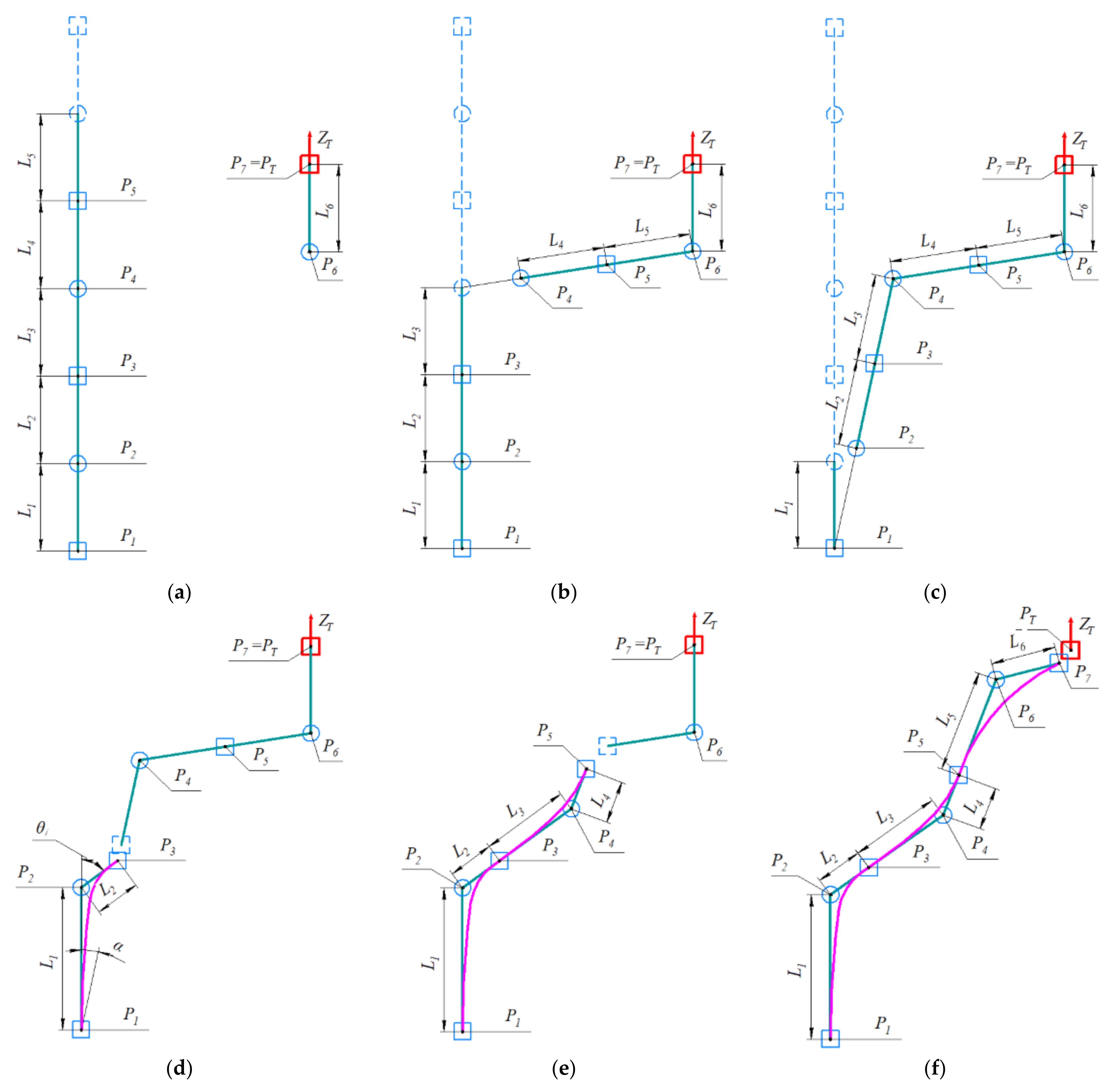
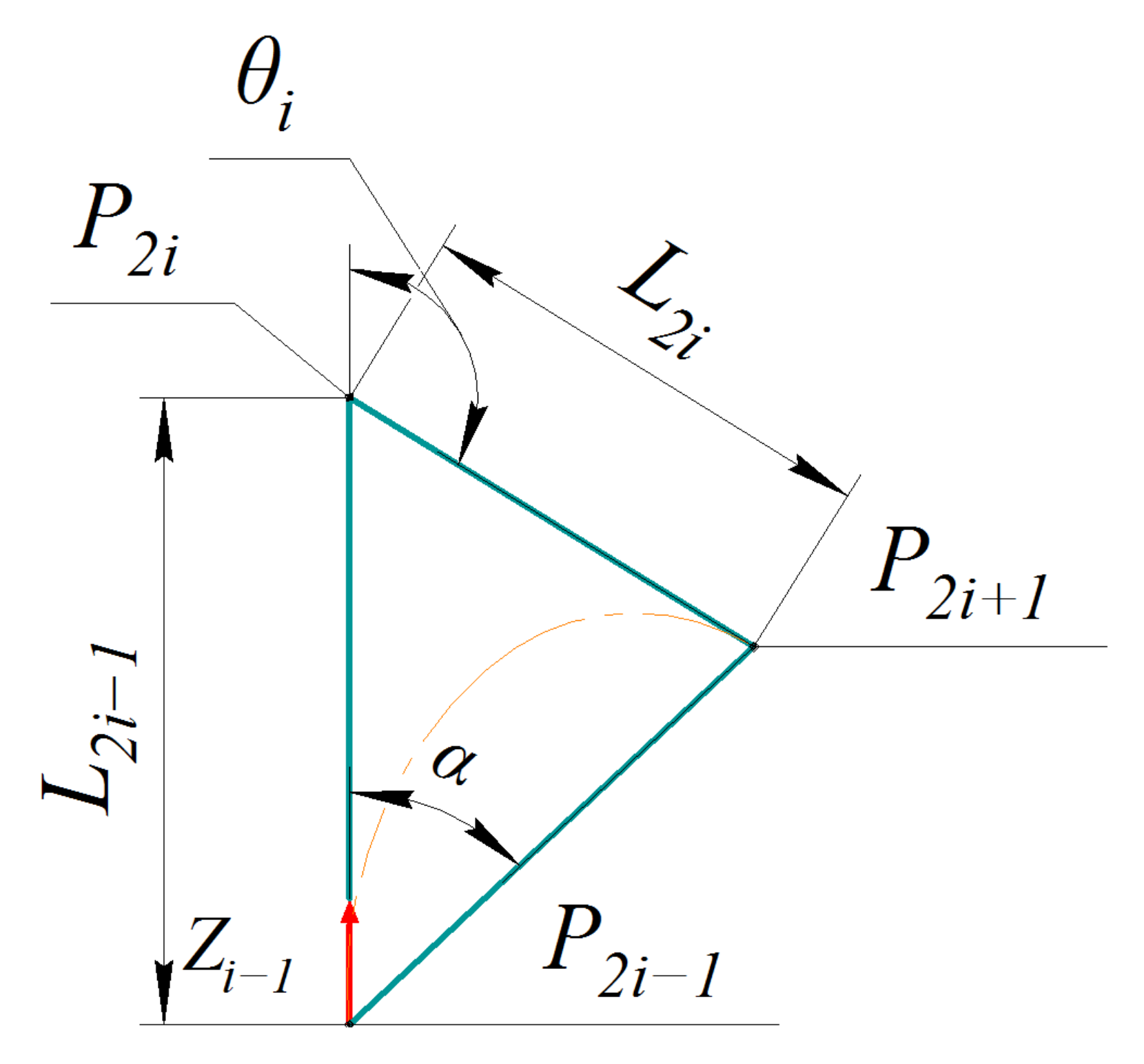
3.2.1. Forward Reaching
3.2.2. Backward Reaching
3.3. Jacobian-Based Inverse Kinematics
4. Simulation
- Three-section robot with three subsections per section.
- Three-section robot with five subsections per section.
- Three-section robot with seven subsections per section.
- Three-section robot with nine subsections per section.
- Five-section robot with three subsections per section.
- Seven-section robot with three subsections per section.
| Section | Subsection Lengths, mm | Subsection Weights | |
|---|---|---|---|
| Robot 1 (3 × 3) | 1 | [20, 40, 10] | [1, 0.001, 3] |
| 2 | [10, 20, 40] | [3, 2, 1] | |
| 3 | [30, 10, 30] | [1, 7, 1] | |
| Robot 2 (3 × 5) | 1 | [20, 20, 40, 10, 10] | [1, 1, 0.001 3, 4] |
| 2 | [10, 10, 20, 40, 20] | [4, 3, 2, 1, 0.001] | |
| 3 | [15, 30, 10, 30, 15] | [0.001, 1, 7, 1, 3] | |
| Robot 3 (3 × 7) | 1 | [30, 20, 20, 40, 10, 10, 10] | [4, 1, 1, 0.001, 3, 4, 1] |
| 2 | [30, 10, 10, 20, 40, 20, 10] | [1, 4, 3, 2, 1, 0.001, 4] | |
| 3 | [20, 15, 30, 10, 30, 15, 20] | [1, 0.001, 1, 7, 1, 3, 1] | |
| Robot 4 (3 × 9) | 1 | [10, 30, 20, 20, 40, 10, 10, 10, 30] | [2, 4, 1, 1, 0.001, 3, 4, 1, 3] |
| 2 | [30, 30, 10, 10, 20, 40, 20, 10, 10] | [4, 1, 4, 3, 2, 1, 0.001, 4, 1] | |
| 3 | [20, 20, 15, 30, 10, 30, 15, 20, 20] | [4, 1, 0.001, 1, 7, 1, 3, 1, 4] | |
| Robot 5 (5 × 3) | 1 | [20, 40, 10] | [1, 0.001, 3] |
| 2 | [10, 20, 40] | [3, 2, 1] | |
| 3 | [30, 10, 30] | [1, 7, 1] | |
| 4 | [10, 50, 10] | [0.001, 1, 0.001] | |
| 5 | [10, 50, 10] | [3, 1, 3] | |
| Robot 6 (7 × 3) | 1 | [20, 40, 10] | [1, 0.001, 3] |
| 2 | [10, 20, 40] | [3, 2, 1] | |
| 3 | [30, 10, 30] | [1, 7, 1] | |
| 4 | [10, 50, 10] | [0.001, 1, 0.001] | |
| 5 | [10, 50, 10] | [3, 1, 3] | |
| 6 | [20, 40, 10] | [3, 0.001, 1] | |
| 7 | [10, 40, 20] | [3, 0.001, 1] |
5. Results and Discussion
| Algorithm | Success Rate, % | Solution Time, ms | Iteration | |||
|---|---|---|---|---|---|---|
| Mean | Median | Mean | Median | |||
| Robot 1 (3 × 3) | FABRIKx (I) | 92.8 | 4.5 | 3.2 | 16 | 11 |
| FABRIKx (P) | 93.8 | 3.3 | 2.1 | 17 | 11 | |
| FABRIKc | 78.5 | 4.4 | 2.3 | 29 | 14 | |
| Jacobian | 81.3 | 8.1 | 5.9 | 34 | 25 | |
| Robot 2 (3 × 5) | FABRIKx (I) | 92.4 | 5.3 | 4.0 | 17 | 12 |
| FABRIKx (P) | 93.6 | 3.6 | 2.4 | 18 | 12 | |
| FABRIKc | 79.5 | 4.3 | 2.2 | 27 | 13 | |
| Jacobian | 83.7 | 7.9 | 6.0 | 32 | 24 | |
| Robot 3 (3 × 7) | FABRIKx (I) | 86.7 | 6.4 | 4.7 | 19 | 13 |
| FABRIKx (P) | 88.5 | 4.2 | 2.8 | 20 | 14 | |
| FABRIKc | 75.8 | 4.9 | 2.6 | 30 | 15 | |
| Jacobian | 84.4 | 7.3 | 5.1 | 28 | 19 | |
| Robot 4 (3 × 9) | FABRIKx (I) | 82.8 | 6.7 | 4.9 | 19 | 14 |
| FABRIKx (P) | 84.9 | 4.4 | 2.9 | 21 | 14 | |
| FABRIKc | 73.4 | 5.0 | 2.7 | 30 | 15 | |
| Jacobian | 84.9 | 7.4 | 5.2 | 27 | 19 | |
| Robot 5 (5 × 3) | FABRIKx (I) | 69.3 | 5.8 | 4.5 | 12 | 10 |
| FABRIKx (P) | 70.7 | 4.1 | 3.1 | 13 | 10 | |
| FABRIKc | 70.0 | 4.0 | 3.0 | 16 | 12 | |
| Jacobian | 0.3 | 26.0 | 26.6 | 28 | 28 | |
| Jacobian (S) | 13.3 | 138.7 | 98.4 | 128 | 90 | |
| Robot 6 (7 × 3) | FABRIKx (I) | 58.9 | 7.4 | 6.0 | 12 | 10 |
| FABRIKx (P) | 60.4 | 5.4 | 4.1 | 13 | 10 | |
| FABRIKc | 53.1 | 8.2 | 6.2 | 24 | 18 | |
| Jacobian | 0 | N/A | N/A | N/A | N/A | |
| Jacobian (S) | 5.2 | 401.3 | 411.0 | 60 | 61 | |
6. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Axinte, D.; Dong, X.; Palmer, D.; Rushworth, A.; Guzman, S.C.; Olarra, A.; Arizaga, I.; Gomez-Acedo, E.; Txoperena, K.; Pfeiffer, K.; et al. MiRoR—Miniaturized Robotic Systems for Holistic In-Situ Repair and Maintenance Works in Restrained and Hazardous Environments. IEEE/ASME Trans. Mechatron. 2018, 23, 978–981. [Google Scholar] [CrossRef]
- Dong, X.; Axinte, D.; Palmer, D.; Cobos, S.; Raffles, M.; Rabani, A.; Kell, J. Development of a Slender Continuum Robotic System for On-Wing Inspection/Repair of Gas Turbine Engines. Robot. Comput. Integr. Manuf. 2017, 44, 218–229. [Google Scholar] [CrossRef]
- Buckingham, R.; Graham, A. Nuclear Snake-Arm Robots. Ind. Rob. 2012, 39, 6–11. [Google Scholar] [CrossRef]
- Dong, X.; Wang, M.; Mohammad, A.; Ba, W.; Russo, M.; Norton, A.; Kell, J.; Axinte, D. Continuum Robots Collaborate for Safe Manipulation of High-Temperature Flame to Enable Repairs in Challenging Environments. IEEE/ASME Trans. Mechatron. 2022, 27, 4217–4220. [Google Scholar] [CrossRef]
- Nahar, D.; Yanik, P.M.; Walker, I.D. Robot Tendrils: Long, Thin Continuum Robots for Inspection in Space Operations. In Proceedings of the 2017 IEEE Aerospace Conference, Big Sky, MT, USA, 4–11 March 2017; pp. 1–8. [Google Scholar]
- Santiago, J.L.C.; Walker, I.D.; Godage, I.S. Continuum Robots for Space Applications Based on Layer-Jamming Scales with Stiffening Capability. In Proceedings of the 2015 IEEE Aerospace Conference, Big Sky, MT, USA, 7–14 March 2015; pp. 1–13. [Google Scholar]
- Liljeback, P.; Mills, R. Eelume: A Flexible and Subsea Resident IMR Vehicle. In Proceedings of the OCEANS 2017–Aberdeen, Aberdeen, UK, 19–22 June 2017; Volume 2017, pp. 1–4. [Google Scholar]
- Burgner-Kahrs, J.; Rucker, D.C.; Choset, H. Continuum Robots for Medical Applications: A Survey. IEEE Trans. Robot. 2015, 31, 1261–1280. [Google Scholar] [CrossRef]
- Zhang, Y.; Lu, M. A Review of Recent Advancements in Soft and Flexible Robots for Medical Applications. Int. J. Med. Robot. Comput. Assist. Surg. 2020, 16, e2096. [Google Scholar] [CrossRef]
- Da Veiga, T.; Chandler, J.H.; Lloyd, P.; Pittiglio, G.; Wilkinson, N.J.; Hoshiar, A.K.; Harris, R.A.; Valdastri, P. Challenges of Continuum Robots in Clinical Context: A Review. Prog. Biomed. Eng. 2020, 2, 032003. [Google Scholar] [CrossRef]
- Hannan, M.W.; Walker, I.D. Novel Kinematics for Continuum Robots. In Advances in Robot Kinematics; Springer: Dordrecht, The Netherlands, 2000; pp. 227–238. [Google Scholar]
- Jones, B.A.; Walker, I.D. Kinematics for Multisection Continuum Robots. IEEE Trans. Robot. 2006, 22, 43–55. [Google Scholar] [CrossRef]
- Wu, H.; Yu, J.; Pan, J.; Ge, G.; Pei, X. A New Geometric Method for Solving the Inverse Kinematics of Two-Segment Continuum Robot. In International Conference on Intelligent Robotics and Applications; Springer: Cham, Switzerland, 2022; pp. 101–112. [Google Scholar]
- Santoso, J.; Onal, C.D. An Origami Continuum Robot Capable of Precise Motion Through Torsionally Stiff Body and Smooth Inverse Kinematics. Soft Robot. 2021, 8, 371–386. [Google Scholar] [CrossRef]
- Garriga-Casanovas, A.; Rodriguez y Baena, F. Kinematics of Continuum Robots With Constant Curvature Bending and Extension Capabilities. J. Mech. Robot. 2019, 11, 011010. [Google Scholar] [CrossRef]
- Wu, L.; Crawford, R.; Roberts, J. Dexterity Analysis of Three 6-DOF Continuum Robots Combining Concentric Tube Mechanisms and Cable-Driven Mechanisms. IEEE Robot. Autom. Lett. 2017, 2, 514–521. [Google Scholar] [CrossRef]
- Li, Z.; Chiu, P.W.Y.; Du, R. Design and Kinematic Modeling of a Concentric Wire-Driven Mechanism Targeted for Minimally Invasive Surgery. In Proceedings of the 2016 IEEE/RSJ International Conference on Intelligent Robots and Systems (IROS), Daejeon, Korea, 9–14 October 2016; Volume 2016, pp. 310–316. [Google Scholar]
- Neppalli, S.; Csencsits, M.A.; Jones, B.A.; Walker, I.D. Closed-Form Inverse Kinematics for Continuum Manipulators. Adv. Robot. 2009, 23, 2077–2091. [Google Scholar] [CrossRef]
- Lai, J.; Huang, K.; Chu, H.K. A Learning-Based Inverse Kinematics Solver for a Multi-Segment Continuum Robot in Robot-Independent Mapping. In Proceedings of the 2019 IEEE International Conference on Robotics and Biomimetics (ROBIO), Dali, China, 6–8 December 2019; pp. 576–582. [Google Scholar]
- Zhang, W.; Yang, Z.; Dong, T.; Xu, K. FABRIKc: An Efficient Iterative Inverse Kinematics Solver for Continuum Robots. In Proceedings of the 2018 IEEE/ASME International Conference on Advanced Intelligent Mechatronics (AIM), Auckland, New Zealand, 9–12 July 2018; Volume 2018, pp. 346–352. [Google Scholar]
- Kolpashchikov, D.; Laptev, N.; Danilov, V.; Skirnevskiy, I.; Manakov, R.; Gerget, O. FABRIK-Based Inverse Kinematics For Multi-Section Continuum Robots. In Proceedings of the 2018 18th International Conference on Mechatronics, Brno, Czech Republic, 5–7 December 2018. [Google Scholar]
- Gonthina, P.S.; Kapadia, A.D.; Godage, I.S.; Walker, I.D. Modeling Variable Curvature Parallel Continuum Robots Using Euler Curves. In Proceedings of the 2019 International Conference on Robotics and Automation (ICRA), Montreal, QC, Canada, 20–24 May 2019; Volume 2019, pp. 1679–1685. [Google Scholar]
- Srivastava, M.; Ammons, J.; Peerzada, A.B.; Krovi, V.N.; Rangaraju, P.; Walker, I.D. 3D Printing of Concrete with a Continuum Robot Hose Using Variable Curvature Kinematics. In Proceedings of the 2022 International Conference on Robotics and Automation (ICRA), Philadelphia, PA, USA, 23–27 May 2022; pp. 3216–3222. [Google Scholar]
- Singh, I.; Amara, Y.; Melingui, A.; Mani Pathak, P.; Merzouki, R. Modeling of Continuum Manipulators Using Pythagorean Hodograph Curves. Soft Robot. 2018, 5, 425–442. [Google Scholar] [CrossRef] [PubMed]
- Godage, I.S.; Medrano-Cerda, G.A.; Branson, D.T.; Guglielmino, E.; Caldwell, D.G. Modal Kinematics for Multisection Continuum Arms. Bioinspir. Biomim. 2015, 10, 035002. [Google Scholar] [CrossRef] [PubMed]
- Mahl, T.; Hildebrandt, A.; Sawodny, O. A Variable Curvature Continuum Kinematics for Kinematic Control of the Bionic Handling Assistant. IEEE Trans. Robot. 2014, 30, 935–949. [Google Scholar] [CrossRef]
- Melingui, A.; Merzouki, R.; Mbede, J.B.; Escande, C.; Benoudjit, N. Neural Networks Based Approach for Inverse Kinematic Modeling of a Compact Bionic Handling Assistant Trunk. In Proceedings of the 2014 IEEE 23rd International Symposium on Industrial Electronics (ISIE), Istanbul, Turkey, 1–4 June 2014; pp. 1239–1244. [Google Scholar]
- Lakhal, O.; Melingui, A.; Merzouki, R. Hybrid Approach for Modeling and Solving of Kinematics of a Compact Bionic Handling Assistant Manipulator. IEEE/ASME Trans. Mechatron. 2016, 21, 1326–1335. [Google Scholar] [CrossRef]
- Ba, W.; Dong, X.; Mohammad, A.; Wang, M.; Axinte, D.; Norton, A. Design and Validation of a Novel Fuzzy-Logic-Based Static Feedback Controller for Tendon-Driven Continuum Robots. IEEE/ASME Trans. Mechatron. 2021, 26, 3010–3021. [Google Scholar] [CrossRef]
- Tan, N.; Yu, P.; Zhang, X.; Wang, T. Model-Free Motion Control of Continuum Robots Based on a Zeroing Neurodynamic Approach. Neural Networks 2021, 133, 21–31. [Google Scholar] [CrossRef]
- Morimoto, R.; Nishikawa, S.; Niiyama, R.; Kuniyoshi, Y. Model-Free Reinforcement Learning with Ensemble for a Soft Continuum Robot Arm. In Proceedings of the 2021 IEEE 4th International Conference on Soft Robotics (RoboSoft), New Haven, CT, USA, 12–16 April 2021; pp. 141–148. [Google Scholar] [CrossRef]
- Djeffal, S.; Amouri, A.; Mahfoudi, C. Kinematics Modeling and Simulation Analysis of Variable Curvature Kinematics Continuum Robots. UPB Sci. Bull. Ser. D Mech. Eng. 2021, 83, 27–42. [Google Scholar]
- Djeffal, S.; Mahfoudi, C.; Amouri, A. Comparison of Three Meta-Heuristic Algorithms for Solving Inverse Kinematics Problems of Variable Curvature Continuum Robots. In Proceedings of the 2021 European Conference on Mobile Robots (ECMR), Bonn, Germany, 31 August–3 September 2021; pp. 1–6. [Google Scholar]
- Amouri, A.; Mahfoudi, C.; Zaatri, A.; Lakhal, O.; Merzouki, R. A Metaheuristic Approach to Solve Inverse Kinematics of Continuum Manipulators. Proc. Inst. Mech. Eng. Part I J. Syst. Control Eng. 2017, 231, 380–394. [Google Scholar] [CrossRef]
- Aristidou, A.; Lasenby, J. FABRIK: A Fast, Iterative Solver for the Inverse Kinematics Problem. Graph. Models 2011, 73, 243–260. [Google Scholar] [CrossRef]
- Kolpashchikov, D.Y.; Gerget, O.M. Comparison of Inverse Kinematics Algorithms for Multi-Section Continuum Robots. Mekhatronika Avtom. Upr. 2021, 22, 420–424. [Google Scholar] [CrossRef]
- Runge, G.; Wiese, M.; Raatz, A. FEM-Based Training of Artificial Neural Networks for Modular Soft Robots. In Proceedings of the 2017 IEEE International Conference on Robotics and Biomimetics (ROBIO), Macau, Macao, 5–8 December 2017; pp. 385–392. [Google Scholar]


| Section Color | Subsection Lengths, mm | Subsection Weights |
|---|---|---|
| Red | [10, 20, 40] | [3, 2, 1] |
| Blue | [10, 20, 40] | [1, 2, 3] |
| Yellow | [40, 20, 10] | [3, 1, 1] |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Kolpashchikov, D.; Gerget, O.; Danilov, V. FABRIKx: Tackling the Inverse Kinematics Problem of Continuum Robots with Variable Curvature. Robotics 2022, 11, 128. https://doi.org/10.3390/robotics11060128
Kolpashchikov D, Gerget O, Danilov V. FABRIKx: Tackling the Inverse Kinematics Problem of Continuum Robots with Variable Curvature. Robotics. 2022; 11(6):128. https://doi.org/10.3390/robotics11060128
Chicago/Turabian StyleKolpashchikov, Dmitrii, Olga Gerget, and Viacheslav Danilov. 2022. "FABRIKx: Tackling the Inverse Kinematics Problem of Continuum Robots with Variable Curvature" Robotics 11, no. 6: 128. https://doi.org/10.3390/robotics11060128
APA StyleKolpashchikov, D., Gerget, O., & Danilov, V. (2022). FABRIKx: Tackling the Inverse Kinematics Problem of Continuum Robots with Variable Curvature. Robotics, 11(6), 128. https://doi.org/10.3390/robotics11060128







