A Novel Adaptive Sliding Mode Controller for a 2-DOF Elastic Robotic Arm †
Abstract
:1. Introduction
- An adaptive control mechanism is proposed to deal with the controlling task of a 2-DOF elastic robot arm. The control mechanism has two loops. The outer loop is an adaptive sliding mode controller (ASMC) to deal with uncertainties and disturbances on the load side of the robot arm. The output of this loop is the desired angular position of the motors. The inner loop consists of the model reference adaptive controllers (MRAC) to stabilise the motor side of the robot arm;
- Extensive simulation experiments and a comparison with the conventional sliding mode controller are conducted to demonstrate the effectiveness of the proposed controller.
2. Related Research Work
3. Mathematical Model of the 2-DOF Elastic Robot Arm
4. Controller Design
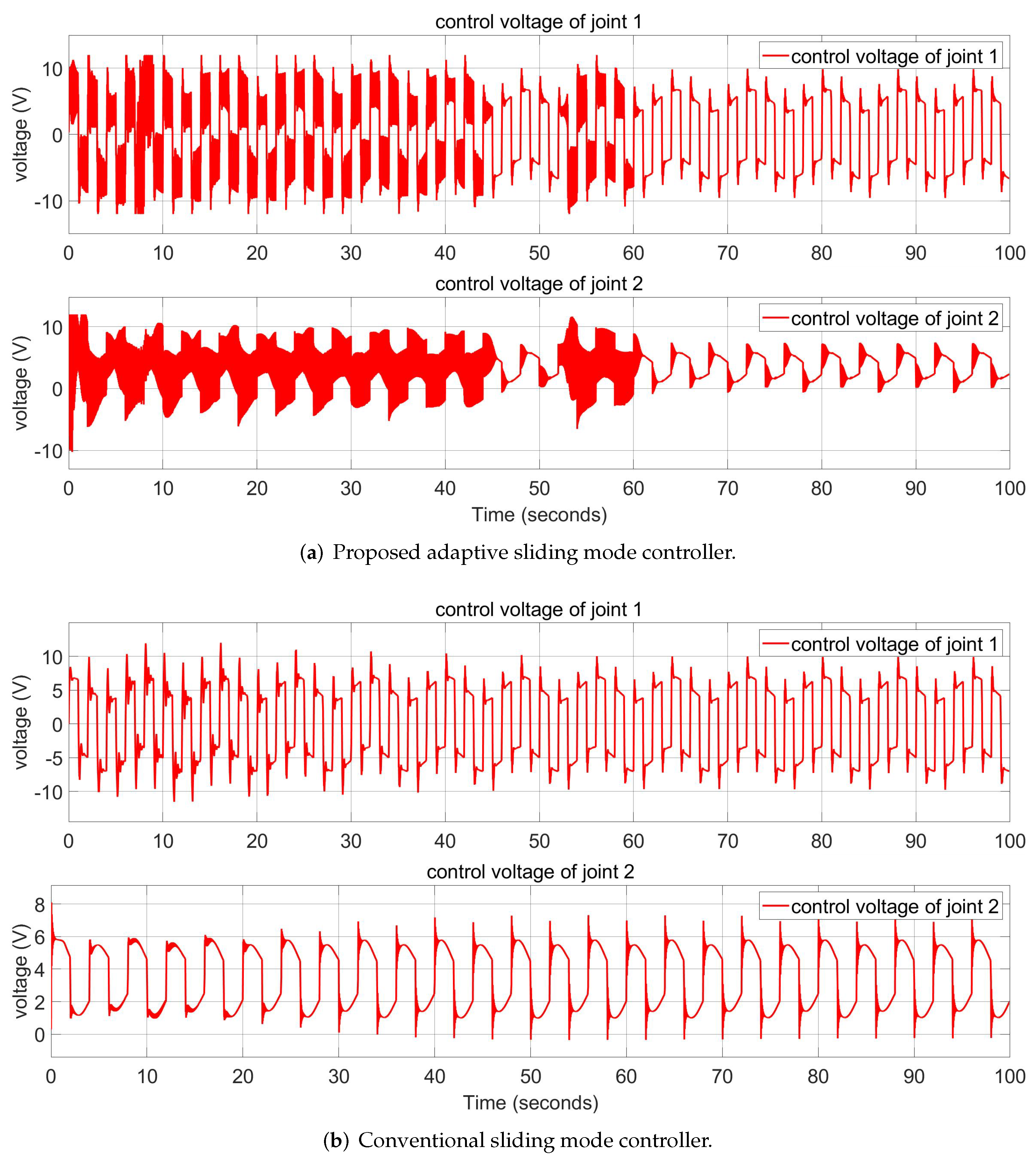
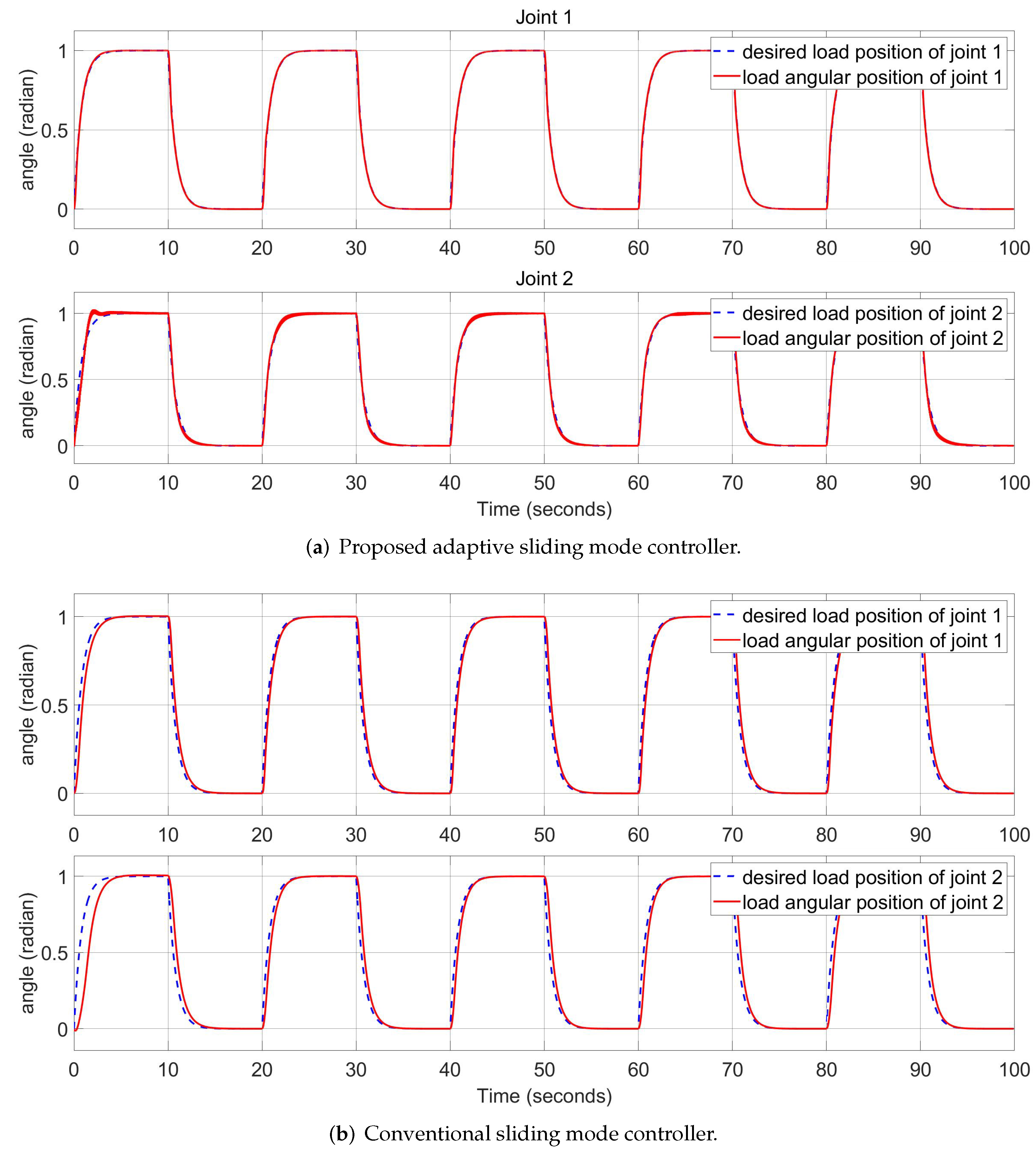
5. Simulation
5.1. Sine Wave Input
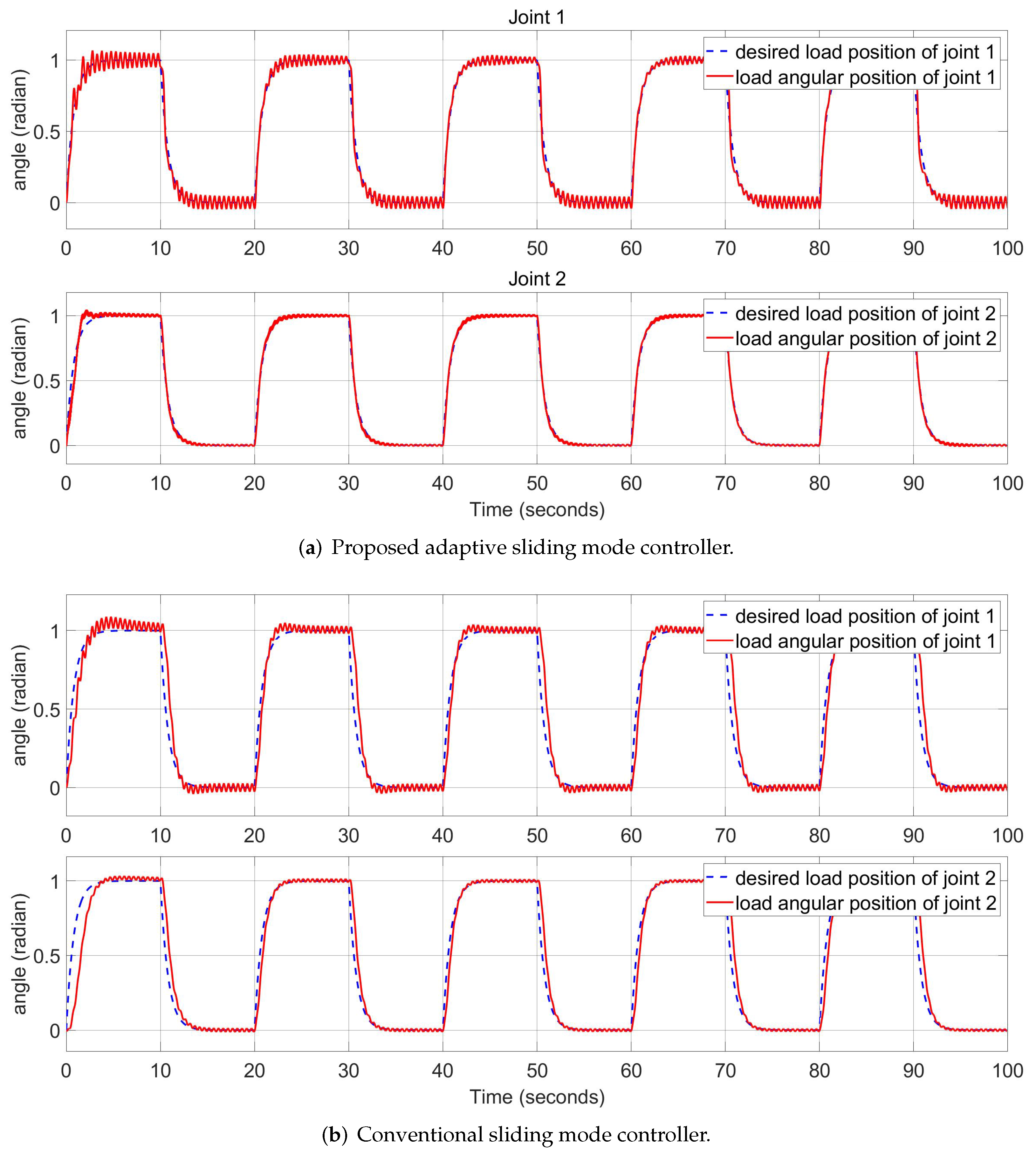
5.2. Square Wave Input
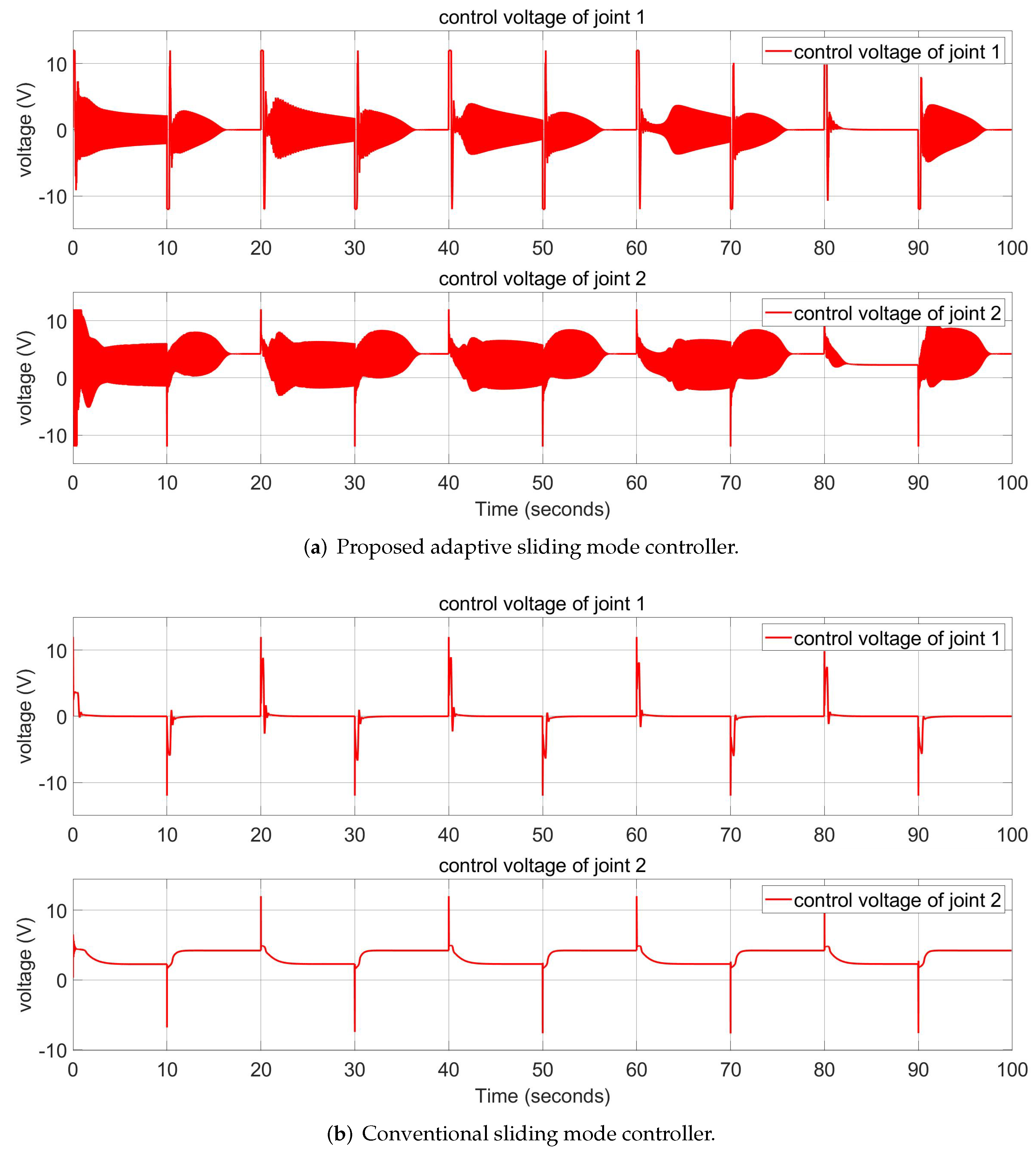
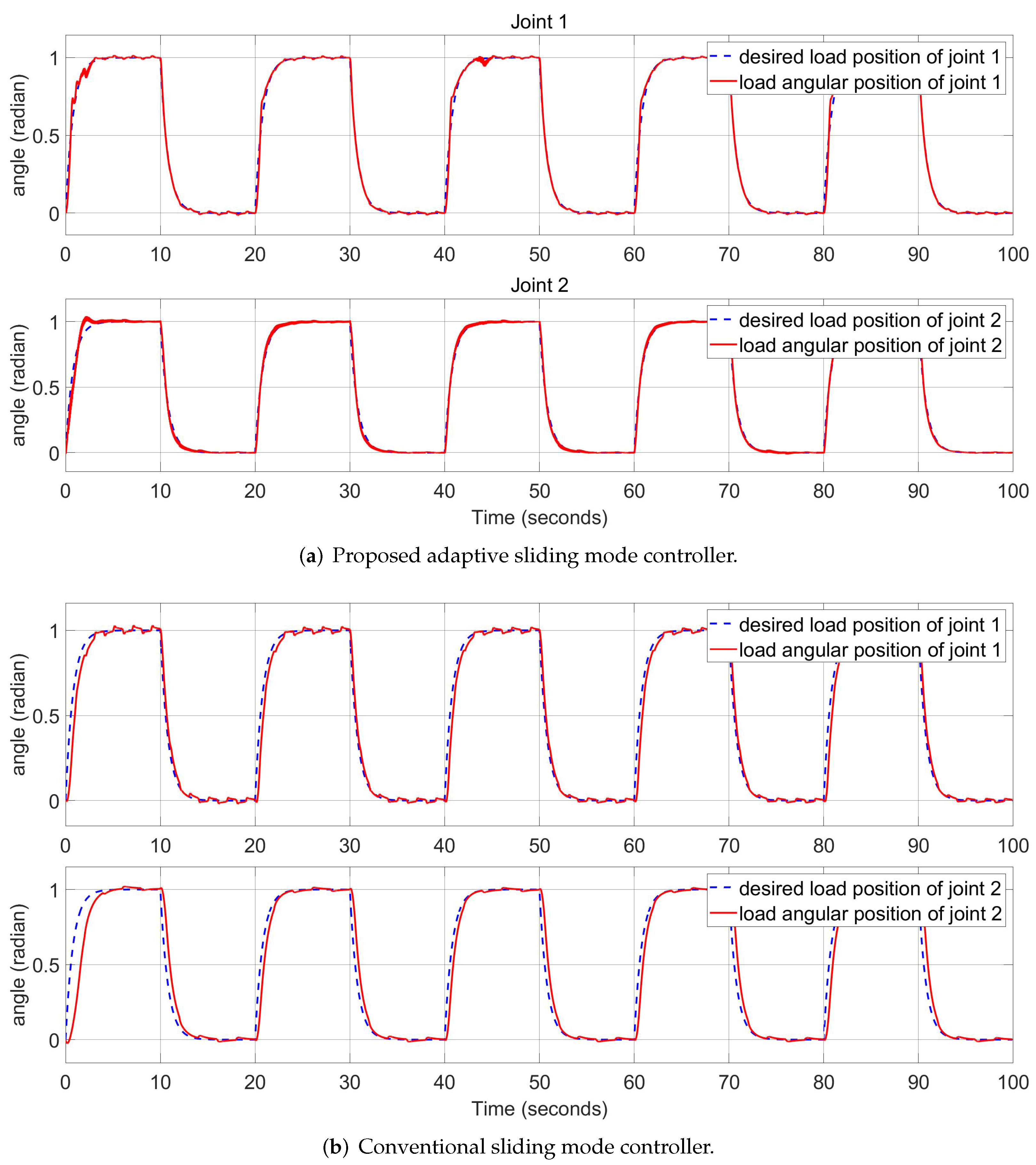
5.3. Step Input
6. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Conflicts of Interest
Abbreviations
| ASMC | Adaptive sliding mode controller |
| MRAC | Model reference adaptive8controllers |
| SAR | Search and rescue |
References
- Govindarajan, V.; Bhattacharya, S.; Kumar, V. Human-robot collaborative topological exploration for search and rescue applications. In Distributed Autonomous Robotic Systems; Springer: Tokyo, Japan, 2016; pp. 17–32. [Google Scholar]
- Brito, T.; Queiroz, J.; Piardi, L.; Fernandes, L.A.; Lima, J.; Leitão, P. A Machine Learning Approach for Collaborative Robot Smart Manufacturing Inspection for Quality Control Systems. Procedia Manuf. 2020, 51, 11–18. [Google Scholar] [CrossRef]
- Mokaram, S.; Aitken, J.M.; Martinez-Hernandez, U.; Eimontaite, I.; Cameron, D.; Rolph, J.; Gwilt, I.; McAree, O.; Law, J. A ROS-integrated API for the KUKA LBR iiwa collaborative robot. IFAC-PapersOnLine 2017, 50, 15859–15864. [Google Scholar] [CrossRef]
- Li, W.; Han, Y.; Wu, J.; Xiong, Z. Collision Detection of Robots Based on a Force/Torque Sensor at the Bedplate. IEEE/ASME Trans. Mechatron. 2020, 25, 2565–2573. [Google Scholar] [CrossRef]
- Xiao, J.; Zhang, Q.; Hong, Y.; Wang, G.; Zeng, F. Collision detection algorithm for collaborative robots considering joint friction. Int. J. Adv. Robot. Syst. 2018, 15, 1729881418788992. [Google Scholar] [CrossRef] [Green Version]
- Jorgensen, S.J.; Lanighan, M.W.; Bertrand, S.S.; Watson, A.; Altemus, J.S.; Askew, R.S.; Bridgwater, L.; Domingue, B.; Kendrick, C.; Lee, J.; et al. Deploying the nasa valkyrie humanoid for ied response: An initial approach and evaluation summary. In Proceedings of the 2019 IEEE-RAS 19th International Conference on Humanoid Robots (Humanoids), Toronto, ON, Canada, 15–17 October 2019; pp. 1–8. [Google Scholar]
- Paine, N.; Mehling, J.S.; Holley, J.; Radford, N.A.; Johnson, G.; Fok, C.L.; Sentis, L. Actuator control for the NASA-JSC Valkyrie humanoid robot: A decoupled dynamics approach for torque control of series elastic robots. J. Field Robot. 2015, 32, 378–396. [Google Scholar] [CrossRef]
- Rollinson, D. Control and Design of Snake Robots. Ph.D. Thesis, Carnegie Mellon University, Pittsburgh, PA, USA, 2014. [Google Scholar]
- Sergi, F.; Lee, M.M.; O’Malley, M.K. Design of a series elastic actuator for a compliant parallel wrist rehabilitation robot. In Proceedings of the 2013 IEEE 13th International Conference on Rehabilitation Robotics (ICORR), Seattle, WA, USA, 24–26 June 2013; pp. 1–6. [Google Scholar]
- Chen, T.; Casas, R.; Lum, P.S. An elbow exoskeleton for upper limb rehabilitation with series elastic actuator and cable-driven differential. IEEE Trans. Robot. 2019, 35, 1464–1474. [Google Scholar] [CrossRef]
- dos Santos, W.M.; Siqueira, A.A. Impedance control of a rotary series elastic actuator for knee rehabilitation. IFAC Proc. Vol. 2014, 47, 4801–4806. [Google Scholar] [CrossRef] [Green Version]
- Tsagarakis, N.G.; Li, Z.; Saglia, J.; Caldwell, D.G. The design of the lower body of the compliant humanoid robot “cCub”. In Proceedings of the 2011 IEEE International Conference on Robotics and Automation, Shanghai, China, 9–13 May 2011; pp. 2035–2040. [Google Scholar]
- Sanfilippo, F.; Azpiazu, J.; Marafioti, G.; Transeth, A.A.; Stavdahl, Ø.; Liljebäck, P. A review on perception-driven obstacle-aided locomotion for snake robots. In Proceedings of the 14th International Conference on Control, Automation, Robotics and Vision (ICARCV), Phuket, Thailand, 13–15 November 2016; pp. 1–7. [Google Scholar]
- Sanfilippo, F.; Azpiazu, J.; Marafioti, G.; Transeth, A.A.; Stavdahl, Ø.; Liljebäck, P. Perception-driven obstacle-aided locomotion for snake robots: The state of the art, challenges and possibilities. Appl. Sci. 2017, 7, 336. [Google Scholar] [CrossRef]
- Williamson, M.M. Series Elastic Actuators. Master’s Thesis, Massachusetts Institute of Technology, Cambridge, MA, USA, 1995. [Google Scholar]
- Li, Y.; Tong, S.; Li, T. Adaptive fuzzy output feedback control for a single-link flexible robot manipulator driven DC motor via backstepping. Nonlinear Anal. Real World Appl. 2013, 14, 483–494. [Google Scholar] [CrossRef]
- Yeon, J.S.; Yim, J.; Park, J.H. Robust control using recursive design method for flexible joint robot manipulators. J. Mech. Sci. Technol. 2011, 25, 3205–3213. [Google Scholar] [CrossRef]
- Barjuei, E.S.; Boscariol, P.; Vidoni, R.; Gasparetto, A. Robust control of three-dimensional compliant mechanisms. J. Dyn. Syst. Meas. Control 2016, 138, 101009. [Google Scholar] [CrossRef]
- Thieffry, M.; Kruszewski, A.; Duriez, C.; Guerra, T.M. Control design for soft robots based on reduced-order model. IEEE Robot. Autom. Lett. 2018, 4, 25–32. [Google Scholar] [CrossRef] [Green Version]
- Shokoohinia, M.R.; Fateh, M.M. Robust dynamic sliding mode control of robot manipulators using the Fourier series expansion. Trans. Inst. Meas. Control 2019, 41, 2488–2495. [Google Scholar] [CrossRef]
- Rsetam, K.; Cao, Z.; Man, Z. Hierarchical non-singular terminal sliding mode controller for a single link flexible joint robot manipulator. In Proceedings of the IEEE 56th Annual Conference on Decision and Control (CDC), Melbourne, VIC, Australia, 12–15 December 2017; pp. 6677–6682. [Google Scholar]
- Soltanpour, M.R.; Moattari, M. Voltage based sliding mode control of flexible joint robot manipulators in presence of uncertainties. Robot. Auton. Syst. 2019, 118, 204–219. [Google Scholar]
- Tajdari, F.; Kabganian, M.; Khodabakhshi, E.; Golgouneh, A. Design, implementation and control of a two-link fully-actuated robot capable of online identification of unknown dynamical parameters using adaptive sliding mode controller. In Proceedings of the Artificial Intelligence and Robotics (IRANOPEN), Qazvin, Iran, 9 April 2017; pp. 91–96. [Google Scholar]
- Guan, P.; Liu, X.J.; Liu, J.Z. Adaptive fuzzy sliding mode control for flexible satellite. Eng. Appl. Artif. Intell. 2005, 18, 451–459. [Google Scholar] [CrossRef]
- Mahmoodabadi, M.; Nejadkourki, N. Trajectory Tracking of a Flexible Robot Manipulator by a New Optimized Fuzzy Adaptive Sliding Mode-Based Feedback Linearization Controller. J. Robot. 2020, 2020, 8813217. [Google Scholar] [CrossRef]
- Zaare, S.; Soltanpour, M.R.; Moattari, M. Adaptive sliding mode control of n flexible-joint robot manipulators in the presence of structured and unstructured uncertainties. Multibody Syst. Dyn. 2019, 47, 397–434. [Google Scholar] [CrossRef]
- Hua, T.M.; Sanfilippo, F.; Helgerud, E. A robust two-feedback loops position control algorithm for compliant low-cost series elastic actuators. In Proceedings of the IEEE International Conference on Systems, Man and Cybernetics (SMC), Bari, Italy, 6–9 October 2019; pp. 2384–2390. [Google Scholar]
- Sanfilippo, F.; Hua, T.M.; Bos, S. A comparison between a two feedback control loop and a reinforcement learning algorithm for compliant low-cost series elastic actuators. In Proceedings of the 53rd Hawaii International Conference on System Sciences (HICSS 2020), Maui, HI, USA, 7–10 January 2020. [Google Scholar]
- Tuan, H.M.; Sanfilippo, F.; Hao, N.V. Modelling and Control of a 2-DOF Robot Arm with Elastic Joints for Safe Human-Robot Interaction. Front. Robot. AI 2021, 8, 679304. [Google Scholar] [CrossRef]
- Tuan, H.M.; Sanfilippo, F.; Hao, N.V. An Adaptive Sliding Mode Controller for a 2-DOF Elastic Robotic Arm. In Proceedings of the 4th International Conference on Intelligent Technologies and Applications (INTAP 2021), Grimstad, Norway, 11–13 October 2021. [Google Scholar]
- Tokat, S.; Fadali, M.S.; Eray, O. A classification and overview of sliding mode controller sliding surface design methods. In Recent Advances in Sliding Modes: From Control to Intelligent Mechatronics; Springer: Cham, Switzerland, 2015; pp. 417–439. [Google Scholar]
- Khan, A.H.; Li, S. Sliding mode control with PID sliding surface for active vibration damping of pneumatically actuated soft robots. IEEE Access 2020, 8, 88793–88800. [Google Scholar] [CrossRef]
- Eker, I. Sliding mode control with PID sliding surface and experimental application to an electromechanical plant. ISA Trans. 2006, 45, 109–118. [Google Scholar] [CrossRef]
- Konno, A.; Uchiyama, M. Vibration suppression control of spatial flexible manipulators. Control Eng. Pract. 1995, 3, 1315–1321. [Google Scholar] [CrossRef]
- Rivera, J.; Garcia, L.; Mora, C.; Raygoza, J.J.; Ortega, S. Super-twisting sliding mode in motion control systems. Sliding Mode Control 2011, 1, 237–254. [Google Scholar]
- Emel’Yanov, S.; Korovin, S.; Levantovskii, L. Higher-order sliding modes in binary control systems. Sov. Phys. Dokl. 1986, 31, 291. [Google Scholar]
- Levant, A. Sliding order and sliding accuracy in sliding mode control. Int. J. Control 1993, 58, 1247–1263. [Google Scholar] [CrossRef]
- Fridman, L.; Levant, A. Higher order sliding modes. Sliding Mode Control Eng. 2002, 11, 53–102. [Google Scholar]
- Levant, A. Robust exact differentiation via sliding mode technique. Automatica 1998, 34, 379–384. [Google Scholar] [CrossRef]
- Lee, S.D.; Lee, B.K.; You, S.S. Sliding Mode Control with Super-Twisting Algorithm for Surge Oscillation of Mooring Vessel System. J. Korean Soc. Mar. Environ. Saf. 2018, 24, 953–959. [Google Scholar] [CrossRef]
- Moreno, J.A.; Osorio, M. A Lyapunov approach to second-order sliding mode controllers and observers. In Proceedings of the 2008 47th IEEE Conference on Decision and Control, Cancun, Mexico, 9–11 December 2008; pp. 2856–2861. [Google Scholar]
- Lavretsky, E. Adaptive control: Introduction, overview, and applications. In Lecture Notes from IEEE Robust and Adaptive Control Workshop; IEEE: Seattle, WA, USA, 9–13 June 2008. [Google Scholar]
- Lin, C.H.; Hsiao, F.Y. Proportional-integral sliding mode control with an application in the balance control of a two-wheel vehicle system. Appl. Sci. 2020, 10, 5087. [Google Scholar] [CrossRef]
- Soon, C.C.; Ghazali, R.; Jaafar, H.I.; Hussien, S.Y.S. Sliding mode controller design with optimized PID sliding surface using particle swarm algorithm. Procedia Comput. Sci. 2017, 105, 235–239. [Google Scholar] [CrossRef]
- Loucif, F.; Kechida, S. Sliding mode control with pid surface for robot manipulator optimized by evolutionary algorithms. In Recent Advances in Engineering Mathematics and Physics; Springer: Cham, Switzerland, 2020; pp. 19–32. [Google Scholar]
- MATLAB Version 9.5.0.944444 (R2018b); The Mathworks, Inc.: Natick, MA, USA, 2018.
- Furat, M.; İlyas, E. Experimental evaluation of sliding-mode control techniques. Çukurova Üniv. Mühendis.-Mimar. Fak. Derg. 2012, 27, 23–37. [Google Scholar]
- Sanfilippo, F.; Helgerud, E.; Stadheim, P.A.; Aronsen, S.L. Serpens, a low-cost snake robot with series elastic torque-controlled actuators and a screw-less assembly mechanism. In Proceedings of the 5th IEEE International Conference on Control, Automation and Robotics (ICCAR), Beijing, China, 19–22 April 2019; pp. 133–139. [Google Scholar]
- Sanfilippo, F.; Helgerud, E.; Stadheim, P.A.; Aronsen, S.L. Serpens: A Highly Compliant Low-Cost ROS-Based Snake Robot with Series Elastic Actuators, Stereoscopic Vision and a Screw-Less Assembly Mechanism. Appl. Sci. 2019, 9, 396. [Google Scholar] [CrossRef] [Green Version]
- Duivon, A.; Kirsch, P.; Mauboussin, B.; Mougard, G.; Woszczyk, J.; Sanfilippo, F. The new design of Serpens, a highly compliant low-cost snake robot. In Proceedings of the 4th International Conference on Intelligent Technologies and Applications (INTAP 2021), Grimstad, Norway, 11–13 October 2021. [Google Scholar]
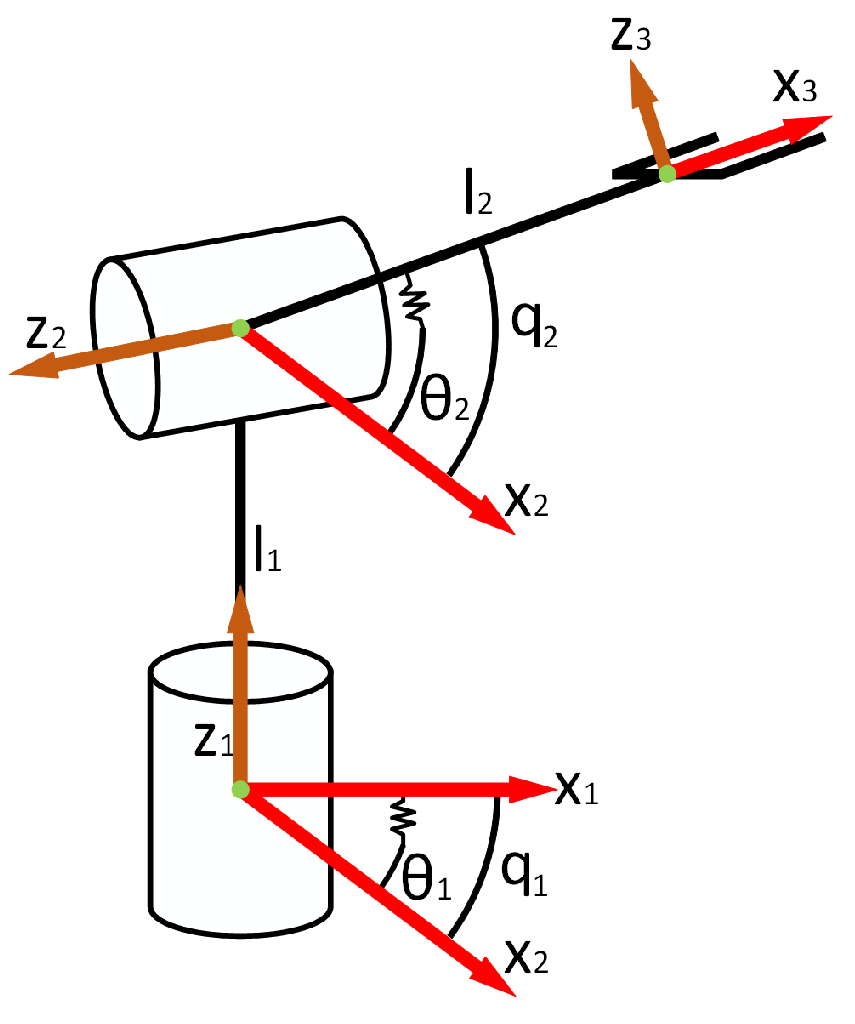
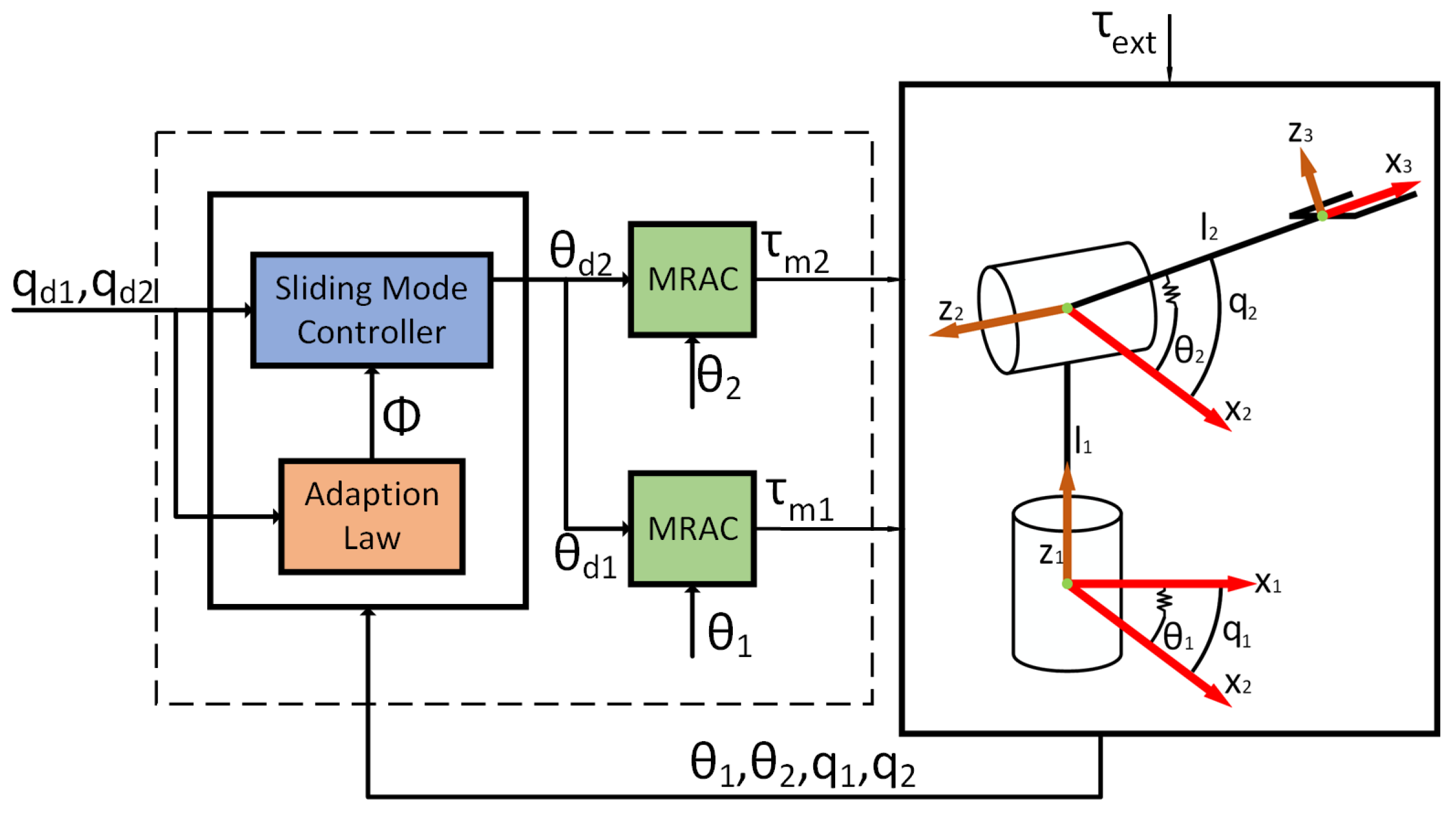









| Type of Robots | Humanoid Robot | Snake Robot | Rehabilitation Robot |
|---|---|---|---|
| Applications | NASA Valkyrie [7] COMAN [12] | POAL [13,14] | RiceWrist [9] ULIX [10] rotary SEA [11] |
| d | a | |||
|---|---|---|---|---|
| Joint 1 | 0 | |||
| Joint 2 | 0 |
| Parameter | Value | Parameter | Value | Parameter | Value |
|---|---|---|---|---|---|
| Gear ratio () | 10 | Spring stiffness () | 1500, 1200 | Load inertia () | 0.1 |
| Load damping coefficient () | 0.2 | Motor damping coefficient () | 0.027 | Motor inertia () | 0.003 |
| Motor mass () | 1 | Link mass () | 6, 4 | Link length () | 0.3 |
| Parameter | Value | Parameter | Value | Parameter | Value |
|---|---|---|---|---|---|
| U | 400 |
| Operating Condition | Normal Condition | Sine Wave Disturbance | Square Wave Disturbance | |
|---|---|---|---|---|
| Controller Type | ||||
| ASMC-MRAC | Joint 1 | 0.009929 | 0.025849 | 0.014397 |
| Joint 2 | 0.026402 | 0.026601 | 0.029558 | |
| SMC-MRAC | Joint 1 | 0.011813 | 0.102562 | 0.017625 |
| Joint 2 | 0.033602 | 0.055017 | 0.038218 |
| Operating Condition | Normal Condition | Sine Wave Disturbance | Square Wave Disturbance | |
|---|---|---|---|---|
| Controller Type | ||||
| ASMC-MRAC | Joint 1 | 0.013186 | 0.033616 | 0.023396 |
| Joint 2 | 0.029123 | 0.028937 | 0.031433 | |
| SMC-MRAC | Joint 1 | 0.049605 | 0.091040 | 0.058128 |
| Joint 2 | 0.085158 | 0.092527 | 0.100103 |
| Performance Specs | RMS Error | Total Variance of Control Signal | |
|---|---|---|---|
| Controller Type | |||
| ASMC-MRAC | Joint 1 | 0.016170 | 0.083913 |
| Joint 2 | 0.025250 | 0.220392 | |
| SMC-MRAC | Joint 1 | 0.064749 | 0.002466 |
| Joint 2 | 0.129457 | 0.002836 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Tuan, H.M.; Sanfilippo, F.; Hao, N.V. A Novel Adaptive Sliding Mode Controller for a 2-DOF Elastic Robotic Arm. Robotics 2022, 11, 47. https://doi.org/10.3390/robotics11020047
Tuan HM, Sanfilippo F, Hao NV. A Novel Adaptive Sliding Mode Controller for a 2-DOF Elastic Robotic Arm. Robotics. 2022; 11(2):47. https://doi.org/10.3390/robotics11020047
Chicago/Turabian StyleTuan, Hua Minh, Filippo Sanfilippo, and Nguyen Vinh Hao. 2022. "A Novel Adaptive Sliding Mode Controller for a 2-DOF Elastic Robotic Arm" Robotics 11, no. 2: 47. https://doi.org/10.3390/robotics11020047
APA StyleTuan, H. M., Sanfilippo, F., & Hao, N. V. (2022). A Novel Adaptive Sliding Mode Controller for a 2-DOF Elastic Robotic Arm. Robotics, 11(2), 47. https://doi.org/10.3390/robotics11020047






