A Deep Reinforcement-Learning Approach for Inverse Kinematics Solution of a High Degree of Freedom Robotic Manipulator
Abstract
:1. Introduction
2. Materials and Methods
2.1. Robotic Arm and PoE-FK Model Description
2.2. Deep Q-Networks for Inverse Kinematics
2.2.1. Background
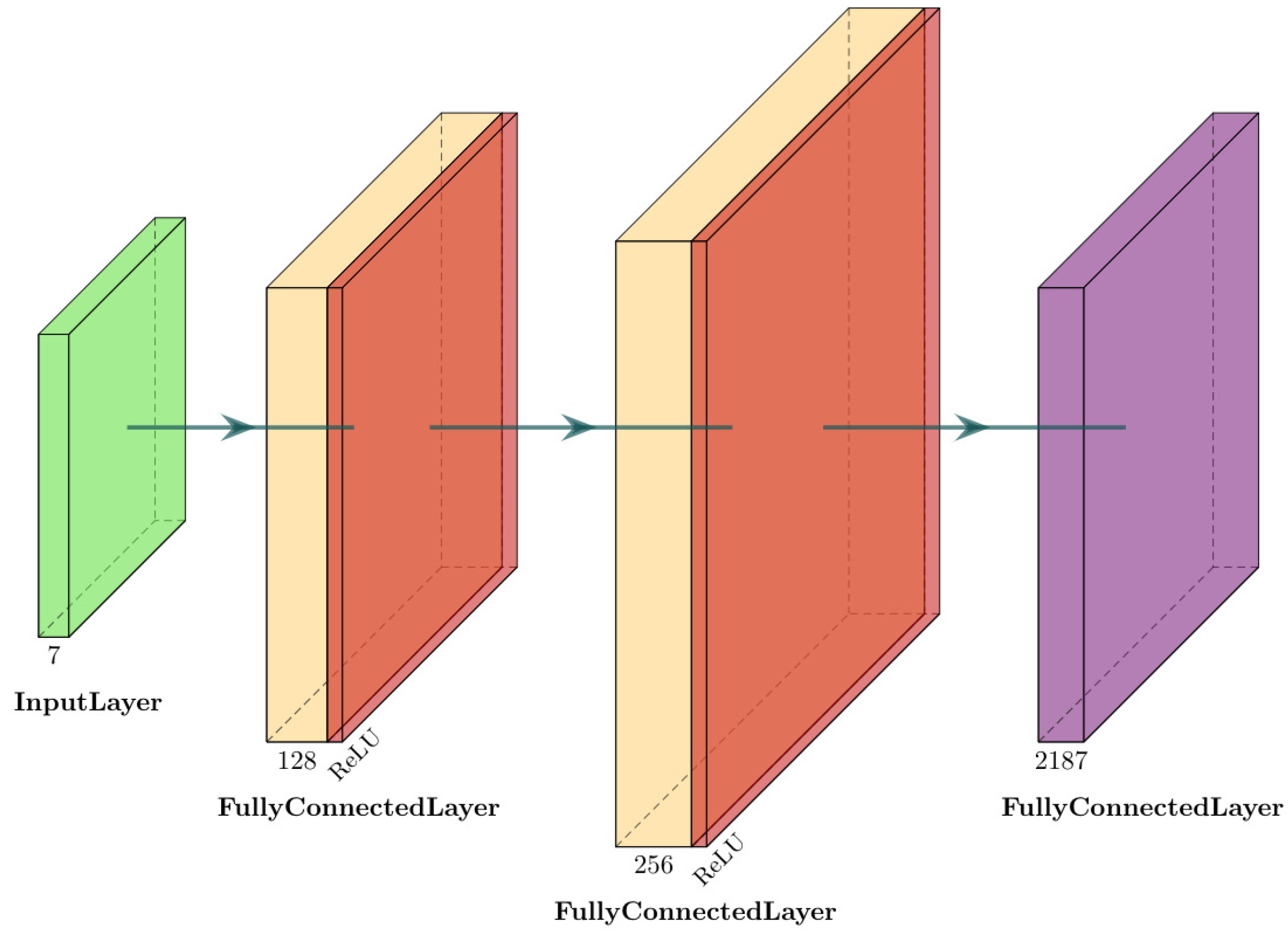
2.2.2. Implementation
| Algorithm 1 Pseudo-code for finding joint positions on the trajectory using DQN. |
| Initialize custom simulated training environment for the DQN agent. |
| Set the initial point of the screw axis to be the closest to the Bézier curve. |
| Initialize the DQN Critic network. |
| Reset initial states: joint positions for the TrajectoryPoint . |
for TrajectoryPoint to MaxTrajectoryPoints do |
for Episode to MaxEpisodes do |
| Observe states for TrajectoryPoint during Episode i. |
| Select action based on DQN Critic network’s weights and the exploration factor. |
| Update states by the amount according to the selected action. |
| Perform action via: |
| Evaluate fitness: |
| Obtain the reward: |
| Store experience in the ExperienceBuffer. |
| Sample random minibatch of transitions from the ExperienceBuffer. |
| Calculate DQN Critic network loss and update network weights. |
| if Fitness == Goal then |
| end if |
| end for |
| end for |
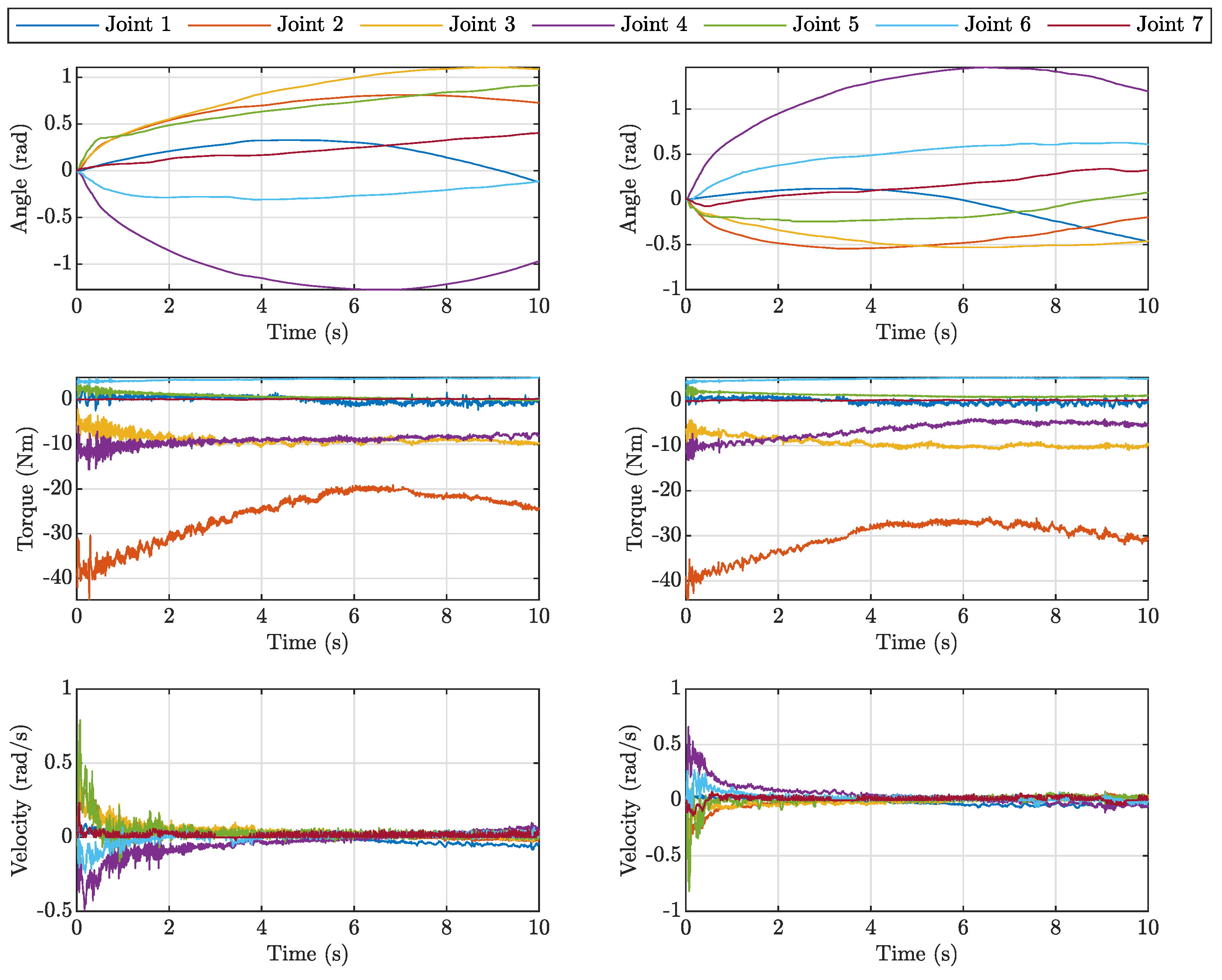
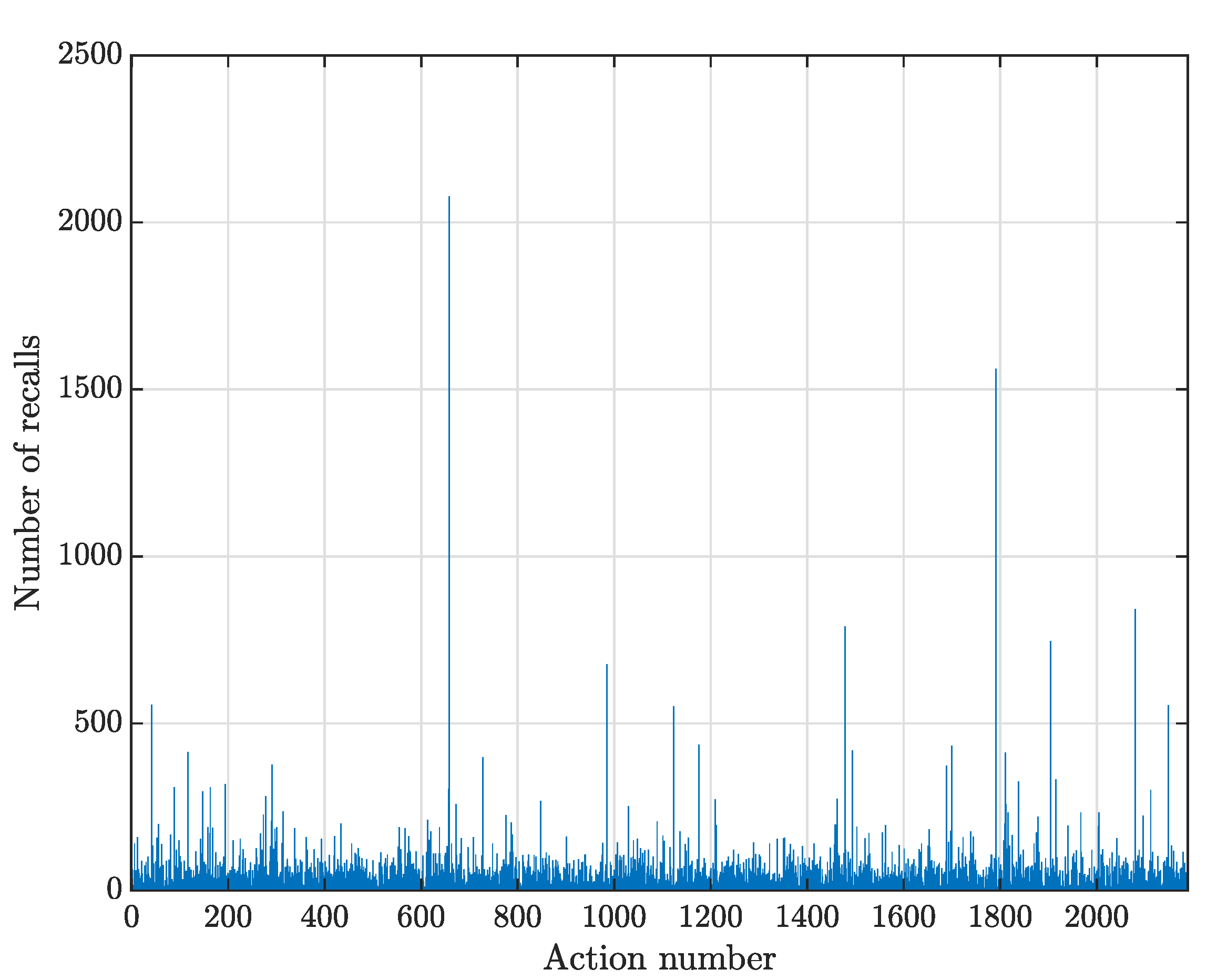
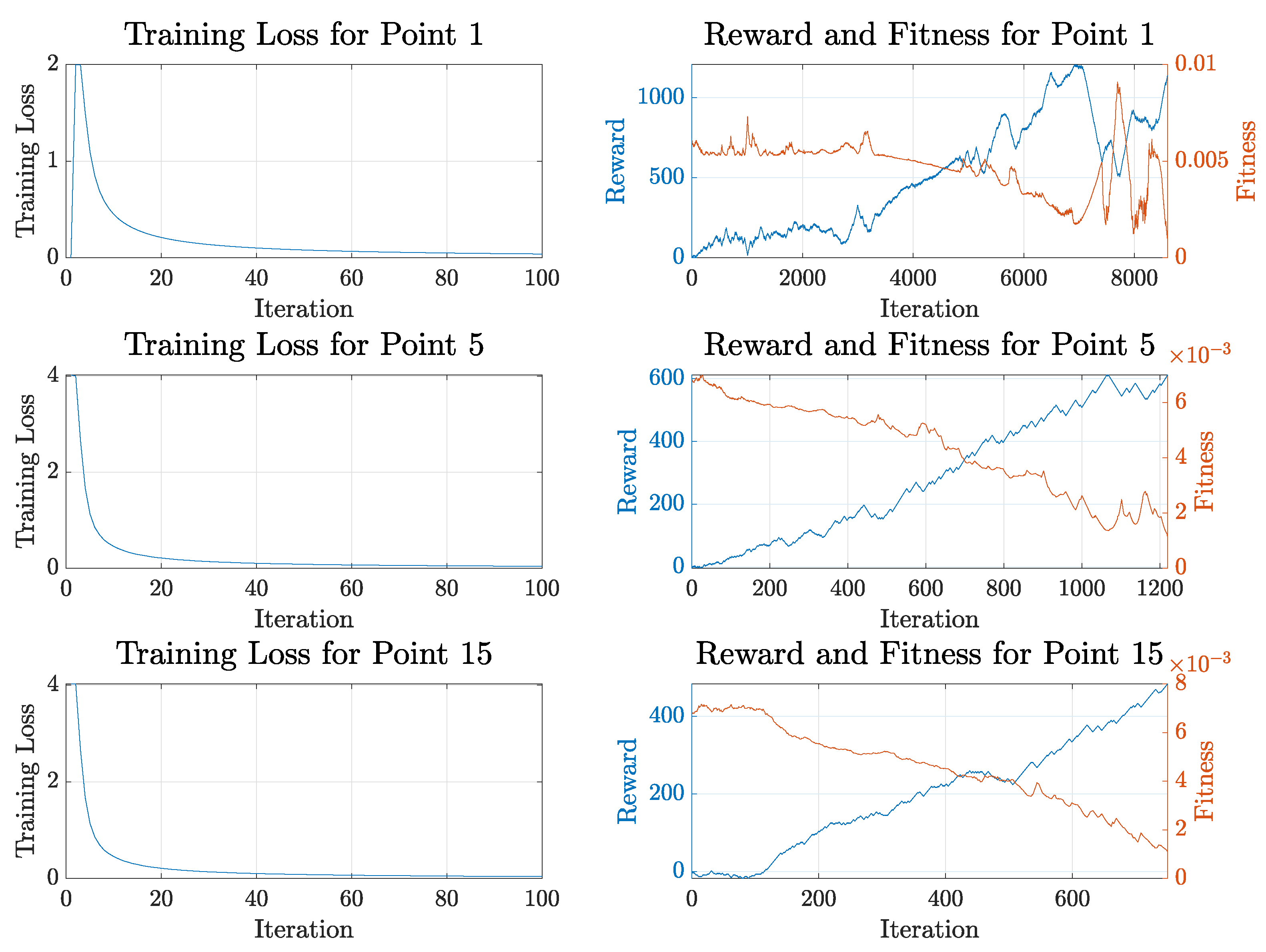
3. Results and Discussion
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Abbreviations
| AI | Artificial Intelligence |
| ANN(s) | Artificial Neural Network(s) |
| CG | Center of Gravity |
| DDPG | Deep Deterministic Policy Gradient |
| DoF | Degree of Freedom |
| DQN | Deep Q-Network |
| D–H | Denavit–Hartenberg |
| FK | Forward Kinematics |
| GA | Genetic Algorithm |
| IK | Inverse Kinematics |
| MDP | Markov Decision Process |
| ML | Machine Learning |
| NAF | Normalized Advantage Function |
| QPFJ | Quintic Polynomial Finite Jerk |
| RL | Reinforcement Learning |
| ROS | Robot Operating System |
| SI | Swarm Intelligence |
| SQP | Sequential-Quadratic Programming |
| PoE | Product of Exponentials |
| PSO | Particle Swarm Optimization |
| URDF | Universal Robot Description Format |
References
- Sridharan, M.; Stone, P. Color Learning on a Mobile Robot: Towards Full Autonomy under Changing Illumination. In Proceedings of the 20th International Joint Conference on Artificial Intelligence, IJCAI 2007, Hyderabad, India, 6–12 January 2007; pp. 2212–2217. [Google Scholar]
- Yip, M.; Das, N. Robot autonomy for surgery. In The Encyclopedia of MEDICAL ROBOTICS: Volume 1 Minimally Invasive Surgical Robotics; World Scientific: Singapore, 2019; pp. 281–313. [Google Scholar]
- Beeson, P.; Ames, B. TRAC-IK: An open-source library for improved solving of generic inverse kinematics. In Proceedings of the 2015 IEEE-RAS 15th International Conference on Humanoid Robots (Humanoids), Seoul, Korea, 3–5 November 2015; pp. 928–935. [Google Scholar]
- Malik, A.; Henderson, T.; Prazenica, R. Multi-Objective Swarm Intelligence Trajectory Generation for a 7 Degree of Freedom Robotic Manipulator. Robotics 2021, 10, 127. [Google Scholar] [CrossRef]
- Collinsm, T.J.; Shen, W.M. Particle swarm optimization for high-DOF inverse kinematics. In Proceedings of the 2017 3rd International Conference on Control, Automation and Robotics (ICCAR), Nagoya, Japan, 24–26 April 2017; pp. 1–6. [Google Scholar]
- Gu, S.; Holly, E.; Lillicrap, T.; Levine, S. Deep reinforcement learning for robotic manipulation with asynchronous off-policy updates. In Proceedings of the 2017 IEEE International Conference on Robotics and Automation (ICRA), Singapore, 29 May–3 June 2017; pp. 3389–3396. [Google Scholar]
- Gu, S.; Holly, E.; Lillicrap, T.; Levine, S. Deep reinforcement learning for robotic manipulation. arXiv 2016, arXiv:1610.00633. [Google Scholar]
- Malik, A. Trajectory Generation for a Multibody Robotic System: Modern Methods Based on Product of Exponentials. Ph.D. Thesis, Embry-Riddle Aeronautical University, Daytona Beach, FL, USA, 2021. [Google Scholar]
- Matheron, G.; Perrin, N.; Sigaud, O. The problem with DDPG: Understanding failures in deterministic environments with sparse rewards. arXiv 2019, arXiv:1911.11679. [Google Scholar]
- Nikishin, E.; Izmailov, P.; Athiwaratkun, B.; Podoprikhin, D.; Garipov, T.; Shvechikov, P.; Vetrov, D.; Wilson, A.G. Improving stability in deep reinforcement learning with weight averaging. In Proceedings of the UAI 2018 Workshop: Uncertainty in Deep Learning, Monterey, CA, USA, 10 August 2018. [Google Scholar]
- Tiong, T.; Saad, I.; Teo, K.T.K.; bin Lago, H. Deep Reinforcement Learning with Robust Deep Deterministic Policy Gradient. In Proceedings of the 2020 2nd International Conference on Electrical, Control and Instrumentation Engineering (ICECIE), Kuala Lumpur, Malaysia, 28 November 2020; pp. 1–5. [Google Scholar]
- Zhang, F.; Leitner, J.; Milford, M.; Upcroft, B.; Corke, P. Towards vision-based deep reinforcement learning for robotic motion control. arXiv 2015, arXiv:1511.03791. [Google Scholar]
- Sasaki, H.; Horiuchi, T.; Kato, S. A study on vision-based mobile robot learning by deep Q-network. In Proceedings of the 2017 56th Annual Conference of the Society of Instrument and Control Engineers of Japan (SICE), Kanazawa, Japan, 19–22 September 2017; pp. 799–804. [Google Scholar]
- Yang, Y.; Li, J.; Peng, L. Multi-robot path planning based on a deep reinforcement learning DQN algorithm. CAAI Trans. Intell. Technol. 2020, 5, 177–183. [Google Scholar] [CrossRef]
- Xin, J.; Zhao, H.; Liu, D.; Li, M. Application of deep reinforcement learning in mobile robot path planning. In Proceedings of the 2017 Chinese Automation Congress (CAC), Jinan, China, 20–22 October 2017; pp. 7112–7116. [Google Scholar]
- Malik, A.; Lischuk, Y.; Henderson, T.; Prazenica, R. Generating Constant Screw Axis Trajectories with Quintic Time Scaling for End-Effector Using Artificial Neural Network and Machine Learning. In Proceedings of the 2021 IEEE Conference on Control Technology and Applications (CCTA), San Diego, CA, USA, 9–11 August 2021; pp. 1128–1134. [Google Scholar]
- Ruan, X.; Ren, D.; Zhu, X.; Huang, J. Mobile robot navigation based on deep reinforcement learning. In Proceedings of the 2019 Chinese Control and Decision Conference (CCDC), Nanchang, China, 3–5 June 2019; pp. 6174–6178. [Google Scholar]
- Zhang, W.; Gai, J.; Zhang, Z.; Tang, L.; Liao, Q.; Ding, Y. Double-DQN based path smoothing and tracking control method for robotic vehicle navigation. Comput. Electron. Agric. 2019, 166, 104985. [Google Scholar] [CrossRef]
- Xue, X.; Li, Z.; Zhang, D.; Yan, Y. A deep reinforcement learning method for mobile robot collision avoidance based on double dqn. In Proceedings of the 2019 IEEE 28th International Symposium on Industrial Electronics (ISIE), Vancouver, BC, Canada, 12–14 June 2019; pp. 2131–2136. [Google Scholar]
- Guo, Z.; Huang, J.; Ren, W.; Wang, C. A reinforcement learning approach for inverse kinematics of arm robot. In Proceedings of the 2019 4th International Conference on Robotics, Control and Automation, Guangzhou, China, 26–28 July 2019; pp. 95–99. [Google Scholar]
- Phaniteja, S.; Dewangan, P.; Guhan, P.; Sarkar, A.; Krishna, K.M. A deep reinforcement learning approach for dynamically stable inverse kinematics of humanoid robots. In Proceedings of the 2017 IEEE International Conference on Robotics and Biomimetics (ROBIO), Macau, China, 5–8 December 2017; pp. 1818–1823. [Google Scholar]
- Zhong, J.; Wang, T.; Cheng, L. Collision-free path planning for welding manipulator via hybrid algorithm of deep reinforcement learning and inverse kinematics. Complex Intell. Syst. 2021, 1–14. [Google Scholar] [CrossRef]
- Bellman, R. Dynamic programming. Science 1966, 153, 34–37. [Google Scholar] [CrossRef] [PubMed]
- Lillicrap, T.P.; Hunt, J.J.; Pritzel, A.; Heess, N.; Erez, T.; Tassa, Y.; Silver, D.; Wierstra, D. Continuous control with deep reinforcement learning. arXiv 2015, arXiv:1509.02971. [Google Scholar]
- Robotics, R. Sawyer. Available online: https://sdk.rethinkrobotics.com/intera/Main_Page (accessed on 10 January 2022).
- Lynch, K.M.; Park, F.C. Modern Robotics; Cambridge University Press: Cambridge, UK, 2017. [Google Scholar]
- Malik, A.; Henderson, T.; Prazenica, R.J. Trajectory Generation for a Multibody Robotic System using the Product of Exponentials Formulation. In AIAA Scitech 2021 Forum; American Institute of Aeronautics and Astronautics: Reston, VA, USA, 2021; p. 2016. [Google Scholar]
- Korczyk, J.J.; Posada, D.; Malik, A.; Henderson, T. Modeling of an On-Orbit Maintenance Robotic Arm Test-Bed. In 2021 AAS/AIAA Astrodynamics Specialist Conference; American Astronautical Society: Big Sky, MT, USA, 2021. [Google Scholar]
- Malik, A.; Henderson, T.; Prazenica, R.J. Using Products of Exponentials to Define (Draw) Orbits and More. Adv. Astronaut. Sci. 2021, 175, 3319. [Google Scholar]
- Silver, D.; Huang, A.; Maddison, C.J.; Guez, A.; Sifre, L.; Van Den Driessche, G.; Schrittwieser, J.; Antonoglou, I.; Panneershelvam, V.; Lanctot, M.; et al. Mastering the game of Go with deep neural networks and tree search. Nature 2016, 529, 484–489. [Google Scholar] [CrossRef] [PubMed]
- Mnih, V.; Kavukcuoglu, K.; Silver, D.; Graves, A.; Antonoglou, I.; Wierstra, D.; Riedmiller, M. Playing atari with deep reinforcement learning. arXiv 2013, arXiv:1312.5602. [Google Scholar]
- Shi, X.; Guo, Z.; Huang, J.; Shen, Y.; Xia, L. A Distributed Reward Algorithm for Inverse Kinematics of Arm Robot. In Proceedings of the 2020 5th International Conference on Automation, Control and Robotics Engineering (CACRE), Dalian, China, 19–20 September 2020; pp. 92–96. [Google Scholar]
- Hester, T.; Vecerik, M.; Pietquin, O.; Lanctot, M.; Schaul, T.; Piot, B.; Horgan, D.; Quan, J.; Sendonaris, A.; Dulac-Arnold, G.; et al. Deep q-learning from demonstrations. arXiv 2017, arXiv:1704.03732. [Google Scholar]
- Hu, Z.; Wan, K.; Gao, X.; Zhai, Y. A dynamic adjusting reward function method for deep reinforcement learning with adjustable parameters. Math. Probl. Eng. 2019, 2019, 7619483. [Google Scholar] [CrossRef]




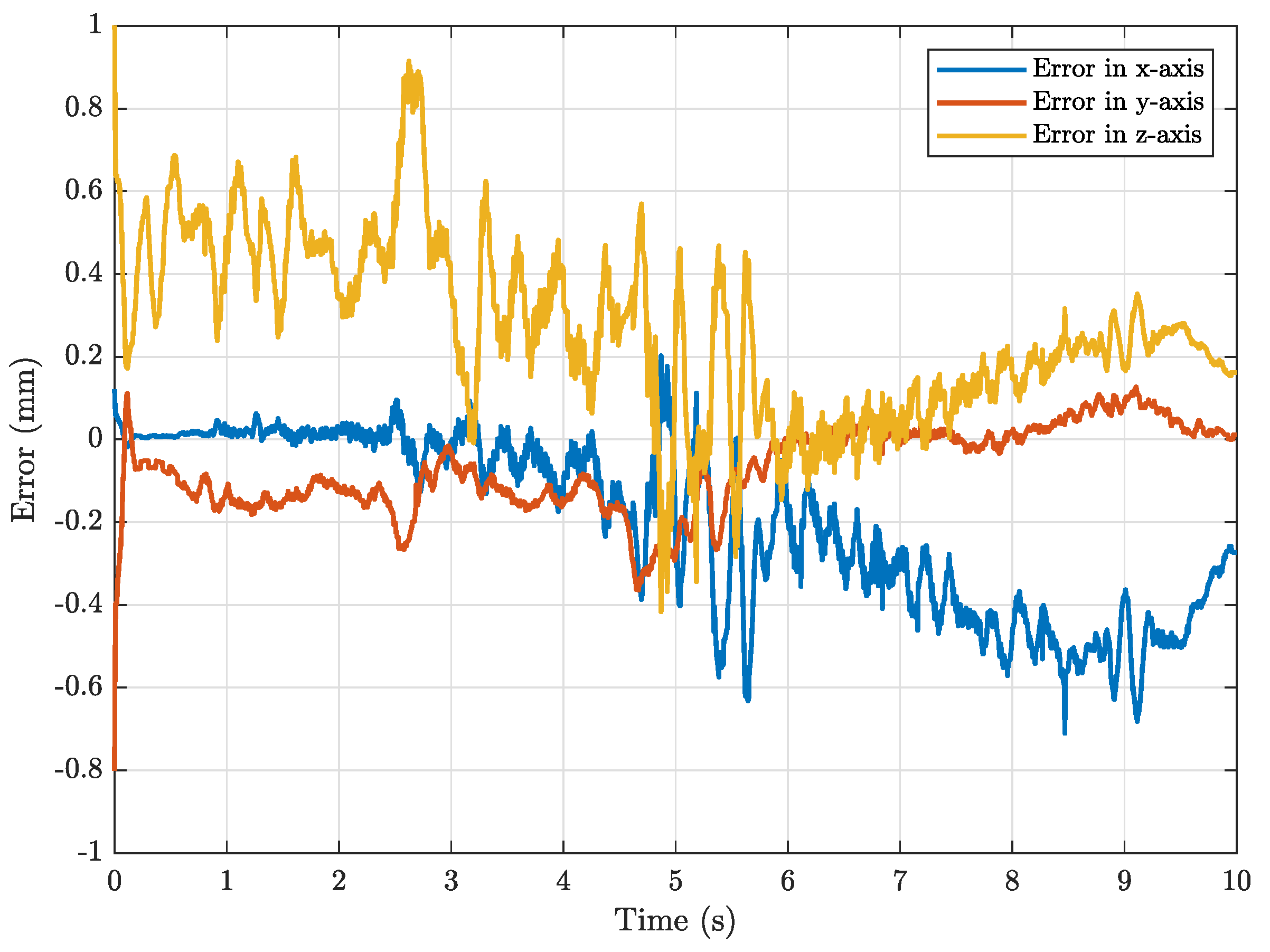

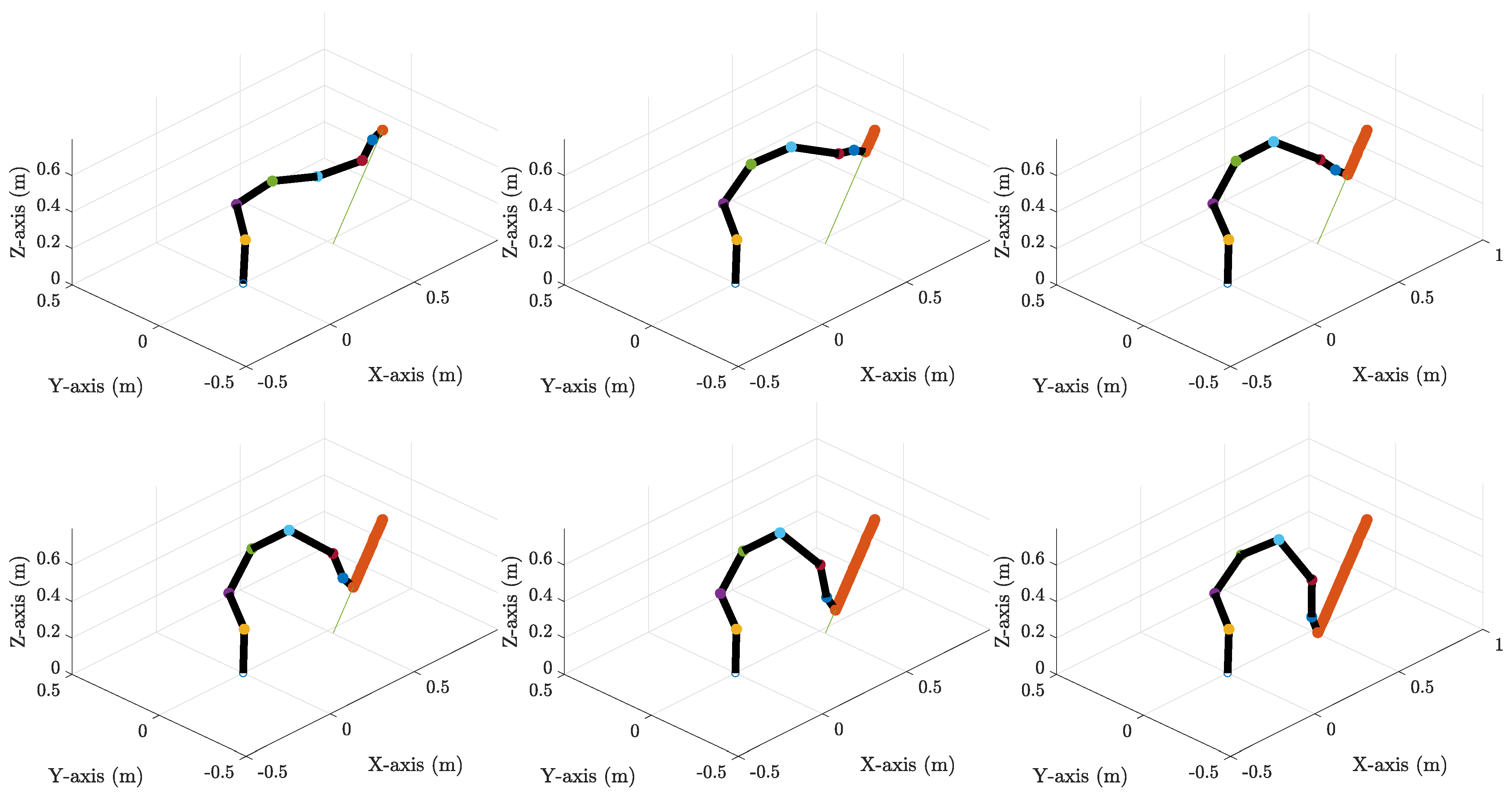
| Parameter | Value |
|---|---|
| Joint-Space Position Step | |
| Learning Rate | 0.01 |
| Discount Factor | 0.9 |
| Gradient Threshold | 1 |
| Mini Batch Size | 64 |
| Target Smooth Factor | |
| Goal Fitness | 0.001 |
| Magnification Factor m | 100 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Malik, A.; Lischuk, Y.; Henderson, T.; Prazenica, R. A Deep Reinforcement-Learning Approach for Inverse Kinematics Solution of a High Degree of Freedom Robotic Manipulator. Robotics 2022, 11, 44. https://doi.org/10.3390/robotics11020044
Malik A, Lischuk Y, Henderson T, Prazenica R. A Deep Reinforcement-Learning Approach for Inverse Kinematics Solution of a High Degree of Freedom Robotic Manipulator. Robotics. 2022; 11(2):44. https://doi.org/10.3390/robotics11020044
Chicago/Turabian StyleMalik, Aryslan, Yevgeniy Lischuk, Troy Henderson, and Richard Prazenica. 2022. "A Deep Reinforcement-Learning Approach for Inverse Kinematics Solution of a High Degree of Freedom Robotic Manipulator" Robotics 11, no. 2: 44. https://doi.org/10.3390/robotics11020044
APA StyleMalik, A., Lischuk, Y., Henderson, T., & Prazenica, R. (2022). A Deep Reinforcement-Learning Approach for Inverse Kinematics Solution of a High Degree of Freedom Robotic Manipulator. Robotics, 11(2), 44. https://doi.org/10.3390/robotics11020044






