Reinforcement Learning for Pick and Place Operations in Robotics: A Survey
Abstract
:1. Introduction
1.1. Robotics Background
1.2. Related Work
1.3. Scope of Review
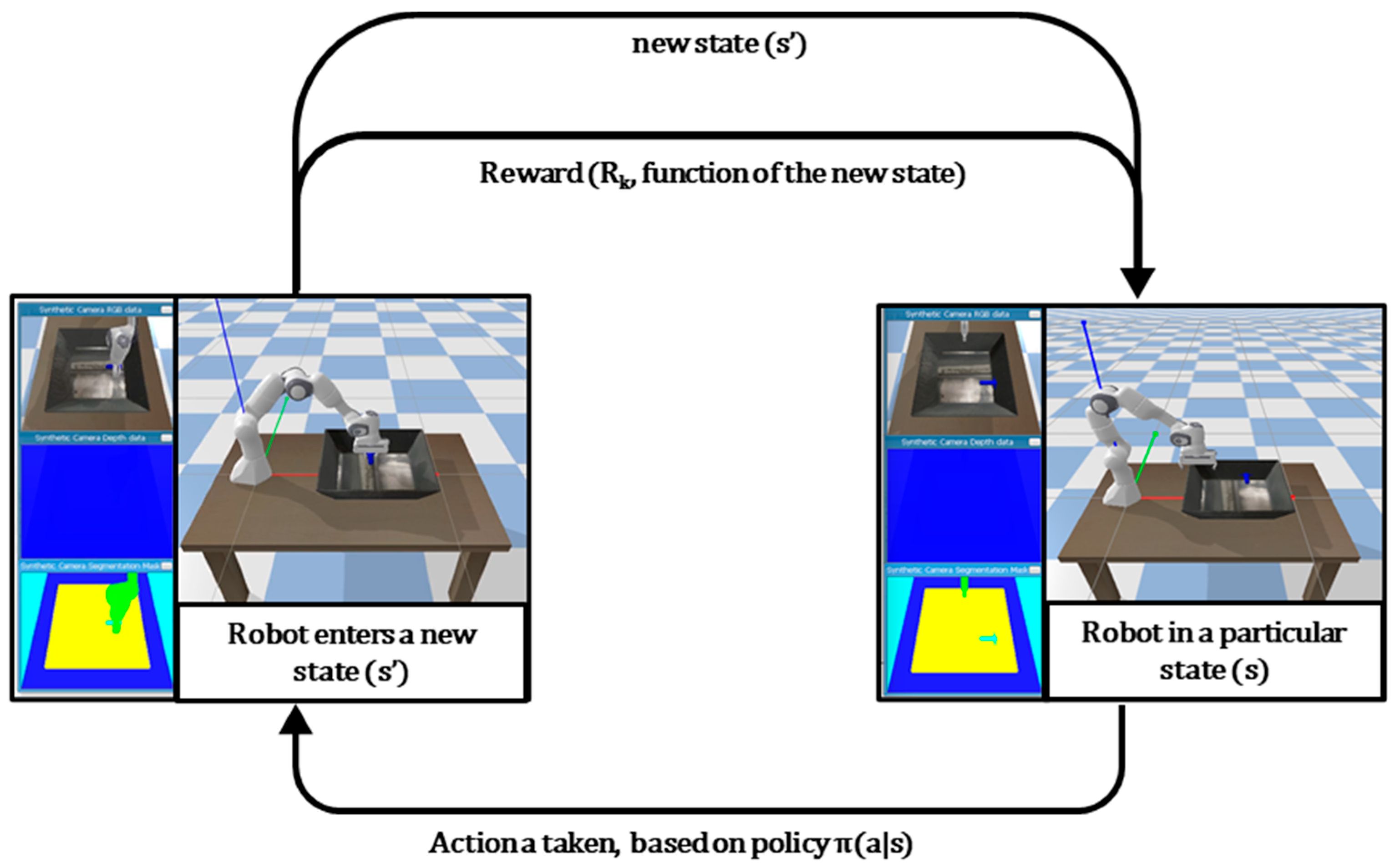
2. RL Formulation
2.1. Markov Decision Process
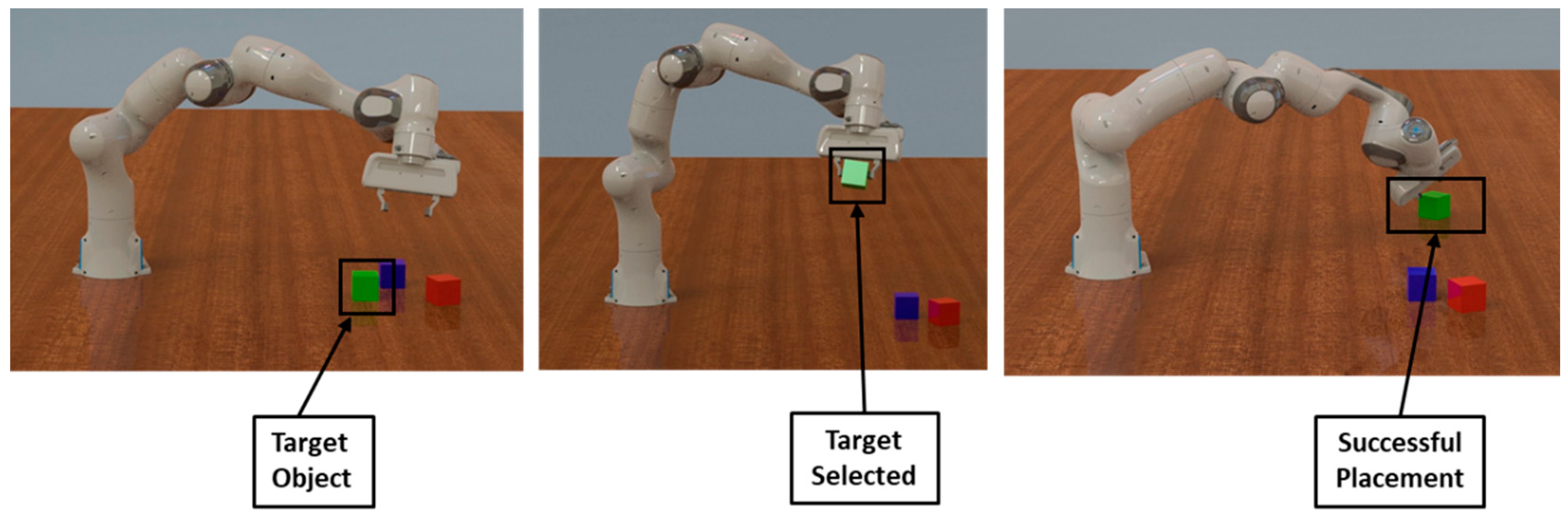
2.2. RL for Pick-and-Place in Robotics
3. Policy Optimization
3.1. Value Function Approach
3.1.1. Value Functions
3.1.2. Dynamic Programming
3.1.3. Model-Free Techniques
3.2. Policy Search Approach
3.2.1. REINFORCE
3.2.2. Actor-Critic Methods
3.2.3. Deterministic Policy Gradient
3.2.4. Proximal Policy Optimization
3.3. Summary
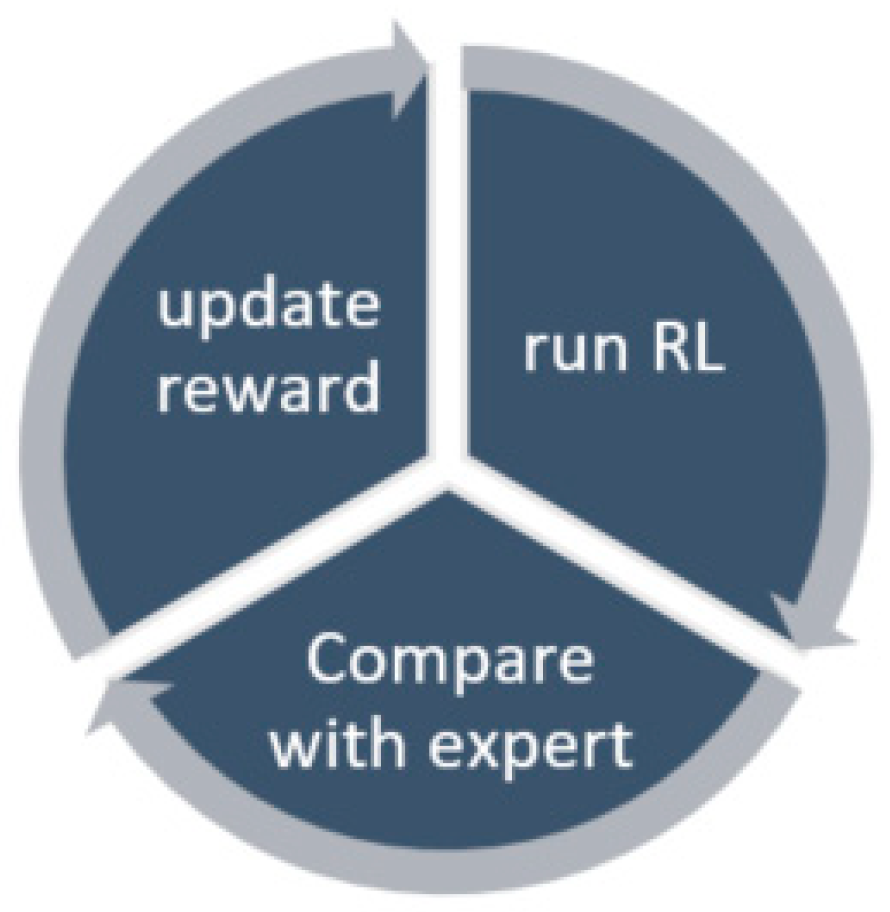
4. Reward Shaping
5. Imitation (Apprenticeship) Learning
5.1. Behavior Cloning
5.2. Inverse Reinforcement Learning
6. Pose Estimation for Grasp Selection
7. Simulation Environment
8. Analysis
8.1. State of Research—Complete Pick-and-Place Task
8.2. State of Research—Pick-and-Place Subtasks
8.3. Critical Discussion
9. Open Problems
10. Conclusions and Future Work
Author Contributions
Funding
Conflicts of Interest
References
- Chang, G.; Stone, W. An effective learning approach for industrial robot programming. In Proceedings of the 2013 ASEE Annual Conference & Exposition, Atlanta, Georgia, 23–26 June 2013. [Google Scholar]
- Massa, D.; Callegari, M.; Cristalli, C. Manual Guidance for Industrial Robot Programming. Ind. Robot Int. J. 2015, 457–465. [Google Scholar] [CrossRef]
- Biggs, G.; MacDonald, B. Survey of robot programming systems. In Proceedings of the Australasian Conference on Robotics and Automation, Brisbane, Australia, 1–3 December 2003; p. 27. [Google Scholar]
- Siciliano, B.; Khatib, O. Springer Handbook of Robotics; Springer: Berlin/Heidelberg, Germany, 2008. [Google Scholar]
- Craig, J.J. Introduction to Robotics Mechanics and Control; Pearson Education International: Upper Saddle River, NJ, USA, 2005. [Google Scholar]
- Hughes, C.; Hughes, T. Robotic Programming: A Guide to Controlling Autonomous Robots; Que: Indianapolis, IN, USA, 2016. [Google Scholar]
- Kumar Saha, S. Introduction to Robotics, 2nd ed.; McGraw Hill Education: New Delhi, India, 2014. [Google Scholar]
- Ajaykumar, G.; Steele, M.; Huang, C.-M. A Survey on End-User Robot Programming. arXiv 2021, arXiv:2105.01757. [Google Scholar] [CrossRef]
- Gasparetto, A.; Scalera, L. A Brief History of Industrial Robotics in the 20th Century. Adv. Hist. Stud. 2019, 8, 24–35. [Google Scholar] [CrossRef] [Green Version]
- Ballestar, M.T.; Díaz-Chao, A.; Sainz, J.; Torrent-Sellens, J. Impact of Robotics on Manufacturing: A Longitudinal Machine Learning Perspective. Technol. Forecast. Soc. Chang. 2020, 162, 120348. [Google Scholar] [CrossRef]
- Pedersen, M.R.; Nalpantidis, L.; Andersen, R.S.; Schou, C.; Bøgh, S.; Krüger, V.; Madsen, O. Robot Skills for Manufacturing: From Concept to Industrial Deployment. Robot. Comput. Integr. Manuf. 2006, 37, 282–291. [Google Scholar] [CrossRef]
- Mohammed, M.Q.; Chung, K.L.; Chyi, C.S. Review of Deep Reinforcement Learning-Based Object Grasping: Techniques, Open Challenges, and Recommendations. IEEE Access 2020, 8, 178450–178481. [Google Scholar] [CrossRef]
- Liu, R.; Nageotte, F.; Zanne, P.; de Mathelin, M.; Dresp-Langley, B. Deep Reinforcement Learning for the Control of Robotic Manipulation: A Focussed Mini-Review. MDPI Robot. 2021, 10, 1–13. [Google Scholar]
- Tai, L.; Zhang, J.; Liu, M.; Boedecker, J.; Burgard, W. Survey of Deep Network Solutions for Learning Control in Robotics: From Reinforcement to Imitation. arXiv 2016, arXiv:1612.07139. [Google Scholar]
- Sutton, R.; Barto, A. Reinforcement Learning: An Introduction; The MIT Press: Cambridge, MA, USA; London, UK, 2018. [Google Scholar]
- Kober, J.; Bagnell, A.; Peters, J. Reinforcement Learning in Robotics: A Survey. Int. J. Robot. Res. 2013, 32, 1238–1274. [Google Scholar] [CrossRef] [Green Version]
- Fu, J.; Levine, S.; Abbeel, P. One-shot learning of manipulation skills with online dynamics adaptation and neural network priors. Proceeding of the 2016 IEEE/RSJ International Conference on Intelligent Robots and Systems (IROS), Daejeon, Korea, 9–14 October 2016; IEEE: New York, NY, USA, 2016; pp. 4019–4026. [Google Scholar]
- Lewis, F.; Dawson, D.; Abdallah, C. Robotic Manipulator Control Theory and Practice, 2nd ed.; Revised and Expanded; Marcel Kekker, Inc.: New York, NY, USA, 2005. [Google Scholar]
- Gualtieri, M.; Pas, A.; Platt, R. Pick and Place without Geometric Object Models; IEEE: Brisbane, QLD, Australia, 2018; pp. 7433–7440. [Google Scholar]
- Stapelberg, B.; Malan, K.M. A Survey of Benchmarking Frameworks for Reinforcement Learning. South Afr. Comput. J. 2020, 32. [Google Scholar] [CrossRef]
- Ng, A.Y.; Harada, D.; Russell, S. Policy Invariance under Reward Transformations Theory and Application to Reward Shaping. In Proceedings of the Sixteenth International Conference on Machine Learning, San Francisco, CA, USA, 27–30 June 1999; pp. 278–287. [Google Scholar]
- Gualtieri, M.; Platt, R. Learning 6-DoF Grasping and Pick-Place Using Attention Focus. In Proceedings of the 2nd Conference on Robot Learning, Zürich, Switzerland, 29 October 2018. [Google Scholar]
- Kleeberger, K.; Bormann, R.; Kraus, W.; Huber, M. A Survey on Learning-Based Robotic Grasping. Curr. Robot. Rep. 2020, 239–249. [Google Scholar] [CrossRef]
- Atkeson, C.; Santamaria, J. A Comparison of Direct and Model-Based Reinforcement Learning. In Proceedings of the 1997 IEEE International Conference on Robotics and Automation, Albuquerque, NM, USA, 25 April 1997. [Google Scholar]
- Sigaud, O.; Buffet, O. Markov Decision Processes in Artificial Intelligence, 2nd ed.; John Wiley & Sons, Inc.: Hoboken, NJ, USA, 2010. [Google Scholar]
- Russell, S.; Norvig, P. Artificial Intelligence A Modern Approach, 4th ed.; Pearson Education, Inc.: Hoboken, NJ, USA; ISBN 978-0-13-461099-3.
- Deisenroth, M.P.; Neumann, G.; Peters, J. A Survey on Policy Search for Robotics. Found. Trends Robot. 2013, 2, 1–114. [Google Scholar] [CrossRef] [Green Version]
- Levine, S.; Koltun, V. Guided policy search. In Proceedings of the Machine Learning Research, Journal of Machine Learning Research, Atlanta, GA, USA, 16 June 2013; Volume 28, pp. 1–9. [Google Scholar]
- Mnih, V.; Badia, A.P.; Mirza, M.; Graves, A.; Lillicrap, T.; Harley, T.; Silver, D.; Kavukcuoglu, K. Asynchronous Methods for Deep Reinforcement Learning. In Proceedings of the 33rd International Conference on Machine Learning, New York, NY, USA, 19–24 June 2016; Volume 48, pp. 1928–1937. [Google Scholar]
- Silver, D.; Lever, G.; Heess, N.; Degris, T.; Wierstra, D.; Riedmiller, M. Deterministic policy gradient algorithms. In Proceedings of the 31st International Conference on Machine Learning, Beijing, China, 16 June 2016; Volume 32. [Google Scholar]
- Schulman, J.; Wolski, F.; Dhariwal, P.; Radford, A.; Klimov, O. Oleg Klimov Proximal Policy Optimization Algorithms. arXiv 2017, arXiv:1707.06347. [Google Scholar]
- Laud, A.D. Theory and Application of Reward Shaping in Reinforcement Learning; University of Illinois at Urbana-Champaign: Champaign, IL, USA, 2004; ISBN 0496782142. [Google Scholar]
- Nagpal, R.; Krishnan, A.U.; Yu, H. Reward Engineering for Object Pick and Place Training. arXiv 2020, arXiv:2001.03792. [Google Scholar]
- Grzes, M.; Kudenko, D. Learning shaping rewards in model-based reinforcement learning. In Proceedings of the AAMAS 2009 Workshop on Adaptive Learning Agents, Budapest, Hungary, 12 May 2009; Volume 115, p. 30. [Google Scholar]
- Mataric, M.J. Reward functions for accelerated learning. In Machine Learning Proceedings, Proceedings of the Eleventh International Conference, Rutgers University, New Brunswick, NJ, USA, 10–13 July 1994; Elsevier: Amsterdam, The Netherlands, 1994; pp. 181–189. [Google Scholar]
- Luo, Y.; Dong, K.; Zhao, L.; Sun, Z.; Zhou, C.; Song, B. Balance between Efficient and Effective Learning: Dense2sparse Reward Shaping for Robot Manipulation with Environment Uncertainty. arXiv 2020, arXiv:2003.02740. [Google Scholar]
- Jang, S.; Han, M. Combining reward shaping and curriculum learning for training agents with high dimensional continuous action spaces. In Proceedings of the 2018 International Conference on Information and Communication Technology Convergence (ICTC), Jeju Island, Korea, 17–19 October 2018; IEEE: New York, NY, USA, 2018; pp. 1391–1393. [Google Scholar]
- Tenorio-Gonzalez, A.C.; Morales, E.F.; Villasenor-Pineda, L. Dynamic Reward Shaping: Training a Robot by Voice. In Proceedings of the Ibero-American Conference on Artificial Intelligence, Bahía Blanca, Argentina, 1–5 November 2010; Springer: New York, NY, USA, 2010; pp. 483–492. [Google Scholar]
- Konidaris, G.; Barto, A. Autonomous shaping: Knowledge transfer in reinforcement learning. In Proceedings of the 23rd International Conference on Machine Learning, Pittsburgh, PA, USA, 25–29 June 2006; pp. 489–496. [Google Scholar]
- Kaelbling, L.P.; Littman, M.L.; Moore, A.W. Reinforcement Learning: A Survey. J. Artif. Intell. Res. 1996, 4, 237–285. [Google Scholar] [CrossRef] [Green Version]
- Ng, A.; Russell, S. Algorithms for Inverse Reinforcement Learning. In Proceedings of the Seventeenth International Conference on Machine Learning, San Francisco, CA, USA, 29 June–2 July 2000. [Google Scholar]
- Osa, T.; Pajarinen, J.; Neumann, G.; Bagnell, J.A.; Abbeel, P.; Peters, J. An Algorithmic Perspective on Imitation Learning. Found. Trends Robot. 2018, 7, 1–179. [Google Scholar] [CrossRef]
- Ho, J.; Ermon, S. Generative Adversarial Imitation Learning. Adv. Neural Inf. Process. Syst. 2016, 29, 4565–4573. [Google Scholar]
- Stephane Ross Interactive Learning for Sequential Decisions and Predictions. Ph.D. Thesis, The Robotics Institute, Carnegie Mellon University, Pittsburgh, PA, USA, 2013.
- Pomerleau, D.A. Alvinn: An Autonomous Land Vehicle in a Neural Network; Technical Report; Carnegie—Mellon University, Artificial Intelligence and Psychology: Pittsburgh, PA, USA, 1989. [Google Scholar]
- Farag, W.; Saleh, Z. Behavior Cloning for Autonomous Driving Using Convolutional Neural Networks. In Proceedings of the 2018 International Conference on Innovation and Intelligence for Informatics, Computing, and Technologies (3ICT), Sakhier, Bahrain, 18–19 November 2018; IEEE: New York, NY, USA, 2018. [Google Scholar]
- Abbeel, P.; Ng, A.Y. Apprenticeship learning via inverse reinforcement learning. In Proceedings of the Twenty-First International Conference on Machine Learning, Banff, AB, Canada, 4–8 July 2004; p. 1. [Google Scholar]
- Bohg, J.; Morales, A.; Asfour, T.; Kragic, D. Data-Driven Grasp Synthesis—A Survey. IEEE Trans. Robot. 2016, 30, 289–309. [Google Scholar] [CrossRef] [Green Version]
- Hodan, T.; Matas, J.; Obdrzalek, S. On evaluation of 6D object pose estimation. In Proceedings of the European Conference on Computer Vision, Amsterdam, The Netherlands, 11–14 October 2016; Springer: Cham, Switzerland, 2016. [Google Scholar]
- Brégier, R.; Devernay, F.; Leyrit, L.; Crowley, J.L. Defining the Pose of Any 3D Rigid Object and an Associated Distance. Int. J. Comput. Vis. 2017, 126, 571–596. [Google Scholar] [CrossRef] [Green Version]
- Gualtieri, M.; Ten Pas, A.; Saenko, K.; Platt, R. High precision grasp pose detection in dense clutter. In Proceedings of the 2016 IEEE/RSJ International Conference on Intelligent Robots and Systems (IROS), Daejeon, Korea, 9–14 October 2016; IEEE: New York, NY, USA, 2016. [Google Scholar]
- Suarez, R.; Roa, M. Grasp Quality Measures: Review and Performance. Auton. Robot. 2014, 38, 65–88. [Google Scholar]
- Sahbani, A.; El-Khoury, S.; Bidaud, P. An Overview of 3D Object Grasp Synthesis Algorithms. Robot. Auton. Syst. 2011, 60, 326–336. [Google Scholar] [CrossRef] [Green Version]
- Jiang, Y.; Moseson, S.; Saxena, A. Efficient grasping from rgbd images: Learning using a New Rectangle Representation. In Proceedings of the IEEE International Conference on Robotics and Automation, Shanghai, China, 9–13 May 2011. [Google Scholar]
- Zeng, A.; Song, S.; Yu, K.-T.; Donlon, E.; Hogan, F. Robotic pick-and-place of novel objects in clutter with multi-affordance grasping and cross-domain image matching. In Proceedings of the 2018 IEEE International Conference on Robotics and Automation (ICRA), Brisbane, QLD, Australia, 21–25 May 2018; IEEE: New York, NY, USA, 2018; pp. 3750–3757. [Google Scholar]
- Tobin, J.; Fong, R.; Ray, A.; Schneider, J.; Zaremba, W.; Abbeel, P. Domain randomization for transferring deep neural networks from simulation to the real world. In Proceedings of the 2017 IEEE/RSJ International Conference on Intelligent Robots and Systems (IROS), Vancouver, BC, Canada, 24–28 September 2017; IEEE: New York, NY, USA, 2017; pp. 23–30. [Google Scholar]
- Huang, S.-W.; Lin, C.-T.; Chen, S.-P.; Wu, Y.-Y.; Hsu, P.-H.; Lai, S.-H. Cross Domain Adaptation with GAN-Based Data Augmentation. In Proceedings of the Lecture Notes in Computer Science: Computer Vision—ECCV 2018, Munich, Germany, 8–14 September 2018; Springer: New York, NY, USA, 2018; Volume 11213, ISBN 978-3-030-01240-3. [Google Scholar]
- Ivaldi, S.; Padois, V.; Nori, F. Tools for Dynamics Simulation of Robots: A Survey based on User Feedback; IEEE: Madrid, Spain, 2014; pp. 842–849. [Google Scholar]
- Erez, T.; Tassa, Y.; Todorov, E. Simulation tools for model-based robotics: Comparison of bullet, Havok, MuJoCo, ODE and PhysX. In Proceedings of the 2015 IEEE International Conference on Robotics and Automation (ICRA), Seattle, WA, USA, 26–30 May 2015; IEEE: New York, NY, USA, 2015; pp. 4397–4404. [Google Scholar]
- Popov, I.; Heess, N.; Lillicrap, T.; Hafner, R.; Barth-Maron, G.; Vecerik, M.; Lampe, T.; Tassa, Y.; Erez, T.; Riedmiller, M. Data-Efficient Deep Reinforcement Learning for Dexterous Manipulation. arXiv 2017, arXiv:1704.03073. [Google Scholar]
- Mahler, J.; Goldberg, K. Learning deep policies for robot bin picking by simulating robust grasping sequences. In Proceedings of the 1st Annual Conference on Robot Learning, Mountain View, CA, USA, 13 November 2017; pp. 515–524. [Google Scholar]
- Sehgal, A.; La, H.; Louis, S.; Nguyen, H. Deep reinforcement learning using genetic algorithm for parameter optimization. In Proceedings of the 2019 Third IEEE International Conference on Robotic Computing (IRC), Naples, Italy, 25–27 February 2019; IEEE: New York, NY, USA, 2019. [Google Scholar]
- Zuo, G.; Lu, J.; Chen, K.; Yu, J.; Huang, X. Accomplishing robot grasping task rapidly via adversarial training. In Proceedings of the 2019 IEEE International Conference on Real-Time Computing and Robotics, Irkutsk, Russia, 4 August 2019. [Google Scholar]
- Chen, C.; Li, H.Y.; Zhang, X.; Liu, X.; Tan, U.X. Towards robotic picking of targets with background distractors using deep reinforcement learning. In Proceedings of the 2nd WRC Symposium on Advanced Robotics and Automation 2019, Beijing, China, 21 August 2019; IEEE: New York, NY, USA, 2019. [Google Scholar]
- Xiao, Y.; Katt, S.; Ten Pas, A.; Chen, S.; Amato, C. Online planning for target object search in clutter under partial observability. In Proceedings of the 2019 International Conference on Robotics and Automation (ICRA), Montreal, QC, Canada, 20 May 2019; IEEE: New York, NY, USA, 2019. [Google Scholar]
- Liu, D.; Wang, Z.; Lu, B.; Cong, M.; Yu, H.; Zou, Q. A Reinforcement Learning-Based Framework for Robot Manipulation Skill Acquisition. IEEE Access 2020, 8, 108429–108437. [Google Scholar] [CrossRef]
- Mohammed, M.Q.; Chung, K.L.; Chyi, C.S. Pick and Place Objects in a Cluttered Scene Using Deep Reinforcement Learning. Int. J. Mech. Mechatron. Eng. 2020, 20, 50–57. [Google Scholar]
- Li, B.; Lu, T.; Li, J.; Lu, N.; Cai, Y.; Wang, S. ACDER: Augmented curiosity-driven experience replay. In Proceedings of the 2020 IEEE International Conference on Robotics and Automation (ICRA), Paris, France, 31 May–31 August 2020; pp. 4218–4224. [Google Scholar]
- Pore, A.; Aragon-Camarasa, G. On simple reactive neural networks for behaviour-based reinforcement learning. In Proceedings of the 2020 IEEE International Conference on Robotics and Automation (ICRA), Paris, France, 31 August 2020. [Google Scholar]
- Al-Selwi, H.F.; Aziz, A.A.; Abas, F.S.; Zyada, Z. Reinforcement learning for robotic applications with vision feedback. In Proceedings of the 2021 IEEE 17th International Colloquium on Signal Processing & Its Applications (CSPA), Langkawi, Malaysia, 5 March 2021; IEEE: New York, NY, USA, 2021. [Google Scholar]
- Marzari, L.; Pore, A.; Dall’Alba, D.; Aragon-Camarasa, G.; Farinelli, A.; Fiorini, P. Towards Hierarchical Task Decomposition Using Deep Reinforcement Learning for Pick and Place Subtasks. arXiv 2021, arXiv:2102.04022. [Google Scholar]
- Anca, M.; Studley, M. Twin delayed hierarchical actor-critic. In Proceedings of the 2021 7th International Conference on Automation, Robotics and Applications (ICARA), Prague, Czech Republic, 4 February 2021; IEEE: New York, NY, USA, 2021. [Google Scholar]
- Morrison, D.; Corke, P.; Leitner, J. Closing the Loop for Robotic Grasping: A Real-Time, Generative Grasp Synthesis Approach. arXiv 2018, arXiv:1804.05172. [Google Scholar]
- Kalashnikov, D.; Irpan, A.; Pastor, P.; Ibarz, J.; Herzog, A.; Jang, E.; Quillen, D.; Holly, E.; Kalakrishnan, M.; Vanhoucke, V.; et al. Scalable deep reinforcement learning for vision-based robotic manipulation. In Proceedings of the 2nd Conference on Robot Learning, Zürich, Switzerland, 29–31 October 2018. [Google Scholar]
- Finn, C.; Levine, S.; Abbeel, P. Guided Cost Learning: Deep inverse optimal control via policy optimization. In Proceedings of the 33rd International Conference on Machine Learning, New York, NY, USA, 19–24 June 2016; Volume 48. JMLR. [Google Scholar]
- Wu, B.; Akinola, I.; Allen, P.K. Allen pixel-attentive policy gradient for multi-fingered grasping in cluttered scenes. In Proceedings of the 2019 IEEE/RSJ International Conference on Intelligent Robots and Systems (IROS), Macau, China, 4 November 2019; IEEE: New York, NY, USA, 2019. [Google Scholar]
- Deng, Y.; Guo, X.; Wei, Y.; Lu, K.; Fang, B.; Guo, D.; Liu, H.; Sun, F. Deep reinforcement learning for robotic pushing and picking in cluttered environment. In Proceedings of the 2019 IEEE/RSJ International Conference on Intelligent Robots and Systems (IROS), Macau, China, 4 November 2019. [Google Scholar]
- Beltrain-Hernandez, C.; Damien, P.; Harada, K.; Ramirez-Alpizar, I. Learning to Grasp with Primitive Shaped Object Policies. 2019 IEEE/SICE Int. Symp. Syst. Integr. 2019, 468–473. [Google Scholar] [CrossRef]
- Berscheid, L.; Meißner, P.; Kröger, T. Robot learning of shifting objects for grasping in cluttered environments. In Proceedings of the 2019 IEEE/RSJ International Conference on Intelligent Robots and Systems, Macau, China, 3–8 November 2019. [Google Scholar]
- Kim, T.; Park, Y.; Park, Y.; Suh, I.H. Acceleration of Actor-Critic Deep Reinforcement Learning for Visual Grasping in Clutter by State Representation Learning Based on Disentanglement of a Raw Input Image. arXiv 2020, arXiv:2002.11903v1. [Google Scholar]

| Paper | Policy Optimization | Pose Estimation | Sim Package | Success Rate | Strengths (S) and Weaknesses (W) |
|---|---|---|---|---|---|
| Fu et al., 2016 [17] | Value function approach with DP using iterative LQR. Basic two-layer NN for updating priors | Model-based approach which combined prior knowledge and online adaptation | MuJoCo | Simulation Testing: 0.80–1.00 Robot Testing: ~0.80 | S: Implemented prior knowledge to reduce the number of samples required W: To create model of system dynamics the NN must be trained on prior examples |
| Gualtieri et al., 2018 [22], Gualtieri et al., 2018 [19] | Value function approach with SARSA. Caffe (NN) used to update the SARSA weights | Model-free data-driven approach which implemented focus. The algorithm allowed for temporary and final placements. Model was trained using 3DNET CAD models | OpenRave (ODE base) | Robot Testing: Picking: 0.88–0.96 Placement: 0.80–0.89 | S: Model-free approach with high picking accuracy W: Low placement accuracy and low overall accuracy in testing |
| Popov et al., 2017 [60] | Distributed Deep DPG (DDPG) method with efficient schedule updates and composite reward functions | Model-free data-driven approach. Reward achieved for appropriate grasp selections. Blocks always oriented in the same manner. | MuJoCo | Simulation Testing: 0.955 | S: Proved that asychronous DDPG has higher data-efficiency then other approaches W: No online testing to validate simulation accuracy |
| Mahler and Goldberg, 2017 [61] | Imitation learning approach in which the robot was trained on data from synthesized grasps. Sample grasps were found by using force and torque space analysis and knowledge of object shapes and poses | Model based approach used for demonstration synthesis. Model free data driven approach for pose selection during training | Pybullet | Simulated Testing: 0.96 Robot Testing: 0.94–0.78 (Testing accuracy depends on the number of objects in the cluttered environment) | S: High picking accuracy on cluttered enviroment of unfamilier objects W: Requires models for the wrench space analysis to develop demonstration samples. Intensive programming effort |
| Sehgal et al., 2018 [62] | DDPG with hindsight experience replay (HER). Parameters tuned using the genetic algorithm | Model-free data-driven approach | MuJoCo | Simulated Testing: ~0.90 | S: Effectively implemented HER for faster convergence W: No improvement in overall task completion performance. No online testing to validate simulation accuracy |
| Zuo et al., 2019 [63] | Deterministic generative adversarial learning (DGAIL) which implemented a policy gradient generator and discriminator trained with IRL (an actor-critic approach) | Data driven approach in which action selection was based on the difference between the demonstrated and generated policy | MuJoCo | Simulated Testing: 0.90 | S: DGAIL had faster convergence then several other RL techniques W: DGAIL was less stable, and less accurate then other modified DDPG techniques |
| Chen et al., 2019 [64] | Two deep Q-Networks (DQN) for pushing and grasping. Mask Region convolutional NN (R-CNN) for object detection | Model based approach where the target object was mixed in clutter. RBGD image was used for target object detection. The scene was rearranged if the target is invisible from the sensor’s perspective | V-REP simulation platform | Simulated Testing: 1.0 3 different scene options were tested. Each seen had the target in a more/less hidden location | S: High target location accuracy. Approach proves that rearranging the enviroment can improve results W: Approach was only applied for known target objects. No online testing to validate the simulation accuracy |
| Xiao et al., 2019 [65] | Parameterized Action Partially Observable Monte-Carlo Planning (PA-POMCP) | Model based approach which implemented known models from a benchmark model set | OpenRAVE & Gazebo | Robot Testing: 1.0 | S: High pick-and-place accuracy W: Model based approach. Grasp poses are pre-defined so the primary task is model recognition. This technique significantly simplifies the problem |
| Liu et al., 2020 [66] | PPO with actor output as manipulation signal (MAPPO) | Data driven approach which extracted target object pose from RGBD sensor | Gazebo | Robotic Testing: Relative improvement of MAPPO to PPO and A3C shown to be >30%. Final accuracy not given | S: Compared various learning and reward shaping approaches W: No final pick-and-place accuracy given. Difficult to guage the performance improvement |
| Mohammed et al., 2020 [67] | Value Function approach with Q-Learning. CNN used to update Q-learning weights. Model pre-trained on Densnet-121. | Data-driven approach. Grasps were generated by using a CNN to identify available poses from a RGB image | Vrep (ODE base) | Simulated Testing: Picking: 0.8–1 Placement: 0.9–1 | S: High placement accuracy considering the absense of model for target object. Short training time W: No online testing to validate the simulation accuracy |
| Li et al., 2020 [68] | DDPG approach with goal-oriented and curiosity driven exploration and dynamic initial states | Data driven approach which used RGBD images to determine object and goal positions | MuJoCo | Simulated Testing: 0.95 Robotic Testing: 0.85 | S: Comparison to several other sampling and learning techniques validated the sample efficiency for this approach W: Deployment on robot showed a reduced overall effectiveness |
| Pore and Aragon- Camarasa, 2020 [69] | Hierarchical RL in which the task was broken into simplified multi-step behaviors with the subsumption architecture (SA). Behavior cloning was used for low-level behavior training. Actor-Critic technique was applied for high level task completion | Data driven approach in which grasp poses were trained with behavior cloning. Target objects were consistent which means that advanced pose estimation was not required | OpenAI Fetch environment with MuJoCo | Simulated Testing: 1.00 | S: Validated that the subsumption architecture improves entire task performance significantly compared to end-to-end approaches W: Technique required behavior cloning samples, and a human for problem breakdown. No online testing to validate simulation accuracy |
| Al-Selwi et al., 2021 [70] | DDPG with HER | Model based approach in which RGB image was used to determine bounding box and rotation angle | MuJoCo | Simulated Testing: 0.502–0.98 (depending on target geometry) | S: Validated that HER DDPG can be used with vision feedback to improve accuracy W: CAD models required for pose selection. No online testing to validate simulation accuracy |
| Marzari et al., 2021 [71] | DDPG with HER and task decomposition | Data driven approach in which grasp poses were learned from a single target object with simple geometry | MuJoCo | Simulation and Robotic Testing: 100% | S: Proved that the DDPG approach with HER can perform excellent task completion accuracy by using task decomposition rather then end-to-end training W: Approach assumed human involvement for task decomposition |
| Anca and Studley, 2021 [72] | Twin delayed hierarchical actor critic (TDHAC) which broke task into high- and low-level goals | Data driven approach which only implemented a 2D motion for picking the action | Pybullet | Simulated Testing: 100% | S: Confirmed that the hierarchical approach improves convergence W: Approach showed no significant improvement over DDPG with HER. The motion was limited to 2D. No online testing to validate simulation accuracy |
| Paper | Policy Optimization | Pose Estimation | Sim Package | Success Rate | Strengths (S) and Weaknesses (W) |
|---|---|---|---|---|---|
| Finn et al., 2016 [75] | Combined relative entropy IRL and path integral IRL with sampling using policy optimization | Algorithm did not incorporate the picking operation so pose selection was not required | MuJoCo | Robotic Testing: Placement: 1 | S: Perfect placement accuracy W: Technique did not incorporate picking action. Online training samples are required |
| Kalashnikov et al., 2018 [74] | QT-Opt, a modified Q-learning algorithm that implemented off-policy training and on-policy fine-tuning | Data-driven approach. Strategy implemented dynamic closed loop control with RL to solve the grasping task. | Bullet Physics Simulator | Robotic Testing: Picking: 0.96 (with object shifting) | S: High picking accuracy in a cluttered environment with unknown objects W: Time-consuming online training required |
| Wu et al., 2019 [76] | Pixel attentive PPO | Data driven approach which learned optimal grasps through trial and error. Pixel attentive method cropped image to focus on local region containing ideal grasp candidates | Pybullet | Simulation and Robotic Testing: 0.911–0.967. Accuracy changed based on the density of the clutter | S: Excellent alignment between simulation and real enviroments. Useful data presented which compared camera orientation and grasp accuracy W:Three finger gripper may contribute to high picking success rate. Most standard grippers are planar (2 fingers) |
| Deng et al., 2019 [77] | Deep Q-Network (DQN) implemented to select actions based on affordance map | Data driven model-free approach in which lifting point candidates were selected based on affordance map showing “hot spots” or ideal grasp candidate locations in the RGBD image. | V-REP | Robotic Testing: Picking: ~0.71 | S: Novel robotic arm design effective for selection of randomly oriented objects in a clutter. W: Picking operation success rate was only 11% better then random grasp actions (very poor) |
| Beltran-Hernandez et al., 2019 [78] | Guided policy search, with image input and grasp pose as output. | Model-based approach. The agent was trained on basic shapes and then tested on complex geometries | Gazebo (ODE Base) | Simulation Testing: Picking: 0.8–1 | S: Approach shows significant controbution to the space by showing effectiveness of using model based techniques for grasping unfamiliar objects W: No online testing to validate simulation accuracy |
| Berscheid et al., 2019 [79] | Modified Q-learning. Upper confidence bound for off-policy exploration. | Model-free approach which implemented NN to generate action values | Online Testing. 25,000 grasps trained in 100 h | Robotic Testing: Picking: 0.92 (with object shifting) | S: High picking accuracy and good recognition of required shifts W: Time-consuming online training required |
| Kim et al., 2020 [80] | A2C with state representation learning (SLR). Involves learning a compressed state representation | Data driven approach which implemented raw image disentanglement | Pybullet | Simulation Testing: Picking: 0.72 | S: Computationally affordable grasping action W: Low picking accuracy. No online testing to validate simulation accuracy |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Lobbezoo, A.; Qian, Y.; Kwon, H.-J. Reinforcement Learning for Pick and Place Operations in Robotics: A Survey. Robotics 2021, 10, 105. https://doi.org/10.3390/robotics10030105
Lobbezoo A, Qian Y, Kwon H-J. Reinforcement Learning for Pick and Place Operations in Robotics: A Survey. Robotics. 2021; 10(3):105. https://doi.org/10.3390/robotics10030105
Chicago/Turabian StyleLobbezoo, Andrew, Yanjun Qian, and Hyock-Ju Kwon. 2021. "Reinforcement Learning for Pick and Place Operations in Robotics: A Survey" Robotics 10, no. 3: 105. https://doi.org/10.3390/robotics10030105
APA StyleLobbezoo, A., Qian, Y., & Kwon, H.-J. (2021). Reinforcement Learning for Pick and Place Operations in Robotics: A Survey. Robotics, 10(3), 105. https://doi.org/10.3390/robotics10030105







