On the Impact of Gravity Compensation on Reinforcement Learning in Goal-Reaching Tasks for Robotic Manipulators
Abstract
1. Introduction
2. Background
2.1. Model-Based Control Using Dynamical System Models
2.2. Reinforcement Learning
2.3. Deep Reinforcement Learning
3. Methods
3.1. Residual Reinforcement Learning
3.2. Torque Control with and without Gravity Compensation
3.3. RL Agents: ACKTR and PPO2
3.3.1. Actor Critic Using Kronecker-Factored Trust Region (ACKTR)
3.3.2. Proximal Policy Optimization (PPO2)
4. Experiments
4.1. Seven-Degree-of-Freedom Robotic Arm
4.2. Reaching Tasks
4.3. RL Agents: ACKTR and PPO2
5. Results
5.1. Hyperparameter Selection in RL Agents
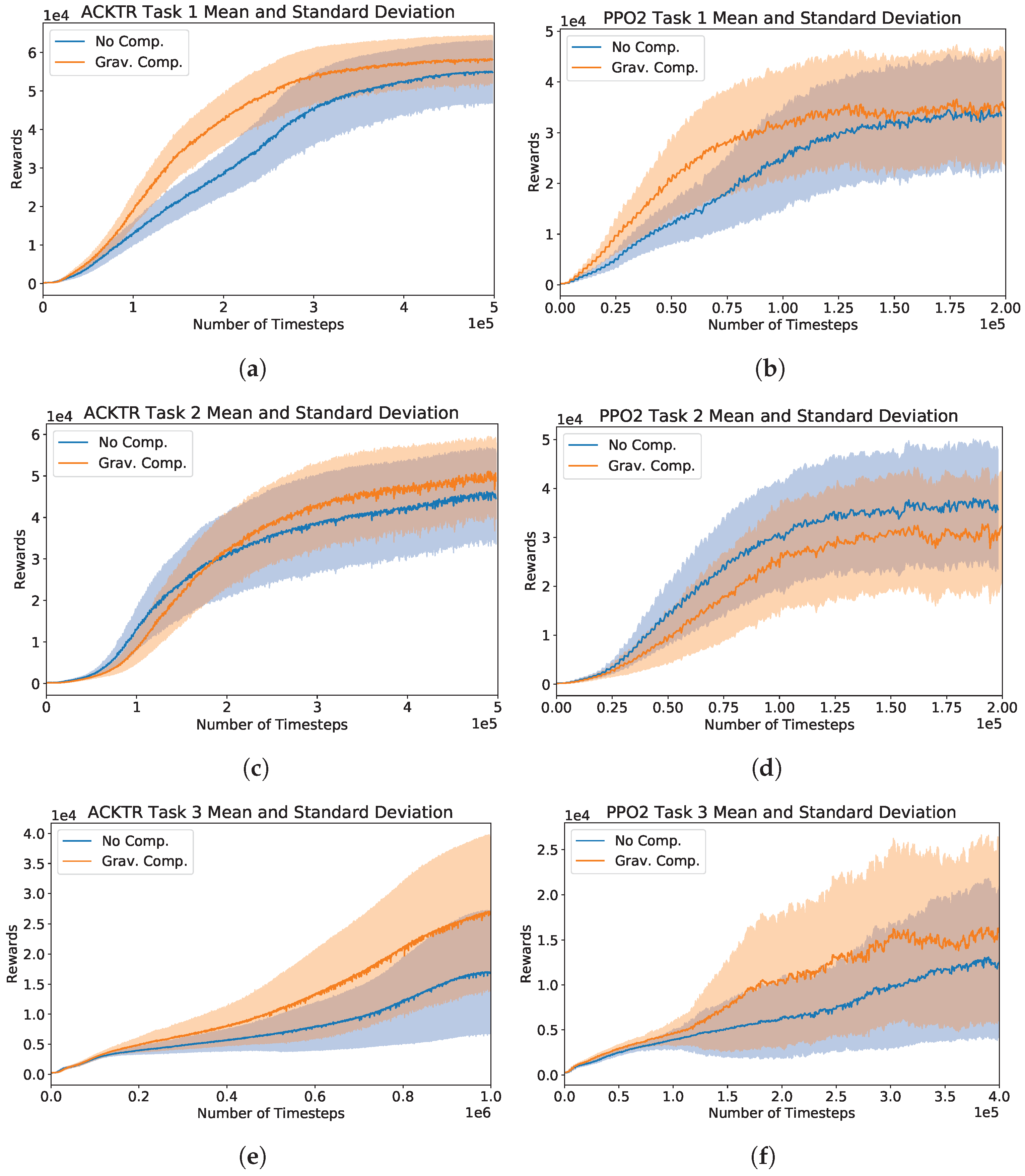
5.2. Performances on Task 1, 2, and 3
5.3. Agents’ Behavioral Evaluation
6. Discussion
7. Conclusions
Supplementary Materials
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Rottmann, A.; Mozos, O.M.; Stachniss, C.; Burgard, W. Semantic Place Classification of Indoor Environments with Mobile Robots Using Boosting. In Proceedings of the 20th National Conference on Artificial Intelligence, AAAI’05, Pittsburgh, PA, USA, 9–13 July 2005; Volume 3, pp. 1306–1311. [Google Scholar]
- Spong, M.W.; Hutchinson, S.; Vidyasagar, M. Robot Modeling and Control; Wiley and Sons: New York, NY, USA, 2006. [Google Scholar]
- Safiotti, A. Fuzzy logic in autonomous robotics: Behavior coordination. In Proceedings of the 6th International Fuzzy Systems Conference, Barcelona, Spain, 5 July 1997; Volume 1, pp. 573–578. [Google Scholar] [CrossRef]
- Chen, C.H.; Wang, C.C.; Wang, Y.T.; Wang, P.T. Fuzzy Logic Controller Design for Intelligent Robots. Math. Probl. Eng. 2017. [Google Scholar] [CrossRef]
- Antonelli, G.; Chiaverini, S.; Sarkar, N.; West, M. Adaptive control of an autonomous underwater vehicle: Experimental results on ODIN. In Proceedings of the 1999 IEEE International Symposium on Computational Intelligence in Robotics and Automation, CIRA’99 (Cat. No.99EX375), Monterey, CA, USA, 8–9 November 1999; pp. 64–69. [Google Scholar] [CrossRef]
- Wei, B. A Tutorial on Robust Control, Adaptive Control and Robust Adaptive Control—Application to Robotic Manipulators. Inventions 2019, 4, 49. [Google Scholar] [CrossRef]
- Bicho, E.; Schöner, G. The dynamic approach to autonomous robotics demonstrated on a low-level vehicle platform. Robot. Auton. Syst. 1997, 21, 23–35. [Google Scholar] [CrossRef]
- Schöner, G.; Dose, M.; Engels, C. Dynamics of behavior: Theory and applications for autonomous robot architectures. Robot. Auton. Syst. 1995, 16, 213–245. [Google Scholar] [CrossRef]
- Fu, J.; Luo, K.; Levine, S. Learning Robust Rewards with Adversarial Inverse Reinforcement Learning. arXiv 2018, arXiv:1710.11248. [Google Scholar]
- Bogert, K.; Doshi, P. Multi-robot inverse reinforcement learning under occlusion with estimation of state transitions. Artif. Intell. 2018, 263, 46–73. [Google Scholar] [CrossRef]
- Kober, J.; Bagnell, J.A.; Peters, J. Reinforcement learning in robotics: A survey. Int. J. Robot. Res. 2013, 32, 1238–1274. [Google Scholar] [CrossRef]
- Gu, S.; Holly, E.; Lillicrap, T.; Levine, S. Deep Reinforcement Learning for Robotic Manipulation with Asynchronous Off-Policy Updates. In Proceedings of the IEEE International Conference on Robotics and Automation (ICRA), Singapore, 29 May–3 June 2017; pp. 3389–3396. [Google Scholar]
- Levine, S.; Finn, C.; Darrell, T.; Abbeel, P. End-to-End Training of Deep Visuomotor Policies. arXiv 2015, arXiv:1504.00702. [Google Scholar]
- Li, W.; Todorov, E. Iterative Linear Quadratic Regulator Design For Nonlinear Biological Movement Systems. In Proceedings of the First International Conference on Informatics in Control, Automation and Robotics, Setúbal, Portugal, 25–28 August 2004. [Google Scholar] [CrossRef]
- DiGiovanna, J.; Mahmoudi, B.; Fortes, J.; Principe, J.C.; Sanchez, J.C. Coadaptive Brain–Machine Interface via Reinforcement Learning. IEEE Trans. Biomed. Eng. 2009, 56, 54–64. [Google Scholar] [CrossRef]
- Bae, J.; Sanchez Giraldo, L.G.; Pohlmeyer, E.A.; Francis, J.T.; Sanchez, J.C.; Príncipe, J.C. Kernel Temporal Differences for Neural Decoding. Intell. Neurosci. 2015, 2015. [Google Scholar] [CrossRef]
- Abbeel, P.; Coates, A.; Quigley, M.; Ng, A.Y. An application of reinforcement learning to aerobatic helicopter flight. In Proceedings of the Advances in Neural Information Processing Systems, Vancouver, BC, Canada, 4–7 December 2007; pp. 1–8. [Google Scholar]
- Martín-Martín, R.; Lee, M.A.; Gardner, R.; Savarese, S.; Bohg, J.; Garg, A. Variable Impedance Control in End-Effector Space: An Action Space for Reinforcement Learning in Contact-Rich Tasks. arXiv 2019, arXiv:1906.08880. [Google Scholar]
- Johannink, T.; Bahl, S.; Nair, A.; Luo, J.; Kumar, A.; Loskyll, M.; Ojea, J.A.; Solowjow, E.; Levine, S. Residual Reinforcement Learning for Robot Control. In Proceedings of the 2019 International Conference on Robotics and Automation (ICRA), Montreal, QC, Canada, 20–24 May 2019. [Google Scholar] [CrossRef]
- Arakelian, V. Gravity compensation in robotics. Adv. Robot. 2015, 30, 1–18. [Google Scholar] [CrossRef]
- Ernesto, H.; Pedro, J.O. Reinforcement learning in robotics: A survey. Math. Probl. Eng. 2015. [Google Scholar] [CrossRef]
- Yu, C.; Li, Z.; Liu, H. Research on Gravity Compensation of Robot Arm Based on Model Learning. In Proceedings of the 2019 IEEE/ASME International Conference on Advanced Intelligent Mechatronics (AIM), Hong Kong, China, 8–12 July 2019; pp. 635–641. [Google Scholar] [CrossRef]
- Montalvo, W.; Escobar-Naranjo, J.; Garcia, C.A.; Garcia, M.V. Low-Cost Automation for Gravity Compensation of Robotic Arm. Appl. Sci. 2020, 10, 3823. [Google Scholar] [CrossRef]
- Alothman, Y.; Gu, D. Quadrotor transporting cable-suspended load using iterative linear quadratic regulator (ilqr) optimal control. In Proceedings of the 2016 8th Computer Science and Electronic Engineering (CEEC), Colchester, UK, 28–30 September 2016; pp. 168–173. [Google Scholar]
- Puterman, M.L. Markov Decision Processes: Discrete Stochastic Dynamic Programming, 1st ed.; John Wiley & Sons, Inc.: Hoboken, NJ, USA, 1994. [Google Scholar]
- Sutton, R.S.; Barto, A.G. Reinforcement Learning: An Introduction, 2nd ed.; Adaptive Computation and Machine Learning Series; The MIT Press: Cambridge, MA, USA, 2018. [Google Scholar]
- Wu, Y.; Mansimov, E.; Liao, S.; Grosse, R.B.; Ba, J. Scalable trust-region method for deep reinforcement learning using Kronecker-factored approximation. arXiv 2017, arXiv:1708.05144. [Google Scholar]
- Schulman, J.; Wolski, F.; Dhariwal, P.; Radford, A.; Klimov, O. Proximal Policy Optimization Algorithms. arXiv 2017, arXiv:1707.06347. [Google Scholar]
- Henderson, P.; Islam, R.; Bachman, P.; Pineau, J.; Precup, D.; Meger, D. Deep Reinforcement Learning that Matters. arXiv 2017, arXiv:1709.06560. [Google Scholar]
- Aumjaud, P.; McAuliffe, D.; Rodriguez Lera, F.J.; Cardiff, P. Reinforcement Learning Experiments and Benchmark for Solving Robotic Reaching Tasks. In Proceedings of the 21st International Workshop of Physical Agents (WAF 2020), Madrid, Spain, 19–20 November 2020. [Google Scholar] [CrossRef]
- Amari, S.I. Natural Gradient Works Efficiently in Learning. Neural Comput. 1998, 10, 251–276. [Google Scholar] [CrossRef]
- Kakade, S.M. A Natural Policy Gradient. In Proceedings of the 14th International Conference on Neural Information Processing Systems: Natural and Synthetic; MIT Press: Cambridge, MA, USA, 2001; pp. 1531–1538. [Google Scholar]
- Schulman, J.; Levine, S.; Moritz, P.; Jordan, M.I.; Abbeel, P. Trust Region Policy Optimization. arXiv 2017, arXiv:1502.05477. [Google Scholar]
- Hill, A.; Raffin, A.; Ernestus, M.; Gleave, A.; Kanervisto, A.; Traore, R.; Dhariwal, P.; Hesse, C.; Klimov, O.; Nichol, A.; et al. Stable Baselines. 2018. Available online: https://github.com/hill-a/stable-baselines (accessed on 1 June 2019).
- Grosse, R.; Martens, J. A Kronecker-factored approximate Fisher matrix for convolution layers. arXiv 2016, arXiv:1602.01407. [Google Scholar]
- Fan, L.; Zhu, Y.; Zhu, J.; Liu, Z.; Zeng, O.; Gupta, A.; Creus-Costa, J.; Savarese, S.; Fei-Fei, L. SURREAL: Open-Source Reinforcement Learning Framework and Robot Manipulation Benchmark. In Proceedings of the Conference on Robot Learning, Zürich, Switzerland, 29–31 October 2018. [Google Scholar]
- Todorov, E.; Erez, T.; Tassa, Y. MuJoCo: A physics engine for model-based control. In Proceedings of the 2012 IEEE/RSJ International Conference on Intelligent Robots and Systems, Vilamoura-Algarve, Portugal, 7–12 October 2012; pp. 5026–5033, ISSN 2153-0858. [Google Scholar] [CrossRef]
- Babaeizadeh, M.; Frosio, I.; Tyree, S.; Clemons, J.; Kautz, J. GA3C: GPU-based A3C for Deep Reinforcement Learning. arXiv 2016, arXiv:1611.06256. [Google Scholar]
- Falkner, S.; Klein, A.; Hutter, F. BOHB: Robust and Efficient Hyperparameter Optimization at Scale. arXiv 2018, arXiv:1807.01774. [Google Scholar]
- Li, L.; Jamieson, K.; DeSalvo, G.; Rostamizadeh, A.; Talwalkar, A. Hyperband: A Novel Bandit-Based Approach to Hyperparameter Optimization. J. Mach. Learn. Res. 2017, 18, 6765–6816. [Google Scholar]
- Paul, S.; Kurin, V.; Whiteson, S. Fast Efficient Hyperparameter Tuning for Policy Gradients. arXiv 2019, arXiv:1902.06583. [Google Scholar]
- Liu, C.; Xu, X.; Hu, D. Multiobjective Reinforcement Learning: A Comprehensive Overview. IEEE Trans. Syst. Man Cybern. Syst. 2015, 45, 385–398. [Google Scholar]
- Pohlmeyer, E.A.; Mahmoudi, B.; Geng, S.; Prins, N.W.; Sanchez, J.C. Using Reinforcement Learning to Provide Stable Brain-Machine Interface Control Despite Neural Input Reorganization. PLoS ONE 2014, 9, e87253. [Google Scholar] [CrossRef]
- An, J.; Yadav, T.; Ahmadi, M.B.; Tarigoppula, V.S.A.; Francis, J.T. Near Perfect Neural Critic from Motor Cortical Activity Toward an Autonomously Updating Brain Machine Interface. In Proceedings of the 2018 40th Annual International Conference of the IEEE Engineering in Medicine and Biology Society (EMBC), Honolulu, HI, USA, 17–21 July 2018; pp. 73–76. [Google Scholar] [CrossRef]
- Shaikh, S.; So, R.; Sibindi, T.; Libedinsky, C.; Basu, A. Towards Autonomous Intra-Cortical Brain Machine Interfaces: Applying Bandit Algorithms for Online Reinforcement Learning. In Proceedings of the 2020 IEEE International Symposium on Circuits and Systems (ISCAS), Seville, Spain, 10–21 October 2020; pp. 1–5. [Google Scholar] [CrossRef]
- Shen, X.; Zhang, X.; Huang, Y.; Chen, S.; Wang, Y. Task Learning Over Multi-Day Recording via Internally Rewarded Reinforcement Learning Based Brain Machine Interfaces. IEEE Trans. Neural Syst. Rehabil. Eng. 2020, 28, 3089–3099. [Google Scholar] [CrossRef]



| Task 1 | (0, , 0, , 0, , ) | 0.0004 |
| Task 2–3 | (, , 0, , 0, , ) | 0.0025 |
| Task 1 | (44.48 ± , 0.0 ± , 10.81 ± ) | (60, −20, 40) |
| Task 2 | (43.70 ± , −43.64 ± , 31.78 ± ) | (40, 40, 0) |
| Task 3 | (43.70 ± , −43.64 ± , 31.78 ± ) | (30, 30, 50) |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Fugal, J.; Bae, J.; Poonawala, H.A. On the Impact of Gravity Compensation on Reinforcement Learning in Goal-Reaching Tasks for Robotic Manipulators. Robotics 2021, 10, 46. https://doi.org/10.3390/robotics10010046
Fugal J, Bae J, Poonawala HA. On the Impact of Gravity Compensation on Reinforcement Learning in Goal-Reaching Tasks for Robotic Manipulators. Robotics. 2021; 10(1):46. https://doi.org/10.3390/robotics10010046
Chicago/Turabian StyleFugal, Jonathan, Jihye Bae, and Hasan A. Poonawala. 2021. "On the Impact of Gravity Compensation on Reinforcement Learning in Goal-Reaching Tasks for Robotic Manipulators" Robotics 10, no. 1: 46. https://doi.org/10.3390/robotics10010046
APA StyleFugal, J., Bae, J., & Poonawala, H. A. (2021). On the Impact of Gravity Compensation on Reinforcement Learning in Goal-Reaching Tasks for Robotic Manipulators. Robotics, 10(1), 46. https://doi.org/10.3390/robotics10010046




