Helical Twist and Rotational Forces in the Mitotic Spindle
Abstract
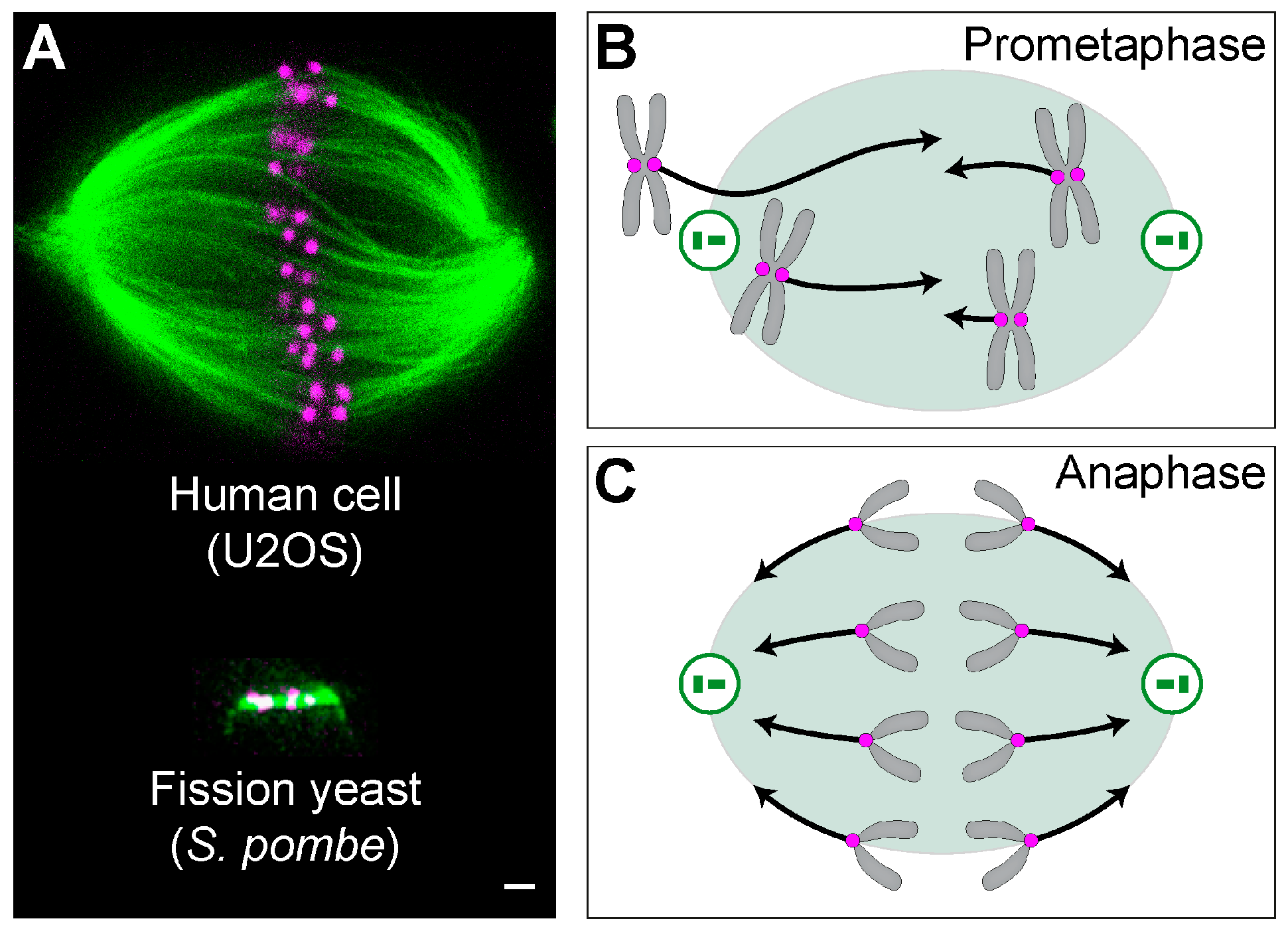
:1. Forces in the Mitotic Spindle
2. From Forces to Shapes and Back
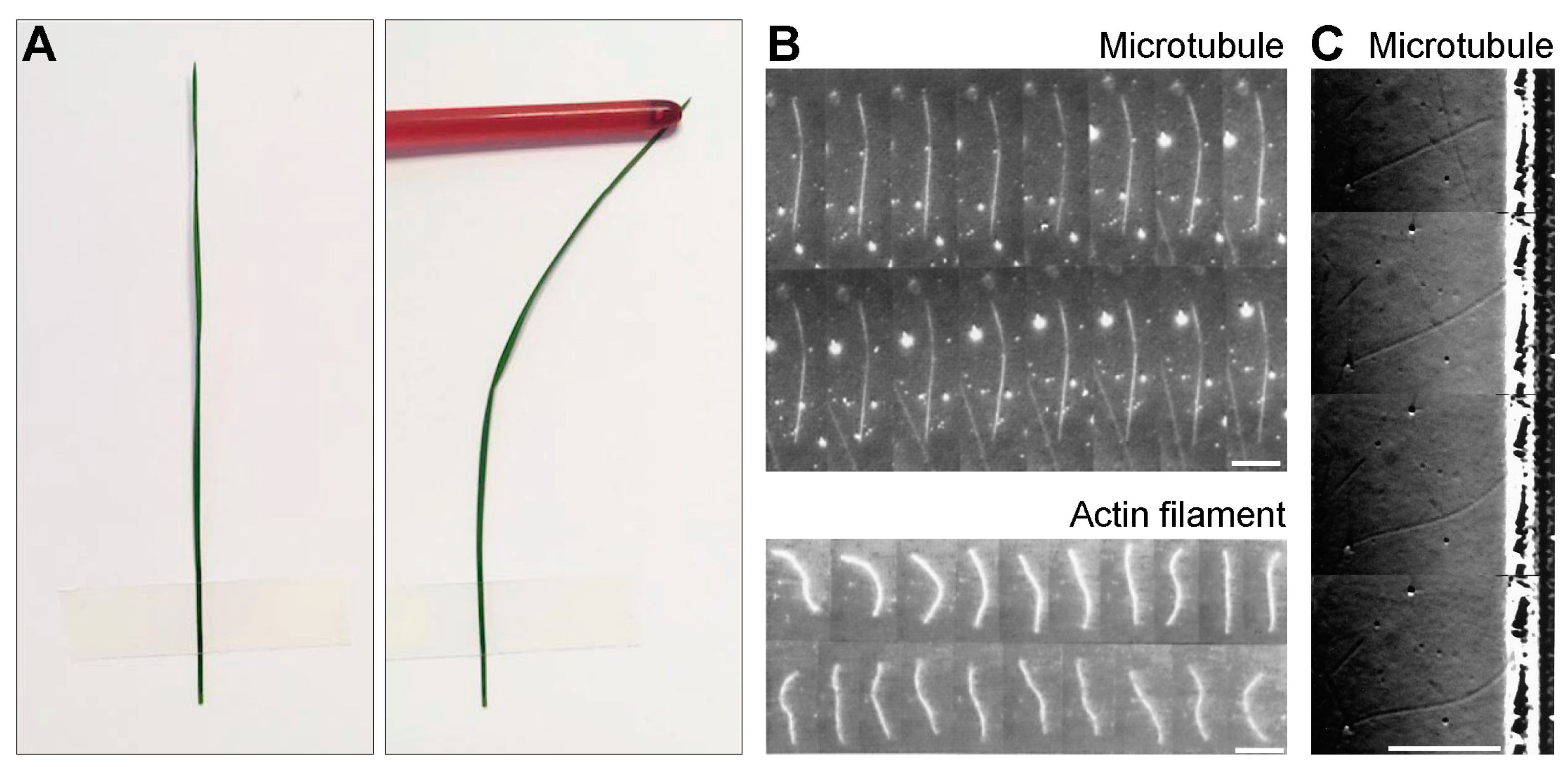
2.1. Deformation of a Slender Elastic Rod
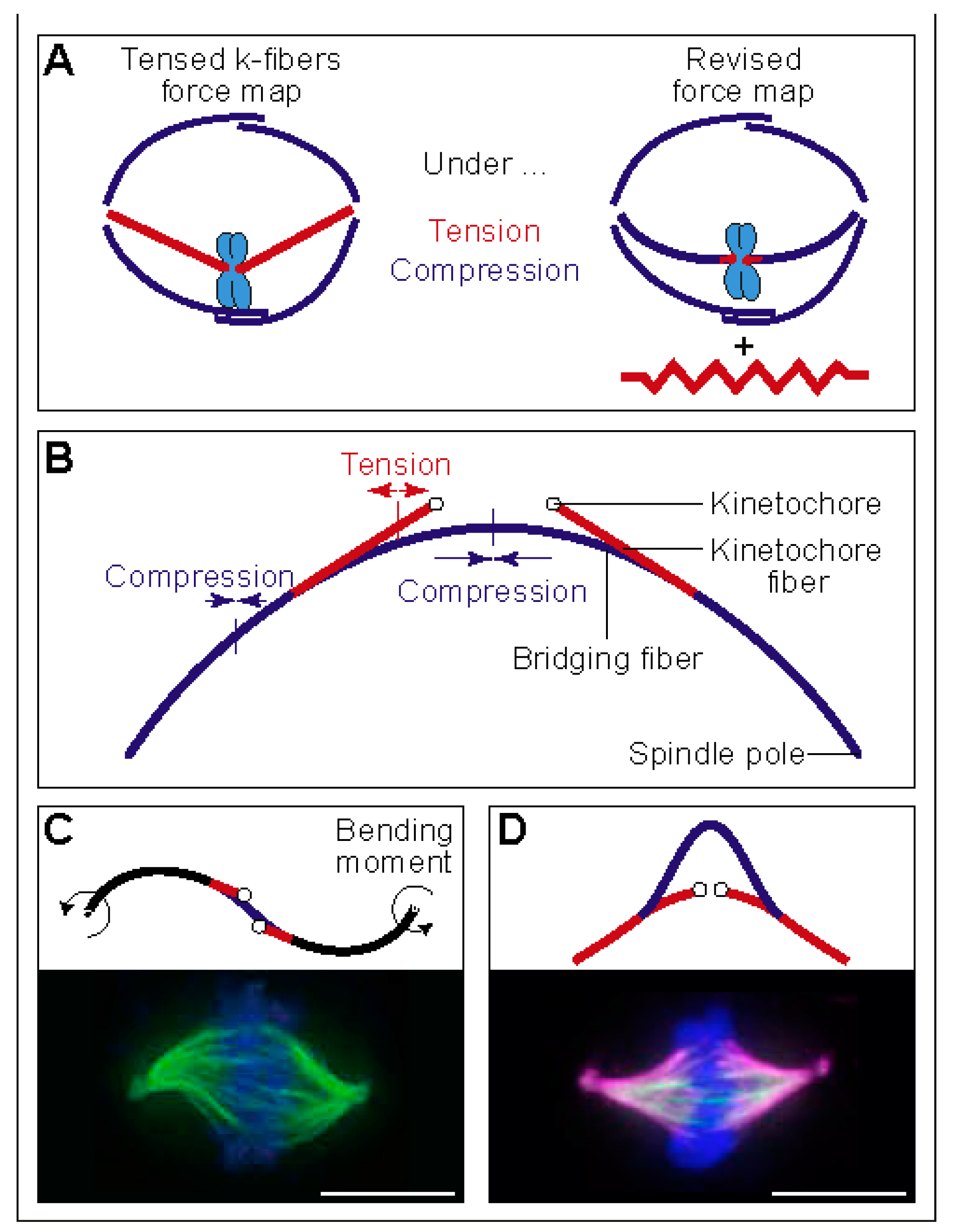
3. Linear and Rotational Forces That Shape the Spindle
4. Twisting Moment in the Spindle Leads to its Chirality
5. Rotational Forces Generated by Motor Proteins
6. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- McIntosh, J.R.; Molodtsov, M.I.; Ataullakhanov, F.I. Biophysics of mitosis. Q. Rev. Biophys. 2012, 45, 147–207. [Google Scholar] [CrossRef] [PubMed]
- Pavin, N.; Tolic, I.M. Self-Organization and Forces in the Mitotic Spindle. Annu Rev. Biophys 2016, 45, 279–298. [Google Scholar] [CrossRef] [PubMed]
- Asbury, C.L. Anaphase A: Disassembling Microtubules Move Chromosomes toward Spindle Poles. Biology 2017, 6, 15. [Google Scholar] [CrossRef] [PubMed]
- Maiato, H.; Gomes, A.; Sousa, F.; Barisic, M. Mechanisms of Chromosome Congression during Mitosis. Biology 2017, 6, 13. [Google Scholar] [CrossRef] [PubMed]
- Scholey, J.M.; Civelekoglu-Scholey, G.; Brust-Mascher, I. Anaphase B. Biology 2016, 5, 51. [Google Scholar] [CrossRef] [PubMed]
- Prosser, S.L.; Pelletier, L. Mitotic spindle assembly in animal cells: A fine balancing act. Nat. Rev. Mol. Cell Biol. 2017, 18, 187–201. [Google Scholar] [CrossRef] [PubMed]
- Nezi, L.; Musacchio, A. Sister chromatid tension and the spindle assembly checkpoint. Curr. Opin. Cell Biol. 2009, 21, 785–795. [Google Scholar] [CrossRef] [PubMed]
- Howard, J. Mechanics of Motor Proteins and the Cytoskeleton; Sinauer Associates: Sunderland, MA, USA, 2001. [Google Scholar]
- Tolic-Norrelykke, I.M. Push-me-pull-you: How microtubules organize the cell interior. Eur. Biophys. J. 2008, 37, 1271–1278. [Google Scholar] [CrossRef]
- Novak, M.; Polak, B.; Simunic, J.; Boban, Z.; Kuzmic, B.; Thomae, A.W.; Tolic, I.M.; Pavin, N. The mitotic spindle is chiral due to torques within microtubule bundles. Nat. Commun 2018, 9, 3571. [Google Scholar] [CrossRef]
- Kalinina, I.; Nandi, A.; Delivani, P.; Chacon, M.R.; Klemm, A.H.; Ramunno-Johnson, D.; Krull, A.; Lindner, B.; Pavin, N.; Tolic-Norrelykke, I.M. Pivoting of microtubules around the spindle pole accelerates kinetochore capture. Nat. Cell Biol. 2013, 15, 82–87. [Google Scholar] [CrossRef]
- Nicklas, R.B. Measurements of the force produced by the mitotic spindle in anaphase. J. Cell Biol. 1983, 97, 542–548. [Google Scholar] [CrossRef] [PubMed]
- Nicklas, R.B. The forces that move chromosomes in mitosis. Annu Rev. Biophys Biophys Chem 1988, 17, 431–449. [Google Scholar] [CrossRef] [PubMed]
- Garzon-Coral, C.; Fantana, H.A.; Howard, J. A force-generating machinery maintains the spindle at the cell center during mitosis. Science 2016, 352, 1124–1127. [Google Scholar] [CrossRef]
- Flemming, W. Zellsubstanz, Kern und Zelltheilung; F. C.W. Vogel: Leipzig, Germany, 1882. [Google Scholar]
- McCully, E.K.; Robinow, C.F. Mitosis in the fission yeast Schizosaccharomyces pombe: A comparative study with light and electron microscopy. J. Cell Sci. 1971, 9, 475–507. [Google Scholar] [PubMed]
- Gittes, F.; Mickey, B.; Nettleton, J.; Howard, J. Flexural rigidity of microtubules and actin filaments measured from thermal fluctuations in shape. J. Cell Biol. 1993, 120, 923–934. [Google Scholar] [CrossRef] [PubMed]
- Dogterom, M.; Yurke, B. Measurement of the force-velocity relation for growing microtubules. Science 1997, 278, 856–860. [Google Scholar] [CrossRef] [PubMed]
- Landau, L.D.; Lifshitz, E.M. Theory of Elasticity, 1st ed.; Pergamon Press: Oxford, UK, 1959; Vol. 7. [Google Scholar]
- Rubinstein, B.; Larripa, K.; Sommi, P.; Mogilner, A. The elasticity of motor-microtubule bundles and shape of the mitotic spindle. Phys. Biol. 2009, 6, 016005. [Google Scholar] [CrossRef] [PubMed]
- Bloom, K.; Joglekar, A. Towards building a chromosome segregation machine. Nature 2010, 463, 446–456. [Google Scholar] [CrossRef]
- Burrack, L.S.; Berman, J. Flexibility of centromere and kinetochore structures. Trends Genet. 2012, 28, 204–212. [Google Scholar] [CrossRef]
- Poirier, M.G.; Marko, J.F. Micromechanical studies of mitotic chromosomes. Curr. Top. Dev. Biol. 2003, 55, 75–141. [Google Scholar]
- Waters, J.C.; Skibbens, R.V.; Salmon, E.D. Oscillating mitotic newt lung cell kinetochores are, on average, under tension and rarely push. J. Cell Sci. 1996, 109 ( Pt. 12), 2823–2831. [Google Scholar]
- Dumont, S.; Mitchison, T.J. Force and length in the mitotic spindle. Curr. Biol. 2009, 19, R749–761. [Google Scholar] [CrossRef] [PubMed]
- Kajtez, J.; Solomatina, A.; Novak, M.; Polak, B.; Vukusic, K.; Rudiger, J.; Cojoc, G.; Milas, A.; Sumanovac Sestak, I.; Risteski, P.; et al. Overlap microtubules link sister k-fibres and balance the forces on bi-oriented kinetochores. Nat. Commun 2016, 7, 10298. [Google Scholar] [CrossRef] [PubMed]
- Simunic, J.; Tolic, I.M. Mitotic Spindle Assembly: Building the Bridge between Sister K-Fibers. Trends Biochem. Sci. 2016, 41, 824–833. [Google Scholar] [CrossRef] [PubMed]
- Tolic, I.M.; Pavin, N. Bridging the gap between sister kinetochores. Cell Cycle 2016, 15, 1169–1170. [Google Scholar] [CrossRef] [PubMed]
- Tolic, I.M. Mitotic spindle: Kinetochore fibers hold on tight to interpolar bundles. Eur. Biophys. J. 2018, 47, 191–203. [Google Scholar] [CrossRef]
- Polak, B.; Risteski, P.; Lesjak, S.; Tolic, I.M. PRC1-labeled microtubule bundles and kinetochore pairs show one-to-one association in metaphase. EMBO Rep. 2017, 18, 217–230. [Google Scholar] [CrossRef]
- Milas, A.; Tolic, I.M. Relaxation of interkinetochore tension after severing of a k-fiber depends on the length of the k-fiber stub. Matters (Zür.) 2016. Published online March 23, 2016. [Google Scholar] [CrossRef]
- Vukusic, K.; Buda, R.; Bosilj, A.; Milas, A.; Pavin, N.; Tolic, I.M. Microtubule Sliding within the Bridging Fiber Pushes Kinetochore Fibers Apart to Segregate Chromosomes. Dev. Cell 2017, 43, 11–23 e16. [Google Scholar] [CrossRef]
- Yang, C.F.; Tsai, W.Y.; Chen, W.A.; Liang, K.W.; Pan, C.J.; Lai, P.L.; Yang, P.C.; Huang, H.C. Kinesin-5 Contributes to Spindle-length Scaling in the Evolution of Cancer toward Metastasis. Sci Rep. 2016, 6, 35767. [Google Scholar] [CrossRef]
- Cai, S.; Weaver, L.N.; Ems-McClung, S.C.; Walczak, C.E. Kinesin-14 family proteins HSET/XCTK2 control spindle length by cross-linking and sliding microtubules. Mol. Biol. Cell 2009, 20, 1348–1359. [Google Scholar] [CrossRef] [PubMed]
- Sawin, K.E.; LeGuellec, K.; Philippe, M.; Mitchison, T.J. Mitotic spindle organization by a plus-end-directed microtubule motor. Nature 1992, 359, 540–543. [Google Scholar] [CrossRef]
- Hagan, I.; Yanagida, M. Novel potential mitotic motor protein encoded by the fission yeast cut7+ gene. Nature 1990, 347, 563–566. [Google Scholar] [CrossRef]
- Gayek, A.S.; Ohi, R. Kinetochore-microtubule stability governs the metaphase requirement for Eg5. Mol. Biol. Cell 2014, 25, 2051–2060. [Google Scholar] [CrossRef] [PubMed]
- Vale, R.D.; Toyoshima, Y.Y. Rotation and translocation of microtubules in vitro induced by dyneins from Tetrahymena cilia. Cell 1988, 52, 459–469. [Google Scholar] [CrossRef]
- Walker, R.A.; Salmon, E.D.; Endow, S.A. The Drosophila claret segregation protein is a minus-end directed motor molecule. Nature 1990, 347, 780–782. [Google Scholar] [CrossRef] [PubMed]
- Yajima, J.; Mizutani, K.; Nishizaka, T. A torque component present in mitotic kinesin Eg5 revealed by three-dimensional tracking. Nat. Struct. Mol. Biol. 2008, 15, 1119–1121. [Google Scholar] [CrossRef] [PubMed]
- Bormuth, V.; Nitzsche, B.; Ruhnow, F.; Mitra, A.; Storch, M.; Rammner, B.; Howard, J.; Diez, S. The highly processive kinesin-8, Kip3, switches microtubule protofilaments with a bias toward the left. Biophys. J. 2012, 103, L4-6. [Google Scholar] [CrossRef]
- Can, S.; Dewitt, M.A.; Yildiz, A. Bidirectional helical motility of cytoplasmic dynein around microtubules. Elife 2014, 3, e03205. [Google Scholar] [CrossRef] [PubMed]
- Ramaiya, A.; Roy, B.; Bugiel, M.; Schaffer, E. Kinesin rotates unidirectionally and generates torque while walking on microtubules. Proc. Natl Acad Sci USA 2017, 114, 10894–10899. [Google Scholar] [CrossRef]


© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Tolić, I.M.; Novak, M.; Pavin, N. Helical Twist and Rotational Forces in the Mitotic Spindle. Biomolecules 2019, 9, 132. https://doi.org/10.3390/biom9040132
Tolić IM, Novak M, Pavin N. Helical Twist and Rotational Forces in the Mitotic Spindle. Biomolecules. 2019; 9(4):132. https://doi.org/10.3390/biom9040132
Chicago/Turabian StyleTolić, Iva M., Maja Novak, and Nenad Pavin. 2019. "Helical Twist and Rotational Forces in the Mitotic Spindle" Biomolecules 9, no. 4: 132. https://doi.org/10.3390/biom9040132
APA StyleTolić, I. M., Novak, M., & Pavin, N. (2019). Helical Twist and Rotational Forces in the Mitotic Spindle. Biomolecules, 9(4), 132. https://doi.org/10.3390/biom9040132




