On Molecular Descriptors of Carbon Nanocones
Abstract
1. Introduction
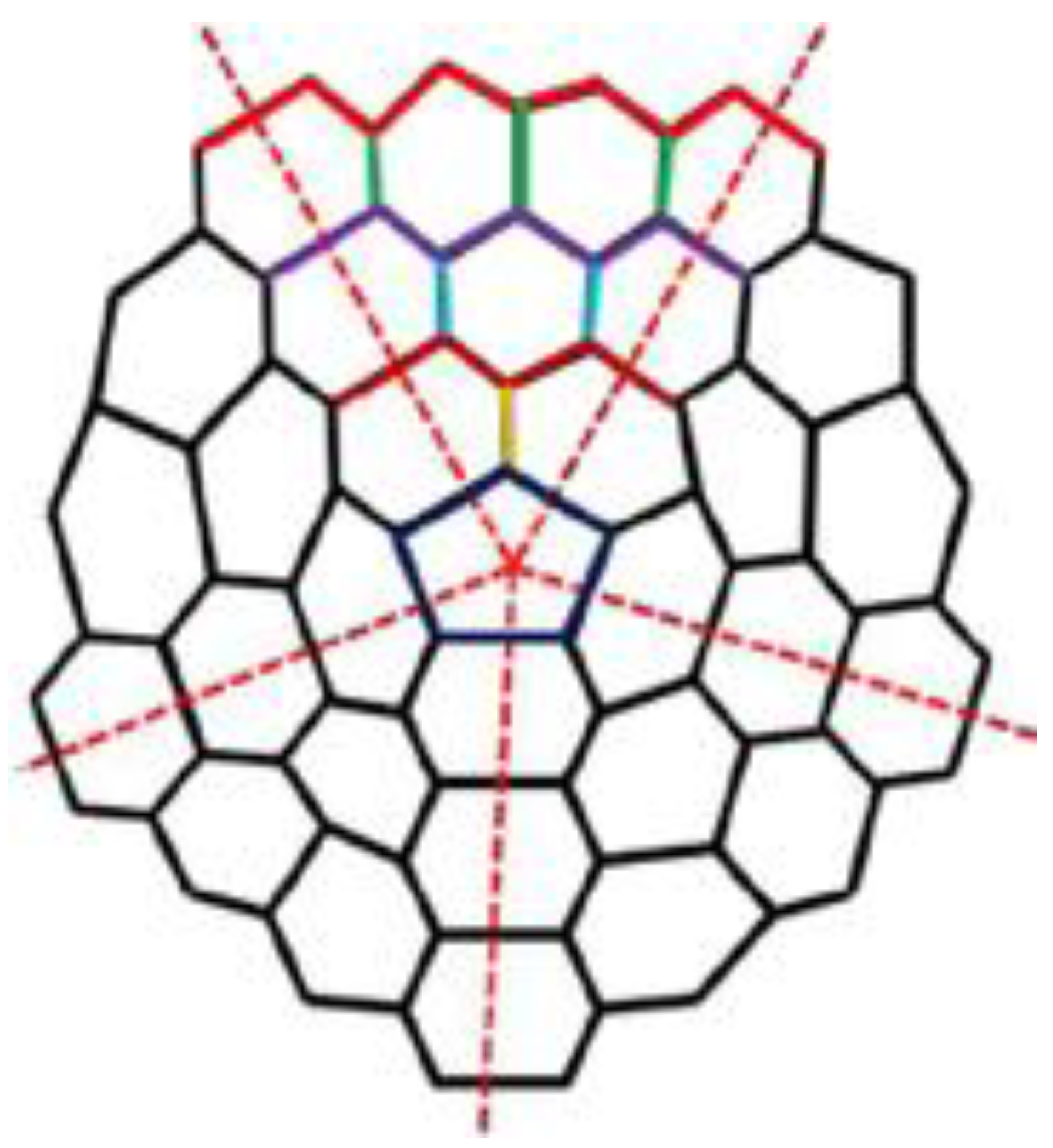
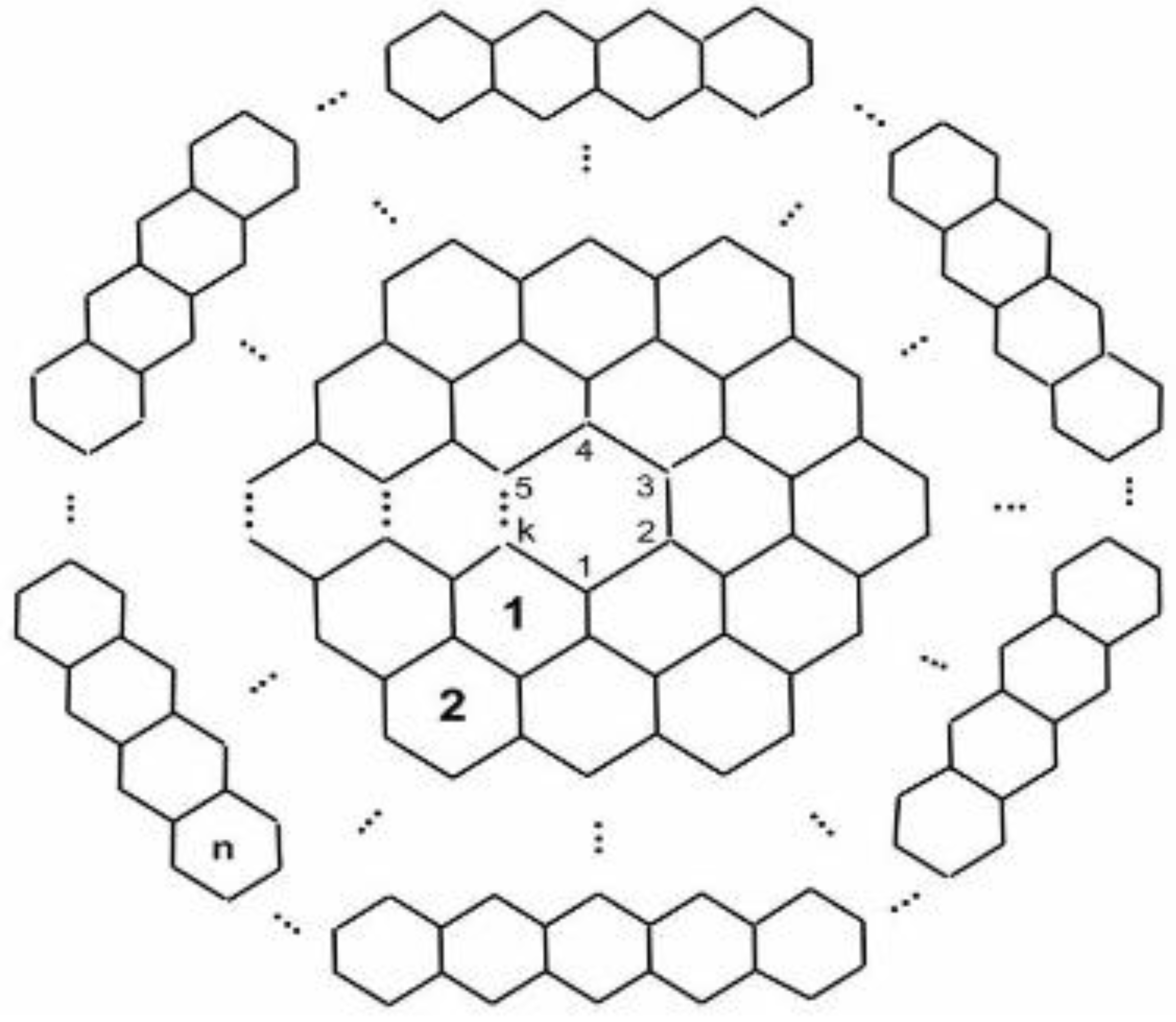
2. Basic Definitions and Notions
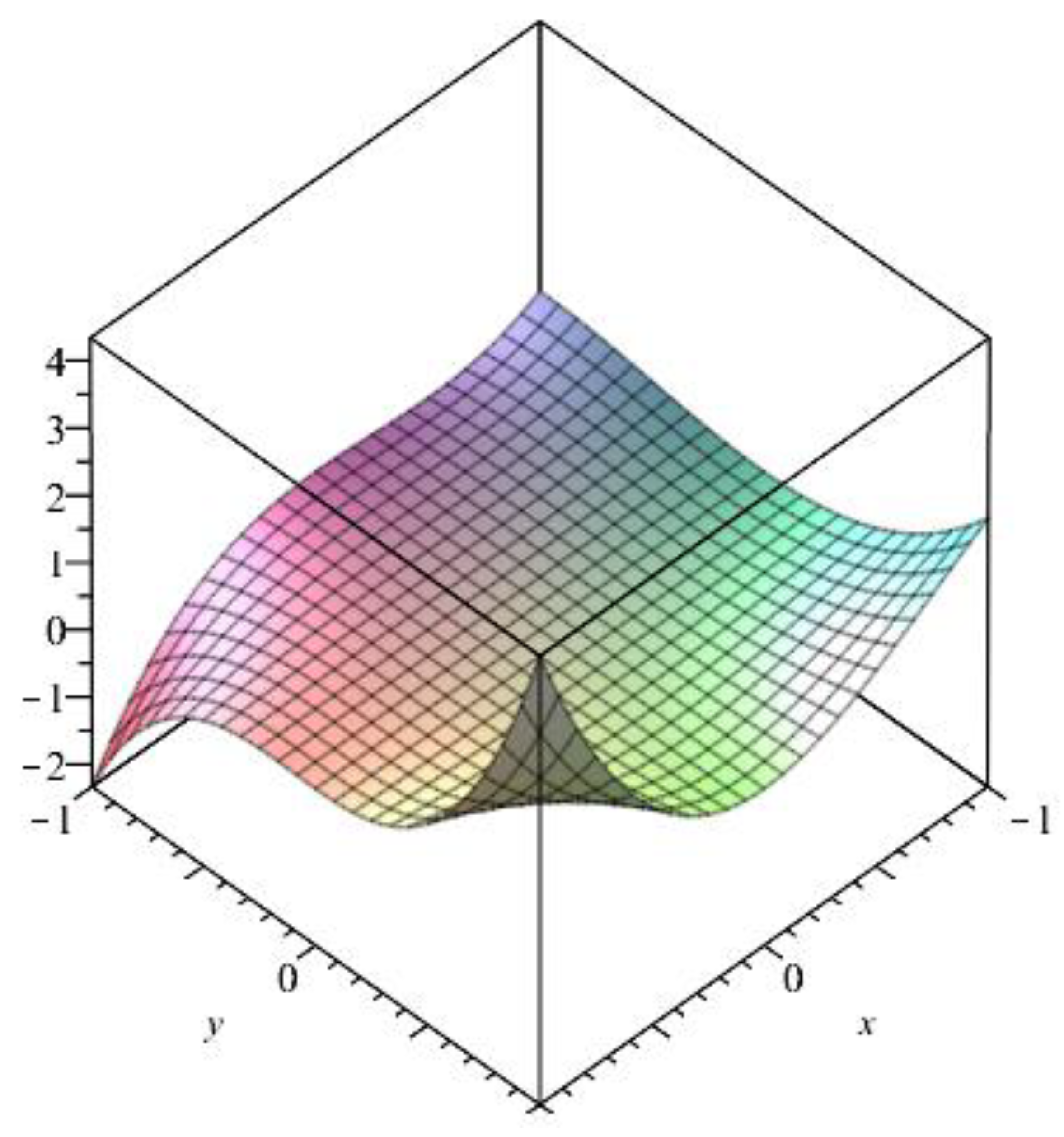
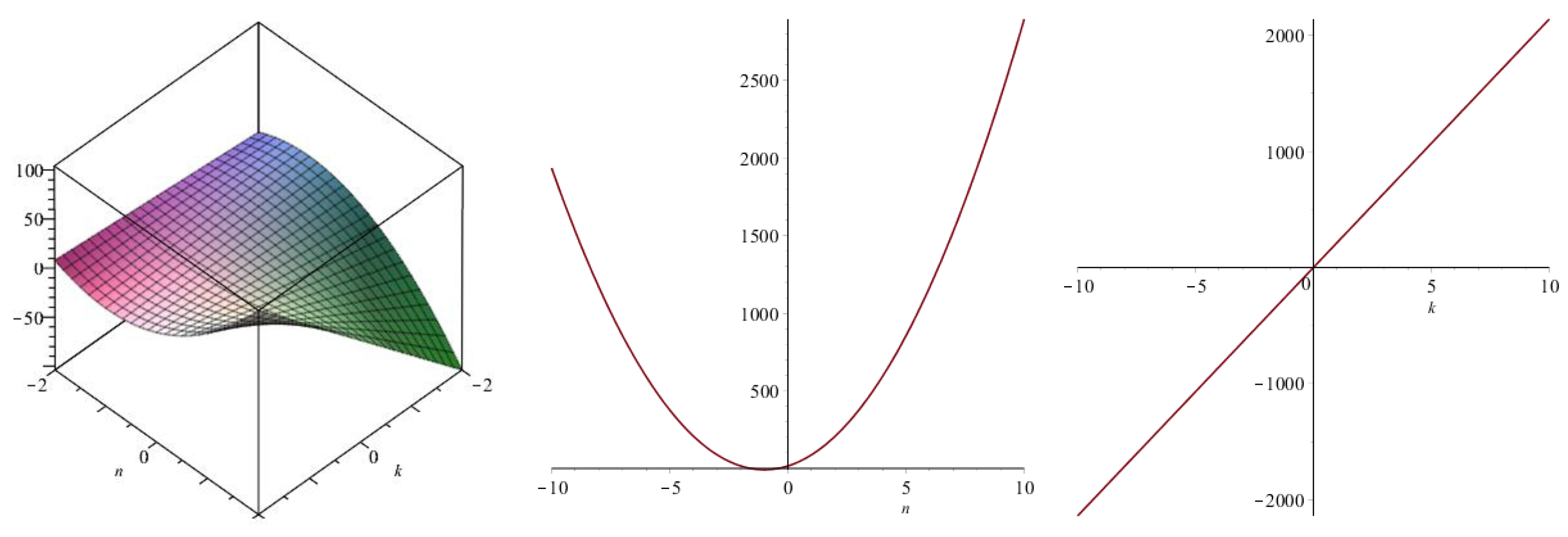
3. Results
4. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Basak, S.C.; Mills, D.; Mumtaz, M.M.; Balasubramanian, K. Use of Topological Indices in Predicting Aryl Hydrocarbon Receptor Binding Potency of Dibenzofurans: A Hierarchical QSAR Approach. Ind. J. Chem. 2003, 42A, 1385–1391. [Google Scholar]
- García, I.; Fall, Y.; Gómez, G. Using topological indices to predict anti-Alzheimer and anti-parasitic GSK-3 inhibitors by multi-target QSAR in silico screening. Molecules 2010, 15, 5408–5422. [Google Scholar] [CrossRef] [PubMed]
- Husin, M.N.; Hasni, R.; Arif, N.E.; Imran, M. On topological indices of certain families of nanostar dendrimers. Molecules 2016, 21, 821. [Google Scholar] [CrossRef] [PubMed]
- Verma, S.; Tripathi, D.; Gupta, P.; Singh, R.; Bahuguna, G.M.; Shivakumark, L.N.; Chauhan, R.K.; Saran, K.S.; Jain, S.L. Highly dispersed palladium nanoparticles grafted onto nanocrystalline starch for the oxidation of alcohols using molecular oxygen as an oxidant. Dalton Trans. 2013, 42, 11522–11527. [Google Scholar] [CrossRef] [PubMed]
- Deutsch, E.; Klavžar, S. M-polynomial and degree-based topological indices. arXiv, 2014; arXiv:1407.1592. [Google Scholar]
- Munir, M.; Nazeer, W.; Rafique, S.; Kang, S.M. M-polynomial and degree-based topological indices of polyhex nanotubes. Symmetry 2016, 8, 149. [Google Scholar] [CrossRef]
- Munir, M.; Nazeer, W.; Rafique, S.; Kang, S.M. M-polynomial and related topological indices of Nanostar dendrimers. Symmetry 2016, 8, 97. [Google Scholar] [CrossRef]
- Munir, M.; Nazeer, W.; Nizami, A.R.; Rafique, S.; Kang, S.M. M-polynomials and topological indices of titania nanotubes. Symmetry 2016, 8, 117. [Google Scholar] [CrossRef]
- Ali, A.; Nazeer, W.; Munir, M.; Kang, S.M. M-polynomials and topological indices of zigzag and rhombic benzenoid systems. Open Chem. 2018, 16, 73–78. [Google Scholar] [CrossRef]
- Munir, M.; Nazeer, W.; Rafique, S.; Nizami, A.R.; Kang, S.M. Some computational aspects of boron triangular nanotubes. Symmetry 2017, 9, 6. [Google Scholar] [CrossRef]
- Kwun, Y.C.; Munir, M.; Nazeer, W.; Rafique, S.; Kang, S.M. M-Polynomials and topological indices of V-Phenylenic Nanotubes and Nanotori. Sci. Rep. 2017, 7, 8756. [Google Scholar] [CrossRef] [PubMed]
- Kang, S.M.; Nazeer, W.; Gao, W.; Afzal, D.; Gillani, S.N. M-polynomials and topological indices of dominating David derived networks. Open Chem. 2018, 16, 201–213. [Google Scholar] [CrossRef]
- Ahmad, M.S.; Nazeer, W.; Kang, S.M.; Jung, C.Y. M-polynomials and degree based topological indices for the line graph of firecracker graph. Glob. J. Pure Appl. Math. 2017, 13, 2749–2776. [Google Scholar]
- Kang, S.M.; Nazeer, W.; Zahid, M.A.; Nizami, A.R.; Aslam, A.; Munir, M. M-polynomials and topological indices of hex-derived networks. Open Phys. 2018, 16, 394–403. [Google Scholar] [CrossRef]
- Gillot, J.; Bollmann, W.; Lux, B. Cigar-shaped graphite crystals with conical structure. Carbon 1968, 6, 381–384. [Google Scholar] [CrossRef]
- Iijima, S. Helical microtubules of graphitic carbon. Nature 1991, 354, 56. [Google Scholar] [CrossRef]
- Adisa, O.O.; Cox, B.J.; Hill, J.M. Modelling the surface adsorption of methane on carbon nanostructures. Carbon 2011, 49, 3212–3218. [Google Scholar] [CrossRef]
- Xu, S.J.; Zhang, Q.X. The hosoya polynomial of one-heptagonal nanocone. Curr. Nanosci. 2013, 9, 411–414. [Google Scholar] [CrossRef]
- Ghorbani, M.; Jalali, M. The vertex PI, szeged and omega polynomials of carbon nanocones CNC4 (n). MATCH Commun. Math. Comput. Chem. 2009, 62, 353–362. [Google Scholar]
- Hosoya, H. On some counting polynomials in chemistry. Dis. Appl. Math. 1988, 19, 239–257. [Google Scholar] [CrossRef]
- Wiener, H.J. Structural determination of paraffin boiling points. J. Am. Chem. Soc. 1947, 69, 17–20. [Google Scholar] [CrossRef] [PubMed]
- Dobrynin, A.A.; Gutman, I. The Wiener index for trees and graphs of hexagonal systems. Acta Appl. Math. 2001, 66, 211–249. [Google Scholar] [CrossRef]
- Gutman, I.; Polansky, O.E. Mathematical Concepts in Organic Chemistry; Springer: New York, NY, USA, 1986. [Google Scholar]
- Randić, M. Characterization of molecular branching. J. Am. Chem. Soc. 1975, 97, 6609–6615. [Google Scholar] [CrossRef]
- Bollobas, B.; Erdos, P. Graphs of extremal weights. Ars Combin. 1998, 50, 225–233. [Google Scholar] [CrossRef]
- Amic, D.; Beslo, D.; Lucic, B.; Nikolic, S.; Trinajstić, N. The Vertex-Connectivity Index Revisited. J. Chem. Inf. Comput. Sci. 1998, 38, 819–822. [Google Scholar] [CrossRef]
- Hu, Y.; Li, X.; Shi, Y.; Xu, T.; Gutman, I. On molecular graphs with smallest and greatest zeroth-order general randić index. MATCH Commun. Math. Comput. Chem. 2005, 54, 425–434. [Google Scholar]
- Caporossi, G.; Gutman, I.; Hansen, P.; Pavlovic, L. Graphs with maximum connectivity index. Comput. Biol. Chem. 2003, 27, 85–90. [Google Scholar] [CrossRef]
- Li, X.; Gutman, I. Mathematical Chemistry Monographs; No. 1; University of Kragujevac and Faculty of Science: Kragujevac, Serbien, 2006. [Google Scholar]
- Nikolić, S.; Kovačević, G.; Miličević, A.; Trinajstić, N. First zagreb index, f-index and f-coindex of the line subdivision graphs. Croat. Chem. Acta 2003, 76, 113–124. [Google Scholar]
- Gutman, I.; Das, K.C. The first zagreb index 30 years after. MATCH Commun. Math. Comput. Chem. 2004, 50, 83–92. [Google Scholar]
- Das, K.C.; Gutman, I. Some properties of the second zagreb index. MATCH Commun. Math. Comput. Chem. 2004, 52, 103–112. [Google Scholar]
- Trinajstić, N.; Nikolić, S.; Miličević, A.; Gutman, I. On Zagreb indices. Kem. Ind. 2010, 59, 577–589. [Google Scholar]
- Vukičcević, D.; Graovac, A. Valence connectivities versus Randić, Zagreb and modified Zagreb index: A linear algorithm to check discriminative properties of indices in acyclic molecular graphs. Croat. Chem. Acta 2004, 77, 501–508. [Google Scholar]
- Huang, Y.; Liu, B.; Gan, L. Augmented zagreb index of connected graphs. MATCH Commun. Math. Comput. Chem. 2012, 67, 483–494. [Google Scholar]

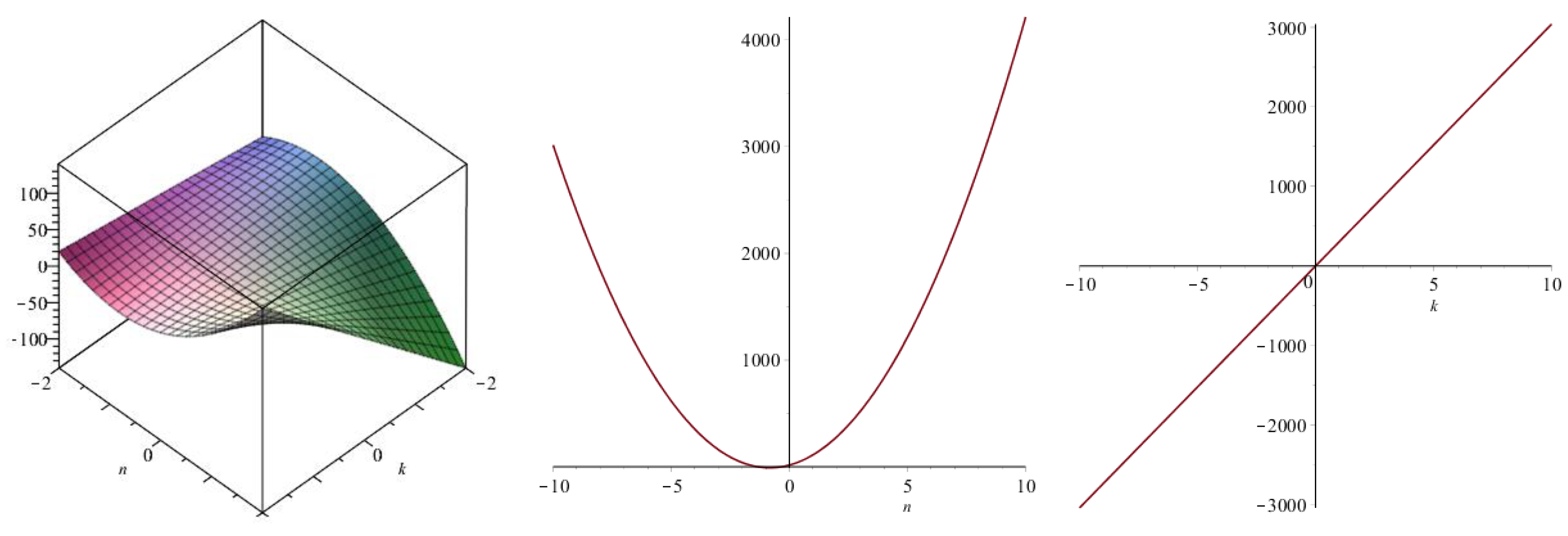
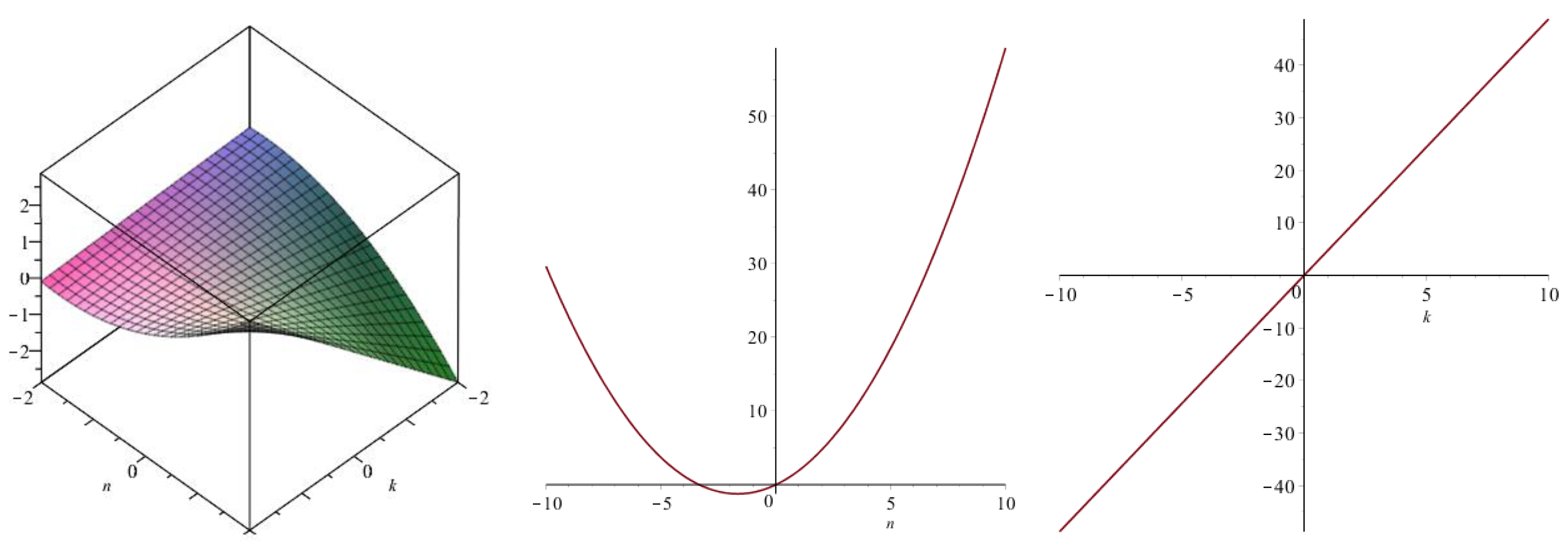
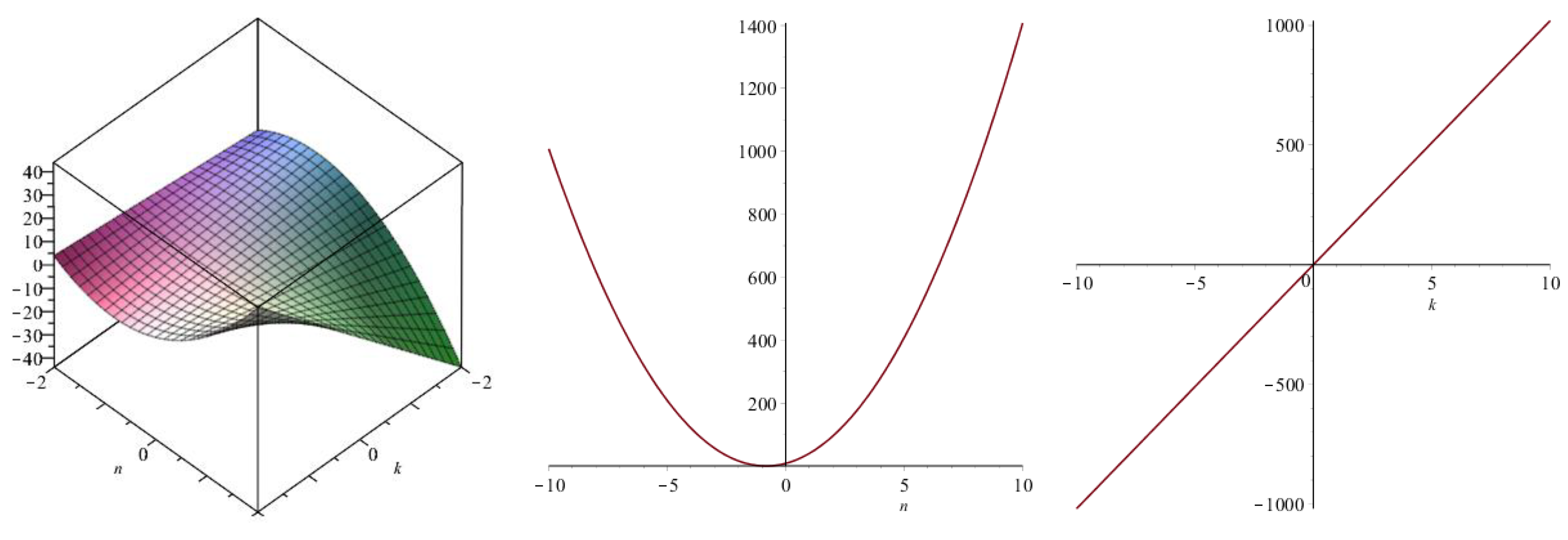
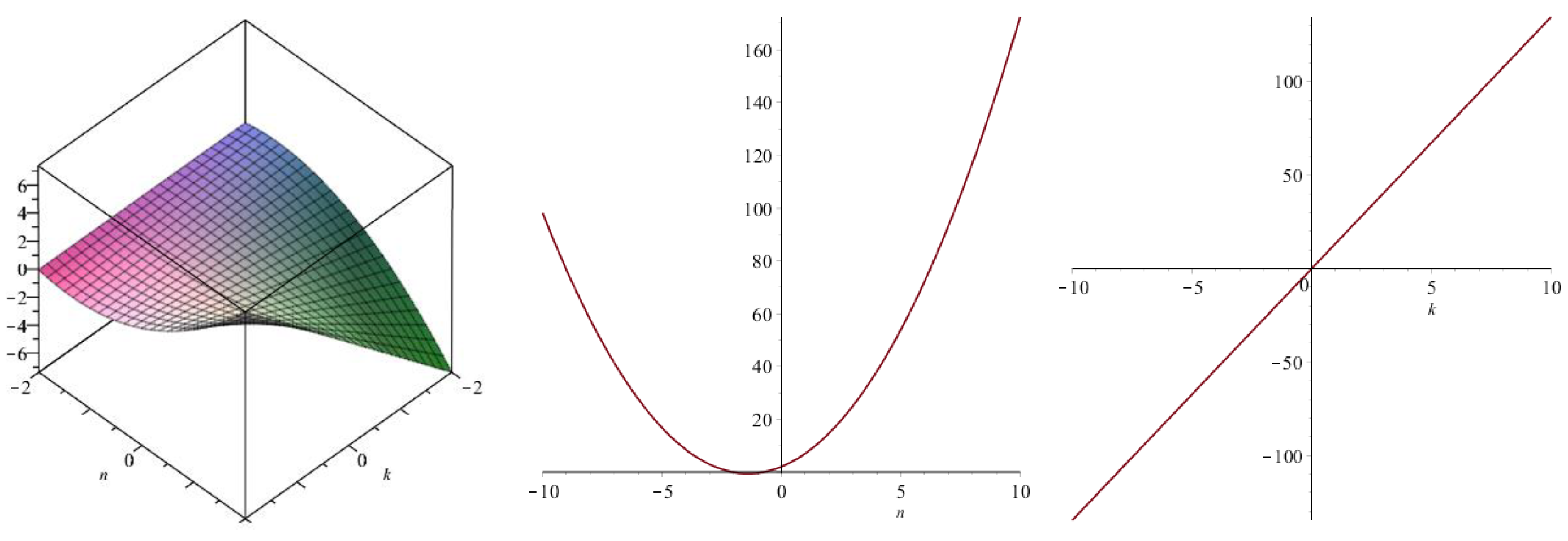
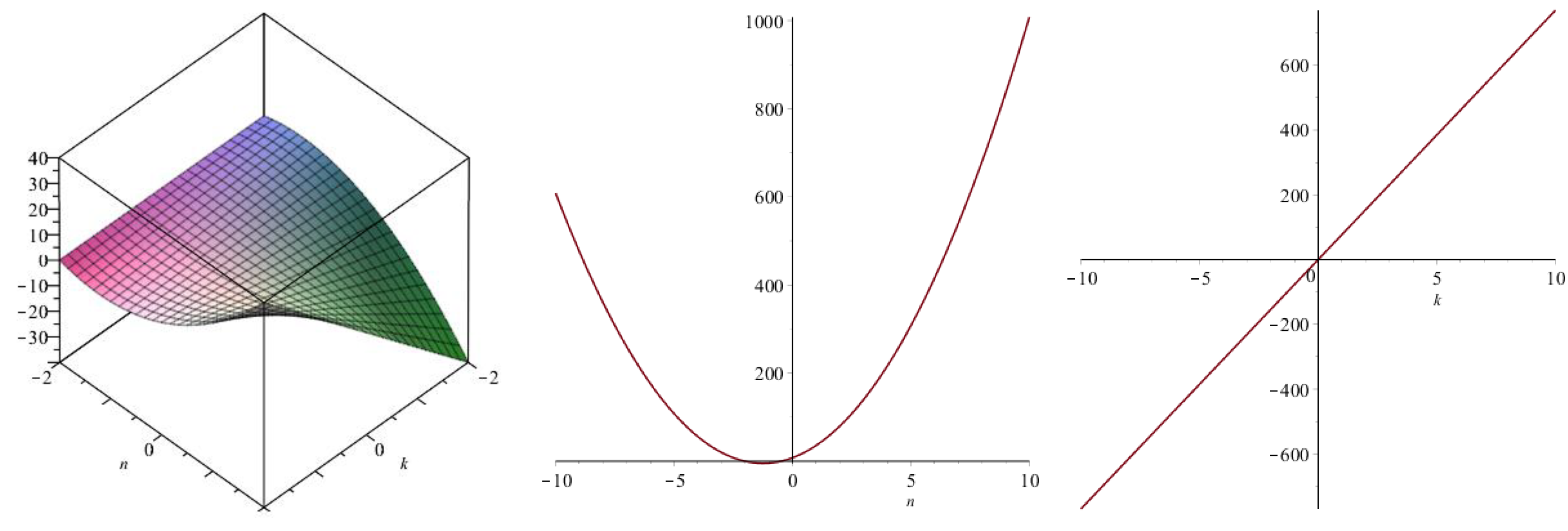
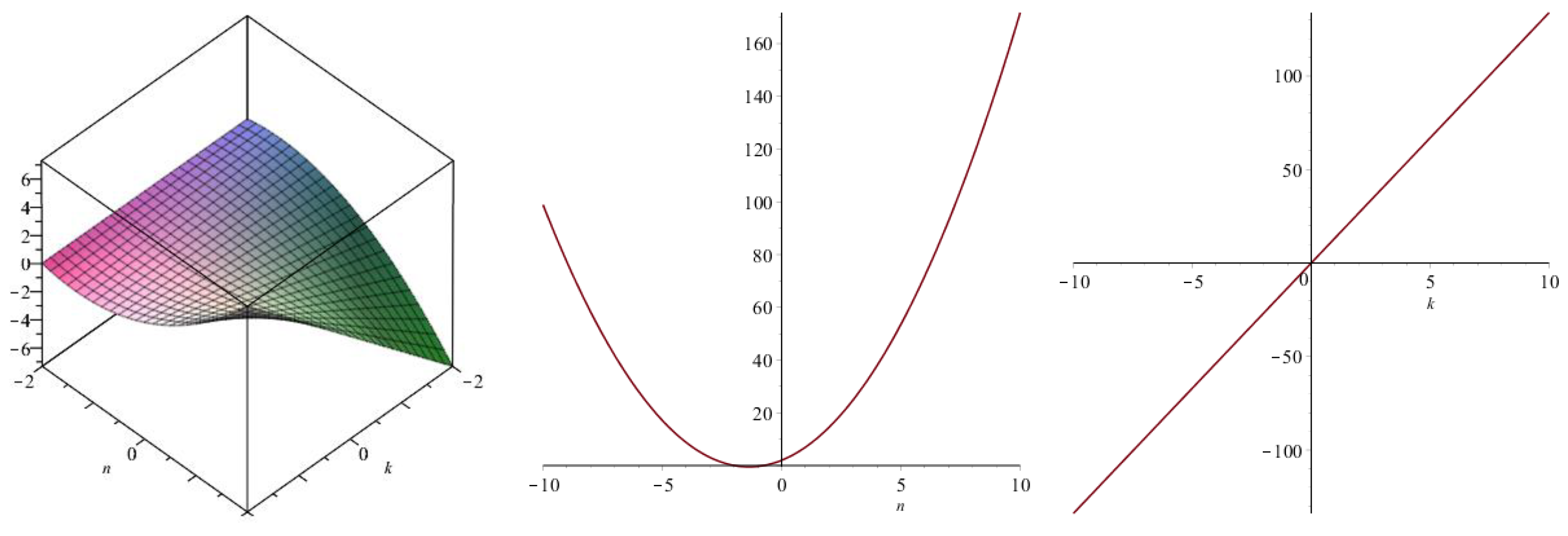
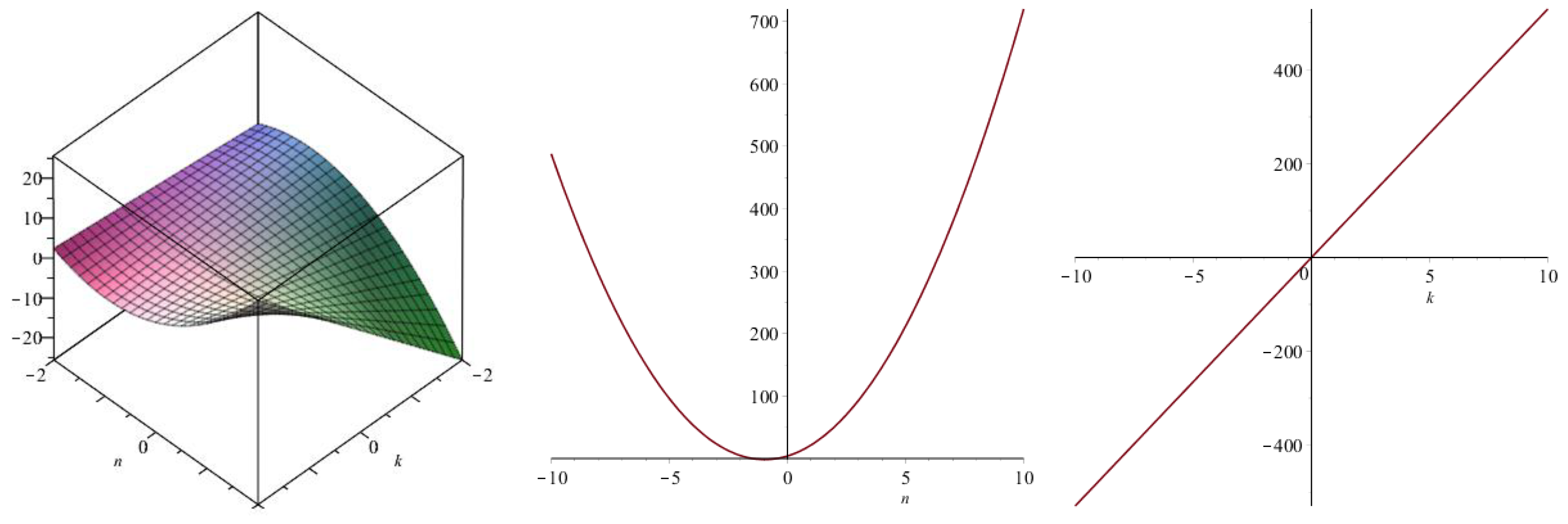

| Topological Index | |
| First Zagreb | |
| Second Zagreb | |
| Second Modified Zagreb | |
| General Randić Index | |
| General inverse Randić Index | |
| Symmetric Division Index | |
| Harmonic Index | |
| Inverse sum Index | |
| Augmented Zagreb Index |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Nazeer, W.; Farooq, A.; Younas, M.; Munir, M.; Kang, S.M. On Molecular Descriptors of Carbon Nanocones. Biomolecules 2018, 8, 92. https://doi.org/10.3390/biom8030092
Nazeer W, Farooq A, Younas M, Munir M, Kang SM. On Molecular Descriptors of Carbon Nanocones. Biomolecules. 2018; 8(3):92. https://doi.org/10.3390/biom8030092
Chicago/Turabian StyleNazeer, Waqas, Adeel Farooq, Muhammad Younas, Mobeen Munir, and Shin Min Kang. 2018. "On Molecular Descriptors of Carbon Nanocones" Biomolecules 8, no. 3: 92. https://doi.org/10.3390/biom8030092
APA StyleNazeer, W., Farooq, A., Younas, M., Munir, M., & Kang, S. M. (2018). On Molecular Descriptors of Carbon Nanocones. Biomolecules, 8(3), 92. https://doi.org/10.3390/biom8030092





