On Eccentricity-Based Topological Indices Study of a Class of Porphyrin-Cored Dendrimers
Abstract
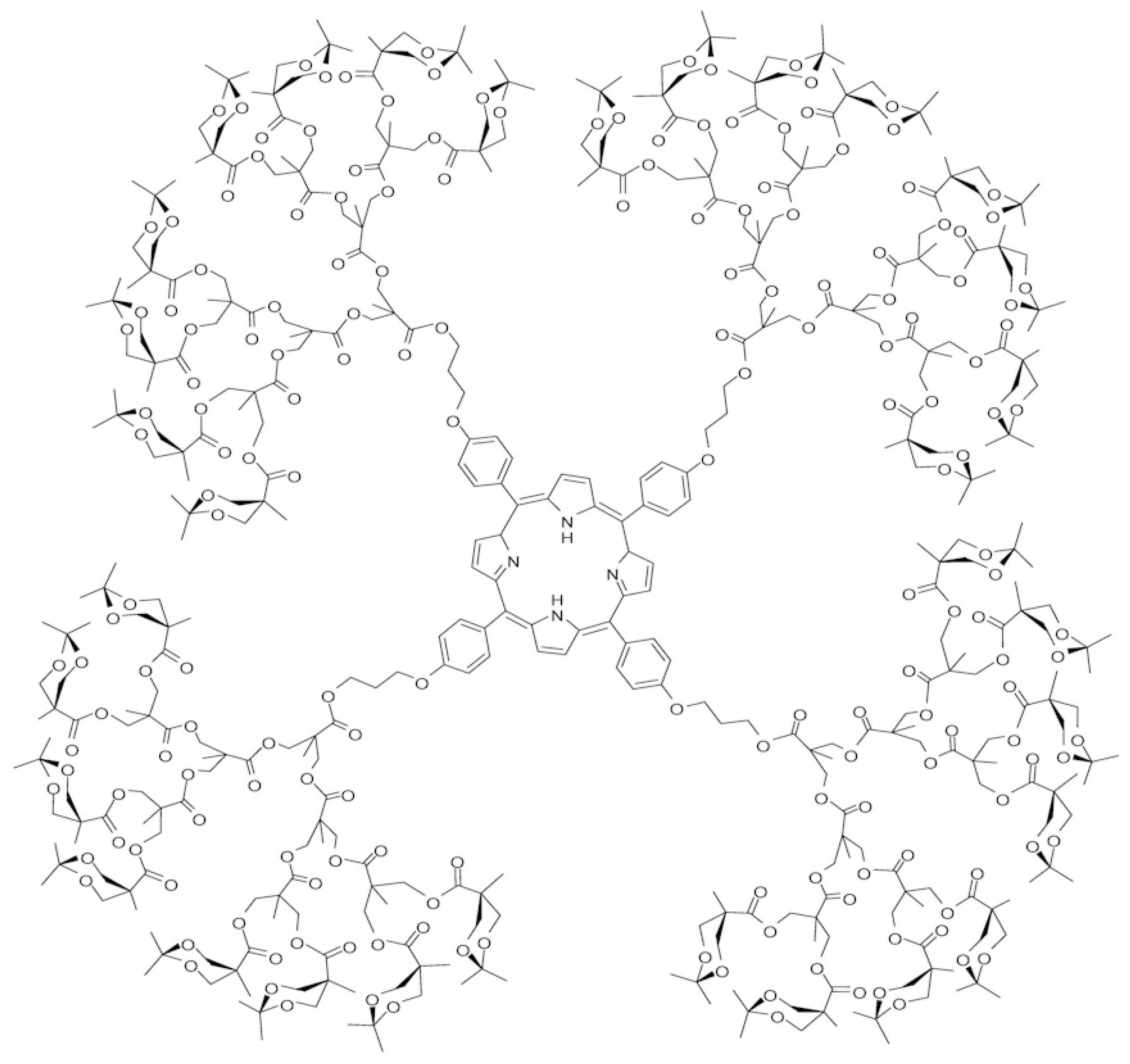
1. Introduction
2. The Eccentricity-Based Indices and Polynomials for the Molecular Graph
3. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- González-Díaz, H.; Vilar, S.; Santana, L.; Uriarte, E. Medicinal chemistry and bioinformatics-current trends in drugs discovery with networks topological indices. Curr. Top. Med. Chem. 2007, 7, 1025–1039. [Google Scholar] [CrossRef]
- Gozalbes, R.; Doucet, J.P.; Derouin, F. Application of topological descriptors in QSAR and drug design: History and new trends. Curr. Drug Targets 2002, 2, 93–102. [Google Scholar] [CrossRef]
- Kier, L.B.; Hall, L.H. Molecular Connectivity in Structure-Activity Analysis; Jhon Wiley and Sons: New York, NY, USA, 1986. [Google Scholar]
- Alaeiyan, M.; Asadpour, J.; Mojarad, R. A numerical method for MEC polynomial and MEC index of one-pentagonal carbon nanocones. Fuller. Nanotub. Carbon Nanostruct. 2013, 2013 21, 825–835. [Google Scholar] [CrossRef]
- Gutman, I.; Trinajstić, N. Graph theory and molecular orbitals Total φ-electron energy of alternant hydrocarbons. Chem. Phys. Lett. 1972, 17, 535–538. [Google Scholar] [CrossRef]
- Rücker, G.; Rücker, C. On topological indices, boiling points, and cycloalkanes. J. Chem. Inf. Comput. Sci. 1999, 39, 788–802. [Google Scholar] [CrossRef]
- Basak, S.C.; Magnuson, V.R.; Niemi, G.J.; Regal, R.R.; Veith, G.D. Topological indices: Their nature, mutual relatedness, and applications. Math. Model. 1987, 8, 300–305. [Google Scholar] [CrossRef]
- Duardo-Sanchez, A.; Patlewicz, G.; González-Díaz, H. A review of network topological indices from chem-bioinformatics to legal sciences and back. Curr. Bioinform. 2011, 6, 53–70. [Google Scholar] [CrossRef]
- Adronov, A.; Frechet, J.M.J. Light-harvesting dendrimers. Chem. Commun. 2000, 33, 1701–1710. [Google Scholar] [CrossRef]
- Naka, K.; Tanaka, Y.; Chujo, Y. Effect of anionic starburst dendrimers on the crystallization of CaCO3 in aqueous solution, Size control of spherical vaterite particles. Langmuir 2002, 18, 3655–3658. [Google Scholar] [CrossRef]
- Suresh, R.; Singh, C.; Rewar, P. Dendrimers as carriers and its application in therapy. Int. J. Anal. Pharm. Biomed. Sci. 2015, 4, 15–23. [Google Scholar]
- Zhao, Z.; Lou, S.; Hu, Y.; Zhu, J.; Zhang, C. A Nano-in-Nano Polymer-Dendrimer Nanoparticle-Based Nanosystem for Controlled Multidrug Delivery. Mol. Pharm. 2017, 14, 2697–2710. [Google Scholar] [CrossRef] [PubMed]
- Abbasi, E.; Aval, S.F.; Akbarzadeh, A.; Milani, M.; Nasrabadi, H.T.; Joo, S.W.; Hanifehpour, Y.; Nejati-Koshki, K.; Pashaei-Asl, R. Dendrimers: Synthesis, applications and properties. Nanoscale Res Lett. 2014, 9, 247–256. [Google Scholar] [CrossRef] [PubMed]
- Wiener, H. Structural determination of paraffin boiling points. J. Am. Chem. Soc. 1947, 69, 17–20. [Google Scholar] [CrossRef] [PubMed]
- Sharma, V.; Goswami, R.; Madan, A.K. Eccentric connectivity index: A novel highly discriminating topological descriptor for structure property and structure activity studies. J. Chem. Inf. Comput. Sci. 1997, 37, 273–282. [Google Scholar] [CrossRef]
- Dureja, H.; Madan, A.K. Topochemical models for prediction of cyclin-dependent kinase 2 inhibitory activity of indole-2-ones. J. Mol. Model. 2005, 11, 525–531. [Google Scholar] [CrossRef] [PubMed]
- Ilic, A.; Gutman, I. Eccentric connectivity index of chemical trees. MATCH Commun. Math. Comput. Chem. 2011, 65, 731–744. [Google Scholar]
- Kumar, V.; Madan, A.K. Application of graph theory: Prediction of cytosolic phospholipase A2 inhibitory activity of propan-2-ones. J. Math. Chem. 2006, 39, 511–521. [Google Scholar] [CrossRef]
- Zhou, B. On eccentric connectivity index. MATCH Commun. Math. Comput. Chem. 2010, 63, 181–198. [Google Scholar]
- Ashrafi, A.R.; Ghorbani, M.; Hossein-Zadeh, M.A. The eccentric connectivity polynomial of some graph operations. Serdica J. Comput. 2011, 5, 101–116. [Google Scholar]
- Ghorbani, M.; Hosseinzadeh, M.A. A new version of Zagreb indices. Filomat 2012, 26, 93–100. [Google Scholar] [CrossRef]
- Gupta, S.; Singh, M.; Madan, A.K. Connective eccentricity index: A novel topological descriptor for predicting biological activity. J. Mol. Graph. Model. 2000, 18, 18–25. [Google Scholar] [CrossRef]
- De, N. Relationship between augmented eccentric connectivity index and some other graph invariants. Int. J. Adv. Math. Sci. 2013, 1, 26–32. [Google Scholar] [CrossRef]
- Doślić, T.; Saheli, M. Augmented eccentric connectivity index. Miskolc Math. Notes. 2011, 12, 149–157. [Google Scholar]
- Sedlar, J. On augmented eccentric connectivity index of graphs and trees. MATCH Commun. Math. Comput. Chem. 2012, 68, 325–342. [Google Scholar]
- Aslam, A.; Ahmed, S.; Gao, W. On topological indices of boron triangular nanotubes. Z. Naturforsch. 2017, 72, 711–716. [Google Scholar] [CrossRef]
- Aslam, A.; Bashir, Y.; Ahmed, S.; Gao, W. On topological indices of certain dendrimer structures. Z. Naturforsch. 2017, 72, 559–566. [Google Scholar] [CrossRef]
- Aslam, A.; Jamil, M.K.; Gao, W.; Nazeer, W. On topological ascpects of some dendrimer structures. Nanotechnol. Rev. 2018, 7, 123–129. [Google Scholar] [CrossRef]
- Aslam, A.; Guirao, J.L.; Ahmad, S.; Gao, W. Topological Indices of the Line Graph of Subdivision Graph of Complete Bipartite Graphs. Appl. Math. Inf. Sci. 2017, 11, 1631–1636. [Google Scholar] [CrossRef]
- Farooq, R.; Malik, M.A. On some eccentricity based topological indices of nanostar dendrimers. Optoelectron. Adv. Mater. Rapid Commun. 2015, 9, 842–849. [Google Scholar]
- Xu, K.; Li, X. Comparison between two eccentricity-based topological indices of graphs. Croat. Chem. Acta 2016, 89, 499–504. [Google Scholar] [CrossRef]
- Bashir, Y.; Aslam, A.; Kamran, M.; Qureshi, I.; Jahangir, A.; Rafiq, M.; Bibi, N.; Muhammad, N. On forgotten topological indices of some dendrimers structure. Molecules 2017, 22, 867. [Google Scholar] [CrossRef] [PubMed]
- Kang, S.M.; Iqbal, Z.; Ishaq, M.; Sarfraz, R.; Aslam, A.; Nazeer, W. On Eccentricity-Based Topological Indices and Polynomials of Phosphorus-Containing Dendrimers. Symmetry 2018, 10, 237–246. [Google Scholar] [CrossRef]
- Jeong, Y.H.; Yoon, H.J.; Jang, W.D. Dendrimer porphyrin-based self-assembled nano-devices for biomedical applications. Polym. J. 2012, 44, 512–521. [Google Scholar] [CrossRef]
- Vestberg, R.; Nyström, A.; Lindgren, M.; Malmström, E.; Hult, A. Porphyrin-cored 2,2-bis (methylol) propionic acid dendrimers. Chem. Master. 2004, 16, 2794–2804. [Google Scholar] [CrossRef]
- Nayak, A.; Stojmenovic, I. Hand Book of Applied Algorithms: Solving Scientific, Engineering, and Practical Problems; John Wiley and Sons: Hoboken, NJ, USA, 2007; 560p. [Google Scholar]
- Sloot, P.; Bubak, M.; Sunderam, V.S.; Alexandrov, V.N.; Albada, G.D.; Dongarra, J.J. Part 3, Lecture notes in computer science. In Computational Science-ICCS; Springer: Krakow, Poland, 2004. [Google Scholar]
- Trinajstic, N. Computational Chemical Graph Theory: Characterization, Enumeration and Generation of Chemical Structures by Computer Methods; Ellis Horwood Ltd.: New York, NY, USA, 1991. [Google Scholar]
- Devillers, J.; Balaban, A.T. Topological Indices and Related Descriptors in QSAR and QSPR; CRC Press: Boca Raton, FL, USA, 2000; 811p. [Google Scholar]
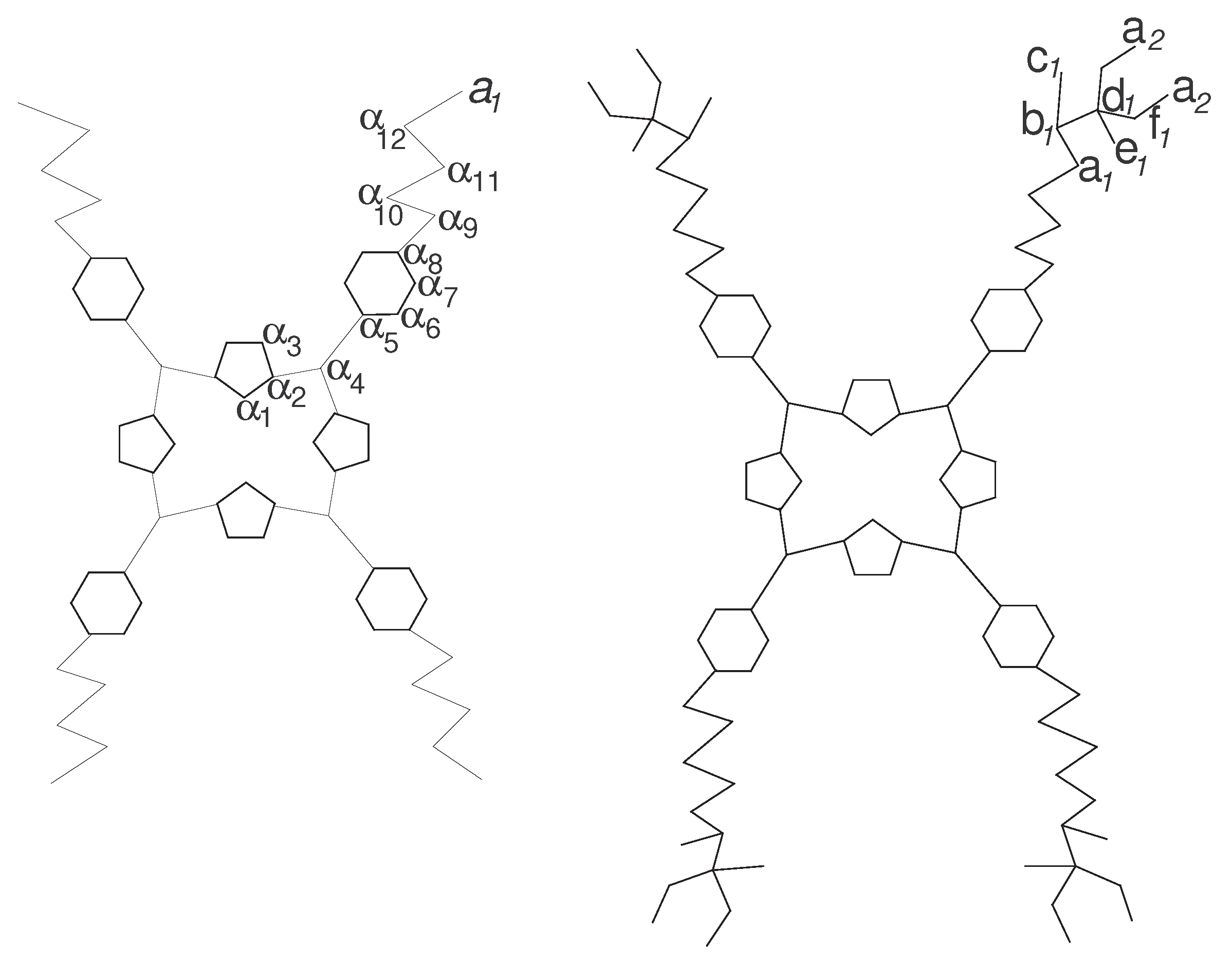
| Representative | Degree | Eccentricity | Frequency | ||
|---|---|---|---|---|---|
| 2 | 6 | 9 | 4 | ||
| 3 | 7 | 12 | 8 | ||
| 2 | 5 | 6 | 8 | ||
| 3 | 9 | 27 | 4 | ||
| 3 | 7 | 12 | 4 | ||
| 2 | 5 | 6 | 8 | ||
| 2 | 5 | 6 | 8 | ||
| 3 | 6 | 8 | 4 | ||
| 2 | 5 | 6 | 4 | ||
| 2 | 4 | 4 | 4 | ||
| 2 | 4 | 4 | 4 | ||
| 2 | 3 | 2 | 4 |
| Representative | Degree | Eccentricity | Frequency | ||
|---|---|---|---|---|---|
| 1 | 2 | 2 | |||
| 2 | 5 | 6 | |||
| 3 | 7 | 8 | |||
| 1 | 3 | 3 | |||
| 4 | 8 | 12 | |||
| 1 | 4 | 4 | |||
| 2 | 5 | 4 |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Gao, W.; Iqbal, Z.; Ishaq, M.; Sarfraz, R.; Aamir, M.; Aslam, A. On Eccentricity-Based Topological Indices Study of a Class of Porphyrin-Cored Dendrimers. Biomolecules 2018, 8, 71. https://doi.org/10.3390/biom8030071
Gao W, Iqbal Z, Ishaq M, Sarfraz R, Aamir M, Aslam A. On Eccentricity-Based Topological Indices Study of a Class of Porphyrin-Cored Dendrimers. Biomolecules. 2018; 8(3):71. https://doi.org/10.3390/biom8030071
Chicago/Turabian StyleGao, Wei, Zahid Iqbal, Muhammad Ishaq, Rabia Sarfraz, Muhammad Aamir, and Adnan Aslam. 2018. "On Eccentricity-Based Topological Indices Study of a Class of Porphyrin-Cored Dendrimers" Biomolecules 8, no. 3: 71. https://doi.org/10.3390/biom8030071
APA StyleGao, W., Iqbal, Z., Ishaq, M., Sarfraz, R., Aamir, M., & Aslam, A. (2018). On Eccentricity-Based Topological Indices Study of a Class of Porphyrin-Cored Dendrimers. Biomolecules, 8(3), 71. https://doi.org/10.3390/biom8030071






