A Physics-Guided Neural Network for Predicting Protein–Ligand Binding Free Energy: From Host–Guest Systems to the PDBbind Database †
Abstract
1. Introduction
2. Background
2.1. Physics-Based Model: GBNSR6
2.2. Data-Driven Model: GCN
3. Materials and Methods
3.1. Featurization and Parameterization
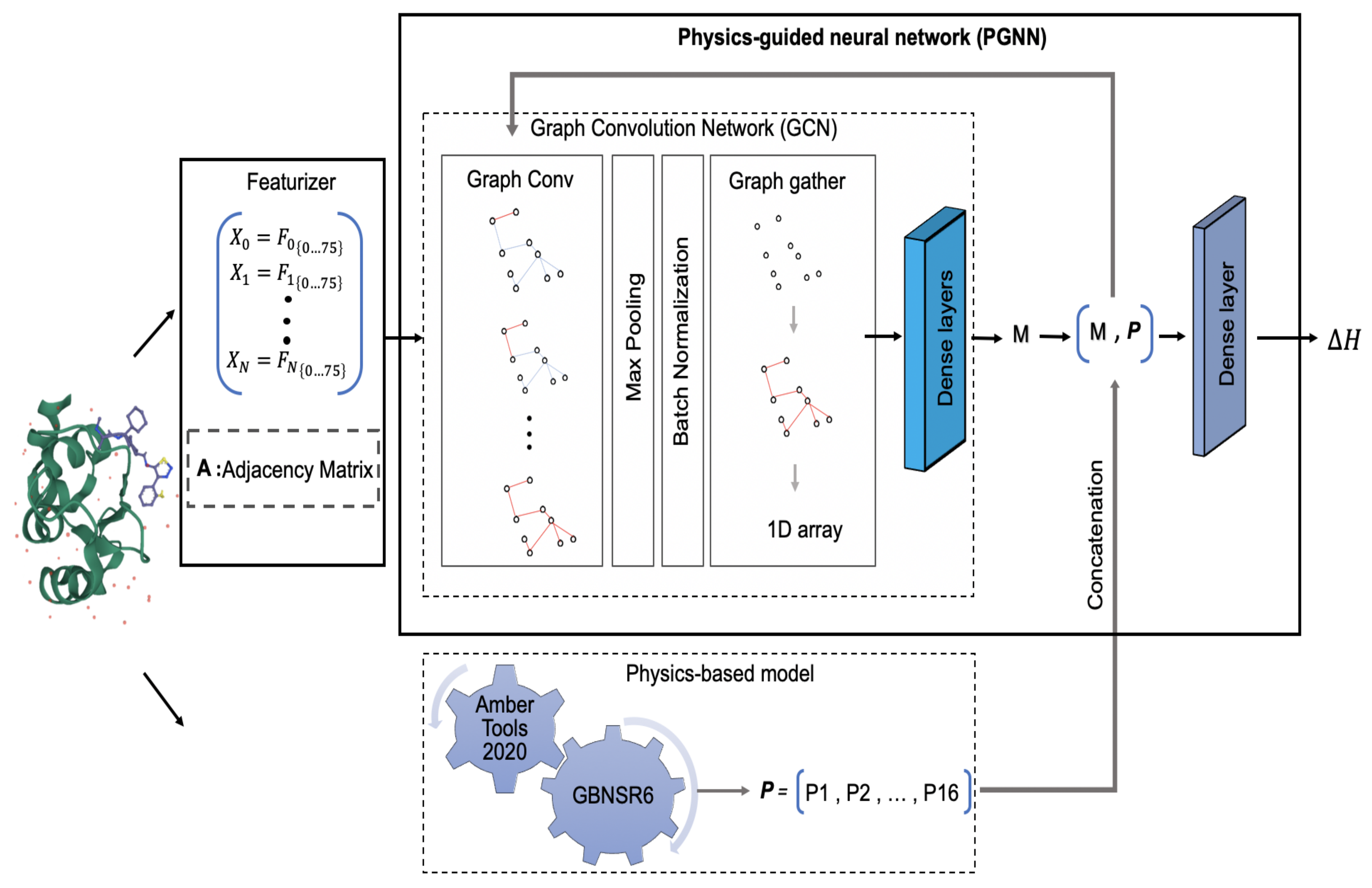
3.2. Hybrid Model: PGNN
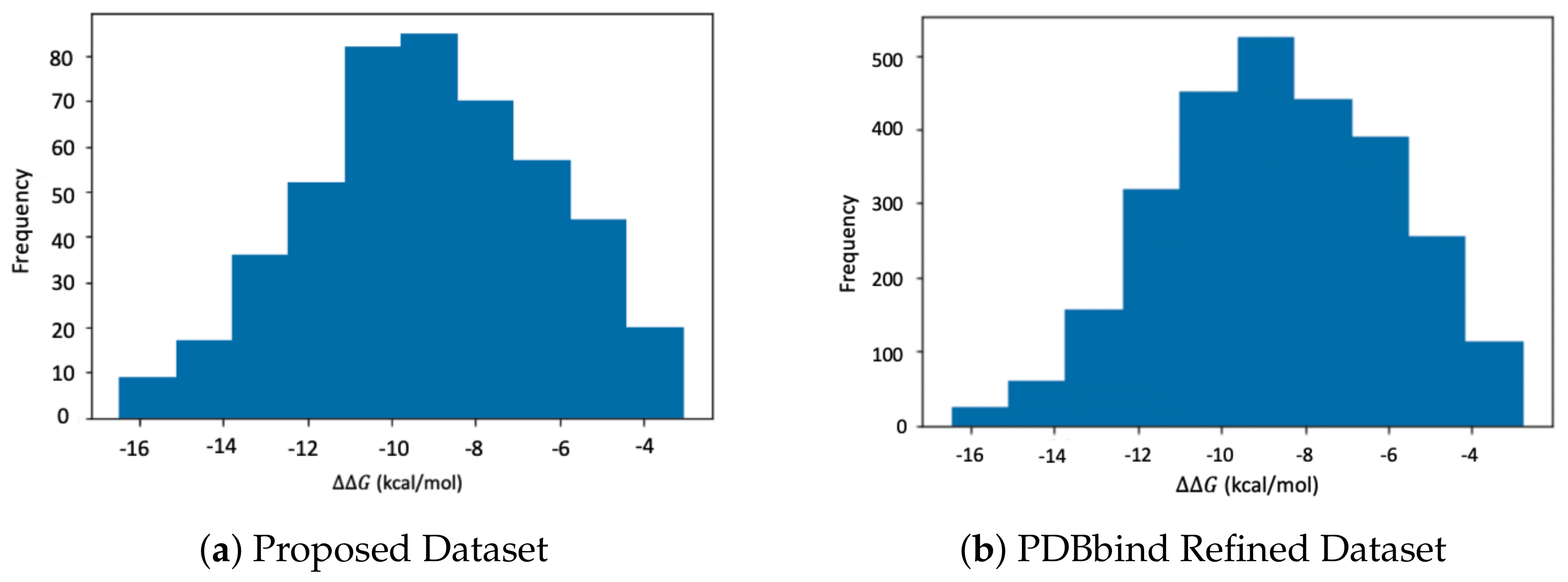
3.3. Datasets
4. Results and Discussion
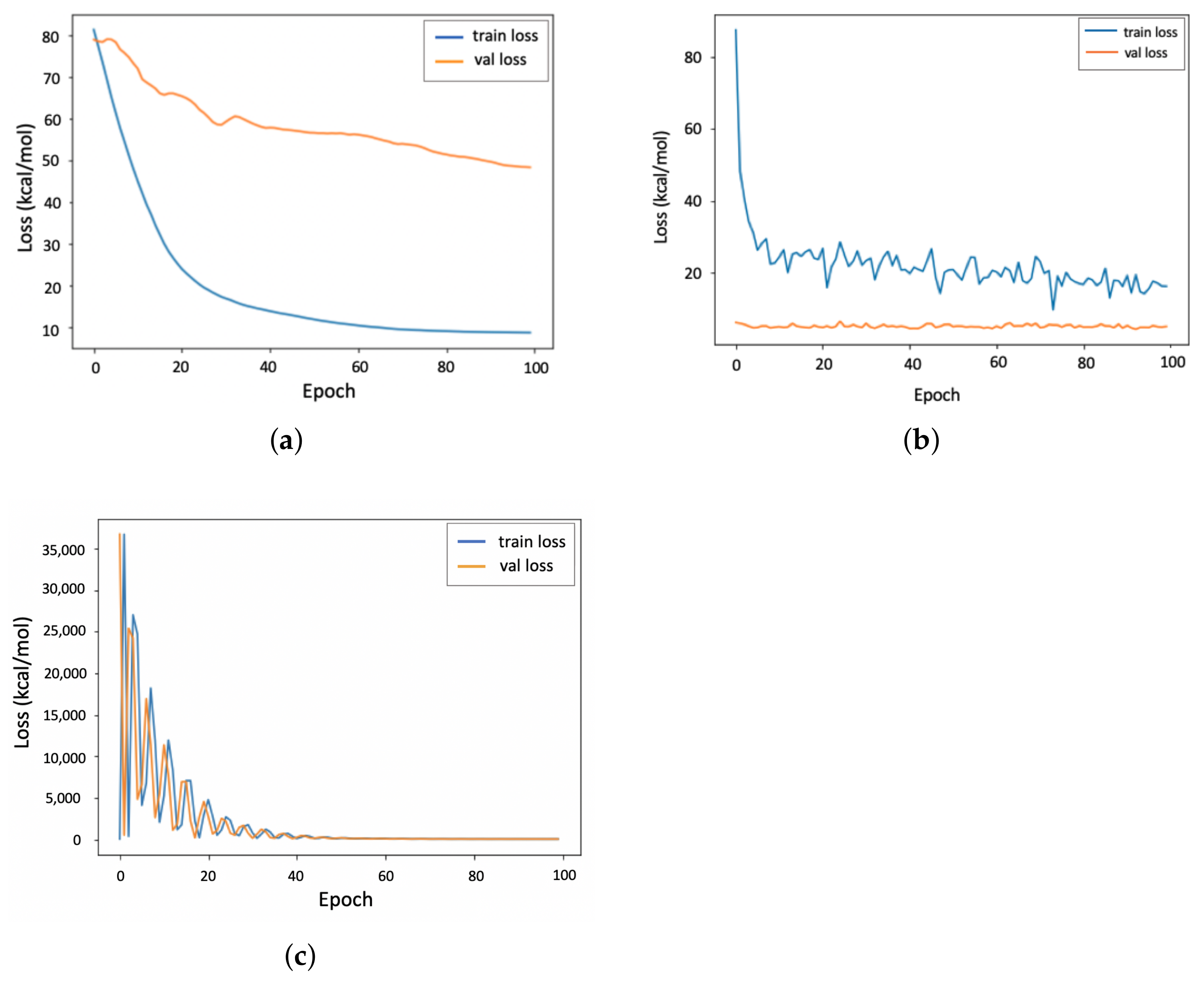
4.1. Accuracy of the PGNN Model
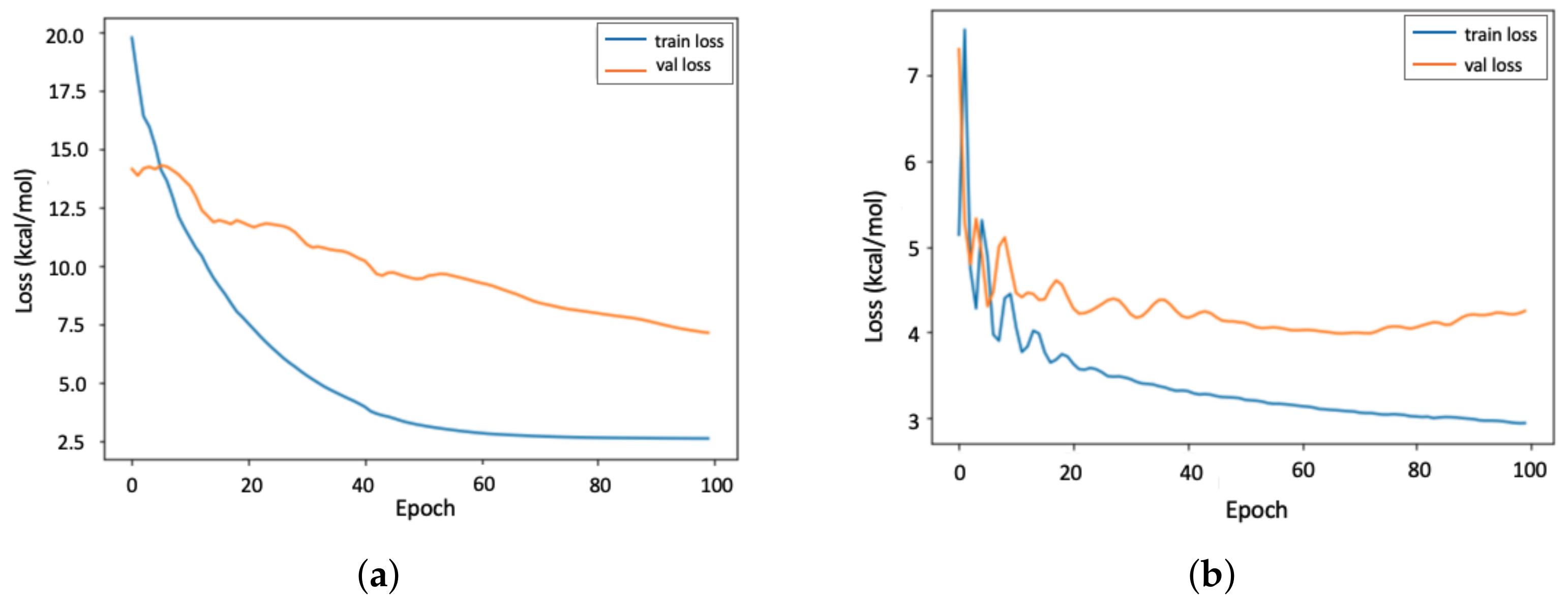
4.2. Transferability of the PGNN Model
4.3. Interpretability of the PGNN Model
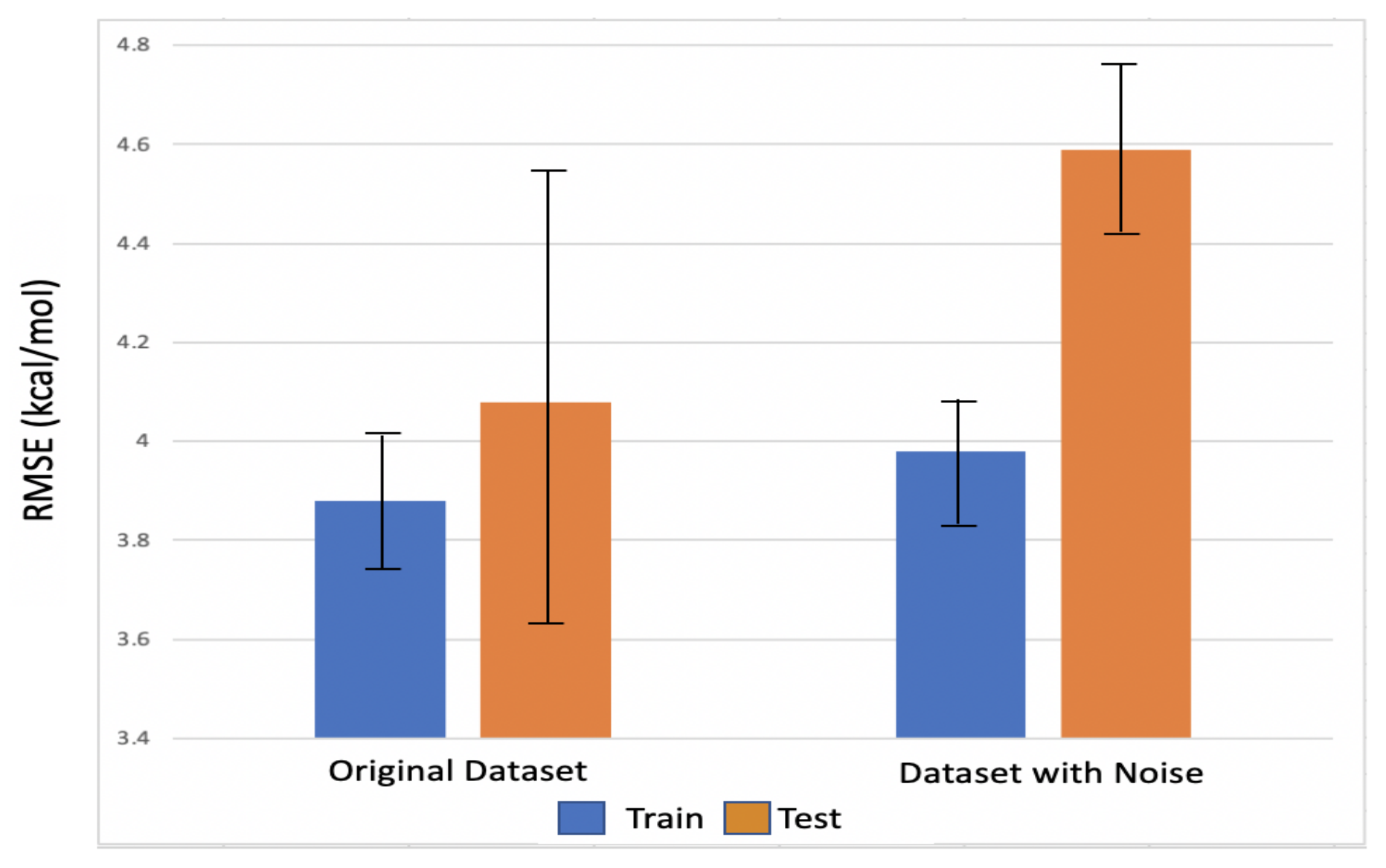
4.4. Robustness Analysis
4.5. Feature Analysis
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Du, X.; Li, Y.; Xia, Y.L.; Ai, S.M.; Liang, J.; Sang, P.; Ji, X.L.; Liu, S.Q. Insights into protein–ligand interactions: Mechanisms, models, and methods. Int. J. Mol. Sci. 2016, 17, 144. [Google Scholar] [CrossRef] [PubMed]
- Woo, H.J.; Roux, B. Calculation of absolute protein–ligand binding free energy from computer simulations. Proc. Natl. Acad. Sci. USA 2005, 102, 6825–6830. [Google Scholar] [CrossRef] [PubMed]
- Jorgensen, W.L. The Many Roles of Computation in Drug Discovery. Science 2004, 303, 1813–1818. [Google Scholar] [CrossRef] [PubMed]
- Mobley, D.L.; Gilson, M.K. Predicting binding free energies: Frontiers and benchmarks. Annu. Rev. Biophys. 2017, 46, 531–558. [Google Scholar] [CrossRef]
- de Ruiter, A.; Oostenbrink, C. Advances in the calculation of binding free energies. Curr. Opin. Struct. Biol. 2020, 61, 207–212. [Google Scholar] [CrossRef]
- Trott, O.; Olson, A.J. AutoDock Vina: Improving the speed and accuracy of docking with a new scoring function, efficient optimization, and multithreading. J. Comput. Chem. 2010, 31, 455–461. [Google Scholar] [CrossRef]
- Allen, W.J.; Balius, T.E.; Mukherjee, S.; Brozell, S.R.; Moustakas, D.T.; Lang, P.T.; Case, D.A.; Kuntz, I.D.; Rizzo, R.C. DOCK 6: Impact of new features and current docking performance. J. Comput. Chem. 2015, 36, 1132–1156. [Google Scholar] [CrossRef]
- Mobley, D.L.; Graves, A.P.; Chodera, J.D.; McReynolds, A.C.; Shoichet, B.K.; Dill, K.A. Predicting absolute ligand binding free energies to a simple model site. J. Mol. Biol. 2007, 371, 1118–1134. [Google Scholar] [CrossRef]
- Chodera, J.D.; Mobley, D.L.; Shirts, M.R.; Dixon, R.W.; Branson, K.; Pande, V.S. Alchemical free energy methods for drug discovery: Progress and challenges. Curr. Opin. Struct. Biol. 2011, 21, 150–160. [Google Scholar] [CrossRef]
- Abel, R.; Wang, L.; Mobley, D.L.; Friesner, R.A. A critical review of validation, blind testing, and real-world use of alchemical protein–ligand binding free energy calculations. Curr. Top. Med. Chem. 2017, 17, 2577–2585. [Google Scholar] [CrossRef]
- Wang, E.; Sun, H.; Wang, J.; Wang, Z.; Liu, H.; Zhang, J.Z.; Hou, T. End-point binding free energy calculation with MM/PBSA and MM/GBSA: Strategies and applications in drug design. Chem. Rev. 2019, 119, 9478–9508. [Google Scholar] [CrossRef]
- Genheden, S.; Ryde, U. The MM/PBSA and MM/GBSA methods to estimate ligand-binding affinities. Expert Opin. Drug Discov. 2015, 10, 449–461. [Google Scholar] [CrossRef]
- Wang, C.; Greene, D.; Xiao, L.; Qi, R.; Luo, R. Recent developments and applications of the MMPBSA method. Front. Mol. Biosci. 2018, 4, 87. [Google Scholar] [CrossRef]
- Hayes, J.M.; Archontis, G. MM-GB (PB) SA calculations of protein–ligand binding free energies. In Molecular Dynamics-Studies of Synthetic and Biological Macromolecules; IntechOpen: London, UK, 2012; pp. 171–190. [Google Scholar]
- Sasmal, S.; El Khoury, L.; Mobley, D.L. D3R Grand Challenge 4: Ligand similarity and MM-GBSA-based pose prediction and affinity ranking for BACE-1 inhibitors. J. Comput.-Aided Mol. Des. 2020, 34, 163–177. [Google Scholar] [CrossRef]
- Wang, Z.; Wang, X.; Li, Y.; Lei, T.; Wang, E.; Li, D.; Kang, Y.; Zhu, F.; Hou, T. farPPI: A webserver for accurate prediction of protein–ligand binding structures for small-molecule PPI inhibitors by MM/PB (GB) SA methods. Bioinformatics 2019, 35, 1777–1779. [Google Scholar] [CrossRef]
- Forouzesh, N.; Mishra, N. An Effective MM/GBSA Protocol for Absolute Binding Free Energy Calculations: A Case Study on SARS-CoV-2 Spike Protein and the Human ACE2 Receptor. Molecules 2021, 26, 2383. [Google Scholar] [CrossRef]
- Sargolzaei, M. Effect of nelfinavir stereoisomers on coronavirus main protease: Molecular docking, molecular dynamics simulation and MM/GBSA study. J. Mol. Graph. Model. 2020, 103, 107803. [Google Scholar] [CrossRef]
- Onufriev, A. Chapter 7—Implicit Solvent Models in Molecular Dynamics Simulations: A Brief Overview. Annu. Rep. Comput. Chem. 2008, 4, 125–137. [Google Scholar] [CrossRef]
- Onufriev, A.V.; Izadi, S. Water models for biomolecular simulations. Wiley Interdiscip. Rev. Comput. Mol. Sci. 2018, 8, e1347. [Google Scholar] [CrossRef]
- Jorgensen, W.L.; Chandrasekhar, J.; Madura, J.D.; Impey, R.W.; Klein, M.L. Comparison of simple potential functions for simulating liquid water. J. Chem. Phys. 1983, 79, 926–935. [Google Scholar] [CrossRef]
- Chen, D.; Chen, Z.; Chen, C.; Geng, W.; Wei, G.W. MIBPB: A software package for electrostatic analysis. J. Comput. Chem. 2011, 32, 756–770. [Google Scholar] [CrossRef] [PubMed]
- Cai, Q.; Ye, X.; Wang, J.; Luo, R. On-the-fly numerical surface integration for finite-difference Poisson–Boltzmann methods. J. Chem. Theory Comput. 2011, 7, 3608–3619. [Google Scholar] [CrossRef] [PubMed]
- Onufriev, A.; Bashford, D.; Case, D.A. Modification of the Generalized Born Model Suitable for Macromolecules. J. Phys. Chem. B 2000, 104, 3712–3720. [Google Scholar] [CrossRef]
- Onufriev, A.; Bashford, D.; Case, D.A. Exploring protein native states and large-scale conformational changes with a modified generalized born model. Proteins Struct. Funct. Bioinform. 2004, 55, 383–394. [Google Scholar] [CrossRef]
- Onufriev, A.V.; Case, D.A. Generalized Born implicit solvent models for biomolecules. Annu. Rev. Biophys. 2019, 48, 275–296. [Google Scholar] [CrossRef]
- Gohlke, H.; Kiel, C.; Case, D.A. Insights into protein–protein binding by binding free energy calculation and free energy decomposition for the Ras–Raf and Ras–RalGDS complexes. J. Mol. Biol. 2003, 330, 891–913. [Google Scholar] [CrossRef]
- Wang, J. Fast identification of possible drug treatment of coronavirus disease-19 (COVID-19) through computational drug repurposing study. J. Chem. Inf. Model. 2020, 60, 3277–3286. [Google Scholar] [CrossRef]
- Zhang, J.; Zhang, H.; Wu, T.; Wang, Q.; van der Spoel, D. Comparison of implicit and explicit solvent models for the calculation of solvation free energy in organic solvents. J. Chem. Theory Comput. 2017, 13, 1034–1043. [Google Scholar] [CrossRef]
- Dzubiella, J.; Swanson, J.; McCammon, J. Coupling nonpolar and polar solvation free energies in implicit solvent models. J. Chem. Phys. 2006, 124, 084905. [Google Scholar] [CrossRef]
- Gomes, J.; Ramsundar, B.; Feinberg, E.N.; Pande, V.S. Atomic convolutional networks for predicting protein–ligand binding affinity. arXiv 2017, arXiv:1703.10603. [Google Scholar]
- Arka, D.; Anuj, K.; William, W.; Jordan, R.; Vipin, K. Physics-guided Neural Networks (PGNN): An Application in Lake Temperature Modeling. arXiv 2021, arXiv:1710.11431. [Google Scholar]
- Karpatne, A.; Atluri, G.; Faghmous, J.H.; Steinbach, M.; Banerjee, A.; Ganguly, A.; Shekhar, S.; Samatova, N.; Kumar, V. Theory-Guided Data Science: A New Paradigm for Scientific Discovery from Data. IEEE Trans. Knowl. Data Eng. 2017, 29, 2318–2331. [Google Scholar] [CrossRef]
- Li, L.; Snyder, J.C.; Pelaschier, I.M.; Huang, J.; Niranjan, U.N.; Duncan, P.; Rupp, M.; Müller, K.R.; Burke, K. Understanding machine-learned density functionals. Int. J. Quantum Chem. 2016, 116, 819–833. [Google Scholar] [CrossRef]
- Liu, J.; Wang, K.; Ma, S.; Huang, J. Accounting for linkage disequilibrium in genome-wide association studies: A penalized regression method. Stat. Its Interface 2013, 6, 99. [Google Scholar]
- Muralidhar, N.; Bu, J.; Cao, Z.; He, L.; Ramakrishnan, N.; Tafti, D.; Karpatne, A. Physics-guided deep learning for drag force prediction in dense fluid-particulate systems. Big Data 2020, 8, 431–449. [Google Scholar] [CrossRef]
- Hautier, G.; Fischer, C.C.; Jain, A.; Mueller, T.; Ceder, G. Finding nature’s missing ternary oxide compounds using machine learning and density functional theory. Chem. Mater. 2010, 22, 3762–3767. [Google Scholar] [CrossRef]
- Fischer, C.C.; Tibbetts, K.J.; Morgan, D.; Ceder, G. Predicting crystal structure by merging data mining with quantum mechanics. Nat. Mater. 2006, 5, 641–646. [Google Scholar] [CrossRef]
- Curtarolo, S.; Hart, G.L.; Nardelli, M.B.; Mingo, N.; Sanvito, S.; Levy, O. The high-throughput highway to computational materials design. Nat. Mater. 2013, 12, 191–201. [Google Scholar] [CrossRef]
- Forouzesh, N.; Izadi, S.; Onufriev, A.V. Grid-based surface generalized Born model for calculation of electrostatic binding free energies. J. Chem. Inf. Model. 2017, 57, 2505–2513. [Google Scholar] [CrossRef]
- Izadi, S.; Harris, R.C.; Fenley, M.O.; Onufriev, A.V. Accuracy comparison of generalized Born models in the calculation of electrostatic binding free energies. J. Chem. Theory Comput. 2018, 14, 1656–1670. [Google Scholar] [CrossRef]
- Forouzesh, N.; Mukhopadhyay, A.; Watson, L.T.; Onufriev, A.V. Multidimensional Global Optimization and Robustness Analysis in the Context of Protein-Ligand Binding. J. Chem. Theory Comput. 2020, 16, 4669–4684. [Google Scholar] [CrossRef]
- Izadi, S.; Aguilar, B.; Onufriev, A.V. Protein–Ligand Electrostatic Binding Free Energies from Explicit and Implicit Solvation. J. Chem. Theory Comput. 2015, 11, 4450–4459. [Google Scholar] [CrossRef]
- Meng, Z.; Xia, K. Persistent spectral–based machine learning (PerSpect ML) for protein–ligand binding affinity prediction. Sci. Adv. 2021, 7, eabc5329. [Google Scholar] [CrossRef]
- Cain, S.; Risheh, A.; Forouzesh, N. Calculation of Protein-Ligand Binding Free Energy Using a Physics-Guided Neural Network. In Proceedings of the 2021 IEEE International Conference on Bioinformatics and Biomedicine (BIBM), Virtual, 9–12 December 2021; IEEE: Piscataway, NJ, USA, 2021; pp. 2487–2493. [Google Scholar]
- Sigalov, G.; Fenley, A.; Onufriev, A. Analytical Electrostatics for Biomolecules: Beyond the Generalized Born Approximation. J. Chem. Phys. 2006, 124, 124902. [Google Scholar] [CrossRef]
- Still, W.C.; Tempczyk, A.; Hawley, R.C.; Hendrickson, T. Semianalytical Treatment of Solvation for Molecular Mechanics and Dynamics. J. Am. Chem. Soc. 1990, 112, 6127–6129. [Google Scholar] [CrossRef]
- Case, D.A.; Cheatham, T.E., III; Darden, T.; Gohlke, H.; Luo, R.; Merz, K.M., Jr.; Onufriev, A.; Simmerling, C.; Wang, B.; Woods, R.J. The Amber biomolecular simulation programs. J. Comput. Chem. 2005, 26, 1668–1688. [Google Scholar] [CrossRef] [PubMed]
- Genheden, S.; Kuhn, O.; Mikulskis, P.; Hoffmann, D.; Ryde, U. The normal-mode entropy in the MM/GBSA method: Effect of system truncation, buffer region, and dielectric constant. J. Chem. Inf. Model. 2012, 52, 2079–2088. [Google Scholar] [CrossRef]
- Numata, J.; Wan, M.; Knapp, E.W. Conformational entropy of biomolecules: Beyond the quasi-harmonic approximation. Genome Informatics 2007, 18, 192–205. [Google Scholar]
- Zhang, S.; Tong, H.; Xu, J.; Maciejewski, R. Graph convolutional networks: A comprehensive review. Comput. Soc. Netw. 2019, 6, 1–23. [Google Scholar] [CrossRef]
- Coley, C.; Barzilay, R.; Green, W.; Jaakkola, T.; Jensen, K. Convolutional Embedding of Attributed Molecular Graphs for Physical Property Prediction. J. Am. Chem. Soc. 2017, 57, 1757–1772. [Google Scholar] [CrossRef]
- Ramsundar, B.; Eastman, P.; Walters, P.; Pande, V. Deep Learning for the Life Sciences: Applying Deep Learning to Genomics, Microscopy, Drug Discovery, and More; O’Reilly Media, Inc.: Sebastopol, CA, USA, 2019. [Google Scholar]
- Duvenaud, D.; Maclaurin, D.; Aguilera-Iparraguirre, J.; Gómez-Bombarelli, R.; Hirzel, T.; Aspuru-Guzik, A.; Adams, R.P. Convolutional Networks on Graphs for Learning Molecular Fingerprints. arXiv 2015, arXiv:1509.09292. [Google Scholar]
- Case, D.A.; Belfon, K.; Ben-Shalom, I.; Brozell, S.R.; Cerutti, D.; Cheatham, T.; Cruzeiro, V.W.D.; Darden, T.; Duke, R.E.; Giambasu, G.; et al. Amber 2020; University of California, San Francisco: San Francisco, CA, USA, 2020. [Google Scholar]
- Luo, R.; David, L.; Gilson, M.K. Accelerated Poisson–Boltzmann Calculations for Static and Dynamic Systems. J. Comput. Chem. 2002, 23, 1244–1253. [Google Scholar] [CrossRef] [PubMed]
- Wang, J.; Luo, R. Assessment of linear finite-difference Poisson–Boltzmann solvers. J. Comput. Chem. 2010, 31, 1689–1698. [Google Scholar] [PubMed]
- Liu, Z.; Li, Y.; Han, L.; Li, J.; Liu, J.; Zhao, Z.; Nie, W.; Liu, Y.; Wang, R. PDB-wide collection of binding data: Current status of the PDBbind database. Bioinformatics 2015, 31, 405–412. [Google Scholar] [CrossRef]
- Wang, B.; Zhao, Z.; Nguyen, D.D.; Wei, G.W. Feature functional theory–Binding predictor (FFT–BP) for the blind prediction of binding free energies. Theor. Chem. Accounts 2017, 136, 1–22. [Google Scholar] [CrossRef]
- Wang, J.; Wolf, R.M.; Caldwell, J.W.; Kollman, P.A.; Case, D.A. Development and testing of a general amber force field. J. Comput. Chem. 2004, 25, 1157–1174. [Google Scholar] [CrossRef]
- Maier, J.A.; Martinez, C.; Kasavajhala, K.; Wickstrom, L.; Hauser, K.E.; Simmerling, C. ff14SB: Improving the accuracy of protein side chain and backbone parameters from ff99SB. J. Chem. Theory Comput. 2015, 11, 3696–3713. [Google Scholar] [CrossRef]
- Ponder, J.W.; Case, D.A. Force fields for protein simulations. Adv. Protein Chem. 2003, 66, 27–85. [Google Scholar]
- Yin, J.; Henriksen, N.M.; Slochower, D.R.; Shirts, M.R.; Chiu, M.W.; Mobley, D.L.; Gilson, M.K. Overview of the SAMPL5 host–guest challenge: Are we doing better? J. Comput.-Aided Mol. Des. 2017, 31, 1–19. [Google Scholar] [CrossRef]
- Gibb, C.L.D.; Gibb, B.C. Binding of cyclic carboxylates to octa-acid deep-cavity cavitand. J. Comput.-Aided Mol. Des. 2014, 28, 319–325. [Google Scholar] [CrossRef]
- Haiying, G.; Christopher, J.B.; Gibb, B.C. Nonmonotonic Assembly of a Deep-Cavity Cavitand. J. Am. Chem. Soc. 2011, 130, 4770–4773. [Google Scholar] [CrossRef]
- Rizzi, A.; Jensen, T.; Slochower, D.R.; Aldeghi, M.; Gapsys, V.; Ntekoumes, D.; Bosisio, S.; Papadourakis, M.; Henriksen, N.M.; De Groot, B.L.; et al. The SAMPL6 SAMPLing challenge: Assessing the reliability and efficiency of binding free energy calculations. J. Comput.-Aided Mol. Des. 2019, 34, 601–633. [Google Scholar] [CrossRef]
- Xie, T.; Li, Y. Adding Gaussian Noise to DeepFool for Robustness based on Perturbation Directionality. Aust. J. Intell. Inf. Process. Syst. 2019, 16, 44–54. [Google Scholar]

| Parameter | Description | Count |
|---|---|---|
| 1–4-eel | 1–4 Electrostatic energy | 3 |
| VDWAALS | Van der Waals energy | 3 |
| EELEC | Electrostatic energy | 3 |
| ESURF | Non-polar solvation energy | 3 |
| EGB | Polar solvation energy | 3 |
| Entropy | Entropy | 1 |
| Total | 16 |
| GraphConv | AtomicConv | PGNN | |
|---|---|---|---|
| Training set | 2.93 ± 0.08 | 16.37 ± 8.3 | 3.88 ± 0.13 |
| Test set | 6.90 ± 0.86 | 5.23 ± 0.40 | 4.08 ± 0.46 |
| GraphConv | PGNN | GBNSR6 | |
|---|---|---|---|
| Training set | 1.61 ± 0.10 | 1.71 ± 0.11 | 8.22 ± 0.11 |
| Test set | 2.43 ± 1.27 | 2.05 ± 0.27 | 8.35 ± 0.34 |
| Physics-Based Parameters | Before Training | After Training |
|---|---|---|
| VDWAALS | ||
| EELEC | ||
| ESURF | ||
| EGB | ||
| 1–4-eel | ||
| Entropy | ||
| Model variable |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Cain, S.; Risheh, A.; Forouzesh, N. A Physics-Guided Neural Network for Predicting Protein–Ligand Binding Free Energy: From Host–Guest Systems to the PDBbind Database. Biomolecules 2022, 12, 919. https://doi.org/10.3390/biom12070919
Cain S, Risheh A, Forouzesh N. A Physics-Guided Neural Network for Predicting Protein–Ligand Binding Free Energy: From Host–Guest Systems to the PDBbind Database. Biomolecules. 2022; 12(7):919. https://doi.org/10.3390/biom12070919
Chicago/Turabian StyleCain, Sahar, Ali Risheh, and Negin Forouzesh. 2022. "A Physics-Guided Neural Network for Predicting Protein–Ligand Binding Free Energy: From Host–Guest Systems to the PDBbind Database" Biomolecules 12, no. 7: 919. https://doi.org/10.3390/biom12070919
APA StyleCain, S., Risheh, A., & Forouzesh, N. (2022). A Physics-Guided Neural Network for Predicting Protein–Ligand Binding Free Energy: From Host–Guest Systems to the PDBbind Database. Biomolecules, 12(7), 919. https://doi.org/10.3390/biom12070919







