ECMpy, a Simplified Workflow for Constructing Enzymatic Constrained Metabolic Network Model
Abstract
:1. Introduction
2. Materials and Methods
2.1. The Workflow of ECMpy
2.2. Calibration of the Original kcat Values
2.3. Simulation
3. Results
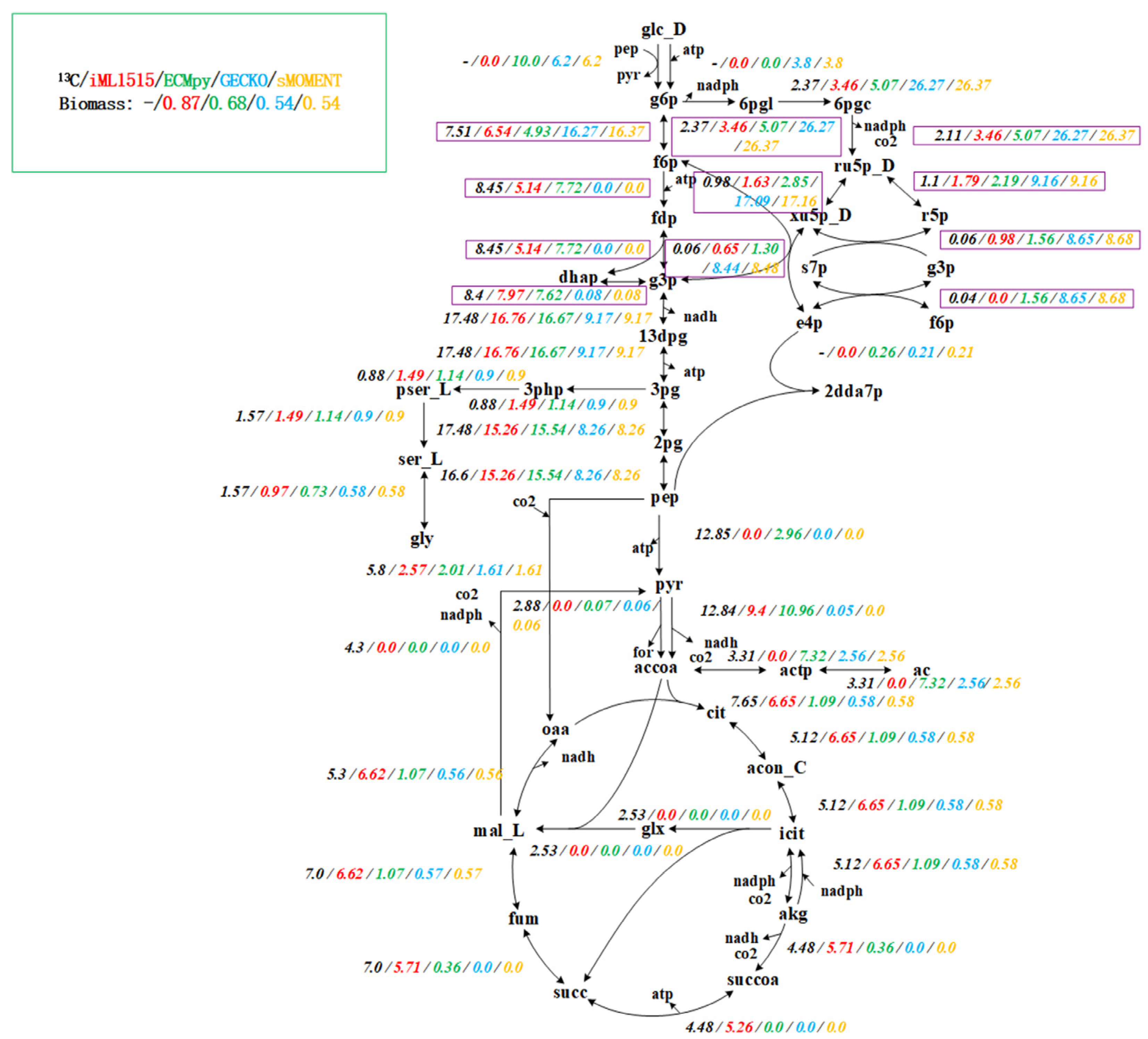
3.1. Construction of the Enzyme-Constrained Model of iML1515 by ECMpy
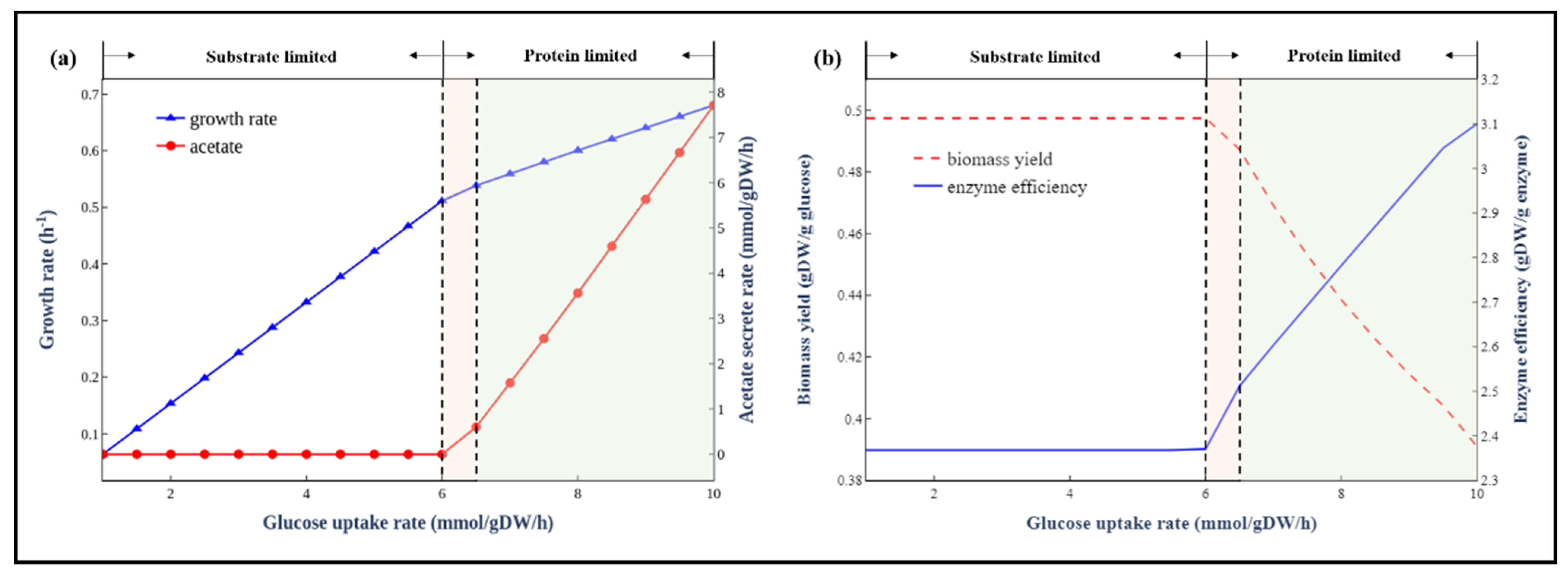
3.2. Overflow Metabolism of E. coli
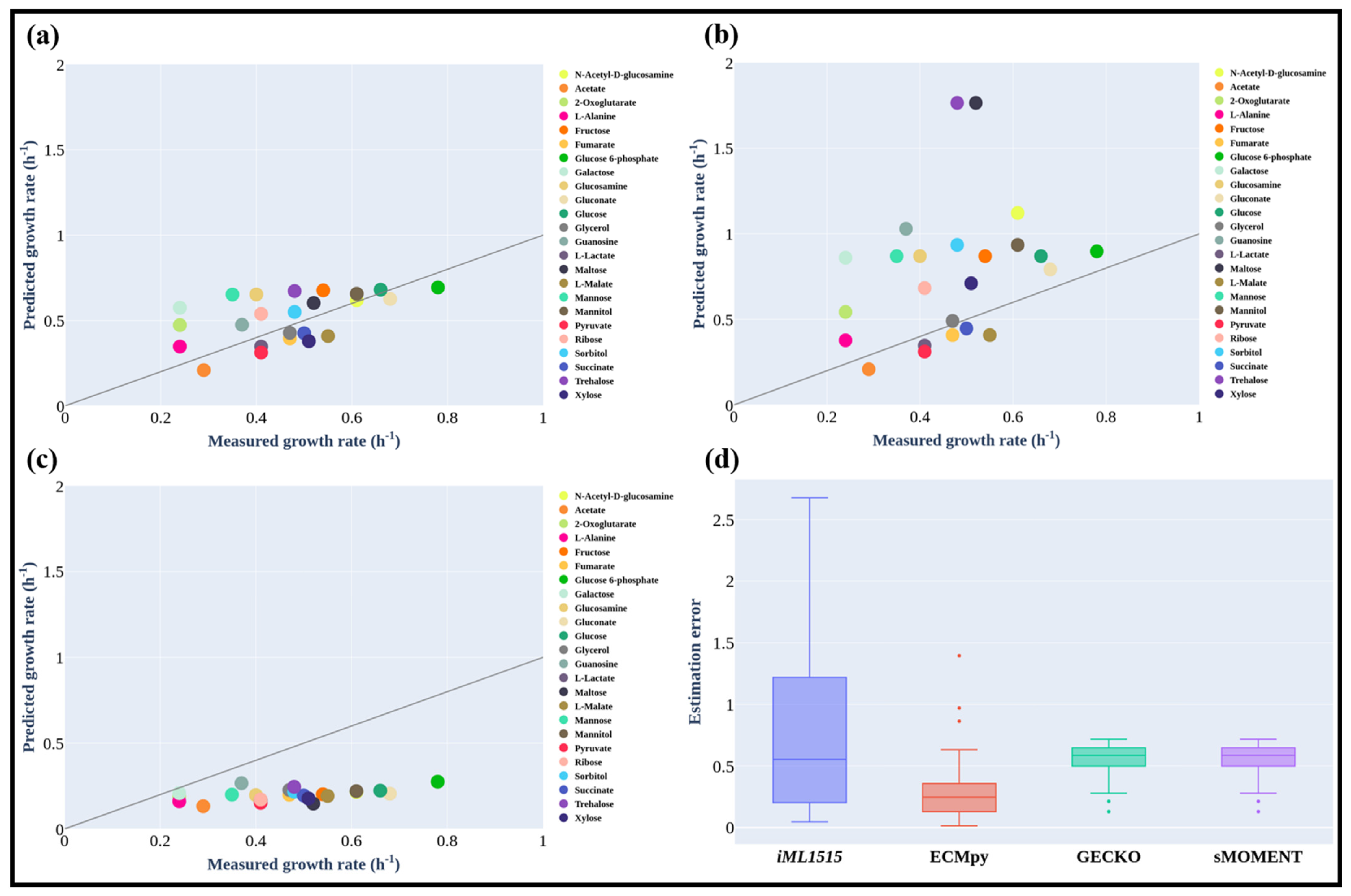
3.3. Maximum Growth Rate of E. coli on Different Carbon Sources
3.4. Simulation of the Trade-Off between Enzyme Usage Efficiency and Biomass Yield
4. Discussion
5. Conclusions
Supplementary Materials
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Edwards, J.S.; Palsson, B.O. Systems Properties of the Haemophilus influenzaeRd Metabolic Genotype. J. Biol. Chem. 1999, 274, 17410–17416. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Gu, C.; Kim, G.B.; Kim, W.J.; Kim, H.U.; Lee, S.Y. Current status and applications of genome-scale metabolic models. Genome Biol. 2019, 20, 1–18. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- O’Brien, E.J.; Monk, J.M.; Palsson, B.O. Using Genome-scale Models to Predict Biological Capabilities. Cell 2015, 161, 971–987. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Kerkhoven, E.; Lahtvee, P.-J.; Nielsen, J. Applications of computational modeling in metabolic engineering of yeast. FEMS Yeast Res. 2014, 15, 1–13. [Google Scholar] [CrossRef] [Green Version]
- Schuetz, R.; Kuepfer, L.; Sauer, U. Systematic evaluation of objective functions for predicting intracellular fluxes in Escherichia coli. Mol. Syst. Biol. 2007, 3, 119. [Google Scholar] [CrossRef]
- Mahadevan, R.; Schilling, C.H. The effects of alternate optimal solutions in constraint-based genome-scale metabolic models. Metab. Eng. 2003, 5, 264–276. [Google Scholar] [CrossRef]
- Lin, Z.; Zhang, Y.; Yuan, Q.; Liu, Q.; Li, Y.; Wang, Z.; Ma, H.; Chen, T.; Zhao, X. Metabolic engineering of Escherichia coli for poly(3-hydroxybutyrate) production via threonine bypass. Microb. Cell Factories 2015, 14, 185. [Google Scholar] [CrossRef] [Green Version]
- Veit, A.; Polen, T.; Wendisch, V.F. Global gene expression analysis of glucose overflow metabolism in Escherichia coli and reduction of aerobic acetate formation. Appl. Microbiol. Biotechnol. 2006, 74, 406–421. [Google Scholar] [CrossRef]
- Basan, M.; Hui, S.; Okano, H.; Zhang, Z.; Shen, Y.; Williamson, J.; Hwa, T. Overflow metabolism in Escherichia coli results from efficient proteome allocation. Nature 2015, 528, 99–104. [Google Scholar] [CrossRef] [Green Version]
- Beg, Q.K.; Vazquez, A.; Ernst, J.; de Menezes, M.A.; Bar-Joseph, Z.; Barabasi, A.; Oltvai, Z.N. Intracellular crowding defines the mode and sequence of substrate uptake by Escherichia coli and constrains its metabolic activity. Proc. Natl. Acad. Sci. USA 2007, 104, 12663–12668. [Google Scholar] [CrossRef] [Green Version]
- Mori, M.; Hwa, T.; Martin, O.; De Martino, A.; Marinari, E. Constrained Allocation Flux Balance Analysis. PLoS Comput. Biol. 2016, 12, e1004913. [Google Scholar] [CrossRef] [Green Version]
- Shlomi, T.; Benyamini, T.; Gottlieb, E.; Sharan, R.; Ruppin, E. Genome-Scale Metabolic Modeling Elucidates the Role of Proliferative Adaptation in Causing the Warburg Effect. PLoS Comput. Biol. 2011, 7, e1002018. [Google Scholar] [CrossRef] [Green Version]
- Zeng, H.; Yang, A. Modelling overflow metabolism in Escherichia coli with flux balance analysis incorporating differential proteomic efficiencies of energy pathways. BMC Syst. Biol. 2019, 13, 3. [Google Scholar] [CrossRef]
- Noor, E.; Flamholz, A.; Bar-Even, A.; Davidi, D.; Milo, R.; Liebermeister, W. The Protein Cost of Metabolic Fluxes: Prediction from Enzymatic Rate Laws and Cost Minimization. PLOS Comput. Biol. 2016, 12, e1005167. [Google Scholar] [CrossRef] [PubMed]
- Adadi, R.; Volkmer, B.; Milo, R.; Heinemann, M.; Shlomi, T. Prediction of Microbial Growth Rate versus Biomass Yield by a Metabolic Network with Kinetic Parameters. PLOS Comput. Biol. 2012, 8, e1002575. [Google Scholar] [CrossRef] [Green Version]
- Sánchez, B.J.; Zhang, C.; Nilsson, A.; Lahtvee, P.-J.; Kerkhoven, E.J.; Nielsen, J. Improving the phenotype predictions of a yeast genome-scale metabolic model by incorporating enzymatic constraints. Mol. Syst. Biol. 2017, 13, 935. [Google Scholar] [CrossRef]
- Bekiaris, P.S.; Klamt, S. Automatic construction of metabolic models with enzyme constraints. BMC Bioinform. 2020, 21, 1–13. [Google Scholar] [CrossRef] [PubMed]
- Massaiu, I.; Pasotti, L.; Sonnenschein, N.; Rama, E.; Cavaletti, M.; Magni, P.; Calvio, C.; Herrgard, M.J. Integration of enzymatic data in Bacillus subtilis genome-scale metabolic model improves phenotype predictions and enables in silico design of poly-γ-glutamic acid production strains. Microb. Cell Fact. 2019, 18, 1–20. [Google Scholar] [CrossRef]
- Chen, Y.; Sun, Y.; Liu, Z.; Dong, F.; Li, Y.; Wang, Y. Genome-scale modeling for Bacillus coagulans to understand the metabolic characteristics. Biotechnol. Bioeng. 2020, 117, 3545–3558. [Google Scholar] [CrossRef] [PubMed]
- Ye, C.; Luo, Q.; Guo, L.; Gao, C.; Xu, N.; Zhang, L.; Liu, L.; Chen, X. Improving lysine production through construction of an Escherichia coli enzyme-constrained model. Biotechnol. Bioeng. 2020, 117, 3533–3544. [Google Scholar] [CrossRef]
- Sulheim, S.; Kumelj, T.; Van Dissel, D.; Salehzadeh-Yazdi, A.; Du, C.; Van Wezel, G.P.; Nieselt, K.; Almaas, E.; Wentzel, A.; Kerkhoven, E.J. Enzyme-Constrained Models and Omics Analysis of Streptomyces coelicolor Reveal Metabolic Changes that Enhance Heterologous Production. iScience 2020, 23. [Google Scholar] [CrossRef]
- Monk, J.M.; Lloyd, C.J.; Brunk, E.; Mih, N.; Sastry, A.; King, Z.; Takeuchi, R.; Nomura, W.; Zhang, Z.; Mori, H.; et al. iML1515, a knowledgebase that computes Escherichia coli traits. Nat. Biotechnol. 2017, 35, 904–908. [Google Scholar] [CrossRef]
- Heckmann, D.; Lloyd, C.J.; Mih, N.; Ha, Y.; Zielinski, D.C.; Haiman, Z.B.; Desouki, A.A.; Lercher, M.J.; Palsson, B.O. Machine learning applied to enzyme turnover numbers reveals protein structural correlates and improves metabolic models. Nat. Commun. 2018, 9, 1–10. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Orth, J.D.; Thiele, I.; Palsson, B.Ø. What is flux balance analysis? Nat. Biotechnol 2010, 28, 245–248. [Google Scholar] [CrossRef] [PubMed]
- Ebrahim, A.; Lerman, J.A.; Palsson, B.O.; Hyduke, D.R. COBRApy: COnstraints-Based Reconstruction and Analysis for Python. BMC Syst. Biol. 2013, 7, 74. [Google Scholar] [CrossRef] [Green Version]
- Motamedian, E.; Mohammadi, M.; Shojaosadati, S.A.; Heydari, M. TRFBA. An algorithm to integrate genome-scale metabolic and transcriptional regulatory networks with incorporation of expression data. Bioinformatics 2017, 33, 1057–1063. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Machado, D.; Herrgård, M. Systematic Evaluation of Methods for Integration of Transcriptomic Data into Constraint-Based Models of Metabolism. PLoS Comput. Biol. 2014, 10, e1003580. [Google Scholar] [CrossRef] [Green Version]
- Lewis, N.; Hixson, K.K.; Conrad, T.M.; Lerman, J.; Charusanti, P.; Polpitiya, A.D.; Adkins, J.; Schramm, G.; Purvine, S.; Lopez-Ferrer, D.; et al. Omic data from evolved E. coli are consistent with computed optimal growth from genome-scale models. Mol. Syst. Biol. 2010, 6, 390. [Google Scholar] [CrossRef]
- Karp, P.D.; Ong, W.K.; Paley, S.; Billington, R.; Caspi, R.; Fulcher, C.; Kothari, A.; Krummenacker, M.; Latendresse, M.; Midford, P.E.; et al. The EcoCyc Database. EcoSal Plus 2018. [Google Scholar] [CrossRef] [Green Version]
- Nilsson, A.; Nielsen, J.; Palsson, B.O. Metabolic Models of Protein Allocation Call for the Kinetome. Cell Syst. 2017, 5, 538–541. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Bremer, H.; Dennis, P.P. Modulation of chemical composition and other parameters of the cell at different exponential growth rates. EcoSal. Plus 2008, 3. [Google Scholar] [CrossRef]
- Brunk, E.; Mih, N.; Monk, J.; Zhang, Z.; O’Brien, E.J.; Bliven, S.E.; Chen, K.; Chang, R.L.; Bourne, P.E.; Palsson, B.O. Systems biology of the structural proteome. BMC Syst. Biol. 2016, 10, 26. [Google Scholar] [CrossRef] [Green Version]
- Wang, M.; Weiss, M.; Simonovic, M.; Haertinger, G.; Schrimpf, S.P.; Hengartner, M.; von Mering, C. PaxDb, a Database of Protein Abundance Averages Across All Three Domains of Life. Mol. Cell. Proteom. 2012, 11, 492–500. [Google Scholar] [CrossRef] [Green Version]
- Okahashi, N.; Kajihata, S.; Furusawa, C.; Shimizu, H. Reliable Metabolic Flux Estimation in Escherichia coli Central Carbon Metabolism Using Intracellular Free Amino Acids. Metabolites 2014, 4, 408–420. [Google Scholar] [CrossRef] [Green Version]
- Chen, Y.; Nielsen, J. Energy metabolism controls phenotypes by protein efficiency and allocation. Proc. Natl. Acad. Sci. USA 2019, 116, 17592–17597. [Google Scholar] [CrossRef] [Green Version]
- Varma, A.; Palsson, B.O. Stoichiometric flux balance models quantitatively predict growth and metabolic by-product secretion in wild-type Escherichia coli W3110. Appl. Environ. Microbiol. 1994, 60, 3724–3731. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Thomas, T.D.; Ellwood, D.C.; Longyear, V.M.C. Change from Homo- to Heterolactic Fermentation by Streptococcus lactis Resulting from Glucose Limitation in Anaerobic Chemostat Cultures. J. Bacteriol. 1979, 138, 109–117. [Google Scholar] [CrossRef] [Green Version]
- van Hoek, M.J.; Merks, R.M. Redox balance is key to explaining full vs. partial switching to low-yield metabolism. BMC Syst. Biol. 2012, 6, 1–10. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Yang, X.; Mao, Z.; Zhao, X.; Wang, R.; Zhang, P.; Cai, J.; Xue, C.; Ma, H. Integrating thermodynamic and enzymatic constraints into genome-scale metabolic models. Metab. Eng. 2021, 67, 133–144. [Google Scholar] [CrossRef] [PubMed]
- Koch, A.L. Microbial physiology and ecology of slow growth. Microbiol Mol. Biol. Rev. 1997, 61, 305–318. [Google Scholar] [PubMed]
- O’Brien, E.J.; Lerman, J.; Chang, R.; Hyduke, D.R.; Palsson, B.Ø. Genome-scale models of metabolism and gene expression extend and refine growth phenotype prediction. Mol. Syst. Biol. 2013, 9, 693. [Google Scholar] [CrossRef]
- Domenzain, I.; Sánchez, B.; Anton, M.; Kerkhoven, E.J.; Millán-Oropeza, A.; Henry, C.; Siewers, V.; Morrissey, J.P.; Sonnenschein, N.; Nielsen, J. Reconstruction of a catalogue of genome-scale metabolic models with enzymatic constraints using GECKO 2.0. bioRxiv 2021. [Google Scholar] [CrossRef]
- Karp, P.D.; Billington, R.; Caspi, R.; Fulcher, C.A.; Latendresse, M.; Kothari, A.; Keseler, I.M.; Krummenacker, M.; Midford, P.E.; Ong, Q.; et al. The BioCyc collection of microbial genomes and metabolic pathways. Briefings Bioinform. 2019, 20, 1085–1093. [Google Scholar] [CrossRef] [PubMed]
- The UniProt Consortium. UniProt: The universal protein knowledgebase in 2021. Nucleic Acids Res. 2021, 49, D480–D489. [Google Scholar] [CrossRef] [PubMed]
- Meldal, B.H.M.; Bye-A-Jee, H.; Gajdoš, L.; Hammerová, Z.; Horáčková, A.; Melicher, F.; Perfetto, L.; Pokorný, D.; Rodriguez-Lopez, M.; Tuerkova, A.; et al. Complex Portal 2018. Extended content and enhanced visualization tools for macromolecular complexes. Nucleic Acids Res. 2019, 47, D550–D558. [Google Scholar] [CrossRef] [PubMed]


| Items | MOMENT | GECKO | AutoPACMEN | ECMpy |
|---|---|---|---|---|
| Subunit number | (not consider) × | (consider) √ | × (provide interface) | √ |
| Proteomics | × | √ | √ | √ |
| Saturation | 1 | 0.46 | 1 | 1 |
| Mass fraction of enzymes | 0.56 | 0.448 | 0.095 | 0.227 |
| Adding methods of enzyme constraints | add enzyme concentrations for each reaction and add the enzymes solvent capacity constraint | change stoichiometric matrix, and introduce a large number of pseudo-reaction and pseudo-metabolite | change stoichiometric matrix, and introduce one pseudo-reaction and pseudo-metabolite | only add a total enzyme constraint |
| Reaction reversibility | not split | split | part split | split |
| Isozyme | a reaction can be catalyzed by multiple enzymes | a reaction can be catalyzed by multiple enzymes | always assumes that the enzyme with the minimal cost is used | a reaction can be catalyzed by multiple enzymes |
| Filling method of missing kcat | the median turnover number across all reactions | match the kcat value to other substrates, organisms, or even introduce wild cards in the EC number. | Similar to GECKO | enzyme cost=0 |
| Model calibration | × | √ | √ | √ |
| Model type | Not provided | XML | XML | JSON |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Mao, Z.; Zhao, X.; Yang, X.; Zhang, P.; Du, J.; Yuan, Q.; Ma, H. ECMpy, a Simplified Workflow for Constructing Enzymatic Constrained Metabolic Network Model. Biomolecules 2022, 12, 65. https://doi.org/10.3390/biom12010065
Mao Z, Zhao X, Yang X, Zhang P, Du J, Yuan Q, Ma H. ECMpy, a Simplified Workflow for Constructing Enzymatic Constrained Metabolic Network Model. Biomolecules. 2022; 12(1):65. https://doi.org/10.3390/biom12010065
Chicago/Turabian StyleMao, Zhitao, Xin Zhao, Xue Yang, Peiji Zhang, Jiawei Du, Qianqian Yuan, and Hongwu Ma. 2022. "ECMpy, a Simplified Workflow for Constructing Enzymatic Constrained Metabolic Network Model" Biomolecules 12, no. 1: 65. https://doi.org/10.3390/biom12010065
APA StyleMao, Z., Zhao, X., Yang, X., Zhang, P., Du, J., Yuan, Q., & Ma, H. (2022). ECMpy, a Simplified Workflow for Constructing Enzymatic Constrained Metabolic Network Model. Biomolecules, 12(1), 65. https://doi.org/10.3390/biom12010065






