Neural Upscaling from Residue-Level Protein Structure Networks to Atomistic Structures
Abstract
:1. Background
2. Methods
3. Results
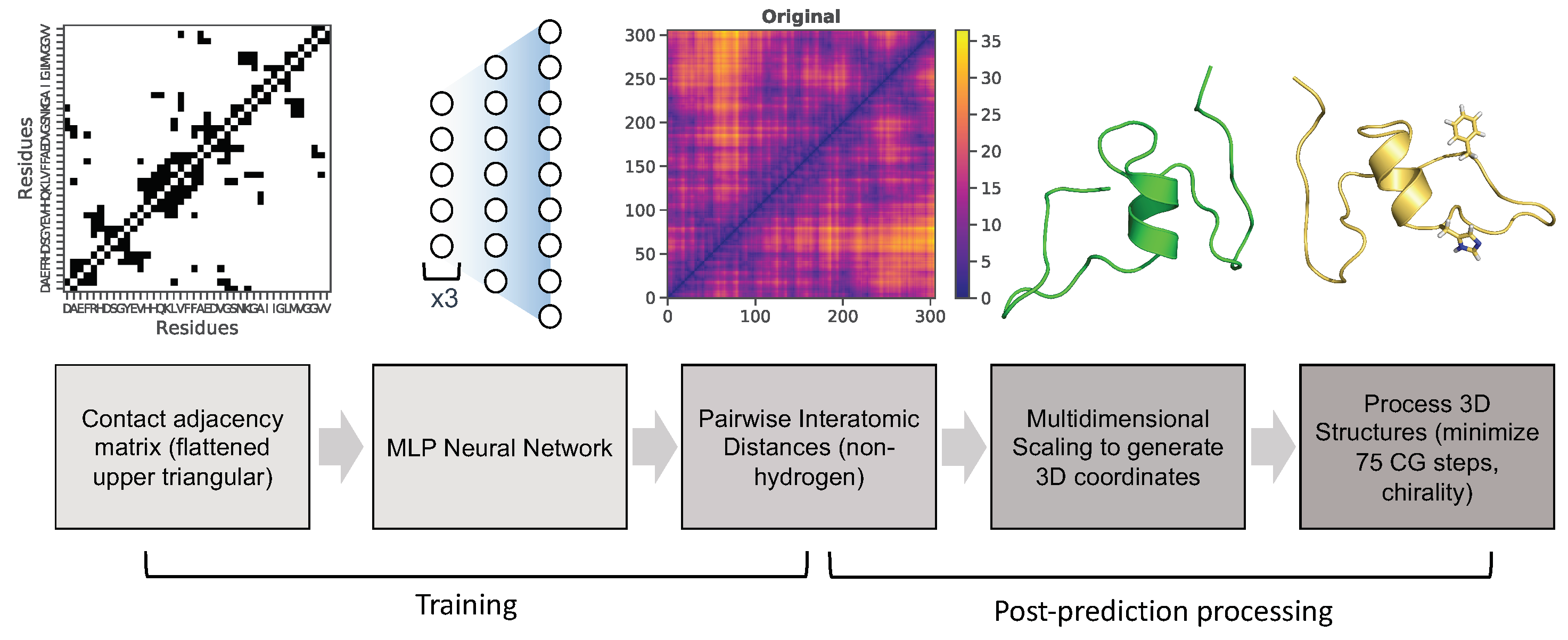
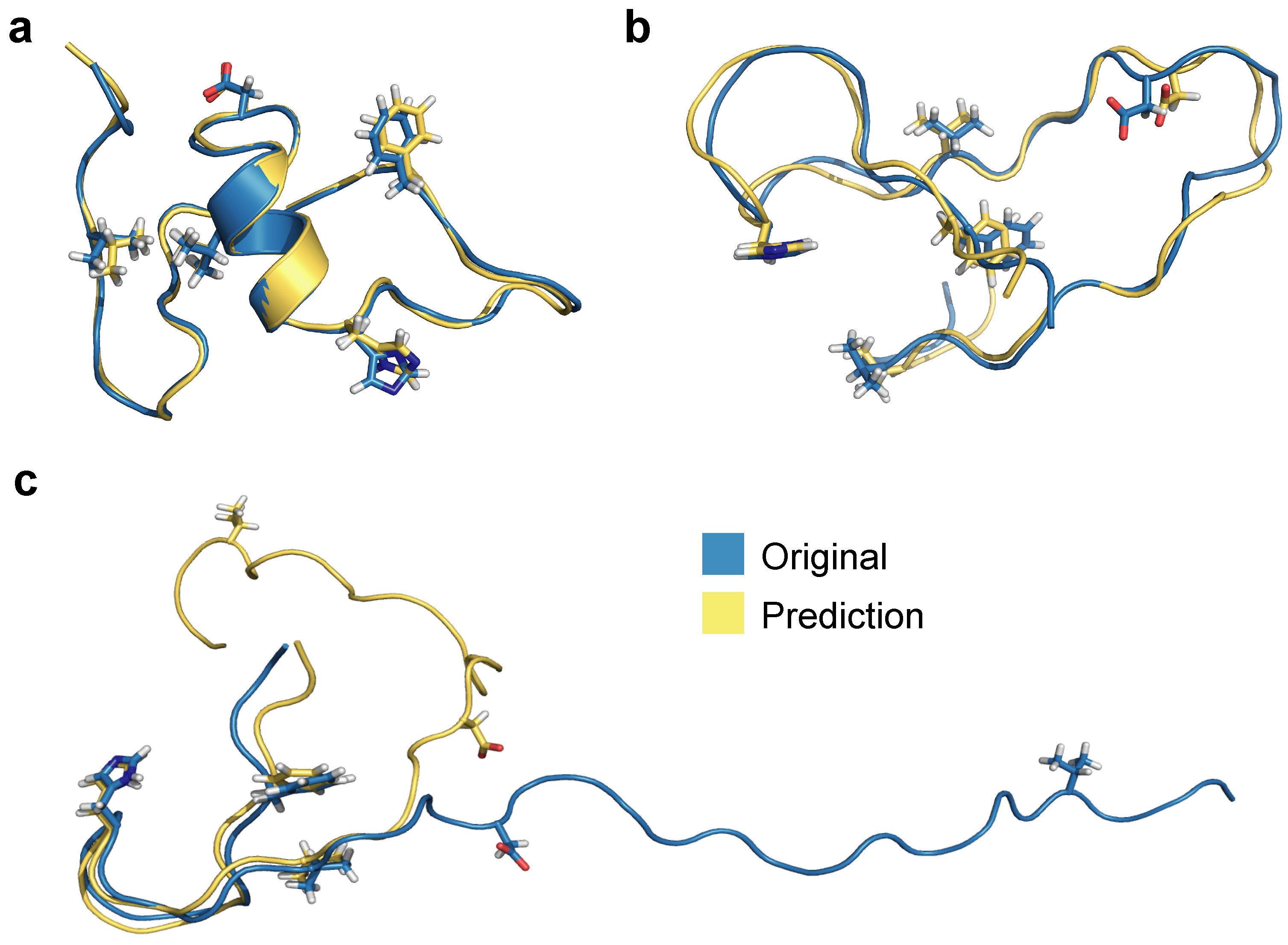
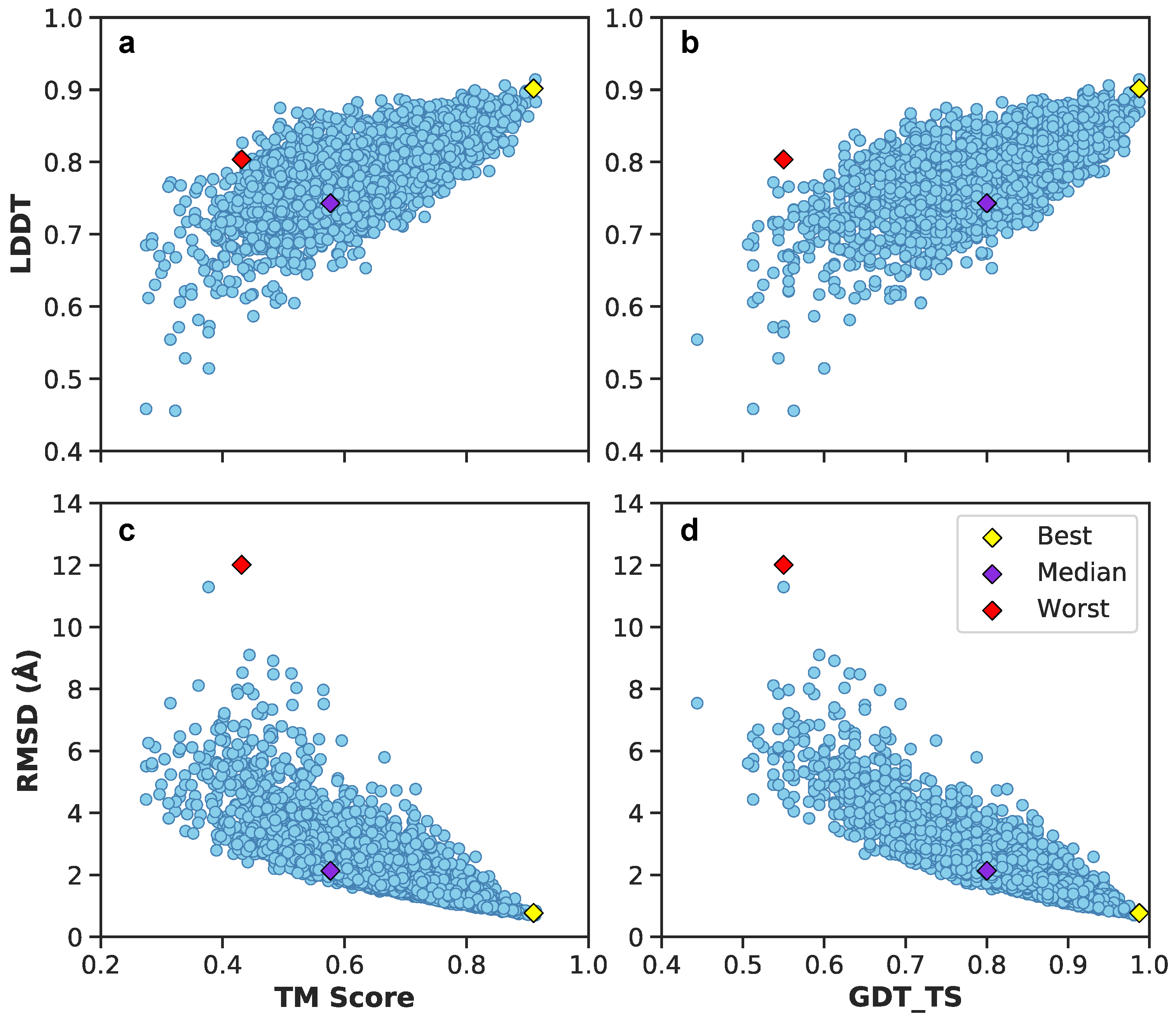
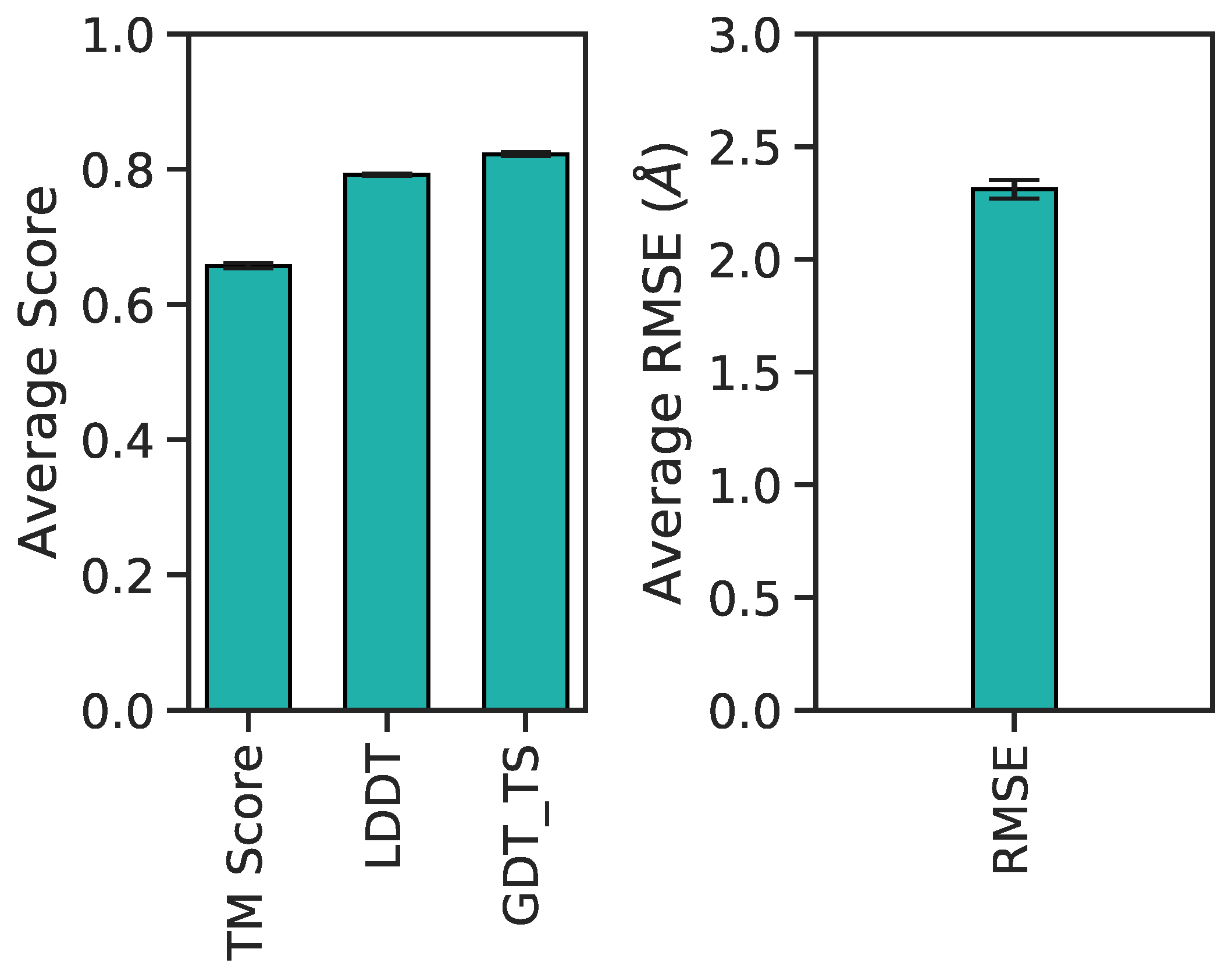
3.1. Multilayer Perceptron (MLP) Neural Network Reconstructs Aβ Conformations with Atomistic Detail
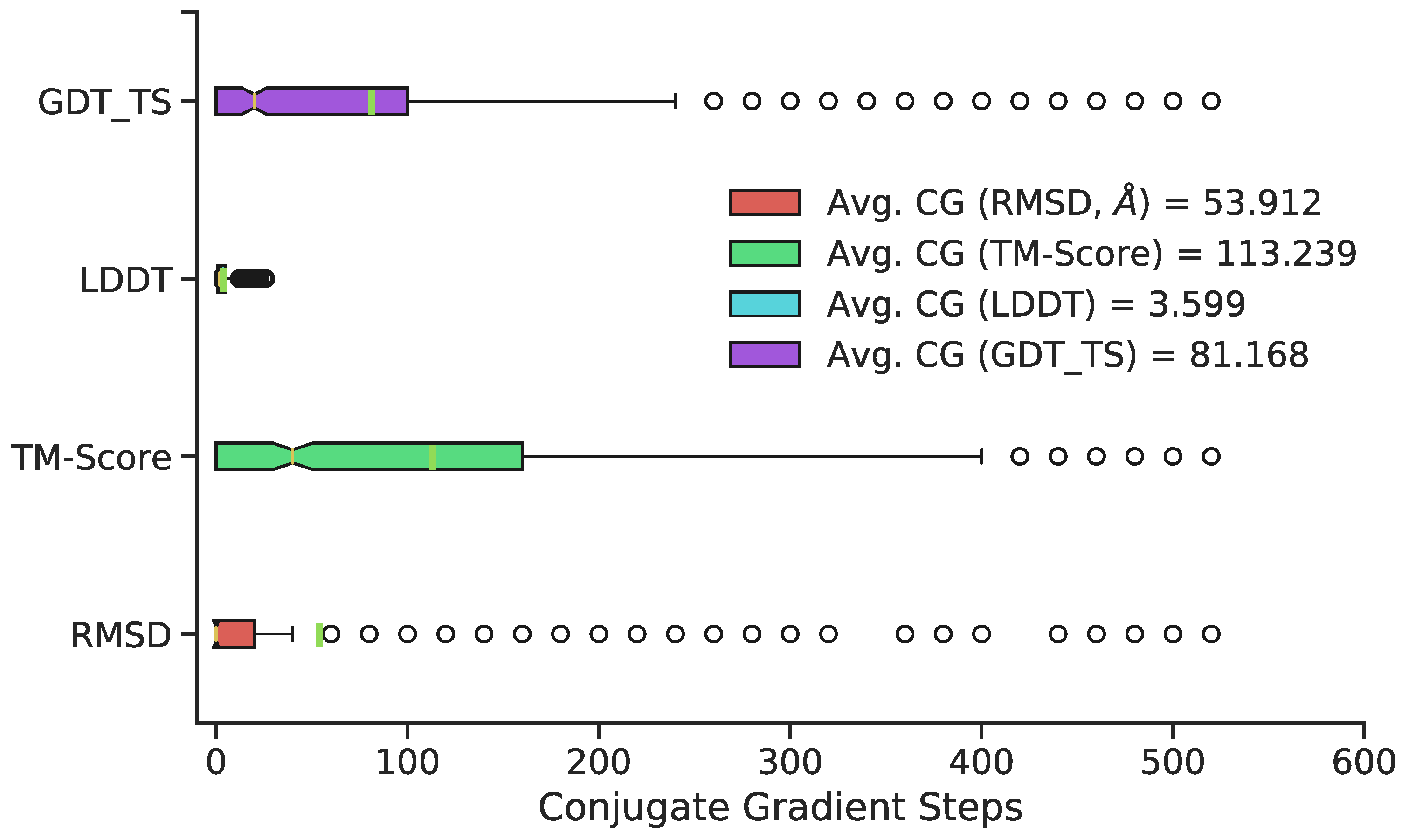
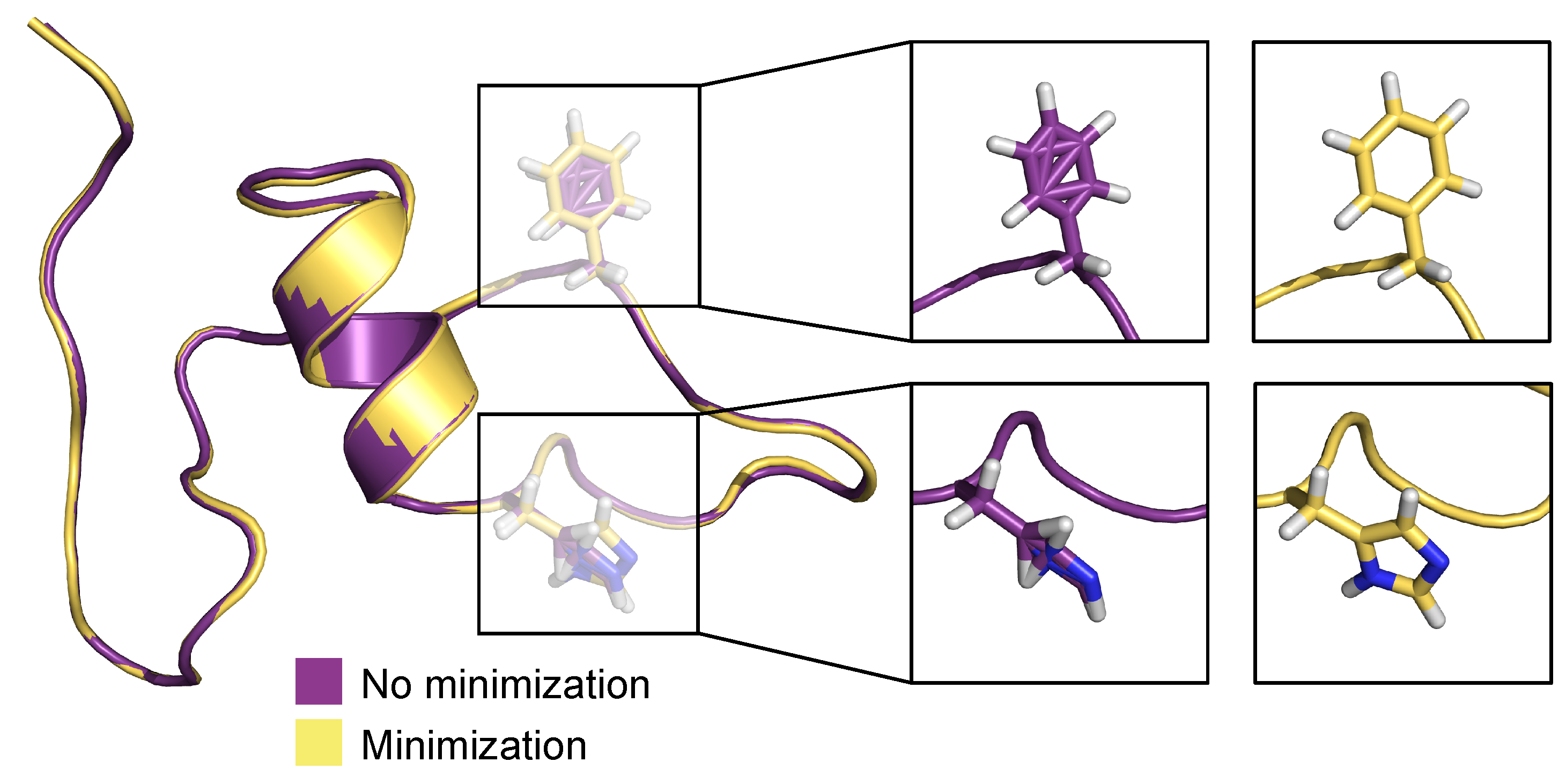
3.2. Generation of 3D Structures and Subsequent Minimization
4. Discussion
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Marrink, S.J.; Risselada, H.J.; Yefimov, S.; Tieleman, D.P.; De Vries, A.H. The Martini Force Field: Coarse Grained Model for Biomolecular Simulations. J. Phys. Chem. B 2007, 111, 7812–7824. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Capelli, R.; Gardin, A.; Empereur-mot, C.; Doni, G.; Pavan, G.M. A Data-Driven Dimensionality Reduction Approach to Compare and Classify Lipid Force Fields. J. Phys. Chem. B 2021, 125, 7785–7796. [Google Scholar] [CrossRef] [PubMed]
- Benson, N.C.; Daggett, V. A Chemical Group Graph Representation for Efficient High-Throughput Analysis of Atomistic Protein Simulations. J. Bioinform. Comput. Biol. 2012, 10, 1250008. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Mustoe, A.M.; Al-Hashimi, H.M.; Brooks, C.L. Coarse Grained Models Reveal Essential Contributions of Topological Constraints to the Conformational Free Energy of RNA Bulges. J. Phys. Chem. B 2014, 118, 2615–2627. [Google Scholar] [CrossRef] [PubMed]
- Wong, E.K.; Prytkova, V.; Freites, J.A.; Butts, C.T.; Tobias, D.J. Molecular Mechanism of Aggregation of the Cataract-Related γD-Crystallin W24r Variant from Multiscale Atomistic Simulations. Biochemistry 2019, 58, 3691–3699. [Google Scholar] [CrossRef]
- Cross, T.J.; Takahashi, G.R.; Diessner, E.M.; Crosby, M.G.; Farahmand, V.; Zhuang, S.; Butts, C.T.; Martin, R.W. Sequence Characterization and Molecular Modeling of Clinically Relevant Variants of the SARS-CoV-2 Main Protease. Biochemistry 2020, 9, 3741–3756. [Google Scholar] [CrossRef]
- Demakis, C.; Childers, M.C.; Daggett, V. Conserved Patterns and Interactions in the Unfolding Transition State Across SH3 Domain Structural Homologues. Protein Sci. 2021, 30, 391–407. [Google Scholar] [CrossRef]
- Grazioli, G.; Martin, R.W.; Butts, C.T. Comparative Exploratory Analysis of Intrinsically Disordered Protein Dynamics Using Machine Learning and Network Analytic Methods. Front. Mol. Biosci. 2019, 6, 42. [Google Scholar] [CrossRef]
- Grazioli, G.; Yu, Y.; Unhelkar, M.H.; Martin, R.W.; Butts, C.T. Network-Based Classification and Modeling of Amyloid Fibrils. J. Phys. Chem. B 2019, 123, 5452–5462. [Google Scholar] [CrossRef]
- Ferrie, J.J.; Petersson, E.J. A Unified De Novo Approach For Predicting The Structures Of Ordered And Disordered Proteins. J. Phys. Chem. B 2020, 124, 5538–5548. [Google Scholar] [CrossRef]
- Rzepiela, A.J.; Schäfer, L.V.; Goga, N.; Risselada, H.J.; De Vries, A.H.; Marrink, S.J. Reconstruction of Atomistic Details from Coarse-Grained Structures. J. Comput. Chem. 2010, 31, 1333–1343. [Google Scholar] [CrossRef] [Green Version]
- Hess, B.; León, S.; Van Der Vegt, N.; Kremer, K. Long Time Atomistic Polymer Trajectories from Coarse Grained Simulations: Bisphenol-A Polycarbonate. Soft Matter 2006, 2, 409–414. [Google Scholar] [CrossRef]
- Peter, C.; Kremer, K. Multiscale Simulation of Soft Matter Systems–From the Atomistic to the Coarse-Grained Level and Back. Soft Matter 2009, 5, 4357–4366. [Google Scholar] [CrossRef]
- Gopal, S.M.; Mukherjee, S.; Cheng, Y.M.; Feig, M. PRIMO/PRIMONA: A Coarse-Grained Model for Proteins and Nucleic Acids That Preserves Near-Atomistic Accuracy. Proteins Struct. Funct. Bioinform. 2010, 78, 1266–1281. [Google Scholar] [CrossRef] [PubMed]
- Brocos, P.; Mendoza-Espinosa, P.; Castillo, R.; Mas-Oliva, J.; Pineiro, Á. Multiscale Molecular Dynamics Simulations of Micelles: Coarse-Grain for Self-Assembly and Atomic Resolution for Finer Details. Soft Matter 2012, 8, 9005–9014. [Google Scholar] [CrossRef]
- Wassenaar, T.A.; Pluhackova, K.; Böckmann, R.A.; Marrink, S.J.; Tieleman, D.P. Going Backward: A Flexible Geometric Approach to Reverse Transformation from Coarse Grained to Atomistic Models. J. Chem. Theory Comput. 2014, 10, 676–690. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Machado, M.R.; Pantano, S. Sirah Tools: Mapping, Backmapping and Visualization of Coarse-Grained Models. Bioinformatics 2016, 32, 1568–1570. [Google Scholar] [CrossRef] [Green Version]
- Bonneau, R.; Tsai, J.; Ruczinski, I.; Chivian, D.; Rohl, C.; Strauss, C.E.M.; Baker, D. Rosetta in CASP4: Progress in Ab Initio Protein Structure Prediction. Proteins Struct. Funct. Bioinform. 2001, 45, 119–126. [Google Scholar] [CrossRef]
- Zhang, Y. Template-Based Modeling and Free Modeling by I-TASSER in CASP7. Proteins Struct. Funct. Bioinform. 2007, 69, 108–117. [Google Scholar] [CrossRef]
- Tyka, M.D.; Keedy, D.A.; André, I.; DiMaio, F.; Song, Y.; Richardson, D.C.; Richardson, J.S.; Baker, D. Alternate States of Proteins Revealed by Detailed Energy Landscape Mapping. J. Mol. Biol. 2011, 405, 607–618. [Google Scholar] [CrossRef] [Green Version]
- Pearce, R.; Zhang, Y. Toward the Solution of the Protein Structure Prediction Problem. J. Biol. Chem. 2021, 297, 100870. [Google Scholar] [CrossRef] [PubMed]
- Smith, S.T.; Meiler, J. Assessing Multiple Score Functions in Rosetta for Drug Discovery. PLoS ONE 2020, 15, e0240450. [Google Scholar] [CrossRef]
- Alford, R.F.; Leaver-Fay, A.; Jeliazkov, J.R.; O’Meara, M.J.; DiMaio, F.P.; Park, H.; Shapovalov, M.V.; Renfrew, P.D.; Mulligan, V.K.; Kappel, K.; et al. The Rosetta All-Atom Energy Function for Macromolecular Modeling and Design. J. Chem. Theory Comput. 2017, 13, 3031–3048. [Google Scholar] [CrossRef] [PubMed]
- Webb, M.A.; Delannoy, J.Y.; de Pablo, J.J. Graph-Based Approach to Systematic Molecular Coarse-Graining. J. Chem. Theory Comput. 2018, 15, 1199–1208. [Google Scholar] [CrossRef] [PubMed]
- Chakraborty, M.; Xu, C.; White, A.D. Encoding and Selecting Coarse-Grain Mapping Operators with Hierarchical Graphs. J. Chem. Phys. 2018, 149, 134106. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Unhelkar, M.H.; Duong, V.T.; Enendu, K.N.; Kelly, J.E.; Tahir, S.; Butts, C.T.; Martin, R.W. Structure Prediction and Network Analysis of Chitinases from the CApe Sundew, DRosera Capensis. Biochim. Biophys. Acta Gen. Subj. 2017, 1861, 636–643. [Google Scholar] [CrossRef] [PubMed]
- Duong, V.T.; Unhelkar, M.H.; Kelly, J.E.; Kim, S.H.; Butts, C.T.; Martin, R.W. Protein Structure Networks Provide Insight into Active Site Flexibility in Esterase/Lipases from the Carnivorous Plant Drosera Capensis. Integr. Biol. 2018, 10, 768–779. [Google Scholar] [CrossRef]
- Yu, Y.; Grazioli, G.; Unhelkar, M.; Martin, R.W.; Butts, C.T. Network Hamiltonian Models Reveal Pathways to Amyloid Fibril Formation. Nat. Sci. Rep. 2020, 10, 15668. [Google Scholar] [CrossRef]
- Bejagam, K.K.; Singh, S.; An, Y.; Deshmukh, S.A. Machine-Learned Coarse-Grained Models. J. Phys. Chem. Lett. 2018, 9, 4667–4672. [Google Scholar] [CrossRef]
- Boninsegna, L.; Gobbo, G.; Noé, F.; Clementi, C. Investigating Molecular Kinetics by Variationally Optimized Diffusion Maps. J. Chem. Theory Comput. 2015, 11, 5947–5960. [Google Scholar] [CrossRef] [Green Version]
- Lemke, T.; Peter, C. Neural Network Based Prediction of Conformational Free Energies—A New Route Toward Coarse-Grained Simulation Models. J. Chem. Theory Comput. 2017, 13, 6213–6221. [Google Scholar] [CrossRef] [PubMed]
- Wang, J.; Olsson, S.; Wehmeyer, C.; Pérez, A.; Charron, N.E.; De Fabritiis, G.; Noé, F.; Clementi, C. Machine Learning of Coarse-Grained Molecular Dynamics Force Fields. ACS Cent. Sci. 2019, 5, 755–767. [Google Scholar] [CrossRef] [Green Version]
- Zhang, L.; Han, J.; Wang, H.; Car, R.; E, W. Deepcg: Constructing Coarse-Grained Models via Deep Neural Networks. J. Chem. Phys. 2018, 149, 034101. [Google Scholar] [CrossRef] [PubMed]
- Vivekanandan, S.; Brender, J.R.; Lee, S.Y.; Ramamoorthy, A. A Partially Folded Structure of Amyloid-Beta (1–40) in an Aqueous Environment. Biochem. Biophys. Res. Commun. 2011, 411, 312–316. [Google Scholar] [CrossRef] [PubMed]
- Phillips, J.C.; Braun, R.; Wang, W.; Gumbart, J.; Tajkhorshid, E.; Villa, E.; Chipot, C.; Skeel, R.D.; Kalé, L.; Schulten, K. Scalable Molecular Dynamics with NAMD. J. Comput. Chem. 2005, 26, 1781–1802. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Jorgensen, W.L.; Chandrasekhar, J.; Madura, J.D.; Impey, R.W.; Klein, M.L. Comparison of Simple Potential Functions for Simulating Liquid Water. J. Chem. Phys. 1983, 79, 926–935. [Google Scholar] [CrossRef]
- Huang, J.; Rauscher, S.; Nawrocki, G.; Ran, T.; Feig, M.; de Groot, B.L.; Grubmüller, H.; MacKerell, A.D.J. CHARMM36m: An Improved Force Field for Folded and Intrinsically Disordered Proteins. Nat. Method 2017, 14, 71–73. [Google Scholar] [CrossRef] [Green Version]
- Martyna, G.J.; Tobias, D.J.; Klein, M.L. Constant Pressure Molecular Dynamics Algorithms. J. Chem. Phys. 1994, 101, 4177–4189. [Google Scholar] [CrossRef]
- Feller, S.E.; Zhang, Y.; Pastor, R.W.; Brooks, B.R. Constant Pressure Molecular Dynamics Simulation: The Langevin Piston Method. J. Chem. Phys. 1995, 103, 4613–4621. [Google Scholar] [CrossRef]
- Humphrey, W.; Dalke, A.; Schulten, K. VMD: Visual Molecular Dynamics. J. Mol. Graph. 1996, 14, 27–28, 33–38. [Google Scholar] [CrossRef]
- Handcock, M.S.; Hunter, D.R.; Butts, C.T.; Goodreau, S.M.; Morris, M. Statnet: Software Tools for the Representation, Visualization, Analysis and Simulation of Network Data. J. Stat. Softw. 2008, 24, 1548. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Butts, C.T. network: A Package for Managing Relational Data in R. J. Stat. Softw. 2008, 24, 1–36. [Google Scholar] [CrossRef] [Green Version]
- Grant, B.J.; Rodrigues, A.P.; ElSawy, K.M.; McCammon, J.A.; Caves, L.S. Bio3D: An R Package for the Comparative Analysis of Protein Structures. Bioinformatics 2006, 22, 2695–2696. [Google Scholar] [CrossRef] [Green Version]
- R Core Team. R: A Language and Environment for Statistical Computing; R Foundation for Statistical Computing: Vienna, Austria, 2018. [Google Scholar]
- Alvarez, S. A Cartography of the Van Der Waals Territories. Dalton Trans. 2013, 42, 8617–8636. [Google Scholar] [CrossRef] [Green Version]
- Chollet, F.; Gibson, A.; Allaire, J.J.; Rahman, F.; Branchaud-Charron, F.; Lee, T.; de Marmiesse, G. Keras. 2015. Available online: https://keras.io (accessed on 2 January 2020).
- Abadi, M.; Barham, P.; Chen, J.; Chen, Z.; Davis, A.; Dean, J.; Devin, M.; Ghemawat, S.; Irving, G.; Isard, M.; et al. Tensorflow: A System for Large-Scale Machine Learning. In Proceedings of the 12th Symposium on Operating Systems Design and Implementation 16, Savannah, GA, USA, 2–4 November 2016; pp. 265–283. [Google Scholar]
- Kotila, M. Autonomio v.0.3.2 User Manual—Autonomio Latest Documentation. 2017. Available online: https://autonom.io (accessed on 2 January 2020).
- McGibbon, R.T.; Beauchamp, K.A.; Harrigan, M.P.; Klein, C.; Swails, J.M.; Hernández, C.X.; Schwantes, C.R.; Wang, L.P.; Lane, T.J.; Pande, V.S. MDTraj: A Modern Open Library for the Analysis of Molecular Dynamics Trajectories. Biophys. J. 2015, 109, 1528–1532. [Google Scholar] [CrossRef] [Green Version]
- Pettersen, E.F.; Goddard, T.D.; Huang, C.C.; Couch, G.S.; Greenblatt, D.M.; Meng, E.C.; Ferrin, T.E. UCSF Chimera—A Visualization System for Exploratory Research and Analysis. J. Comput. Chem. 2004, 25, 1605–1612. [Google Scholar] [CrossRef] [Green Version]
- Zhang, Y.; Skolnick, J. Scoring Function for Automated Assessment of Protein Structure Template Quality. Proteins Struct. Funct. Bioinform. 2004, 57, 702–710. [Google Scholar] [CrossRef]
- Mariani, V.; Biasini, M.; Barbato, A.; Schwede, T. lddt: A Local Superposition-Free Score for Comparing Protein Structures and Models Using Distance Difference Tests. Bioinformatics 2013, 29, 2722–2728. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Zemla, A. LGA: A Method for Finding 3d Similarities in Protein Structures. Nucleic Acids Res. 2003, 31, 3370–3374. [Google Scholar] [CrossRef] [Green Version]
- Kryshtafovych, A.; Schwede, T.; Topf, M.; Fidelis, K.; Moult, J. Critical Assessment of Methods of Protein Structure Prediction (CASP)—Round Xiii. Proteins Struct. Funct. Bioinform. 2019, 87, 1011–1020. [Google Scholar] [CrossRef] [Green Version]
- Kaźmierkiewicz, R.; Liwo, A.; Scheraga, H.A. Energy-based Reconstruction of a Protein Backbone from Its Alpha-carbon Trace by a Monte-carlo Method. J. Comput. Chem. 2002, 23, 715–723. [Google Scholar] [CrossRef] [PubMed]
- Wang, W.; Gómez-Bombarelli, R. Coarse-Graining Auto-Encoders for Molecular Dynamics. Npj Comput. Mater. 2019, 5, 125. [Google Scholar] [CrossRef] [Green Version]
- Senior, A.W.; Evans, R.; Jumper, J.; Kirkpatrick, J.; Sifre, L.; Green, T.; Qin, C.; Žídek, A.; Nelson, A.W.; Bridgland, A.; et al. Improved Protein Structure Prediction Using Potentials from Deep Learning. Nature 2020, 577, 706–710. [Google Scholar] [CrossRef] [PubMed]
- Scholkopf, B.; Smola, A.J. Learning with Kernels: Support Vector Machines, Regularization, Optimization, and Beyond; MIT Press: Cambridge, MA, USA, 2001. [Google Scholar]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Duong, V.T.; Diessner, E.M.; Grazioli, G.; Martin, R.W.; Butts, C.T. Neural Upscaling from Residue-Level Protein Structure Networks to Atomistic Structures. Biomolecules 2021, 11, 1788. https://doi.org/10.3390/biom11121788
Duong VT, Diessner EM, Grazioli G, Martin RW, Butts CT. Neural Upscaling from Residue-Level Protein Structure Networks to Atomistic Structures. Biomolecules. 2021; 11(12):1788. https://doi.org/10.3390/biom11121788
Chicago/Turabian StyleDuong, Vy T., Elizabeth M. Diessner, Gianmarc Grazioli, Rachel W. Martin, and Carter T. Butts. 2021. "Neural Upscaling from Residue-Level Protein Structure Networks to Atomistic Structures" Biomolecules 11, no. 12: 1788. https://doi.org/10.3390/biom11121788
APA StyleDuong, V. T., Diessner, E. M., Grazioli, G., Martin, R. W., & Butts, C. T. (2021). Neural Upscaling from Residue-Level Protein Structure Networks to Atomistic Structures. Biomolecules, 11(12), 1788. https://doi.org/10.3390/biom11121788





