Abstract
More than one hundred years of experimental and theoretical investigations of electron scattering in gases delivered cross-sections in a wide energy range, from few meV to keV. An analogy in optics, characterizing different materials, comes under the name of the dispersion relation, i.e., of the dependence of the refraction index on the light wavelength. The dispersion relation for electron (and positron) scattering was hypothesized in the 1970s, but without clear results. Here, we review experimental, theoretical, and semi-empirical cross-sections for N, CO, CH, and CF in search of any hint for such a relation—unfortunately, without satisfactory conclusions.
1. The Need for Cross Sections
Cross sections for electron scattering are the input data in modeling and diagnostics of industrial plasma, gas discharge [1], thermonuclear plasma [2,3], biological media [4,5], and atmospheric processes, including extra-solar planets [6]. Such modeling requires the knowledge of the total and partial (elastic, ionization, dissociation, and electronic, vibrational, rotational excitation) cross sections in a broad energy range. Out of the gases considered in this paper, CF is used for etching SiO, in spite of the disadvantages resulting from the presence of hot radicals (with the energy of few eV) in Ar/O/CF plasmas. CH acts as an intrinsic cooler in carbon-lined tokamaks like JET, thanks to its high cross sections for the vibrational excitations in the region of a few eV, see reference [7]. Resonant processes in electron scattering in N and CO at a few eV (2.1 and 3.9 eV, respectively), enhancing the vibrational and rotational transitions, are the basis of high-power IR lasers [8]. For thermonuclear plasmas, the energy range up to 1 keV is of interest [9].
Experimental determinations are relatively easy for total cross section (TCS) in the energy range 1–100 eV, using beam methods [10]. In some gases, like N and CH [7], the uncertainty on the TCS is as low as 5%. At very low energies, swarm measurements, especially in gas mixtures, obtain self-consistent sets of partial cross sections, also for rotational and vibrational excitations [11]. However, as discussed for HO (e.g., reference [12]), such sets may not be unique. Good agreements (e.g., within few per cent) exist for ionization cross sections [13]. Scarce data are available for electronic excitations; however, their contribution to the TCS are usually only a few per cent. Measurements of vibrational excitations are difficult; similar to electronic excitations, they require a good energy resolution of analyzers and integrating differential cross sections (DCS) in the whole 0–180 angular range (see [14]). A “missing channel” in the measurements of partial cross sections in molecules is, frequently, the dissociation into neutral fragments (see [15]). All these partial cross sections should sum-up to the TCS. Our question is: may we deduce some more information from (pretty precise) measurements of total cross sections to derive partial ones? Are there any schemes of partitioning and/or semi-empirical indications?
The knowledge of positron-scattering cross sections is rather fragmentary. Positrons may be considered as complementary to electron scattering [16,17,18]; no exchange effects occur for positrons and the overall interaction is weaker, as the attractive polarization potential (of the electronic cloud) subtracts from the repulsive static potential of the nuclear core. Modeling is needed in studies of positron annihilation for the defectoscopy of the solid state [19] and for medical applications (positron emission tomography—PET). Experiments, theory, and semi-empirical models are the input data for further modeling, yielding improved sets of data (see [20]).
2. Semi-Empirical Models
Semi-empirical models have been developed to estimate partial cross sections. The models try to relate electron (and positron) scattering cross sections in different energy ranges to some molecular features, like the “radii” [21], total atomic number Z, dipole polarizability, electron binding energies in the target, etc. At the very low energy range, in particular for noble gases, the modified effective range theory (MERT) [22,23] extrapolates the elastic (integral and differential) cross section down to zero energy. The input data for MERT are the dipole polarizability and the integral and/or differential cross sections in the range of sub-eV, see the detailed discussion for CH in reference [24]. MERT has also been applied to positron scattering, say in Ar and N, up to the energies of a few eV [25].
The relation to the dipole polarizability appears again in the intermediate (about 100 eV) energy range. Several authors [26,27] have indicated that the maxima of the ionization cross sections rise with the rise of dipole polarizability. As the ionization at these energies constitutes a significant part of the TCS, other works [28,29] suggested that the TCS in its maximum also depends on the polarizability. Thus, the question arises: why are the same molecular feature governed/reflected in the cross sections in two distant energy ranges?
For ionization cross sections, the most widely used is the Born-Bethe binary encounter model (BEB) [30]. It requires as input, data on the binding and kinetic energies of electrons on given electronic orbitals. However, as far as the BEB model is successful in calculating the total ionization cross section, i.e., the sum of ionization from single orbitals, it hardly predicts these partial ionization cross sections, see, for example, reference [31].
A modified version of BEB is also used to predict electronic excitation cross sections [32]. The input for this model is the optical oscillator strength that can be deduced from experimental zero-angle DCS for electronic excitations [33] at high (i.e., “Born”, see reference [34]) energies.
Born approximation is also used for vibrational excitations in the region above the threshold. For infrared-active modes it is quite successful both for electron and positron [35] scattering. It is not useful in predicting the vibrational excitation in resonances. Note, in this issue, two papers going beyond Born approximation: by Ayouz et al. [36] for electron scattering on HO and by Poveda, do N. Varella and Mohallem [37] for positron scattering on H.
The region of few eV is the domain of resonant states in electron-molecule scattering. These states are usually classified as: (1) Feshbach resonances, resulting from the capturing of the incoming electron to a free electronic orbital of the target, and showing up as narrow structures in the elastic and TCS; and (2) shape resonances, due to temporary trapping of the incoming electron inside the effective (i.e., comprising the centrifugal barrier) potential well of the target, and showing-up as relatively broad maxima in TCS, frequently with a vibrational-like structure superimposed, see Figure 1 for N, and compare the highlighted figure of reference [38] showing the two types of resonances in TCS in N.
The contribution of Feshbach resonances to TCS is insignificant, but the shape resonances, say in N (Figure 1) and CO (Figure 2) give the maxima of TCS even by few folds higher than the potential-scattering “background” [39,40,41]. The contribution of the vibrational excitations in these maxima is high, roughly 1/6 of TCS in molecules like N and CO and as much as 1/3 of TCS in resonances in CO, NO, OCS, see Figure 2 for CO.
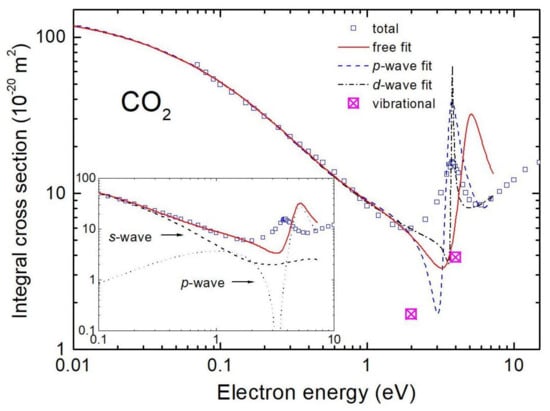
Figure 2.
Integral (elastic and vibrational) cross sections for electron—CO scattering in the low energy range. As for N, the MERT analysis [40] predicts a shape resonance. Elastic cross sections re-edited from reference [40], vibrational—measurements from the Kaiserslautern group [44], TCS—recommended values from reference [45].

Figure 1.
Integral (elastic, vibrational, total) cross sections for electron—N scattering in the low energy range. MERT analysis [39] predicts a shape resonance: its position and width depend on the choice of the low-energy data used as the input for the analysis. Elastic cross sections re-edited from reference [39], vibrational excitation by Michael Allan [42], elaborated in reference [43]. TCS values are taken from reference [10].
Advanced theories, like complex Kohn [46], Schwinger multi-channel [47], Schwinger multi-channel with pseudo-potentials [48], close-coupling [49], and R-matrix [50] are needed to reproduce the existence of resonances, especially shape ones. However, extending the MERT analysis [25] to energies of a few eV (as compared to ca. 1 eV in previous works [23]) produced a rather unexpected result, namely resonant-like maxima in the integral elastic cross sections [24,39,40,41], see Figure 1, Figure 2, Figure 3 and Figure 4 for N, CO, CH, and CF, respectively. These maxima appear from a fast change of single (s, p, d) phase shifts at energies of a few eV, see the insets in Figure 1 and Figure 2. The positions, amplitudes, and widths of maxima depend on the partial-wave channel in which the resonance appears as small variations within the experimental uncertainties; the low-energy experimental data used for the MERT lead to the resonances in different channels (Figure 1 and Figure 2). In CH and CF the resonances are broad and result from the contribution of more than one partial wave [24,41].
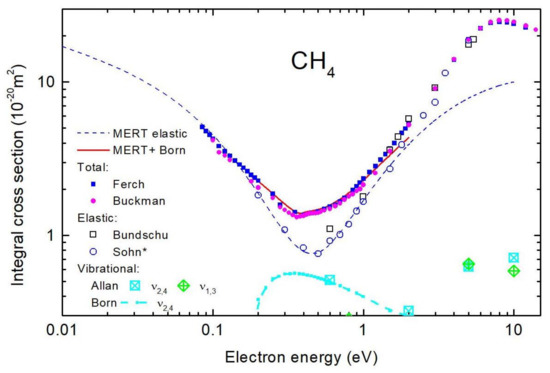
Figure 3.
Integral (elastic, vibrational, total) cross sections for electron—CH scattering in the low energy range. For references see reference [24].
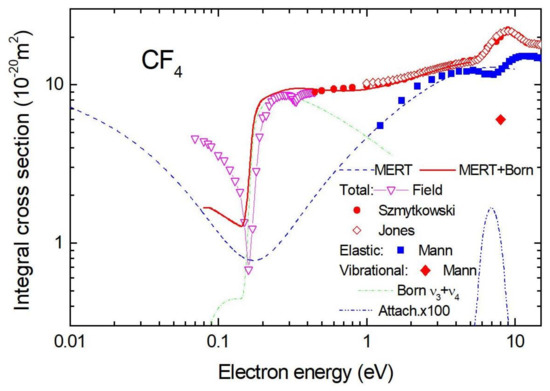
Figure 4.
Integral (elastic, vibrational, total, dissociative electron attachment) cross sections for electron—CF scattering in the low energy range. For references see reference [41].
Obviously, semi-empirical analyses can not substitute more rigorous theories, but the lesson from such “MERT resonances [24,39,40,41]” is that the same potential may govern elastic cross sections in the few meV and few eV energy ranges (this is not the case of some ab-intio methods, using three different potentials in different energy ranges [51]).
3. Is Total Cross Section Merely a Sum of Partials?
Conceptually, TCS is considered as a sum of partial cross sections, that are usually regarded as independent quantities: this is a hidden hypothesis in many of the semi-empirical approaches. Furthermore, theories usually treat the elastic and inelastic channels independently. The approaches most successful recently, like the R-matrix [50] and Schwinger multi-channels [48] stop before the thresholds for electronic excitations and/or ionization. In the intermediate energy range, a so-called optical potential [52] is commonly used in calculations of the summed inelastic cross sections (i.e., all electronic excitations and the ionization, also called "absorption" cross section), see, for example, [53]. Then, via some assuptions on the partitioning scheme, the ionization cross sections were derived [5]. However, relations between these schemes and the parameters used in BEB models for ionizations are not clear.
These approaches would suggest that scattering channels are independent. However, other theories indicate that including additional channels influences results. This is well seen in calculations of electronic excitations, say in HO [54] and also in calculations that go beyond the Born approximation of the near-threshold vibrational excitation for the same molecule, see reference [36] in this volume.
Generally, experimental hints for channel coupling are faint. Figure 4 for CF would suggest that the vibrational excitation in CF in the threshold region is simply summed to the elastic (MERT) part. However, in the resonant regions, the two channels are clearly coupled. The maximum in the vibrational channels anticipates the one in the elastic scattering; moreover, in the elastic channel, a kind of shoulder is seen, instead. A similar picture holds for NF [31]. Does this phenomenon reflect a high value of the transition dipole moment (0.122ae in CF as compared to 0.021 ae in CH [55]) for the asymmetric stretching vibrational modes?
In some molecules, like N and CO (see Figure 19 in reference [43]), a progression of high (up to ) vibrational overtones in shape resonances was observed, but excitations of these modes are shifted in energy, see Figure 1 for N. This behavior has been recently reproduced in N (and NO) shape resonances by the local optical potential model [56,57] that assumes coupling between the discrete and continuum states of the colliding system. The superposition of the elastic scattering and vibrational modes makes the whole resonance peak much broader (but lower), resulting from the MERT model.
For positron scattering, it seems rather clear that inelastic channels, like positronium-formation, sum-up with elastic channels, see Figure 5 for N. In the case of Ar, the theory that included absorption [58] indicated a step of the integral elastic cross section at the opening of the absorption channels, but the effect is too small to be proved experimentally at present. Another application of the optical potential for positron scattering at 100–300 eV in argon [59] showed that “absorption” effects reduce the DCS at intermediate (30–120) angles but raise it by a factor of a few folds in the zero-angle limit.
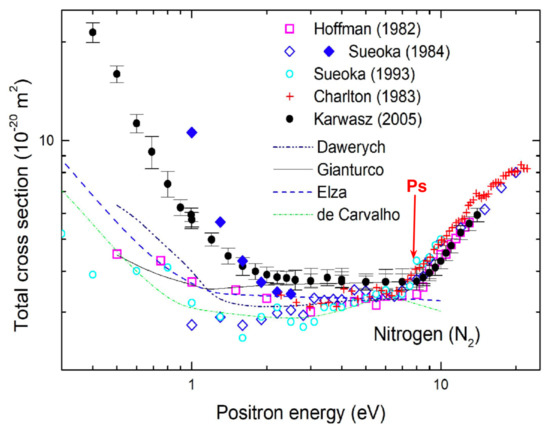
Figure 5.
Total cross section for positron scattering on N. All experiments (in spite of their methodological uncertainties) indicate the rise of TCS towards zero energy (MERT domain), a flat, hard sphere-like region up to the threshold for the positronium formation (Ps—indicated by vertical arrow), and the rapid (a Wannier-like) rise of TCS above this threshold. For references see [60].
Figure 5 shows another interesting feature of the low-energy positron-scattering cross sections: a constant value of TCS in range up to the threshold for positronium formation. This feature is present in many targets, including H, CO, SF. Taking a geometrical cross section, one derives hard-sphere “dimensions” of the molecules, see reference [16]. Detailed models [21,61] explain that this feature comes from an inter-play between the short-range repulsive (i.e., of the nuclear core) and long-range attractive (due to the polarization) interactions. Note also that a hard-sphere model applied successfully by Borghesani [62] to electron-helium scattering (this issue).
Apart from He, TCS for electron scattering hardly relates to any “hard-sphere” radii. In N, the TCS at 5 eV (i.e., outside the resonance and still below the thresholds for electronic excitations) is lower by a factor of three for positrons than for electrons. Does it reflect a mere difference in the interaction potential or exchange effects? As the exchange effects should be less significant at high energies, it is worth exploiting the TCS in a broad energy range. This will be done via the dispersion relation that considers the high and very low energy ranges together.
4. Dispersion Relation
In optics, the dispersion relation, i.e., the dependence of the complex refraction index on the wavelength (Kronig-Kramers relations [52]) gives complete information on the optical properties of the material. The dispersion relation for electron (and positron) scattering has been formulated by Gerjuoy and Krall [63]. It relates the real part of the scattering amplitude f(E,0) at a given energy E and zero scattering angle with the Born amplitude for direct (f) and exchange (g) scattering [64].
Kauppila et al. [65], already in the 1980s, performed measurements of TCS up to 700 eV and checked the validity of the dispersion relation for electron and positron scattering on He, Ne, Ar. Their conclusion for electron scattering was negative (the relation does not hold) and the relation seemed valid for positron scattering on these three atoms, within the experimental uncertainties. Note, however, that in that time positron measurements at low energies were subject to big uncertainties, see Figure 5; similarly, in the high energy part, no Born region was reached, see Figure 6 (and compare with a similar Figure 7 for CO).
An extra term for electrons, as compared to positron scattering, comes from the exchange part of the scattering amplitude (), that is non-analytic for negative energies [52]. However, the very idea of a dispersion relation led to the method of optical potential [6,59,66] widely used in calculations of absorption (i.e., electronic excitation and ionization) cross sections adding the elastic part and TCS.
The dispersion relation should hold for any arbitrarily chosen lower limit of integration, i.e., for any energy, like it was checked by de Heer and collaborators for H and He [67]. Choosing the low limit of integration at simplifies the analysis: for non-polar molecules (like the four considered here) the scattering at zero energy is isotropic and the scattering amplitude equals the minus scattering length. Consequently, the dispersion relation simplifies to:
The Born amplitude is the Fourier transform of the scattering potential corresponding to the wave vector transferred ( and being the initial and final scattering vector).
In principle, for an energy-independent potential (as should be the case of the static interaction), the Born amplitude for the zero-momentum transferred (i.e., for scattering into the forward direction) should also be energy independent. Further, DCS is the square of the scattering amplitude—in the Born approximation, it remains unchanged when the sign of the interaction potential changes. This should be the case of electron and positron scattering at “sufficiently” high energies, where the polarization potential may be disregarded. A series of works [68,69,70] started in the 1970s to verify the Born conditions in elastic scattering on molecules, see Figure 8 for CO.
For positron scattering, we are not aware of similar DCSs extending to zero angles as those shown in Figure 8. Kauppila et al. [71] measured DCS in Ar for electron and positron scattering at 300 eV; the experimental points at 30–90 coincide within experimental uncertainties, but the ab inito optical model [72] predicts the DCS at the zero angle by a factor of two lower for positrons than for electrons.
One could expect that the information on the opposite-sign of the short-range scattering potentials for positrons and electrons is “hidden” in the MERT parameters, in particular the “effective range”. However, as one of us shows (KF) in this issue [73] it is not so straightforward. Nevertheless, in the next section we resume experimental data that can be useful in evaluation of the dispersion relation.
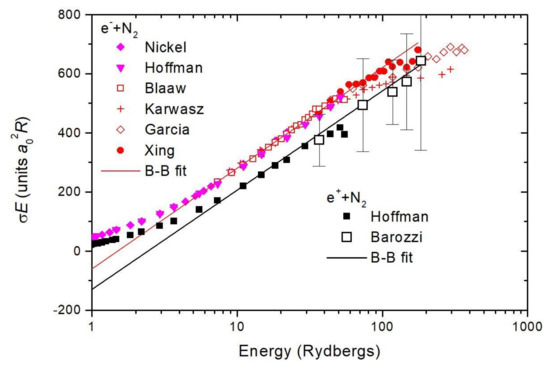
Figure 6.
High-energy total cross sections for electron and positron scattering on N. The lines are the Bethe-Born fit, Equation (4). For references for electron scattering see the review [43]; for positrons Detroit [74] and Trento data [75] are used.
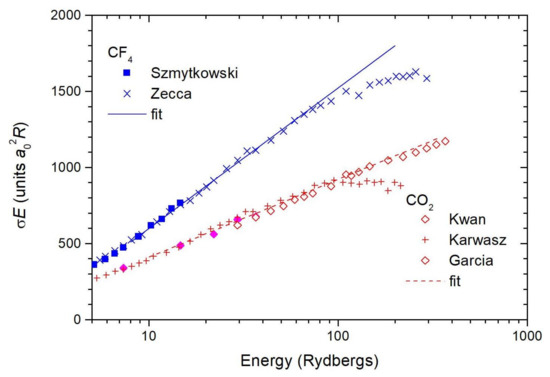
Figure 7.
High-energy total cross sections for electron—CO and CF scattering. The line is the Bethe-Born fit, Equation (4). Experimental data are from Madrid laboratory [76], Trento [77,78], Detroit [79] and Gdańsk [80].
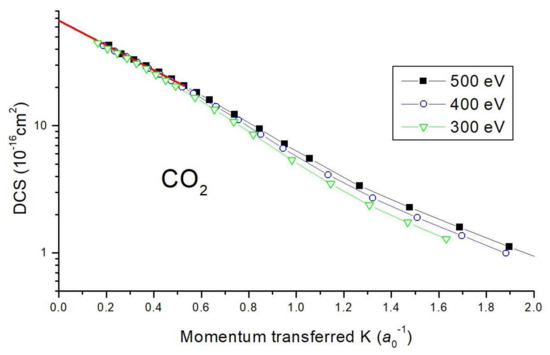
Figure 8.
In search of the forward Born amplitude. Do DCSs at high energies tend to a constant value? Data for CO are by Bromberg [69]; a single point for 10 at 400 eV by Iga et al. [81] coincides with Bromberg’s data.
5. Experimental Input
Lack of experimental data was one of the obstacles in verifying the dispersion relation and its modifications in the past [64]. Here, we propose an “experimental” dispersion relation that requires, apart from total cross sections in a wide energy range (asymptotically from 0 to ∞), scattering length, i.e., the integral cross sections at zero energy and the elastic DCS at zero momentum transferred (i.e., asymptotically at zero angle) and high (“Born” [34]) energy.
In the zero-energy limit, the already mentioned new approach to MERT [24,39] consisted of fitting the phase shifts and cross sections directly, to increase the fidelity in the zero-energy limit and extend its applicability above 1 eV.
At high energies, two groups—from Trento [82,83,84] and Madrid University [76,85]—extended TCS measurements on molecules up to 3–5 keV. Trento measurements [83] above 1 keV were subject to the angular resolution error (mainly in the inelastic channel) underestimating the TCS at their highest energies by some 20–30% [7]. The Madrid group [76] used the energy analyzer at the exit of the scattering channel (therefore excluding electron scattered inelastically into forward angles), so their TCS are reliable up to their highest energies. They also promptly applied the Bethe-Born formula, extrapolating TCS into very high (up to relativistic) energies. This formula contains a logarithmic term that reflects the infinite range of the Coulomb interaction between target electrons and the incoming electron/positron [86].
The scattering length A was adopted from the MERT-free fit in reference [39,40] for N and CO, respectively, and from MERT fits in references [24,41] for CH and CF, respectively.
Born forward scattering amplitude has been deduced from low-angle elastic differential cross sections at high energies. For N, numerous elastic DCS measurements were completed [68,70,87]; Zhang et al. [70] extrapolated them to the zero-angle, obtaining the value of 17.4 × 10 cm/sr (and declaring 1% error bar). For CO, the DCS measured [69] down to 2 already at 300–500 eV indicates a constant zero-angle value, of about 67 × 10 cm (with an uncertainty of %), see Figure 8.
For CH and CF we used the data of Sakae et al. [88], extending up to 700 eV, but the uncertainty of these values is high (some 20%). The lowest angle measured was 5, the extrapolation was done via a polynomial fit (no details given), and the experimental data agree in shape with the model of Jain [51] but are a factor of three lower at the zero angle, agreeing with much earlier theory of Szabo and Ostlund [89].
Parameters A and B of the Born-Bethe fit to the electron TCS (Equation (4), Figure 6 and Figure 7) are: , 310; , 510; 52, 232; and 317, 923, for N, CO, CH (see ref. [7]), and CF, respectively. Note that the parameter B scales with the total number n of electrons in the target (the ratio amounting to about 22 in units) — a similar conclusion in the high energy limit was drawn by García and Manero [90]. On the other hand, the TCS in its maximum (but outside resonance) correlates well [29] with the polarizability, see TCS values at 30 eV (around the maximum) in Table 1.

Table 1.
In search for dispersion relation in electron-molecule scattering.
The integral over the TCS in Formula (2) was completed in the energy range from 10 eV to 10 eV: such a choice assures that the value of the integral does not depend significantly (less than 1%) on the integration limits. The integral was performed in three sub-sets: (i) MERT region from 10 eV to 1 eV, see the discussion in Figure 1, Figure 2, Figure 3 and Figure 4, (ii) the low and intermediate energy range 1–1000 eV, using the recommended TCS from reference [45], (iii) high energy range—using the extrapolations via Bethe-Born fit, see Figure 6 and Figure 7. Results for electrons are given in Table 1.
The check of the dispersion relation for positrons is given in Table 2. The scattering length for N, CO, and CH were taken from our previous papers [25,94]. We are not aware of the experimental TCS for CF positron-scattering in the very low energy range. In the high energy limit it was noted [75] that TCS (for N, Ar, Kr) merge in the range of a few keV. As shown in Figure 6, for N, the coefficient B of the high-energy Bethe-Born fit is, within experimental uncertainties, equal for positrons and electrons. This result is also supported by the optical-model calculations by Khander et al. [95] (this issue) for electron and positron scattering on such a heavy atoms as radon. Parameters A and B of the Born-Bethe fit to positron TCS, Equation (4), are: , 310, , 510, 0, 232, 317, and 923, for N, CO, CH, and CF, respectively.

Table 2.
In search for dispersion relation in positron-molecule scattering.
Let us review the main points from the present comparisons (see columns 4 and 5 in Table 1 and Table 2). The dispersion relation, as proposed originally, seems to be quite reasonable in the case of positron scattering. The optical model [72] tells us that the Born amplitude for the real (static + polarization + absorption) potential may be lower for positrons than for electrons. In fact, for CH, where the DCS for electrons are probably underestimated (we are not aware of the data similar to these in Figure 8), the values in column four (the difference of terms) and column five (the integral) in Table 2 are equal within uncertainties. This would confirm the conclusion of Kauppila et al. that the dispersion relation holds for positron scattering on noble gases, and also on noble-like CH. To resolve the answer for N and CO, the ab initio (i.e., not semi-empirical) Born amplitude for positrons is needed.
For electrons, the situation is more unclear; the very sign of the terms disagree. Moreover, the results suggest that the contribution of the Born exchange scattering amplitude () should be significantly greater than the Born direct scattering amplitude () to hold the dispersion relation. What remains is the question of resonances, does the dispersion relation holds when the projectile and the target molecule do not form bound states [98]? Out of the four discussed molecules none showed stable negative ions, only temporary negative states [99] decaying into radicals/atoms are formed via resonances (see example for CF on Figure 4). In turn, detailed searches for resonances in positron scattering gave a negative result [100].
We are not able to draw clear conclusions from the present comparisons. Still, many of the experiment-deduced components of the dispersion relation lay within high uncertainty limits. For sure, different quantities in the dispersion relation are interlinked. The input from the theory is necessary.
Author Contributions
Conceptualization, supervision and original draft preparation, G.K.; formal analysis and investigation, F.C. and K.F. All authors have read and agreed to the published version of the manuscript.
Funding
This research received no external funding.
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
Not applicable.
Acknowledgments
One of us recalls his very fruitful conceptual stay in Detroit (AD 1991), and especially the extraordinary hospitality of Walter Kauppila and Talbert S. Stein. F.C. thanks J. Franz for the hospitality in Poland in September 2021.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Dodt, D.; Dinklage, A.; Bartschat, K.; Zatsarinny, O. Validation of atomic data using a plasma discharge. New J. Phys. 2010, 12, 073018. [Google Scholar] [CrossRef]
- Nakano, T.; Higashijima, S.; Kubo, H.; Asakura, N.; Fukumoto, M. The emission rates of CH, CD and C2 spectral bands and a re-evaluation of the chemical sputtering yield of the JT-60U carbon divertor plates. Nucl. Fusion 2014, 54, 043004. [Google Scholar] [CrossRef]
- Sahoo, A.K.; Sharma, L. Electron Impact Excitation of Extreme Ultra-Violet Transitions in Xe7 – Xe10 Ions. Atoms 2021, 9, 76. [Google Scholar] [CrossRef]
- Munoz, A.; Blanco, F.; García, G.; Thorne, P.A.; Brunger, M.J.; Sullivan, J.P.; Buckman, S.J. Single electron tracks in water vapour for energies below 100 eV. Int. J. Mass Spectrom. 2008, 277, 175. [Google Scholar] [CrossRef]
- Sinha, N.; Antony, B. Mean Free Paths and Cross Sections for Electron Scattering from Liquid Water. J. Phys. Chem. B 2021, 125, 5479. [Google Scholar] [CrossRef] [PubMed]
- Modak, P.; Antony, B. Electron scattering from HNCO. Eur. Phys. J. D 2021, 75, 54. [Google Scholar] [CrossRef]
- Song, M.Y.; Yoon, J.S.; Cho, H.; Itikawa, Y.; Karwasz, G.P.; Kokoouline, V.; Nakamura, Y.; Tennyson, J. Cross Sections for Electron Collisions with Methane. J. Phys. Chem. Ref. Data 2015, 44, 023101. [Google Scholar] [CrossRef]
- Pietanza, L.D.; Guaitella, O.; Aquilanti, V.; Armenise, I.; Bogaerts, A.; Capitelli, M.; Colonna, G.; Guerra, V.; Engeln, R.; Kustova, E.; et al. Advances in non-equilibrium CO2 plasma kinetics: A theoretical and experimental review. Eur. Phys. J. D 2021, 75, 237. [Google Scholar] [CrossRef]
- Yoon, J.S.; Song, M.Y.; Han, J.M.; Hwang, S.H.; Chang, W.S.; Lee, B.; Itikawa, Y. Cross Sections for Electron Collisions with Hydrogen Molecules. J. Phys. Chem. Ref. Data 2008, 37, 913. [Google Scholar] [CrossRef]
- Szmytkowski, C.; Możejko, P. Recent total cross section measurements in electron scattering from molecules. Eur. Phys. J. D 2020, 74, 90. [Google Scholar] [CrossRef]
- Kawaguchi, S.; Takahashi, K.; Satoh, K. Electron collision cross section set for N2 and electron transport in N2, N2/He, and N2/Ar. Plasma Sources Sci. Technol. 2021, 30, 035010. [Google Scholar] [CrossRef]
- Song, M.Y.; Yoon, J.S.; Cho, H.; Karwasz, G.P.; Kokoouline, V.; Nakamura, Y.; Tennyson, J. “Recommended” cross sections for electron collisions with molecules. Eur. Phys. J. D 2020, 74, 60. [Google Scholar] [CrossRef]
- Lindsay, B.G.; Mangan, M.A. 5.1 Ionization: Datasheet from Landolt-Börnstein—Group I Elementary Particles, Nuclei and Atoms. In Interactions of Photons and Electrons with Molecules; Springer Materials; Springer: Berlin/Heidelberg, Germany, 2003; Volume 17C. [Google Scholar] [CrossRef]
- Kłosowski, Ł.; Piwiński, M. Magnetic Angle Changer for Studies of Electronically Excited Long-Living Atomic States. Atoms 2021, 9, 71. [Google Scholar] [CrossRef]
- Ptasińska, S. A Missing Puzzle in Dissociative Electron Attachment to Biomolecules: The Detection of Radicals. Atoms 2021, 9, 77. [Google Scholar] [CrossRef]
- Karwasz, G.P. Positrons—An alternative probe to electron scattering. Eur. Phys. J. D 2005, 35, 267. [Google Scholar] [CrossRef]
- Campeanu, R.I.; Whelan, C.T. Few Body Effects in the Electron and Positron Impact Ionization of Atoms. Atoms 2021, 9, 33. [Google Scholar] [CrossRef]
- Carelli, F.; Gianturco, F.A.; Franz, J.; Satta, M. A dipole-driven path for electron and positron attachments to gas-phase uracil and pyrimidine molecules: A quantum scattering analysis. Eur. Phys. J. D 2015, 69, 143. [Google Scholar] [CrossRef]
- Karwasz, G.P.; Zecca, A.; Brusa, R.S.; Pliszka, D. Application of positron annihilation techniques for semiconductor studies. Alloy. Compd. 2004, 382, 244. [Google Scholar] [CrossRef]
- García-Abenza, A.; Lozano, A.I.; Oller, J.C.; Blanco, F.; Gorfinkiel, J.D.; Limao-Vieira, P.; García, G. Evaluation of Recommended Cross Sections for the simulation of Electron Tracks in Water. Atoms 2021, 9, 98. [Google Scholar]
- Franz, J.; Fedus, K.; Karwasz, G.P. Do positrons measure atomic and molecular diameters? Eur. Phys. J. D 2016, 70, 155. [Google Scholar] [CrossRef]
- O’Malley, T.F.; Spruch, L.; Rosenberg, L. Modification of Effective-Range Theory in the Presence of a Long—Range r-4 Potential. J. Math. Phys. 1961, 2, 491. [Google Scholar] [CrossRef]
- Buckman, S.J.; Mitroy, J. Analysis of low-energy electron scattering cross sections via effective-range theory. J. Phys. B. 1989, 22, 1365. [Google Scholar] [CrossRef]
- Fedus, K.; Karwasz, G.P. Ramsauer-Townsend minimum in methane—Modified effective range analysis. Eur. Phys. J. D 2014, 68, 93. [Google Scholar] [CrossRef]
- Idziaszek, Z.; Karwasz, G. Applicability of modified effective-range theory to positron-atom and positron-molecule scattering. Phys. Rev. A 2006, 73. [Google Scholar] [CrossRef]
- Harland, P.W.; Vallance, C. Ionization cross-sections and ionization efficiency curves from polarizability volumes and ionization potentials. Int. J. Mass Spectr. Ion Proc. 1997, 171, 173–181. [Google Scholar] [CrossRef]
- Karwasz, G.P.; Możejko, P.; Song, M.Y. Electron-impact ionization of fluoromethanes—Review of experiments and binary-encounter models. Int. J. Mass Spectrom. 2014, 365–366, 232–237. [Google Scholar] [CrossRef]
- Szmytkowski, C. On trends in total cross sections for electron (positron) scattering on atoms and molecules at intermediate energies. Z. Phys. D 1989, 13, 69–73. [Google Scholar] [CrossRef]
- Karwasz, G.P.; Brusa, R.S.; Piazza, A.; Zecca, A. Total cross sections for electron scattering on chloromethanes: Formulation of the additivity rule. Phys. Rev. A 1999, 59, 1341. [Google Scholar] [CrossRef]
- Kim, Y.K.; Rudd, M.E. Binary-encounter-dipole model for electron-impact ionization. Phys. Rev. A 1994, 50, 3954. [Google Scholar] [CrossRef]
- Song, M.; Yoon, J.; Cho, H.; Karwasz, G.; Kokoouline, V.; Nakamura, Y.; Hamilton, J.R.; Tennyson, J. Cross Sections for Electron Collisions with NF3. J. Phys. Chem. Ref. Data 2017, 46, 043104. [Google Scholar] [CrossRef]
- Kawahara, H.; Suzuki, D.; Kato, H.; Hoshino, M.; Tanaka, H.; Ingolfsson, O.; Campbell, L.; Brunger, M.J. Cross sections for electron impact excitation of the C1Π and D1Σ+ electronic states in N2O. J. Chem. Phys. 2009, 131, 114307. [Google Scholar] [CrossRef] [PubMed]
- Xu, W.Q.; Ma, Z.R.; Peng, Y.G.; Du, X.J.; Xu, Y.C.; Wang, L.H.; Li, B.; Zhang, H.R.; Zhang, B.Y.; Zhu, J.H.; et al. Cross sections for the electron-impact excitations A˜1B1 and B˜1A1 of H2O determined by high-energy electron scattering. Phys. Rev. A 2021, 103, 032808. [Google Scholar] [CrossRef]
- Kang, X.; Xu, L.Q.; Liu, Y.W.; Wang, S.X.; Yang, K.; Peng, Y.G.; Ni, D.D.; Hiraoka, N.; Tsuei, K.D.; Zhu, L.F. A study on the validity of the first Born approximation for high-energy electron scattering with nitrogen molecules. J. Phys. B At. Mol. Opt. Phys. 2019, 52, 245202. [Google Scholar] [CrossRef]
- Marler, J.P.; Surko, C.M. Systematic comparison of positron—And electron-impact excitation of the ν3 vibrational mode of CF4. Phys. Rev. A 2005, 72, 062702. [Google Scholar] [CrossRef]
- Ayouz, M.; Faure, A.; Tennyson, J.; Kokoouline, V.; Tudorovskaya, M. Cross Sections and Rate Coefficients for Vibrational Excitation of H2O by Electron Impact. Atoms 2021, 9, 62. [Google Scholar] [CrossRef]
- Poveda, L.A.; Varella, M.T.d.N.; Mohallem, J.R. Vibrational Excitation Cross-Section by Positron Impact: A Wave-Packet Dynamics Study. Atoms 2021, 9, 64. [Google Scholar] [CrossRef]
- Kitajima, M.; Kishino, T.; Okumura, T.; Kobayashi, N.; Sayama, A.; Mori, Y.; Kosaka, K.; Odigiri, F.; Hoshino, M.; Tanaka, H. Low-energy and very-low energy total cross sections for electron collisions with N2. Eur. Phys. J. D 2017, 71, 139. [Google Scholar] [CrossRef]
- Idziaszek, Z.; Karwasz, G.P. Modified effective-range theory for low energy e -N2 scattering. Eur. Phys. J. D 2009, 51, 347–355. [Google Scholar] [CrossRef]
- Idziaszek, Z.; Karwasz, G.P.; Brusa, R.S. Modified effective range analysis of low energy electron and positron scattering on CO2. J. Phys. Conf. Ser. 2008, 115, 012002. [Google Scholar] [CrossRef]
- Fedus, K.; Karwasz, G. Ramsauer–Townsend minimum in electron scattering from CF4: Modified effective range analysis. Eur. Phys. J. D 2021, 75, 76. [Google Scholar] [CrossRef]
- Allan, M. Excitation of vibrational levels up to ν = 17 in N2 by electron impact in 0-5 eV region. J. Phys. B 1986, 18, 4511. [Google Scholar] [CrossRef]
- Zecca, A.; Karwasz, G.P.; Brusa, R.S. One century of experiments on electron-atom and molecule scattering: A critical review of integral cross-sections. La Riv. del Nuovo C. 1996, 19, 1–146. [Google Scholar] [CrossRef]
- Antoni, T.; Jung, K.; Ehrhardt, H.; Chang, E.S. Rotational branch analysis of the excitation of the fundamental vibrational modes of CO2 by slow electron collisions. J. Phys. B 1986, 19, 1377. [Google Scholar] [CrossRef]
- Karwasz, G.P.; Brusa, R.S.; Zecca, A. 6.1 Total scattering cross sections: Datasheet from Landolt-Börnstein—Group I Elementary Particles, Nuclei and Atoms. In Interactions of Photons and Electrons with Molecules; Springer Materials; Springer: Berlin/Heidelberg, Germany, 2003; Volume 17C. [Google Scholar] [CrossRef]
- Isaacs, W.A.; McCurdy, C.W.; Rescigno, T.N. Theoretical support for a Ramsauer-Townsend minimum in electron-CF4 scattering. Phys. Rev. A 1998, 58, 309. [Google Scholar] [CrossRef]
- Winstead, C.; McKoy, V.; Sun, Q. Low-energy elastic electron scattering by tetrafluoromethane (CF4). J. Chem. Phys. 1993, 98, 1105–1109. [Google Scholar] [CrossRef]
- Costa, R.F.d.; Varella, M.T.D.N.; Bettega, M.H.F.; Lima, M.A.P. Recent advances in the application of the Schwinger multichannel method with pseudopotentials to electron-molecule collisions. Eur. Phys. J. D 2015, 69, 159. [Google Scholar] [CrossRef]
- Gianturco, F.A.; Lucchese, R.R. The elastic scattering of electrons from molecules: II. Molecular features and spatial symmetries of some resonant states. J. Phys. B. 1996, 29, 3955. [Google Scholar] [CrossRef]
- Hamilton, J.R.; Tennyson, J.; Huang, S.; Kushner, M.J. Calculated cross sections for electron collisions with NF3, NF2 and NF with applications to remote plasma sources. Plasma Sources Sci. Technol. 2017, 26, 065010. [Google Scholar] [CrossRef]
- Jain, A. Total (elastic+absorption) cross sections for e-CH4 collisions in a spherical model at 0.10–500 eV. Phys. Rev. A 1986, 34, 3707. [Google Scholar] [CrossRef] [PubMed]
- Thirumalai, D.; Staszewska, G.; Truhlar, D.G. Dispersion Relation Techniques for Approximating the Optical Model Potential for Electron Scattering. Comments At. Mol. Phys. 1987, 20, 217–243. [Google Scholar]
- Goswami, B.; Naghma, R.; Antony, B. Calculation of electron impact total ionization cross sections for tungsten, uranium and their oxide radicals. Int. J. Mass Spectr. 2014, 372, 8. [Google Scholar] [CrossRef]
- Gorfinkiel, J.D.; Morgan, L.A.; Tennyson, J. Electron impact dissociative excitation of water within the adiabatic nuclei approximation. J. Phys. B. 2002, 35, 543. [Google Scholar] [CrossRef]
- Bishop, D.M.; Cheung, L.M. Vibrational Contributions to Molecular Dipole Polarizabilities. J. Phys. Chem. Ref. Data 1982, 11, 119. [Google Scholar] [CrossRef][Green Version]
- Laporta, V.; Celiberto, R.; Vadehra, J.M. Theoretical vibrational-excitation cross sections and rate coefficients for electron-impact resonant collisions involving rovibrationally excited N2 and NO molecules. Plasma Sources Sci. Technol. 2012, 21, 055018. [Google Scholar] [CrossRef]
- Trevisan, C.S.; Houfek, K.; Shang, Z.; Orel, A.E.; McCurdy, C.W.; Rescigno, T.N. Nonlocal model of dissociative electron attachment and vibrational excitation of NO. Phys. Rev. A 2005, 71, 052714. [Google Scholar] [CrossRef]
- Bartschat, K.; McEachran, R.P.; Stauffer, A.D. Optical potential approach to electron and positron scattering from noble gases. I. Argon. J. Phys. B. 1988, 21, 2789. [Google Scholar] [CrossRef]
- Joachain, C.J.; Potvliege, R.M. Importance of absorption effects on fast positron-argon differential cross sections. Phys. Rev. A 1987, 35, 4873. [Google Scholar] [CrossRef]
- Karwasz, G.P.; Pliszka, D.; Brusa, R.S. Total cross sections for positron scattering in argon, nitrogen and hydrogen below 20 eV. Nucl. Instr. Meth. B 2006, 247, 68. [Google Scholar] [CrossRef]
- Fedus, K. A rigid sphere approach to positron elastic scattering by noble gases, molecular hydrogen, nitrogen and methane. Eur. Phys. J. D 2016, 70, 261. [Google Scholar] [CrossRef][Green Version]
- Borghesani, F.A. Accurate Electron Drift Mobility Measurements in Moderately Dense Helium Gas at Several Temperatures. Atoms 2021, 9, 52. [Google Scholar] [CrossRef]
- Gerjuoy, E.; Krall, N.A. Dispersion Relations in Atomic Scattering Problems. Phys. Rev. 1960, 119, 705. [Google Scholar] [CrossRef]
- Temkin, A.; Bhatia, A.K.; Kim, Y.S. A new dispersion relation for electron-atom scattering. J. Phys. B. 1986, 19, L701. [Google Scholar] [CrossRef]
- Kauppila, W.E.; Stein, T.S.; Smart, J.H.; Dababneh, M.S.; Ho, Y.K.; Downing, J.P.; Pol, V. Measurements of total scattering cross sections for intermediate-energy positrons and electrons colliding with helium, neon, and argon. Phys. Rev. A 1982, 24, 725. [Google Scholar] [CrossRef]
- Salvat, F. Optical-model potential for electron and positron elastic scattering by atoms. Phys. Rev. A 2003, 68, 012708. [Google Scholar] [CrossRef]
- Heer, F.J.d.; McDowell, M.R.C.; Wagenaar, R.W. Numerical study of the dispersion relation for e–H scattering. J. Phys. B. 1977, 10, 1945. [Google Scholar] [CrossRef]
- Jansen, R.H.J.; Heer, F.J.d.; Luyken, H.J.; Wingerden, B.v.; Blaauw, H.J. Absolute differential cross sections for elastic scattering of electrons by helium, neon, argon and molecular nitrogen. J. Phys. B. 1975, 9, 185. [Google Scholar] [CrossRef]
- Bromberg, J.P. Absolute differential cross sections of elastically scattered electrons. V. O2 and CO2 at 500, 400, and 300 eV. J. Chem. Phys. 1974, 60, 1717. [Google Scholar] [CrossRef]
- Zhang, Y.; Ross, A.W.; Fink, M. Electron correlation and charge density study of N2 and O2 by high energy electron scattering. Z. Phys. D 1991, 18, 163–169. [Google Scholar] [CrossRef]
- Hyder, M.A.; Dababneb, M.S.; Hsieh, Y.F.; Kauppila, W.E.; Kwan, C.K.; Mahdavi-Hezaveh, M.; Stein, T.S. Positron Differential Elastic-Scattering Cross-Section Measurements for Argon. Phys. Rev. Lett. 1986, 57, 2252. [Google Scholar] [CrossRef]
- Joachain, C.J.; Vanderpoorten, R.; Winters, K.H.; Byron, F.W., Jr. Optical model theory of elastic electron- and positron-argon scattering at intermediate energies. J. Phys. B 1977, 10, 227. [Google Scholar] [CrossRef]
- Fedus, K. Elastic Scattering of Slow Electrons by Noble Gases—The Effective Range Theory and the Rigid Sphere Model. Atoms 2021, 9, 91. [Google Scholar] [CrossRef]
- Hoffman, K.R.; Dababneh, M.S.; Hsieh, Y.F.; Kauppila, W.E.; Pol, V.; Smart, J.H.; Stein, T.S. Total-cross-section measurements for positrons and electrons colliding with H2, N2, and CO2. Phys. Rev. A 1982, 25, 1393. [Google Scholar] [CrossRef]
- Barozzi, M. Misure di Sezione d’Urto Positrone-Molecola: Realizzazione dell’Apparato Sperimentale e Prime Misure. Master’s Thesis, Universita’ degli Studi di Trento, Trento, Italy, 1997. [Google Scholar]
- Garcia, G.; Manero, F. Total cross sections for electron scattering by CO2 molecules in the energy range 400–5000 eV. Phys. Rev. A 1996, 53, 250. [Google Scholar] [CrossRef]
- Szmytkowski, C.; Zecca, A.; Karwasz, G.; Oss, S.; Maciąg, K.; Marinković, B.; Brusa, R.S.; Grisenti, R. Absolute total cross sections for electron-CO2 scattering at energies form 0.5 to 3000 eV. J. Phys. B. 1987, 20, 5817. [Google Scholar] [CrossRef][Green Version]
- Zecca, A.; Karwasz, G.P.; Brusa, R.S. Total-cross-section measurements for electron scattering by NH3, SiH4, and H2S in the intermediate-energy range. Phys. Rev. A 1992, 45, 2777. [Google Scholar] [CrossRef]
- Kwan, C.K.; Hsieh, Y.F.; Kauppila, W.E.; Smith, S.J.; Stein, T.S.; Uddin, M.N.; Dababneh, M.S. e±—CO and e±—CO2 total cross-section measurements. Phys. Rev. A 1983, 27, 1328. [Google Scholar] [CrossRef]
- Szmytkowski, C.; Krzysztofowicz, A.; Janicki, P.; Rosenthal, L. Electron scattering from CF4 and CCl4. Total cross section measurements. Chem. Phys. Lett. 1992, 199, 191. [Google Scholar] [CrossRef]
- Iga, I.; Homem, M.G.P.; Mazon, K.T.; Lee, M.T. Elastic and total cross sections for electron-carbon dioxide collisions in the intermediate energy range. J. Phys. B. 1999, 32. [Google Scholar] [CrossRef]
- Karwasz, G.P. Intermediate-energy total cross sections for electron scattering on GeH4. J. Phys. B. 1995, 28, 1301. [Google Scholar] [CrossRef]
- Zecca, A.; Szmytkowski, C.; Karwasz, G.; Brusa, R.S. Absolute total cross sections for electron scattering on CH4 molecules in the 1-4000 eV energy range. J. Phys. B. 1991, 24, 2547–2554. [Google Scholar] [CrossRef]
- Karwasz, G.; Brusa, R.S.; Gasparoli, A.; Zecca, A. Total cross-section measurements for e-—CO scattering: 80–4000 eV. Chem. Phys. Lett. 1993, 211, 529–533. [Google Scholar] [CrossRef]
- García, G.; Manero, F. Electron scattering by CH4 molecules at intermediate energies (400–5000 eV). Phys. Rev. A 1998, 57, 1069. [Google Scholar] [CrossRef]
- Bransden, B.H.; Joachain, C.J. Physics of Atoms and Molecules, 2nd ed.; Prentice-Hall: Hoboken, NJ, USA, 2003. [Google Scholar]
- Dubois, R.D.; Rudd, M.E. Differential cross sections for elastic scattering of electrons from argon, neon, nitrogen and carbon monoxide. J. Phys. B 1976, 9, 2657. [Google Scholar] [CrossRef]
- Sakae, T.; Sumiyoshi, S.; Murakami, E.; Matsumoto, Y.; Ishibashi, K.; Katase, A. Scattering of electrons by CH4, CF4 and SF6 in the 75–700 eV range. J. Phys. B. 1989, 22, 1385. [Google Scholar] [CrossRef]
- Szabo, A.; Ostlund, N.S. Calculation of high energy elastic electron-molecule scattering cross sections with CNDO wavefunctions. J. Chem. Phys. 1974, 60, 946–950. [Google Scholar] [CrossRef]
- Garcia, G.; Manero, F. Correlation of the total cross section for electron scattering by molecules with 10–22 electrons, and some molecular parameters at intermediate energies. Chem. Phys. Lett. 1997, 280, 4373. [Google Scholar] [CrossRef]
- Nickel, J.C.; Kanik, I.; Trajmar, S.; Imre, K. Total cross section measurements for electron scattering on H2 and N2 from 4 to 300 eV. J. Phys. B 2017, 25, 2427–2431. [Google Scholar] [CrossRef]
- Kanik, I.; Trajmar, S.; Nickel, J.C. Total cross section measurements for electron scattering on CH4 from 4 to 300 eV. Chem. Phys. Lett. 1992, 193, 281–286. [Google Scholar] [CrossRef]
- Experimental values of Polarizability. Available online: https://cccbdb.nist.gov/xp1x.asp?prop=9 (accessed on 1 September 2021).
- Fedus, K.; Karwasz, G.P.; Idziaszek, Z. Analytic approach to modified effective-range theory for electron and positron elastic scattering. Phys. Rev. A 2013, 88, 012704. [Google Scholar] [CrossRef]
- Khandker, M.H.; Haque, A.K.F.; Haque, M.M.; Billah, M.M.; Watabe, H.; Uddin, M.A. Relativistic Study on the Scattering of e± from Atoms and Ions of the Rn Isonuclear Series. Atoms 2021, 9, 59. [Google Scholar] [CrossRef]
- Dababneh, M.S.; Hsieh, Y.F.; Kauppila, W.E.; Kwan, C.K.; Smith, S.J.; Stein, T.S.; Uddin, M.N. Total-cross-section measurements for positron and electron scattering by O2, CH4, and SF6. Phys. Rev. A 1988, 38, 1207. [Google Scholar] [CrossRef] [PubMed]
- Sueoka, O.; Mori, S. Total cross sections for low and intermediate energy positrons and electrons colliding with CH4, C2H4 and C2H6 molecules. J. Phys. B 1986, 19, 4035. [Google Scholar] [CrossRef]
- Vrinceanu, D.; Msezane, A.Z.; Bessis, D.; Temkin, A. Exchange Forces in Dispersion Relations Investigated Using Circuit Relations. Phys. Rev. Lett. 2001, 86, 3256. [Google Scholar] [CrossRef] [PubMed]
- Coat, Y.L.; Ziesel, J.P.; Guillotin, J.P. Negative ion resonances in CF4 probed by dissociative electron attachment. J. Phys. B. 1994, 27, 965. [Google Scholar] [CrossRef]
- Sullivan, J.P.; Gilbert, S.J.; Buckman, S.; Surko, C. Search for resonances in the scattering of low-energy positrons from atoms and molecules. J. Phys. B 2001, 34, L467. [Google Scholar] [CrossRef]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).