Relativistic Configuration-Interaction and Perturbation Theory Calculations of the Sn XV Emission Spectrum
Abstract
:1. Introduction
2. Theory
2.1. CI-MBPT Framework
2.2. CI-MBPT Numerical Procedure
2.3. Input Configurations
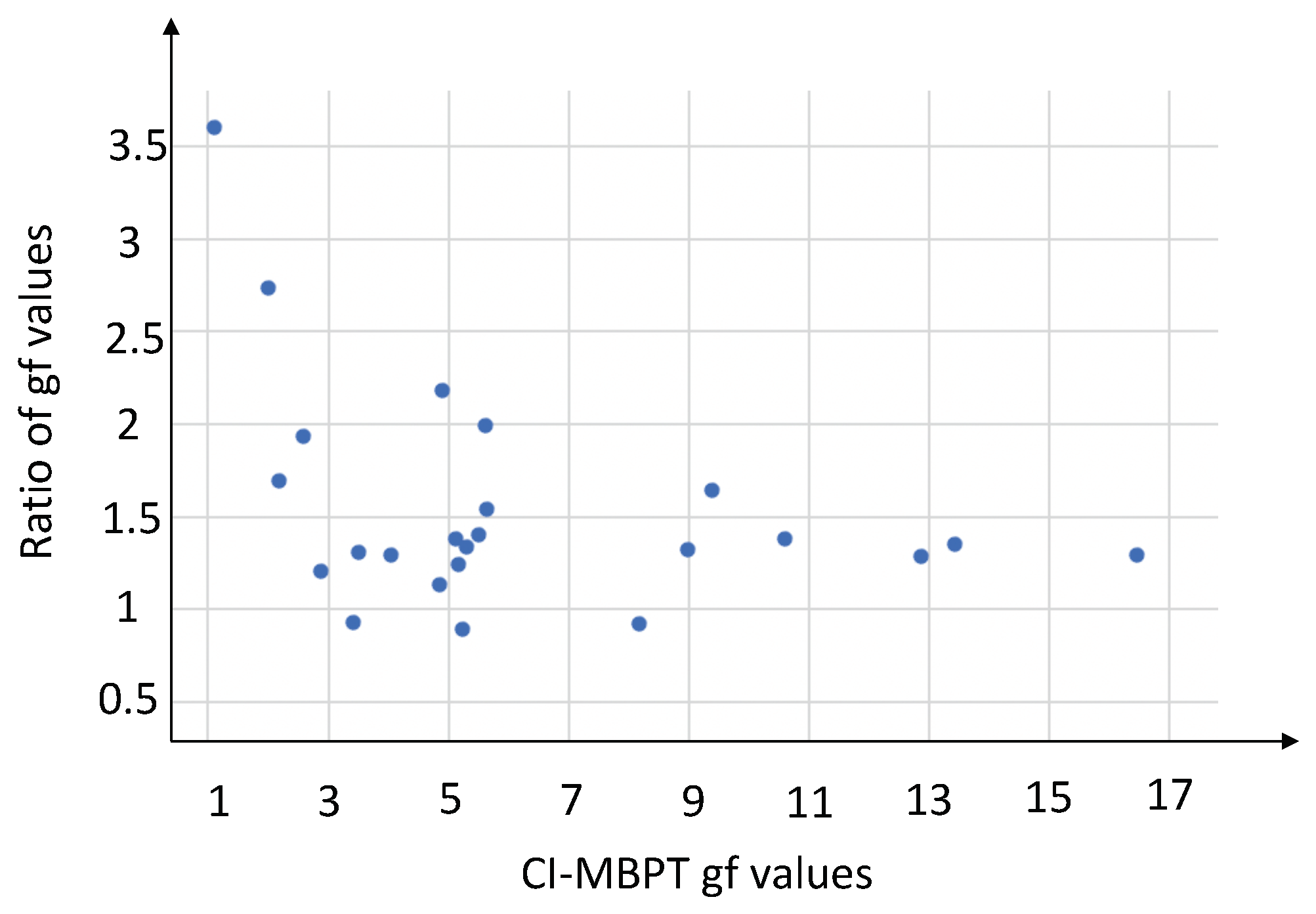
2.4. Wavelengths and gf-Values
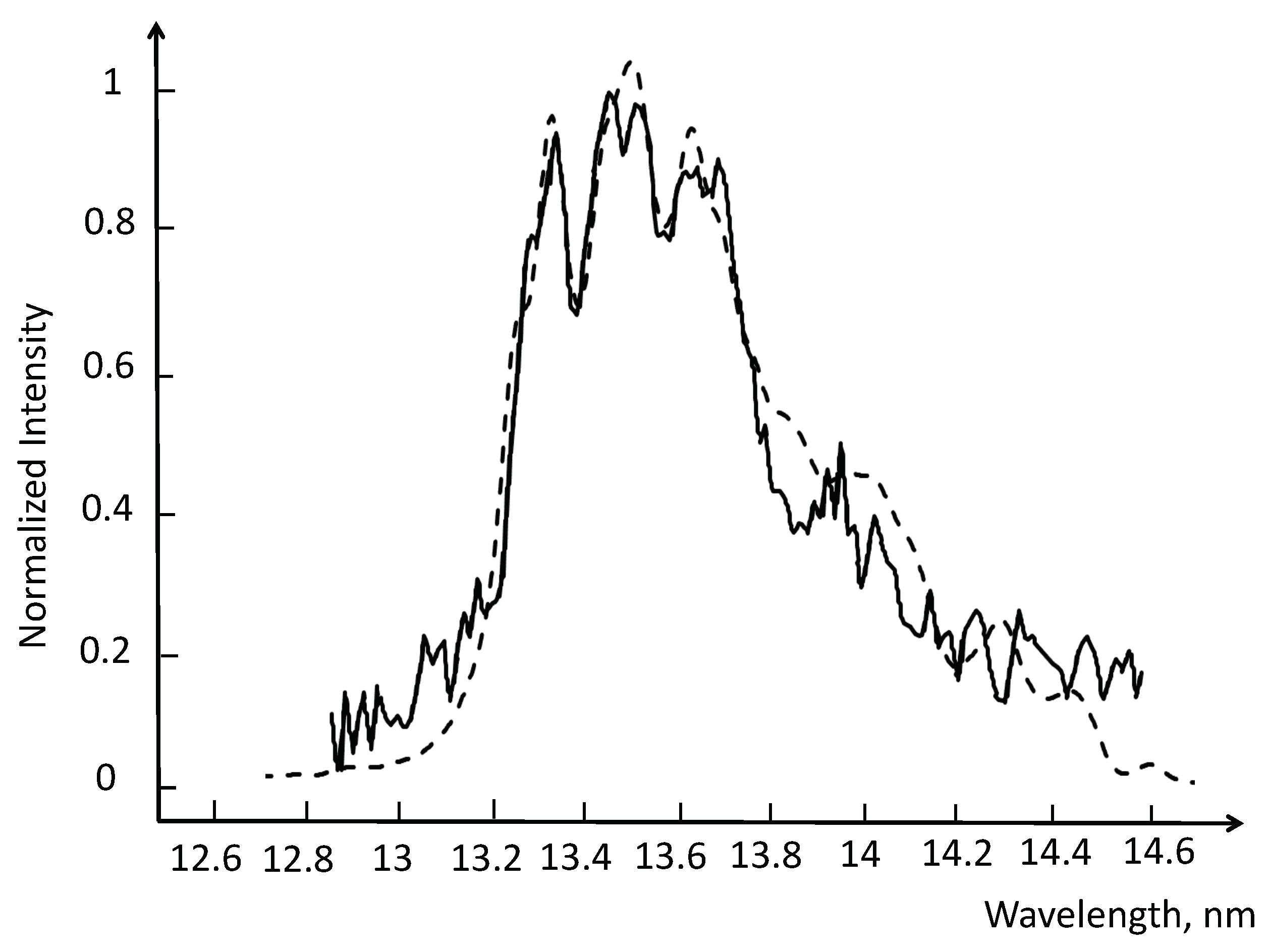
2.5. CI-MBPT Intensities
3. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Versolato, O. Physics of laser-driven tin plasma sources of EUV radiation for nanolithography. Plasma Sources Sci. Technol. 2019, 28, 083001. [Google Scholar] [CrossRef] [Green Version]
- O’Sullivan, G.; Li, B.; D’Arcy, R.; Dunne, P.; Hayden, P.; Kilbane, D.; McCormack, T.; Ohashi, H.; O’Reilly, F.; Sheridan, P.; et al. Spectroscopy of highly charged ions and its relevance to EUV and soft X-ray source development. J. Phys. B At. Mol. Opt. Phys. 2015, 48, 144025. [Google Scholar] [CrossRef]
- Colgan, J.; Kilcrease, D.; Abdallah, J.; Sherrill, M.; Fontes, C.; Hakel, P.; Armstrong, G. Atomic structure considerations for the low-temperature opacity of Sn. High Energy Density Phys. 2017, 23, 133. [Google Scholar] [CrossRef] [Green Version]
- Torretti, F.; Sheil, J.; Schupp, R.; Basko, M.M.; Bayraktar, M.; Meijer, R.A.; Witte, S.; Ubachs, W.; Hoekstra, R.; Versolato, O.O.; et al. Prominent radiative contributions from multiply-excited states in laser-produced tin plasma for nanolithography. Nat. Commun. 2020, 11, 2334. [Google Scholar] [CrossRef]
- Filin, D.; Colgan, J.; Savukov, I.M. Ab initio CI-MBPT Energy levels and Line Strengths of the Sn XIII-Sn XVI Ions. In Proceedings of the International Conference on Numerical Simulation of Plasmas (ICNSP), Santa Fe, NM, USA, 3–5 September 2019. [Google Scholar]
- D’Arcy, R.; Ohashi, H.; Suda, S.; Tanuma, H.; Fujioka, S.; Nishimura, H.; Nishihara, K.; Suzuki, C.; Kato, T.; Koike, F.; et al. Transitions and the effects of configuration interaction in the spectra of Sn XV–Sn XVIII. Phys. Rev. A 2009, 79, 042509. [Google Scholar] [CrossRef]
- Savukov, I.M. Relativistic configuration-interaction perturbation-theory method with application to intercombination and allowed transitions of light Be-like ions. Phys. Rev. A 2004, 70, 042502. [Google Scholar] [CrossRef]
- Savukov, I.M.; Johnson, W.R.; Berry, H.G. Mixed configuration-interaction and many-body perturbation-theory calculations of energies and oscillator strengths of J = 1 odd states of neon. Phys. Rev. A 2002, 66, 052501. [Google Scholar] [CrossRef] [Green Version]
- Savukov, I.M. Accurate calculations of energies and oscillator strengths for light neon-like ions. J. Phys. B At. Mol. Opt. Phys. 2003, 36, 4789–4797. [Google Scholar] [CrossRef]
- Dzuba, V.A. Calculation of the energy levels of Ge, Sn, Pb, and their ions in the VN-4 approximation. Phys. Rev. A 2005, 71, 062501. [Google Scholar] [CrossRef] [Green Version]
- Dzuba, V.A.; Flambaum, V.V.; Silvestrov, P.G.; Sushkov, O.P. Calculation of parity non-conservation in thallium. J. Phys. B 1987, 20, 3297. [Google Scholar] [CrossRef]
- Dzuba, V.A.; Flambaum, V.V.; Sushkov, O.P. Summation of the perturbation theory high order contributions to the correlation correction for the energy levels of the caesium atom. Phys. Lett. A 1989, 140, 493. [Google Scholar]
- Dzuba, V.A.; Flambaum, V.V.; Kozlov, M.G. Combination of the many-body perturbation theory with the configuration-interaction method. Phys. Rev. A 1996, 54, 3948–3959. [Google Scholar] [PubMed] [Green Version]
- Savukov, I. Configuration-interaction many-body-perturbation-theory energy levels of four-valent Si i. Phys. Rev. A 2015, 91, 022514. [Google Scholar] [CrossRef] [Green Version]
- Savukov, I.M. Configuration-interaction plus many-body-perturbation-theory calculations of Si i transition probabilities, oscillator strengths, and lifetimes. Phys. Rev. A 2016, 93, 022511. [Google Scholar] [CrossRef] [Green Version]
- Scheers, J.; Shah, C.; Ryabtsev, A.; Bekker, H.; Torretti, F.; Sheil, J.; Czapski, D.A.; Berengut, J.C.; Ubachs, W.; López-Urrutia, J.R.C.; et al. EUV spectroscopy of highly charged Sn13+-Sn15+ ions in an electron-beam ion trap. Phys. Rev. A 2020, 101, 062511. [Google Scholar] [CrossRef]
- Ryabtsev, A.N.; Kononov, É.Y.; Churilov, S.S. Spectra of rubidium-like Pd X-Sn XIV ions. Opt. Spectrosc. 2008, 105, 844–850. [Google Scholar] [CrossRef]
- Churilov, S.S.; Ryabtsev, A.N. Analysis of the spectra of In XII–XIV and Sn XIII–XV in the far-VUV region. Opt. Spectrosc. 2006, 101, 169–178. [Google Scholar] [CrossRef]
- Sugar, J.; Rowan, W.L.; Kaufman, V. Resonance lines 4p6–4p54d of the Kr i isoelectronic sequence. J. Opt. Soc. Am. B 1991, 8, 2026–2027. [Google Scholar] [CrossRef]
- Churilov, S.S.; Ryabtsev, A.N. Analysis of the 4p64d7-(4p64d64f + 4p54d8) transitions in the Sn VIII spectrum. Opt. Spectrosc. 2006, 660, 729. [Google Scholar]
- Churilov, S.S.; Ryabtsev, A.N. Analyses of the Sn IX–Sn XII spectra in the EUV region. Phys. Scr. 2006, 73, 614. [Google Scholar] [CrossRef]
| 1 | 4s4p | 12 | 4s4p4d4f | 23 | 4s4p4f | 34 | 4s4p4d5s |
| 2 | 4s4p5s | 13 | 4s4p4d5f | 24 | 4s4p4d | 35 | 4s4p4d5p |
| 3 | 4s4p6s | 14 | 4s4p4d5p | 25 | 4s4p4d5d | 36 | 4s4p4d5d |
| 4 | 4s4p4d | 15 | 4s4p4d6p | 26 | 4s4p5p4f | 37 | 4s4p4d5p4f |
| 5 | 4s4p5d | 16 | 4s4p5d5p | 27 | 4s4p5p6p | 38 | 4s4p4d4f |
| 6 | 4s4p6d | 17 | 4s4p5d6p | 28 | 4s4p4d5s | 39 | 4s4p4d5p |
| 7 | 4s4p4f | 18 | 4s4p5s5p | 29 | 4s4p5d5s | 40 | 4s4p4d5s4f |
| 8 | 4s4p5f | 19 | 4s4p5s6p | 30 | 4s4p4d6s | 41 | 4s4p4d5s5p |
| 9 | 4s4p6f | 20 | 4s4p6s5p | 31 | 4s4p4d5d | 42 | 4s4p4d4f |
| 10 | 4s4p5p | 21 | 4s4p5s4f | 32 | 4s4p4d | 43 | 4s4p4d |
| 11 | 4s4p6p | 22 | 4s4p5p | 33 | 4s4p4d4f | 44 | 4p4d |
| 1 | 4s4p4f | 13 | 4s4p4f | 25 | 4s4p5s4f | 37 | 4s4p4d4f |
| 2 | 4s4p5f | 14 | 4s4p5p | 26 | 4s4p5s5f | 38 | 4s4p4d |
| 3 | 4s4p5p | 15 | 4s 4p4d5s | 27 | 4s4p6s4f | 39 | 4s4p4d5d |
| 4 | 4s4p6p | 16 | 4s 4p4d5d | 28 | 4s4p6s5f | 40 | 4s4p4d5s |
| 5 | 4s4p4d | 17 | 4s 4p5p4f | 29 | 4s4p4d4f | 41 | 4s4p4d6s |
| 6 | 4s4p5s | 18 | 4p4d | 30 | 4s4p4d5f | 42 | 4s4p4d5p4f |
| 7 | 4s4p6s | 19 | 4s4p4d5p | 31 | 4s4p4d4f | 43 | 4s4p4d |
| 8 | 4s4p5d | 20 | 4s4p4d6p | 32 | 4s4p4d5f | 44 | 4s4p4d4f |
| 9 | 4s4p6d | 21 | 4s4p5d5p | 33 | 4s4p4d5p | 45 | 4s4p4d5s |
| 10 | 4s4p5s | 22 | 4s4p5d6p | 34 | 4s4p4d6p | 46 | 4s4p 4d5p |
| 11 | 4s4p6s | 23 | 4s4p5s5p | 35 | 4s4p4d5s4f | 47 | 4s4p4d5d |
| 12 | 4s4p4d | 24 | 4s4p5s6p | 36 | 4s4p4d5p |
| Lower State | CI-MBPT | Upper State | CI-MBPT | CI-MBPT | [6] | [6] | [6] | ||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| Config. | Config. | ||||||||||
| 0 | 0 | 0.979 | 1.000 | 1.87 | 4.3 | 13.23 | 13.25 | 13.29 | 5.8 | ||
| 1.215 | 1.333 | 1.123 | 1.25 | 4.64 | 10.6 | 13.29 | 13.35 | 14.65 | |||
| 1.250 | 1.250 | 1.192 | 1.200 | 7.21 | 16.45 | 13.31 | 13.34 | 13.34 | 21.22 | ||
| 1.250 | 1.250 | 1.199 | 1.250 | 2.47 | 5.61 | 13.38 | 13.46 | 11.16 | |||
| 0.950 | 1.000 | 1.051 | 1.083 | 3.6 | 8.18 | 13.39 | 13.44 | 7.54 | |||
| 1.112 | 1.000 | 1.076 | 1.000 | 5.68 | 12.86 | 13.4 | 13.49 | 16.54 | |||
| 1.197 | 1.167 | 1.069 | 1.083 | 2.14 | 4.85 | 13.41 | 13.42 | 13.46 | 5.5 | ||
| 1.090 | 1.083 | 1.075 | 1.050 | 4.15 | 9.39 | 13.42 | 13.54 | 15.43 | |||
| 1.417 | 1.500 | 1.085 | 1.167 | 1 | 2.26 | 13.44 | |||||
| 1.369 | 1.500 | 1.378 | 1.500 | 2.35 | 5.31 | 13.45 | 13.45 | 7.08 | |||
| 1.369 | 1.500 | 1.120 | 1.083 | 2.32 | 5.23 | 13.47 | 13.63 | 4.67 | |||
| 0.950 | 1.000 | 0.890 | 1.000 | 2.3 | 5.17 | 13.49 | 13.55 | 13.57 | 6.44 | ||
| 0.817 | 0.667 | 0.794 | 0.667 | 2.27 | 5.11 | 13.5 | 13.54 | 7.07 | |||
| 1.197 | 1.167 | 1.115 | 1.167 | 2.45 | 5.51 | 13.52 | 13.53 | 7.74 | |||
| 1.215 | 1.333 | 1.196 | 1.083 | 4 | 8.99 | 13.52 | 13.47 | 11.88 | |||
| 0.817 | 0.667 | 0.977 | 0.750 | 2.18 | 4.89 | 13.53 | 13.68 | 10.66 | |||
| 0.604 | 0.500 | 0.770 | 0.500 | 1.81 | 4.05 | 13.55 | 13.53 | 13.53 | 5.25 | ||
| 1.112 | 1.000 | 1.069 | 1.000 | 2.52 | 5.64 | 13.57 | 13.54 | 8.68 | |||
| 1.197 | 1.167 | 1.279 | 1.500 | 1.57 | 3.51 | 13.59 | 13.62 | 13.62 | 4.58 | ||
| 0.817 | 0.667 | 1.005 | 1.083 | 2.31 | 5.15 | 13.61 | |||||
| 1.215 | 1.333 | 1.090 | 1.250 | 1.18 | 2.63 | 13.62 | |||||
| 1.417 | 1.500 | 1.108 | 1.167 | 1.16 | 2.6 | 13.62 | |||||
| 0.979 | 1.000 | 0.996 | 1.000 | 6.03 | 13.43 | 13.63 | 13.66 | 13.65 | 18.14 | ||
| 1.25 | 1.333 | 1.170 | 1.250 | 1.85 | 4.11 | 13.65 | |||||
| 1.215 | 1.333 | 1.086 | 1.167 | 1.54 | 3.42 | 13.68 | 13.75 | 13.76 | 3.18 | ||
| 0.604 | 0.500 | 1.178 | 0.667 | 0.5 | 1.11 | 13.7 | 13.82 | 13.79 | 4 | ||
| 1.197 | 1.167 | 0.977 | 1.083 | 1.2 | 2.64 | 13.85 | |||||
| 1.197 | 1.167 | 1.005 | 1.083 | 0.91 | 1.99 | 13.94 | 14.05 | 14.03 | 5.44 | ||
| 1.112 | 1.083 | 1.005 | 1.083 | 1.02 | 2.19 | 14.11 | 14.2 | 14.17 | 3.71 | ||
| 0.817 | 1.000 | 1.030 | 1.000 | 1.34 | 2.87 | 14.22 | 14.27 | 14.26 | 3.45 | ||
| 1.112 | 1.000 | 1.005 | 1.000 | 1.21 | 2.58 | 14.32 | 14.39 | 14.36 | 4.98 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Filin, D.; Savukov, I.; Colgan, J. Relativistic Configuration-Interaction and Perturbation Theory Calculations of the Sn XV Emission Spectrum. Atoms 2021, 9, 96. https://doi.org/10.3390/atoms9040096
Filin D, Savukov I, Colgan J. Relativistic Configuration-Interaction and Perturbation Theory Calculations of the Sn XV Emission Spectrum. Atoms. 2021; 9(4):96. https://doi.org/10.3390/atoms9040096
Chicago/Turabian StyleFilin, Dmytro, Igor Savukov, and James Colgan. 2021. "Relativistic Configuration-Interaction and Perturbation Theory Calculations of the Sn XV Emission Spectrum" Atoms 9, no. 4: 96. https://doi.org/10.3390/atoms9040096
APA StyleFilin, D., Savukov, I., & Colgan, J. (2021). Relativistic Configuration-Interaction and Perturbation Theory Calculations of the Sn XV Emission Spectrum. Atoms, 9(4), 96. https://doi.org/10.3390/atoms9040096






