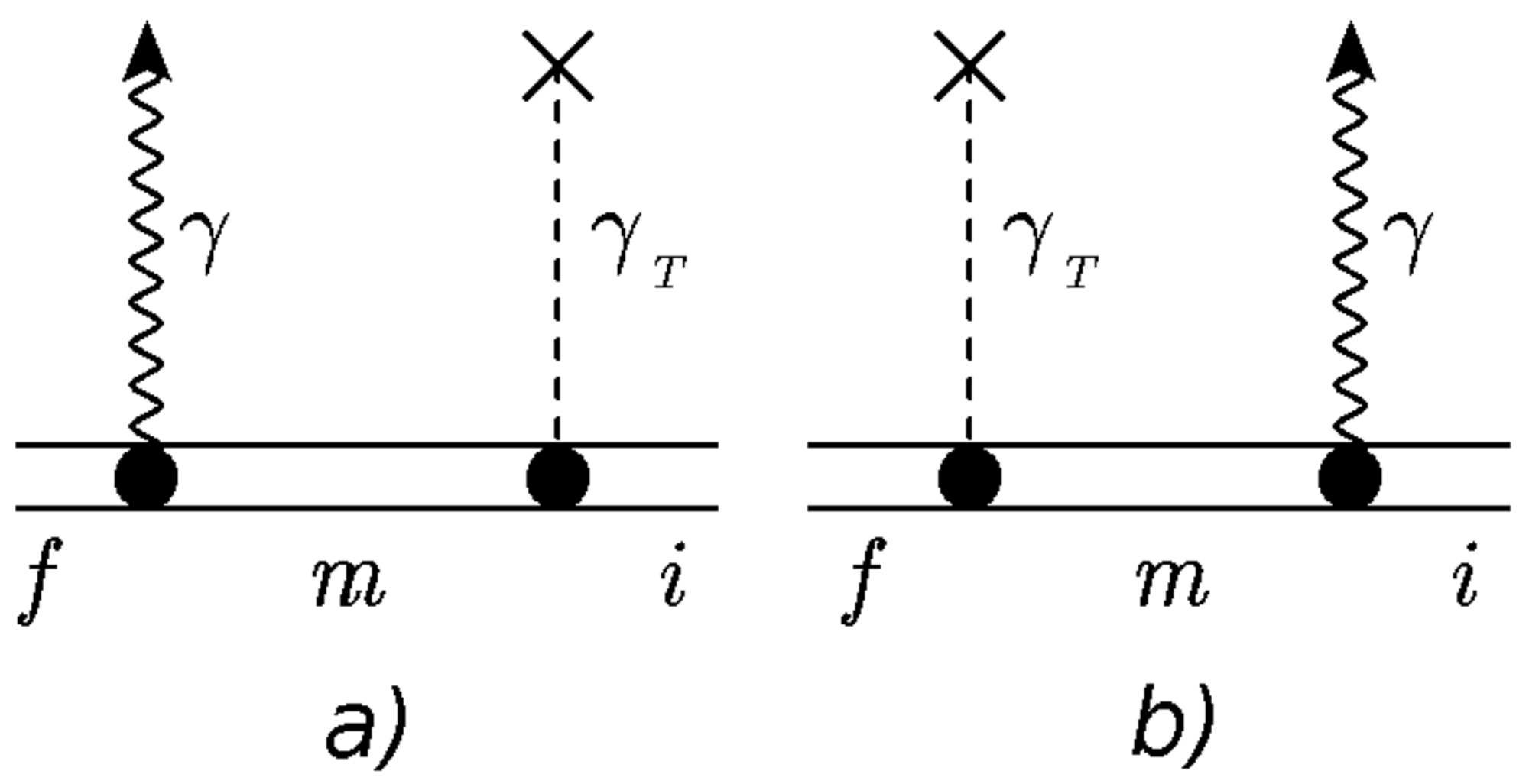Lowest-Order Thermal Correction to the Hydrogen Recombination Cross-Section in Presence of Blackbody Radiation

Abstract

In the present paper, the correction of the recombination and ionization processes of the hydrogen atom due to the thermal interaction of two charges was considered. The evaluation was based on a rigorous quantum electrodynamic (QED) approach within the framework of perturbation theory. The lowest-order radiative correction to the recombination/ionization cross-section was examined for a wide range of temperatures corresponding to laboratory and astrophysical conditions. The found thermal contribution was discussed both for specific states and for the total recombination and ionization coefficients.

1. Introduction

The electron recombination/ionization process has been widely discussed in the literature. Since the end of the 20th century, the study of this effect has found application in modern physics with the aim of a detailed description of laboratory experiments and the cosmological evolution of the early Universe. The theoretical prescription for electron recombination is precisely given within the framework of the quantum mechanical (QM) approach, which allows one to carry out the non-relativistic evaluation (based on the solution of the Schrödinger equation) for light atomic systems and easily extends to the relativistic case within the Dirac formalism. Recently, focusing on simple examples of the hydrogen atom, a rigorous derivation of the corresponding cross-section was obtained within the framework of quantum electrodynamics (QED) [1]. In particular, quantum mechanical results were obtained by considering a one-loop self-energy Feynman diagram. In addition, in [1], it was demonstrated that the QED approach accommodates a thorough description of the effects induced by the blackbody radiation and, by excellence, strictly take into account the finite lifetimes of atomic levels.

One of the advantages of the QED approach is its ability to consistently take into account the radiative corrections to the recombination and ionization processes. For example, the derivation of the corresponding radiative QED corrections in the framework of the two-time Green function method using the adiabatic S-matrix formalism can be found in [2]. Concentrating on the development of the thermal QED theory (TQED), in this paper, we describe the lowest-order radiative correction that occurs when evaluating the exchange of thermal photons between two charges [3]. A consistent calculation of thermal corrections to the emission probabilities in hydrogen and singly ionized helium atoms were presented in [4,5], and the correction due to thermal interaction was recently evaluated in [6], showing its importance for the study radiation processes.

Adopting the formalism developed in [1,6] for the vertex-type radiative thermal correction to a particular case of the radiative recombination process, we estimate the Feynman graphs shown in Figure 1.

The process of electron transition from the initial state of the continuous spectrum $i=\epsilon$ to the bound state with the emission of a photon is considered here for the hydrogen atom placed in a heat bath. Working in non-relativistic approximation, the wave function of the incident electron can be described as the series expansion over spherical waves [7,8,9,10,11]. The cross-section of the recombination process, ${\sigma }^{\mathrm{rec}}$, can be expressed via the ionization cross-section, ${\sigma }^{\mathrm{ion}}$, by the detailed balance relation (in relativistic units $\hslash =c=m=1$):

$$\begin{array}{c}\hfill {\sigma }_{nl}^{\mathrm{rec}}=2(2l+1){\sigma }_{nl}^{\mathrm{ion}}\frac{k^2}{p^2},\end{array}$$

(1)

where k is the momentum of the emitted photon, $p\equiv |\overrightarrow{p}|$ is the incident electron momentum and $nl$ is the principal quantum number and orbital momentum of the bound atomic state, respectively. The corresponding QED derivation of the cross-section for the radiative recombination process using the one-loop self-energy correction can be found in [1].

In the following section, we briefly present the mathematical derivations for the vertex thermal correction to the one-electron recombination process. Numerical calculations of this correction to the partial cross-sections and then to the total recombination and ionization coefficients are presented in Section 3. A discussion and conclusions of the obtained results are presented in the last section and can be found throughout the paper.

2. Thermal Vertex Correction to the Recombination Process

To obtain the lowest-order thermal correction to the recombination cross-section, it is convenient to use the adiabatic S-matrix formalism for reducible Feynman graphs (Figure 1), when each interaction vertex contains an additional exponential factor $\exp (-\eta |t\left|\right)$. The exponential pre-factor, however, is not necessarily needed at the top of the thermal interaction indicated by the cross in these diagrams. The S-matrix element corresponding to Figure 1a) is:

$$\begin{array}{c}\hfill S_{\eta }^{\left(3\right)}={(-\mathrm{i}e)}^{2}iZe\int d^4{x}_1{d}^4{x}_2{d}^4{x}_3{\overline{\psi }}_f\left(x_1\right){\gamma }^{\mu }{A}_{\mu }\left(x_1\right)\\ \hfill \times e^{-\eta |t_1|}S(x_1,x_2)e^{-\eta |t_2|}{\gamma }^{\nu }{D}_{\nu \lambda }^{\beta }(x_2,x_3)j^{\lambda }\left(x_3\right){\psi }_i\left(x_2\right),\end{array}$$

(2)

where integration is extended over space–time variables $x_i$ which denote the spatial position vector $\overrightarrow{r}$ and the time variable t. The Dirac matrices are denoted as ${\gamma }^{\mu }$, where $\mu$ takes the values $\mu =(0,1,2,3)$, ${\psi }_a\left(x\right)={\psi }_a\left(\overrightarrow{r}\right)e^{-\mathrm{i}{E}_{a}t}$ is the one-electron Dirac wave function, $\overline{{\psi }_a}$ is the Dirac conjugated wave function and $j^{\sigma }\left(x\right)$ is the four-dimensional nuclear current.

The standard electron propagator defined as the vacuum-expectation value of the time-ordered product of electron-positron field operators can be represented in terms of an eigenmode decomposition with respect to one-electron eigenstates [11,12]:

$$\begin{array}{c}\hfill S(x_1,x_2)=\frac{\mathrm{i}}{2\pi }\underset{-\infty }{\overset{\infty }{\int }}d\omega e^{-\mathrm{i}\omega (t_1-t_2)}\sum _n\frac{{\psi }_n\left({\overrightarrow{r}}_1\right){\overline{\psi }}_n\left({\overrightarrow{r}}_2\right)}{\omega -E_n(1-\mathrm{i}0)},\end{array}$$

(3)

where summation runs over the entire Dirac spectrum. The photon wave function, $A_{\mu }\left(x\right)$, is:

$$\begin{array}{c}\hfill A_{\mu }\left(x\right)=\sqrt{\frac{2\pi }{\omega }}{e}_{\mu }^{\left(\lambda \right)}{e}^{i{k}_{\mu }{x}^{\mu }}.\end{array}$$

(4)

Here, $e_{\mu }^{\left(\lambda \right)}$ are the components of the photon polarization four-vector, $x_{\mu }$ is the space–time four-vector, $k_{\mu }$ is the photon momentum four-vector with the space vector $\overrightarrow{k}$ and photon frequency $\omega =|\overrightarrow{k}|$. Using the transversality condition ${\gamma }_{\mu }{e}_{\mu }^{\left(\lambda \right)}=\overrightarrow{e}\overrightarrow{\alpha }$ ($\overrightarrow{e}$ is a transverse space vector of the photon polarization), the wave function for the emitted/absorbed real photon takes the form:

$$\begin{array}{c}\hfill \overrightarrow{A}\left(x\right)=\sqrt{\frac{2\pi }{\omega }}\overrightarrow{e}{e}^{i(\overrightarrow{k}\overrightarrow{r}-\omega t)}\equiv \sqrt{\frac{2\pi }{\omega }}{e}^{-i\omega t}\overrightarrow{A}(\overrightarrow{k},\overrightarrow{r}).\end{array}$$

(5)

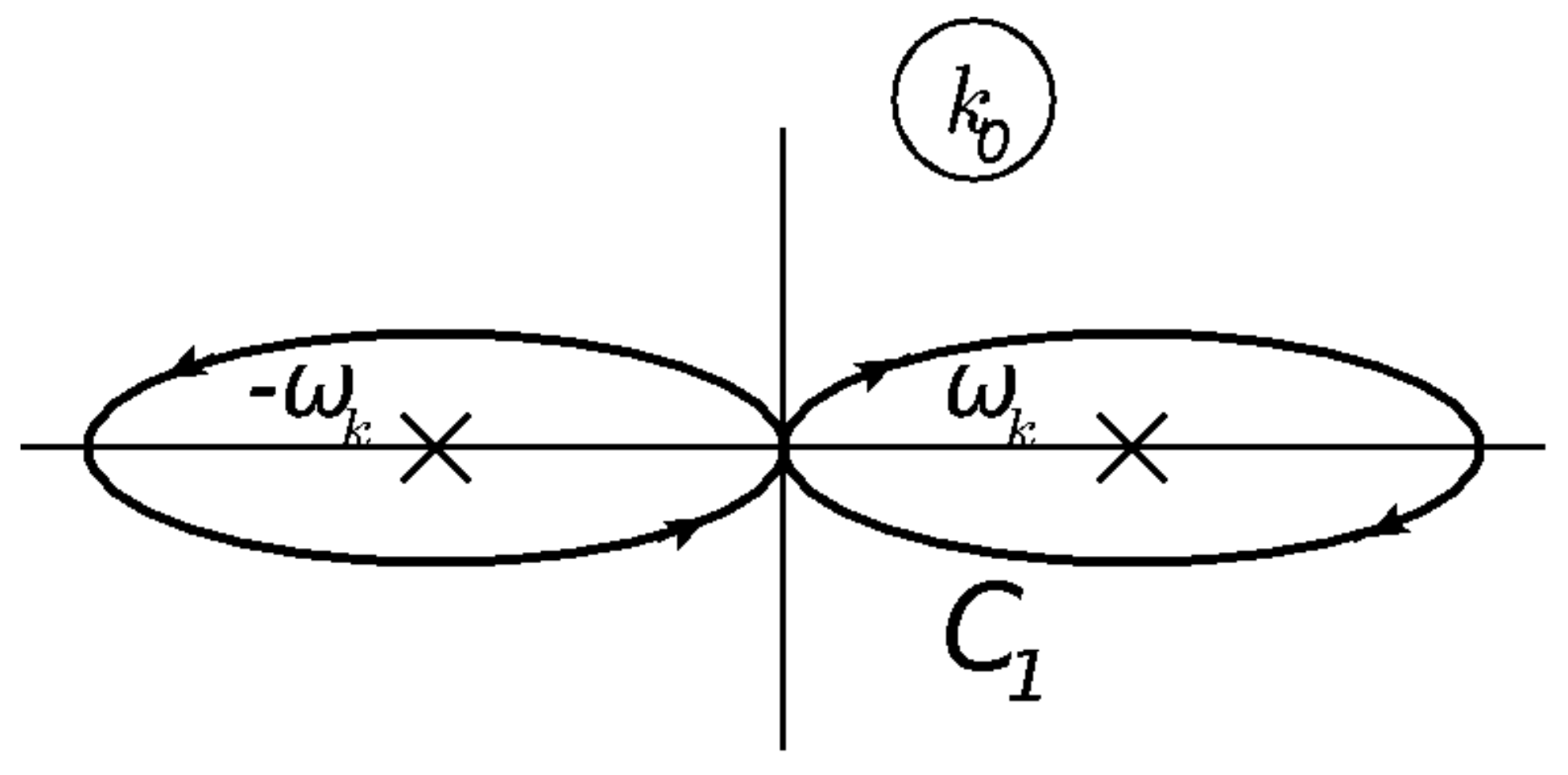
The thermal part of photon propagator was found in [3] in the form:

$$\begin{array}{c}\hfill D_{\lambda \sigma }^{\beta }\left(x_2{x}_3\right)=4\pi \underset{C_1}{\int }\frac{d^{4}k}{{\left(2\pi \right)}^4}\frac{e^{ik(x_2-x_3)}}{k^2}{n}_{\beta }\left(\right|\overrightarrow{k}\left|\right),\end{array}$$

(6)

where $k^2\equiv k_0^2-{\overrightarrow{k}}^2$, $n_{\beta }\left(\right|\overrightarrow{k}\left|\right)$ represents the Planck distribution function $\left(\exp \right(\beta |\overrightarrow{k}{\left|\right)-1)}^{-1}$, $\beta =1/\left(k_{B}T\right)$, $k_B$ is the Boltzmann constant and T is the temperature in Kelvin. The notation $C_1$ in Equation (5) denotes integration in the $k_0$ plane over the contour shown in Figure 2.

At first, one can integrate over the $d^4{x}_3$ variables in Equation (2) which leads to the four-dimensional Fourier transform of the nuclear current $j^{\sigma }\left(k\right)$. For the point-like nucleus within the static limit, it can be simplified to $j^{\sigma }\left(k\right)=j^0\left(k\right)=2\pi \delta \left(k_0\right)\rho \left(\overrightarrow{k}\right)=2\pi \delta \left(k_0\right)$. Then, the arising $\delta$-function leads to the doubled three-dimensional Fourier transform of the function $n_{\beta }\left(\right|\overrightarrow{k}\left|\right)/{\overrightarrow{k}}^2$. A rigorous derivation of the remaining integrals can be found in [3], which gives rise to the thermal Coulomb potential.

Then, the S-matrix element, Equation (2), can be found by

$$\begin{array}{c}\hfill S_{\eta }^{\left(3\right)}=-4\pi Z{e}^3\int d^4{x}_1{d}^4{x}_2{\overline{\psi }}_f\left(x_1\right){\gamma }^{\mu }{A}_{\mu }\left(x_1\right)e^{-\eta |t_1|}\\ \hfill \times S(x_1,x_2)e^{-\eta |t_2|}\int \frac{d^{3}k}{{\left(2\pi \right)}^3}\frac{e^{i\overrightarrow{k}{\overrightarrow{r}}_2}}{{\overrightarrow{k}}^2}{n}_{\beta }\left(\right|\overrightarrow{k}\left|\right){\psi }_i\left(x_2\right).\end{array}$$

(7)

It should be noted here that the same expression could be immediately written in the thermal Coulomb gauge and must be regularized at $|\overrightarrow{k}|\equiv \kappa \to 0$, as can be seen in [3,6]. In the interest of brevity, we subsequently omit the evaluation of the Feynman graphs in Figure 1 (as the corresponding calculations completely repeat the evaluation of bound–bound transition probability presented in [6]).

According to [6], the regularized thermal correction to the emission probability is reduced to:

$$\begin{array}{c}\hfill \mathsf{\Delta }{W}_{if}^{\mathrm{rad}}=\frac{4Z{e}^4\zeta \left(3\right)}{9{\pi }^2{\beta }^3}\langle i|\overrightarrow{\alpha }\overrightarrow{A}|f\rangle {\omega }_{if}d\overrightarrow{\nu }\times \\ \hfill \left[\underset{m}{{\sum }^{\prime }}\frac{\langle f|\overrightarrow{\alpha }{\overrightarrow{A}}^{*}|m\rangle \langle m|r^2|i\rangle }{E_i-E_m}+\underset{m}{{\sum }^{\prime }}\frac{\langle f|r^2|m\rangle \langle m|\overrightarrow{\alpha }{\overrightarrow{A}}^{*}|i\rangle }{E_f-E_m}\right.\\ \hfill \left.+\frac{1}{2}\frac{\langle f|\overrightarrow{\alpha }{\overrightarrow{A}}^{*}|i\rangle \langle i|r^2|i\rangle }{{\omega }_{if}}-\frac{1}{2}\frac{\langle f|r^2|f\rangle \langle f|\overrightarrow{\alpha }{\overrightarrow{A}}^{*}|i\rangle }{{\omega }_{if}}\right],\end{array}$$

(8)

where $\zeta \left(3\right)$ is the Riemann zeta function. The recombination cross-section $d\sigma$ is related to the transition probability by the relation $d\sigma =dW/j$, where $j=\upsilon$ is the particle flux density per unit volume ($\upsilon$ is the velocity of particles equal to the speed of light for photons).

One of the conclusions following from the result of Equation (8) is that matrix elements contain the scalar operator $r^2$ that preserves the parity of the state, i.e., the matrix element ${\left(r^2\right)}_{nm}$ is nonzero for states with the same orbital angular momentum due to the orthogonality property. Thus, further integration over the angles of the momentum $\overrightarrow{p}$ represented in the electron wave function for the continuum state can be performed in an ordinary manner using the orthogonality property for the Legendre polynomials, $P_l(cos\theta )$:

$$\begin{array}{c}\hfill \int d{\theta }_{\overrightarrow{p}}{P}_{l^{\prime }}(cos{\theta }_{\overrightarrow{p}\overrightarrow{r^{\prime }}})P_l(cos{\theta }_{\overrightarrow{p}\overrightarrow{r}})=\frac{4\pi }{2l+1}{P}_l(cos{\theta }_{\overrightarrow{r}\overrightarrow{r^{\prime }}}),\end{array}$$

(9)

and the recurrent formula:

$$\begin{array}{c}\hfill x{P}_l\left(x\right)=\frac{(l+1)}{(2l+1)}{P}_{l+1}\left(x\right)+\frac{l}{(2l+1)}{P}_{l-1}\left(x\right).\end{array}$$

(10)

The wave function for the state from the continuum with the energy $\epsilon =p^2/2$ can be written in the form:

$$\begin{array}{c}\hfill {\psi }_p=\frac{1}{2p}\sum _{l=0}^{\infty }{\mathrm{i}}^l(2l+1)e^{\mathrm{i}{\delta }_l}{R}_{pl}\left(r\right)P_l(cos{\theta }_{\overrightarrow{p}\overrightarrow{r}}),\end{array}$$

(11)

where $R_{pl}\left(r\right)$ is the radial part of the wave function and the phase factor ${\delta }_l$ can be omitted as immaterial for our purposes.

The result for the electric dipole photon emission is well known and leads to:

$$\begin{array}{c}\hfill \int d{\theta }_{\overrightarrow{p}}d{\theta }_{\overrightarrow{r}}d{\theta }_{\overrightarrow{r^{\prime }}}\langle \epsilon l^{\prime }|\overrightarrow{r}|nl\rangle \langle nl|\overrightarrow{r^{\prime }}|m{l}^{\prime }\rangle =\\ \hfill l\frac{{\left(4\pi \right)}^2}{2l+1}{I}_{pl-1;nl}{I}_{nl;ml-1}+(l+1)\frac{{\left(4\pi \right)}^2}{2l+1}{I}_{pl+1;nl}{I}_{nl;ml+1},\end{array}$$

(12)

which holds for $n=m$ and $l^{\prime }=l\mp 1$, respectively. Here:

$$\begin{array}{c}\hfill I_{p{l}^{\prime };nl}=\underset{0}{\overset{\infty }{\int }}dr{r}^3{R}_{nl}\left(r\right)R_{p{l}^{\prime }}\left(r\right),\end{array}$$

(13)

Analytical representation of the radial wave functions of discrete $R_{nl}\left(r\right)$ and the continuum $R_{p{l}^{\prime }}\left(r\right)$ states for the hydrogen atom can be found in textbooks [8,11]. Then, radial integrals of the type Equation (13) are usually calculated employing the Gordon formula, as can be seen, for example, in [13,14,15]. The expression (12) is written for the first term in Equation (8) and easily adapts to the second one.

Combining all the results, the final expression for recombination to an arbitrary bound $nl$ state can be written as

$$\begin{array}{c}\hfill \mathsf{\Delta }{\sigma }_{nl}=\frac{64Z{e}^4\zeta \left(3\right)}{9(2l+1){\beta }^3}{l}_{>}\left[-\frac{1}{2}{I}_{p{l}^{\prime };nl}{R}_{nl;nl}{I}_{nl;p{l}^{\prime }}+\right.\\ \hfill +\sum _{\genfrac{}{}{0pt}{}{m}{(m\ne \epsilon )}}\frac{E_n-E_m}{E_{\epsilon }-E_m}{I}_{p{l}^{\prime };nl}{I}_{nl;m{l}^{\prime }}{R}_{m{l}^{\prime };p{l}^{\prime }}+\\ \hfill \left.+\sum _{\genfrac{}{}{0pt}{}{m}{(m\ne n)}}\frac{E_m-E_{\epsilon }}{E_n-E_m}{I}_{p{l}^{\prime };nl}{I}_{ml;p{l}^{\prime }}{R}_{nl;ml}\right]{(E_{\epsilon }-E_n)}^2,\end{array}$$

(14)

where $l_{>}=\max (l,l^{\prime })$ and the expression (14) consists of two contributions with $l^{\prime }=l-1$ and $l^{\prime }=l+1$ according to (12). Pointing out that the third term in Equation (8) is a correction to the wave function of the continuum state, it can be excluded from consideration, as can be seen in [2]. Here, we introduce the notation:

$$\begin{array}{c}\hfill R_{nl;p{l}^{\prime }}=\underset{0}{\overset{\infty }{\int }}dr{r}^4{R}_{nl}\left(r\right)R_{p{l}^{\prime }}\left(r\right)=\\ \hfill \frac{2^{l+l^{\prime }+1}{p}^{l^{\prime }}{n}^{-l-2}}{{[(2l+1)!]}^2}\sqrt{\frac{(n+l)!}{(n-l-1)!}}{\left[\frac{8\pi p}{1-e^{-\frac{2\pi }{p}}}\right]}^{1/2}\\ \hfill \times \prod _{s=1}^{l^{\prime }}\sqrt{s^2+\frac{1}{p^2}}\underset{0}{\overset{\infty }{\int }}dr{r}^{4+l+l^{\prime }}{e}^{-\frac{r}{n}-ipr}\times \\ \hfill F\left(-n+l+1,2l+2,\frac{2r}{n}\right)F\left(\frac{i}{p}+l^{\prime }+1,2l^{\prime }+2,2ipr\right)\end{array}$$

(15)

The integral (15) (as well as (13) which leads to Gordon’s formula) can be analytically calculated using the derivative with respect to the parameter before r in the exponent, and the multiplicity of the derivative is determined by reducing it to a tabular integral:

$$\begin{array}{c}\hfill \underset{0}{\overset{\infty }{\int }}dt{t}^{c-1}{e}^{-st}{}_1{F}_1\left(a;c;t\right){}_1{F}_1\left(\alpha ;c;\lambda t\right)=\\ \hfill \frac{(c-1)!}{{(s-1)}^a{(s-\lambda )}^{\alpha }}{s}^{a+\alpha -c}{}_2{F}_1\left(a,\alpha ;c;\frac{\lambda }{(s-1)(s-\lambda )}\right).\end{array}$$

(16)

Here, ${}_1{F}_1$ is the confluent hypergeometric functions of the first kind and ${}_2{F}_1$ is Gauss’s hypergeometric functions. The first contribution in Equation (14) is also given by $R_{nl;nl}=\frac{n^2}{2}(5n^2+1-3l(l+1))$.

The analytical result for $R_{nl;nl}$ shows impetuous growth with an increase of n, which makes us conclude the significance of the correction of Equation (14) for highly excited states. Nonetheless, as pointed out in [6], the approximation $r\ll 1$ is valid for low-lying states and may be violated for Rydberg states. The legitimacy of using such an approximation is dictated by the series expansion of the potential found in [3] in the vicinity $\frac{r}{\beta }\ll 1$. In [6], it was found (see Table IV there) that the calculations of the full form for the thermal potential and approximated by the $r^2$ contribution deviate starting from $n=20$ at 300 K and $n=10$ at 3000 K. However, we now found that the $r/\beta$ thermal potential argument was incorrectly parameterized (the $\alpha$ was omitted). Numerical values corresponding to the correction of the lowest order [6] were recalculated with the correct scaling and are listed in

Table 1. Numerical values of energy shifts $\mathsf{\Delta }{E}_A^{\beta }=\langle A|V^{\beta }\left(r\right)|A\rangle$ for different atomic states A at temperatures $T=300$ K (upper line) and $T=3000$ K (lower line) in a hydrogen atom. The first column shows the considered state $(n_A,l_A)$. In the second column, the energy shift is calculated with the approximate potential $V^{\beta }\left(r\right)$ given by Equations (38) and (52) in [6]. In the third column, the energy shift is calculated with the potential $V^{\beta }\left(r\right)$ given by Equation (51) in [6]. All values are in Hz.

$({\mathit{n}}_{\mathit{A}},{\mathit{l}}_{\mathit{A}})$	$\mathsf{\Delta }{\mathit{E}}_{{\mathit{n}}_{\mathit{A}}{\mathit{l}}_{\mathit{A}}}^{\mathit{\beta }}$, Equation (38)	$\mathsf{\Delta }{\mathit{E}}_{{\mathit{n}}_{\mathit{A}}{\mathit{l}}_{\mathit{A}}}^{\mathit{\beta }}$, Equation (51)
(1,0)	$-3.36$	$-3.36$
	$-3.36\times {10}^3$	$-3.36\times {10}^3$
(2,0)	$-46.98$	$-46.98$
	$-4.698\times {10}^4$	$-4.698\times {10}^4$
(10,0)	$-2.80\times {10}^4$	$-2.80\times {10}^4$
	$-2.80\times {10}^7$	$-2.80\times {10}^7$
(10,9)	$-1.29\times {10}^4$	$-1.29\times {10}^4$
	$-1.29\times {10}^7$	$-1.29\times {10}^7$
(20,0)	$-4.48\times {10}^5$	$-4.48\times {10}^5$
	$-4.48\times {10}^8$	$-4.47\times {10}^8$
(20,19)	$-1.93\times {10}^5$	$-1.93\times {10}^5$
	$-1.93\times {10}^8$	$-1.93\times {10}^8$
(100,0)	$-2.80\times {10}^8$	$-2.78\times {10}^8$
	$-2.80\times {10}^{11}$	$-2.78\times {10}^{11}$
(100,99)	$-1.14\times {10}^8$	$-1.13\times {10}^8$
	$-1.14\times {10}^{11}$	$-9.171\times {10}^{10}$
(200,0)	$-4.47\times {10}^9$	$-4\times {10}^9$
	$-4.47\times {10}^{12}$	$-3.72\times {10}^{11}$
(200,99)	$-1.80\times {10}^9$	$-1.73\times {10}^9$
	$-1.80\times {10}^{12}$	$-5.06\times {10}^{11}$

.

As a result, it turns out that there is no deviation up to $n\approx 100$ at such temperatures. The numerical values of the thermal corrections to the transition rates taking into account thermal shifts listed in Table 1 are given in

Table 2. Recalculated transition rates and thermal corrections at $T=300$ K to one-photon electric dipole transitions between highly excited states due to the thermal energy shift, see Equations (53) and (54) in [6] for details. All values are given in s${}^{-1}$.

${\mathit{n}}_{\mathit{i}},{\mathit{l}}_{\mathit{i}}$	${\mathit{n}}_{\mathit{f}},{\mathit{l}}_{\mathit{f}}$	${\mathit{W}}_{\mathbf{if}}$	$\mathsf{\Delta }{\mathit{W}}_{\mathbf{if}}^{\mathbf{ind}}$	$\mathsf{\Delta }{\mathit{W}}_{\mathbf{if}}^{\mathbf{v}}$	$\mathsf{\Delta }{\mathit{W}}_{\mathbf{if}}^{\mathbf{v},\mathbf{ind}}$
$(10,9)$	$(9,8)$	$1.320\times {10}^4$	$5.419\times {10}^3$	$2.213\times {10}^{-5}$	$2.811\times {10}^{-6}$
$(50,1)$	$(49,0)$	$2.682$	$3.077\times {10}^2$	$1.998\times {10}^{-4}$	$1.524\times {10}^{-2}$
$(50,49)$	$(49,48)$	$7.137\times {10}^{-1}$	$81.861$	$2.190\times {10}^{-5}$	$1.671\times {10}^{-3}$
$(70,1)$	$(69,0)$	$4.840\times {10}^{-1}$	$1.541\times {10}^2$	$2.759\times {10}^{-4}$	$5.852\times {10}^{-2}$
$(70,69)$	$(69,68)$	$9.369\times {10}^{-2}$	$29.830$	$2.186\times {10}^{-5}$	$4.636\times {10}^{-3}$
$(100,1)$	$(99,0)$	$7.953\times {10}^{-2}$	$74.387$	$3.858\times {10}^{-4}$	$2.407\times {10}^{-1}$
$(100,99)$	$(99,98)$	$1.093\times {10}^{-2}$	$10.221$	$2.175\times {10}^{-5}$	$1.356\times {10}^{-2}$

and can be directly compared with the results presented in Table V from ref. [6].

3. Recombination and Ionization Coefficients

The thermal correction to the effective cross-sections evaluated in the previous section allows one to define the corresponding correction to the recombination and ionization coefficients [10]. The rate of recombination to the n-th level due to the spontaneous recombination processes, ${\alpha }_{nl}$, is given by

$$\begin{array}{c}\hfill {\alpha }_{nl}=\underset{0}{\overset{\infty }{\int }}{\sigma }_{nl}^{\mathrm{rec}}f\left(v\right)vdv,\end{array}$$

(17)

where ${\sigma }_{nl}^{\mathrm{rec}}$ represents the spontaneous recombination cross-section, $f\left(v\right)$ is the Maxwell–Boltzmann distribution function with the velocity of incident electrons v ($v=p$ in our units):

$$\begin{array}{c}\hfill f\left(v\right)dv=4\pi {\left(\frac{1}{2\pi k_{B}T}\right)}^{3/2}{v}^2{e}^{-\frac{v^2}{2k_B{T}_e}}dv.\end{array}$$

(18)

The presence of the Maxwell–Boltzmann distribution function in the recombination coefficient restricts the magnitude of the incident electron momentum p. The typical speed can be estimated as $p^2\sim 2k_{B}T\ll 1$ up to $T\sim {10}^5$ K, which justifies the used non-relativistic approximation.

The similar expression can be written for the stimulated recombination coefficient:

$$\begin{array}{c}\hfill {\alpha }_{nl}^{\beta }=\underset{0}{\overset{\infty }{\int }}{\sigma }_{nl}^{\mathrm{rec},\beta }f\left(v\right)vdv,\end{array}$$

(19)

and the total recombination coefficient is:

$$\begin{array}{c}\hfill {\alpha }^{\mathrm{total}}\equiv {\alpha }_A=\sum _{nl}{\alpha }_{nl},\end{array}$$

(20)

where index A corresponds to the so-called case A when the coefficient ${\alpha }^{\mathrm{total}}$ includes the direct recombination process to the ground state, while case B in astrophysical studies excludes this process.

Recently, the influence of finite lifetimes on the stimulated transition rates in hydrogen and helium atoms was studied in [16,17,18], while this effect for bound-free transitions is described in detail in [1]. In the latter case, the numerical calculations become much more complicated when summing over $nl$ for the recombination/ionization coefficients due to the presence of the Lorentz factor. The effect of finite lifetimes itself in the recombination process reaches the level of few percent of the ‘ordinary’ stimulated transitions, leveling out at high temperatures and large values of $nl$. Although the corresponding widths of atomic levels can be taken into account here, we will leave it and focus on numerical calculations of the corresponding well-known spontaneous and stimulated rates. The latter can be expressed, as can be seen in [9,10], as

$$\begin{array}{c}\hfill {\sigma }_{nl}^{\mathrm{rec},\beta }={\sigma }_{nl}^{\mathrm{rec}}{n}_{\beta }(\epsilon +E_{nl}),\end{array}$$

(21)

where $E_{nl}$ is the ionization potential of the $nl$ state.

The corrections to the partial spontaneous and stimulated recombination coefficients ($\mathsf{\Delta }{\alpha }_{nl}$ and $\mathsf{\Delta }{\alpha }_{nl}^{\beta }$, respectively), partial ionization coefficient ($\mathsf{\Delta }{\beta }_{nl}$), that we are interested in can also be calculated using Equations (1), (17), (19)–(21). The corresponding numerical results for the $1s$ and $2s$ states in the hydrogen atom are given in

Table 3. Thermal corrections to the partial recombination and ionization coefficients for spontaneous and stimulated processes for the $1s$ and $2s$ states at different temperatures. The coefficients ${\alpha }_{nl}$ are calculated using Equation (14), the first, second and third contributions are denoted as $\mathsf{\Delta }{\alpha }_{1s}^{\left(1\right)}$, $\mathsf{\Delta }{\alpha }_{1s}^{\left(2\right)}$, $\mathsf{\Delta }{\alpha }_{1s}^{\left(3\right)}$, respectively. Values with index $\beta$ denote corresponding stimulated recombination corrections. Summation over m in Equation (14) was performed in the range $m\in [1,100]$, which guarantees the given numbers in the table. The correction to the partial ionization coefficient $\mathsf{\Delta }{\beta }_{nl}$ is given as a total contribution and coincides with the sum of $\mathsf{\Delta }{\alpha }_{nl}^{\left(1\right)}$, $\mathsf{\Delta }{\alpha }_{nl}^{\left(2\right)}$, $\mathsf{\Delta }{\alpha }_{nl}^{\left(3\right)}$, $\mathsf{\Delta }{\alpha }_{nl}^{\beta ,\left(1\right)}$, $\mathsf{\Delta }{\alpha }_{and}^{\beta ,\left(2\right)}$ and $\mathsf{\Delta }{\alpha }_{and}^{\beta ,\left(3\right)}$, as it should be according to the detailed balance. All values are given in ${\mathrm{m}}^3{\mathrm{s}}^{-1}$.

	T = 300 K	T = 1000 K	T = 3000 K	T = 5000 K	T = 10,000 K	T = 20,000 K
${\alpha }_{1s}$	$9.4939\times {10}^{-19}$	$5.1848\times {10}^{-19}$	$2.9688\times {10}^{-19}$	$2.2812\times {10}^{-19}$	$1.5819\times {10}^{-19}$	$1.0787\times {10}^{-19}$
${\alpha }_{1s}^{\beta }$	$0.0$	$6.9968\times {10}^{-88}$	$2.0781\times {10}^{-42}$	$2.2263\times {10}^{-33}$	$1.1211\times {10}^{-26}$	$2.0858\times {10}^{-23}$
$\mathsf{\Delta }{\alpha }_{1s}^{\left(1\right)}$	$-3.3362\times {10}^{-29}$	$-6.6434\times {10}^{-28}$	$-1.0148\times {10}^{-26}$	$-3.5689\times {10}^{-26}$	$-1.9282\times {10}^{-25}$	$-1.0049\times {10}^{-24}$
$\mathsf{\Delta }{\alpha }_{1s}^{\beta ,\left(1\right)}$	$0.0$	$-8.9930\times {10}^{-97}$	$-7.1673\times {10}^{-50}$	$-3.5334\times {10}^{-40}$	$-1.4032\times {10}^{-32}$	$-2.0339\times {10}^{-28}$
$\mathsf{\Delta }{\alpha }_{1s}^{\left(2\right)}$	$-1.4502\times {10}^{-24}$	$-1.0971\times {10}^{-23}$	$-6.3683\times {10}^{-23}$	$-1.4172\times {10}^{-22}$	$-4.1445\times {10}^{-22}$	$-1.1997\times {10}^{-21}$
$\mathsf{\Delta }{\alpha }_{1s}^{\beta ,\left(2\right)}$	$0.0$	$-2.6489\times {10}^{-92}$	$-8.3235\times {10}^{-46}$	$-2.6099\times {10}^{-36}$	$-5.5717\times {10}^{-29}$	$-4.3721\times {10}^{-25}$
$\mathsf{\Delta }{\alpha }_{1s}^{\left(3\right)}$	$-3.3162\times {10}^{-29}$	$-6.4671\times {10}^{-28}$	$-9.4444\times {10}^{-27}$	$-3.2380\times {10}^{-26}$	$-1.6872\times {10}^{-25}$	$-8.5139\times {10}^{-25}$
$\mathsf{\Delta }{\alpha }_{1s}^{\beta ,\left(3\right)}$	$0.0$	$-8.9365\times {10}^{-97}$	$-6.8742\times {10}^{-50}$	$-3.3163\times {10}^{-40}$	$-1.2731\times {10}^{-32}$	$-1.7797\times {10}^{-28}$
$\mathsf{\Delta }{\beta }_{1s}$	$-1.4503\times {10}^{-24}$	$-1.0972\times {10}^{-23}$	$-6.3702\times {10}^{-23}$	$-1.4178\times {10}^{-22}$	$-4.1479\times {10}^{-22}$	$-1.2019\times {10}^{-21}$
${\alpha }_{2s}$	$1.3919\times {10}^{-19}$	$7.6117\times {10}^{-20}$	$4.3716\times {10}^{-20}$	$3.3664\times {10}^{-20}$	$2.3419\times {10}^{-20}$	$1.5998\times {10}^{-20}$
${\alpha }_{2s}^{\beta }$	$5.02703\times {10}^{-77}$	$2.7449\times {10}^{-37}$	$4.2385\times {10}^{-26}$	$6.3229\times {10}^{-24}$	$2.3283\times {10}^{-22}$	$1.2711\times {10}^{-21}$
$\mathsf{\Delta }{\alpha }_{2s}^{\left(1\right)}$	$-1.9237\times {10}^{-29}$	$-3.8311\times {10}^{-28}$	$-5.6857\times {10}^{-27}$	$-1.9496\times {10}^{-26}$	$-1.0001\times {10}^{-25}$	$-4.8333\times {10}^{-25}$
$\mathsf{\Delta }{\alpha }_{2s}^{\beta ,\left(1\right)}$	$-6.9737\times {10}^{-87}$	$-1.3982\times {10}^{-45}$	$-5.6939\times {10}^{-33}$	$-3.8470\times {10}^{-30}$	$-1.0792\times {10}^{-27}$	$-4.3657\times {10}^{-26}$
$\mathsf{\Delta }{\alpha }_{2s}^{\left(2\right)}$	$-1.8429\times {10}^{-26}$	$-1.3955\times {10}^{-24}$	$-8.1121\times {10}^{-24}$	$-1.8065\times {10}^{-23}$	$-5.2879\times {10}^{-23}$	$-1.5317\times {10}^{-22}$
$\mathsf{\Delta }{\alpha }_{2s}^{\beta ,\left(2\right)}$	$-1.0928\times {10}^{-82}$	$-9.0071\times {10}^{-42}$	$-1.4704\times {10}^{-29}$	$-6.4156\times {10}^{-27}$	$-1.0055\times {10}^{-24}$	$-2.4067\times {10}^{-23}$
$\mathsf{\Delta }{\alpha }_{2s}^{\left(3\right)}$	$-2.6134\times {10}^{-28}$	$-5.0962\times {10}^{-27}$	$-7.4361\times {10}^{-26}$	$-2.5487\times {10}^{-25}$	$-1.3296\times {10}^{-24}$	$-6.7418\times {10}^{-24}$
$\mathsf{\Delta }{\alpha }_{2s}^{\beta ,\left(3\right)}$	$-3.5101\times {10}^{-52}$	$-1.8839\times {10}^{-44}$	$-7.5179\times {10}^{-32}$	$-5.0406\times {10}^{-29}$	$-1.4108\times {10}^{-26}$	$-5.7965\times {10}^{-25}$
$\mathsf{\Delta }{\beta }_{2s}$	$-1.8458\times {10}^{-25}$	$-1.4010\times {10}^{-24}$	$-8.1921\times {10}^{-24}$	$-1.8346\times {10}^{-23}$	$-5.5330\times {10}^{-23}$	$-1.8508\times {10}^{-22}$

separately for each of the three summands in Equation (14). It should be noted here that the calculations are well converged upon the summation over the intermediate spectrum m, which were carried out by the direct summation of each individual state $ml<\epsilon$ to $m=100$. The values listed in Table 3 are guaranteed to be within five digits.

The numerical results in Table 3 show mostly insignificant contributions to the partial coefficients ${\alpha }_{1s\left(2s\right)}$, ${\alpha }_{1s\left(2s\right)}^{\beta }$ and ${\beta }_{1s\left(2s\right)}$. However, according to the discussion at the end of the previous section and the definition in Equation (20), summation over $nl$ leads to an increase in the heat correction for the total coefficients ${\alpha }_A$, ${\alpha }_A^{\beta }$ and ${\beta }_A$ to such an extent that the summation result does not converge. Situations in which the same pattern occurs were discussed in [19,20]. A stocktaking of the effects limiting the divergent partition sum $\sum _{nl}(2l+1)n_{nl}^{\left(\mathrm{Boltzmann}\right)}$ is described in detail in [19]. The simplified model in our case is as follows. The probability $w_n$ that the state n is not destroyed by the mixing thermal interaction corresponding to the matrix element ${\left(r^2\right)}_{ab}$ between two arbitrary states a and b should be inserted into the sum over $nl$ states in Equation (20). Then, according to Equation (8), we compare the thermal correction $\mathsf{\Delta }{E}_{nl}^{\beta }\sim {\beta }^{-3}{n}^2(5n^2+1-3l(l+1))$, as can be seen in [3], with the Lamb shift scaled $\mathsf{\Delta }{E}_L\sim 1.24214\times {10}^{-6}{n}^{-3}$ for the $ns(l=0)$ state in atomic units [12]. We solved equation $\mathsf{\Delta }{E}_L=\mathsf{\Delta }{E}_{ns}^{\beta }$ for a specified temperature, which gives the same results if the partition function $\exp (-\left(\mathsf{\Delta }{E}_{ns}^{\beta }\right)/\mathsf{\Delta }{E}_L)$ equaled to $e^{-1}$. The result can be written as

$$\begin{array}{ccc}\hfill n^{*}& =& \frac{1.14026}{{\left(k_{B}T\right)}^{\frac{3}{7}}},\hfill \\ \hfill w_n& =& e^{-{\left(\frac{n}{n^{*}}\right)}^7}\approx e^{-0.399{\left(k_{B}T\right)}^3{n}^7}\hfill \end{array}$$

(22)

in atomic units.

Still, one should take into account the thermal energy shift for the energy levels of the atom in the unperturbed cross-section. This can be done by modifying the unperturbed cross-section by replacing $E_a\to E_a+\mathsf{\Delta }{E}_a^{\beta }$. Then, it can be found that the third and fourth contributions in Equation (8) (or the first one in Equation (14)) are canceled out by this replacement, and contributions proportional to the cube and the square of $\mathsf{\Delta }{E}_a^{\beta }$ remain. However, these corrections are of the next order in $\alpha$, so we omit their further calculations.

Below are the results of numerical calculations of the total ionization and recombination coefficients and thermal corrections to them. The case B can be easily obtained by the subtraction of corresponding values of ${\alpha }_{1s}$ from ${\alpha }_A$, as can be seen in Table 3. Numerical values of the total coefficients ${\alpha }_A$, ${\alpha }_A^{\beta }$, $\mathsf{\Delta }{\alpha }_A$, ${\beta }_A$ and $\mathsf{\Delta }{\beta }_A$ are collected in

Table 4. The corrections to the total recombination and ionization coefficients for spontaneous and stimulated processes for case A at different temperatures. All values are given in ${\mathrm{m}}^3{\mathrm{s}}^{-1}$.

	T = 300 K	T = 700 K	T = 1000 K	T = 3000 K	T = 5000 K	T = 10,000 K	T = 20,000 K
${\alpha }_A$	$4.32385\times {10}^{-18}$	$2.52126\times {10}^{-18}$	$2.00071\times {10}^{-18}$	$9.63800\times {10}^{-19}$	$6.78908\times {10}^{-19}$	$4.16397\times {10}^{-19}$	$2.50652\times {10}^{-19}$
${\alpha }_A^{\beta }$	$2.15163\times {10}^{-18}$	$1.72895\times {10}^{-18}$	$1.56064\times {10}^{-18}$	$1.10529\times {10}^{-18}$	$9.29960\times {10}^{-19}$	$7.28372\times {10}^{-19}$	$5.65045\times {10}^{-19}$
$\mathsf{\Delta }{\alpha }_A$	$-2.29004\times {10}^{-20}$	$-1.41894\times {10}^{-20}$	$-1.16107\times {10}^{-20}$	$-6.26605\times {10}^{-21}$	$-5.04184\times {10}^{-21}$	$-2.74662\times {10}^{-21}$	$-2.64351\times {10}^{-21}$
$\mathsf{\Delta }{\alpha }_A^{\beta }$	$2.56355\times {10}^{-21}$	$1.50305\times {10}^{-21}$	$1.16062\times {10}^{-21}$	$4.99707\times {10}^{-22}$	$8.75126\times {10}^{-23}$	$2.46134\times {10}^{-22}$	$-6.53582\times {10}^{-23}$
${\beta }_A$	$6.47549\times {10}^{-18}$	$4.25021\times {10}^{-18}$	$3.56135\times {10}^{-18}$	$2.06909\times {10}^{-18}$	$1.60887\times {10}^{-18}$	$1.14477\times {10}^{-18}$	$8.15697\times {10}^{-19}$
$\mathsf{\Delta }{\beta }_A$	$-2.03369\times {10}^{-20}$	$-1.26864\times {10}^{-20}$	$-1.04501\times {10}^{-20}$	$-5.76635\times {10}^{-21}$	$-4.95433\times {10}^{-21}$	$-2.50048\times {10}^{-21}$	$-2.70887\times {10}^{-21}$

for different temperatures. The values are obtained by the direct summation of partial coefficients with the partition function Equation (22) up to $n,m=100$.

4. Discussion and Conclusions

The numerical results obtained in this work for the thermal correction Equation (14) for specific $1s$ and $2s$ states are given in Table 3. One can find an increasing value of the correction with elevating temperature. In particular, considering the recombination process at room temperature 300 K, the thermal contribution is $-1.4503\times {10}^{-24}$, whereas the spontaneous recombination coefficient for the $1s$ state is approximately ${10}^{-18}$. This relation is valid for the $2s$ state, which leads to the conclusion that for a ratio of approximately ${10}^{-6}$, this correction is rather insignificant in laboratory experiments. The opposite case corresponds to higher temperatures. For example, at 20,000 K, the thermal correction to the recombination cross-section reaches a level of $1.1\%$ with respect to the spontaneous one and is two orders of magnitude larger than the stimulated recombination coefficient ${\alpha }_{1s}^{\beta }$. The relative value of the order of $1.1\%$ with respect to spontaneous recombination into the $2s$ state is retained, but the thermal correction is an order of magnitude less than the stimulated coefficient. Thus, one can expect a significant contribution of the thermal correction to the total (summed over all $nl$ states) recombination coefficient. Moreover, directly following from the discussion presented above, as can also be seen in [3], the increasing value of the correction with the principal quantum number n sets the need for such a calculation.

Performing a direct summation over $nl$ of the thermal correction Equation (14) results in a diverging contribution. To ’streamline’ this, we followed the procedure described in [19,20], where physical conditions are discussed in detail. According to [19], the probability $w_n$ that the state n is not destroyed by the mixing thermal interaction should be introduced, limiting the divergent partition sum. The numerical results of the summation with the probability $w_n$, as in Equation (22), are listed in Table 4.

In particular, as follows from Table 4, the thermal correction to the total recombination coefficient is approximately $0.3\%$ at any temperature. This value can be compared with the achieved accuracy of astrophysical experiments aimed at studying the recombination of the early Universe. Then, considering the thermal effect giving by Equation (14) in the astrophysical context of the recombination of the early universe, the fitting formula for the total recombination coefficient (the same as in [21]) is:

$$\begin{array}{c}\hfill {\alpha }_B^S={10}^{-19}\frac{a{t}^b}{1+c{t}^d}{\mathrm{m}}^3{\mathrm{s}}^{-1},\end{array}$$

(23)

can be found with the parameters $a=4.4648$, $b=-0.6092$, $c=0.7470$ and $d=0.5049$ ($t=T_M/{10}^4$ K) instead of $a=4.309$, $b=-0.6166$, $c=0.6703$, and $d=0.5300$ known from [22,23]. We used the data from Table 4 to find the estimate in the modification of the ionization fraction. As in [1], a change in the coefficients a, b, c and d can lead to a $0.2\%$ contribution to the ionization fraction of the primordial plasma, repeating the effect of the finite lifetimes of atomic states (the contribution decreases with increasing temperature and is more significant for low temperatures). However, such a seemingly insignificant contribution is of interest for further planned experimental data and is highlighted by the constantly produced new data with unprecedented precision [24].