Abstract
The quest for stabilizing planar forms of tetracoordinate carbon started five decades ago and intends to achieve interconversion between [R]- and [S]-stereoisomers without breaking covalent bonds. Several strategies are successful in making the planar tetracoordinate form a minimum on its potential energy surface. However, the first examples of systems where stereomutation is possible were reported only recently. In this study, the possibility of neutral and dications of simple hydrocarbons (cyclopentane, cyclopentene, spiropentane, and spiropentadiene) and their counterparts with the central carbon atom replaced by elements from groups 13, 14, and 15 are explored using ab initio MP2 calculations. The energy difference between the tetrahedral and planar forms decreases from row II to row III or IV substituents. Additionally, aromaticity involving the delocalization of the lone pair on the central atom appears to help in further stabilizing the planar form compared to the tetrahedral form, especially for the row II substituents. We identified 11 systems where the tetrahedral state is a minimum on the potential energy surface, and the planar form is a transition state corresponding to stereomutation. Interestingly, the planar structures of three systems were found to be minimum, and the corresponding tetrahedral states were transition states. The energy profiles corresponding to such transitions involving both planar and tetrahedral states without the breaking of covalent bonds were examined. The systems showcased in this study and research in this direction are expected to realize molecules that experimentally exhibit stereomutation.
1. Introduction
The paradigm of the tetrahedral structure of tetracoordinated carbon centers (ttC) is powerful and uncontested [,]. However, designing molecules with unusual planar tetracoordinated carbon centers (ptC) has been an interesting area of research for about five decades. The availability of a lone pair of electrons on the central planar tetracoordinate carbon and electron deficient 3 centered-2 electron (3c-2e) bonds makes the system unstable. Hence, different approaches to stabilize the ptC have been used, and several molecules containing ptC have been reported [].
The utilization of -donor and -acceptor substituents helps in the stabilization of ptC by accepting the unfavorable electron density on the hybridized C-atom and providing electron density to the electron deficient 3c-2e bonds, respectively [,]. The removal of the lone pair of electrons leading to the formation of a dicationic species also has been shown as a viable technique to stabilize the ptC center. Moreover, the implementation of small rings to the tetracoordinated C center—hence, making the system sterically rigid—has been a promising strategy for the stabilization of ptC [,,].
Utilizing these concepts, the first ever stable ptC’s were reported by Schleyer and coworkers in 1976. They identified the di-lithium substituted ptC’s of cyclopropane and cyclopropene analogues to be minima on the potential energy surface (PES) []. Following this, in 1977, Cotton and Miller synthesized the first compound with a ptC center []. Since then, a large number of stable planar tetracoordinated centers (ptX’s) in general have been identified both experimentally [,,,,,,,,,,,,,] and theoretically [,,,,,,,,,,,,,,,,,,,,,] by exploiting the electronic and steric factors as explained earlier.
Multiple efforts towards stabilizing the planar state, so that it can act as a transition state for the stereomutation process, have been futile. Monkhorst showed that the streomutation barrier (interconversion between stereoisomers without bond breaking) via a planar state is much higher as compared to the energy required for C–C bond breaking [], which signifies the difficulty of the problem. Since then, scientists have attempted to attain a thermally accessible ptC for stereomutation. However, less results have been achieved as, for systems with stable ptC, the ttC was found to be a higher order saddle point or vice-versa.
Recently, Raghunathan et. al reported the first possible stereomutation via a thermally accessible ptX []. They used high level ab initio calculations, Born–Oppenheimer molecular dynamics studies using DFT, and classical dynamics to study the thermodynamic and kinetic factors corresponding to stereomutation. Moreover, they identified systems where both tetrahedral and planar forms are minima on their potential energy surface, and located a transition state that connects these two forms. The whole process happens without the breaking of any covalent bonds involving the central tetracoordinate atom.
In this paper, we endeavor to stabilize possible ptX’s by exploiting the electronic and steric factors. A set of four model systems (CH, CH, CH, and CH) were considered in this study. The model systems CH and CH were previously studied by Schleyer and co-workers []. The central C-atom was substituted by possible valence isoelectronic elements from group 13, 14, and 15 in order to isolate stable ptX’s (Figure 1). We used ab initio MP2 calculations to carefully design and showcase possible stereomutations in multiple systems.
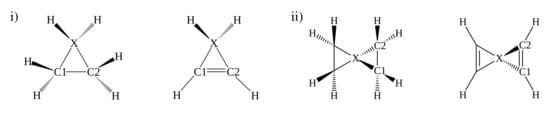
Figure 1.
Two different types of tetracoordinated molecular systems (i) and (ii) considered in the present study (X = B, C, N, Al, Si, P, Ga, Ge, and As).
2. Methods
Two classes of systems were considered in the present study to investigate the stability of a planar tetracoordinated system (ptX): (i) three-membered cyclic- and (ii) spiro[2,2]-type analogues (Figure 1). The tetrahedral-tetracoordinated and the planar-tetracoordinated geometries (ttX and ptX) for the various systems were optimized at the MP2/cc-pVTZ level of theory [,]. The stationary points on the potential energy surface (PES) were characterized using frequency calculations at the same level. The transition states associated with the stereomutation process were connected to the respective minimum energy structures using the intrinsic reaction coordinate (IRC) analysis.
Higher-order saddle points were characterized as nth-order saddle points based on the number of imaginary frequencies obtained in the normal mode analysis. To examine the possible role of aromaticity in stabilizing planar states, the nuclear independent chemical shift (NICS) [] values were calculated for ptC systems at the MP2/cc-pVTZ level of theory. A ghost atom was placed at the geometric center of the rings to calculate the isotropic magnetic shielding.
A negative NICS value indicates that the system is aromatic while a positive value is obtained for antiaromatic systems. NICS values have been shown to provide insights on the extent of aromatic stabilization in different classes of molecules. All the calculations were performed using the Gaussian16 software package []. The relative energies of the stationary points with respect to the tetrahedral structures, the number of imaginary frequencies (), and important geometrical parameters for all the molecular systems investigated are given in Table 1, which are discussed in detail in the following sections. The relative energies of the stationary points with zero point energy correction are given in the Supplementary Materials.

Table 1.
Relative energies ( in kcal/mol), number of imaginary frequencies (), geometric parameters (C-X bond lengths in Å) of the neutral and dicationic species of cyclopropene, spiropentadiene, cyclopropane, and spiropentane along with the skeletally substituted derivatives calculated at the MP2/cc-pVTZ level of theory. The relative energies reported here do not include zero-point energies.
3. Results and Discussion
3.1. Stabilization of ptC
The cyclopropene molecule, [CH], in its tetrahedral form, is undoubtedly a minimum on the PES. However, the corresponding planar structure is a third-order saddle point and is ∼117 kcal/mol higher is energy as compared to the ttC (Table 1). In Table 1, a positive relative energy value of the planar form indicates destabilization compared to the tetrahedral form, and a negative value indicates that the planar form is more stable as compared to its tetrahedral counterpart. Previous studies attempted to stabilize this by using different strategies.
Just by removing two electrons (the lone pair on the central carbon), the ptC for the dicationic species [CH] was found to be a minimum on the PES []. This phenomenon is understandable from the change in the electronic structure of the system. The molecular orbitals of the ttC and ptC structure of CH are shown in Figure 2. On going from ttC to ptC, one of the bond MOs is converted to a lone pair orbital, and this leaves only six electrons for four covalent bonds making the system unstable.
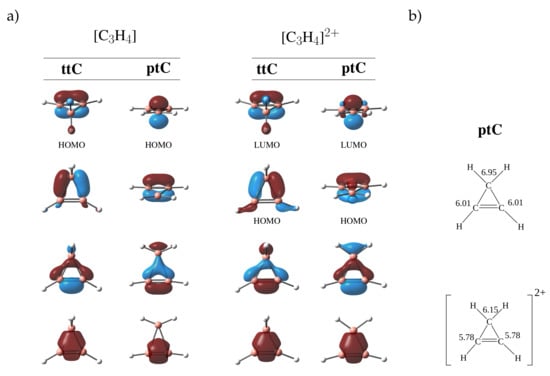
Figure 2.
(a) Molecular orbitals (MO) of ttC and ptC geometries for CH and [CH] molecules calculated at HF/cc-pVTZ level of theory. (b) Atomic electron populations obtained from natural population analysis at the HF/cc-pVTZ level of theory.
As explained in the introduction, one can expect the presence of acceptor ligands or the removal of the lone pair of electrons to stabilize the ptC compounds []. Thus, in the dicationic species [CH], the electronic charge on the central carbon is expected to reduce and, hence, stabilize the system. The molecular orbitals of the [CH] (Figure 2) clearly show the reduction in the natural electronic charge on the central carbon by delocalization.
The saturated analogue cyclopropane, CH also shows a similar trend. The ttC is a minimum, whereas the ptC is a second-order saddle point on the PES with an energy of ∼111 kcal/mol (Table 1). The planar form of the dicationic counterpart of cyclopropane could not be optimized at the current level of theory, whereas the ttC is a second order saddle point on the PES.
Introducing mechanical strain by the formation of a cage-like structures around the central carbon have been shown to be effective in the stabilization of ptC [,,,]. To this end, spiropentadiene CH and its saturated analogue were then considered in the present study. The ptC geometry of the spiropentadiene was found to be a fourth-order saddle point on the PES as compared to the ttC minima. However, the energy difference between the planar and tetrahedral form was now reduced to ∼92.7 kcal/mol as compared to ∼117.4 kcal/mol in the case of cyclopropene (Table 1).
However, in the dicationic species of spiropentadiene, the ptC was found to be a minimum on the PES while the tetrahedral structure a higher order saddle point. The ptC was stabilized by ∼20 kcal/mol as compared to the ttC spiropentadiene. Similar to cyclopropane, the saturated ttC spiropentane was found to be a minimum whereas the ptC, which was a higher order saddle point. However, the removal of two electrons from spiropentane i.e., [CH] led to the stabilization of the ptC, which is a minimum on the PES (Table 1).
A comparison of the unsaturated and the saturated systems investigated above reveals that the stabilization of the ptC in the dications is due to the reduction of the electronic charge on the central carbon facilitated by electron delocalization in the rings. Moreover, the cyclopropene and spiropentadiene dications are cyclic conjugated systems with 4n + 2 electrons with and can be considered aromatic. From Figure 2, the possible aromatic stabilization of the dicationic species is reflected in the nature of the HOMO orbital. This resembles very closely the HOMO of the classic cyclopropyl cation system.
A similar effect is also observed in the planar form of the dicationic spiropentene molecule. Such an aromatic stabilization is deemed to be responsible for the extra stabilization of the planar as compared to the tetrahedral state upon removal of two electrons from cyclopentene. This is further examined by using NICS calculations. The computed NICS values at the geometric centers of the rings change from 11.28 for the ptC CH to −41.76 for ptC [CH] clearly indicating the aromatic nature of the systems. The negative NICS value pointing to the aromatic nature of planar tetracoordinated systems have also been reported in literature [,,]. In the case of ptC [CH] system, the NICS value was found to be −45.96. The planar form of a neutral cyclopropene system leads to elongated CC bonds (∼1.83 Å) possibly due to anti-aromatic destabilization. Further investigations have concentrated on the effect of skeletal substitutions by atoms/ions isoelectronic to carbon to examine how this modulates the difference between the planar and tetrahedral forms, and to identify possible molecular models that exhibit stereomutation.
3.2. Heteroatom Substitution for the Stabilization of ptX
To identify stable model ptC systems, the central C-atoms of the saturated and unsaturated analogues of cyclopropane and spiropentane were substituted with different valence isoelectronic (four valence electrons) heteroatoms from Group 13, 14, and 15 (X = B, Al, Ga, C, Si, Ge, N, P, and As) (Figure 1). For example, the model cyclopropane systems can be expressed as [XCH] (X = B, Al, and Ga), [XCH] (X = C, Si, and Ge), and [XCH] (X = N, P, and As).
As seen above in the saturated and unsaturated analogues of cyclopropane and spiropentane molecules, here, as well the ttX geometries were found to be minima on the PES. However, the ptX geometries were either a transition state or a higher order saddle point. It was observed that on going down the group, the relative energies of the ptXs, () decreased (B→ Al, C → Si, N→ P) and then increased (Al→ Ga, Si → Ge, P→ As) following a trend similar to their electronegativities.
The X–C bond length decreases when moving along a period and increases down the group (e.g., >> and <<), consistent with the change in the atomic radii, and the bond lengths indicate that the skeletal substitutions do not destabilize the three membered rings. The Wiberg bond index (WBI) [] was also calculated for the different skeletally substituted systems (see Supplementary Materials). The WBI for most of the system indicates the presence of a stable X–C bond. However, in some systems, the bond index was found to be very low.
As noted above, the stabilization of the ptX can be achieved by reducing the electronic charge on the central atom (X). To this end, the electronic structure of the saturated and unsaturated analogues of cyclopropane and spiropentane derivatives with two valence electrons on the central atom were investigated. The ptX [XCH] (X belongs to group 13 and 14, i.e., B, Al, Ga, Si, and Ge) structures were found to a minima on the PES and their corresponding ttX were higher order saddle points. For X= B and Ga, the ttX structures could not be stabilized.
In contrast, the ptXs in [XCH] (X = N, P, and As) were transition states with eigen vectors (for the imaginary frequency) corresponding to the X–C bond stretches that will lead to ring opening, which is not interesting in the context of this study. In the saturated analogues [XCH] (X = B, Al, and Ga) the ptXs were minima on the PES, whereas the ttXs were transition states corresponding to stereomutation. However, in the group 14 and 15 analogues, both the ttX and ptX structures were unstable.
In the hetero-atom centered [XCH] spiro compounds, the ttXs were either transition states or higher order saddle points except for [GaCH] for which the ttX stationary point structure could not be obtained. For the group 13 compounds, the ptXs structures of [XCH for X = B and Ga were the minima, while, for X = Al, it was a transition state. In the other [XCH] (X = hetero-atom) spiro compounds, the ptXs structures were transition states (TSs) or higher order saddle points.
In the complementary saturated spiropentane-type [XCH] systems, the ttXs were high energy saddle points, except for X = B and N where the ttX structures could not be optimized. In addition, the ptX geometries were also found to be transition states or higher order saddle points on the PES. This indicates the possibility of multiple systems where the tetrahedral state is a minimum and it can rotate around the central atom to go to an equivalent tetrahedral form via a planar transition state. Similarly, there are systems where the planar form is a minimum, and it can be converted to an identical planar form via the corresponding tetrahedral transition state. These aspects are addressed in the following section.
3.3. Stereomutation in Model Systems
To investigate possible stereomutation in the above systems, molecules where the ptX is a transition state connecting two isoenergic ttX minima or vice versa were considered. The IRC calculations were done to follow the normal mode corresponding to the transition state on either sides to connect to the respective minima.
The angle between the planes () formed by the two three-membered rings were followed to account for the stereomutation event as it changes from 90° to 0° going from ttX to ptX. The potential energy profile for the stereomutation in XCH systems via ptX TSs is given in Figure 3a. The barriers for stereomutation were found to be 29.0, 49.5, 59.6, 75.2, and 80.6 kcal/mol for X = Al, Si, Ge, P, and As, respectively. The stereomutation barrier increases on moving along a period and on going down the group.
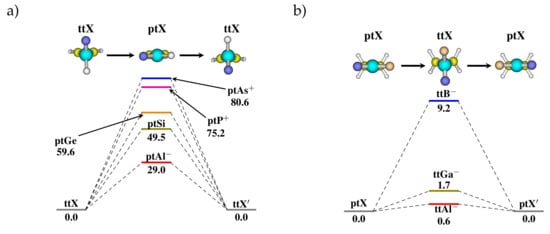
Figure 3.
Potential energy profile for possible stereomutation pathway in (a) cyclopropene ([XCH) and (b) cyclopropane derivatives ([XCH) calculated at MP2/cc-pVTZ level of theory. The hybridized C-atom is substituted by different valence isoelectronic heteroatoms of group 13, 14, and 15 of the periodic table to stabilize the ptX geometry. The energies are reported in kcal/mol.
In the saturated [XCH] systems where X = group 13 elements, (i.e., B, Al, and Ga) the ttXs are the TSs that connect the minima ptXs, and thus the stereomutation here is ptX→ttX→ ptX. The stereomutation barrier for X = Al and Ga is lower than X = B. In addition, the spiropentene analogues were found to show similar features. The ptX were found to be a transition state whereas the ttX were minima on the PES. Moreover, the stereomutation barrier increases on moving down the group and along the period (Figure 4). In contrast, the saturated spiropentane i.e., ptX [XCH] were found to be higher order saddle points except for X = Al where the ptX is a transition state leading to stereomutation.
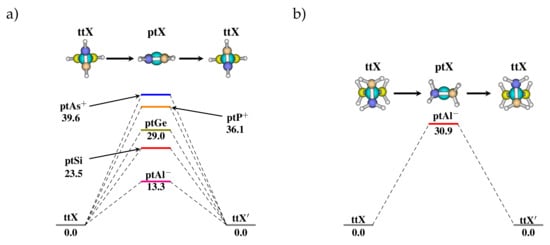
Figure 4.
PES for possible stereomutation pathway in (a) spiropentadiene ([XCH) and (b) spiropentane derivatives ([XCH) calculated at MP2/cc-pVTZ level of theory. The central hybridized C-atom is substituted by different valence isoelectronic heteroatoms of group 13, 14, and 15 of the periodic table to stabilize the ptX geometry. Energies are given in kcal/mol.
4. Conclusions
Five decades of research have resulted in significant progress in understanding the factors that stabilize the planar form of tetracoordinated centers, and some have been experimentally realized. The original objective of work in this area was to achieve stereomutation where the interconversion between [R]- and [S]-isomers of tetracoordinate tetrahedral centers via a planar state could be observed. Most of the molecular models proposed until recently effectively stabilize the planar state compared to the tetrahedral state. However, in these models, the tetrahedral state is destabilized or is a higher order saddle point precluding the possibility of stereomutation.
In the present study, we explored the possibility of stereomutation in simple systems containing a central tetracoordinate center isoelectronic to carbon. We demonstrated that the combination of introducing a three-membered ring, enabling aromatic stabilization, and heteroatom substitution is a viable strategy to modulate the energy difference between the planar and tetrahedral states of tetracoordinate systems. Aromaticity, assessed by molecular orbitals and NICS calculations, appears to stabilize the dicationic planar forms in the parent hydrocarbons. Introducing skeletal substitutions to the central carbon by isoelectronic species from rows III and IV of the periodic table effectively stabilizes the planar state. However, the effect of aromaticity is not crucial in this case.
We successfully demonstrated the identification of systems where stereomutation about a stereocenter is possible via a planar transition state without any bond dissociation. We hope that further work in this direction by improving the model systems and incorporating asymmetry in the central atom will result in the experimental realization of elusive systems.
Supplementary Materials
The following are available online at https://www.mdpi.com/article/10.3390/atoms9040079/s1. Figure S1: Representative structures for the calculation of bond indexes, Table S1: Relative energies in kcal/mol including the zero point energies for various systems studied, Table S2: Wiberg Bond index (WBI) for cyclopropene derivatives, Table S3: WBI for cyclopropane derivatives, Table S4: WBI for spiropentene derivatives (X having four valence electrons), Table S5: WBI for spiropentene derivatives (X having two valence electrons), Table S6: WBI for spiropentane derivatives (X having four valence electrons), Table S7: WBI for spiropentane derivatives (X having two valence electrons).
Author Contributions
Conceptualization, U.D.P. and U.L.; methodology, K.Y., U.D.P. and U.L.; investigation, K.Y.; writing—original draft preparation, K.Y.; writing—review and editing, U.D.P. and U.L.; supervision, U.D.P. and U.L.; All authors have read and agreed to the published version of the manuscript.
Funding
The authors would like to thank NISER Bhubaneswar for computational facilities.
Data Availability Statement
Data available in article or Supplementary Materials.
Conflicts of Interest
The authors declare no conflict of interest.
Abbreviations
The following abbreviations are used in this manuscript:
| ttC | tetrahedral tetracoordinated carbon |
| ptC | planar tetracoordinated carbon |
| ttX | tetrahedral tetracoordinated system with X as the substituent |
| ptX | planar tetracoordinated system with X as the substituent |
| PES | potential energy surface |
| IRC | intrinsic reaction coordinate |
| NICS | nuclear independent chemical shift |
| TS | transition state |
References
- Le Bel, J.A. Sur les relations qui existent entre les formules atomiques des corps organiques et le pouvoir rotatoire de leurs dissolutions. Bull. Soc. Chim. Fr 1874, 22, 337–347. [Google Scholar]
- Van’t Hoff, J. A suggestion looking to the extension into space of the structural formulas at present used in chemistry, and a note upon the relation between the optical activity and the chemical constitution of organic compounds. Arch. Neerl. Sci. Exact. Nat. 1874, 9, 445. [Google Scholar]
- Hoffmann, R.; Alder, R.W.; Wilcox, C.F., Jr. Planar tetracoordinate carbon. J. Am. Chem. Soc. 1970, 92, 4992–4993. [Google Scholar] [CrossRef]
- Krogh-Jespersen, M.B.; Chandrasekhar, J.; Wuerthwein, E.U.; Collins, J.B.; Von Rague Schleyer, P. Molecular orbital study of tetrahedral, planar, and pyramidal structures of the isoelectronic series BH, CH4, NH, AlH, SiH4, and PH. J. Am. Chem. Soc. 1980, 102, 2263–2268. [Google Scholar] [CrossRef]
- Von Ragué Schleyer, P.; Boldyrev, A.I. A new, general strategy for achieving planar tetracoordinate geometries for carbon and other second row periodic elements. J. Chem. Soc. Chem. Commun. 1991, 1536–1538. [Google Scholar] [CrossRef]
- Li, Y.; Liao, Y.; Chen, Z. Be2C Monolayer with Quasi-Planar Hexacoordinate Carbons: A Global Minimum Structure. Angew. Chem. Int. Ed. 2014, 53, 7248–7252. [Google Scholar] [CrossRef] [PubMed]
- Yañez, O.; Vásquez-Espinal, A.; Báez-Grez, R.; Rabanal-León, W.A.; Osorio, E.; Ruiz, L.; Tiznado, W. Carbon rings decorated with group 14 elements: New aromatic clusters containing planar tetracoordinate carbon. New J. Chem. 2019, 43, 6781–6785. [Google Scholar] [CrossRef]
- Collins, J.B.; Dill, J.D.; Jemmis, E.D.; Apeloig, Y.; Schleyer, P.v.R.; Seeger, R.; Pople, J.A. Stabilization of planar tetracoordinate carbon. J. Am. Chem. Soc. 1976, 98, 5419–5427. [Google Scholar] [CrossRef]
- Cotton, F.A.; Millar, M. The probable existence of a triple bond between two vanadium atoms. J. Am. Chem. Soc. 1977, 99, 7886–7891. [Google Scholar] [CrossRef]
- Erker, G. Planar-Tetracoordinate Carbon: Making Stable Anti-van’t Hoff/LeBel Compounds. Comment Inorg. Chem. 1992, 13, 111–131. [Google Scholar] [CrossRef]
- Xu, J.; Zhang, X.; Yu, S.; Ding, Y.H.; Bowen, K.H. Identifying the Hydrogenated Planar Tetracoordinate Carbon: A Combined Experimental and Theoretical Study of CAl4H and CAl4H−. J. Phys. Chem. Lett. 2017, 8, 2263–2267. [Google Scholar] [CrossRef] [Green Version]
- Ebner, F.; Greb, L. Calix[4]pyrrole Hydridosilicate: The Elusive Planar Tetracoordinate Silicon Imparts Striking Stability to Its Anionic Silicon Hydride. J. Am. Chem. Soc. 2018, 140, 17409–17412. [Google Scholar] [CrossRef]
- Li, X.; Zhang, H.F.; Wang, L.S.; Geske, G.; Boldyrev, A. Pentaatomic Tetracoordinate Planar Carbon, [CAl4]2−: A New Structural Unit and Its Salt Complexes. Angew. Chem. Int. Ed. 2000, 39, 3630–3632. [Google Scholar] [CrossRef]
- Röttger, D.; Erker, G. Compounds Containing Planar-Tetracoordinate Carbon. Angew. Chem. Int. Ed. 1997, 36, 812–827. [Google Scholar] [CrossRef]
- Li, X.; Wang, L.S.; Boldyrev, A.I.; Simons, J. Tetracoordinated Planar Carbon in the Al4C− Anion. A Combined Photoelectron Spectroscopy and ab Initio Study. J. Am. Chem. Soc. 1999, 121, 6033–6038. [Google Scholar] [CrossRef]
- Ghana, P.; Rump, J.; Schnakenburg, G.; Arz, M.I.; Filippou, A.C. Planar Tetracoordinated Silicon (ptSi): Room-Temperature Stable Compounds Containing Anti-van’t Hoff/Le Bel Silicon. J. Am. Chem. Soc. 2020, 143, 420–432. [Google Scholar] [CrossRef]
- Driess, M.; Aust, J.; Merz, K.; van Wüllen, C. van’t Hoff–Le Bel Stranger: Formation of a Phosphonium Cation with a Planar Tetracoordinate Phosphorus Atom. Angew. Chem. Int. Ed. 1999, 38, 3677–3680. [Google Scholar] [CrossRef]
- Li, S.D.; Ren, G.M.; Miao, C.Q.; Jin, Z.H. M4H4X: Hydrometals (M = Cu, Ni) Containing Tetracoordinate Planar Nonmetals (X=B, C, N, O). Angew. Chem. Int. Ed. 2004, 43, 1371–1373. [Google Scholar] [CrossRef] [PubMed]
- Li, Y.; Li, F.; Zhou, Z.; Chen, Z. SiC2 Silagraphene and Its One-Dimensional Derivatives: Where Planar Tetracoordinate Silicon Happens. J. Am. Chem. Soc. 2011, 133, 900–908. [Google Scholar] [CrossRef] [PubMed]
- Guo, J.C.; Miao, C.Q.; Ren, G.M. Planar tetracoordinate Si and Ge in π-aromatic X3Cu (X = Si, Ge) cations. Comput. Theor. Chem. 2014, 1032, 7–11. [Google Scholar] [CrossRef]
- Guo, J.C.; Wu, H.X.; Ren, G.M.; Miao, C.Q.; Li, Y.X. D3h X3Li (X = C, Si and Ge): Superalkali cations containing three planar tetracoordinate X atoms. Comput. Theor. Chem. 2016, 1083, 1–6. [Google Scholar] [CrossRef] [Green Version]
- Sui, J.J.; Xu, J.; Ding, Y.H. A template for a planar tetracoordinate heavier group 14 atom: A global study of C2Si2Xq (X = C, Si, Ge, Sn, Pb; q = +1, 0, − 1). Dalton Trans. 2016, 45, 56–60. [Google Scholar] [CrossRef]
- Xu, J.; Ding, Y.H. Pentaatomic planar tetracoordinate silicon with 14 valence electrons: A large-scale global search of (n + m = 4; q = 0, ±1, −2; X, Y = main group elements from H to Br). J. Comput. Chem. 2015, 36, 355–360. [Google Scholar] [CrossRef]
- Keese, R. Carbon Flatland: Planar Tetracoordinate Carbon and Fenestranes. Chem. Rev. 2006, 106, 4787–4808. [Google Scholar] [CrossRef]
- Siebert, W.; Gunale, A. Compounds containing a planar-tetracoordinate carbon atom as analogues of planar methane. Chem. Soc. Rev. 1999, 28, 367–371. [Google Scholar] [CrossRef]
- Yang, L.M.; Ganz, E.; Chen, Z.; Wang, Z.X.; Schleyer, P.v.R. Four Decades of the Chemistry of Planar Hypercoordinate Compounds. Angew. Chem. Int. Ed. 2015, 54, 9468–9501. [Google Scholar] [CrossRef] [PubMed]
- Pancharatna, P.D.; Méndez-Rojas, M.A.; Merino, G.; Vela, A.; Hoffmann, R. Planar Tetracoordinate Carbon in Extended Systems. J. Am. Chem. Soc. 2004, 126, 15309–15315. [Google Scholar] [CrossRef] [PubMed]
- Merino, G.; Mendez-Rojas, M.A.; Vela, A.; Heine, T. Recent advances in planar tetracoordinate carbon chemistry. J. Comput. Chem. 2007, 28, 362–372. [Google Scholar] [CrossRef]
- Zheng, H.F.; Xu, J.; Ding, Y.H. A sixteen-valence-electron carbon-group 13 family with global penta-atomic planar tetracoordinate carbon: An ionic strategy. Phys. Chem. Chem. Phys. 2020, 22, 3975–3982. [Google Scholar] [CrossRef] [PubMed]
- Thirumoorthy, K.; Thimmakondu, V.S. Flat crown ethers with planar tetracoordinate carbon atoms. Int. J. Quantum Chem. 2021, 121, e26479. [Google Scholar] [CrossRef]
- Wang, Z.X.; Schleyer, P.v.R. A New Strategy To Achieve Perfectly Planar Carbon Tetracoordination. J. Am. Chem. Soc. 2001, 123, 994–995. [Google Scholar] [CrossRef]
- Thirumoorthy, K.; Chandrasekaran, V.; Cooksy, A.L.; Thimmakondu, V.S. Kinetic Stability of Si2C5H2 Isomer with a Planar Tetracoordinate Carbon Atom. Chemistry 2021, 3, 13–27. [Google Scholar] [CrossRef]
- Job, N.; Khatun, M.; Thirumoorthy, K.; CH, S.S.R.; Chandrasekaran, V.; Anoop, A.; Thimmakondu, V.S. CAl4Mg0/−: Global Minima with a Planar Tetracoordinate Carbon Atom. Atoms 2021, 9, 24. [Google Scholar] [CrossRef]
- Boldyrev, A.I.; Simons, J. Tetracoordinated Planar Carbon in Pentaatomic Molecules. J. Am. Chem. Soc. 1998, 120, 7967–7972. [Google Scholar] [CrossRef]
- Suresh, C.H.; Frenking, G. Direct 1- 3 Metal- Carbon Bonding and Planar Tetracoordinated Carbon in Group 6 Metallacyclobutadienes. Organometallics 2010, 29, 4766–4769. [Google Scholar] [CrossRef]
- Thirumoorthy, K.; Karton, A.; Thimmakondu, V.S. From High-Energy C7H2 Isomers with A Planar Tetracoordinate Carbon Atom to An Experimentally Known Carbene. J. Phys. Chem. A 2018, 122, 9054–9064. [Google Scholar] [CrossRef] [Green Version]
- Sateesh, B.; Srinivas Reddy, A.; Narahari Sastry, G. Towards design of the smallest planar tetracoordinate carbon and boron systems. J. Comput. Chem. 2007, 28, 335–343. [Google Scholar] [CrossRef] [PubMed]
- Priyakumar, U.D.; Sastry, G.N. A system with three contiguous planar tetracoordinate carbons is viable: A computational study on a C6H isomer. Tetrahedron Lett. 2004, 45, 1515–1517. [Google Scholar] [CrossRef]
- Cui, Z.H.; Contreras, M.; Ding, Y.H.; Merino, G. Planar Tetracoordinate Carbon versus Planar Tetracoordinate Boron: The Case of CB4 and Its Cation. J. Am. Chem. Soc. 2011, 133, 13228–13231. [Google Scholar] [CrossRef]
- Cui, Z.H.; Ding, Y.H.; Cabellos, J.L.; Osorio, E.; Islas, R.; Restrepo, A.; Merino, G. Planar tetracoordinate carbons with a double bond in CAl3E clusters. Phys. Chem. Chem. Phys. 2015, 17, 8769–8775. [Google Scholar] [CrossRef]
- Nandula, A.; Trinh, Q.T.; Saeys, M.; Alexandrova, A.N. Origin of Extraordinary Stability of Square-Planar Carbon Atoms in Surface Carbides of Cobalt and Nickel. Angew. Chem. Int. Ed. 2015, 54, 5312–5316. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Guo, J.C.; Feng, L.Y.; Dong, C.; Zhai, H.J. Ternary 12-electron CBe3X(X = H, Li, Na, Cu, Ag) clusters: Planar tetracoordinate carbons and superalkali cations. Phys. Chem. Chem. Phys. 2019, 21, 22048–22056. [Google Scholar] [CrossRef] [PubMed]
- Guo, J.C.; Feng, L.Y.; Dong, C.; Zhai, H.J. Planar Pentacoordinate versus Tetracoordinate Carbons in Ternary CBe4Li4 and CBe4Li Clusters. J. Phys. Chem. A 2018, 122, 8370–8376. [Google Scholar] [CrossRef] [PubMed]
- Priyakumar, U.D.; Reddy, A.S.; Sastry, G.N. The design of molecules containing planar tetracoordinate carbon. Tetrahedron Lett. 2004, 45, 2495–2498. [Google Scholar] [CrossRef]
- Xie, H.B.; Ding, Y.H. CAl4X (X = Si, Ge): Molecules with simultaneous planar tetracoordinate carbon, aluminum, and silicon/germanium. J. Chem. Phys. 2007, 126, 184302. [Google Scholar] [CrossRef] [Green Version]
- Monkhorst, H. Activation energy for interconversion of enantiomers containing an asymmetric carbon atom without breaking bonds. Chem. Commun. 1968, 1111–1112. [Google Scholar] [CrossRef]
- Raghunathan, S.; Yadav, K.; Rojisha, V.C.; Jaganade, T.; Prathyusha, V.; Bikkina, S.; Lourderaj, U.; Priyakumar, U.D. Transition between [R]-and [S]-stereoisomers without bond breaking. Phys. Chem. Chem. Phys. 2020, 22, 14983–14991. [Google Scholar] [CrossRef]
- Lammertsma, K.; Schleyer, P.v.R. Structures and energies of isomeric carbodications (C5H and C6H). J. Phys. Chem. 1988, 92, 881–886. [Google Scholar] [CrossRef]
- Frisch, M.J.; Head-Gordon, M.; Pople, J.A. A direct MP2 gradient method. Chem. Phys. Lett. 1990, 166, 275–280. [Google Scholar] [CrossRef]
- Kendall, R.A.; Dunning, T.H., Jr.; Harrison, R.J. Electron affinities of the first-row atoms revisited. Systematic basis sets and wave functions. J. Chem. Phys. 1992, 96, 6796–6806. [Google Scholar] [CrossRef] [Green Version]
- Schleyer, P.v.R.; Maerker, C.; Dransfeld, A.; Jiao, H.; van Eikema Hommes, N.J. Nucleus-Independent Chemical Shifts: A Simple and Efficient Aromaticity Probe. J. Am. Chem. Soc. 1996, 118, 6317–6318. [Google Scholar] [CrossRef]
- Frisch, M.J.; Trucks, G.W.; Schlegel, H.B.; Scuseria, G.E.; Robb, M.A.; Cheeseman, J.R.; Scalmani, G.; Barone, V.; Petersson, G.A.; Nakatsuji, H.; et al. Gaussian 16 Revision C.01; Gaussian Inc.: Wallingford, CT, USA, 2016. [Google Scholar]
- McGrath, M.P.; Radom, L. Alkaplanes: A class of neutral hydrocarbons containing a potentially planar tetracoordinate carbon. J. Am. Chem. Soc. 1993, 115, 3320–3321. [Google Scholar] [CrossRef]
- Rasmussen, D.R.; Radom, L. Planar-Tetracoordinate Carbon in a Neutral Saturated Hydrocarbon: Theoretical Design and Characterization. Angew. Chem. Int. Ed. 1999, 38, 2875–2878. [Google Scholar] [CrossRef]
- Zhang, C.; Sun, W.; Cao, Z. Zigzag boron- carbon nanotubes with quasi-planar tetracoordinate carbons. J. Am. Chem. Soc. 2008, 130, 5638–5639. [Google Scholar] [CrossRef]
- Yañez, O.; Vásquez-Espinal, A.; Pino-Rios, R.; Ferraro, F.; Pan, S.; Osorio, E.; Merino, G.; Tiznado, W. Exploiting electronic strategies to stabilize a planar tetracoordinate carbon in cyclic aromatic hydrocarbons. Chem. Comm. 2017, 53, 12112–12115. [Google Scholar] [CrossRef] [PubMed]
- Thimmakondu, V.S.; Thirumoorthy, K. Si3C2H2 isomers with a planar tetracoordinate carbon or silicon atom (s). Comput. Theor. Chem. 2019, 1157, 40–46. [Google Scholar] [CrossRef] [Green Version]
- Wiberg, K.B. Application of the pople-santry-segal CNDO method to the cyclopropylcarbinyl and cyclobutyl cation and to bicyclobutane. Tetrahedron 1968, 24, 1083–1096. [Google Scholar] [CrossRef]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).