Stereomutation in Tetracoordinate Centers via Stabilization of Planar Tetracoordinated Systems
Abstract
:1. Introduction
2. Methods
3. Results and Discussion
3.1. Stabilization of ptC
3.2. Heteroatom Substitution for the Stabilization of ptX
3.3. Stereomutation in Model Systems
4. Conclusions
Supplementary Materials
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Abbreviations
| ttC | tetrahedral tetracoordinated carbon |
| ptC | planar tetracoordinated carbon |
| ttX | tetrahedral tetracoordinated system with X as the substituent |
| ptX | planar tetracoordinated system with X as the substituent |
| PES | potential energy surface |
| IRC | intrinsic reaction coordinate |
| NICS | nuclear independent chemical shift |
| TS | transition state |
References
- Le Bel, J.A. Sur les relations qui existent entre les formules atomiques des corps organiques et le pouvoir rotatoire de leurs dissolutions. Bull. Soc. Chim. Fr 1874, 22, 337–347. [Google Scholar]
- Van’t Hoff, J. A suggestion looking to the extension into space of the structural formulas at present used in chemistry, and a note upon the relation between the optical activity and the chemical constitution of organic compounds. Arch. Neerl. Sci. Exact. Nat. 1874, 9, 445. [Google Scholar]
- Hoffmann, R.; Alder, R.W.; Wilcox, C.F., Jr. Planar tetracoordinate carbon. J. Am. Chem. Soc. 1970, 92, 4992–4993. [Google Scholar] [CrossRef]
- Krogh-Jespersen, M.B.; Chandrasekhar, J.; Wuerthwein, E.U.; Collins, J.B.; Von Rague Schleyer, P. Molecular orbital study of tetrahedral, planar, and pyramidal structures of the isoelectronic series BH, CH4, NH, AlH, SiH4, and PH. J. Am. Chem. Soc. 1980, 102, 2263–2268. [Google Scholar] [CrossRef]
- Von Ragué Schleyer, P.; Boldyrev, A.I. A new, general strategy for achieving planar tetracoordinate geometries for carbon and other second row periodic elements. J. Chem. Soc. Chem. Commun. 1991, 1536–1538. [Google Scholar] [CrossRef]
- Li, Y.; Liao, Y.; Chen, Z. Be2C Monolayer with Quasi-Planar Hexacoordinate Carbons: A Global Minimum Structure. Angew. Chem. Int. Ed. 2014, 53, 7248–7252. [Google Scholar] [CrossRef] [PubMed]
- Yañez, O.; Vásquez-Espinal, A.; Báez-Grez, R.; Rabanal-León, W.A.; Osorio, E.; Ruiz, L.; Tiznado, W. Carbon rings decorated with group 14 elements: New aromatic clusters containing planar tetracoordinate carbon. New J. Chem. 2019, 43, 6781–6785. [Google Scholar] [CrossRef]
- Collins, J.B.; Dill, J.D.; Jemmis, E.D.; Apeloig, Y.; Schleyer, P.v.R.; Seeger, R.; Pople, J.A. Stabilization of planar tetracoordinate carbon. J. Am. Chem. Soc. 1976, 98, 5419–5427. [Google Scholar] [CrossRef]
- Cotton, F.A.; Millar, M. The probable existence of a triple bond between two vanadium atoms. J. Am. Chem. Soc. 1977, 99, 7886–7891. [Google Scholar] [CrossRef]
- Erker, G. Planar-Tetracoordinate Carbon: Making Stable Anti-van’t Hoff/LeBel Compounds. Comment Inorg. Chem. 1992, 13, 111–131. [Google Scholar] [CrossRef]
- Xu, J.; Zhang, X.; Yu, S.; Ding, Y.H.; Bowen, K.H. Identifying the Hydrogenated Planar Tetracoordinate Carbon: A Combined Experimental and Theoretical Study of CAl4H and CAl4H−. J. Phys. Chem. Lett. 2017, 8, 2263–2267. [Google Scholar] [CrossRef] [Green Version]
- Ebner, F.; Greb, L. Calix[4]pyrrole Hydridosilicate: The Elusive Planar Tetracoordinate Silicon Imparts Striking Stability to Its Anionic Silicon Hydride. J. Am. Chem. Soc. 2018, 140, 17409–17412. [Google Scholar] [CrossRef]
- Li, X.; Zhang, H.F.; Wang, L.S.; Geske, G.; Boldyrev, A. Pentaatomic Tetracoordinate Planar Carbon, [CAl4]2−: A New Structural Unit and Its Salt Complexes. Angew. Chem. Int. Ed. 2000, 39, 3630–3632. [Google Scholar] [CrossRef]
- Röttger, D.; Erker, G. Compounds Containing Planar-Tetracoordinate Carbon. Angew. Chem. Int. Ed. 1997, 36, 812–827. [Google Scholar] [CrossRef]
- Li, X.; Wang, L.S.; Boldyrev, A.I.; Simons, J. Tetracoordinated Planar Carbon in the Al4C− Anion. A Combined Photoelectron Spectroscopy and ab Initio Study. J. Am. Chem. Soc. 1999, 121, 6033–6038. [Google Scholar] [CrossRef]
- Ghana, P.; Rump, J.; Schnakenburg, G.; Arz, M.I.; Filippou, A.C. Planar Tetracoordinated Silicon (ptSi): Room-Temperature Stable Compounds Containing Anti-van’t Hoff/Le Bel Silicon. J. Am. Chem. Soc. 2020, 143, 420–432. [Google Scholar] [CrossRef]
- Driess, M.; Aust, J.; Merz, K.; van Wüllen, C. van’t Hoff–Le Bel Stranger: Formation of a Phosphonium Cation with a Planar Tetracoordinate Phosphorus Atom. Angew. Chem. Int. Ed. 1999, 38, 3677–3680. [Google Scholar] [CrossRef]
- Li, S.D.; Ren, G.M.; Miao, C.Q.; Jin, Z.H. M4H4X: Hydrometals (M = Cu, Ni) Containing Tetracoordinate Planar Nonmetals (X=B, C, N, O). Angew. Chem. Int. Ed. 2004, 43, 1371–1373. [Google Scholar] [CrossRef] [PubMed]
- Li, Y.; Li, F.; Zhou, Z.; Chen, Z. SiC2 Silagraphene and Its One-Dimensional Derivatives: Where Planar Tetracoordinate Silicon Happens. J. Am. Chem. Soc. 2011, 133, 900–908. [Google Scholar] [CrossRef] [PubMed]
- Guo, J.C.; Miao, C.Q.; Ren, G.M. Planar tetracoordinate Si and Ge in π-aromatic X3Cu (X = Si, Ge) cations. Comput. Theor. Chem. 2014, 1032, 7–11. [Google Scholar] [CrossRef]
- Guo, J.C.; Wu, H.X.; Ren, G.M.; Miao, C.Q.; Li, Y.X. D3h X3Li (X = C, Si and Ge): Superalkali cations containing three planar tetracoordinate X atoms. Comput. Theor. Chem. 2016, 1083, 1–6. [Google Scholar] [CrossRef] [Green Version]
- Sui, J.J.; Xu, J.; Ding, Y.H. A template for a planar tetracoordinate heavier group 14 atom: A global study of C2Si2Xq (X = C, Si, Ge, Sn, Pb; q = +1, 0, − 1). Dalton Trans. 2016, 45, 56–60. [Google Scholar] [CrossRef]
- Xu, J.; Ding, Y.H. Pentaatomic planar tetracoordinate silicon with 14 valence electrons: A large-scale global search of (n + m = 4; q = 0, ±1, −2; X, Y = main group elements from H to Br). J. Comput. Chem. 2015, 36, 355–360. [Google Scholar] [CrossRef]
- Keese, R. Carbon Flatland: Planar Tetracoordinate Carbon and Fenestranes. Chem. Rev. 2006, 106, 4787–4808. [Google Scholar] [CrossRef]
- Siebert, W.; Gunale, A. Compounds containing a planar-tetracoordinate carbon atom as analogues of planar methane. Chem. Soc. Rev. 1999, 28, 367–371. [Google Scholar] [CrossRef]
- Yang, L.M.; Ganz, E.; Chen, Z.; Wang, Z.X.; Schleyer, P.v.R. Four Decades of the Chemistry of Planar Hypercoordinate Compounds. Angew. Chem. Int. Ed. 2015, 54, 9468–9501. [Google Scholar] [CrossRef] [PubMed]
- Pancharatna, P.D.; Méndez-Rojas, M.A.; Merino, G.; Vela, A.; Hoffmann, R. Planar Tetracoordinate Carbon in Extended Systems. J. Am. Chem. Soc. 2004, 126, 15309–15315. [Google Scholar] [CrossRef] [PubMed]
- Merino, G.; Mendez-Rojas, M.A.; Vela, A.; Heine, T. Recent advances in planar tetracoordinate carbon chemistry. J. Comput. Chem. 2007, 28, 362–372. [Google Scholar] [CrossRef]
- Zheng, H.F.; Xu, J.; Ding, Y.H. A sixteen-valence-electron carbon-group 13 family with global penta-atomic planar tetracoordinate carbon: An ionic strategy. Phys. Chem. Chem. Phys. 2020, 22, 3975–3982. [Google Scholar] [CrossRef] [PubMed]
- Thirumoorthy, K.; Thimmakondu, V.S. Flat crown ethers with planar tetracoordinate carbon atoms. Int. J. Quantum Chem. 2021, 121, e26479. [Google Scholar] [CrossRef]
- Wang, Z.X.; Schleyer, P.v.R. A New Strategy To Achieve Perfectly Planar Carbon Tetracoordination. J. Am. Chem. Soc. 2001, 123, 994–995. [Google Scholar] [CrossRef]
- Thirumoorthy, K.; Chandrasekaran, V.; Cooksy, A.L.; Thimmakondu, V.S. Kinetic Stability of Si2C5H2 Isomer with a Planar Tetracoordinate Carbon Atom. Chemistry 2021, 3, 13–27. [Google Scholar] [CrossRef]
- Job, N.; Khatun, M.; Thirumoorthy, K.; CH, S.S.R.; Chandrasekaran, V.; Anoop, A.; Thimmakondu, V.S. CAl4Mg0/−: Global Minima with a Planar Tetracoordinate Carbon Atom. Atoms 2021, 9, 24. [Google Scholar] [CrossRef]
- Boldyrev, A.I.; Simons, J. Tetracoordinated Planar Carbon in Pentaatomic Molecules. J. Am. Chem. Soc. 1998, 120, 7967–7972. [Google Scholar] [CrossRef]
- Suresh, C.H.; Frenking, G. Direct 1- 3 Metal- Carbon Bonding and Planar Tetracoordinated Carbon in Group 6 Metallacyclobutadienes. Organometallics 2010, 29, 4766–4769. [Google Scholar] [CrossRef]
- Thirumoorthy, K.; Karton, A.; Thimmakondu, V.S. From High-Energy C7H2 Isomers with A Planar Tetracoordinate Carbon Atom to An Experimentally Known Carbene. J. Phys. Chem. A 2018, 122, 9054–9064. [Google Scholar] [CrossRef] [Green Version]
- Sateesh, B.; Srinivas Reddy, A.; Narahari Sastry, G. Towards design of the smallest planar tetracoordinate carbon and boron systems. J. Comput. Chem. 2007, 28, 335–343. [Google Scholar] [CrossRef] [PubMed]
- Priyakumar, U.D.; Sastry, G.N. A system with three contiguous planar tetracoordinate carbons is viable: A computational study on a C6H isomer. Tetrahedron Lett. 2004, 45, 1515–1517. [Google Scholar] [CrossRef]
- Cui, Z.H.; Contreras, M.; Ding, Y.H.; Merino, G. Planar Tetracoordinate Carbon versus Planar Tetracoordinate Boron: The Case of CB4 and Its Cation. J. Am. Chem. Soc. 2011, 133, 13228–13231. [Google Scholar] [CrossRef]
- Cui, Z.H.; Ding, Y.H.; Cabellos, J.L.; Osorio, E.; Islas, R.; Restrepo, A.; Merino, G. Planar tetracoordinate carbons with a double bond in CAl3E clusters. Phys. Chem. Chem. Phys. 2015, 17, 8769–8775. [Google Scholar] [CrossRef]
- Nandula, A.; Trinh, Q.T.; Saeys, M.; Alexandrova, A.N. Origin of Extraordinary Stability of Square-Planar Carbon Atoms in Surface Carbides of Cobalt and Nickel. Angew. Chem. Int. Ed. 2015, 54, 5312–5316. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Guo, J.C.; Feng, L.Y.; Dong, C.; Zhai, H.J. Ternary 12-electron CBe3X(X = H, Li, Na, Cu, Ag) clusters: Planar tetracoordinate carbons and superalkali cations. Phys. Chem. Chem. Phys. 2019, 21, 22048–22056. [Google Scholar] [CrossRef] [PubMed]
- Guo, J.C.; Feng, L.Y.; Dong, C.; Zhai, H.J. Planar Pentacoordinate versus Tetracoordinate Carbons in Ternary CBe4Li4 and CBe4Li Clusters. J. Phys. Chem. A 2018, 122, 8370–8376. [Google Scholar] [CrossRef] [PubMed]
- Priyakumar, U.D.; Reddy, A.S.; Sastry, G.N. The design of molecules containing planar tetracoordinate carbon. Tetrahedron Lett. 2004, 45, 2495–2498. [Google Scholar] [CrossRef]
- Xie, H.B.; Ding, Y.H. CAl4X (X = Si, Ge): Molecules with simultaneous planar tetracoordinate carbon, aluminum, and silicon/germanium. J. Chem. Phys. 2007, 126, 184302. [Google Scholar] [CrossRef] [Green Version]
- Monkhorst, H. Activation energy for interconversion of enantiomers containing an asymmetric carbon atom without breaking bonds. Chem. Commun. 1968, 1111–1112. [Google Scholar] [CrossRef]
- Raghunathan, S.; Yadav, K.; Rojisha, V.C.; Jaganade, T.; Prathyusha, V.; Bikkina, S.; Lourderaj, U.; Priyakumar, U.D. Transition between [R]-and [S]-stereoisomers without bond breaking. Phys. Chem. Chem. Phys. 2020, 22, 14983–14991. [Google Scholar] [CrossRef]
- Lammertsma, K.; Schleyer, P.v.R. Structures and energies of isomeric carbodications (C5H and C6H). J. Phys. Chem. 1988, 92, 881–886. [Google Scholar] [CrossRef]
- Frisch, M.J.; Head-Gordon, M.; Pople, J.A. A direct MP2 gradient method. Chem. Phys. Lett. 1990, 166, 275–280. [Google Scholar] [CrossRef]
- Kendall, R.A.; Dunning, T.H., Jr.; Harrison, R.J. Electron affinities of the first-row atoms revisited. Systematic basis sets and wave functions. J. Chem. Phys. 1992, 96, 6796–6806. [Google Scholar] [CrossRef] [Green Version]
- Schleyer, P.v.R.; Maerker, C.; Dransfeld, A.; Jiao, H.; van Eikema Hommes, N.J. Nucleus-Independent Chemical Shifts: A Simple and Efficient Aromaticity Probe. J. Am. Chem. Soc. 1996, 118, 6317–6318. [Google Scholar] [CrossRef]
- Frisch, M.J.; Trucks, G.W.; Schlegel, H.B.; Scuseria, G.E.; Robb, M.A.; Cheeseman, J.R.; Scalmani, G.; Barone, V.; Petersson, G.A.; Nakatsuji, H.; et al. Gaussian 16 Revision C.01; Gaussian Inc.: Wallingford, CT, USA, 2016. [Google Scholar]
- McGrath, M.P.; Radom, L. Alkaplanes: A class of neutral hydrocarbons containing a potentially planar tetracoordinate carbon. J. Am. Chem. Soc. 1993, 115, 3320–3321. [Google Scholar] [CrossRef]
- Rasmussen, D.R.; Radom, L. Planar-Tetracoordinate Carbon in a Neutral Saturated Hydrocarbon: Theoretical Design and Characterization. Angew. Chem. Int. Ed. 1999, 38, 2875–2878. [Google Scholar] [CrossRef]
- Zhang, C.; Sun, W.; Cao, Z. Zigzag boron- carbon nanotubes with quasi-planar tetracoordinate carbons. J. Am. Chem. Soc. 2008, 130, 5638–5639. [Google Scholar] [CrossRef]
- Yañez, O.; Vásquez-Espinal, A.; Pino-Rios, R.; Ferraro, F.; Pan, S.; Osorio, E.; Merino, G.; Tiznado, W. Exploiting electronic strategies to stabilize a planar tetracoordinate carbon in cyclic aromatic hydrocarbons. Chem. Comm. 2017, 53, 12112–12115. [Google Scholar] [CrossRef] [PubMed]
- Thimmakondu, V.S.; Thirumoorthy, K. Si3C2H2 isomers with a planar tetracoordinate carbon or silicon atom (s). Comput. Theor. Chem. 2019, 1157, 40–46. [Google Scholar] [CrossRef] [Green Version]
- Wiberg, K.B. Application of the pople-santry-segal CNDO method to the cyclopropylcarbinyl and cyclobutyl cation and to bicyclobutane. Tetrahedron 1968, 24, 1083–1096. [Google Scholar] [CrossRef]
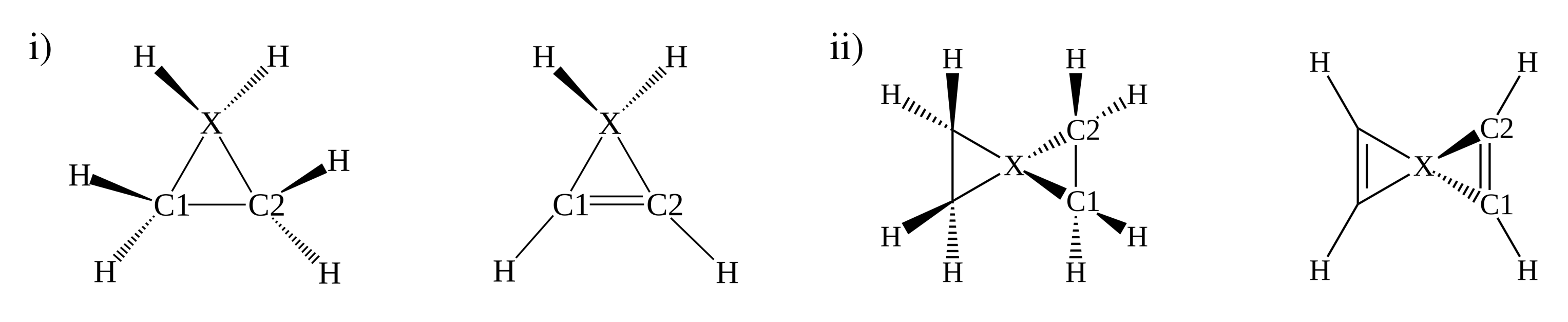
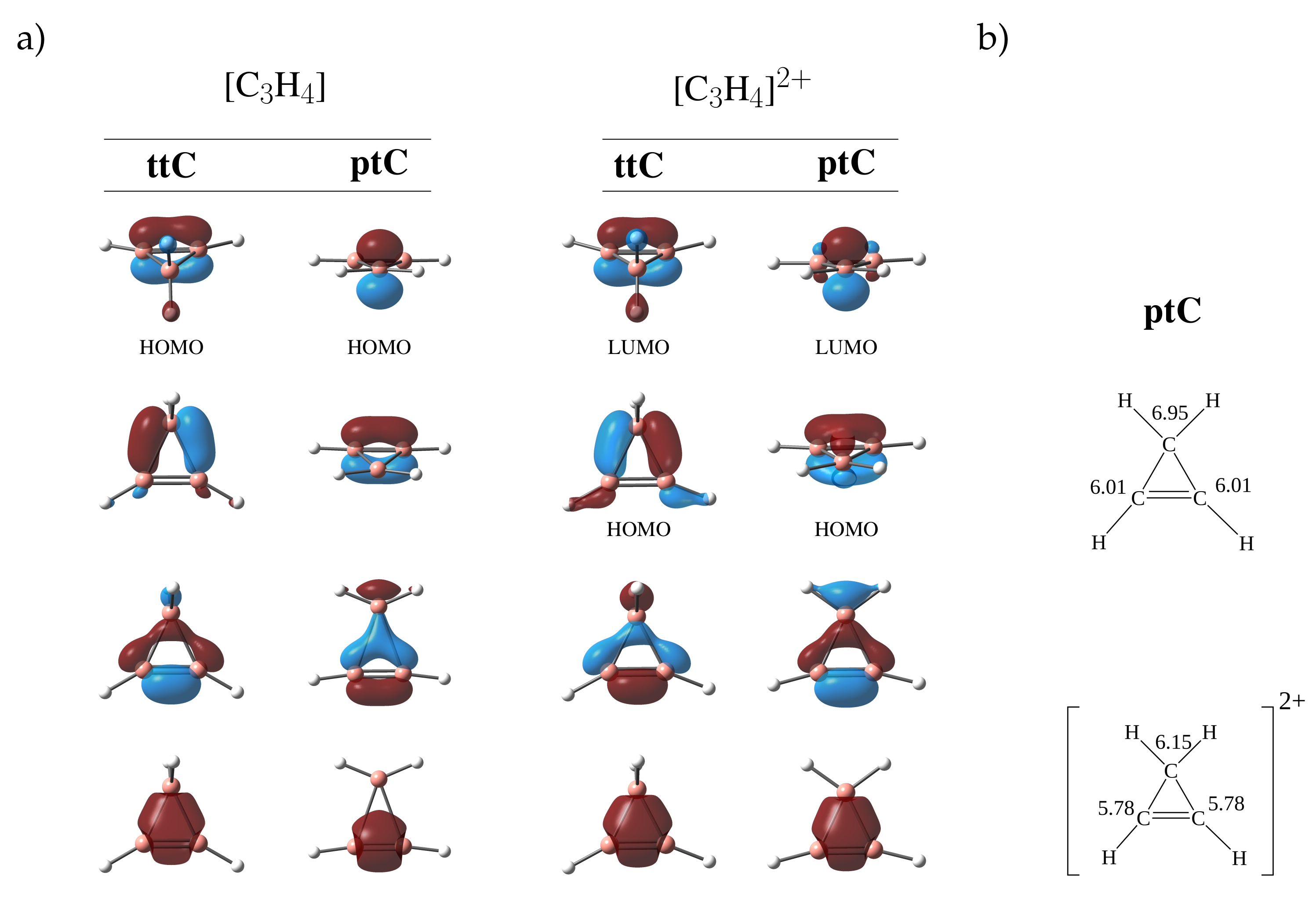
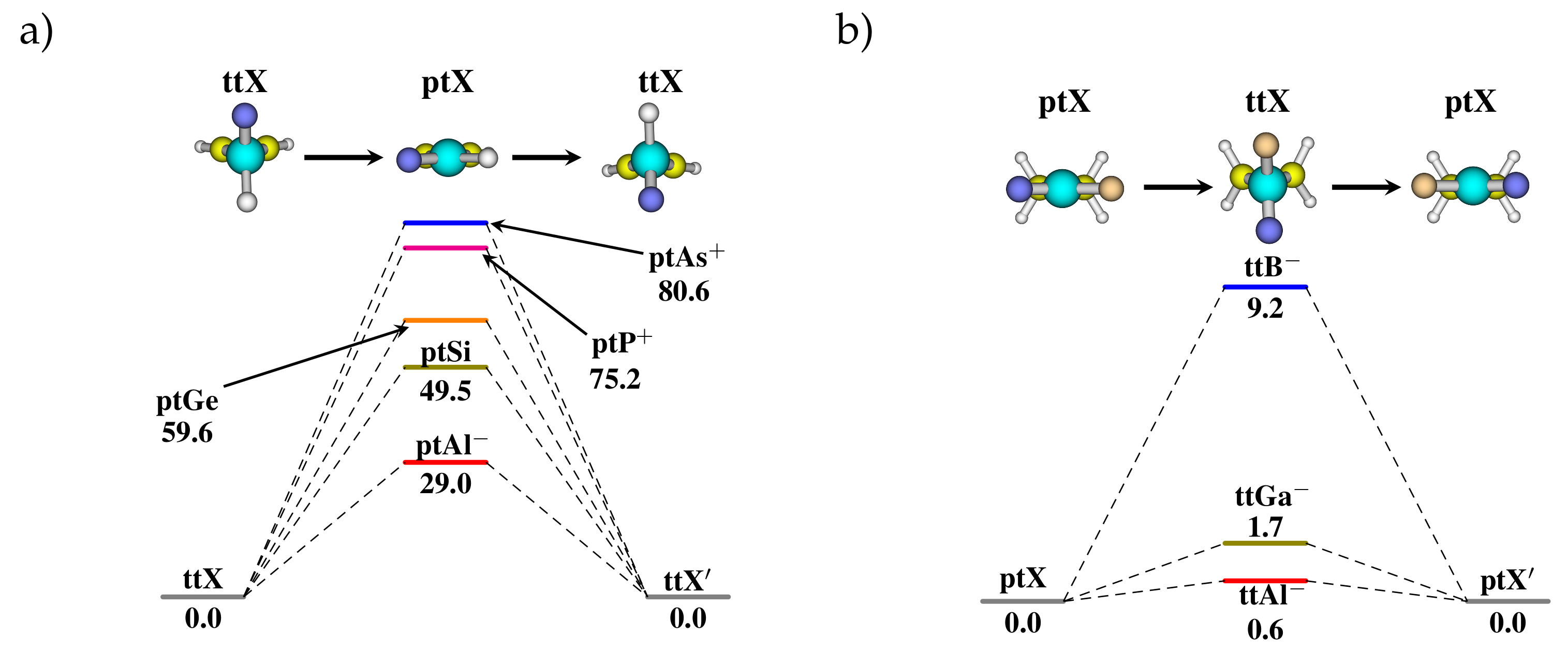
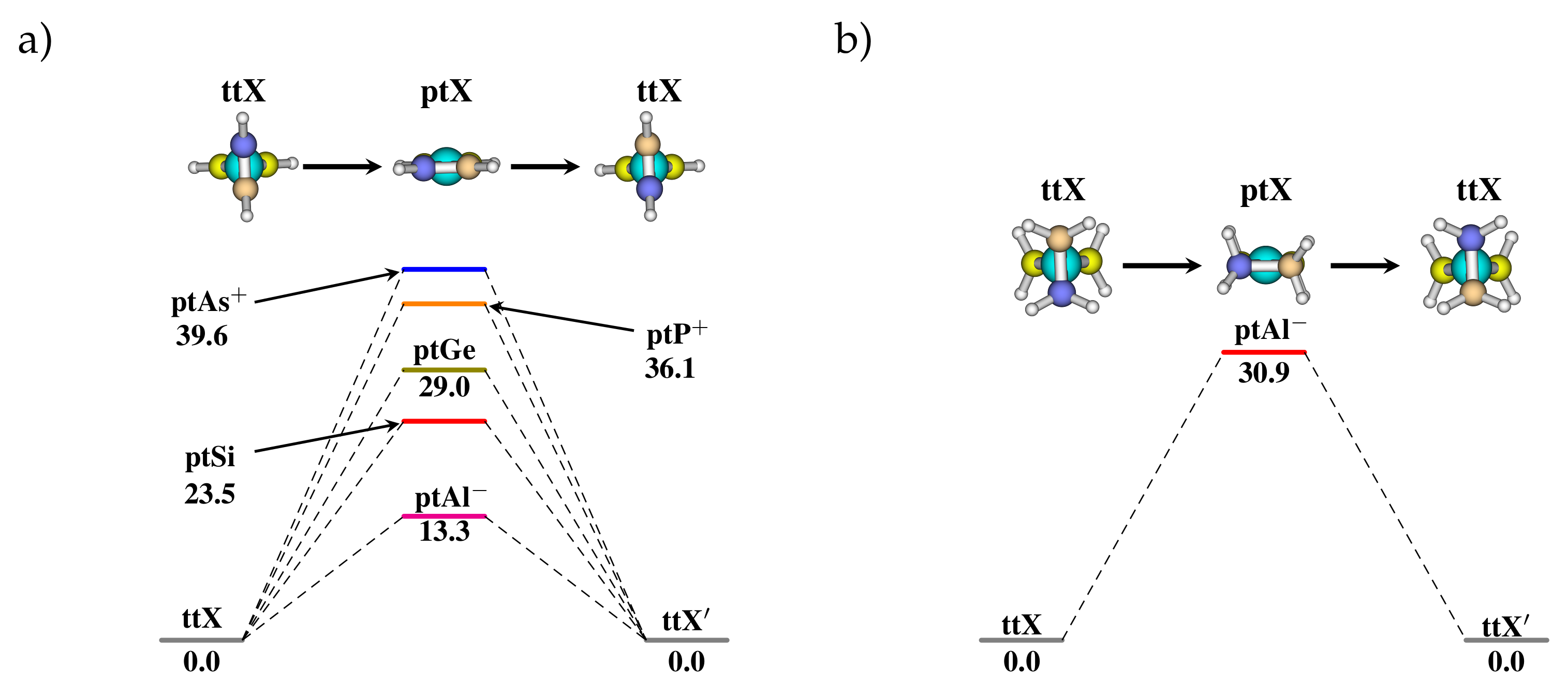
| Four Valence Electrons | Two Valence Electrons | ||||||||
|---|---|---|---|---|---|---|---|---|---|
| ttX | ptX | ttX | ptX | ||||||
| X | 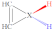 |  |  |  |  |  |  |  | |
| B | , | 0.0, 0 | 0.0, 0 | 81.5, 3 | 46.5, 3 | 0.0,- | 0.0, 1 | −29.1, 0 | −27.2, 0 |
| X–C1 | 1.61 | 1.58 | 1.66 | 1.62 | 1.43 | 1.84 | 1.68 | 1.55 | |
| Al | , | 0.0, 0 | 0.0, 0 | 29.0, 1 | 13.3, 1 | 0.0, 2 | 0.0, 1 | −149.7, 0 | −7.5, 1 |
| X–C1 | 1.95 | 1.93 | 1.96 | 1.94 | 1.97 | 2.29 | 2.32 | 1.97 | |
| Ga | , | 0.0, 0 | 0.0, 0 | 40.5, 2 | 19.3, 2 | 0.0,2 | 0.0,- | −152.9,0 | −69.4,0 |
| X–C1 | 1.99 | 1.96 | 2.01 | 1.98 | 1.99 | 1.97 | 2.31 | 1.95 | |
| C | , | 0.0, 0 | 0.0, 0 | 117.4, 3 | 92.7, 4 | 0.0,- | 0.0, 2 | −62.6,0 | , 0 |
| X–C1 | 1.53 | 1.48 | 1.83 | 1.53 | 1.46 | 1.76 | 1.50 | 1.48 | |
| Si | , | 0.0, 0 | 0.0, 0 | 49.5, 1 | 23.5, 1 | 0.0, 2 | 0.0, 1 | −9.5, 0 | −6.4, 1 |
| X–C1 | 1.82 | 1.80 | 1.81 | 1.80 | 2.20 | 2.15 | 2.06 | 1.88 | |
| Ge | , | 0.0, 0 | 0.0, 0 | 59.6, 1 | 28.9, 1 | 0.0, 2 | 0.0, 1 | −9.5, 0 | −12.7, 1 |
| X–C1 | 1.91 | 1.89 | 1.91 | 1.90 | 2.30 | 2.22 | 2.13 | 1.93 | |
| N | , | 0.0, 0 | 0.0, 0 | 77.0, 3 | 97.0, 4 | 0.0, 0 | 0.0, 2 | −4.5, 1 | −0.8, 1 |
| X–C1 | 1.50 | 1.46 | 1.72 | 1.56 | 1.40 | 1.89 | 1.48 | 1.50 | |
| P | , | 0.0, 0 | 0.0, 0 | 75.2, 1 | 36.1, 1 | 0.0, 2 | 0.0, 2 | −64.9, 1 | −3.6, 1 |
| X–C1 | 1.75 | 1.72 | 1.73 | 1.72 | 1.85 | 2.12 | 2.01 | 1.83 | |
| As | , | 0.0, 0 | 0.0, 0 | 80.6, 1 | 39.8, 1 | 0.0, 1 | 0.0, 2 | −79.9, 1 | −5.7, 2 |
| X–C1 | 1.88 | 1.85 | 1.86 | 1.84 | 1.97 | 2.25 | 2.13 | 1.94 | |
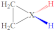 | 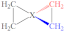 | 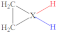 |  |  |  |  |  | ||
| B | , | 0.0, 0 | 0.0, 0 | 140.5, 3 | 105.1, 3 | 0.0, 1 | 0.0,- | −9.2, 0 | −129.5, 0 |
| X–C1 | 1.61 | 1.58 | 1.60 | 1.68 | 2.02 | 1.37 | 1.82 | 1.61 | |
| Al | , | 0.0, 0 | 0.0, 0 | 43.0, 1 | 30.9, 1 | 30.9, 1 | 0.0, 1 | −0.6, 0 | −13.8, 1 |
| X–C1 | 1.99 | 1.97 | 2.0 | 1.99 | 2.42 | 2.38 | 2.39 | 2.03 | |
| Ga | , | 0.0, 0 | 0.0, 0 | 58.6, 2 | 51.8, 3 | 0.0, 1 | 0.0, 1 | −1.7, 0 | −24.2, 1 |
| X–C1 | 2.0 | 1.98 | 2.06 | 2.03 | 2.42 | 2.33 | 2.35 | 2.0 | |
| C | , n | 0.0, 0 | 0.0, 0 | 110.9, 2 | 102.4, 3 | 0.0, 2 | 0.0, 3 | 29.4, - | −20.0, 0 |
| X–C1 | 1.50 | 1.48 | 1.66 | 1.53 | 1.90 | 1.91 | 1.54 | 1.55 | |
| Si | , | 0.0, 0 | 0.0, 0 | 77.7, 1 | 60.5, 1 | 0.0, 2 | 0.0, 2 | −0.9, 1 | 10.4, 1 |
| X–C1 | 1.86 | 1.84 | 1.86 | 1.85 | 2.42 | 2.28 | 2.22 | 1.94 | |
| Ge | , | 0.0, 0 | 0.0, 0 | 83.4, 2 | 70.9, 1 | 0.0, 2 | 0.0, 2 | −1.9, 1 | −16.9, 1 |
| X–C1 | 1.93 | 1.91 | 2.36 | 1.95 | 2.31 | 2.34 | 2.27 | 2.00 | |
| N | , | 0.0, 0 | 0.0, 0 | 71.6, 2 | 65.5, 2 | 0.0, - | 0.0, - | −6.1, 3 | −9.8, 3 |
| X–C1 | 1.49 | 1.46 | 1.66 | 1.52 | 1.68 | 1.59 | 1.68 | 1.58 | |
| P | , | 0.0, 0 | 0.0, 0 | 74.5, 2 | 105.5, 1 | 0.0, 2 | 0.0, 3 | −1.2, 1 | −4.1, 2 |
| X–C1 | 1.80 | 1.78 | 2.14 | 1.77 | 2.42 | 2.43 | 2.36 | 1.97 | |
| As | , | 0.0, 0 | 0.0, 0 | 64.6, 2 | 109.7, 2 | 0.0, 2 | 0.0, 3 | −1.5, 1 | −9.7, 1 |
| X–C1 | 1.91 | 1.90 | 2.42 | 1.91 | 2.46 | 2.50 | 2.40 | 2.08 | |
| Single point energies, since energy minimization failed to result in stationary points with these geometries at the current level of theory. | |||||||||
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Yadav, K.; Lourderaj, U.; Priyakumar, U.D. Stereomutation in Tetracoordinate Centers via Stabilization of Planar Tetracoordinated Systems. Atoms 2021, 9, 79. https://doi.org/10.3390/atoms9040079
Yadav K, Lourderaj U, Priyakumar UD. Stereomutation in Tetracoordinate Centers via Stabilization of Planar Tetracoordinated Systems. Atoms. 2021; 9(4):79. https://doi.org/10.3390/atoms9040079
Chicago/Turabian StyleYadav, Komal, Upakarasamy Lourderaj, and U. Deva Priyakumar. 2021. "Stereomutation in Tetracoordinate Centers via Stabilization of Planar Tetracoordinated Systems" Atoms 9, no. 4: 79. https://doi.org/10.3390/atoms9040079
APA StyleYadav, K., Lourderaj, U., & Priyakumar, U. D. (2021). Stereomutation in Tetracoordinate Centers via Stabilization of Planar Tetracoordinated Systems. Atoms, 9(4), 79. https://doi.org/10.3390/atoms9040079






