Linear and Nonlinear Optical Absorption of CdSe/CdS Core/Shell Quantum Dots in the Presence of Donor Impurity
Abstract
:1. Introduction
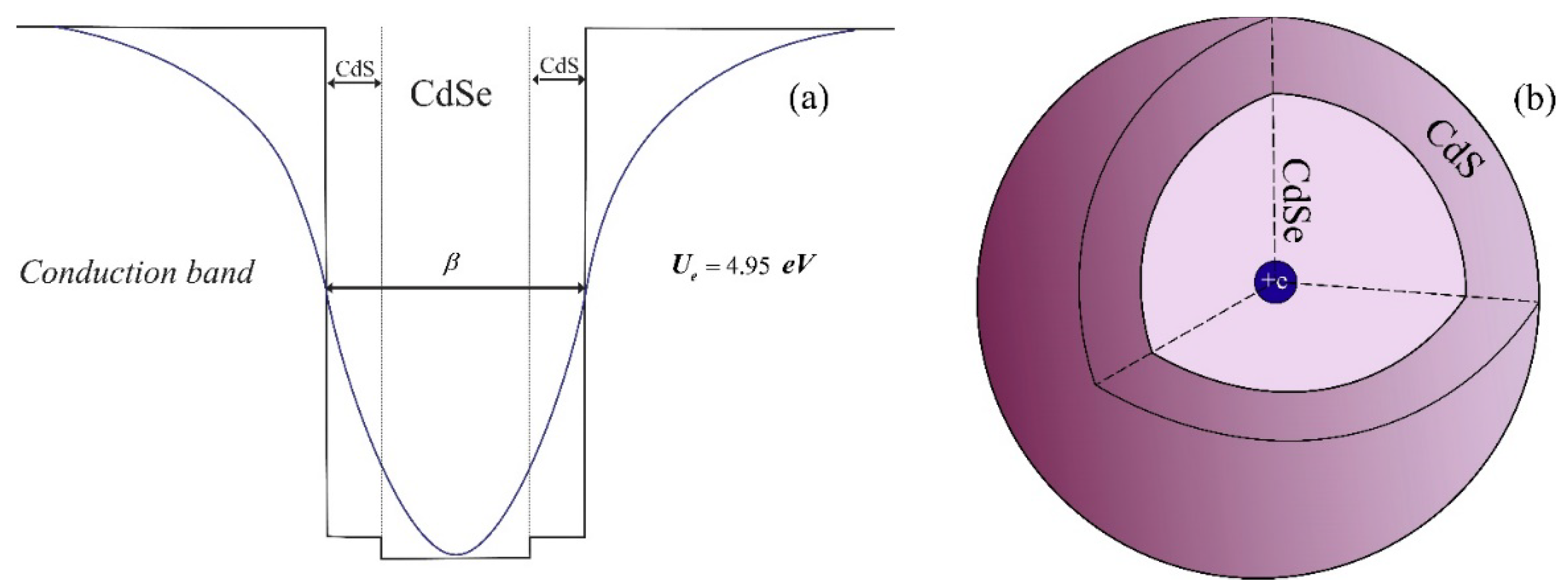
2. Theory
3. Linear and Nonlinear Optical Properties
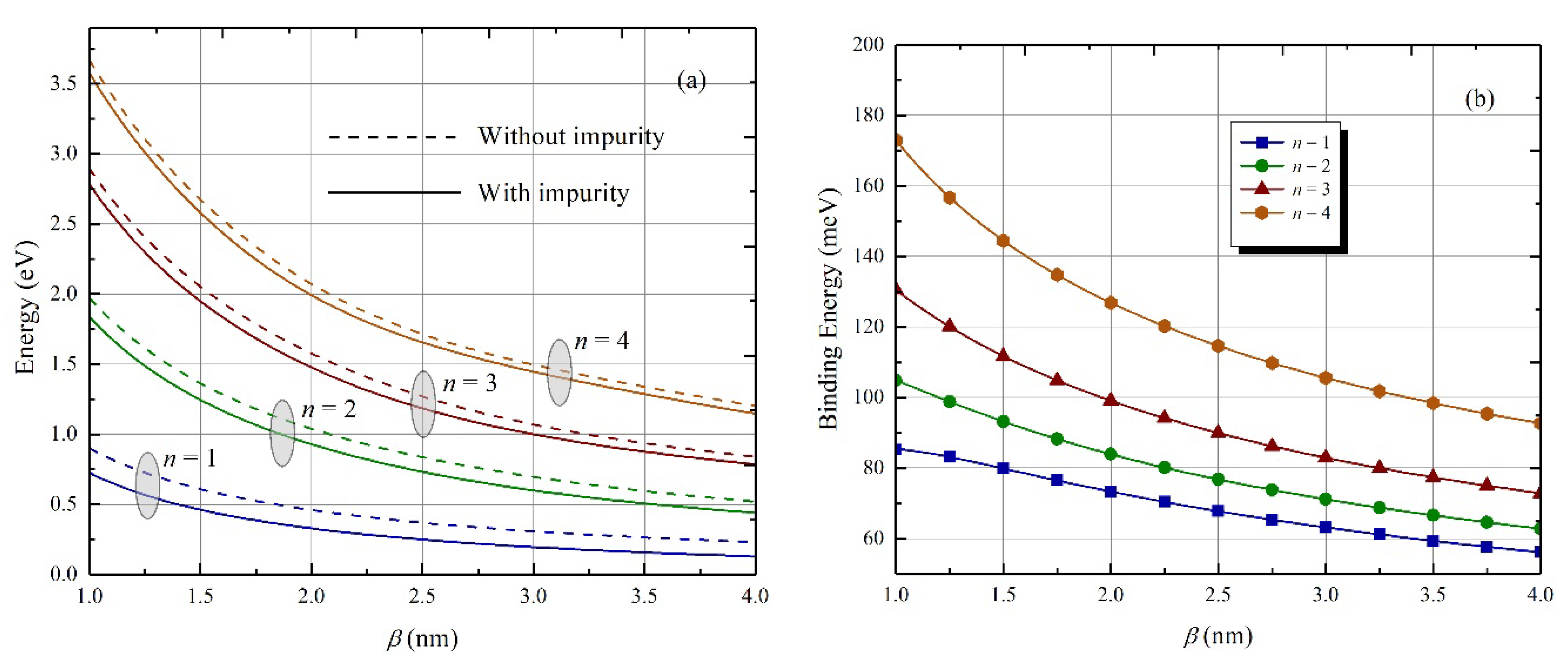
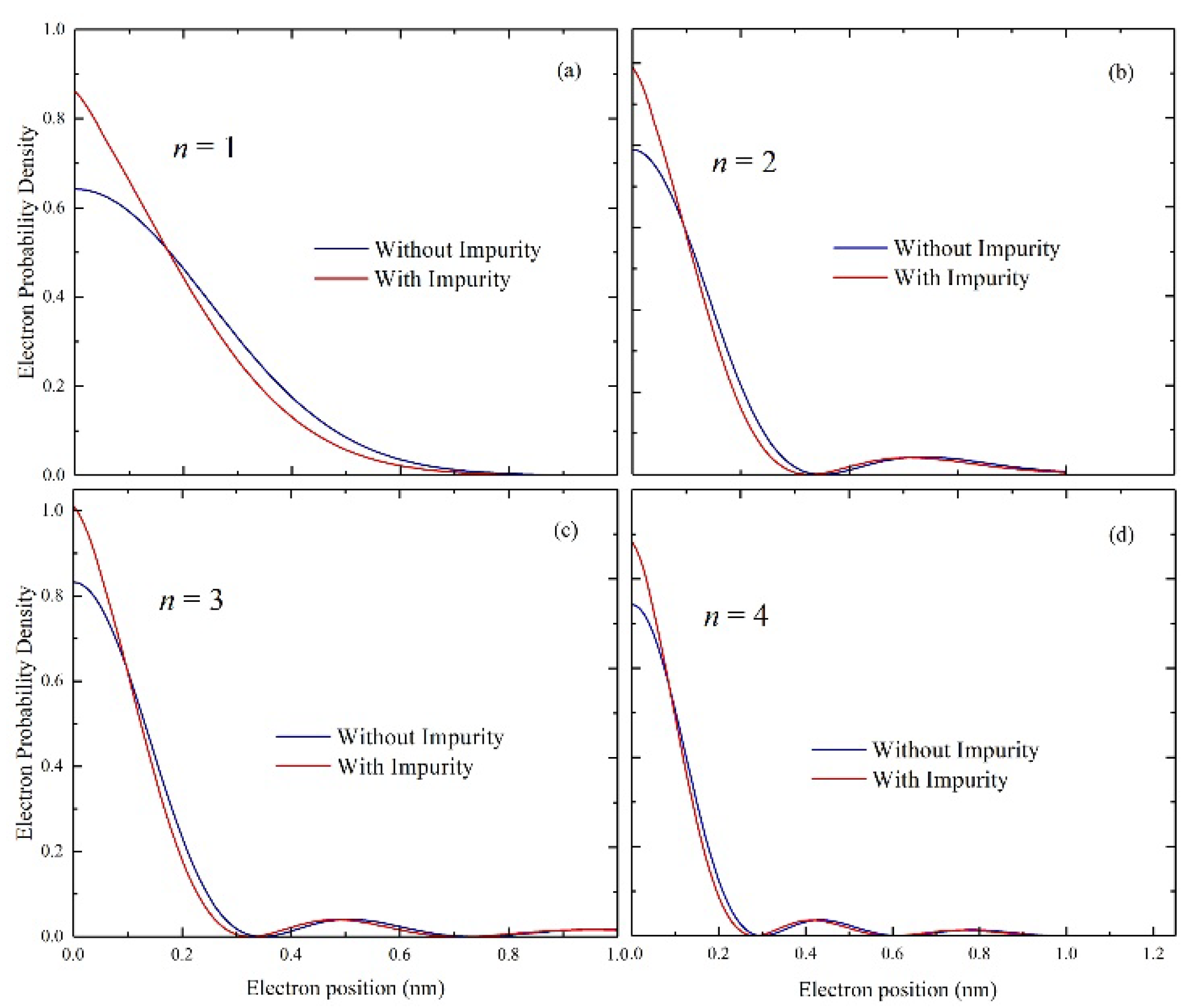
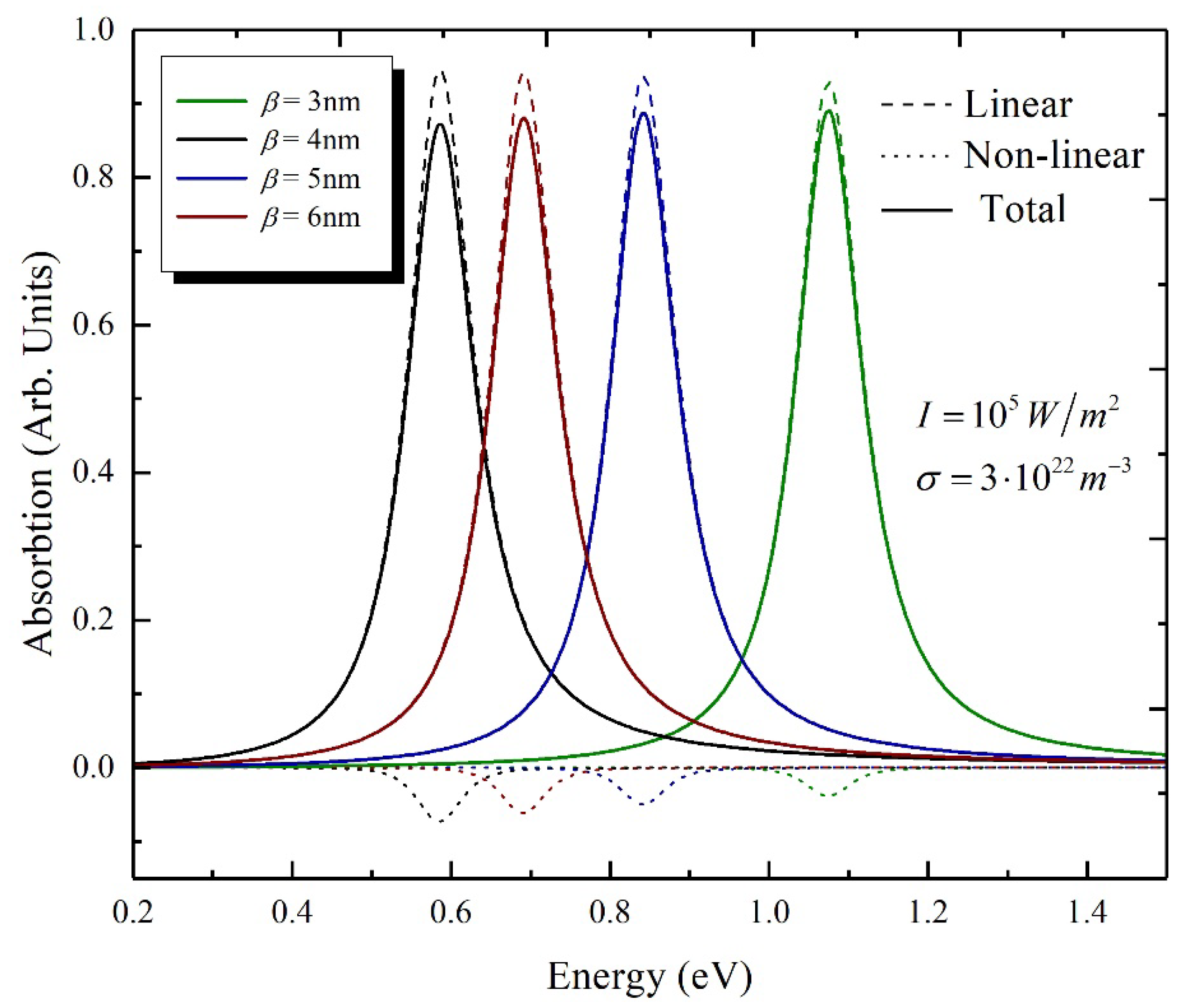
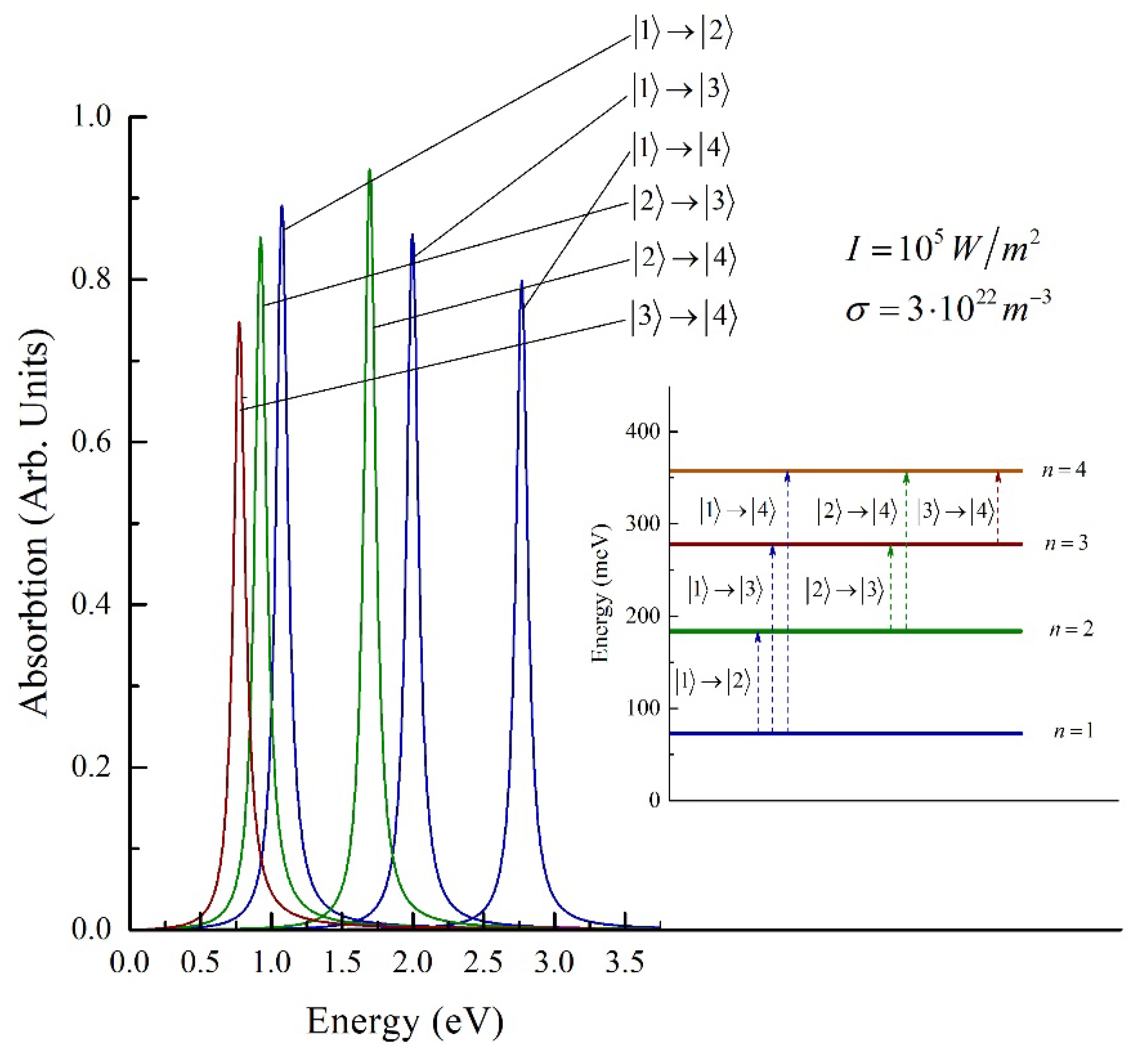
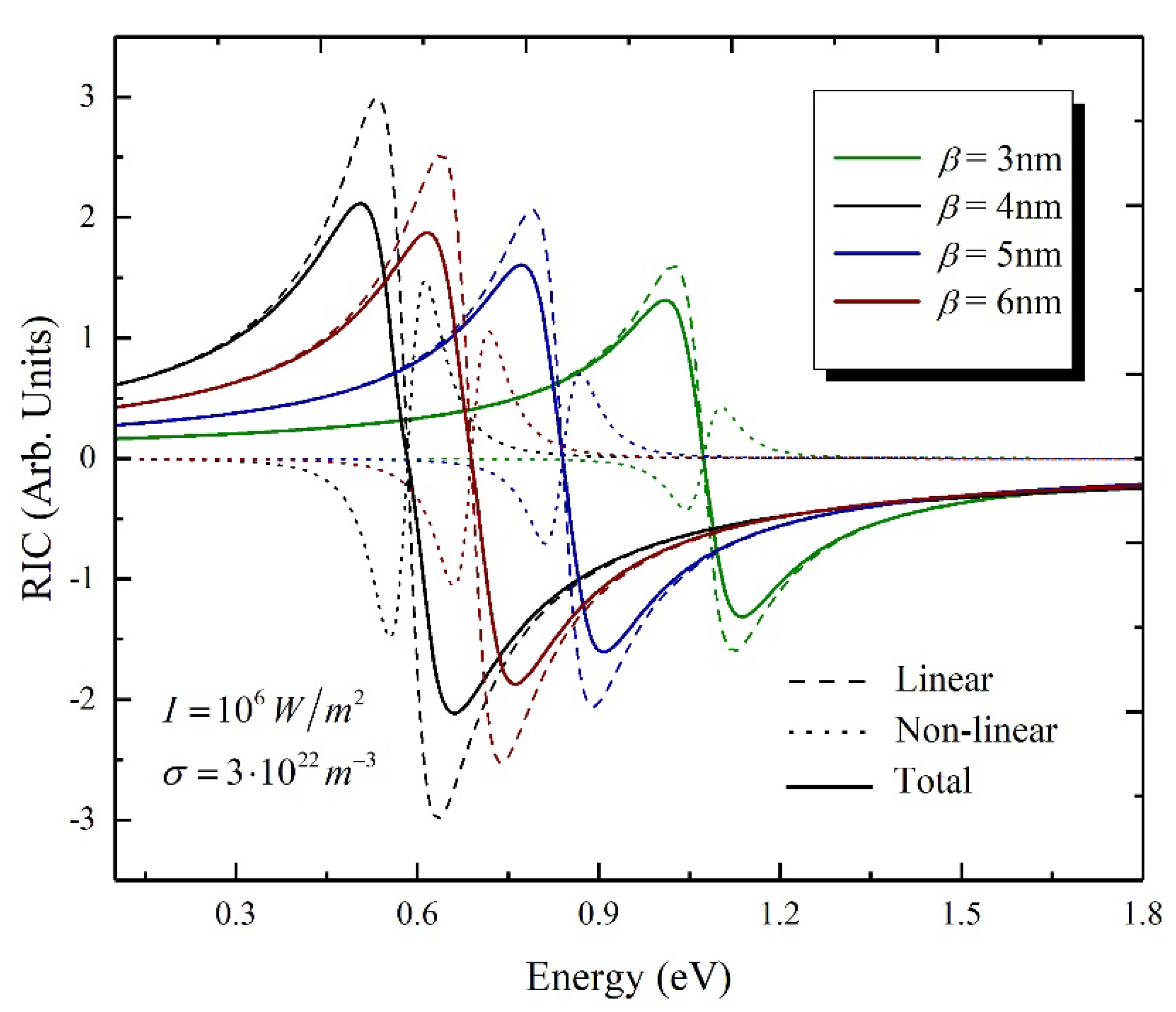
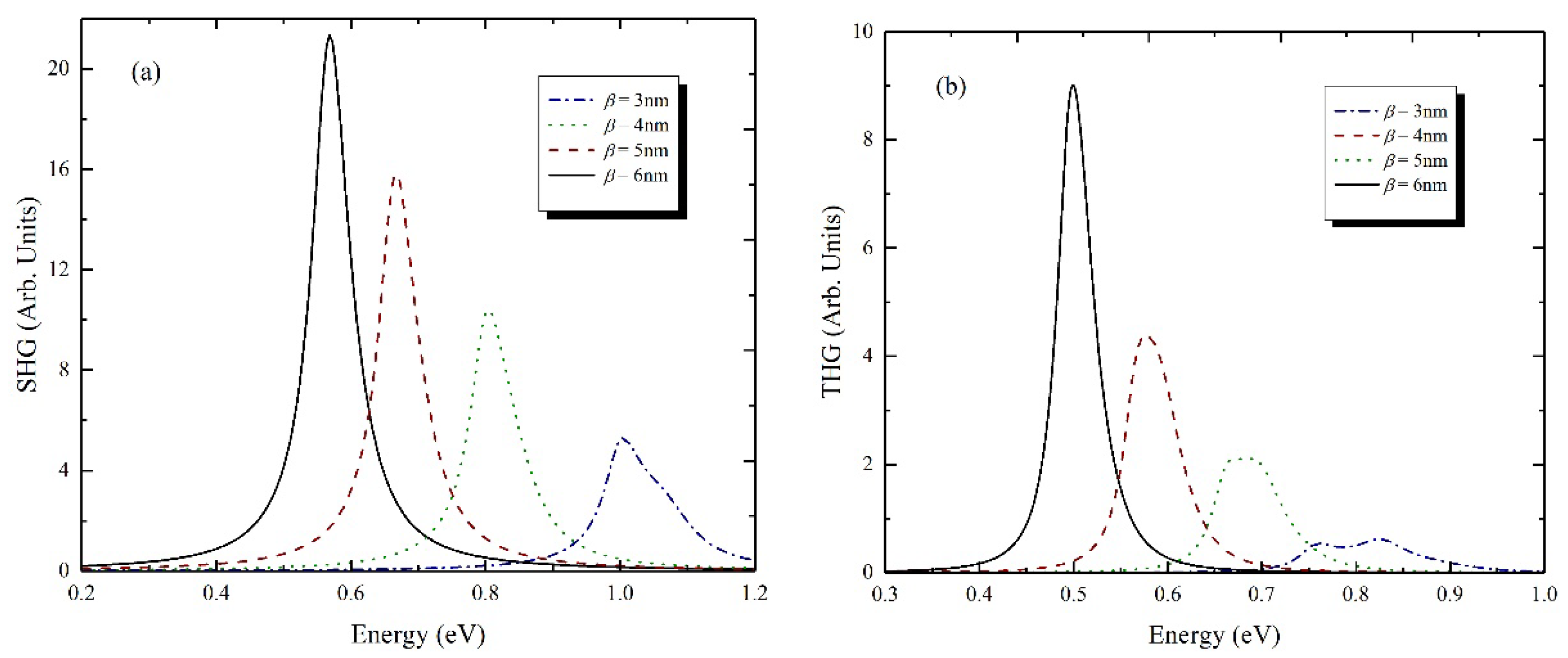
4. Results and Discussion
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Bimberg, D.; Grundmann, M.; Ledentsov, N.N.; Ruvimov, S.S.; Werner, P.; Richter, U.; Heydenreich, J.; Ustinov, V.M.; Kop’ev, P.S.; Alferov, Z.I. Self-organization processes in MBE-grown quantum dot structures. Thin Solid Films 1995, 267, 32–36. [Google Scholar] [CrossRef]
- Bosacchi, A.; Frigeri, P.; Franchi, S.; Allegri, P.; Avanzini, V. InAsGaAs self-assembled quantum dots grown by ALMBE and MBE. J. Cryst. Growth 1997, 175, 771–776. [Google Scholar] [CrossRef]
- Nötzel, R.; Ploog, K.H. MBE of quantum wires and quantum dots. J. Cryst. Growth 2001, 227, 8–12. [Google Scholar] [CrossRef]
- Mahler, B.; Spinicelli, P.; Buil, S.; Quelin, X.; Hermier, J.P.; Dubertret, B. Towards non-blinking colloidal quantum dots. Nat. Mater. 2008, 7, 659–664. [Google Scholar] [CrossRef]
- Baskoutas, S.; Terzis, A.F. Size-dependent band gap of colloidal quantum dots. J. Appl. Phys. 2006, 99, 013708. [Google Scholar] [CrossRef]
- Litvin, A.P.; Martynenko, I.V.; Purcell-Milton, F.; Baranov, A.V.; Fedorov, A.V.; Gun’Ko, Y.K. Colloidal quantum dots for optoelectronics. J. Mater. Chem. A 2017, 5, 13252–13275. [Google Scholar] [CrossRef]
- Kagan, C.R.; Lifshitz, E.; Sargent, E.H.; Talapin, D.V. Building devices from colloidal quantum dots. Science 2016, 353. [Google Scholar] [CrossRef]
- Lu, W.; Guo, X.; Luo, Y.; Li, Q.; Zhu, R.; Pang, H. Core-shell materials for advanced batteries. Chem. Eng. J. 2019, 355, 208–237. [Google Scholar] [CrossRef]
- Clifford, J.P.; Konstantatos, G.; Johnston, K.W.; Hoogland, S.; Levina, L.; Sargent, E.H. Fast, sensitive and spectrally tuneable colloidal-quantum-dot photodetectors. Nat. Nanotechnol. 2009, 4, 40–44. [Google Scholar] [CrossRef]
- Konstantatos, G.; Howard, I.; Fischer, A.; Hoogland, S.; Clifford, J.; Klem, E.; Levina, L.; Sargent, E.H. Ultrasensitive solution-cast quantum dot photodetectors. Nature 2006, 442, 180–183. [Google Scholar] [CrossRef] [PubMed]
- Chen, O.; Zhao, J.; Chauhan, V.P.; Cui, J.; Wong, C.; Harris, D.K.; Wei, H.; Han, H.S.; Fukumura, D.; Jain, R.K.; et al. Compact high-quality CdSe–CdS core–shell nanocrystals with narrow emission linewidths and suppressed blinking. Nat. Mater. 2013, 12, 445–451. [Google Scholar] [CrossRef] [Green Version]
- Vasudevan, D.; Gaddam, R.R.; Trinchi, A.; Cole, I. Core–shell quantum dots: Properties and applications. J. Alloys Compd. 2015, 636, 395–404. [Google Scholar] [CrossRef]
- Selopal, G.S.; Zhao, H.; Wang, Z.M.; Rosei, F. Core/shell quantum dots solar cells. Adv. Funct. Mater. 2020, 30, 1908762. [Google Scholar] [CrossRef]
- Yuan, X.; Zheng, J.; Zeng, R.; Jing, P.; Ji, W.; Zhao, J.; Yang, W.; Li, H. Thermal stability of Mn2+ ion luminescence in Mn-doped core–shell quantum dots. Nanoscale 2014, 6, 300–307. [Google Scholar] [CrossRef]
- Bhattacharyya, B.; Pandey, A. CuFeS2 quantum dots and highly luminescent CuFeS2 based core/shell structures: Synthesis, tunability, and photophysics. J. Am. Chem. Soc. 2016, 138, 10207–10213. [Google Scholar] [CrossRef]
- Zeiri, N.; Naifar, A.; Nasrallah, S.A.B.; Said, M. Third nonlinear optical susceptibility of CdS/ZnS core-shell spherical quantum dots for optoelectronic devices. Optik 2019, 176, 162–167. [Google Scholar] [CrossRef]
- Loitsch, B.; Winnerl, J.; Grimaldi, G.; Wierzbowski, J.; Rudolph, D.; Morkoötter, S.; Doöblinger, M.; Abstreiter, G.; Koblmüller, G.; Finley, J.J. Crystal phase quantum dots in the ultrathin core of GaAs–AlGaAs core–shell nanowires. Nano Lett. 2015, 15, 7544–7551. [Google Scholar] [CrossRef] [PubMed]
- Zhu, X.; Yang, X.; Lv, C.; Guo, S.; Li, J.; Zheng, Z.; Zhu, H.; Yang, D. New approach to create TiO2 (B)/carbon core/shell nanotubes: Ideal structure for enhanced lithium ion storage. ACS Appl. Mater. Interfaces 2016, 8, 18815–18821. [Google Scholar] [CrossRef]
- Jiang, H.; Chen, Y.; Li, L.; Liu, H.; Ren, C.; Liu, X.; Tian, G. Hierarchical ZnO nanorod/ZnFe2O4 nanosheet core/shell nanoarray decorated with PbS quantum dots for efficient photoelectrochemical water splitting. J. Alloys Compd. 2020, 828, 154449. [Google Scholar] [CrossRef]
- Kayaci, F.; Vempati, S.; Ozgit-Akgun, C.; Donmez, I.; Biyikli, N.; Uyar, T. Transformation of polymer-ZnO core–shell nanofibers into ZnO hollow nanofibers: Intrinsic defect reorganization in ZnO and its influence on the photocatalysis. Appl. Catal. B Environ. 2015, 176, 646–653. [Google Scholar] [CrossRef]
- Wang, M.; Peng, Z.; Qian, J.; Li, H.; Zhao, Z.; Fu, X. Highly efficient solar-driven photocatalytic degradation on environmental pollutants over a novel C fibers@ MoSe2 nanoplates core-shell composite. J. Hazard. Mater. 2018, 347, 403–411. [Google Scholar] [CrossRef] [PubMed]
- Mantashian, G.A.; Mantashyan, P.A.; Sarkisyan, H.A.; Kazaryan, E.M.; Bester, G.; Baskoutas, S.; Hayrapetyan, D.B. Exciton-Related Raman Scattering, Interband Absorption and Photoluminescence in Colloidal CdSe/CdS Core/Shell Quantum Dots Ensemble. Nanomaterials 2021, 11, 1274. [Google Scholar] [CrossRef] [PubMed]
- Schmitt-Rink, S.D.A.B.M.; Miller, D.A.B.; Chemla, D.S. Theory of the linear and nonlinear optical properties of semiconductor microcrystallites. Phys. Rev. B 1987, 35, 8113. [Google Scholar] [CrossRef] [PubMed]
- Takagahara, T. Excitonic optical nonlinearity and exciton dynamics in semiconductor quantum dots. Phys. Rev. B 1987, 36, 9293. [Google Scholar] [CrossRef]
- Li, B.; Guo, K.X.; Zhang, C.J.; Zheng, Y.B. The second-harmonic generation in parabolic quantum dots in the presence of electric and magnetic fields. Phys. Lett. A 2007, 367, 493–497. [Google Scholar] [CrossRef]
- Shao, S.; Guo, K.X.; Zhang, Z.H.; Li, N.; Peng, C. Studies on the third-harmonic generations in cylindrical quantum dots with an applied electric field. Superlattices Microstruct. 2010, 48, 541–549. [Google Scholar] [CrossRef]
- Liu, G.; Guo, K.; Wu, Q.; Wu, J.H. Polaron effects on the optical rectification and the second harmonic generation in cylindrical quantum dots with magnetic field. Superlattices Microstruct. 2013, 53, 173–183. [Google Scholar] [CrossRef]
- Portacio, A.A.; Rodríguez, B.A.; Villamil, P. Influence of the position of a donor impurity on the second-order nonlinear optical susceptibility in a cylindrical quantum dot. Superlattices Microstruct. 2018, 113, 550–557. [Google Scholar] [CrossRef]
- Xie, W. Nonlinear optical properties of a hydrogenic donor quantum dot. Phys. Lett. A 2008, 372, 5498–5500. [Google Scholar] [CrossRef]
- Zielinski, M.; Oron, D.; Chauvat, D.; Zyss, J. Second-Harmonic Generation from a Single Core/Shell Quantum Dot. Small 2009, 5, 2835–2840. [Google Scholar] [CrossRef] [PubMed]
- Bera, A.; Ghosh, A.; Ghosh, M. Nonlinear optical properties of doped quantum dots: Interplay between noise and carrier density. Opt. Mater. 2017, 69, 352–357. [Google Scholar] [CrossRef]
- Poerschke, O.R. Madelung, Semiconductors: Other than Group IV Elements and 2I-V Compounds; Springer: Berlin/Heidelberg, Germany, 1992. [Google Scholar]
- Parang, Z.; Keshavarz, A.; Zamani, N. Optimization of optical absorption coefficient in double modified Pöschl–Teller quantum wells. J. Comput. Electron. 2014, 13, 1020–1025. [Google Scholar] [CrossRef]
- Hayrapetyan, D.B.; Kazaryan, E.M.; Tevosyan, H.K. Optical properties of spherical quantum dot with modified Pöschl–Teller potential. Superlattices Microstruct. 2013, 64, 204–212. [Google Scholar] [CrossRef]
- Sargsian, T.A.; Mkrtchyan, M.A.; Sarkisyan, H.A.; Hayrapetyan, D.B. Effects of external electric and magnetic fields on the linear and nonlinear optical properties of InAs cylindrical quantum dot with modified Pöschl-Teller and Morse confinement potentials. Phys. E Low-Dimens. Syst. Nanostructures 2021, 126, 114440. [Google Scholar] [CrossRef]
- Ünlü, S.; Karabulut, İ.; Şafak, H. Linear and nonlinear intersubband optical absorption coefficients and refractive index changes in a quantum box with finite confining potential. Phys. E Low-Dimens. Syst. Nanostructures 2006, 33, 319–324. [Google Scholar] [CrossRef]
- Chuu, D.S.; Hsiao, C.M.; Mei, W.N. Hydrogenic impurity states in quantum dots and quantum wires. Phys. Rev. B 1992, 46, 3898. [Google Scholar] [CrossRef] [Green Version]
- Badlyan, N.M.; Biermann, A.; Aubert, T.; Hens, Z.; Maultzsch, J. Thermal expansion of colloidal CdSe/CdS core/shell quantum dots. Phys. Rev. B 2019, 99, 195425. [Google Scholar] [CrossRef]
- İbrahim, K.; Baskoutas, S. Linear and nonlinear optical absorption coefficients and refractive index changes in spherical quantum dots: Effects of impurities, electric field, size, and optical intensity. J. Appl. Phys. 2008, 103, 073512. [Google Scholar] [CrossRef]
- Xie, W. Impurity effects on optical property of a spherical quantum dot in the presence of an electric field. Phys. B Condens. Matter 2010, 405.16, 3436–3440. [Google Scholar] [CrossRef]
- Baira, M.; Salem, B.; Madhar, N.A.; Ilahi, B. Linear and Nonlinear Intersubband Optical Properties of Direct Band Gap GeSn Quantum Dots. Nanomaterials 2019, 9, 124. [Google Scholar] [CrossRef] [Green Version]
- Liu, C.H.; Xu, B.R. Theoretical study of the optical absorption and refraction index change in a cylindrical quantum dot. Phys. Lett. A 2008, 372, 888–892. [Google Scholar] [CrossRef]
- Pandey, A.; Guyot-Sionnest, P. Intraband spectroscopy and band offsets of colloidal II-VI core/shell structures. J. Chem. Phys. 2007, 127, 104710. [Google Scholar] [CrossRef] [PubMed]
- Duque, C.M.; Mora-Ramos, M.E.; Duque, C.A. Properties of the second and third harmonics generation in a quantum disc with inverse square potential. A modeling for nonlinear optical responses of a quantum ring. J. Lumin. 2013, 138, 53–60. [Google Scholar] [CrossRef]
- Bahramiyan, H.; Khordad, R. Optical properties of a GaAs pyramid quantum dot: Second-and third-harmonic generation. Int. J. Mod. Phys. B 2014, 28, 1450053. [Google Scholar] [CrossRef]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Mantashian, G.A.; Zaqaryan, N.A.; Mantashyan, P.A.; Sarkisyan, H.A.; Baskoutas, S.; Hayrapetyan, D.B. Linear and Nonlinear Optical Absorption of CdSe/CdS Core/Shell Quantum Dots in the Presence of Donor Impurity. Atoms 2021, 9, 75. https://doi.org/10.3390/atoms9040075
Mantashian GA, Zaqaryan NA, Mantashyan PA, Sarkisyan HA, Baskoutas S, Hayrapetyan DB. Linear and Nonlinear Optical Absorption of CdSe/CdS Core/Shell Quantum Dots in the Presence of Donor Impurity. Atoms. 2021; 9(4):75. https://doi.org/10.3390/atoms9040075
Chicago/Turabian StyleMantashian, Grigor A., Nare A. Zaqaryan, Paytsar A. Mantashyan, Hayk A. Sarkisyan, Sotirios Baskoutas, and David B. Hayrapetyan. 2021. "Linear and Nonlinear Optical Absorption of CdSe/CdS Core/Shell Quantum Dots in the Presence of Donor Impurity" Atoms 9, no. 4: 75. https://doi.org/10.3390/atoms9040075
APA StyleMantashian, G. A., Zaqaryan, N. A., Mantashyan, P. A., Sarkisyan, H. A., Baskoutas, S., & Hayrapetyan, D. B. (2021). Linear and Nonlinear Optical Absorption of CdSe/CdS Core/Shell Quantum Dots in the Presence of Donor Impurity. Atoms, 9(4), 75. https://doi.org/10.3390/atoms9040075







