Calculation of the Lowest Resonant States of H− and Li by the Complex Absorbing Potential Method
Abstract
1. Introduction
2. Theory
3. Calculation Method
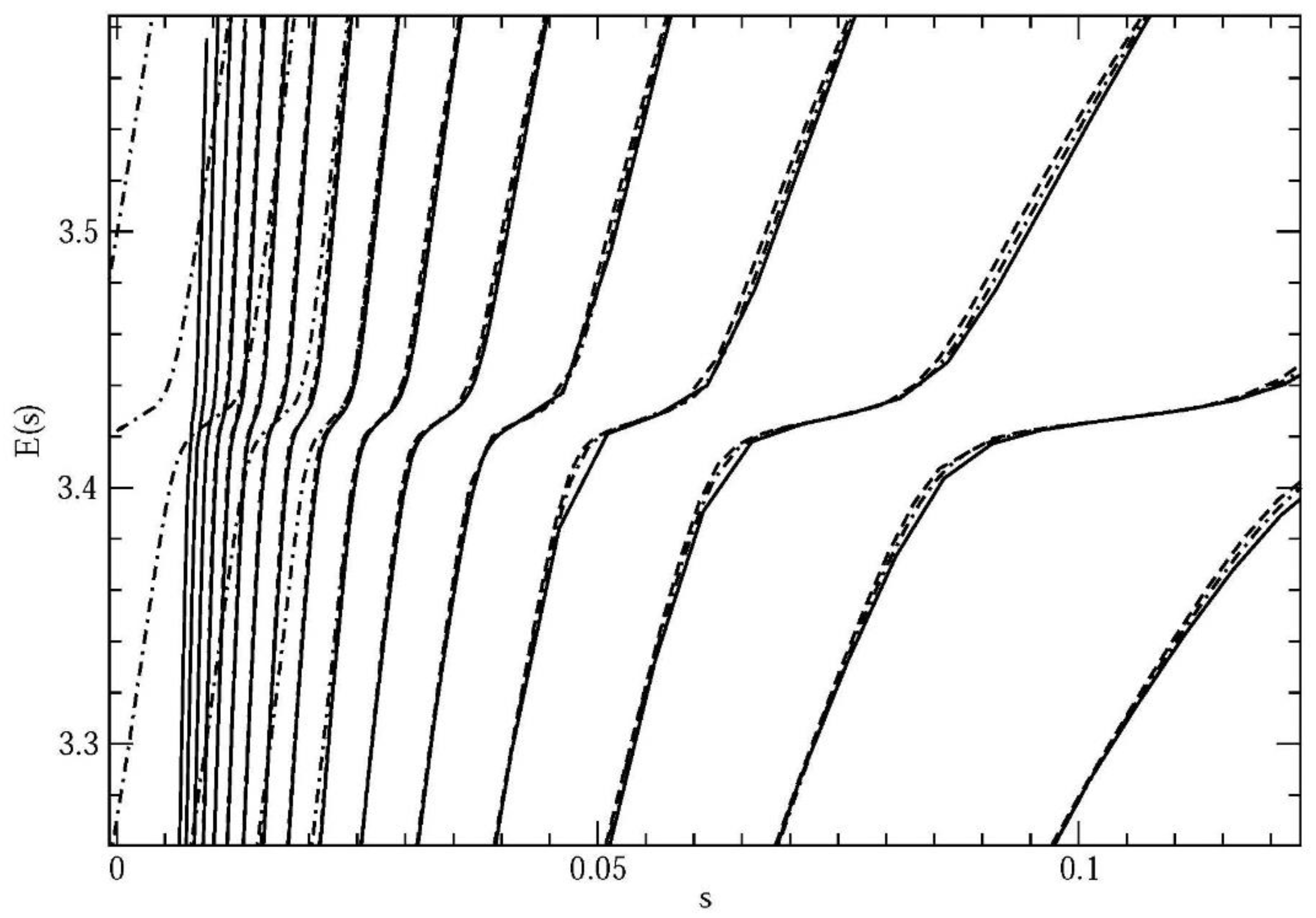
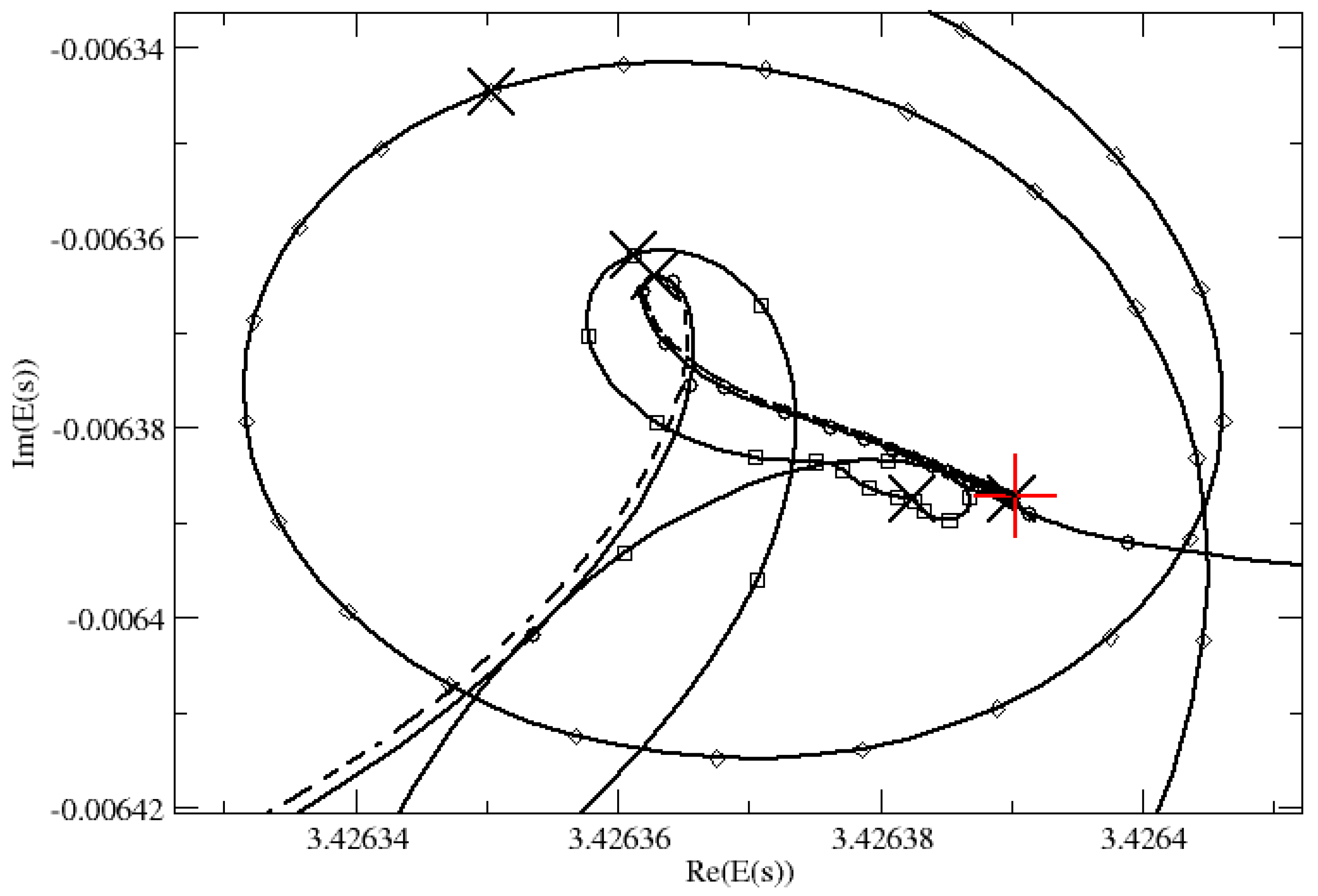
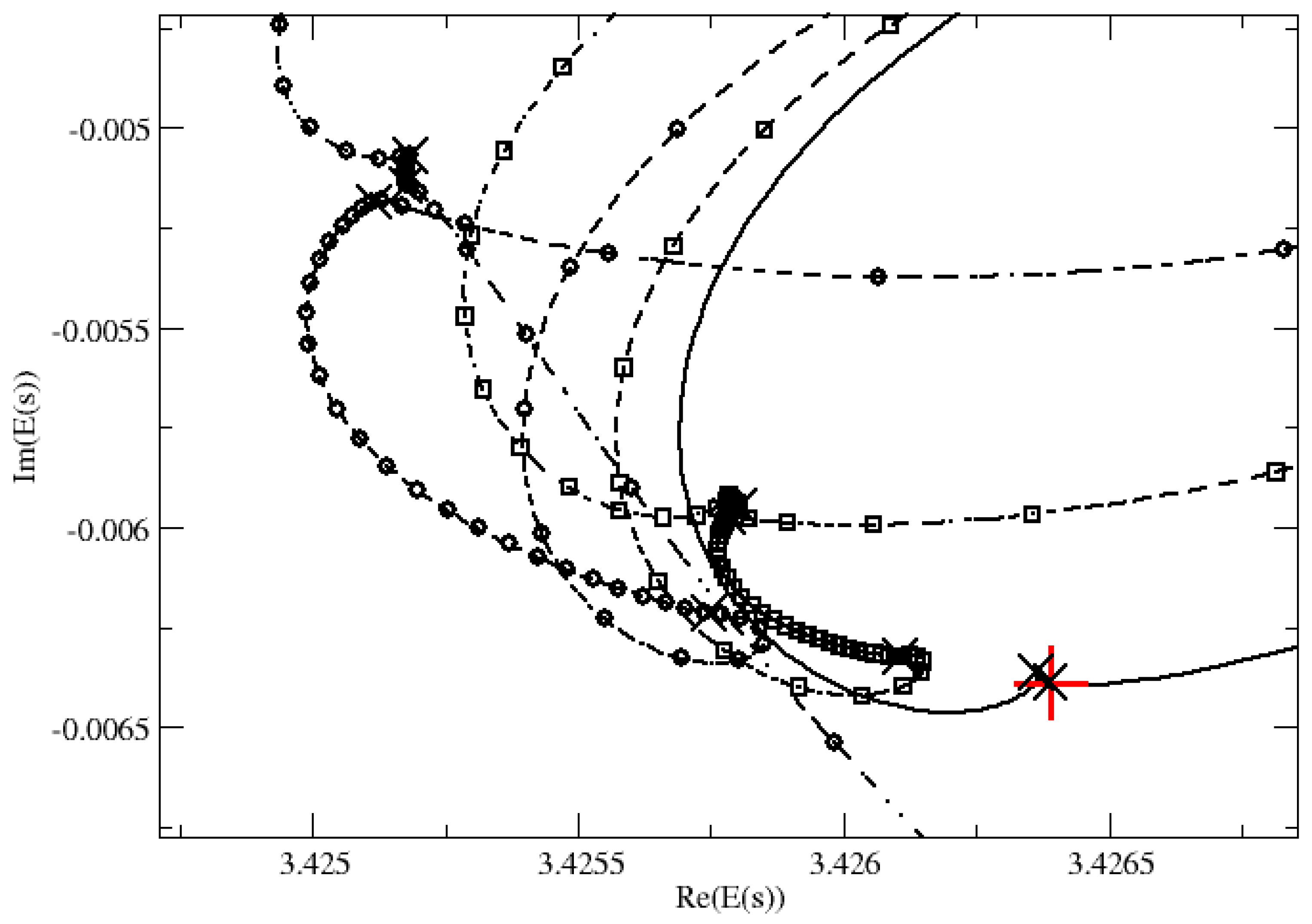
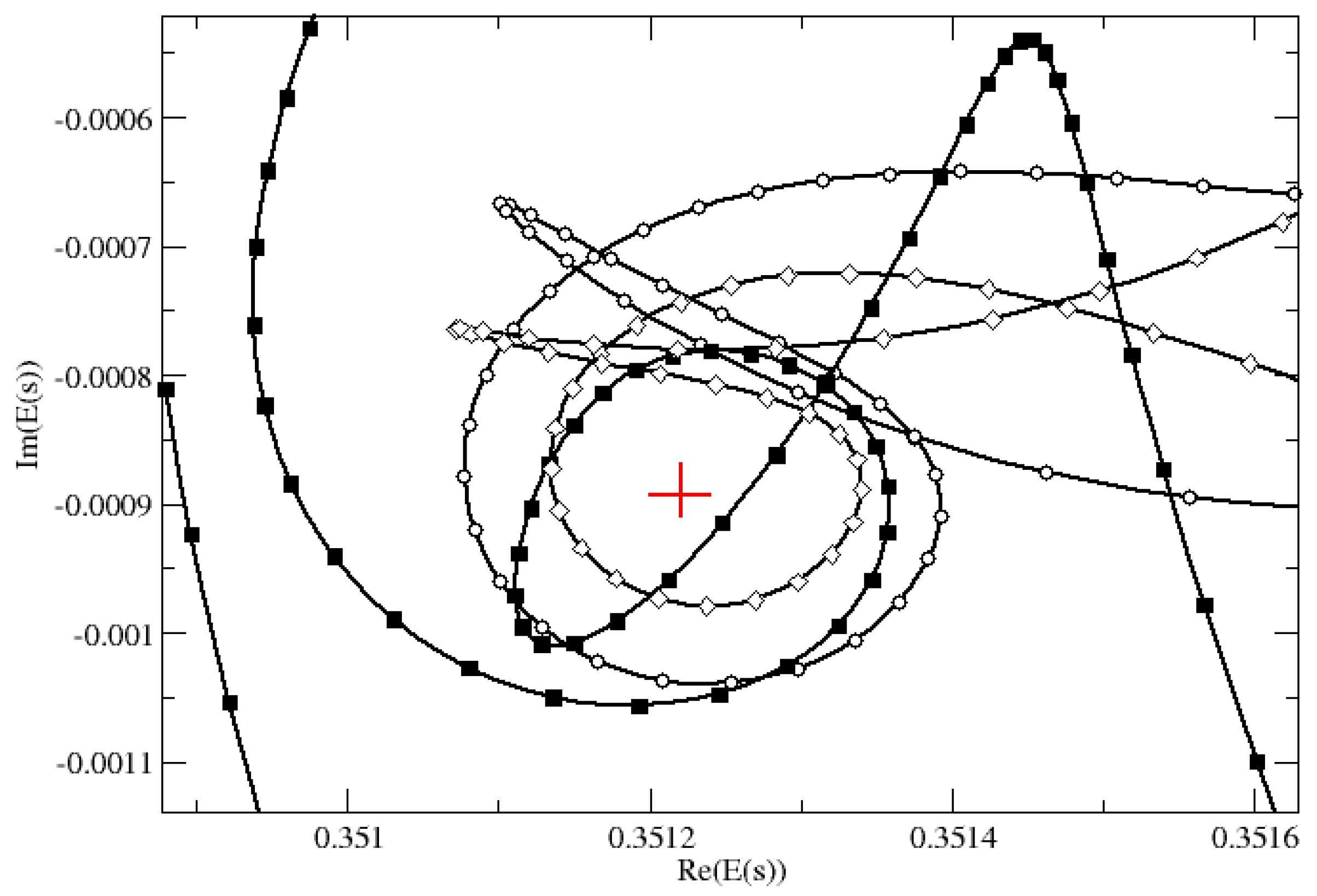
4. Results and Discussion
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Appendix A
References
- Jolicard, G.; Austin, E.J. Optical potential stabilization method for predicting resonance levels. Chem. Phys. Lett. 1985, 121, 106–110. [Google Scholar] [CrossRef]
- Jolicard, G.; Austin, E.J. Optical potential method of calculating resonance energies and widths. Chem. Phys. 1986, 103, 295–302. [Google Scholar] [CrossRef]
- Jolicard, G.; Perrin, M.Y. A perturbational treatment of the resonance eigenvalue problem using the optical potential model. Chem. Phys. 1987, 116, 1–10. [Google Scholar] [CrossRef]
- Jolicard, G.; Humbert, J. Study of the one-channel resonance states. Method without a stabilization procedure in the framework of the optical potential model. Chem. Phys. 1987, 118, 397–405. [Google Scholar] [CrossRef]
- Jolicard, G.; Leforestier, C.; Austin, E.J. Resonance states using the optical potential model. Study of Feshbach resonances and broad shape resonances. J. Chem. Phys. 1988, 88, 1026–1031. [Google Scholar] [CrossRef]
- Rom, N.; Lipkin, N.; Moiseyev, N. Optical potentials by the complex coordinate method. Chem. Phys. 1991, 151, 199–204. [Google Scholar] [CrossRef]
- Riss, U.V.; Meyer, H.D. Calculation of resonance energies and widths using the complex absorbing potential method. J. Phys. B At. Mol. Opt. Phys. 1993, 26, 4503–4536. [Google Scholar] [CrossRef]
- Riss, U.V.; Meyer, H.D. Reflection-free complex absorbing potentials. J. Phys. B At. Mol. Opt. Phys. 1995, 28, 1475–1493. [Google Scholar] [CrossRef]
- Reinhardt, W.P. Complex coordinates in the theory of atomic and molecular structure and dynamics. Ann. Rev. Phys. Chem. 1982, 33, 223–255. [Google Scholar] [CrossRef]
- Sommerfeld, T.; Riss, U.V.; Meyer, H.D.; Cederbaum, L.S. Metastable C22− dianion. Phys. Rev. Lett. 1997, 79, 1237–1240. [Google Scholar] [CrossRef]
- Sommerfeld, T.; Riss, U.V.; Meyer, H.D.; Cederbaum, L.S.; Engels, B.; Suter, H.U. Temporary anions—Calculation of energy and lifetime by absorbing potentials: The resonance. J. Phys. B At. Mol. Opt. Phys. 1998, 31, 4107–4122. [Google Scholar] [CrossRef]
- Sommerfeld, T.; Cederbaum, L.S. Long-lived states of . Phys. Rev. Lett. 1998, 80, 3723–3726. [Google Scholar] [CrossRef]
- Dreuw, A.; Sommerfeld, T.; Cederbaum, L.S. Possible long-lived quartet resonance states of CO−. Theor. Chem. Acc. 1998, 100, 60–64. [Google Scholar] [CrossRef]
- Ingr, M.; Meyer, H.D.; Cederbaum, L.S. Potential energy curve of the X resonance state of computed by CAP/CI. J. Phys. B At. Mol. Opt. Phys. 1999, 32, L547–L556. [Google Scholar] [CrossRef]
- Santra, R.; Cederbaum, L.S.; Meyer, H.D. Electronic decay of molecular clusters: Non-stationary states computed by standard quantum chemistry methods. Chem. Phys. Lett. 1999, 303, 413–419. [Google Scholar] [CrossRef]
- Sahoo, S.; Ho, Y.K. The complex absorbing potential method (CAP) to study the Stark effect in hydrogen and lithium. J. Phys. B At. Mol. Opt. Phys. 2000, 33, 2195–2206. [Google Scholar] [CrossRef]
- Sommerfeld, T. FCN− and FNC− radical anions. Phys. Chem. Chem. Phys. 2001, 3, 2394–2399. [Google Scholar] [CrossRef]
- Sommerfeld, T.; Santra, R. Efficient method to perform CAP/CI calculations for temporary anions. Int. J. Quant. Chem. 2001, 82, 218–226. [Google Scholar] [CrossRef]
- Santra, R.; Cederbaum, L.S. An efficient combination of computational techniques for investigating electronic resonance states in molecules. J. Chem. Phys. 2001, 115, 6853–6861. [Google Scholar] [CrossRef]
- Santra, R.; Cederbaum, L.S. Non-Hermitian electronic theory and applications to clusters. Phys. Rep. 2002, 368, 1–117. [Google Scholar] [CrossRef]
- Sommerfeld, T. Coupling between dipole-bound and valence states: The nitromethane anion. Phys. Chem. Chem. Phys. 2002, 4, 2511–2516. [Google Scholar] [CrossRef]
- Sommerfeld, T.; Meyer, H.D. Computing the energy-dependent width of temporary anions L2 from ab initio methods. J. Phys. B At. Mol. Opt. Phys. 2002, 35, 1841–1863. [Google Scholar] [CrossRef]
- Dreuw, A.; Sommerfeld, T.; Cederbaum, L.S. Short- and long-lived electronic states of BF−. J. Chem. Phys. 2002, 116, 6039–6044. [Google Scholar] [CrossRef]
- Feuerbacher, S.; Sommerfeld, T.; Santra, R.; Cederbaum, L.S. Complex absorbing potentials in the framework of electron propagator theory. II. Application to temporary anions. J. Chem. Phys. 2003, 118, 6188–6199. [Google Scholar] [CrossRef]
- Muga, J.G.; Palao, J.P.; Navarro, B.; Equsquiza, I.L. Complex absorbing potentials. Phys. Rep. 2004, 395, 357–426. [Google Scholar] [CrossRef]
- Sajeev, Y.; Santra, R.; Pal, S. Analytically continued Fock space multireference coupled-cluster theory: Application to the 2Πg shape resonance in e-N2 scattering. J. Chem. Phys. 2005, 122, 234320. [Google Scholar] [CrossRef]
- Sajeev, Y.; Santra, R.; Pal, S. Correlated complex independent particle potential for calculating electronic resonances. J. Chem. Phys. 2005, 123, 204110:1–204110:10. [Google Scholar] [CrossRef]
- Sajeev, Y.; Vysotskiy, V.; Cederbaum, L.S.; Moiseyev, N. Continuum remover-complex absorbing potential: Efficient removal of the nonphysical stabilization points. J. Chem. Phys. 2009, 131, 211102:1–211102:4. [Google Scholar] [CrossRef]
- Ehara, M.; Sommerfeld, T. CAP/SAC-CI method for calculating resonance states of metastable anions. Chem. Phys. Lett. 2012, 537, 107–112. [Google Scholar] [CrossRef]
- Ghosh, A.; Vaval, N.; Pal, S.; Bartlett, R.J. Complex absorbing potential based equation-of-motion coupled cluster method for the potential energy curve of CO2−. J. Chem. Phys. 2014, 141, 164113:1–164113:6. [Google Scholar] [CrossRef]
- Ghosh, A.; Vaval, N.; Pal, S. Equation-of-motion coupled-cluster method for the study of shape resonance. J. Chem. Phys. 2012, 136, 234110:1–234110:6. [Google Scholar] [CrossRef]
- Jagau, T.C.; Zuev, D.; Bravaya, K.B.; Epifanovsky, E.; Krylov, A.I. A fresh look at resonances and complex absorbing potentials: Density matrix-based approach. J. Phys. Chem. Lett. 2014, 5, 310–315, J. Phys. Chem. Lett.2015, 6, 3866. [Google Scholar] [CrossRef]
- Zuev, D.; Jagau, T.C.; Bravaya, K.B.; Epifanovsky, E.; Shao, Y.; Sundstrom, E.; Head-Gordon, M.; Krylov, A.I. Complex absorbing potentials within EOM-CC family of methods: Theory, implementation, and benchmarks. J. Chem. Phys. 2014, 141, 024102:1–024102:19, Erratum: J Chem. Phys. 2015, 143, 149901:1. [Google Scholar] [CrossRef]
- Jagau, T.C.; Krylov, A.I. Complex absorbing potential equation-of-motion coupled-cluster method yields smooth and internally consistent potential energy surfaces and lifetimes for molecular resonances. J. Phys. Chem. Lett. 2014, 5, 3078–3085. [Google Scholar] [CrossRef]
- Jagau, T.C.; Dao, D.B.; Holtgrewe, N.S.; Krylov, A.I.; Mabbs, R. Same but different: Dipole-stabilized shape resonances in CuF− and AgF−. J. Phys. Chem. Lett. 2015, 6, 2786–2793. [Google Scholar] [CrossRef]
- Ehara, M.; Fukuda, R.; Sommerfeld, T. Projected CAP/SAC-CI method with smooth Voronoi potential for calculating resonance states. J. Comp. Chem. 2016, 37, 242–249. [Google Scholar] [CrossRef]
- Kunitsa, A.A.; Bravaya, K.B. First-principles calculations of the energy and width of the 2Au shape resonance in p-benzoquinone: A gateway state for electron transfer. J. Phys. Chem. Lett. 2015, 6, 1053–1058. [Google Scholar] [CrossRef]
- Kanazawa, Y.; Ehara, M.; Sommerfeld, T. Low-lying π* resonances of standard and rare DNA and RNA bases studied by the projected CAP/SAC–CI method. J. Phys. Chem. A 2016, 120, 1545–1553. [Google Scholar] [CrossRef]
- Jagau, T.C.; Krylov, A.I. Characterizing metastable states beyond energies and lifetimes: Dyson orbitals and transition dipole moments. J. Chem. Phys. 2016, 144, 054113:1–054113:10. [Google Scholar] [CrossRef]
- Jagau, T.C.; Bravaya, K.B.; Krylov, A.I. Extending quantum chemistry of bound states to electronic resonances. Ann. Rev. Phys. Chem. 2017, 68, 525–553. [Google Scholar] [CrossRef]
- Kunitsa, A.A.; Granovsky, A.A.; Bravaya, K.B. CAP-XMCQDPT2 method for molecular electronic resonances. J. Chem. Phys. 2017, 146, 184107:1–184107:8. [Google Scholar] [CrossRef]
- Ehara, M.; Kanazawa, Y.; Sommerfeld, T. Low-lying π* resonances associated with cyano groups: A CAP/SAC-CI study. Chem. Phys. 2017, 482, 169–177. [Google Scholar] [CrossRef]
- White, A.F.; Epifanovsky, E.; McCurdy, C.W.; Head-Gordon, M. Second order Moller-Plesset and coupled cluster singles and doubles methods with complex basis functions for resonances in electron-molecule scattering. J. Chem. Phys. 2017, 146, 234107:1–234107:10. [Google Scholar] [CrossRef] [PubMed]
- Thodika, M.; Fennimore, M.; Karsili, T.N.V.; Matsika, S. Comparative study of methodologies for calculating metastable states of small to medium-sized molecules. J. Chem. Phys. 2019, 151, 244104:1–244104:16. [Google Scholar] [CrossRef] [PubMed]
- Phung, Q.M.; Komori, Y.; Yanai, T.; Sommerfeld, T.; Ehara, M. Combination of a Voronoi-type complex absorbing potential with the XMS-CASPT2 method and pilot applications. J. Chem. Theor. Comp. 2020, 16, 2606–2616. [Google Scholar] [CrossRef] [PubMed]
- Adamson, S.O.; Kharlampidi, D.D.; Golubkov, G.V.; Dyakov, Y.A.; Morozov, I.I.; Shestakov, D.V.; Golubkov, M.G. Calculation of the lowest resonance 1S state of H− ion by complex absorbing potential method. Russ. J. Phys. Chem. B 2020, 14, 742–751. [Google Scholar] [CrossRef]
- Belogolova, A.V.; Dempwolff, A.I.; Dreuw, A.; Trofimov, A.V. A complex absorbing potential electron propagator approach to resonance states of metastable anions. J. Phys. Conf. Ser. 2021, 1847, 012050:1–012050:10. [Google Scholar] [CrossRef]
- Bylicki, M.; Nicolaides, C.A. Theoretical resolution of the H− resonance spectrum up to the n = 4 threshold. II. States of 1S and 1D symmetries. Phys. Rev. A 2000, 61, 052509:1–052509:10. [Google Scholar] [CrossRef]
- Bylicki, M. The Hermitian representation of the complex-rotation method and its application to the 1s2s2 2S resonance of He−. J. Phys. B At. Mol. Opt. Phys. 1991, 24, 413–422. [Google Scholar] [CrossRef]
- Gopalan, A.; Bömmels, J.; Götte, S.; Landwehr, A.; Franz, K.; Ruf, M.-W.; Hotop, H.; Bartschat, K. A novel electron scattering apparatus combining a laser photoelectron source and a triply differentially pumped supersonic beam target: Characterization and results for the resonance. Eur. Phys. J. D 2003, 22, 17–29. [Google Scholar] [CrossRef]
- Cederquist, H.; Mannervik, S. On the core-excited doublets of Li I: Accurate determination of autoionisation rates. J. Phys. B At. Mol. Phys. 1982, 15, L807–L812. [Google Scholar] [CrossRef]
- Mannervik, S.; Cederquist, H. Absolute term energies of core-excited doublets of Li I determined experimentally. Phys. Scr. 1985, 31, 79–82. [Google Scholar] [CrossRef]
- Cederquist, H.; Mannervik, S. Autoionizing states in Li I observed in optical-emission spectra. Phys. Rev. A 1985, 31, 171–176. [Google Scholar] [CrossRef]
- Cardona, J.C.; Sanz-Vicario, J.L.; Martín, F. Complete Feshbach-type calculations of energy positions and widths of autoionizing states Li-like atoms. Phys. Rev. A 2010, 82, 022501:1–022501:13. [Google Scholar] [CrossRef]
- Landau, A.; Moiseyev, N. Molecular resonances by removing complex absorbing potentials via Padé; Application to CO− and N2−. J. Chem. Phys. 2016, 145, 164111:1–164111:8. [Google Scholar] [CrossRef]
- Ehrhardt, H.; Langhans, L.; Linder, F.; Taylor, H.S. Resonance scattering of slow electrons from H2 and CO angular distributions. Phys. Rev. 1968, 173, 222–230. [Google Scholar] [CrossRef]
- Berman, M.; Estrada, H.; Cederbaum, L.S.; Domcke, W. Nuclear dynamics in resonant electron-molecule scattering beyond the local approximation: The 2.3-eV shape resonance in N2. Phys. Rev. A 1983, 28, 1363–1381. [Google Scholar] [CrossRef]
- Lefebvre, R.; Sindelka, M.; Moiseyev, N. Resonance positions and lifetimes for flexible complex absorbing potentials. Phys. Rev. A 2005, 72, 052704:1–052704:6. [Google Scholar] [CrossRef]
- Bloch, C. Une formulation unifiée la théorie des réactions nucléares. Nucl. Phys. 1957, 4, 503–528. [Google Scholar] [CrossRef]
- Zvijac, D.J.; Heller, E.J.; Light, J.C. Variational correction to Wigner R-matrix theory of scattering. J. Phys. B At. Mol. Opt. Phys. 1975, 8, 1016–1033. [Google Scholar] [CrossRef]
- Halley, M.H.; Delande, D.; Taylor, K.T. The combination of R-matrix and complex coordinate methods: Application to resonances in the diamagnetic Rydberg spectra of Li. J. Phys. B At. Mol. Opt. Phys. 1992, 25, L525–L532. [Google Scholar] [CrossRef]
- Halley, M.H.; Delande, D.; Taylor, K.T. The combination of R-matrix and complex coordinate methods: Application to the diamagnetic Rydberg spectra of Ba and Sr. J. Phys. B At. Mol. Opt. Phys. 1993, 26, 1775–1790. [Google Scholar] [CrossRef]
- Huarte-Larranaga, F.; Gimenez, H.; Aguilar, A.; Baer, M. On the accuracy of reactive scattering calculations with absorbing potentials: A new implementation based on a generalized R-matrix propagation. Chem. Phys. Lett. 1998, 291, 346–350. [Google Scholar] [CrossRef]
- Huarte-Larranaga, F.; Gimenez, H.; Aguilar, A. The application of complex absorbing potentials to an invariant embedding scattering method: I. Theory and computational details. J. Chem. Phys. 1998, 109, 5761–5769. [Google Scholar] [CrossRef]
- Huarte-Larranaga, F.; Gimenez, H.; Lucas, J.M.; Aguilar, A. The application of complex absorbing potentials to an invariant embedding scattering method. II. Applications. J. Chem. Phys. 1999, 111, 1979–1987. [Google Scholar] [CrossRef]
- Szegö, G. Orthogonal Polynomials; American Mathematical Society: Providence, RI, USA, 1939; p. 432. ISBN 978-147-043-171-6. [Google Scholar]
- Akhiezer, N.I.; Glazman, A.I. Theory of Linear Operators in Hilbert Space; Pittman Publishing Inc.: Marshfield, MA, USA, 1981; p. 347. ISBN 027-308-495-X. [Google Scholar]
- Bateman, H.; Erdelyi, A. Higher Transcendental Functions; McGraw-Hill Book Company, Inc.: New York, NY, USA, 1953; p. 324. ISBN 089-874-206-4. [Google Scholar]
- Kazmin, Y.A. On subsequences of Hermite and Laguerre polynomials. Vestn. Mosk. Univ. Ser. Mat. Mekhaniki 1960, 2, 6–9. [Google Scholar]
- Ryndina, V.V. Approximation by Laguerre polynomials in the complex domain. Izv. Akad. Nauk. USSR Ser. Mat. 1962, 26, 143–160. [Google Scholar]
- Gradshteyn, I.S.; Ryzhik, I.M. Table of Integrals, Series and Products; Academic Press, Inc.: New York, NY, USA, 1980; p. 1191. ISBN 012-294-760-6. [Google Scholar]
- Davies, K.T.R.; Baranger, M. Symmetry properties of the S-matrix with application to resonance reactions. Ann. Phys. 1962, 19, 383–427. [Google Scholar] [CrossRef]
- Bain, R.A.; Bardsley, J.N.; Junker, B.R.; Sukumar, C.V. Complex coordinate studies of resonant electron-atom scattering. J. Phys. B At. Mol. Opt. Phys. 1974, 7, 2189–2202. [Google Scholar] [CrossRef]
- Zhang, S.; Jin, J. Computation of Special Functions; John Wiley & Sons: New York, NY, USA, 1996; p. 717. ISBN 047-111-963-6. [Google Scholar]
- Ting, T.C.T. A method of solving a system of linear equations whose coefficients form a tridiagonal matrix. Quart. Appl. Math. 1964, 22, 105–116. [Google Scholar] [CrossRef][Green Version]
- Pedrotti, K.D. Extinction spectroscopy: A novel laser spectroscopic technique. Opt. Commun. 1987, 62, 250–255. [Google Scholar] [CrossRef]
- Cantù, A.M.; Parkinson, W.H.; Tondello, G.; Tozzi, G.P. Observations of Li i and Li ii absorption spectra in the grazing incidence region. J. Opt. Soc. Am. 1977, 67, 1030–1033. [Google Scholar] [CrossRef]
- Ederer, D.L.; Lucatorto, T.; Madden, R.P. Autoionization Spectra of Lithium. Phys. Rev. Lett. 1970, 25, 1537–1539. [Google Scholar] [CrossRef]
- Davis, B.; Chung, K.T. Widths of 2S, 2Po, and 2D resonances in Li I, Be II, and B III. Phys. Rev. A 1985, 31, 3017–3026. [Google Scholar] [CrossRef]
- Chung, K.T. Photoionization of lithium below the Li+ 1s2s3 S threshold. Phys. Rev. A 1997, 56, R3330–R3333. [Google Scholar] [CrossRef]
- Zatsarinny, O.; Fischer, C.F. The use of basis splines and nonorthogonal orbitals in R-matrix calculations: Application to Li photoionization. J. Phys. B At. Mol. Opt. Phys. 2000, 33, 313–342. [Google Scholar] [CrossRef]
- Verbockhaven, G.; Hansen, J.E. Energies and autoionization widths in the lithium isoelectronic sequence. J. Phys. B At. Mol. Opt. Phys. 2001, 34, 2337–2361. [Google Scholar] [CrossRef]
- Adamson, S.; Kharlampidi, D.; Preobrazhenskaya, A.A.; Dementiev, A. Calculation of the lowest 2S resonance state of He− by a stabilization method. Russ. J. Phys. Chem. B 2017, 11, 894–902. [Google Scholar] [CrossRef]
- Adamson, S.; Kharlampidi, D.; Dementiev, A. Application of the uniformly charged sphere stabilization for calculating the lowest 1S resonances of H−. In Advances in Quantum Methods and Applications in Chemistry, Physics, and Biology. Progress in Theoretical Chemistry and Physics; Hotokka, M., Brandas, E., Maruani, J., Delgado-Barrio, G., Eds.; Springer: Cham, Switzerland, 2012; Volume 27, pp. 101–118. ISBN 978-331-901-528-6. [Google Scholar]
- Preobrazhenskaya, A.A.; Adamson, S.O.; Kharlampidi, D.D.; Dement’ev, A.I. Calculation of the lowest 1S resonance state of the H− anion by the stabilization method. Russ. J. Phys. Chem. B 2014, 8, 22–29. [Google Scholar] [CrossRef]
- Preobrazhenskaya, A.A.; Adamson, S.O.; Kharlampidi, D.D.; Dementiev, A.I. Ab initio calculations of lower resonant states of two-electron systems. Russ. J. Phys. Chem. B 2016, 10, 133–142. [Google Scholar] [CrossRef]
- Adamson, S.; Kharlampidi, D.; Dementiev, A. Stabilization of resonance states by an asymptotic Coulomb potential. J. Chem. Phys. 2008, 128, 024101:1–024101:7. [Google Scholar] [CrossRef] [PubMed]



| 0.01 | 0.0031 | 3.426390 | 0.006388 | 0.0031 | 3.426441 | 0.006375 |
| 0.01 | 1.0803 | 3.426363 | 0.006364 | 1.0803 | 3.426443 | 0.006411 |
| 0.12 | 0.1760 | 3.426382 | 0.006388 | 0.1608 | 3.426446 | 0.006380 |
| 0.12 | 1.0560 | 3.426361 | 0.006362 | 1.0560 | 3.426443 | 0.006414 |
| 0.36 | 1.0324 | 3.426350 | 0.006345 | 1.0142 | 3.426441 | 0.006435 |
| N | |||||||
|---|---|---|---|---|---|---|---|
| 0.01 | 100 | 0.0016 | 3.425115 | 0.005185 | 0.0017 | 3.426867 | 0.008752 |
| 100 | 0.7347 | 3.425747 | 0.006216 | 0.7438 | 3.426845 | 0.006961 | |
| 600 | 0.0018 | 3.425785 | 0.005974 | 0.0018 | 3.426641 | 0.007170 | |
| 600 | 0.6559 | 3.426108 | 0.006324 | 0.6622 | 3.426608 | 0.006624 | |
| 0.12 | 100 | 0.0579 | 3.425567 | 0.005875 | 0.0576 | 3.426796 | 0.007439 |
| 100 | 0.6863 | 3.425744 | 0.006194 | 0.6883 | 3.426835 | 0.007100 | |
| 600 | 0.1227 | 3.426042 | 0.006248 | 0.1157 | 3.426605 | 0.006735 | |
| 600 | 0.6494 | 3.426105 | 0.006318 | 0.6494 | 3.426604 | 0.006629 | |
| 0.36 | 100 | 0.6622 | 3.425754 | 0.006172 | 0.6621 | 3.426812 | 0.006999 |
| 600 | 0.6751 | 3.426096 | 0.006321 | 0.6751 | 3.426614 | 0.006633 | |
| N | |||||||
|---|---|---|---|---|---|---|---|
| 0.01 | 100 | 0.00085 | 3.425175 | 0.005144 | 0.00085 | 3.426723 | 0.008766 |
| 100 | 1.29522 | 3.425184 | 0.005068 | 1.29517 | 3.426633 | 0.008886 | |
| 600 | 0.00006 | 3.425804 | 0.005947 | 0.00006 | 3.426600 | 0.007182 | |
| 600 | 1.10547 | 3.425784 | 0.005917 | 1.09122 | 3.426597 | 0.007227 | |
| 0.12 | 100 | 0.00446 | 3.425645 | 0.005787 | 0.00437 | 3.426641 | 0.007474 |
| 100 | 1.13039 | 3.425628 | 0.005754 | 1.13039 | 3.426633 | 0.007523 | |
| 600 | 0.00035 | 3.426059 | 0.006163 | 0.00034 | 3.426531 | 0.006789 | |
| 600 | 1.10547 | 3.426035 | 0.006138 | 1.09122 | 3.426532 | 0.006828 | |
| 0.36 | 100 | 0.00855 | 3.425804 | 0.005947 | 0.00862 | 3.426599 | 0.007181 |
| 600 | 1.10547 | 3.425785 | 0.005919 | 1.10505 | 3.426597 | 0.007225 | |
| λ | A | B | ||
|---|---|---|---|---|
| −Eres | Г | −Eres | Г | |
| 1.00 | 0.3512175 | 172.73 | 0.3512240 | 132.32 |
| 1.20 | 0.3512303 | 176.65 | 0.3511645 | 144.03 |
| 1.40 | 0.3512224 | 176.73 | 0.3510555 | 164.30 |
| 1.60 | 0.3512307 | 179.65 | 0.3513016 | 199.75 |
| 1.80 | 0.3512312 | 178.95 | 0.3511226 | 193.48 |
| Averaged value a | 0.3512250 | 175.83 | 0.3512137 | 164.51 |
| Reference value b | 0.35122025/173.870 | |||
| λ | 2P0 [1s(2s2p) 3P] | 2P0 [1s(2s2p) 1P] | ||||||
|---|---|---|---|---|---|---|---|---|
| A | B | A | B | |||||
| −Eres | Г | −Eres | Г | −Eres | Г | −Eres | Г | |
| 3.1 | 5.312252 | 11.55 | 5.312185 | 13.46 | 5.256965 | 35.74 | 5.256806 | 23.22 |
| 3.3 | 5.312212 | 12.95 | 5.312199 | 4.62 | 5.256608 | 46.32 | - | - |
| 3.5 | 5.312070 | 11.70 | 5.312001 | 14.08 | 5.256063 | 34.58 | 5.255900 | 22.91 |
| 3.7 | 5.311837 | 13.11 | 5.311827 | 4.50 | 5.255298 | 44.33 | 5.255332 | 14.07 |
| Averaged value a | 5.312107 | 13.33 | 5.312083 | 7.67 | 5.256247 | 39.97 | 5.256179 | 20.02 |
| Experimental and theoretical values | ||||||||
| 5.31307(3)/9.6(4) b | ||||||||
| 5.31183/13.5 c | 5.25624/34.5 c | |||||||
| 5.256864/36.79 d | ||||||||
| λ | 2P0 [1s(2s2p) 3P] | 2P0 [1s(2s2p) 1P] | ||||||
|---|---|---|---|---|---|---|---|---|
| 1 | 2 | 1 | 2 | |||||
| −Eres | Г | −Eres | Г | −Eres | Г | −Eres | Г | |
| 3.1 | 5.312253 | 14.02 | 5.312252 | 11.55 | 5.256920 | 40.71 | 5.256965 | 35.74 |
| 3.3 | 5.312205 | 10.08 | 5.312212 | 12.95 | 5.256598 | 33.97 | 5.256608 | 46.32 |
| 3.5 | 5.312082 | 14.33 | 5.312070 | 11.70 | 5.256039 | 43.46 | 5.256063 | 34.58 |
| 3.7 | 5.311828 | 10.05 | 5.311837 | 13.11 | 5.255292 | 32.61 | 5.255298 | 44.33 |
| Averaged value a | 5.312106 | 11.98 | 5.312107 | 13.33 | 5.256243 | 38.37 | 5.256247 | 39.97 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Adamson, S.O.; Kharlampidi, D.D.; Dyakov, Y.A.; Golubkov, G.V.; Golubkov, M.G. Calculation of the Lowest Resonant States of H− and Li by the Complex Absorbing Potential Method. Atoms 2021, 9, 72. https://doi.org/10.3390/atoms9040072
Adamson SO, Kharlampidi DD, Dyakov YA, Golubkov GV, Golubkov MG. Calculation of the Lowest Resonant States of H− and Li by the Complex Absorbing Potential Method. Atoms. 2021; 9(4):72. https://doi.org/10.3390/atoms9040072
Chicago/Turabian StyleAdamson, Sergey O., Daria D. Kharlampidi, Yurii A. Dyakov, Gennady V. Golubkov, and Maxim G. Golubkov. 2021. "Calculation of the Lowest Resonant States of H− and Li by the Complex Absorbing Potential Method" Atoms 9, no. 4: 72. https://doi.org/10.3390/atoms9040072
APA StyleAdamson, S. O., Kharlampidi, D. D., Dyakov, Y. A., Golubkov, G. V., & Golubkov, M. G. (2021). Calculation of the Lowest Resonant States of H− and Li by the Complex Absorbing Potential Method. Atoms, 9(4), 72. https://doi.org/10.3390/atoms9040072






