Abstract
A detailed study of positron impact elastic scattering from methane and silane is carried out using a model potential consisting of static and polarization potentials. The static potential for the molecular target is obtained analytically by using accurate Gaussian molecular wavefunctions. The molecular orbitals are expressed as a linear combination of Gaussian atomic orbitals. Along with the analytically obtained static potential, a correlation polarization potential is also added to construct the model potential. Utilizing the model potential, the Schrödinger equation is solved using the partial wave phase shift analysis method, and the scattering amplitude is obtained in terms of the phase shifts. Thereafter, the differential, integrated and total cross sections are calculated. These cross-section results are compared with the previously reported measurements and theoretical calculations.
1. Introduction
Studies on positron scattering from atoms and molecules are important due to their relevance in understanding different plasma and astronomical environments [1,2]. Positrons are produced mainly in the beta decay process from radioactive isotopes or through the interaction of the gamma–rays radiated from radioactive nuclei with matter. Additionally, in astronomical environments, positron annihilation radiation has been detected from various directions of the Milky Way galaxy, particularly from its central region [3]. The gamma–rays from the positron-emitting radionuclide are detected in positron emission tomography (PET) scanners for determining the metabolic activity through three-dimensional images of a human body [4]. The positron annihilation spectroscopy (PAS) is widely used in material science to identify defects, density alterations and displacements within a solid material [5].
In the recent review of Brunger et al. [6], they mentioned the previously available measurements and theoretical calculations and reported the recommended positron-molecule scattering cross sections. These cross section results are very important in the different positron transport simulations [7,8]. According to Brunger et al. [6], there are very few reports on the positron-molecule scattering cross-section results and more experimental and theoretical studies are required in this direction. Therefore, in the present work, we study positron impact elastic scattering from methane (CH4) and silane (SiH4) which are simple symmetrical molecules. Interaction of positrons with these molecules casts light on the various processes taking places in the plasma and astronomical environments [9,10,11]. In fact, the scattering cross-section results from such molecules are the basic inputs for the characterization of their plasma.
There is very little attention paid to positron impact elastic scattering studies from CH4 and SiH4 molecules, especially for the differential cross section (DCS). The only experimental DCS results for CH4 are available from Przybyla et al. [12], who performed the relative DCS measurements with angular distribution ranging from 30° to 135° in the incident positron energy range 4–200 eV. On the theoretical end, a few old calculations from Jain [13], Jain and Thompson [14,15] and Jain and Gianturco [16] are available for positron-CH4 scattering. These calculations are based on the optical model potential method using different polarization and correlation potentials. Out of these calculations, Jain and Gianturco [16] presented the detailed DCS and integrated cross section (ICS) results from 0.2 eV to 200 eV incident positron energy by employing a parameter-free model polarization potential within the density function description of the target correlation. Further, there are no specific experimental results available for ICS; however, a few theoretical calculations have been reported in the low energy region. Zecca et al. [17] calculated the ICS results in the energy range of 0.001 eV to 10 eV using the Schwinger multichannel method at both static and static plus polarization levels of approximation. Franz [18] performed the ICS calculations up to 10 eV by taking different forms of short-range correlation polarization potentials. In contrast, for the total cross section (TCS) results, several measurements and theoretical calculations have been reported in the past. Charlton et al. [19] measured the TCS for positron-CH4 scattering in the incident positron energy range from 15 eV to 600 eV by using a slow positron beam time of flight (TOF) system. Further, with the minor modifications in the experimental set up, the same group of Charlton [20] reported TCS results in the low energy range from 2 eV to 20 eV. Floeder et al. [21] measured the TCS results in the incident positron energy from 5 eV to 400 eV by producing the low-energy positrons using a combination of the 22Na positron emitter and tungsten-vane moderator. Dababneh et al. [22] used a beam transmission technique and carried out the measurements in the range of 1 eV to 500 eV positron energy. Sueoka and Mori [23] reported the positron impact total cross section in the energy range varying from 0.7 eV to 400 eV, using a retarding potential TOF method. Zecca et al. [17] reported the latest TCS measurements for positron-CH4 scattering in the incident positron energy ranging from 0.1 eV to 50 eV. On the theoretical side, Jain [24] performed the TCS calculations for 2–600 eV positron energies by taking three different positronium formation energies and using a local spherically complex optical potential (SCOP). Further, Baluja and Jain [25] reported the TCS results up to 5000 eV. Raizada and Baluja [26] calculated TCS using the additivity rule in the energy range from 10 eV to 5000 eV. Recently, Singh et al. [27] employed a modified spherically complex optical potential (mSCOP) to calculate the TCS results for CH4 in the incident positron energy range from the positronium formation threshold to 5000 eV.
There are no experimental DCS results reported for the positron-SiH4 scattering; only old theoretical calculations of Jain [28], Gianturco et al. [29], and Jain and Gianturco [16] are available in the literature. However, recently, Barbosa and Bettega [30] performed the Schwinger multichannel approach calculations to find the DCS and ICS results for positron scattering from SiH4 in the incident positron impact energies up to 10 eV. Similar to CH4, there are no specific measurements for the ICS results. Further, only a few results have been reported for TCS. For example, Sueoka et al. [31] measured the TCS for positron-SiH4 scattering in the 0.7–400 eV incident positron energy range, using a TOF set up with a retarding potential method (RP–TOF). Besides this experimental work, Baluja and Jain [25] calculated TCS up to 5 keV, using SCOP formalism. Further, Raizada and Baluja [32] reported the TCS results using the additivity rule in the energy range from 10 eV to 5000 eV. Sinha et al. [33] calculated the TCS for the 1 eV to 5 keV incident positron energy region with SCOP formalism.
Recently, we successfully applied our analytical static potential approach to study the electron and positron impact elastic scattering from some molecular targets [34,35,36]. In the present work, we extend our method to report the different cross section results for positron scattering from CH4 and SiH4 in a wide range of incident positron energies of 1–500 eV. We calculate the charge densities of these molecules by using the STO-6G Gaussian wavefunction obtained from GAUSSIAN 16 software with the Hartree–Fock method. Subsequently, the static potential is calculated analytically in a fixed molecular frame of reference. We construct the model potential consisting of the calculated static potential, adding to it the suitable polarization potential. This potential is further used in the Schrödinger equation to solve the scattering problem by adopting the method of partial wave phase shift analysis [37,38]. The scattering amplitude in terms of the phase shift is obtained. Thereafter, the differential and integrated cross-section results are calculated, utilizing the scattering amplitude in a conventional manner. Additionally, we also add the imaginary part of the potential, i.e., the absorption potential to the model potential, and calculate the TCS which takes into account all the inelastic scattering channels. In our present work, we do not explicitly consider the positronium formation contribution while calculating TCS. Here, our focus is to study positron-CH4/SiH4 elastic scattering. In addition, the effect of the positronium formation is known to affect the magnitude and nature of TCS more only at low incident positron energies.
In the next section, we describe the theoretical methodology adopted, and the results are presented and discussed in Section 3.
2. Theoretical Methodology
The interaction between the incident positron with the target molecule is similar to that of electron scattering; only the sign of the interaction potential changes. Additionally, the exchange part is dropped for positron scattering, as it is only applicable for electron scattering due to its indistinguishability with the target electrons. At an arbitrary point r from the center of mass of the molecule, the static potential of the target molecule as experienced by the projectile positron can be expressed as
Here, the first term in Equation (1) stands for the nuclear charge distribution, and the second term is due to the electronic contribution. Here, Z is the total charge of the target molecule. The molecular electronic charge density p(r′) at point r′ can be written in terms of the molecular wavefunction by taking its square modulus. Further, the molecular orbitals are expressed as a linear combination of the Gaussian atomic orbitals. As a result, the charge density p(r′) can be written as [39]
Here, represents the molecular orbital coefficient, Nkj refers to the normalization constants and denotes the coefficients of the un–normalized form of the Gaussian basis function . Here, summations over i and k are, respectively, on the number of molecular orbitals and the total number of atomic orbitals, while j is over the Gaussian basis which is taken as 6 in the present case. We obtain the STO-6G Gaussian wavefunction and its related constants in Equation (2) using the GAUSSIAN 16 software with the Hartree–Fock method. The choice of taking the STO-6G basis set of the Gaussian wavefunctions provides quite accurate cross section results as demonstrated in our previous publications [34,35,36]. However, to check the accuracy of the wavefunction, we can compare our obtained ground state energies for CH4 and SiH4 molecules with other available reliable calculations. We find that the ground state energies for CH4 and SiH4 molecules in the present calculations are −40.11 and −290.21 Hartree, respectively. The corresponding values obtained from the DFT/B3LYP method with cc–pVTZ basis set [40] are −40.54 and −291.91 Hartree, and thus show close agreement with our results.
The un–normalized form of the Gaussian basis function with center at A with its coordinates , and can be represented as
Here, mx, my and mz are non–negative integers and αkj is the exponents of the Gaussian basis function. The values of the exponents and coefficients of atomic and molecular wavefunctions viz. αij, Nkj, ckj and αkj are taken from our previous paper [39]. Now using the property of Gaussian multiplication, i.e., the product of the exponential parts of two orbitals with different centers, A and B can be written as an exponential of the same form at a center P on the line joining A and B,
where rp is the position vector of P in the molecular frame and can be expressed as
Further, using the expression for charge density as in Equation (2) and expanding the denominator of Equation (1) and following the property of spherical harmonics, we can write the spherically averaged static potential over all the orientations of the molecule as
Here, is greater than and . In order to evaluate the above integral, we multiply two different atomic Gaussian orbitals, i.e., two s-orbitals of hydrogen atoms (i.e., H (1s)), the s-orbital of a carbon or silicon atom (i.e., C (1s22s22p2), Si (1s22s22p63s23p2)), the s-orbital of H atom with the p-orbital of C or Si atom, or two s-orbitals or two p-orbitals of C or Si atom. For CH4 and SiH4 molecules, the molecular frame is fixed with the C or Si atom at the origin and the four H atoms at the positions (a, a, a), (a, −a, −a), (−a, a, −a) and (−a, −a, a), where the values of ‘a’ are 0.6261 Å and 0.8544 Å for CH4 and SiH4, respectively. We evaluate Equation (6) in a particular molecular frame of reference using the Euler angle transformation. The values of the calculated Euler angles are taken from our previous paper [39].
Along with the spherically averaged static potential, we also include the polarization effect, which rearranges the charge distribution of the target molecule in the presence of the incident positron. We uses the expression for the polarization potential as given by Jain and Gianturco [16]
Here, is the point where the short–range correlation and long–range dipole parts cross each other for the first time. is the polarizability of the target and its value is taken to be 16.54 a.u. for CH4 [41] and 32.24 a.u. for SiH4 [41]. The expression for the short–range correlation potential is taken from Jain and Gianturco [16] as given below
Here, and is the charge density of the target molecule. Thus, the model potential for positron impact elastic scattering can expressed as
In the case of TCS calculations, we further add the absorption potential as an imaginary part in the above equation so that the model potential becomes complex and can be expressed as
The expression for the absorption potential for positron scattering is taken from Reid and Wadehra [42] and can be written as
Here, is the local speed of the incident positron and is the average binary collision cross section as expressed below
Here, is the Bohr radius and is the Rydberg constant. , and . and are, respectively, the incident positron energy and Fermi kinetic energy. is an important parameter for positron scattering and for the absorption potential in the low to high impact energies. We choose it as followed by Chiari et al. [43],
Here, is the first electronic excitation energy of the target molecule and is the energy which the maximum inelastic cross section reaches without considering the positronium (Ps) formation. In the present case, the value of is taken to be 10.9 eV for CH4 [44] and 8.7 eV for SiH4 [44]. is the positronium formation energy given by eV, where is the ionization energy of the target molecule. The ionization energies are 12.61 eV for CH4 [45] and 11.7 eV for SiH4 [45].
The scattering of positrons from CH4 and SiH4 molecule can be described in a non-relativistic manner using the model potential (Equations (9) and (10)) in the Schrödinger equation (in atomic units),
Here is the total scattering wavefunction. By expanding the wavefunction in terms of its partial waves and phase shifts in the usual standard manner and then substituting in Equation (14), we obtain the following radial equation
where is the momentum of positron and is the radial wavefunction associated with the th partial wave satisfying Equation (15), which can be solved subjecting to the following asymptotic boundary conditions,
Here, is the phase shift of th outgoing partial wave with respect to the free spherical wave in the presence of the potential. Further, the solution of Equation (15) gives us the phase shift at each kinetic energy of the incident positron [37,38]. Further, we can express the scattering amplitude in terms of phase shift by the following expression
where, is the th order Legendre polynomial. gives differential cross section, while total elastic integrated () and absorption cross sections () are finally obtained by using the following expressions [37,38]
Here, is the imaginary part of the complex phase shift obtained when the model potential has the absorption potential included. Further, the total cross section () is obtained by adding the total elastic integrated cross section () to the absorption cross section ().
3. Results and Discussion
3.1. Positron-CH4 Scattering
3.1.1. Differential Cross Sections
In the present work, we calculated the DCS results for positron-CH4 scattering in a wide range of incident positron energies from 1 eV to 500 eV. These DCS results are compared with the only available measurement of Przybyla et al. [12] and theoretical calculation of Jain and Gianturco [16]. The experimental cross-section results of Przybyla et al. [12] are relative measurements; therefore, we normalized them with our calculated DCS at 90° angle to obtain an overall best agreement with the experiment.
In Figure 1a–d, we show our DCS at 1 eV to 4 eV incident positron energies. The DCS results at 1 eV are compared with the theoretical calculations of Jain and Gianturco [16] in Figure 1a. We notice that the shapes of the DCS curves are similar, but their positions of the minimum are slightly shifted from each other. In fact, the polarization potential is very important to provide the correct information about the position of the minimum of a DCS curve. However, in both calculations, the polarization potentials are taken to be the same, and the shift in the position of the minimum of the curves may be due to the different wavefunctions used in both calculations through which the charge densities or the static potentials are obtained in the calculations. Further, from Figure 1b,c at 2 eV and 3 eV, we observed a similar behavior of the DCS results as seen in Figure 1a, but the difference in the position of their minimum decreases as the energy increases. At the incident positron energy 4 eV, the experimental results of Przybyla et al. [12] are available, while the calculations of Jain and Gianturco [16] were not reported. Therefore, we compared our DCS results with these measurements [12] in Figure 1d and found a very good agreement. Additionally, both the DCS curves have their position of minimum very close to 65°. This comparison also provides the accuracy of our DCS calculations at low energies for positron-CH4 scattering.
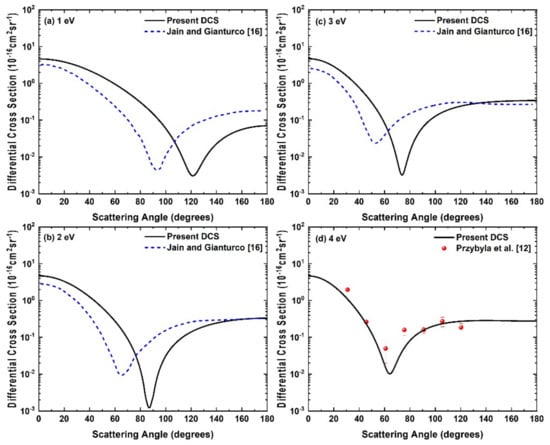
Figure 1.
Differential cross sections for positron-CH4 elastic scattering at incident positron energies (a) 1 eV, (b) 2 eV, (c) 3 eV and (d) 4 eV. Solid line, present DCS; dashed line, Jain and Gianturco [16]; solid sphere with error bars, Przybyla et al. [12].
In Figure 2a–d, we display our DCS results for 6–10 eV incident positron energies. We compare them with the calculations of Jain and Gianturco [16] as well as the experimental results of Przybyla et al. [12] at 6 and 10 eV. Here again, we observe similar kind of comparisons between the two theoretical results as seen in Figure 1. Further, from the Figure 2b,d, we see that the present DCS curves show overall good agreement with the experimental DCS results of Przybyla et al. [12] at 6 and 10 eV with respect to their behavior as well as the occurrence of the positions of minimum. However, in the scattering angle range of 40–90°, we observe that the theoretical calculations of Jain and Gianturco [16] show better agreement with measurements.
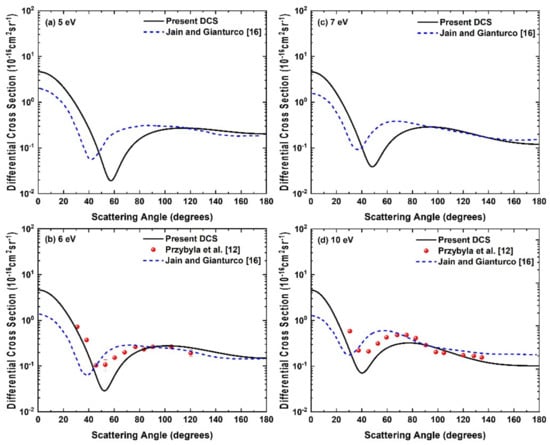
Figure 2.
Differential cross sections for positron-CH4 elastic scattering at incident positron energies (a) 5 eV, (b) 6 eV, (c) 7 eV and (d) 10 eV. Solid line, present DCS; dashed line, Jain and Gianturco [16]; solid sphere with error bars, Przybyla et al. [12].
The present DCS for 15, 20, 30 and 50 eV incident positron energies are shown and compared with the measurement of Przybyla et al. [12] and the theoretical calculation of Jain and Gianturco [16] in Figure 3a–d. We see from Figure 3a that our DCS results for 15 eV are in very good agreement with the experimental results of Przybyla et al. [12] with a similar minimum position around 35°. A very similar nature of the comparison can be noticed for 20 eV in Figure 3b. At 30 eV, our results, as shown in Figure 3c, are also in good agreement with the measurement [12], except in the 40–70° angular range, where these are slightly higher than the measurements [12]. From Figure 3d, we find that our DCS at 50 eV shows overall better agreement with the measurements [12] as compared to the other calculations [16], which show somewhat higher cross sections in the near forward scattering angles.
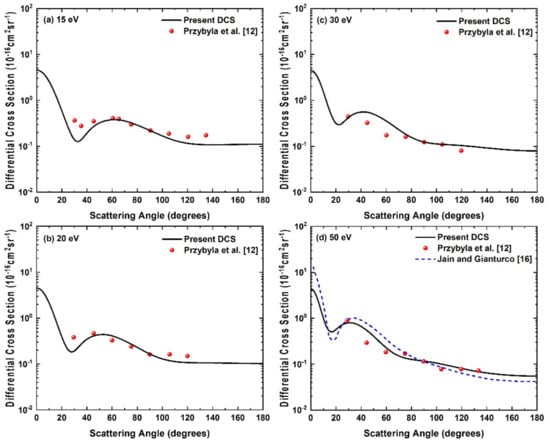
Figure 3.
Differential cross sections for positron-CH4 elastic scattering at incident positron energies (a) 15 eV, (b) 20 eV, (c) 30 eV and (d) 50 eV. Solid line, present DCS; dashed line, Jain and Gianturco [16]; solid sphere, Przybyla et al. [12].
The comparison of our DCS results with experimental [12] and theoretical results [16] at 100, 200, and 300–500 eV energies is shown through Figure 4a–c. We find excellent agreement between the present DCS results and the measurement [12] at 100 and 200 eV as shown in Figure 4a,b respectively. Our DCS results also agree well with the calculations of Jain and Gianturco [16] at 200 eV. We find from all the DCS results presented through Figure 1, Figure 2, Figure 3 and Figure 4 that the minimum of the cross-section curves shift toward the lower angles and DCS curves fall off at a slow pace as the energy increases.
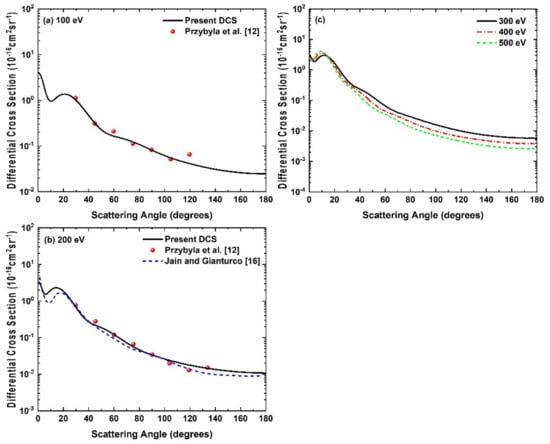
Figure 4.
Differential cross sections for positron-CH4 elastic scattering at incident positron energies (a) 100 eV, (b) 200 eV and (c) 300–500 eV. In (a) and (b); Solid line, present DCS; dashed line, Jain and Gianturco [16]; solid sphere, Przybyla et al. [12].
3.1.2. Elastic Integrated and Total Cross Sections
We also calculate the elastic ICS and TCS results for positron-CH4 scattering in the incident positron energy range from 1 eV to 500 eV. In Figure 5a, we show our elastic ICS results in the entire energy range, and we compare these with the theoretical calculations of Jain and Gianturco [16], Zecca et al. [17] and Franz [18] available in the range of up to 10 eV only. All the calculations show deviations up to 10 eV, which may be either due to the difference in the methods of calculations or the utilized charge densities obtained from different wavefunctions. The cross sections reported in [16] have smaller values in comparison to our results, except at 10 eV. The calculated ICS results of Zecca et al. [17] also have lower cross sections than the present results but the nature of the curve is very similar. However, the ICS results of Franz [18] are higher than all the cross sections reported.
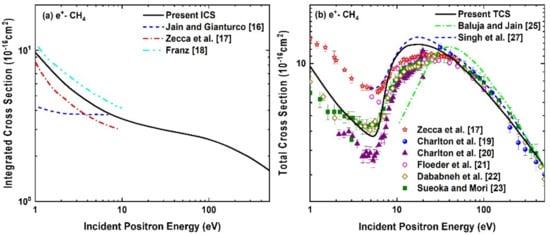
Figure 5.
(a) Elastic integrated and (b) total cross section for positron-CH4 scattering as a function of incident positron energy. In (a); solid line, present ICS; dashed line, Jain and Gianturco [16]; dashed dot line, Zecca et al. [17]; dashed double dot line, Franz [18]; in (b); solid line, present TCS, dashed dot line, Baluja and Jain [25]; dashed line, Singh et al. [27]; open star, Zecca et al. [17]; solid sphere Charlton [19]; solid up triangle Charlton [20]; open solid sphere, Floeder et al. [21]; open diamond, Dababneh et al. [22]; solid square, Sueoka and Mori [23].
The present TCS results for positron-CH4 scattering are shown in Figure 5b, and these are compared with the measurements of Charlton et al. [19,20], Floeder et al. [21], Dababneh et al. [22], Sueoka and Mori [23] and Zecca et al. [17], and the theoretical calculations of Baluja and Jain [25] and Singh et al. [27]. Below the positronium formation energy (i.e., 5.81 eV), the experimental results have different values and are not in agreement among themselves. In this region, our TCS results are in good agreement with the measurements of Dababneh et al. [22], and Sueoka and Mori [23]. The measurements of Charlton [20] are lower than the present TCS results, whereas those of Zecca et al. [17] are somewhat higher. In fact, Zecca et al. [17] measured the cross sections with the angular resolution of 4° with an estimated energy-dependent angular distribution varying from ∼17° at 1 eV to 5.4° at 10 eV positron energy. Thus the experimental results of Zecca et al. [17] are more accurate in comparison with the previously available other measurements, where the angular resolutions were relatively smaller. Above the positronium formation energy, our TCS results are in very good agreement with all the measurements [17,19,20,21,22,23] except in the energy region from 10 eV to 30 eV, where these are slightly higher. On comparison with the theoretical calculations of Singh et al. [27], we see that our TCS results are in overall good agreement with only small differences, whereas the TCS results of Baluja and Jain [25] have lower cross sections below 30 eV, but match with our results as the energy increases. This may be due to the different absorption potentials taken in these calculations [25] as compared to ours.
Overall, we can say that all our results for DCS, ICS and TCS are in reasonable agreement with the previously reported measurements and calculations for the positron-CH4 scattering in a wide range of incident positron energy from 1 eV to 500 eV.
3.2. Positron-SiH4 Scattering
3.2.1. Differential Cross Sections
Figure 6a–d exhibits our present DCS results at positron-SiH4 scattering from 1 eV to 4 eV incident positron energies and their comparison with the theoretical calculations of Jain and Gianturco [16] and Barbosa and Bettega [30]. The DCS curves from all the three calculations show similar behavior as well as positions of the minimum, almost at the same angle. As far as the magnitude of the cross sections is concerned, the calculations of Barbosa and Bettega [30] are higher, while those of Jain and Gianturco [16] are lower than the present DCS results.
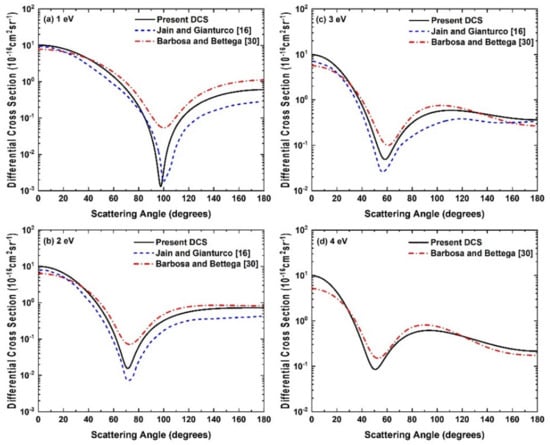
Figure 6.
Differential cross sections for positron-SiH4 elastic scattering at incident positron energies (a) 1 eV, (b) 2 eV, (c) 3 eV and (d) 4 eV. Solid line, present DCS; dashed line, Jain and Gianturco [16]; dashed dot line, Barbosa and Bettega [30].
We show our DCS results at 5–8 eV energies in Figure 7a–d. From these figures, we find that our results are in overall agreement with the calculations of Barbosa and Bettega [30], except at the near forward scattering angles, where our DCS results are higher. Figure 7a also includes the available results of Jain and Gianturco [16] for comparison and shows that they are not in good agreement with the present DCS calculations.
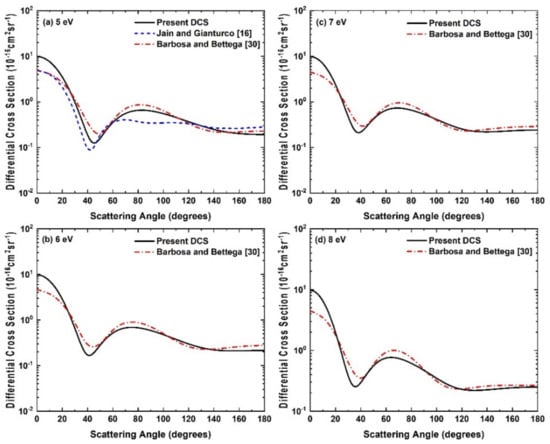
Figure 7.
Differential cross sections for positron-SiH4 elastic scattering at incident positron energies (a) 5 eV, (b) 6 eV, (c) 7 eV and (d) 8 eV. Solid line, present DCS; dashed line, Jain and Gianturco [16]; dashed dot line, Barbosa and Bettega [30].
There are no other theoretical or experimental results available for the positron scattering from SiH4 at intermediate and higher energies for comparison. Since our results for CH4 at higher energies, as presented above, compare with the available experimental results in a favorable manner, it would be worthwhile to also present similar results for SiH4 so that these are available for future comparison purposes. We show our DCS results for SiH4 in the intermediate (10–50 eV) and high (100–500 eV) energy regions in Figure 8a,b. We observe the following general features here, i.e., the minimum position of the DCS curves shift toward the forward angles as the energy increases, and at higher energies the DCS curves fall off smoothly with respect to the scattering angles. Although the reason for this shift of the minimum is not very clear to us, this effect may be attributed to the behavior of the polarization potential [16] as pointed out from the similar positron-molecule scattering calculations.
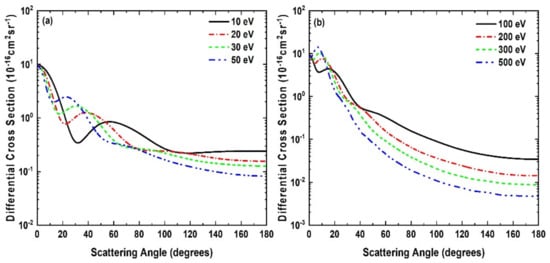
Figure 8.
Differential cross sections for positron-SiH4 elastic scattering at incident positron energies (a) 10–50 eV and (b) 100–500 eV.
3.2.2. Elastic Integrated and Total Cross Sections
In Figure 9, we display our elastic ICS and TCS results for positron-SiH4 scattering at the incident positron energies from 1 eV to 500 eV. There are no experimental results available for ICS; therefore, we compare in Figure 9a the present elastic ICS results with the theoretical results of Jain and Gianturco [16] and Barbosa and Bettega [30] that are available up to 10 eV. We see a perfect agreement of our results with the theoretical calculations of Barbosa and Bettega [30]. Further, all the theoretical ICS curves show a similar nature, but the results of Jain and Gianturco [16] have lower magnitude of the cross section than the other two calculations. This difference can also be traced back to the DCS results comparisons as shown in Figure 6 and Figure 7, where the DCS results of [16] also show a lower cross section, especially in the forward direction. We report our ICS calculations up to 500 eV incident positron energies for the sake of future comparisons, in case further studies are performed theoretically or experimentally in this energy range.
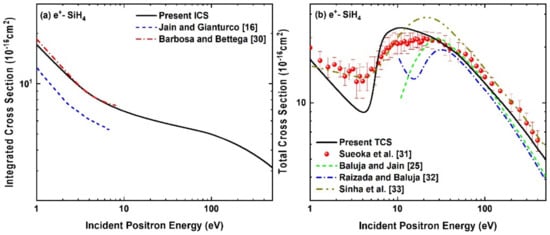
Figure 9.
(a) Elastic integrated and (b) total cross section for positron-SiH4 scattering as a function of incident positron energy. In (a); solid line, present ICS; dashed line, Jain and Gianturco [16]; dashed dot line, Barbosa and Bettega [30]; in (b); solid line, present TCS; solid sphere, Sueoka et al. [31]; dashed line, Baluja and Jain [25]; dashed dot line, Raizada and Baluja [32]; dashed double dot, Sinha et al. [33].
In Figure 9b, the present TCS results are shown in the energy range from 1 eV to 500 eV and compared with the measurements of Sueoka et al. [31] and the theoretical calculations of Baluja and Jain [25], Raizada and Baluja [32] and Sinha et al. [33]. Below the positronium formation energy (i.e., 4.9 eV), our TCS results have lower magnitude than the experimental results [31]. Beyond the positronium formation energy, our results lie almost within the error considerations of the measurements [31], whereas the theoretical calculations [25,32] show lower cross sections below 30 eV and above 100 eV than the present results as well as the measurements [31]. On comparison with the calculations of Sinha et al. [33], we find that their results are somewhat higher than the present TCS.
Since there are very few experimental and theoretical results available for positron-SiH4 scattering, we show the comparison of our calculated DCS, ICS, and TCS results, wherever possible. We find reasonably good agreement with the previously reported measurements and calculations.
4. Conclusions
We presented a detailed study of positron impact elastic scattering from CH4 and SiH4 molecules in a wide range of incident energies from 1 eV to 500 eV. We obtained the static potential for CH4 and SiH4 molecules analytically, utilizing the Gaussian wavefunctions. A model potential consisting of static and polarization potential was constructed to study the scattering problem. Further, using the model potential, the Schrödinger equation was solved with the partial wave analysis method to obtain the scattering amplitude and phase shifts with which the DCS and ICS results were calculated. Further, the absorption potential was added to the model potential to include the inelastic part in the scattering process. Thereafter, the TCS results, that have both the inelastic and elastic components included, were obtained for positron-CH4/SiH4 scattering. Where possible, we compared our present cross section results with the available experimental and other theoretical results and found quite good agreement. More experimental and theoretical studies are needed for the positron-CH4/SiH4 scattering in future to verify the present cross section results, especially for SiH4. Thus, we successfully applied our analytical static potential approach to describe the positron scattering elastic scattering from CH4 and SiH4 molecules in the present work. We feel that our present method can be further extended and applied to more complex molecules.
Author Contributions
Conceptualization, D.M., L.S. and R.S.; methodology, D.M., L.S. and R.S.; software, D.M..; validation, D.M., L.S. and R.S.; formal analysis, D.M., L.S. and R.S.; investigation, D.M., L.S. and R.S.; resources, D.M., L.S. and R.S.; data curation, D.M.; writing—original draft preparation, D.M.; writing—review and editing, D.M., L.S. and R.S.; visualization, D.M., L.S. and R.S.; supervision, L.S. and R.S.; project administration, L.S. and R.S.; funding acquisition, L.S. and R.S. All authors have read and agreed to the published version of the manuscript.
Funding
This research was funded by SERB–DST, New Delhi, Govt. of India through Grants No: CRG/2020/005597 and DST/ICPS/QuST/Theme–3/2019/General.
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
Can be obtained from the authors on request.
Acknowledgments
The author, D.M., is thankful to the Ministry of Human Resources and Development (MHRD), Govt. of India, for the financial assistance to carry out his research. R.S. and L.S. are thankful to SERB–DST, New Delhi, Govt. of India for the sanction of research grants No: CRG/2020/005597, and DST/ICPS/QuST/Theme–3/2019/General.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Surko, C.M.; Murphy, T.J. Use of the positron as a plasma particle. Phys. Fluids B Plasma Phys. 1990, 2, 1372–1375. [Google Scholar] [CrossRef]
- Guessoum, N. Positron astrophysics and areas of relation to low-energy positron physics. Eur. Phys. J. D 2014, 68, 137. [Google Scholar] [CrossRef]
- Johnson, W.N., III; Harnden, F.R., Jr.; Haymes, R.C. The spectrum of low-energy gamma radiation from the galactic-center region. Astrophys. J. 1972, 172, L1–L7. [Google Scholar] [CrossRef]
- Kropotov, J.D. Positron emission tomography. In Functional Neuromarkers for Psychiatry; Elsevier: Amsterdam, The Netherlands, 2016; pp. 27–30. ISBN 9780124105133. [Google Scholar] [CrossRef][Green Version]
- Dlubek, G.; Meyendorf, N. Positron annihilation spectroscopy (PAS). In Annual Review of Materials Science; Springer Series in Statistics; Springer: New York, NY, USA, 2004; pp. 374–411. ISBN 978-0-387-98134-5. [Google Scholar]
- Brunger, M.J.; Buckman, S.J.; Ratnavelu, K. Positron scattering from molecules: An experimental cross section compilation for positron transport studies and benchmarking theory. J. Phys. Chem. Ref. Data 2017, 46, 023102. [Google Scholar] [CrossRef]
- Blanco, F.; Muñoz, A.; Almeida, D.; da Silva, F.F.; Limão-Vieira, P.; Fuss, M.C.; Sanz, A.G.; García, G. Modelling low energy electron and positron tracks in biologically relevant media. Eur. Phys. J. D 2013, 67, 199. [Google Scholar] [CrossRef]
- Fuss, M.C.; Ellis-Gibbings, L.; Jones, D.B.; Brunger, M.J.; Blanco, F.; Muñoz, A.; Limão-Vieira, P.; García, G. The role of pyrimidine and water as underlying molecular constituents for describing radiation damage in living tissue: A comparative study. J. Appl. Phys. 2015, 117, 214701. [Google Scholar] [CrossRef]
- Song, M.-Y.; Yoon, J.-S.; Cho, H.; Itikawa, Y.; Karwasz, G.P.; Kokoouline, V.; Nakamura, Y.; Tennyson, J. Cross sections for electron collisions with methane. J. Phys. Chem. Ref. Data 2015, 44, 023101. [Google Scholar] [CrossRef]
- Broadfoot, A.L.; Belton, M.J.S.; Takacs, P.Z.; Sandel, B.R.; Shemansky, D.E.; Holberg, J.B.; Ajello, J.M.; Atreya, S.K.; Donahue, T.M.; Moos, H.W.; et al. Extreme ultraviolet observations from voyager 1 encounter with Jupiter. Science 1979, 204, 979–982. [Google Scholar] [CrossRef]
- Goldhaber, D.M.; Betz, A.L. Silane in IRC +10216. Astrophys. J. 1984, 279, L55–L58. [Google Scholar] [CrossRef]
- Przybyla, D.A.; Kauppila, W.E.; Kwan, C.K.; Smith, S.J.; Stein, T.S. Measurements of positron-methane differential scattering cross sections. Phys. Rev. A 1997, 55, 4244–4247. [Google Scholar] [CrossRef]
- Jain, A. Elastic scattering of electrons and positrons by CH4 at 25–800 eV. J. Chem. Phys. 1983, 78, 6579–6583. [Google Scholar] [CrossRef]
- Jain, A.; Thompson, D.G. The scattering of slow positrons by CH4 and NH3. J. Phys. B At. Mol. Phys. 1983, 16, 1113–1123. [Google Scholar] [CrossRef]
- Jain, A.; Thompson, D.G. Rotational excitation of CH4 molecules by low-energy positrons. Phys. Rev. A 1984, 30, 1098–1100. [Google Scholar] [CrossRef]
- Jain, A.; Gianturco, F.A. Low-energy positron collisions with CH4 and SiH4 molecules by using new positron polarization potentials. J. Phys. B At. Mol. Opt. Phys. 1991, 24, 2387–2398. [Google Scholar] [CrossRef]
- Zecca, A.; Chiari, L.; Trainotti, E.; Sarkar, A.; Sanchez, S.D.A.; Bettega, M.H.F.; Varella, M.D.N.; Lima, M.A.P.; Brunger, M.J. Positron scattering from methane. Phys. Rev. A 2012, 85, 012707. [Google Scholar] [CrossRef]
- Franz, J. Positron-electron correlation-polarization potentials for the calculation of positron collisions with atoms and molecules. Eur. Phys. J. D 2017, 71, 44. [Google Scholar] [CrossRef]
- Charlton, M.; Griffith, T.C.; Heyland, G.R.; Wright, G.L. Total scattering cross sections for intermediate-energy positrons in the molecular gases H2, O2, N2, CO2 and CH4. J. Phys. B At. Mol. Phys. 1980, 13, L353–L356. [Google Scholar] [CrossRef]
- Charlton, M.; Griffith, T.C.; Heyland, G.R.; Wright, G.L. Total scattering cross sections for low-energy positrons in the molecular gases H2, N2, CO2, O2 and CH4. J. Phys. B At. Mol. Phys. 1983, 16, 323–341. [Google Scholar] [CrossRef]
- Floeder, K.; Fromme, D.; Raith, W.; Schwab, A.; Sinapius, G. Total cross section measurements for positron and electron scattering on hydrocarbons between 5 and 400 eV. J. Phys. B At. Mol. Phys. 1985, 18, 3347–3359. [Google Scholar] [CrossRef]
- Dababneh, M.S.; Hsieh, Y.-F.; Kauppila, W.E.; Kwan, C.K.; Smith, S.J.; Stein, T.S.; Uddin, M.N. Total-cross-section measurements for positron and electron scattering by O2, CH4, and SF6. Phys. Rev. A 1988, 38, 1207–1216. [Google Scholar] [CrossRef]
- Sueoka, O.; Mori, S. Total cross sections for low and intermediate energy positrons and electrons colliding with CH4, C2H4 and C2H6 molecules. J. Phys. B At. Mol. Phys. 1986, 19, 4035–4050. [Google Scholar] [CrossRef]
- Jain, A. Total (elastic plus inelastic) cross sections for positron-methane (helium) collisions at low, intermediate, and high energies. Phys. Rev. A 1987, 35, 4826–4829. [Google Scholar] [CrossRef] [PubMed]
- Baluja, K.L.; Jain, A. Total (elastic and inelastic) scattering cross sections for several positron-molecule systems at 10—5000 eV: H2, H2O, NH3, CH4, N2, CO, C2H2, O2, SiH4, CO2, N2O, and CF4. Phys. Rev. A 1992, 45, 7838–7845. [Google Scholar] [CrossRef]
- Raizada, R.; Baluja, K.L. Positron scattering from hydrocarbons. Pramana 1996, 46, 431–449. [Google Scholar] [CrossRef]
- Singh, S.; Dutta, S.; Naghma, R.; Antony, B. Positron scattering from simple molecules. J. Phys. B At. Mol. Opt. Phys. 2017, 50, 135202. [Google Scholar] [CrossRef]
- Jain, A. Positron-monosilane (SiH4) collisions at low, intermediate and high energies using a spherical complex optical potential approach. J. Phys. B At. Mol. Phys. 1986, 19, L807–L813. [Google Scholar] [CrossRef]
- Gianturco, F.A.; Jain, A.; Pantano, L.C. Positron collisions by methane and monosilane molecules below 10 eV. Phys. Rev. A 1987, 36, 4637–4643. [Google Scholar] [CrossRef] [PubMed]
- Barbosa, A.S.; Bettega, M.H.F. Calculated cross sections for elastic scattering of slow positrons by silane. Phys. Rev. A 2017, 96, 042715. [Google Scholar] [CrossRef]
- Sueoka, O.; Mori, S.; Hamada, A. Total cross section measurements for positrons and electrons colliding with molecules. I. SiH 4 and CF 4. J. Phys. B At. Mol. Opt. Phys. 1994, 27, 1453–1465. [Google Scholar] [CrossRef]
- Raizada, R.; Baluja, K.L. Total cross sections of positron scattering from various molecules using the rule of additivity. Phys. Rev. A 1997, 55, 1533–1536. [Google Scholar] [CrossRef]
- Sinha, N.; Singh, S.; Antony, B. Theoretical study of positron scattering by group 14 tetra hydrides: A quantum mechanical approach. Int. J. Quantum Chem. 2018, 118, e25679. [Google Scholar] [CrossRef]
- Mahato, D.; Sharma, L.; Srivastava, R. An approach to study electron and positron scattering from NH3 and PH3 using the analytic static potential. J. Phys. B At. Mol. Opt. Phys. 2020, 53, 225204. [Google Scholar] [CrossRef]
- Mahato, D.; Sharma, L.; Srivastava, R. Study of electron and positron elastic scattering from hydrogen sulphide using analytically obtained static potential. Atoms 2020, 8, 83. [Google Scholar] [CrossRef]
- Mahato, D.; Sharma, L.; Srivastava, R. A new approach to study electron and positron scattering from acetylene. J. Electron Spectros. Relat. Phenom. 2021, 252, 147118. [Google Scholar] [CrossRef]
- Joachain, C.J. Quantum Collision Theory, 3rd ed.; North-Holland Physics Publishing: Amsterdam, The Netherland, 1983. [Google Scholar]
- Schiff, L.I. Quantum Mechanics, 3rd ed.; Tata McGraw-Hill: New York, NY, USA, 2010. [Google Scholar]
- Mahato, D.; Sharma, L.; Stauffer, A.D.; Srivastava, R. Electron impact elastic scattering from methane and silane molecules. Eur. Phys. J. D 2019, 73, 189. [Google Scholar] [CrossRef]
- Johnson Russell, D., III. NIST Computational Chemistry Comparison and Benchmark Database; 2020. Available online: http://cccbdb.nist.gov/ (accessed on 9 August 2021).
- Olney, T.N.; Cann, N.M.; Cooper, G.; Brion, C.E. Absolute scale determination for photoabsorption spectra and the calculation of molecular properties using dipole sum-rules. Chem. Phys. 1997, 223, 59–98. [Google Scholar] [CrossRef]
- Reid, D.D.; Wadehra, J.M. A quasifree model for the absorption effects in positron scattering by atoms. J. Phys. B At. Mol. Opt. Phys. 1996, 29, L127–L133. [Google Scholar] [CrossRef]
- Chiari, L.; Zecca, A.; Girardi, S.; Trainotti, E.; García, G.; Blanco, F.; McEachran, R.P.; Brunger, M.J. Positron scattering from O2. J. Phys. B At. Mol. Opt. Phys. 2012, 45, 215206. [Google Scholar] [CrossRef]
- Curtis, M.G.; Walker, I.C. Low-energy electron-impact excitation of methane, silane, tetrafluoromethane and tetrafluorosilane. J. Chem. Soc. Faraday Trans. 2 1989, 85, 659. [Google Scholar] [CrossRef]
- NIST Chemistry Webbook. Available online: http://webbook.nist.gov/chemistry (accessed on 12 August 2021).
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).