Vibrational Excitation Cross-Section by Positron Impact: A Wave-Packet Dynamics Study
Abstract
:1. Introduction
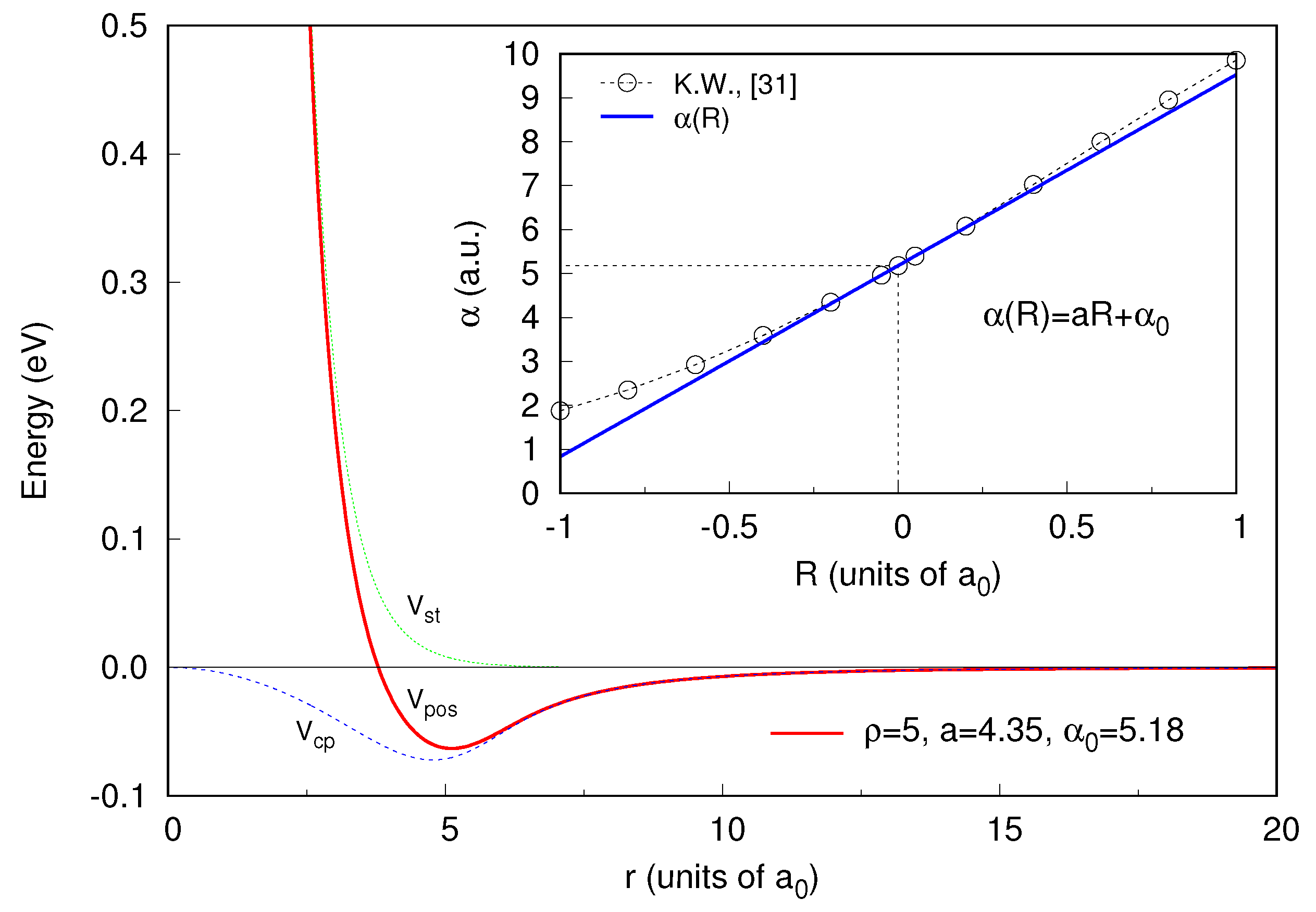
2. The Model Potential
3. Wave-Packet Dynamics
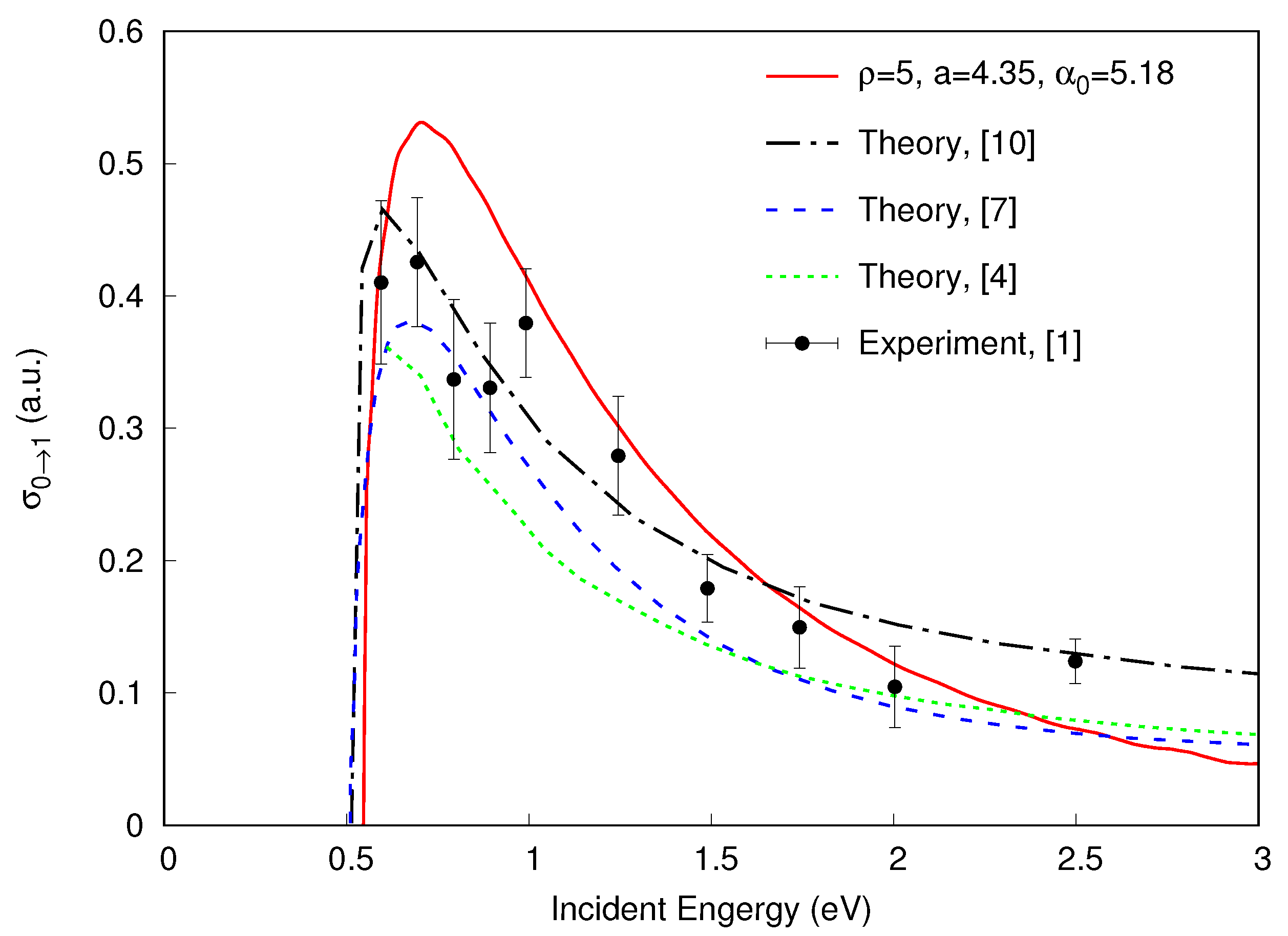
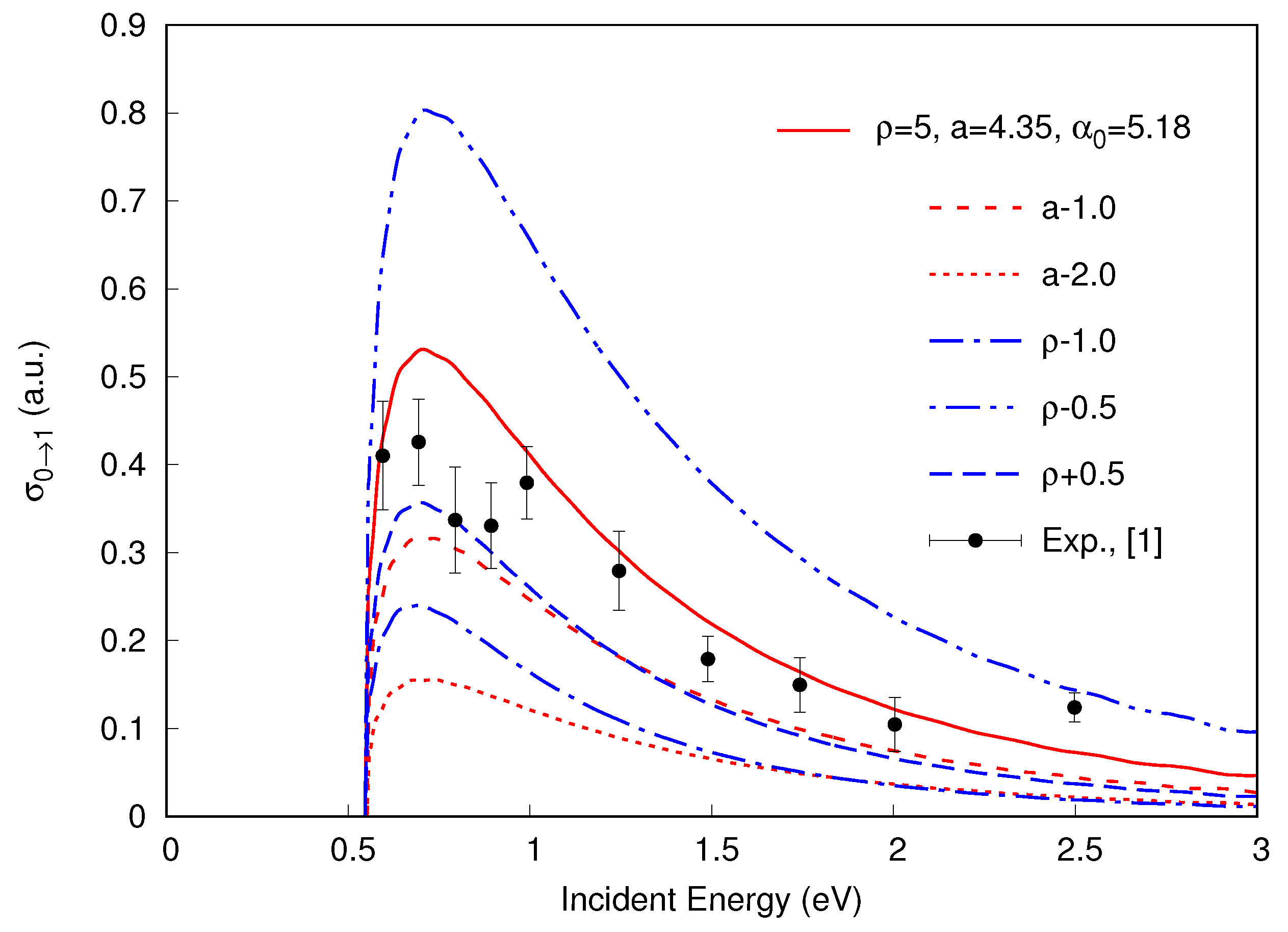
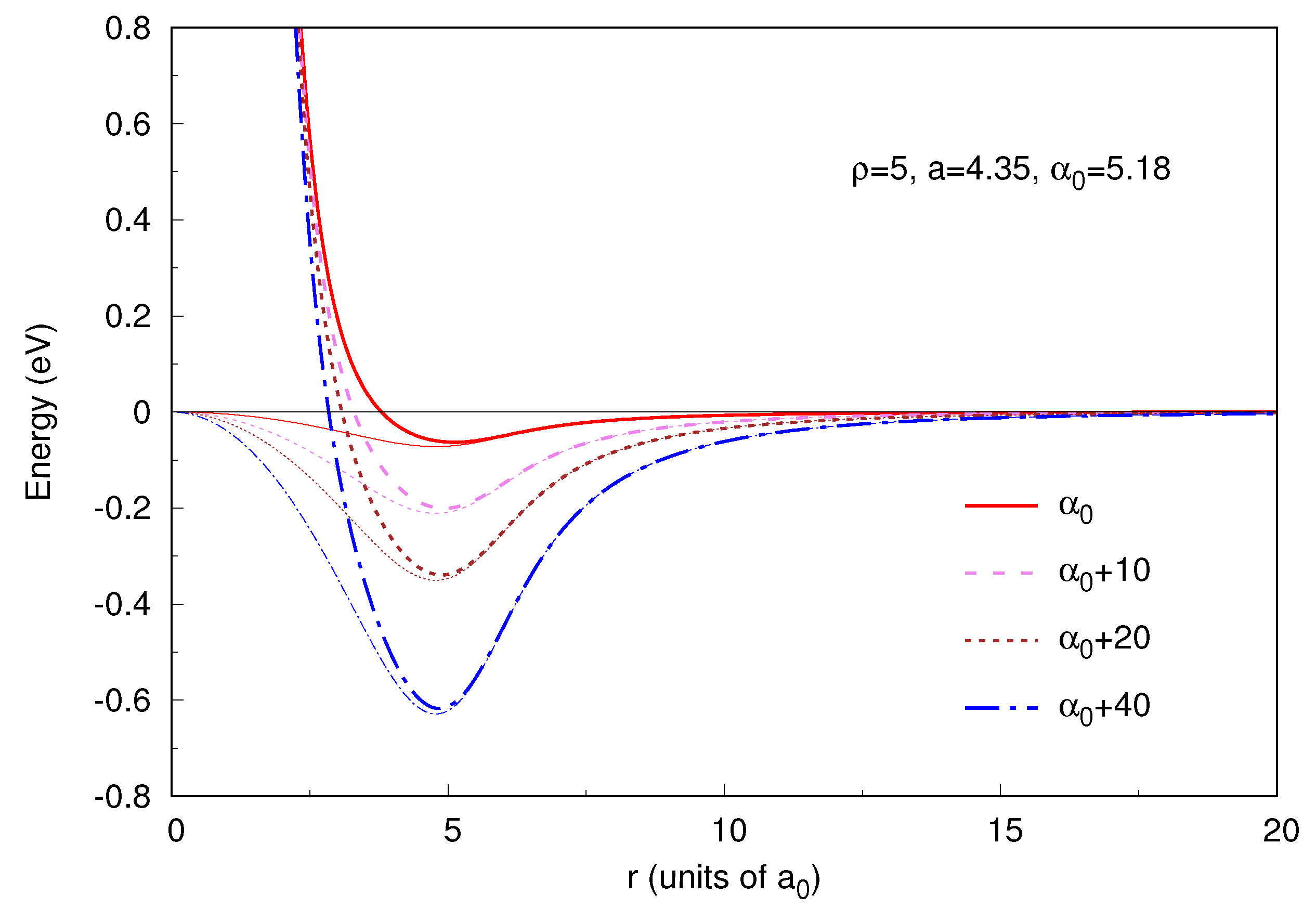
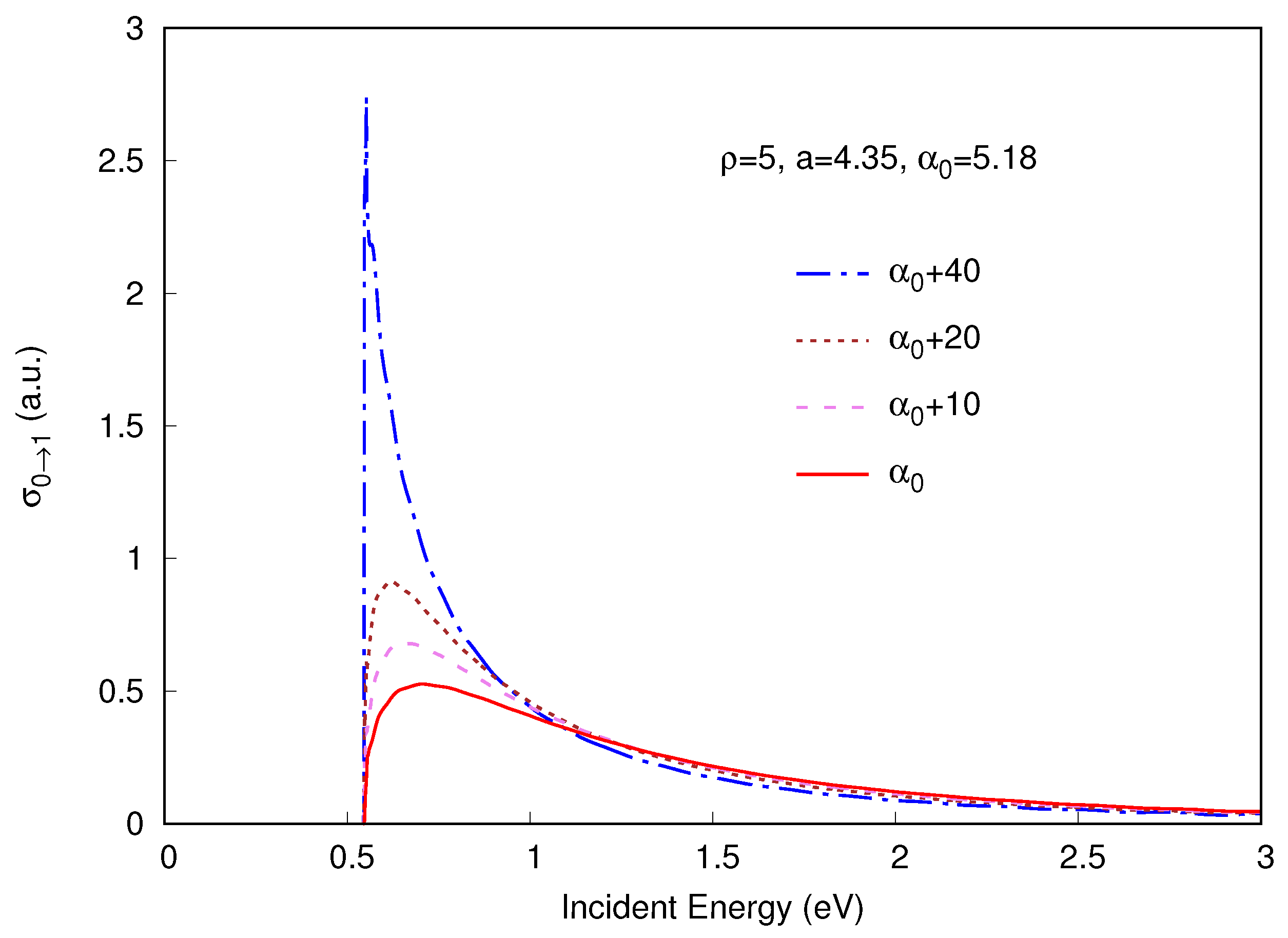
4. Results and Discussion
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Acknowledgments
Conflicts of Interest
References
- Sullivan, J.P.; Gilbert, S.J.; Surko, C.M. Excitation of Molecular Vibrations by Positron Impact. Phys. Rev. Lett. 2001, 86, 1494. [Google Scholar] [CrossRef] [Green Version]
- Gilbert, S.J.; Greaves, R.G.; Surko, C.M. Positron Scattering from Atoms and Molecules at Low Energies. Phys. Rev. Lett. 1999, 82, 5032–5035. [Google Scholar] [CrossRef] [Green Version]
- Marler, J.P.; Surko, C.M. Systematic comparison of positron- and electron-impact excitation of the ν3 vibrational mode of CF4. Phys. Rev. A 2005, 72, 062702. [Google Scholar] [CrossRef] [Green Version]
- Gianturco, F.A.; Mukherjee, T. Dynamical coupling effects in the vibrational excitation of H2 and N2 colliding with positrons. Phys. Rev. A 1997, 55, 1044–1055. [Google Scholar] [CrossRef]
- Mukherjee, T.; Ghosh, A.S.; Jain, A. Low-energy positron collisions with H2 and N2 molecules by using a parameter-free positron-correlation-polarization potential. Phys. Rev. A 1991, 43, 2538–2543. [Google Scholar] [CrossRef] [PubMed]
- Varella, M.T.D.N.; Lima, M.A.P. Near-threshold vibrational excitation of H2 by positron impact: A projection-operator approach. Phys. Rev. A 2007, 76, 052701. [Google Scholar] [CrossRef] [Green Version]
- Varella, M.T.D.N.; de Oliveira, E.M.; Lima, M.A. Near threshold vibrational excitation of molecules by positron impact: A projection operator approach. Nucl. Instr. Meth. B 2008, 266, 435–440. [Google Scholar] [CrossRef]
- Mazon, K.T.; Tenfen, W.; Michelin, S.E.; Arretche, F.; Lee, M.T.; Fujimoto, M.M. Vibrational cross sections for positron scattering by nitrogen molecules. Phys. Rev. A 2010, 82, 032704. [Google Scholar] [CrossRef]
- Mukherjee, T.; Mukherjee, M. Low-energy positron–nitrogen-molecule scattering: A rovibrational close-coupling study. Phys. Rev. A 2015, 91, 062706. [Google Scholar] [CrossRef]
- Zammit, M.C.; Fursa, D.V.; Savage, J.S.; Bray, I.; Chiari, L.; Zecca, A.; Brunger, M.J. Adiabatic-nuclei calculations of positron scattering from molecular hydrogen. Phys. Rev. A 2017, 95, 022707. [Google Scholar] [CrossRef] [Green Version]
- Poveda, L.A.; Assafrão, D.; Pinheiro, J.G.; Mohallem, J.R. Close-coupling scattering cross sections and a model for positron cooling in a buffer gas of molecular nitrogen. Phys. Rev. A 2019, 100, 062706. [Google Scholar] [CrossRef]
- Gilbert, S.J.; Kurz, C.; Greaves, R.G.; Surko, C.M. Creation of a monoenergetic pulsed positron beam. App. Phys. Lett. 1997, 70, 1944–1946. [Google Scholar] [CrossRef]
- Danielson, J.R.; Dubin, D.H.E.; Greaves, R.G.; Surko, C.M. Plasma and trap-based techniques for science with positrons. Rev. Mod. Phys. 2015, 87, 247–306. [Google Scholar] [CrossRef]
- Natisin, M.R.; Danielson, J.R.; Surko, C.M. Positron cooling by vibrational and rotational excitation of molecular gases. J. Phys. B At. Mol. Opt. Phys. 2014, 47, 225209. [Google Scholar] [CrossRef]
- Young, J.A.; Surko, C.M. Feshbach-resonance-mediated positron annihilation in small molecules. Phys. Rev. A 2008, 78, 032702. [Google Scholar] [CrossRef] [Green Version]
- Young, J.A.; Surko, C.M. Feshbach-resonance-mediated annihilation in positron interactions with large molecules. Phys. Rev. A 2008, 77, 052704. [Google Scholar] [CrossRef] [Green Version]
- Gribakin, G.F.; Young, J.A.; Surko, C.M. Positron-molecule interactions: Resonant attachment, annihilation, and bound states. Rev. Mod. Phys. 2010, 82, 2557–2607. [Google Scholar] [CrossRef] [Green Version]
- Gribakin, G.F.; Lee, C.M.R. Positron Annihilation in Molecules by Capture into Vibrational Feshbach Resonances of Infrared-Active Modes. Phys. Rev. Lett. 2006, 97, 193201. [Google Scholar] [CrossRef] [Green Version]
- d’A Sanchez, S.; Lima, M.A.P.; Varella, M.T.D.N. Feshbach projection operator approach to positron annihilation. Phys. Rev. A 2009, 80, 052710. [Google Scholar] [CrossRef] [Green Version]
- d’A Sanchez, S.; Lima, M.A.; Varella, M.T.D.N. Multimode vibrational couplings in resonant positron annihilation. Phys. Rev. Lett. 2011, 107, 103201. [Google Scholar] [CrossRef]
- Jones, A.C.L.; Danielson, J.R.; Natisin, M.R.; Surko, C.M.; Gribakin, G.F. Ubiquitous Nature of Multimode Vibrational Resonances in Positron-Molecule Annihilation. Phys. Rev. Lett. 2012, 108, 093201. [Google Scholar] [CrossRef] [Green Version]
- Danielson, J.R.; Young, J.A.; Surko, C.M. Analysis of experimental positron-molecule binding energies. J. Phys. Conf. Ser. 2010, 199, 012012. [Google Scholar] [CrossRef]
- Danielson, J.R.; Jones, A.C.L.; Gosselin, J.J.; Natisin, M.R.; Surko, C.M. Interplay between permanent dipole moments and polarizability in positron-molecule binding. Phys. Rev. A 2012, 85, 022709. [Google Scholar] [CrossRef] [Green Version]
- Amaral, P.H.R.; Mohallem, J.R. Positron binding to atoms and apolar molecules: A convergence of theory and experiment. Phys. Rev. A 2012, 86, 042708. [Google Scholar] [CrossRef]
- Romero, J.; Charry, J.A.; Flores-Moreno, R.; Varella, M.T.D.N.; Reyes, A. Calculation of positron binding energies using the generalized any particle propagator theory. J. Chem. Phys. 2014, 141, 114103. [Google Scholar] [CrossRef] [PubMed]
- Swann, A.R.; Gribakin, G.F. Positron Binding and Annihilation in Alkane Molecules. Phys. Rev. Lett. 2019, 123, 113402. [Google Scholar] [CrossRef] [Green Version]
- Suzuki, H.; Otomo, T.; Iida, R.; Sugiura, Y.; Takayanagi, T.; Tachikawa, M. Positron binding in chloroethenes: Modeling positron-electron correlation-polarization potentials for molecular calculations. Phys. Rev. A 2020, 102, 052830. [Google Scholar] [CrossRef]
- Amaral, P.H.R.; Mohallem, J.R. Machine-learning predictions of positron binding to molecules. Phys. Rev. A 2020, 102, 052808. [Google Scholar] [CrossRef]
- Hofierka, J.; Cunningham, B.; Rawlins, C.M.; Patterson, C.H.; Green, D.G. Many-body theory of positron binding in polyatomic molecules. arXiv 2021, arXiv:2105.06959. [Google Scholar]
- Sugiura, Y.; Suzuki, K.; Koido, S.; Takayanagi, T.; Kita, Y.; Tachikawa, M. Quantum dynamics calculation of the annihilation spectrum for positron–proline scattering. Comp. Theor. Chem. 2019, 1147, 1–7. [Google Scholar] [CrossRef]
- Kołos, W.; Wolniewicz, L. Polarizability of the Hydrogen Molecule. J. Chem. Phys. 1967, 46, 1426–1432. [Google Scholar] [CrossRef]
- Mitroy, J.; Ivanov, I.A. Semiempirical model of positron scattering and annihilation. Phys. Rev. A 2002, 65, 042705. [Google Scholar] [CrossRef] [Green Version]
- Marston, C.; Balint-Kurti, G.; Dixon, R. Time dependent quantum dynamics of reactive scattering and the calculation of product quantum state distributions—A study of the collinear F + H2(v = 0)->HF(v’) + H reaction. Theor. Chim. Acta 1991, 79, 313–322. [Google Scholar] [CrossRef]
- Bradley, K.S.; Schatz, G.C.; Balint-Kurti, G.G. Wave Packet Methods for the Direct Calculation of Energy-Transfer Moments in Molecular Collisions. J. Phys. Chem. A 1999, 103, 947–952. [Google Scholar] [CrossRef]
- Vibók, Á.; Halász, G.J. Parametrization of complex absorbing potentials for time-dependent quantum dynamics using multi-step potentials. Phys. Chem. Chem. Phys. 2001, 3, 3048–3051. [Google Scholar] [CrossRef]
- Dixon, R.N.; Marston, C.C.; Balint-Kurti, G.G. Photodissociation dynamics and emission spectroscopy of H2S in its first absorption band: A time dependent quantum mechanical study. J. Chem. Phys. 1990, 93, 6520–6534. [Google Scholar] [CrossRef]
- Takatsuka, K.; Hashimoto, N. A novel method to calculate eigenfunctions and eigenvalues in a given energy range. J. Chem. Phys. 1995, 103, 6057–6067. [Google Scholar] [CrossRef]
| Parameter | Value |
|---|---|
| Grid parameters | |
| 1200 | |
| 1024 | |
| 32 | |
| 200 | |
| 950 | |
| 1000 | |
| Initial WP parameters | |
| 100 | |
| 20 | |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Poveda, L.A.; Varella, M.T.d.N.; Mohallem, J.R. Vibrational Excitation Cross-Section by Positron Impact: A Wave-Packet Dynamics Study. Atoms 2021, 9, 64. https://doi.org/10.3390/atoms9030064
Poveda LA, Varella MTdN, Mohallem JR. Vibrational Excitation Cross-Section by Positron Impact: A Wave-Packet Dynamics Study. Atoms. 2021; 9(3):64. https://doi.org/10.3390/atoms9030064
Chicago/Turabian StylePoveda, Luis A., Marcio T. do N. Varella, and José R. Mohallem. 2021. "Vibrational Excitation Cross-Section by Positron Impact: A Wave-Packet Dynamics Study" Atoms 9, no. 3: 64. https://doi.org/10.3390/atoms9030064
APA StylePoveda, L. A., Varella, M. T. d. N., & Mohallem, J. R. (2021). Vibrational Excitation Cross-Section by Positron Impact: A Wave-Packet Dynamics Study. Atoms, 9(3), 64. https://doi.org/10.3390/atoms9030064






