Accurate Electron Drift Mobility Measurements in Moderately Dense Helium Gas at Several Temperatures
Abstract
1. Introduction
2. Experimental Details
3. Experimental Results and Discussion
3.1. The Need for Accurate Measurements
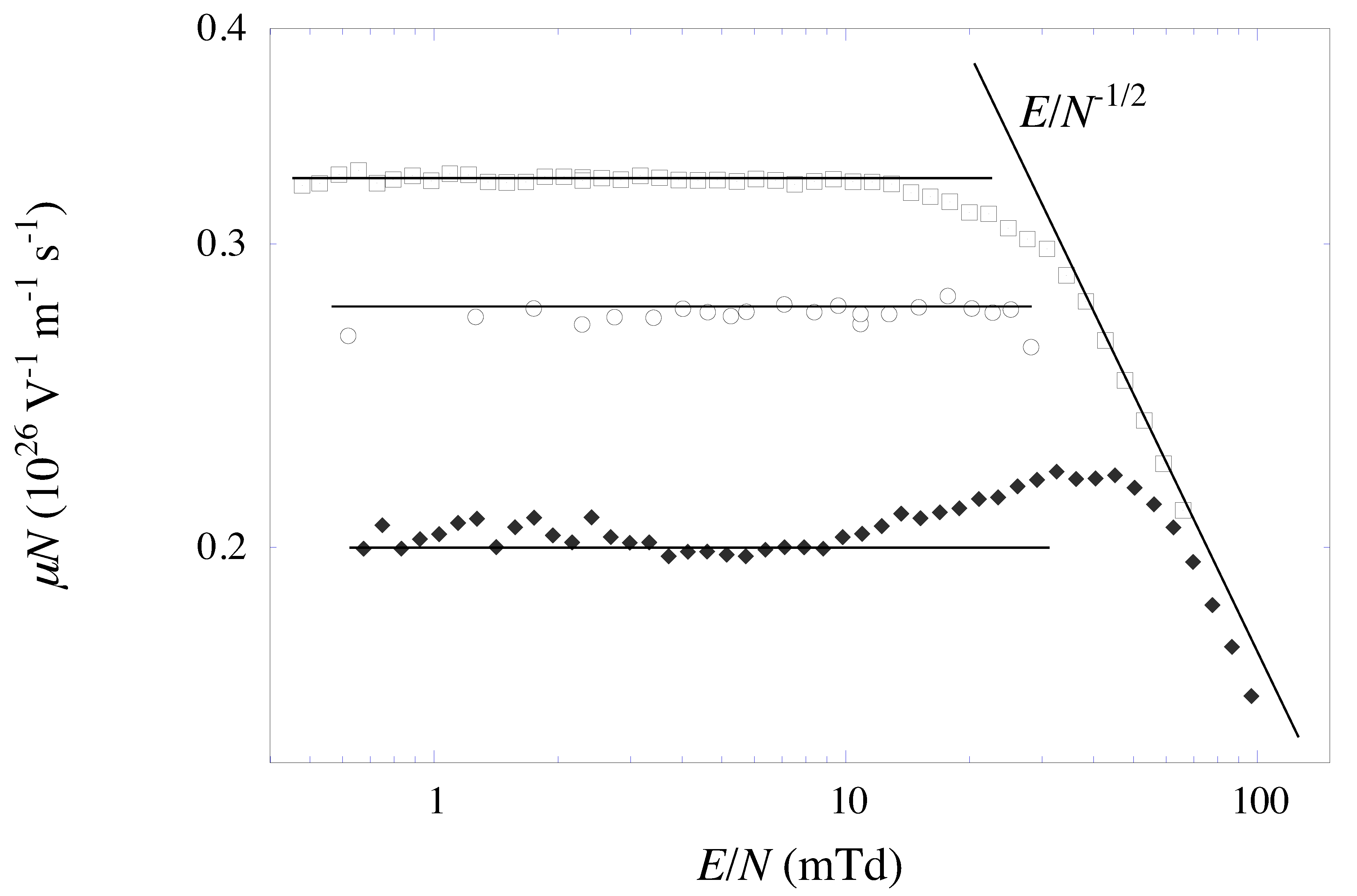
3.2. Choice of the Correct Density Range to Explore
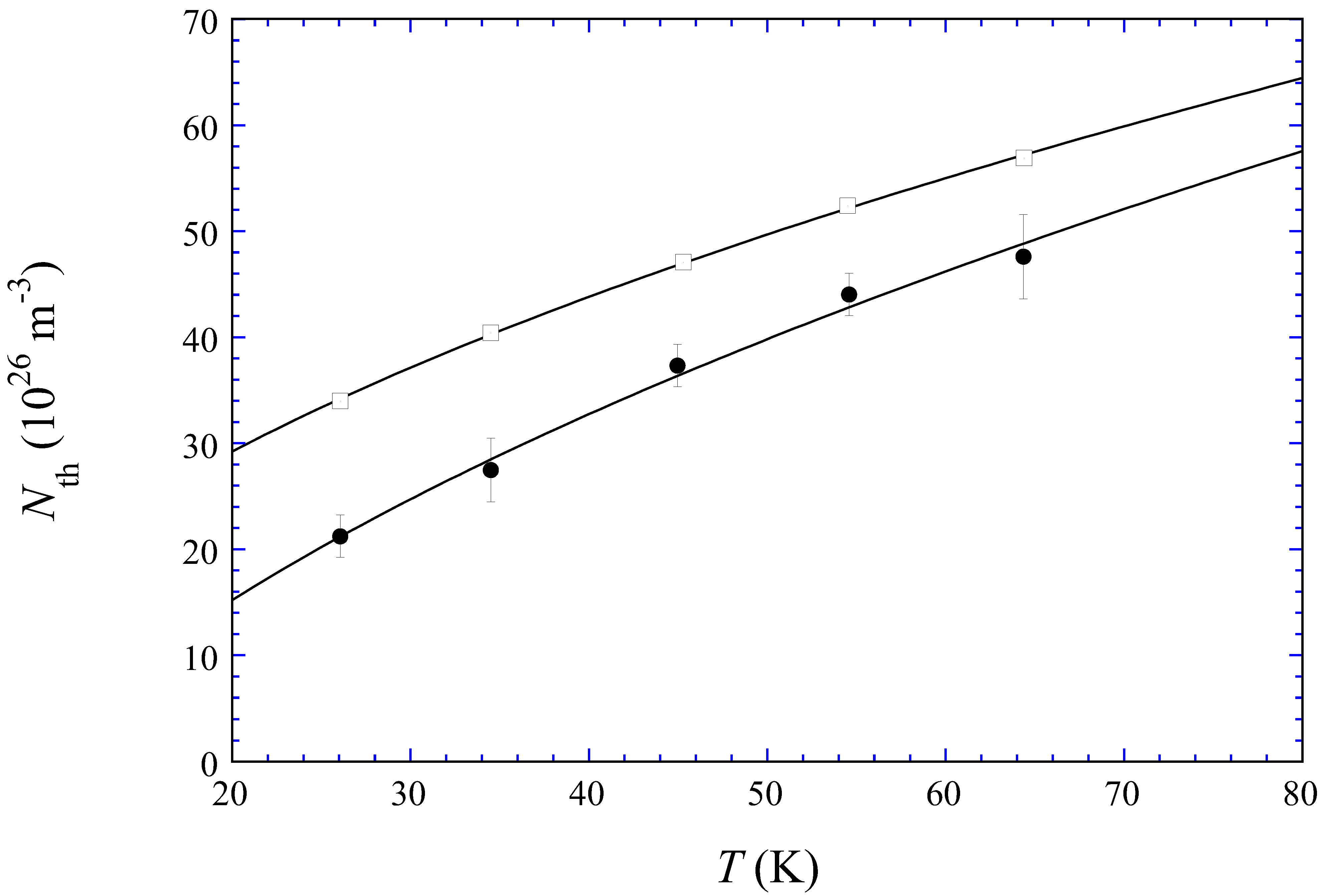
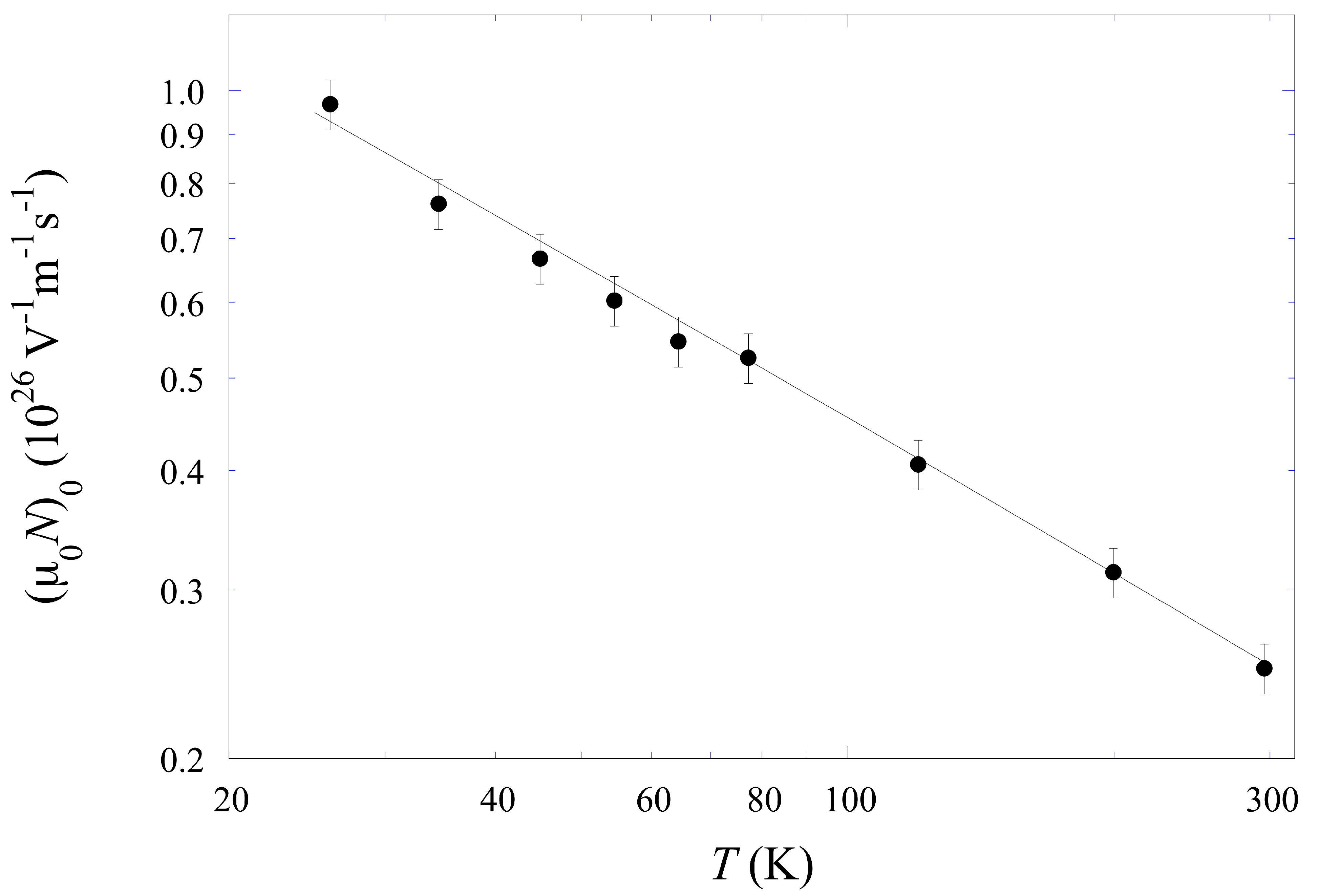
3.3. Density Dependence of the Zero-Field Limit of the Density Normalized Mobility
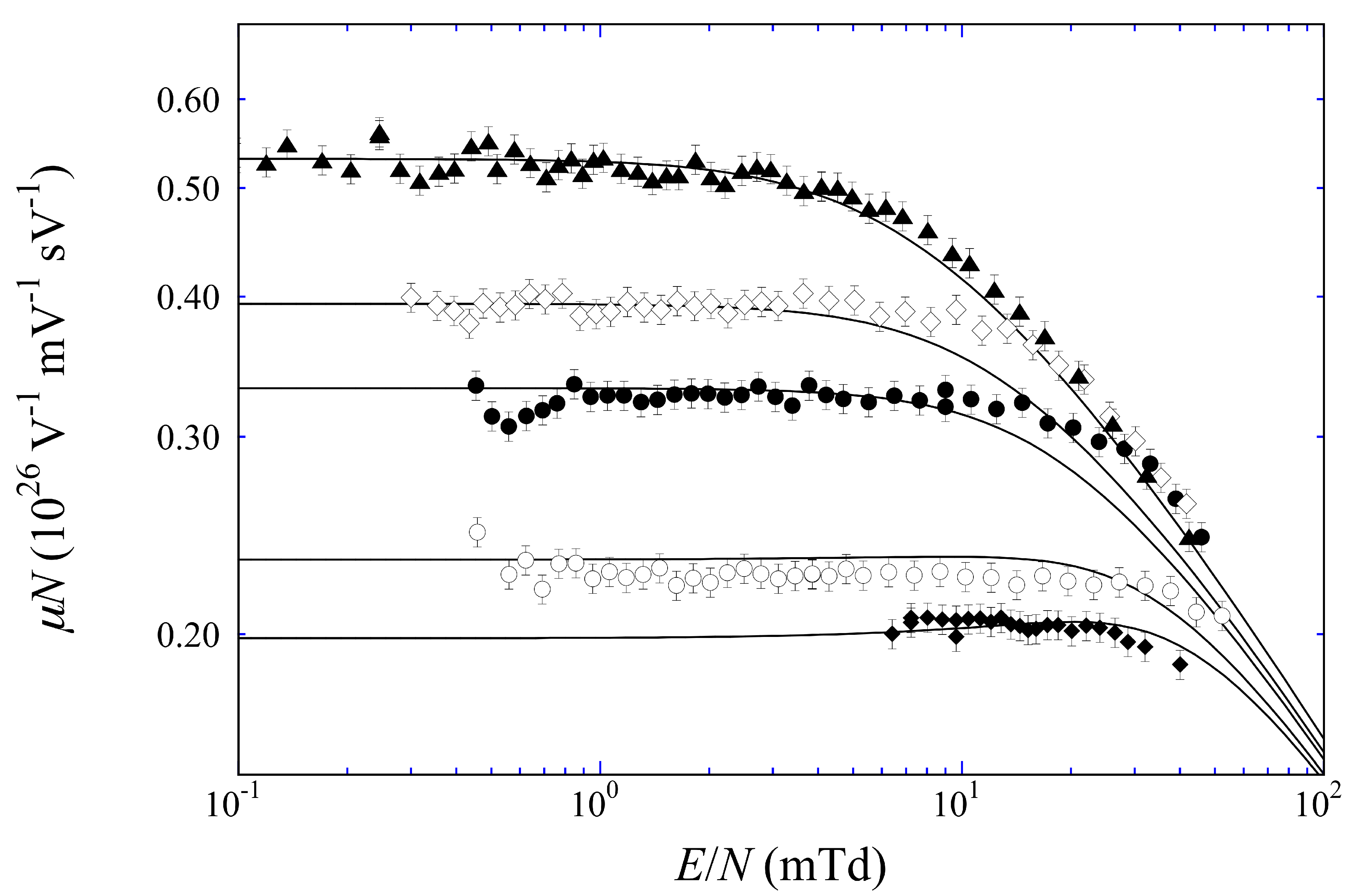
3.4. Validation of the Accuracy of the Present Experiment and of Its Outcome
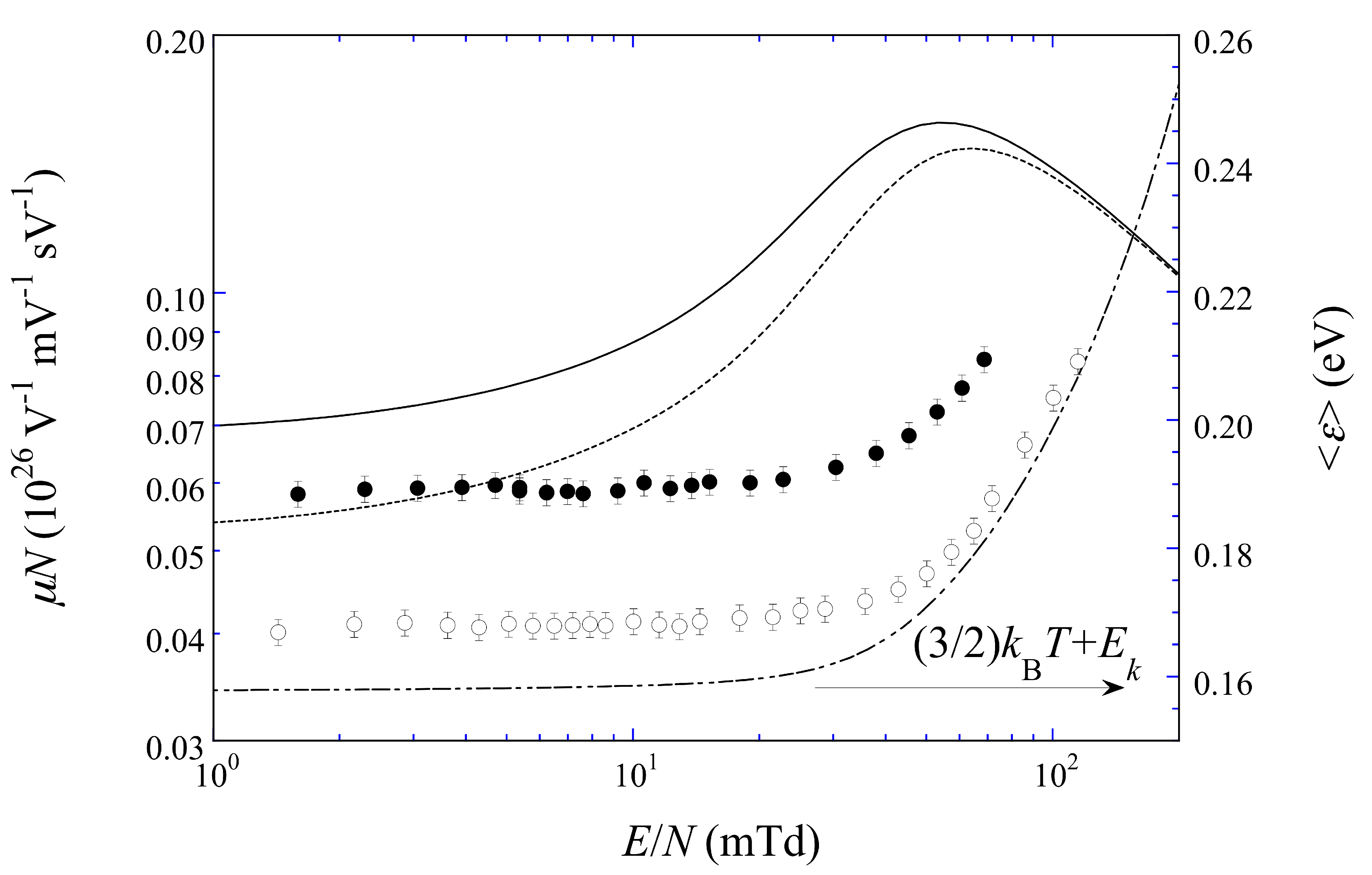
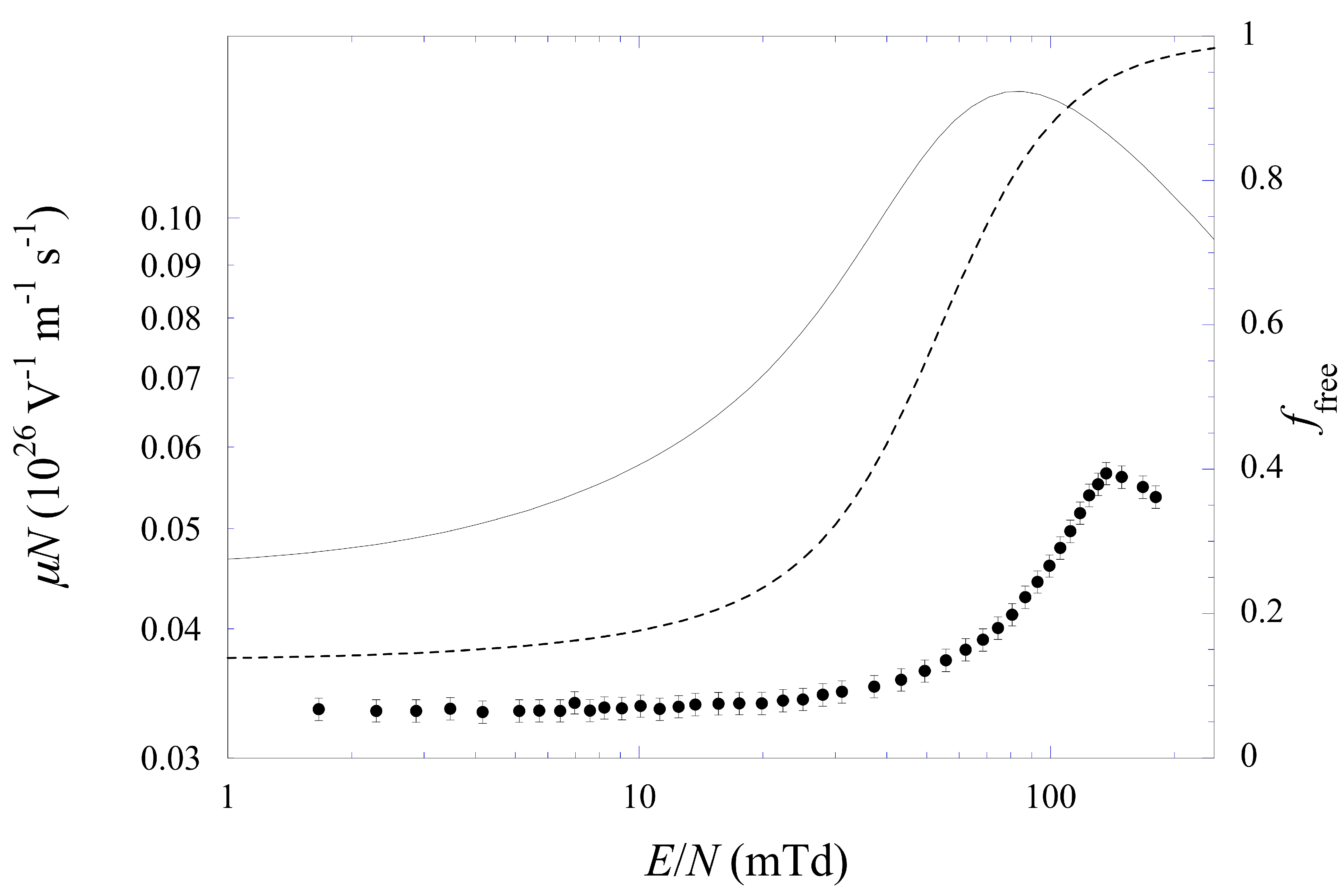
4. Weakly Localized States vs. Electron Bubble States
5. Conclusions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
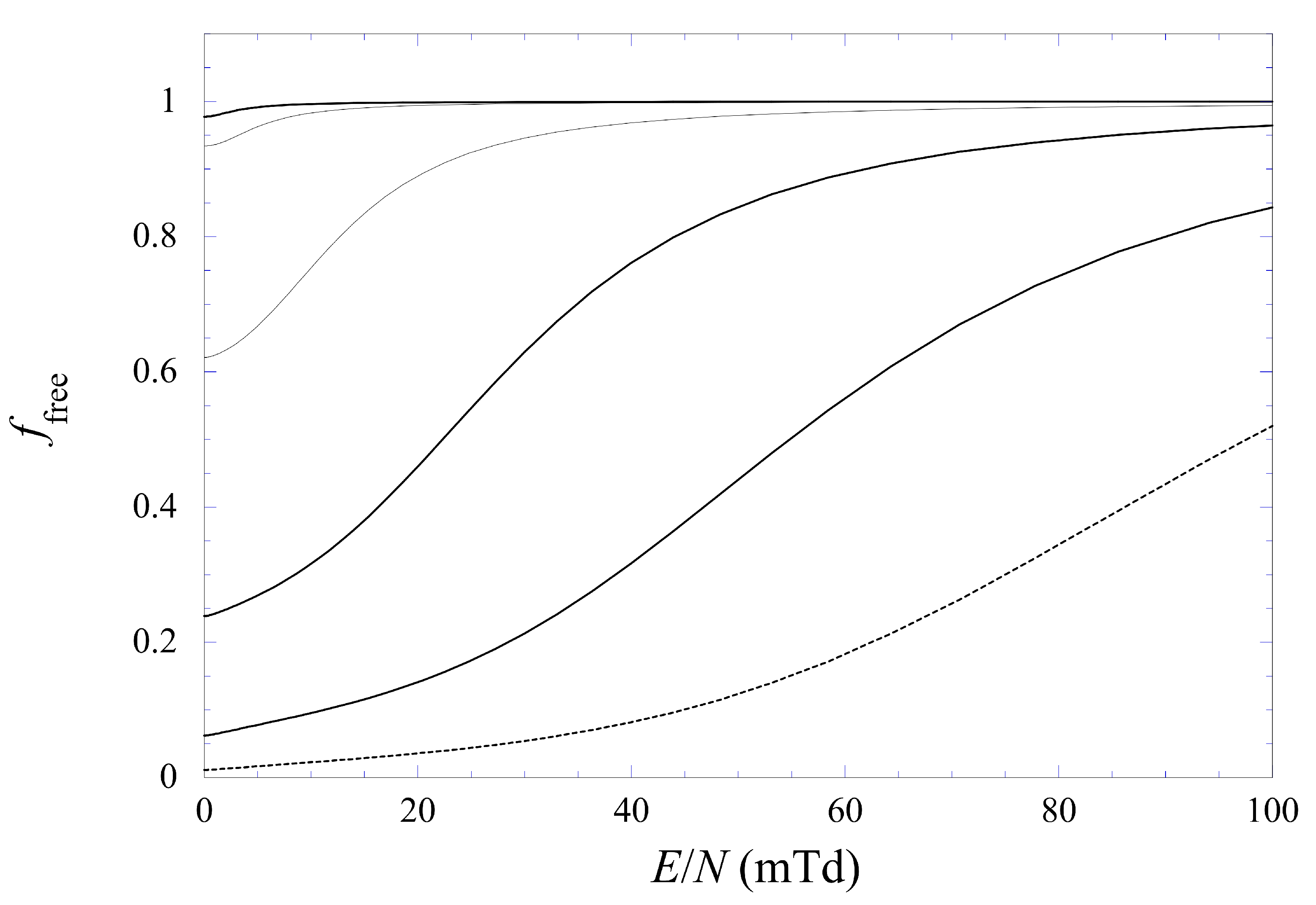
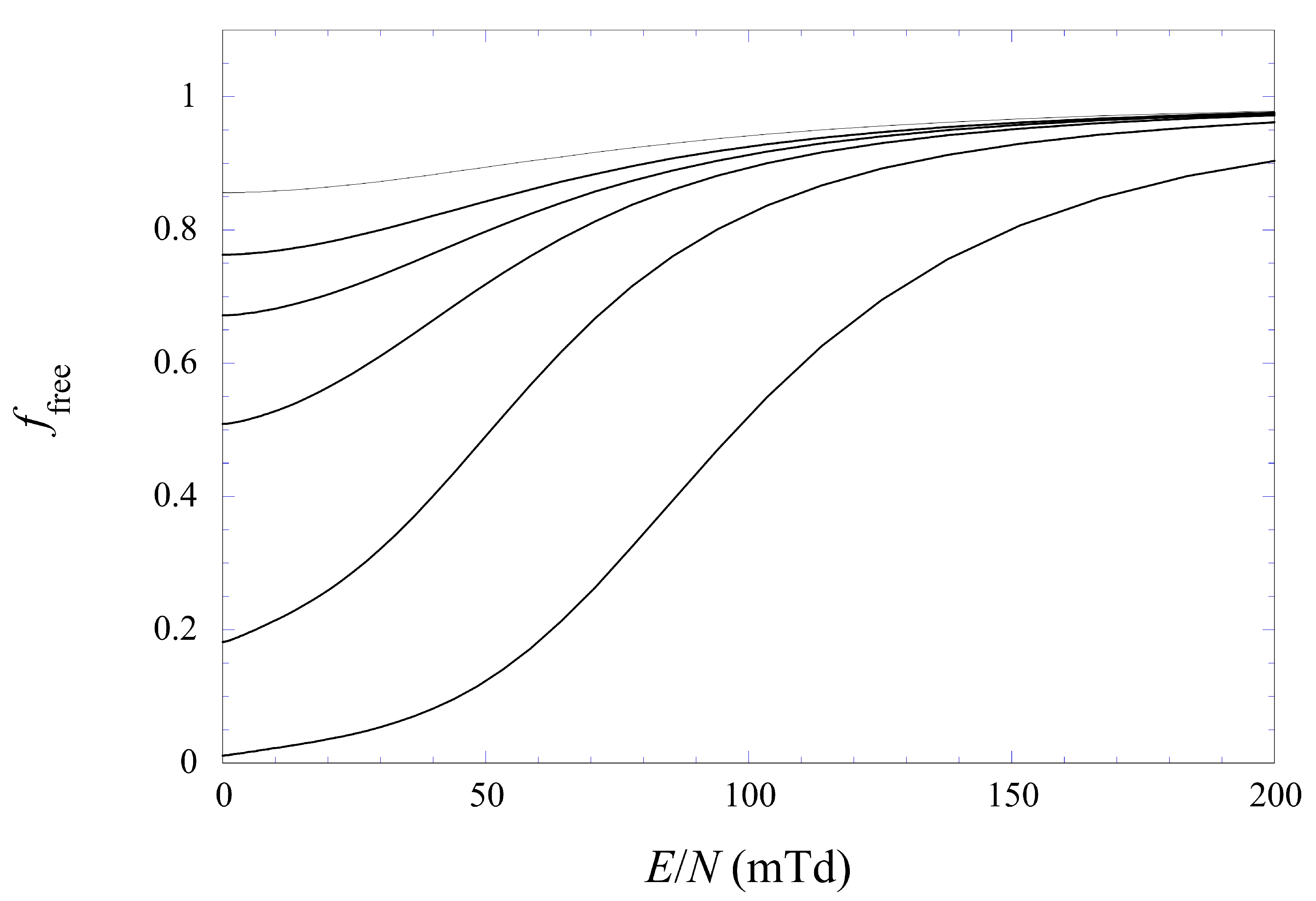
Appendix A. Influence of and of on the Mobility of Quasifree Electrons

References
- Levine, J.; Sanders, T.M. Anomalous electron mobility and complex negative ion formation in low-temperature helium vapor. Phys. Rev. Lett. 1962, 8, 159–161. [Google Scholar] [CrossRef]
- Levine, J.L.; Sanders, T.M. Mobility of electrons in low-temperature helium gas. Phys. Rev. 1967, 154, 138–149. [Google Scholar] [CrossRef]
- Harrison, H.R.; Sander, L.M.; Springett, B.E. Electron mobility and localization in dense He4 gas. J. Phys. B At. Mol. Phys. 1973, 6, 908–917. [Google Scholar] [CrossRef]
- Bartels, A. Density dependence of electron drift velocities in helium and hydrogen at 77.6 K. Appl. Phys. 1975, 8, 59–64. [Google Scholar] [CrossRef]
- Schwarz, K.W.; Prasad, B. Dynamics of electron localization in dense helium gas. Phys. Rev. Lett. 1976, 36, 878–881. [Google Scholar] [CrossRef]
- Schwarz, K.W. Anomalous electron mobilities in dense helium gas. Phys. Rev. Lett. 1978, 41, 239–242. [Google Scholar] [CrossRef]
- Schwarz, K.W. Electron localization in dense helium gas: New experimental results. Phys. Rev. B 1980, 21, 5125–5136. [Google Scholar] [CrossRef]
- Iakubov, I.T.; Polischuk, A.Y. Influence of multiple scattering processes on the electron mobility in moderately dense gases. Phys. Lett. A 1982, 91, 67–69. [Google Scholar] [CrossRef]
- Iakubov, I.T.; Polischuk, A.Y. Quantum density corrections to mobility and dispersion law for electrons in a medium of disordered scatterers. J. Phys. B At. Mol. Phys. 1982, 15, 4029–4041. [Google Scholar] [CrossRef]
- Atrazhev, V.M.; Iakubov, I.T. The electron drift velocity in dense gases. J. Phys. D Appl. Phys. 1977, 10, 2155–2163. [Google Scholar] [CrossRef]
- Ya Polischuk, A. Quantum corrections to electron conductivity in a disordered medium of anisotropic scatterers. J. Phys. B At. Mol. Phys. 1983, 16, 3853–3858. [Google Scholar] [CrossRef]
- Polischuk, A.Y. Theory of electron mobility in dense gases with small polarizability. Phys. B+C 1984, 124, 91–95. [Google Scholar] [CrossRef]
- O’Malley, T.F. Multiple scattering effect on electron mobilities in dense gases. J. Phys. B At. Mol. Phys. 1980, 13, 1491–1504. [Google Scholar] [CrossRef]
- Braglia, G.L.; Dallacasa, V. Theory of electron mobility in dense gases. Phys. Rev. A 1982, 26, 902–914. [Google Scholar] [CrossRef]
- O’Malley, T.F. General Model For Electron Drift and Diffusion in a Dense Gas. J. Phys. B At. Mol. Opt. Phys. 1992, 25, 163–180. [Google Scholar] [CrossRef]
- Anderson, P.W. Absence of diffusion in certain random lattices. Phys. Rev. 1958, 109, 1492–1505. [Google Scholar] [CrossRef]
- Cutler, M.; Mott, N.F. Observation of Anderson localization in an electron gas. Phys. Rev. 1969, 181, 1336–1340. [Google Scholar] [CrossRef]
- Foldy, L.L. The multiple scattering of waves. I. General theory of isotropic scattering by randomly distributed scatterers. Phys. Rev. 1945, 67, 107–119. [Google Scholar] [CrossRef]
- Lax, M. Multiple scattering of waves. Rev. Mod. Phys. 1951, 23, 287–310. [Google Scholar] [CrossRef]
- Ya Polischuk, A. Quantum corrections to the Boltzmann equation for electrons in a disordered medium. J. Phys. B At. Mol. Phys. 1983, 16, 3845–3851. [Google Scholar] [CrossRef]
- Borghesani, A.F.; Bruschi, L.; Santini, M.; Torzo, G. Electron mobility in neon at high densities. Phys. Rev. A 1988, 37, 4828–4835. [Google Scholar] [CrossRef]
- Bartels, A. Density dependence of the electron drift velocity in argon. Phys. Lett. A 1973, 44, 403–404. [Google Scholar] [CrossRef]
- Borghesani, A.F.; Santini, M.; Lamp, P. Excess electron mobility in high-density argon gas. Phys. Rev. A 1992, 46, 7902–7909. [Google Scholar] [CrossRef]
- Borghesani, A.F.; Santini, M. Electron localization-delocalization transition in high-density neon gas. Phys. Rev. A 1992, 45, 8803–8810. [Google Scholar] [CrossRef]
- Ioffe, A.F.; Regel, A.R. Non-crystalline, amorphous and liquid electronic semiconductors. In Progress in Semiconductors; Gibson, A.F., Ed.; Wiley: Hoboken, NJ, USA, 1960; Volume 4, pp. 237–291. [Google Scholar]
- Huxley, L.G.; Crompton, R.W. The Diffusion and Drift of Electrons in Gases; Wiley: New York, NY, USA, 1974. [Google Scholar]
- Springett, B.E.; Jortner, J.; Cohen, M.H. Stability criterion for the localization of an excess electron in a nonpolar fluid. J. Chem. Phys. 1968, 48, 2720–2731. [Google Scholar] [CrossRef]
- Wigner, E.; Seitz, F. On the constitution of metallic sodium. Phys. Rev. 1933, 43, 804–810. [Google Scholar] [CrossRef]
- Hernandez, J.P.; Martin, L.W. Analysis of excess electron states in neon gas. Phys. Rev. A 1991, 43, 4568–4571. [Google Scholar] [CrossRef] [PubMed]
- O’Malley, T.F. Extrapolation of electron-rare gas atom cross sections to zero energy. Phys. Rev. 1963, 130, 1020–1029. [Google Scholar] [CrossRef]
- Lekner, J. Scattering of waves by an ensemble of fluctuating potentials. Philos. Mag. 1968, 18, 1281–1286. [Google Scholar] [CrossRef]
- Ascarelli, G. Hall mobility of electrons in liquid xenon. J. Phys. Condens. Matter 1992, 4, 6055–6072. [Google Scholar] [CrossRef]
- Adams, P.W.; Paalanen, M.A. Localization in a Nondegenerate Two-Dimensional Electron Gas. Phys. Rev. Lett. 1987, 58, 2106. [Google Scholar] [CrossRef] [PubMed]
- Adams, P.W.; Paalanen, M.A. Anderson Localization of Electrons in Dense He4 Gas. Phys. Rev. Lett. 1988, 61, 451. [Google Scholar] [CrossRef] [PubMed]
- Mott, N.F. Electrons in disordered structures. Adv. Phys. 1967, 16, 49–144. [Google Scholar] [CrossRef]
- Mott, N. Metal-Insulator Transitions; Taylor & Francis: Abingdon, UK, 1974. [Google Scholar]
- Cohen, M.H.; Lekner, J. Theory of hot electrons in gases, liquids, and solids. Phys. Rev. 1967, 158, 305–309. [Google Scholar] [CrossRef]
- Stanley, H.E. Introduction to Phase Transitions and Critical Phenomena; International Series of Monographs on Physics; Oxford University Press: Oxford, UK, 1971; Volume 46. [Google Scholar]
- Thomas, J.E.; Schmidt, P.W. X-ray study of critical opalescence in argon. J. Chem. Phys. 1963, 39, 2506–2516. [Google Scholar] [CrossRef]
- Borghesani, A.F. Electron mobility maximum in dense argon gas at low temperature. J. Electrostat. 2001, 53, 89–106. [Google Scholar] [CrossRef][Green Version]
- Jahnke, J.A.; Silver, M.; Hernandez, J.P. Mobility of excess electrons and O2- formation in dense fluid helium. Phys. Rev. B 1975, 12, 3420–3427. [Google Scholar] [CrossRef]
- Borghesani, A.F.; Santini, M. High-temperature electron localization in dense He gas. Phys. Rev. E 2002, 65, 8. [Google Scholar] [CrossRef] [PubMed]
- Borghesani, A.; Bruschi, L.; Santini, M.; Torzo, G. Density dependence of the electronic mobility in high density neon gas. Phys. Lett. A 1985, 108, 255–258. [Google Scholar] [CrossRef]
- Borghesani, A.F.; Santini, M. Electron mobility and localization effects in high-density Ne gas. Phys. Rev. A 1990, 42, 7377–7388. [Google Scholar] [CrossRef]
- Borghesani, A.F.; Neri, D.; Santini, M. Low-temperature mobility in high-density neon gas. Phys. Rev. E 1993, 48, 1379–1389. [Google Scholar] [CrossRef]
- Neri, D.; Borghesani, A.F.; Santini, M. Electron attachment to O2 molecules in dense helium and argon gases. Phys. Rev. E 1997, 56, 2137–2142. [Google Scholar] [CrossRef]
- Borghesani, A.F. Resonant low-energy electron attachment to O2 impurities in dense neon gas. Plasma Sources Sci. Technol. 2020, 29, 35024. [Google Scholar] [CrossRef]
- Torzo, G. A simple recirculating pump for high-pressure high-purity gas. Rev. Sci. Instrum. 1990, 61, 1162–1163. [Google Scholar] [CrossRef]
- Angus, S.; Reuck, K.M.D.; McCarty, R.D. International Thermodynamic Tables of the Fluid State—4 Helium; Pergamon: New York, NY, USA, 1977. [Google Scholar]
- Sychev, V.V.; Vasserman, A.A.; Kozlov, A.D.; Spiridonov, G.A.; Tsymarny, V.A. Thermodynamic Properties of Helium; Hemisphere: Washington, DC, USA, 1987. [Google Scholar]
- Borghesani, A.F.; Delfitto, G. A low-cost, continuously adjustable, high-voltage, regulated DC power supply. Meas. Sci. Technol. 1990, 1, 825–827. [Google Scholar] [CrossRef]
- Borghesani, A.F.; Bruschi, L.; Santini, M.; Torzo, G. Simple photoelectronic source for swarm experiments in high-density gases. Rev. Sci. Instrum. 1986, 57, 2234–2237. [Google Scholar] [CrossRef]
- Borghesani, A.F.; Santini, M. Electron swarm experiments in fluids-signal waveform analysis. Meas. Sci. Technol. 1990, 1, 939–947. [Google Scholar] [CrossRef]
- Miyakawa, T.; Dexter, D.L. Stability of electronic bubbles in liquid neon and hydrogen. Phys. Rev. 1969, 184, 166–172. [Google Scholar] [CrossRef]
- Atrazhev, V.M. Delocalisation of electrons in dense helium gas by external electric field. J. Phys. D: Appl. Phys. 1984, 17, 889–902. [Google Scholar] [CrossRef]
- Sakai, Y.; Schmidt, W.F.; Khrapak, A. High- and low-mobility electrons in liquid neon. Chem. Phys. 1992, 164, 139–152. [Google Scholar] [CrossRef]
- Bartels, A.K. Messungen der Elektronendriftgeschwindigkeit in He, Ar, H2 und N2 bei Sehr Hohen Gasdichten (zur Frage der kollektiven WechselWirkung von Elektronen mit dem Gas). Ph.D. Thesis, Hamburg University, Hamburg, Germany, 1974. [Google Scholar]
- Borghesani, A.F.; Santini, M. Electron mobility maximum in near-critical argon gas. Int. J. Thermophys. 2001, 22, 1109–1121. [Google Scholar] [CrossRef]
- Borghesani, A.F.; Lamp, P. Injection of photoelectrons into dense argon gas. Plasma Sources Sci. Technol. 2011, 20, 34001. [Google Scholar] [CrossRef]
- Weyhreter, M.; Barzick, B.; Mann, A.; Linder, F. Measurements of differential cross sections for e-Ar, Kr, Xe scattering at E = 0.05 - 2 eV. Zeitschrift Phys. D Atoms Mol. Clust. 1988, 7, 333–347. [Google Scholar] [CrossRef]
- Borghesani, A.F. Ions and Electrons in Liquid Helium; International Series of Monographs on Physics; Oxford University Press: Oxford, UK, 2007; Volume 137. [Google Scholar]
- McCarty, R.D.; Arp, V.D. A New Wide Range Equation of State for Helium. In Advances in Cryogenic Engineering; ACRE; Springer: Boston, MA, USA, 1990; Volume 35, pp. 1465–1475. [Google Scholar] [CrossRef]
- Haddad, G.N.; Elford, M.T. Low-energy electron scattering cross sections in carbon dioxide. J. Phys. B At. Mol. Phys. 1979, 12, L743. [Google Scholar] [CrossRef]
- Elford, M.; Haddad, G. The Drift Velocity of Electrons in Carbon Dioxide at Temperatures between 193 and 573 K. Aust. J. Phys. 1980, 33, 517–530. [Google Scholar] [CrossRef]
- Krebs, P.; Giraud, V.; Wantschik, M. Electron Localization in Dense Ammonia Vapor. Phys. Rev. Lett. 1980, 44, 211. [Google Scholar] [CrossRef]
- Krebs, P.; Lang, U. Electron Mobility and Multiple Scattering Effects in Dense Methanol Gas. J. Phys. Chem. 1996, 100, 10482–10489. [Google Scholar] [CrossRef]


Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Borghesani, A.F. Accurate Electron Drift Mobility Measurements in Moderately Dense Helium Gas at Several Temperatures. Atoms 2021, 9, 52. https://doi.org/10.3390/atoms9030052
Borghesani AF. Accurate Electron Drift Mobility Measurements in Moderately Dense Helium Gas at Several Temperatures. Atoms. 2021; 9(3):52. https://doi.org/10.3390/atoms9030052
Chicago/Turabian StyleBorghesani, Armando Francesco. 2021. "Accurate Electron Drift Mobility Measurements in Moderately Dense Helium Gas at Several Temperatures" Atoms 9, no. 3: 52. https://doi.org/10.3390/atoms9030052
APA StyleBorghesani, A. F. (2021). Accurate Electron Drift Mobility Measurements in Moderately Dense Helium Gas at Several Temperatures. Atoms, 9(3), 52. https://doi.org/10.3390/atoms9030052





