Abstract
We have applied the full-relativistic Dirac B-Spline R-matrix method to obtain cross sections for electron scattering from ytterbium atoms. The results are compared with those obtained from a semi-relativistic (Breit-Pauli) model-potential approach and the few available experimental data.
Keywords:
electron scattering; elastic; excitation; ionization; ytterbium; close-coupling; B-Spline R-matrix 1. Introduction
Electron collisions with ytterbium atoms are of interest for both fundamental studies by experimental and theoretical methods [1,2]. While the ground state has a closed-shell configuration, one of the electrons as well as one of the electrons can easily be promoted. Furthermore, with a nuclear charge of , Yb is a heavy atom for which relativistic effects are important. All the above lead to a very dense energy level structure and, consequently, to complex line spectra [3]. This also makes the theoretical description of collision processes involving Yb very challenging and hence suitable for benchmark testing.
In addition to being of fundamental interest, ytterbium is important for a number of practical plasma applications. A list of references can be found in Bostock et al. [2]. As one specific recent example, accurate cross sections for electron collisions with ytterbium atoms are needed in the modelling of the enrichment process that is the basis for the creation of Lu-177, which carries great promise in the treatment of a variety of cancers [4]. While some experimental data and theoretical predictions are available in the literature [2,5,6,7,8,9], the comprehensive dataset needed for the modeling requires calculations for a large number of discrete transitions as well as ionization over an extended energy range. In this context, it also important to have reliable absolute cross sections. This can be a serious challenge for both experiment and theory. The former often needs help from theory, while the latter can be seriously affected by both channel coupling and the quality of the target structure description. See, for example, the discussions in refs. [2,8].
In this paper, we report our initial calculations of e-Yb scattering, using a full-relativistic 20-state close-coupling model. The resulting equations are solved with the Dirac B-spline R-matrix (DBSR) code developed by Zatsarinny and described by Zatsarinny and Bartschat [10]. Since this is the very last project that Oleg Zatsarinny worked on until his untimely death on 2 March 2021, it appears to be an appropriate start of this Special Issue of ATOMS that is dedicated to his legacy.
Section 2 of this manuscript gives a brief description of the numerical methods used in both the atomic structure and the subsequent collision calculations. In addition to the DBSR-20 model, we carried out standard Breit-Pauli R-matrix (BPRM) calculations with 10 and 28 coupled states, respectively. While we believe that the superior structure model of DBSR yields the most accurate results of the three models, the BPRM-10 and BPRM-28 results provide some indication about the sensitivity of these theoretical predictions to details of the model. Section 3 exhibits our results and the corresponding discussion, before we finish with some conclusions and an outlook in Section 4.
2. Numerical Method
We used the full-relativistic Dirac B-Spline R-matrix (DBSR) method developed by Zatsarinny [10] to perform the calculations. The first challenge in a complex target such as Yb is the structure calculation. Looking at the NIST tables [3], one notices that the subshell is opened up at relatively low energies, which results in a very rich target structure. Accurately including all the states that can be built from, e.g., and , is not possible with currently available computer programs. Hence, we only include the one state of the configuration that can have a total electronic angular momentum , since it can be excited via an optically allowed single-electron transition from the ground state.
There is also a substantial term dependence in the one-electron orbitals, as well as strong configuration mixing. For the DBSR-20 model, we employed the programs grasp2K [11] and DBSR_HF [12] to generate the orbitals for Yb+ in the basis configurations , , and . With these orbitals in hand, we carried out a bound-state close-coupling calculation, i.e., we looked for bound-state solutions of the scattering problem [13]. This method has the advantage that it enables us to systematically increase the number of states ultimately included in the close-coupling collision calculation for scattering. Specifically, so-called pseudo-states can easily be generated by forcing the orbitals to vanish at the boundary of the R-matrix box. These pseudo-states represent a finite discretization of the infinite number of high-lying Rydberg states as well as the target continuum. Excitation cross sections for the pseudo-states then provide estimates for excitation of the Rydberg series as well as the ionization cross section. In order to further improve the structure description, a few “perturbers”, i.e., doubly-excited states, were added to the configurations ultimately used for the neutral Yb atom.
Table 1 shows a comparison between the values obtained originally and the recommended excitation thresholds [3]. Not surprisingly, there remain differences, generally of the order of a few percent. Due to the high density of states, even the order of states could not be correctly reproduced in some cases. The largest discrepancy of about 10% occurs for the relatively high-lying state. Overall, one can see that the total energy of the ground state is not low enough, which will result in an underestimate of about 0.3 eV of the ionization potential. In order to allow for a meaningful comparison with experiment (if available) and to ensure that the levels are in the correct order for modelling applications, we adjusted the theoretical thresholds to the recommended ones.

Table 1.
Excitation energies (eV) in the DBSR-20 compared to the recommended NIST values.
The stucture calculations for the BPRM-10 and BPRM-28 models were performed with the program AUTOSTRUCTURE [14]. The 10-state model included all states that can be built from the , , and configurations. In the 28-state model, all states originating from the , , and configurations were added. In practice, the Belfast R-matrix program [15] for such large targets uses a core potential provided by AUTOSTRUCTURE to describe the inner 68 electrons and only treats the two outer valence electrons explicitly. Generally, the excitation energies were significantly inferior to those used in the DBSR-20 model. This is mainly due to the fact that not enough correlation is included to properly describe the binding energy of the two electrons in the ground state. While there are ways to fix this, the BPRM calculations are only meant to serve as some indicator for the sensitivity of the predictions. Hence, any deviations seen in the next section effectively represent the “worst-case scenario”.
We used an R-matrix radius of ≈ (where m is the Bohr radius) in the DBSR-20 and ≈ and ≈ in the BPRM-10 and BPRM-28 calculations, respectively. In the DBSR model, we employed 138 splines of order 8 (9) to expand the large (small) component of the projectile orbitals inside the R-matrix box. Using different spline orders for the two components prevents the occurrence of spurious structures [16]. In the BPRM calculations, 35 numerical continuum orbitals and partial waves up to a total electronic angular momentum of were used. This value of , as well as number of basis functions, limits the energy range for which the predictions for the cross sections are converged with the number of partial waves, especially for optically allowed transitions. In the DBSR-20 model, we therefore increased to 49.5. We employed a top-up procedure based on a geometric series extrapolation in all calculations. The suitability was tested by switching from numerical to estimated partial-wave contributions at different values. For DBSR-20, this allowed us to generate partial-wave-converged results up to 150 eV shown in the next section.
3. Results and Discussion
Figure 1 shows our initial results for elastic scattering from the ground state. Comparing the DBSR predictions with those obtained from the BPRM-10 and BPRM-28 models and the experimental data of Predojević et al. [6] shows good agreement for incident energies above ≈ eV, while the results are extremely sensitive to the details of the model in the low-energy regime. More work would be required to carefully study these very low energies in order to extract, for example, a reliable value for the scattering length. We also see very narrow dips and peaks in the DBSR-20 results between about 2 eV and 4 eV collision energy. They are not numerical artifacts but most likely not observable experimentally with realistic current energy resolution.
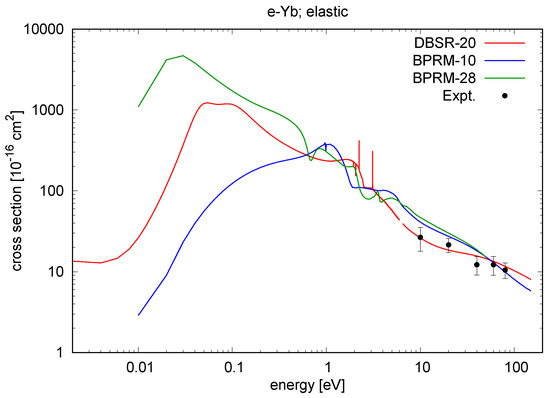
Figure 1.
Cross section for elastic e-Yb scattering obtained in the DBSR-20, BPRM-10, and BPRM-28 models. The experimental data are from Predojević et al. [6].
Figure 2 and Figure 3 exhibit results for excitation of the and states from the ground state. Except for a small admixture to the state, these are mostly exchange transitions and hence the cross sections peak at low incident energies just above threshold. In this energy region, there is significant resonance structure, which would need to be analyzed in more detail if this information is needed. For many modeling applications, however, it is sufficient to obtain the rate coefficients, which are obtained by integrating the (properly weighted) cross sections over the energy and, therefore, are generally much less sensitive to the details of the resonance positions.
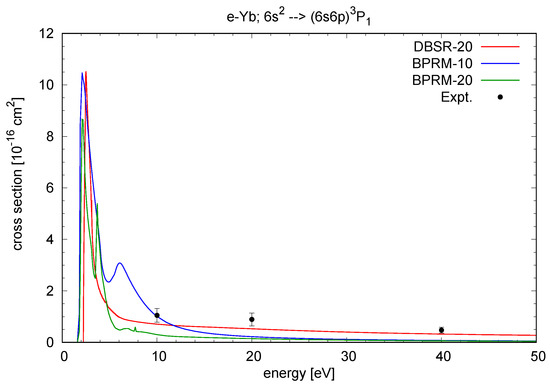
Figure 2.
Cross section for electron impact excitation of the transition in Yb. The DBSR-20 results are compared with the BPRM-10 and BPRM-28 predictions and the experimental data of Predojević et al. [7].
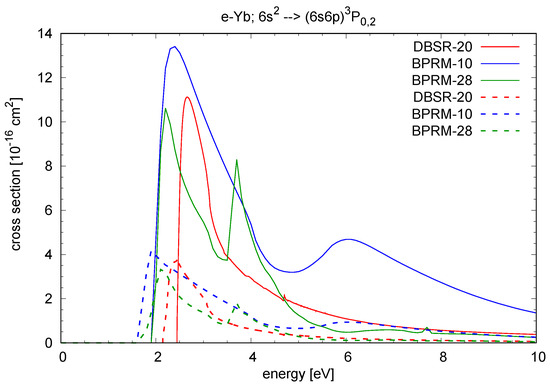
Figure 3.
Cross section for electron impact excitation of the (solid lines) and (dashed lines) transitions in Yb. The DBSR-20 results are compared with the BPRM-10 and BPRM-28 predictions.
Unfortunately, no experimental data are available near threshold. For the higher energies, the agreement between the DBSR-20 prediction and the experimental data of Predojević et al. [7] (only available for the state) is very good.
Figure 4 and Figure 5 display our results for excitation of two optically allowed transitions, namely and , respectively. In the latter case, the subshell is opened for a dipole-allowed one-electron transition. Hence, the cross section is substantial, which may be important for plasma modeling. Again, only a few experimental data, with significant uncertainties, are available for comparison. Given the difficulty of describing the state in the first place, the level of agreement seen in Figure 5 is certainly encouraging.
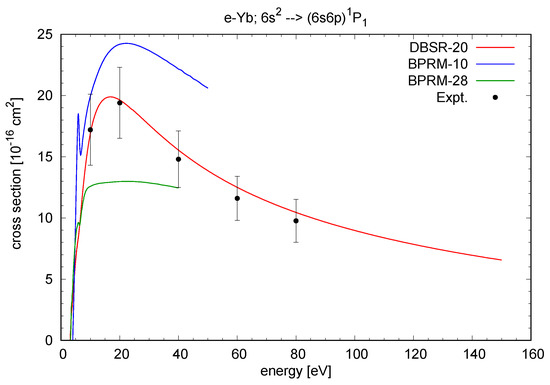
Figure 4.
Cross section for electron impact excitation of the transition in Yb. The DBSR-20 results are compared with the BPRM-10 and BPRM-28 predictions and the experimental data of Predojević et al. [6].
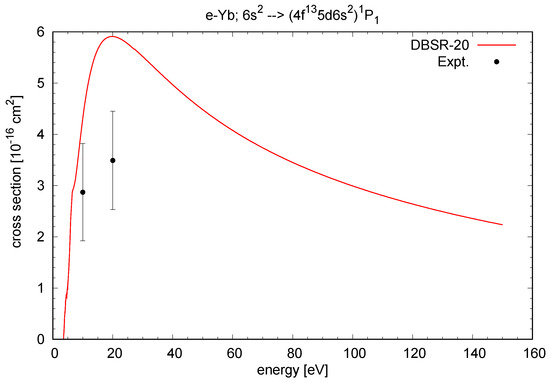
Figure 5.
Cross section for electron impact excitation of the transition in Yb. The DBSR-20 results are compared with the experimental data of Predojević et al. [7]. The BPRM models did not include this state.
Next, we consider a spin-allowed quadrupole transition, namely . Results are shown in Figure 6. As in spin-forbidden cases, theoretical predictions for such transitions can be strongly affected by coupling to higher Rydberg states as well as the ionization continuum. It is, once again, encouraging to see that the DBSR-20 model overshoots the experimental data by less than the BPRM-28 model, presumably due to the better structure description. Based on our experience with many other collisions problems, we expect that larger DBSR calculations, which are planned in the future, will bring the predictions down and improve the agreement with experiment. Qualitatively, this can be understood as follows: Larger calculations would open up the possibility for both excitation of higher Rydberg levels and ionization, thereby generally reducing the flux into lower excited levels.

Figure 6.
Cross section for electron impact excitation of the transition in Yb. The DBSR-20 results are compared BPRM-28 predictions (BPRM-10 did not include this state) and the experimental data of Predojević et al. [7].
We finish with some results for optically allowed transitions between excited states. These cross sections can be very large and, therefore, may also be of great importance for modeling applications, especially if the electron temperature is high enough to enable substantial populations of the metastables or of optically excited atoms, for example, in a laser trap. Figure 7 exhibits our predictions for four such transitions between states of the and manifolds. In the interest of visibility, we only show the DBSR-20 results.
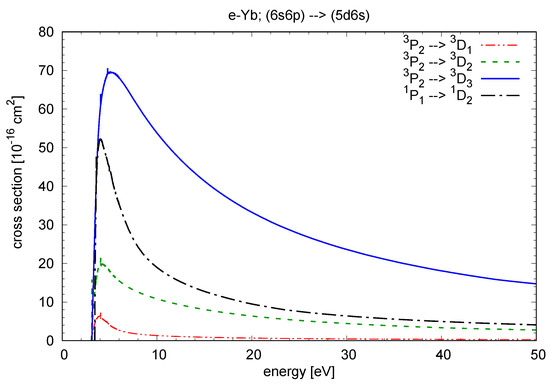
Figure 7.
DBSR-20 predictions of cross sections for electron-induced transitions between the states indicated in the legend.
4. Conclusions and Outlook
In this manuscript, we have presented initial results from an ongoing project to produce an extensive set of reliable cross sections for electron collisions with ytterbium atoms. The work was initiated by Oleg Zatsarinny. Our future calculations will benefit greatly from his providing us an excellent start and the suite of computer programs that he developed over decades. These suites of BSR and DBSR codes are publicly available on GitHub [17]. Compiled versions of the BSR programs (using non-relativistic and semi-relativistic models) and examples are also implemented on the Atomic and Molecular Physics Gateway [18]. More details will be provided in a later publication of this Special Issue.
Author Contributions
The calculations were initiated by O.Z. and completed by K.R.H. and K.B. The latter two authors prepared this manuscript. All authors have read and agreed to the published version of the manuscript.
Funding
This work was supported by the United States National Science Foundation under grant Nos. PHY-1803844, OAC-1834740, PHY-2110023, and the XSEDE allocation TG-PHY-090031, and by the Texas Advanced Computing Center through the Frontera allocation PHY-20028.
Conflicts of Interest
The authors declare no conflict of interest. The funders had no role in the design of the study; in the collection, analyses, or interpretation of data; in the writing of the manuscript, or in the decision to publish the results.
Sample Availability
Tabulated results of the cross sections are available from the authors upon request.
Abbreviations
The following abbreviations are used in this manuscript:
| BSR | B-Spline R-matrix |
| DBSR | Dirac B-Spline R-matrix |
| BPRM | Breit-Pauli R-matrix |
References
- Zetner, P.W.; Johnson, P.V.; Li, Y.; Csanak, G.; Clark, R.E.H.; Abdallah, J., Jr. Electron impact excitation of the (…6s6p3PJ) levels in ytterbium. J. Phys. B 2001, 34, 1619–1639. [Google Scholar] [CrossRef]
- Bostock, C.J.; Fursa, D.V.; Bray, I. Calculation of electron scattering from the ground state of ytterbium. Phys. Rev. A 2011, 83, 052710. [Google Scholar] [CrossRef]
- Kramida, A.; Ralchenko, Y.; Reader, J.; NIST ASD Team. NIST Atomic Spectra Database (ver. 5.8). 2020. Available online: https://physics.nist.gov/asd (accessed on 11 June 2021).
- ORNL News. 2020. Available online: https://www.oakridger.com/news/20190312/ornls-enriching-isotopes-again (accessed on 11 June 2021).
- Shimon, L.L.; Golovchak, N.V.; Garga, I.I.; Kurta, I.V. Electron-impact excitation of atomic-ytterbium spectral lines: An experimental study. Opt. Spektrosk. 1981, 50, 1037. [Google Scholar]
- Predojević, B.; Šević, D.; Pejčev, V.; Marinković, B.P.; Filipović, D.M. Electron scattering by ytterbium: I. Excitation of the 4f146s6p1P1 resonance state and elastic collision. J. Phys. B 2005, 38, 1329. [Google Scholar] [CrossRef]
- Predojević, B.; Šević, D.; Pejčev, V.; Marinković, B.P.; Filipović, D.M. Electron scattering by ytterbium: II. Excitation of the 4f14(6s6p3P1,5d6s1D2,and6s7p1P1) and 4f135d6s2(7/2,5/2) states. J. Phys. B 2005, 38, 3489. [Google Scholar] [CrossRef]
- Das, T.; Sharma, L.; Srivastava, R.; Stauffer, A.D. Electron-impact excitation of zinc and ytterbium atoms. Phys. Rev. A 2012, 86, 022710. [Google Scholar] [CrossRef]
- Kelemen, V.I.; Remeta, E.Y. Elastic scattering of electrons by europium and ytterbium atoms. Technol. Phys. 2013, 58, 1749, Originally published in Zhurnal Tekhniceskoj Fiziki 2013, 83, 46. [Google Scholar] [CrossRef]
- Zatsarinny, O.; Bartschat, K. Relativistic B-spline R-matrix method for electron collisions with atoms and ions: Application to low-energy electron scattering from Cs. Phys. Rev. A 2008, 77, 062701. [Google Scholar] [CrossRef]
- Jönsson, P.; He, X.; Fischer, C.F.; Grant, I.P. The grasp2K relativistic atomic structure package. Comp. Phys. Commun. 2007, 177, 597. [Google Scholar] [CrossRef]
- Zatsarinny, O.; Fischer, C.F. DBSR_HF: A B-spline Dirac–Hartree–Fock program. Comp. Phys. Commun. 2016, 202, 287. [Google Scholar] [CrossRef] [Green Version]
- Zatsarinny, O.; Fischer, C.F. Atomic structure calculations using MCHF and BSR. Comp. Phys. Commun. 2009, 180, 2041. [Google Scholar] [CrossRef]
- AUTOSTRUCTURE Code. Available online: http://amdpp.phys.strath.ac.uk/autos/ (accessed on 11 June 2021).
- Berrington, K.A.; Eissner, W.B.; Norrington, P.H. Belfast atomic R-matrix codes. Comp. Phys. Commun. 1995, 92, 290. [Google Scholar] [CrossRef]
- Fischer, C.F.; Zatsarinny, O. A B-spline Galerkin method for the Dirac equation. Comp. Phys. Commun. 2009, 180, 879. [Google Scholar] [CrossRef] [Green Version]
- Oleg Zatsarinny GitHub Repository. Available online: https://github.com/zatsaroi/ (accessed on 16 July 2021).
- Atomic and Molecular Physics Gateway. Available online: https://ampgateway.org/ (accessed on 16 July 2021).
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).