Classical Description of Resonant Charge Exchange Involving the Second Flavor of Hydrogen Atoms

Abstract

We studied the consequences of the existence of the second flavor of hydrogen atoms (SFHA)—the existence proven by atomic experiments and evidenced by astrophysical observations—on the resonant charge exchange. We found analytically that there is indeed an important difference in the corresponding cross-sections for the SFHA compared to the usual hydrogen atoms. This difference could serve as an additional tool for distinguishing between the two kinds of hydrogen atoms in future experiments/observations. We also show that the SFHA does not exhibit any Stark effect—whether in a uniform or a non-uniform electric field—in any order of the perturbation theory.

1. Introduction

There is a proof from atomic experiments that there are two kinds—or two flavors—of hydrogen atoms: the usual ones and the second flavor [1]. The second flavor of hydrogen atoms (SFHA) has only states of zero angular momentum (the S-states) both in the discrete and the continuous spectra. Therefore, due to the selection rules (presented, e.g., in the textbook [2])—the rules prohibiting the transition between the S-states—the SFHA does not have states that can be coupled by the electric dipole radiation [1,3,4].

It should be noted that the theoretical part of the discovery of the SFHA was based on solving the standard Dirac equation for a hydrogen atom. The Dirac equation allows two solutions at a relatively small distance from the origin: the regular solution and the singular solution. For models with the point-like nucleus (i.e., the point-like proton), the singular solution is justifiably rejected. However, in Paper [1], it was shown that with the allowance for the finite size of the proton and for its electromagnetic form factor, the inner (i.e., inside the proton) wave function and its derivative at the proton boundary can satisfy the standard continuity requirement with the wave function and its derivative for the singular solution outside the proton for the ground state. In Paper [4], it was shown that the same is true for all l = 0 states of the discrete and continuous spectra. Thus, the singular solution outside the proton was proven to be legitimate. This result was obtained without introducing any new physical laws. Only the allowance for the SFHA eliminated a huge (by many orders of magnitude) discrepancy between the experimental and theoretical results for the high-energy tail of the linear momentum distribution in the ground state of hydrogen atoms [1]. This constituted the experimental proof of the existence of the SFHA.

There is also another piece of evidence in favor of the existence of the SFHA—from astrophysics. Their existence can explain recent puzzling astrophysical observations concerning the redshifted radio line 21 cm from the early Universe [5]: the explanation presented in Paper [4] did not require resorting to hypothetical, never discovered subatomic particles—in distinction to the explanation from Paper [6]. It follows that the SFHA is a viable candidate for dark matter or at least a part of it.

In the present paper, we study the consequences of the existence of the SFHA on the resonant charge exchange for hydrogen atoms. Charge exchange is one of the most important processes in atomic physics and astrophysics—see, e.g., Book [7], Reviews [8,9], and references therein. In particular, on the resonant charge exchange between the usual atoms, one could see, e.g., Papers and Reviews [10,11,12,13,14,15] (listed chronologically) and references therein. We remind that, specifically for hydrogen atoms (of any kind), the resonant charge exchange is the process where the electron in the hydrogen atom, being initially in the state of the principal quantum number n ≥ 1 (including n >> 1)—the state described by a set of parabolic or spherical quantum numbers—ends up bound to the nearby proton in the state of exactly the same set of quantum numbers.

Our focus here is at the distinction in the description of the resonant charge exchange (along the lines of Paper [10]) between the SFHA and a proton, compared to the corresponding charge exchange between the usual hydrogen atom and a proton—the distinction caused by the specific structure of the SFHA. We show analytically that there is indeed an important difference in the classical cross-section of the resonant charge exchange during the collision of the proton with the SFHA compared to the collision of the proton with the usual hydrogen atom.

2. Analytic Calculations for Usual Hydrogen Atoms

For relatively slow collisions, the classical cross-section σ of the resonant charge exchange, specifically for the transition of a classical electron from the field of influence of one ion into the field of influence of another one, is the following (according to Paper [10]):

σ = (8π/I²)(1 − 0.8z^2/5), z = v/(2I)^1/2

(1)

where I is the ionization potential from the particular state of the atom and v is the relative velocity of the colliding nuclei. Here and below, we use atomic units, unless specified to the contrary. The Expression (1) for the cross-section is valid under the condition:

v << v_max = (2I)^1/2

(2)

We specifically study the corresponding resonant charge exchange between a hydrogen atom in the state of the principal quantum number n and a proton. In this section, we consider the usual hydrogen atom—the situation where the hydrogen atom is of the second flavor will be considered in the next section. In the zeroth approximation, the ionization potential is:

I₀ = 1/(2n²)

(3)

so that in the zeroth approximation one has

σ₀ = 32πn⁴[1 − 0.8(nv)^2/5]

(4)

In the next approximation, we take into account the Stark shift of the sublevels of the hydrogen atom in the field of the proton located at the distance R from the atom. The first non-vanishing correction to the ionization potential of the hydrogen atom from a particular state originates from the linear Stark effect:

I = [1/(2n²)](1 − 3n³q/R²), q = n₁ − n₂

(5)

where n₁ and n₂ are the parabolic quantum numbers.

As noted in Paper [10], a barrierless transition of an electron from one ion to another one is possible if the potential for the interaction between electrons and nuclei at the midpoint of the axis joining them exceeds the ionization potential. This leads to the following charge-exchange-effective separation between the atom and the proton [10]:

R₀ = 4/I

(6)

After substituting R = R₀ in the second term in the parenthesis in the right side of Equation (5) and using I = I₀ = 1/(2n²) in that term (since the term is much smaller than the first term), this equation becomes:

I = [1/(2n²)][1 − 3q/(64n)]

(7)

On substituting Equation (7) in Equation (1) and utilizing the smallness of the second term in the parenthesis in the right side of Equation (7), we finally obtain:

σ = 32πn⁴[1 − 0.8(nv)^2/5 + 3q/(32n)]

(8)

3. The Corresponding Results for the Second Flavor of Hydrogen Atoms

Now we consider the situation where the hydrogen atom (colliding with the proton) is of the second flavor. Let us first explain that the SFHA does not exhibit any Stark effect in any order of the perturbation theory, neither in the uniform electric field nor in the non-uniform electric field of the proton.

In a uniform electric field F, the interaction term in the Hamiltonian of an atom is V = –dF, where d is the operator of the electric dipole moment of the atomic electron (dF is the scalar product of these two vectors, also known as the dot-product). The SFHA has only the S-states. Therefore, due to the selection rules, all matrix elements (both diagonal and non-diagonal) of the operator d are zeros. Thus, the SFHA does not exhibit any Stark effect in a uniform electric field in any order of the perturbation theory.

Now, let us analyze whether there is any Stark effect when the SFHA is subjected to the non-uniform electric field of an ion of the charge Z separated from the SFHA by the distance R. The dipole interaction term (~1/R²) yields zero in all orders of the perturbation theory—for the same reason as in the case of the uniform electric field.

In the usual hydrogen atom, the next contribution (~1/R³) originates from the quadrupole interaction calculated in the first order, and the higher contribution (~1/R⁴) is due to the following three sources: dipole interaction calculated in the second order, the quadrupole interaction calculated in the second order, and the octupole interaction calculated in the first order—as shown in Paper [16]. However, for the SFHA, the quadrupole, octupole, and all higher multipole terms, containing linear combinations of various powers of the radius-vector operator r of the atomic electron, yield zeros in all orders of the perturbation theory—both diagonal and non-diagonal matrix elements of the operator r are zeros.

For completeness, we also note that for the usual hydrogen atom, there is a relatively small contribution to the electric quadrupole moment of the atomic electron due to the magnetic dipole and electric quadrupole hyperfine interactions with the nucleus—see, e.g., Paper [17] and references therein. For the S-states of the usual hydrogen atom, this contribution arises due to the admixture of the D-states, the admixture being caused by the hyperfine interactions. However, since the SFHA does not have D-states (it has only the S-states), this effect for the SFHA is also zero.

From the above follows an important new result. Namely, the SFHA does not couple not only to the electric dipole radiation (as noted in Papers [3,4]), but also does not couple to the electric quadrupole of any higher multipole radiation. From the absence of the Stark effect in any order for the SFHA, it also follows that for the SFHA the corresponding cross-section σ₂ of the resonant charge exchange is:

σ₂ = 32πn⁴[1 − 0.8(nv)^2/5]

(9)

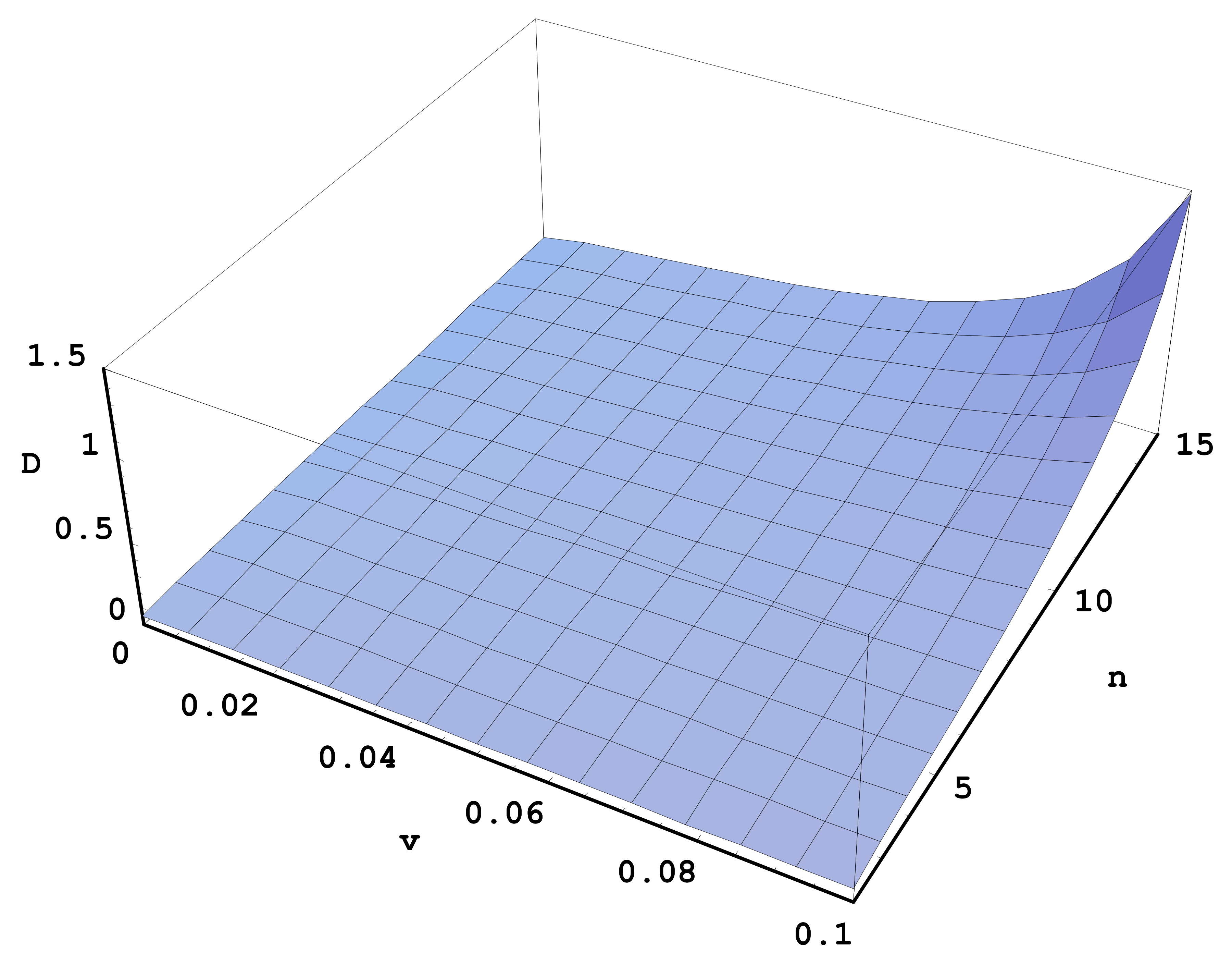
Figure 1 illustrates the relative difference D = (σ − σ₂)/σ₂, where σ and σ₂ are given by Equations (8) and (9), respectively, versus the relative velocity v of the colliding particles and the principal quantum number n for the quantum number q = n − 1. It is seen that the relative difference can reach values ~1.

Thus, there is a significant difference in the classical cross-section of the resonant charge exchange when the proton collides with the SFHA rather than with the usual hydrogen atom. Namely, in the latter case there is an additional (third) term in the cross-section (see Equation (8)), which is absent in the former case (see Equation (9)). This is yet another important fundamental distinction between the SFHA and the usual hydrogen atom—in addition to the fact that the SFHA does not have states that can be coupled by the electric dipole radiation.

4. Conclusions

We analyzed whether the classical cross-section of the resonant charge exchange would be different for the SFHA (compared to the usual hydrogen atoms) due to the fact that the SFHA has only S-states. We found analytically that there is indeed an important difference in the corresponding cross-sections: the relative difference can reach values ~1.

We also analytically studied the Stark effect for the SFHA. It turned out that the SFHA does not exhibit any Stark effect in a uniform electric field in any order of the perturbation theory. As for the SFHA in the non-uniform field of the proton at the distance R, it does not exhibit any Stark effect in any order of 1/R—even after allowing for hyperfine interactions with the nucleus.

The SFHA does not engage in the electric dipole, quadrupole, or any higher multipole radiation and could be a viable candidate for dark matter or a part of it, as shown in Paper [4]. In the present paper, we revealed additional important distinctive features of the SFHA. We hope that our findings will motivate further laboratory experiments and astrophysical observations on the issue of the SFHA. In particular, the difference in the cross-section of the resonant charge exchange for the SFHA compared to the usual hydrogen atoms could serve as an additional tool for distinguishing between the two kinds of hydrogen atoms in future experiments/observations.