“Amplified Spontaneous Emission” in Micro- and Nanolasers

Abstract

Amplified Spontaneous Emission is ubiquitous in systems with optical gain and is responsible for many opportunities and shortcomings. Its role in the progression from the simplest form of thermal radiation (single emitter spontaneous emission) all the way to coherent radiation from inverted systems is still an open question. We critically review observations of photon bursts in micro- and nanolasers, in the perspective of currently used measurement techniques, in relation to threshold-related questions for small devices. Corresponding stochastic predictions are analyzed, and contrasted with burst absence in differential models, in light of general phase space properties. A brief discussion on perspectives is offered in the conclusions.

1. Introduction

Amplified Spontaneous Emission (ASE) is a pervasive phenomenon ever present in any optical system which exhibits gain. Its origin lies in the existence of the induced emission, symmetric of absorption, postulated by Einstein [1] in his seminal paper on radiation. In the field of lasers and optical amplifiers, which has grown a few decades later, it has progressively gained importance as a competitor [2], precursor [3] or substitute [4] of lasing and broadband noise source [5] or pulsed source in optical amplifiers (cf. [6] and references therein for numerous applications).

From the laser point of view, fundamental aspects of ASE begin with the realization of the existence of a threshold for the spontaneous amplification [7,8]. Overcoming this threshold amounts to enabling the amplification of a signal at the end of a pumped sample to be spontaneously amplified through propagation in the medium—whence the term ASE. In such a case a “mirrorless laser” can be built [9], and one of its early experimental realization is the (transversely excited, high pressure) $N_2$ laser [10,11]. As already mentioned, and to be expected, systems with high gain—which make for excellent oscillators—have been very well sought after for their ease in realizing a laser [12,13], as well as the more versatile dye-based counterparts, for which a thorough characterization of the combined ASE and coherent emission has been conducted [14] (corrections to initially established relations, mostly applicable to solid state lasers, have been later determined [15]). An alternative representation of ASE, seen as amplified noise, has been also proposed [16].

At the macroscopic scale, ASE is responsible for astrophysical laser sources [8,17], on the one hand, and has been exploited to strongly improve the efficiency of the Free Electron Laser, using a self-amplification regime [18,19,20], or for UV amplification [21]. ASE, exploited as a biocompatible nonlinear, scattering induced amplifier [22], is the natural precursor of random lasing [23,24] and is predicted to appear in concomitance with a reduction in the number of degrees of freedom in such systems [25].

From the point of view of field monochromaticity, a large amount of ASE is detrimental in conjuction with coherent emission in bulk lasers [2] or fiber amplifiers [26]. However, it enables pulse shortening [27] and very broadband lasers and amplifiers [28], whose current application is the generation of ultrashort pulses [29] approaching the attosecond regime. In this sense, ASE is strongly beneficial to the realization of sources with extreme performance. Current interest, at an entirely different lengthscale, covers the micro- and nanoscopic regime, where on the one hand solid-state microdisk lasers suffer from the incoherent emission component [30], while ASE is used as a measure of the potential for obtaining lasing action in nanodevices [31,32] even before achieving actual lasing—its usefulness is therefore in validating the selection of candidates for nanolasing emission. Strong technological interest in ASE appears in the investigation of colloidal systems [33] and their threshold engineering [34] as well as in organic lasers [35,36] as reviewed in [37].

A very interesting regime in superluminescent diodes has been identified, where the superpossonian statistics approaches the lasing regime as the current supplied to the device is increased [38]. In addition to the potential technological interest proposed in the original paper, this observation may suggest the emission of frequent, ultrashort ASE pulses which amount to a quasi-continuous emission. Whether this is a generic kind of emission is a question which is now of great interest in relation with photon condensation. Without entering into a detailed discussion of this line of research, which escapes the scope of this contribution, we highlight this emerging topic, susceptible of leading to a more complete description of the physics of radiation in its evolution from the entirely spontaneous emitter relaxation into the purely coherent (lasing) emission.

The observation of the condensation of photons in interaction with a resonant medium in a cavity [39], and of its different statistical and non-stationary properties [40,41], has prompted the investigation of its occurrence even in other systems [42,43], hinting to a phenomenon more general than what initially considered (even without considering polariton and excitons which lie outside the realm of this discussion). A generalized thermodynamical treatment of Kirchoff’s law [44] enables the description of subsystems with different temperatures—thus out of equilibrium—bridging the gap between the traditional thermal point of view and more modern devices. Its applications are numerous and, in addition to enabling more efficient, tailored coupling between emitters and space, offers one more step in the description of the radiation field starting from the ideal spontaneous emission (one single emitter in vacuum) all the way to the non-equilibrium situation, eventually represented by the laser [45]. Potential interest for futuristic high-speed communications rests on the development of these concepts [46].

A complete overview of spontaneous emission is outside the scope of the present contribution; however, aspects which are important for our scopes include the filtering action of a cavity [47] or the relation between spontaneous emission and gain in Quantum Well semiconductor devices [48]. Fundamental features of the relationship between the so-called “Dicke superradiance” and ASE are discussed in [49,50], and provide the foundations of the transition between the spontaneous and the stimulated regimes. Finally, it is worth pointing out recent investigations on the coherence properties of ASE and the possibility for obtaining lasing action—through ASE—in a cavity-less system [51,52]. A good overview of the physics of small-sized lasers and of many of their threshold features—including discussions on noise properties and quantum-mechanical considerations—can be found in [53] (and references therein).

In this contribution, we concentrate on pre-threshold photon bursts that have been experimentally observed in micro- and nanolasers, whose existence can be (mostly) predicted by a stochastic modelling approach based on Einstein’s semiclassical theory of radiation [1]. At the present stage, no definite answers exist on their actual nature, aside from the fact that they appear unusual from a traditional laser physics point of view. We compare observed and predicted features, and comment on the technological limitations which constrain their experimental detection. Topological considerations, based on standard laser models, provide guidance in interpreting the observations and in reconstructing their physical origin. Second-order zero-delay autocorrelations are the most widespread means of characterizing very weak signals, such as those emitted by nanolasers, and have been widely employed also for thermal or quasi-thermal sources [38]. A simple analysis of the autocorrelation of a pulsed source complements the guidance provided by the topological analysis and helps securing a grip onto some of the observed characteristics of pre-threshold photon bursts.

This paper is work in progress and aims at proposing more questions than it can provide answers. As such, it is possible that several Readers may have diverging views from the writer, but also that the latter may revise his position on some of the exposed points in the near or far future. Thus Readers should take this contribution not so much as a finished product, but, rather, as a stimulus to delve more deeply in the points that are raised and in the much more numerous ones which are only hinted upon as related issues.

The paper touches on different aspects of photon bursts, directly and indirectly observed in micro- and nanolaser experiments, predicted by fully stochastic models and (mostly) missed by differential models. The presentation is divided into 6 main sections, followed by conclusions (Section 8). The question of the nature of a laser threshold in micro- and nanolaser is discussed in Section 2 starting from the proof of its equivalence to a phase transition for macroscopic lasers and leading into the paradoxical case of the thresholdless nanolaser. The experimental constraints, whose origin resides in the technological limitations of current instrumentation, are highlighted together with the potentially crucial role that models may play in directing the investigations on this topic. Since photon bursts appear in the smooth transition region from incoherent to coherent emission, this point is central to the discussion. The (scarce) collected evidence on photon bursts is summarized in Section 3, with reference to the publications in which this is found, and a physical role in the incoherent→coherent transition is proposed (Section 3.2). Since direct measurements of the temporal evolution of laser emission are possible only with microdevices, most of the information is gathered through the use of autocorrelation functions obtained through photon counting. A simple model, Section 4, is used to show that the presence photon bursts can be statistically identified through the appearance of superthermal statistics (of course in the single-mode emission regime, as it is well-known that mode competition leads to strong bunching). The model, based on a sequence of pulses of variable amplitude sitting on an adjustable background, is used to show the limitations of this approach, where superthermal bunching disappears when the background grows too large or when the pulses become too frequent. A brief overview of the two main classes of models (Section 5), differential and stochastic (Section 5.2), is given, summarizing their main characteristics and their ability (Section 5.1) to include some of the crucial aspects for a thorough description of the physics of laser threshold in small devices. The predictions of different implementations of stochastic models are summarized in Section 5.3 in relationship to photon bursts. Up until here, the paper summarizes observations (both experimental and numerical) and examines the characteristics of models or analysis tools in relationship to their potential for describing photon bursts. Some clearer understanding, accompanied by predictive power and insight into the dynamics, is offered by a topological analysis of the phase space which underlies the description of laser physics is presented in Section 6. Here, the eigenvalues emerging from the linear stability analysis are examined for nano-, micro-, and macrolasers, together with their accompanying eigenvectors. This analysis enables a clearer view of the stability of each kind of laser and of the possibility for adequate noise to give rise to photon bursts. One last section examines the features of a phenomenological modifications of the Rate Equations, very recently proposed, where photon bursts have been observed: a first in the ability for a differential model in predicting the emission of large photon bunches. Through the topological analysis (Section 7), we see how the proposed modification may enable the more modest amount of noise which accompanies the differential description to give rise to photon bursts.

The schematic representation of Figure 1 shows in graphical form the different topics which are going to be addressed in the discussion. On a typical nanolaser response curve (black line) which shows the photon number as a function of pump, we qualitatively indicate the threshold region, in which photon bursts are observed (stochastically computed dark green trace). A physical interpretation on their origin will be offered on the basis of the phase space properties, showing that before continuous coherent emission any fluctuation (purple arrow) possesses a small likelihood of relaxing into the photon field, and thus easily grows extremely large, with the consequent emission of a photon burst (in a qualitatively similar way of what is achieved in laser Q-switching). Along the way, we examine the experimental aspects of the problem on the basis of existing results, but also considering the experimental limitations and offering some insight into the main analysis tool: the second order autocorrelation. The current models’ predictive abilities in regard to photon bursts are also reviewed, considering both differential and stochastic methods.

In the following, we will refer to spontaneous emission in the traditional sense used in laser physics, rather than in the thermal radiation sense partly discussed in this introduction. The term laser threshold is used to denote the true threshold point, as defined in a phase transition (but also in bifurcation theory), but also to identify the region in which the electromagnetic field evolves from the emission of (mainly) incoherent photons to the coherent regime. Threshold region is used when emphasizing the extent of the transition in pump range.

2. Laser Threshold at the Micro- and Nanoscale

The question of laser threshold, a non-issue in the macroscopic devices used for decades, has come to the forefront with the considerable cavity volume reduction introduced by the Vertical Cavity Surface Emitting Laser (VCSEL) design [54], which led, in less than two decades, to ultralow currents for coherent emission [55]. The impressive reduction in cavity volume achieved by these devices brought a substantial increase in the fraction of spontaneous emission coupled into the lasing mode ($\beta$ factor) with the consequent linear relationship between input and output for $\beta =1$. As a result, based on the traditional macroscopic laser point of view, threshold was extrapolated to a zero pump value; the devices fitting this condition became therefore known as thresholdless lasers [56] or zero-threshold lasers [57,58].

While in macroscopic lasers threshold is compatible with a phase transition definition [59,60,61,62], with nearly unmeasurable deviations from the thermodynamic limit, the strong finite size effects typical of nanocavities introduce a smooth change from the non-lasing to the lasing solution [56,63] and open questions about the nature of the transition [64]. The extended pump range over which the transition takes place demonstrates an unfolding of the thermodynamical discontinuity and the suggest the name of threshold region for the corresponding pump interval. The practical consequence of the uncertainty surrounding a clear definition of threshold in small devices has led to the call for more stringent criteria to identify lasing [65], particularly in the technologically very active field of organic devices [66]. From a quantum-statistical point of view, the definition of threshold is legitimate only in the thermodynamic limit and for devices which approach such a regime (thus macroscopic lasers, only), as clearly demonstrated in a seminal paper [67]. However, the rigorous analysis does not provide any useful answers to the practical question of whether and when does the emission of a small source become (sufficiently) coherent, at least to be accepted as a laser. This question carries far reaching consequences, since many of the applications for which lasers are selected require a (sufficiently) good level of coherence, which has to be ensured for their usefulness. Luckily, statistical theories are not the only tools to define a transition and a very recent contribution has shown that through bifurcation analysis it is possible—in a suitably extended model (cf. Section 5.1)—to predict the existence of a true laser threshold even in a thresholdless laser [68].

In spite of recent advances, a clear description of the physics of the radiation emitted by a nanolaser in the transition from incoherent to coherent emission is still lacking. Two concomitant reasons contribute to the uncertainty. On the one hand, measurements are very difficult in the threshold region due to the extremely reduced photon flux which, coupled to extremely short evolution timescales, imposes a currently unsurmountable double constraint on instrumentation: high sensitivity and large bandwidth. Experimental schemes to circumvent the limitations vary from devising alternative (somewhat larger) sources with (hopefully) similar (enough) characteristics [69], to better detectors [70] or to more advanced correlation techniques [38,71]. However, none can entirely compensate for the required extreme performance, and the information that can be experimentally gathered remains partial. On the other hand, models have so far failed to provide a clear picture of the physics of radiation in the threshold region, leaving the more detailed predictions to fully numerical, stochastic approaches. The compounded experimental and theoretical difficulties have left the investigations in a state where progress is slow and difficult. A brief discussion of the current state of modelling is offered in Section 5.

In this contribution we focus our attention onto the region which precedes coherent emission (even a very noisy one, with a broadband radiofrequency spectrum [72]) where we observe pulses whose features resemble those of ASE. So far the number of reports concerning this kind of emission at the micro- and nanoscale is relatively small, nonetheless it has been seen—directly or indirectly—in different kinds of devices and at different laser scales. An interesting question, for future consideration, concerns the possible relationship between this regime of emission and what can be expected from thermal sources in a condensed photon phase. From a practical point of view, spontaneous photon bursts may bring along alternative ways of encoding information in small devices at lower power consumption, provided suitable schemes are employed [73].

3. Summary of Existing Evidence for Photon Bursts

We first summarize the observations of photon bursts (Section 3.1) which precede the establishment of cw coherent emission, referring the Reader to the original publications for details. Section 3.2 then offers an interpretation of the observations.

3.1. Experimental Observations

Direct and indirect experimental observations of photon burst emission can be summarized as follows.

E.1

Finite width of $g^{\left(2\right)}\left(\tau \right)$ and of $g^{\left(2X\right)}\left(\tau \right)$ (the latter measured with a Michelson interferometer) obtained from a photonic crystal nanolaser and ascribed to amplitude fluctuations of a coherent state (cf. Figures 2 and 3 in [71] and Figures 4 and 5 in [74]). Observation compatible with the emission of photon bursts;

E.2

Direct observation of photon bursts in a narrow, but well accessible interval of pump values before the onset of (noisy) cw laser oscillation in a microlaser (cf. Figure 3 in [72]);

E.3

Narrow, structureless decay of the second-order time-delayed autocorrelation $g^{\left(2\right)}\left(\tau \right)$ with typical width $O\left({10}^{-9}s\right)$ both in microlasers and metallo-dielectric nanolasers (cf. Figure 5 in [72], Figure 3 in [75] and Figure 3 in [76]). Similar observation in lasing devices built upon photonic crystal nanostructures (cf. Figure 4 in [77]);

E.4

Report of a peak superimposed on the second-order time-delayed autocorrelation, $g^{\left(2\right)}\left(\tau \right)$, for same-(pump)-pulse, attributed to ASE in a metallo-dielectric nanolaser (cf. Figure 3 in [75]). This additional peak disappears as lasing is established;

E.5

Low-frequency broadband rf spectrum with cutoff compatible with the width of $g^{\left(2\right)}\left(\tau \right)$ (cf. Figure 8 in [78]) (micro-VCSEL). The lack of spectral structure (except a gradual decay towards the cutoff) is compatible with irregularly occurring bursts;

E.6

Observation of a superthermal $g^{\left(2\right)}\left(0\right)$, compatible with sharp emission bursts in micro-VCSELs (cf. Figure 6 in [76]). Superthermal autocorrelation values have also been obtained in metallo-dielectric nanolasers (cf. Figure 4 in [79]).

Direct measurements of $g\left(1\right)\left(\tau \right)$ would be desirable, as the first-order autocorrelation would offer a direct measurement of the photon burst’s coherence time. Although cumbersome, they have been performed in other nanolaser contexts [80], but so far not for photon bursts. However, equivalent information has been gathered from the second-order cross-correlation $g^{\left(2X\right)}\left(\tau \right)$ [71], corroborating the temporal features observed by direct means [72].

3.2. Interpretation

The traditional picture of laser threshold, developed for macroscopic devices, assimilates it to a second-order phase transition where diverging fluctuations (infinite correlation length) develop at the crossing point. The evolution from incoherent to coherent emission is described as a statistical superposition of coherent and incoherent photons [81], as a stepping stone between the two regimes. Although never explicitly stated, the statistical superposition hypothesis is suggestive of a transient mixture (at equilibrium) of incoherent and coherent photons which make up the emission.

This picture may now be revised in light of the observations summarized above. Under the assumption that the photon bursts can be considered to be sufficiently coherent (cf. later), we may think of the transition as constituted by coherent temporal islands bathed in an incoherent sea of spontaneous emission. In macroscopic lasers, the transition could only be observed as a (temporally) transient state [82] given the narrowness of the transition region, which shrinks to a single pump value in the true thermodynamic limit. The intrinsic stability constraints associated to the extremely narrow pump range, coupled to the technical state of the instrumentation of the late 1960’s (or early 70’s) could only offer a temporal glimpse into the averaged structure of the intermediate state. The information could, in fact, be gathered only extracting the photon statistics at fixed delay times in an experiment conducted by preparing the laser in a same state below threshold and suddenly decreasing the cavity losses (at the reference 0 time) to bring it above threshold. This way, the only time information was contained in the delay at which the convolution between coherent and incoherent photon fraction was measured. The need for long term averaging to collect the statistics washed out any detailed information on the temporal evolution (cf. Figure 2 in [82]).

In small lasers, instead, the extended transition region transforms the sudden jump into a progressive sequence of steps where, for each pump value, the ratio between the (time) fraction occupied by the islands and the sea evolves in favour of the former, until coherence is reached when the water dries out. However, the possibility of monitoring the temporal evolution in these devices at fixed, stable pump values sheds further insight into the internal dynamics of the radiation, showing an interplay between “coherent” bursts and an incoherent background emission. Figure 2 gives a qualitative illustration of the concept: the red islands show the time interval in which the photon number overcomes a set level (chosen here for best graphical illustration) for two different levels of pump, below the one for which the emission ceases to fall to the spontaneous emission level. Adding up the contributions to the upper and lower levels and considering them to correspond to a spontaneous ($a_s$, lower) and coherent ($a_c$, upper) contribution we can picture the averaged state as being made up of a state mixture $\langle \psi \rangle =a_s{\psi }_s+a_c{\psi }_c$, where ${\psi }_s$ and ${\psi }_c$ represent the spontaneous and coherent component, respectively. The latter information is the main one which could be accessed in macrolasers at the time of their photons statistical characterization (mostly in the 1970s), due to instrumental limitations. The narrowness of the region in such devices where photon bursts may appear, due to the sharpness of the transition, may make direct measurements almost impossible even nowadays.

The photon bursts observed in a microlaser [72,84] have an apparent duration of the order of ${\tau }_b\approx 0.4$ ns. Although there may be bandwidth limitations which intervene in the measurement, this value agrees with time-delayed second-order autocorrelation measurements taken with a fast photocounting system (∼40 ps time jitter) [76]. Similar values are obtained from the observation of the mixture of incoherent and coherent radiation in a nanolaser [71]. Burst durations close to one nanosecond correspond to sub-Å spectral widths, which are well below the selectivity of cavity mirrors (in terms of spectral width). This strongly suggest a good degree of coherence in each burst (even though below lasing standard), accompanied by a randomness in the choice of the emission wavelength from one burst to the next, thereby leading to an average broad line (of the order of one nanometer), at least in the microlaser observations [76]. This remark supports the previous picture of independent “coherent” bursts interspersed by incoherent emission.

Before concluding this section, it is important to insist on the distinction between coherence time and linewidth, which lays at the root of the previous conclusion. Indeed, the coherence time is associated with the individual photon burst, while the linewidth is the result of the ensemble of bursts, whose central optical frequency can take any value within the amplification line. This not only illustrates the distinction between the two pieces of information, but also highlights the reason why linewidth measurements are not accepted as proof of coherent emission.

4. Relationship between Bursts and ${\mathit{g}}^{\left(\mathbf{2}\right)}\left(\mathbf{0}\right)$—Experimental Considerations

Some simple mathematical considerations help highlighting some of the issues which connect the (indirect) observations of photon bursts with the zero-delay second-order autocorrelation. Since the basic properties that we intend to point out are general, we can base our observations on a simple model where we compute the autocorrelation of a single rectangular pulse defined by

$$\begin{array}{ccc}\hfill s\left(t\right)& =& \left\{\begin{array}{ccc}A& ,& 0\le t\le T·\delta \\ \alpha A& ,& T·\delta \le t\le T\end{array}\right.,\hfill \end{array}$$

(1)

$$\begin{array}{ccc}\hfill 0\le & \alpha & \le 1,\hfill \end{array}$$

(2)

where T represents the period, A is the amplitude of the signal and $\alpha$ represents the fraction of the maximum A by which the bottom level (background) is raised. Its zero-delay second-order autocorrelation, defined by [85]

$$\begin{array}{ccc}\hfill g^{\left(2\right)}(\tau =0)& =& \frac{{\langle s\left(t\right)s(t+\tau )\rangle }_{\tau =0}}{{\langle s\rangle }^2}\hfill \end{array}$$

(3)

where $\langle ·\rangle$ stands for the temporal average, straightforwardly gives the following expression:

$$\begin{array}{ccc}\hfill g^{\left(2\right)}\left(0\right)& =& \frac{A^2\delta +{\alpha }^2{A}^2(1-\delta )}{{\left[A\delta +\alpha A(1-\delta )\right]}^2}.\hfill \end{array}$$

(4)

Two limits can be readily obtained: $\alpha =0$ and $\alpha =1$, which correspond to the disappearance of background and disappearance of the peak, respectively. The former gives

$$\begin{array}{ccc}\hfill {\left.g^{\left(2\right)}\left(0\right)\right|}_{\alpha =0}& =& \frac{1}{\delta },\hfill \end{array}$$

(5)

while from the latter it is immediate to see that

$$\begin{array}{ccc}\hfill {\left.g^{\left(2\right)}\left(0\right)\right|}_{\alpha =1}& =& 1.\hfill \end{array}$$

(6)

Thus, in the total absence of a background (unlikely in an experiment, where there is at least some detection noise) the autocorrelation is inversely proportional to the width of the pulse and can diverge as this quantity goes to zero. Although the limit does not hold in a real system, it is easy to see how a single pulse can give rise to superthermal statistics, which occurs every time $\delta <0.5$. When, instead, the pulse disappears ($\alpha =1$) the statistics becomes that of Poisson, or coherent radiation.

From an experimental point of view, the intermediate cases are most interesting, especially because the number of pulses may be variable and background is unavoidable. First of all, the consideration of a single pulse in the period T (and consideration of a periodic function itself) is not a restriction. In practice, the observation window is of finite size, which can be assumed to be the duration T (periodicity is not a necessary hypothesis in the computation we have performed). The presence of more than one pulse (as long as we consider them to be all the same height) amounts to changing the fraction $\delta T$ of the time interval occupied by the pulses themselves. The computation is insensitive to the presence of N pulses of duration $\delta T$ or of a single pulse of duration $N\delta T$, as long as $N\delta \le 1$. The pulses can even be different in duration, what matters is only the fraction of the time interval T which they fill.

Figure 3 clearly shows the inverse relationship with the duty cycle in the absence of an offset (baseline $\alpha =0$, black line) and the degradation of the expected value of $g^{\left(2\right)}\left(0\right)$ as a function of the duty cycle $\delta$. It is interesting to notice that $g^{\left(2\right)}\left(0\right)$ decreases rapidly as the pulse width (or number of pulses) progressively fill the (measurement) time interval T and fall below 2 (subthermal statistics) when $\delta \ge 0.5$, as already stated. More interesting is the fact that the background (noise) rapidly reduces the autocorrelation, which becomes subthermal for any value of $\delta$ when $\alpha \gtrsim 0.2$ (magenta line in Figure 3). While in itself there is no particular reason for preferring $g^{\left(2\right)}\left(0\right)>2$, its practical usefulness is clear, since it helps identifying a regime of photon bursts in experiments where $g^{\left(2\right)}\left(0\right)$ is the only easily accessible quantity. Whenever the statistics becomes subthermal it is impossible to distinguish between a regime with burst emission and a dynamically different one (photon bunched in a subthermal way, for instance, dynamical oscillations [72,86], or background effects [84]). This simple example immediately shows the limitations of the autocorrelation measurement in the identification of bursts and highlights the difficulties inherent in the presence of too large a number of pulses (fractional filling of the measurement interval T) and of the influence of background.

The picture does not substantially change, up to numerical factors (e.g., in the value of $\delta$ and $\alpha$ for which the statistics becomes subthermal), if the pulses are of unequal height. In practice, experiments will also suffer from bandwidth limitations which are going to broaden the pulses, an instrumental factor which contributes to reducing the actual value of $g^{\left(2\right)}\left(0\right)$. Amplitude reduction, due to detector sensitivity, also contributes to a degradation of $g^{\left(2\right)}\left(0\right)$, especially since the background may not be affected (if due to electronics). Overall, these factors compound and it is not uncommon to observe experimentally measured functional dependences in the autocorrelation where a growth from shot noise ($g^{\left(2\right)}\left(0\right)=1$) towards thermal statistics is observed as the pump is increased, followed by a decrease towards Poisson statistics (not necessarily reached, cf. e.g., Figure 2c in [87]). The subthermal value of $g^{\left(2\right)}\left(0\right)$ at low pump is to be ascribed to the strong filtering of the instrumentation (and insufficient sampling, also observed in some stochastic numerical simulations, Section 5.2). Of course, such functional dependences cannot be univocally interpreted: it is impossible to tell whether the failure to reach thermal statistics is simply due to instrumental limitations or whether a burst regime remains undetected, due to possible confusion with a noisy but coherent signal. Indeed, a subthermal, but superpossonian, regime on the decreasing slope of $g^{\left(2\right)}\left(0\right)$ may be due to statistical properties of the radiation, to dynamics, to frequent photon bursts which fill the observation window, or to instrumental background: the multiplicity of causes prevents a univocal interpretation of the observation. It is, however, interesting to notice that this simple picture may help interpret the observation of $g^{\left(2\right)}\left(0\right)<2$ in a regime of ASE with decreasing values as the power supplied to the superluminescent diode is increased [38]: frequent, short ASE pulses may very well produce autocorrelation values compatible with the observations.

Table 1. Summary of the influence of different factors in the (experimental) identification of photon bursts through $g^{\left(2\right)}\left(0\right)$.

Feature	Consequence	Comment
$g^{\left(2\right)}\left(0\right)$	>2	Allows for a univocal identification of the presence of photon bursts (superthermal bunching) in the temporal laser emission
$g^{\left(2\right)}\left(0\right)$	$1\le g^{\left(2\right)}\left(0\right)\le 2$	Does not exclude the presence of photon bursts, but does not allow the certain identification, since other kinds of signals, such as strongly oscillating photon numbers, may give the same value of $g^{\left(2\right)}\left(0\right)$ (cf. e.g., Figure 4c in [76]).
Frequent bursts	Filling of the measurement window	Frequent bursts increase the fraction of the temporal window in which the photon bursts are measured, reducing the value of $g^{\left(2\right)}\left(0\right)$. This is not a parasitic effect and signals convergence towards cw laser emission
Detection bandwidth	Smaller and broader pulses	Controls the measured value of the autocorrelation signal reducing its value relative to the real one; reduces the range of pump values for the observation of photon bursts
Detection background	Lower contrast	Reduces the estimated value of $g^{\left(2\right)}\left(0\right)$; reduces the range of pump values for the observation of photon bursts
Signal contrast	Ratio between photon bursts and background	Directly affects the estimate of $g^{\left(2\right)}\left(0\right)$. Improvements in height detection or reduction in background lead towards a more realistic evaluation of $g^{\left(2\right)}\left(0\right)$
Far below threshold	Very infrequent bursts	Likelihood of detecting an actual burst very low compared to the accumulation of background shot noise; results in often-observed drop in $g^{\left(2\right)}\left(0\right)\to 1$ at very low pump

summarizes the main results of this section, by identifying the main consequence of each feature and explaining the influence that it has on the measurement. These constraints are crucial in experiments, even though they control the computation of the autocorrelation even from signals obtained from a numerical integration. In the latter case, however, most of the constraints can be lifted (up to the difficulty of obtaining sufficient statistics below threshold), thus we focus on the experimental side.

As already explained, photon bursts can occur with a subthermal $g^{\left(2\right)}\left(0\right)$ (cf. e.g., Figure 4b in [76]), but similar autocorrelation values can also be obtained with strong oscillations (Figure 4c in [76]). The lack of bijectivity prevents all conclusions. Frequent bursts increase $\delta$ (Figure 3), while a degradation in the signal-to-noise ratio (or signal-to-background ratio), represented by increasing values of $\alpha$ (e.g., along a vertical cut in Figure 3), reduces again $g^{\left(2\right)}\left(0\right)$. Not surprisingly, in the detection system high sensitivity and low noise are therefore crucial, a difficult set of requirements to match for any kind of micro- or nanolaser. For simplicity, the table has been prepared with a detection scheme in mind where a linear detector samples the full temporal signal with sufficient resolution. In photon counting the requirements are the same; there, the signal-to-noise ratio is represented by the dark count rate and the integration window (number of samples required to obtain a good signal on top of noise). The latter can often be large (overcoming very easily hundreds of thousands of measurements) and require long measurement times, with the consequent stability issues for the experiment. The longer the time windows, the stronger the perturbations, thus the difficulties are equivalent to those outlined in the table, even though they may appear in a different form. The same holds for measurements carried out far below threshold, where the occurrence of a burst is extremely unlikely: the accumulated background noise takes over and the autocorrelation is governed by the shot noise (cf. e.g., Figure 2c in [87]). Finally, in photon counting the detection bandwidth is replaced by the finite detector averaging time.

5. Theoretical Models

The above-mentioned technological limitations which strongly limit the experimental characterization of nanodevices lend a prominent role to the theoretical description of nanolasers. Here, models take a particular importance for their predictive power, since crucial features can be actively sought with complex experimental techniques only if there is valid proof motivating the investment. In addition, numerical predictions provide information on how to search for interesting features. Below, we briefly outline two main classes of theoretical approaches, without offering a complete overview, but, rather, highlighting their main features. By necessity, only a few of the relevant papers are cited, just as examples and sources of additional references.

5.1. Differential Models

As for most physical phenomena, the traditional and most successful way of modeling laser emission is based on a differential approach where an infinitesimal description of the physical interactions predicts the evolution of the electromagnetic field (thus, of the photon number). While various approaches have been used in the past six decades, the most widespread rests on the so-called Maxwell-Bloch equations (proposed by Arecchi and Bonifacio [88,89]), for the electromagnetic field (simplified Maxwell equations [90]) in interaction with the material (Bloch equations [91]). Two features distinguish this powerful technique, successfully used to describe temporal, spatio-temporal and nonlinear phenomena [92]: the absence of spontaneous emission in its formulation and the assumption that the photon number is very large (justifying the differential description). Both hold excellently well above the laser threshold, particularly for the macroscopic lasers for which the model was derived. Of course, neither of these hypotheses can hold at the nanoscale.

A class of models which avoid these pitfalls has been based on a quantum-mechanical derivation of equations, specific to semiconductor-based devices, where equivalent variables are used for the description: a photon-assisted polarization, the photon field and the population [93,94]. While solving the two previous shortcomings, and allowing for a self-consistent derivation of fluctuations, these models still do not predict the occurrence of superthermal emission which can only be obtained, in this framework, from purely probabilistic considerations [95].

Laser Rate Equations (REs) are derived on the basis of phenomenological considerations [50,96] and have been modified early on to include finite-size effects through the average contribution of the spontaneous emission to the laser field [56,63]. The REs, which can be retraced to the semiclassical Einstein’s theory of radiation [1], are often preferred for their simplicity and direct physical interpretation. Furthermore, the addition of the average spontaneous emission in the photon number provides a degree of statistical information on the fluctuations.

The following list highlights some aspects of the physics of (micro- and) nanolasers which emerge at the modelling stage but which cannot always be described by (at least some of) the previous approaches:

D.1

The addition of spontaneous emission, for instance as a constant contribution (cf. Equation (7)), breaks the transcritical bifurcation [97,98,99] which characterizes the standard REs written for macroscopic lasers [50,96]. This is a consequence of the finite cavity volume (expressed by the fraction of spontaneous emission coupled into the lasing mode, $\beta$) and is related to the disappearance of the thermodynamic limit, recovered when $\beta \to 0$ (cf. [67] for details). Its immediate, and partly counterintuitive, consequence is a progressive stabilization of the laser operation as $\beta$ increases (cf. Section 6): nanodevices are more stable than their macroscopic counterparts. For an interesting physical application of imperfect bifurcations, cf. [100].

D.2

Differential models have so far considered only the coherent part of the electromagnetic field, without introducing an independent random field for the description of spontaneous emission. The latter is added onto the coherent part (as a coherent contribution from the spontaneous relaxation processes, e.g., in REs) but does not exist as a variable in itself. This is an important conceptual point which prevents a correct description of the below-threshold region. Some stochastic models (Section 5.2) introduce the incoherent field as an independent variable, albeit without the concept of random phase, since they are based on a photon number concept.

D.3

As noted in [101] through a numerical integration of discretized REs, the integer nature of photons and emitters makes itself felt at the nanoscale (and even at the mesoscale [102]). This introduces an intrinsic noise, entirely missed by the differential models, and leads to a background granularity which cannot be replaced by other means. In this sense, discrete models (cf. Section 5.2 and Section 5.3) hold superior predictive power for small devices.

D.4

The introduction of Langevin terms in differential models to simulate fluctuations has two shortcomings: it may lead to negative photon numbers (thus numerical instabilities) when the latter is very small (thus close to threshold, especially in nanolasers) and to an incorrect approximation of the noise distribution. The former problem could be solved by abandoning the photon number representation, but the latter reposes on the approximation of Poissonian processes (true physical statistics of light-matter interaction) with Gaussian ones; such replacement holds only for large arguments, a condition violated at small photon numbers [103].

Two very recent modelling ideas attract the attention, as they do not directly fit in the previous summary. They are based on hypotheses which haven’t been considered so far and therefore do not match the literature outline offered above. We therefore highlight these new ideas which are proposed for the description of nanolasers.

A modification of the REs introduces a new element in the class of discrete models, allowing for the observation of photon bursts [104]. Its central point lies in the introduction, in a rate equation description, of correlations among emitters, recently predicted and observed in different contexts, as we now outline.

Searching for ultranarrow linewidths, superradiant states have been exploited to obtain extreme phase locking, thus extreme phase coherence, in samples of cooled alkaline atoms [105,106,107]. Using a Maxwell-Bloch model for nanolasers, a splitting in the field and polarization operators’ spectrum is predicted in presence of sufficiently strong coupling—needed to pass lasing threshold [108]; for insufficient coupling (nanoleds) only one spectral component appears: the collective oscillations are thus attributed inter-emitter correlations [108]. Sub- and superradiant coupling between Quantum Dots in nanolasers is investigated using a quantum mechanical description of nanolasers, thus including correlations which are expanded to sufficiently high order to retain pairwise emitter interactions [109]. Radiative coupling is thus predicted and correlated to the statistical properties of the photon field. A similar approach predicts the appearance of superradiant pulses identifiable by the temporal evolution of the second-order autocorrelation function [110]. Finally, experimental observations of sub- and superradiant emission are reported in [111] for Quantum Dot based microcavities.

Based on this bulk of evidence, ref. [104] makes the hypothesis that a phenomenological asymmetry between the relaxation rates of spontaneous and stimulated emission, in a RE model with Pauli blocking [112], may qualitatively provide an acceptable description of correlations at the semiclassical level. The resulting modified REs predict the appearance of photon bursts in the presence of subradiant coupling. Without entering into a discussion on the underlying assumptions, it is worth noting the strong novelty which [104] brings to the class of differential models, as it is the only one capable of predicting any form of bursts with Langevin noise. Since below and near threshold the latter is quite small (proportional to the photon number), it is in general not surprising that bursts should be excluded from the dynamical predictions obtained from the integration of stochastic differential equations for nanolasers. Thus, it is worth trying to gain some topological understanding of the reasons why photon bunching should appear in [104]. This point will be examined in Section 7, after the topological investigation (Section 6) of the phase space properties of the radiation-matter interaction and of its relation with the photon bursts numerically predicted by fully Stochastic, discrete models (Section 5.2 and Section 5.3).

A new quantum-mechanical model, instead, derived without limitation in the number of emitters or cavity size, computes from first principles the interaction between a semiconductor and the electromagnetic field [68]. Its main novelty consists in the inclusion of an independent incoherent field, in addition to the coherent one, thus enabling a proper description of laser operation over the entire range of pump values, from below to above threshold. A bifurcation analysis univocally identifies the threshold position as a function of emitters and $\beta$, and the existence of a minimum number of emitters experimentally found [111] and forecasted by REs [112]. The use of bifurcation theory circumvents the limitations coming from the definitions based on statistically-defined phase transitions [67] and enables the clear and univocal identification of a finite threshold [68]—as the pump rate for which a coherent field emerges from 0—even for $\beta =1$, the so-called thresholdless laser.

5.2. Stochastic Simulators

The shortcomings of the differential approach can be solved by approaching nanolaser modelling as a fully stochastic problem. Here, not much can be done analytically, but the agreement between experimental measurements and numerical predictions is excellent [72], as proven not only by the numerical existence of photon bursts, but also by the reproduction of details in the functional dependence of $g^{\left(2\right)}\left(0\right)$ on pump, without any adjustment parameters (cf. Figures 4 and 6 in [72]). In addition, good qualitative agreement is obtained in the comparison between experiments with pump modulation to identify the laser threshold (cf. Figures 5 and 6 in [86]), or to study the response of a modulation through the threshold region (cf. Figures 3 and 6 in [73]), as well in the microlaser response to feedback (Figures 3 and 8, and Figures 6 and 9 in [113]).

The gold standard for a stochastic model is the Master Equation, but its prohibitive dimensionality renders its numerical simulation impossible for any realistic situation. The usual way of solving the problem is to follow individual trajectories and repeat the process starting from different initial conditions to obtain statistically significant results. Two different approaches have been explored in the last decade, the first one based on Monte Carlo realizations of a random walk on the lattice of the allowed states (thus including the intrinsic discreteness of the variables and of the transitions) [114,115], according to a scheme proposed in [67], but not numerically implemented there. Following previous developments, a sophisticated Monte Carlo method has been applied to the stochastic simulation of a Quantum Well semiconductor laser, including the electron population in the bands [116] for a laser whose dynamics is included between the classes A and B [117].

A parallel approach, preceded by a discretization of the Rate Equations implemented in stochastic terms [101], directly implements the physical processes as a sequence of probabilistic events, either computed at fixed steps [83], or by (probabilistically) computing the time at which an event takes place [104] (using a Gillespie-like algorithm [118] also used in [116]). The two approaches are equivalent [118] provided that conditions on additivity are fulfilled [83], with the Gillespie-like strategy leading to much shorter computing times [104,116].

5.3. Stochastic Predictions

Stochastic numerical predictions of photon bursts have been independently obtained with the different schemes previously cited. A brief summary of the results is the following:

N.1

Photon bursts are observed in the laser output for a semiconductor laser model derived from the Master Equation (cf. Figure 4 in [114] and Figure 5 in [115]);

N.2

Photon bursts appear in the laser output for Class B lasers both at the micro- and nanoscale (cf. Figure 5 in the Supplementary Material of [72] and Figure 3a in [84]);

N.3

Prediction of photon bursts in the laser output for semiconductor nanolaser in dynamical regimes between Classes A and B (cf. Figure 7 in [116]);

N.4

Prediction of superthermal statistics (free-running, Quantum Well laser, Figure 7 in [119]);

N.5

Prediction of superthermal statistics using a Gillespie algorithm in a model with pump blocking, suited to Quantum Dot modelling (cf. Figure 5 in [104]).

With the notable exception of the phenomenologically modified REs discussed in [104], only stochastic models [83,104,114,115,116] are presently capable of predicting photon bursts. While for the moment there is no clear understanding of the failure of differential models in this respect, we can speculate that: (1) it may originate from the continuous action of the noise perturbation, which is added at each step in the Langevin scheme of the REs—this contrasts with the random times at which (larger) fluctuations spontaneously appear in the stochastic approach; and (2) that the Gaussian statistics, as opposed to the more physical Poissonian one, may modify the fluctuations in a way that suppresses large deviations. The discussion on the phase space features, Section 6, helps understanding the dynamical behaviour of the photon bursts, whose stochastically predicted statistical properties almost invariably match a superpoissonian statistics.

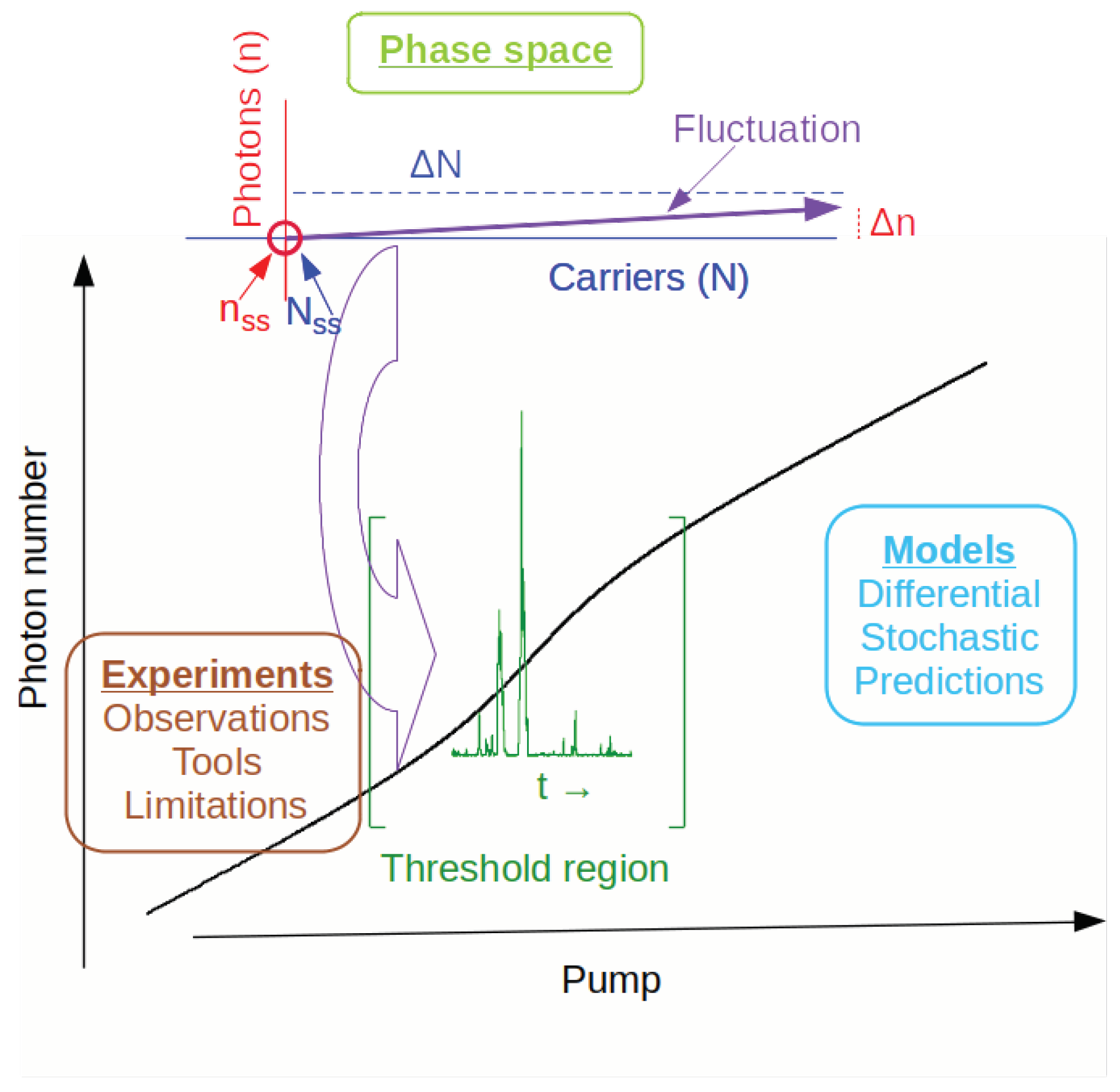
6. Phase Space Information

While only a proper stochastic simulation is currently capable of reproducing the observed dynamics [84], a topological investigation of the phase space properties of the rate equations, with the added contribution of the average spontaneous emission, provides useful information. This is not surprising, given that the underlying topological structure on which the random walk takes place (e.g., [67,114]) is the same as the one of the stochastic laser simulators [83] (both derive from the semiclassical description of radiation [1]).

The traditional rate equations with the spontaneous emission contribution to the lasing mode read for a Quantum Well system [96] (equivalent to a “four-level” laser model):

$$\begin{array}{ccc}\hfill \dot{n}& =& -{\mathsf{\Gamma }}_{c}n+\beta \gamma N(n+1),\hfill \end{array}$$

(7)

$$\begin{array}{ccc}\hfill \dot{N}& =& P-\beta \gamma Nn-\gamma N,\hfill \end{array}$$

(8)

where n and N represent the photon and carrier number (or population inversion), respectively, ${\mathsf{\Gamma }}_c$ and $\gamma$ are the relaxation rates for the intra-cavity photons and for the population inversion, respectively, P is the pump rate and $\beta$ is the previously defined fraction of spontaneous emission coupled into the lasing mode. This set of REs includes the average contribution of the spontaneous emission to the number of coherent photons in the cavity mode through the term $\beta \gamma N$ (Equation (7)). The steady state (equilibrium) values for the photon number and the population inversion, as directly obtained from Equations (7) and (8), are:

$$\begin{array}{ccc}\hfill \overline{n}& =& \left\{\left(\frac{C-1}{2}\right)+\sqrt{{\left(\frac{C-1}{2}\right)}^2+\beta C}\right\}{\beta }^{-1},\hfill \end{array}$$

(9)

$$\begin{array}{ccc}\hfill \overline{N}& =& \frac{{\mathsf{\Gamma }}_c}{\beta \gamma }\frac{C}{1+\beta \overline{n}},\hfill \end{array}$$

(10)

$$\begin{array}{ccc}\hfill C& =& \frac{P}{P_{th}},P_{th}=\frac{{\mathsf{\Gamma }}_c}{\beta },\hfill \end{array}$$

(11)

where the over-strike represents equilibrium.

The linear stability analysis (lsa) [97] of Equations (7) and (8), performed around the steady-state values for the two variables, is readily obtained from:

$$\begin{array}{ccc}\hfill \frac{d}{dt}\left(\begin{array}{c}\nu \\ \mu \end{array}\right)& =& \overline{\overline{\mathcal{S}}}\left(\begin{array}{c}\nu \\ \mu \end{array}\right),\hfill \end{array}$$

(12)

$$\begin{array}{ccc}\hfill \overline{\overline{\mathcal{S}}}& =& \left(\begin{array}{cc}\beta \gamma \overline{N}-{\mathsf{\Gamma }}_c-\lambda & \beta \gamma (\overline{n}+1)\\ -\beta \gamma \overline{N}& -\gamma -\beta \gamma \overline{n}-\lambda \end{array}\right),\hfill \end{array}$$

(13)

where we have defined the perturbations

$$\begin{array}{ccc}\hfill n\left(t\right)& =& \overline{n}+\nu e^{\lambda t},\hfill \end{array}$$

(14)

$$\begin{array}{ccc}\hfill N\left(t\right)& =& \overline{N}+\mu e^{\lambda t}.\hfill \end{array}$$

(15)

The full analysis is performed here for ${\mathsf{\Gamma }}_c={10}^{11}{s}^{-1}$ and $\gamma ={10}^9{s}^{-1}$. The “threshold”, Equation (11), is the one defined in [67].

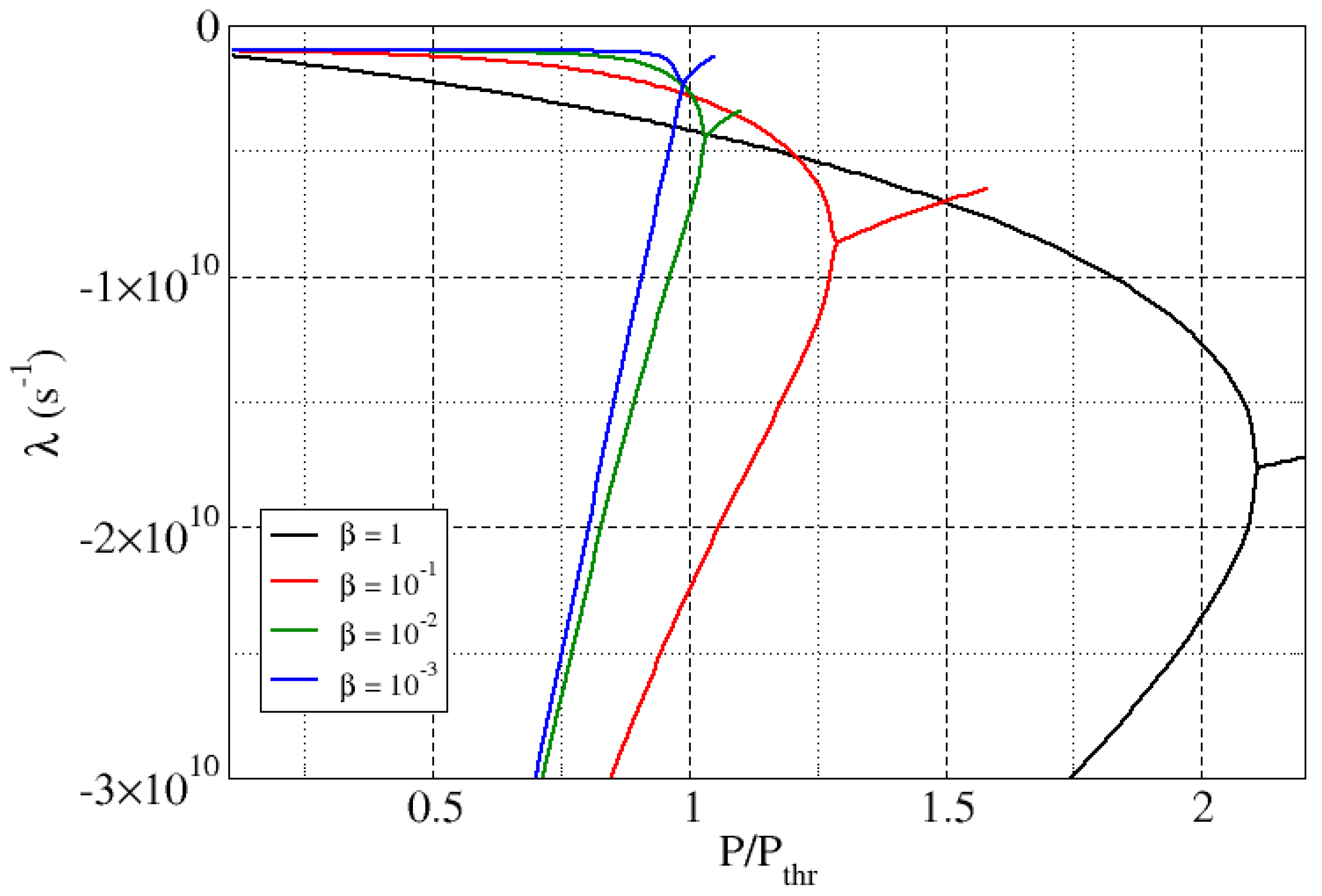
6.1. Eigenvalue Analysis

The lsa provides information on the laser’s return (or lack thereof) to its stationary emission state when a perturbation is applied to its two variables. The eigenvalues give a measure of the state’s robustness and are shown in Figure 4 for different values of $\beta$.

For ease of comparison, the horizontal scale plots the pump rate relative to the threshold value (Equation (11)) for the matching laser (i.e., normalized to $\beta$). The first observation is that below a critical pump rate, there are two distinct real eigenvalues; however, they collapse into a pair of complex conjugate eigenvalues for instance at $\frac{P}{P_{thr}}\approx 2.1$ for $\beta =1$ (black curve). From this point on, the real parts of the two eigenvalues coincide, since they distinguish themselves only for their imaginary parts (not shown). There are two important remarks which arise from this figure: (1) as the fraction of spontaneous emission coupled into the lasing mode decreases, the eigenvalues become complex conjugate at an earlier (normalized) pump rate; (2) as $\beta$ decreases, the eigenvalue closer to the real axis becomes progressively less negative, thus indicating that the corresponding laser is less stable. Notice that the traditional rate equations model devoid of the spontaneous emission contribution predicts one zero eigenvalue at threshold, matching the indifferent stability responsible for the divergence of fluctuations and for the presence of a phase transition [59,60,61,62]. This corresponds to a device where $\beta \to 0$. Here, the finiteness of $\beta$ stabilizes the solution, giving rise to a so-called imperfect bifurcation [99] whose features have a certain resemblance to those of an avoided level crossing in quantum mechanics [120]. Figure 4 clearly shows that the stabilization effect is much stronger at the nanoscopic than at the microscopic scale, since a more negative eigenvalue represents a faster convergence to 0 of the corresponding perturbation (Equations (14) and (15)).

As an aside, it is interesting to notice the displacement of the threshold, compared to the standard predicted value [67], which corresponds to 1 on the (normalized) pump axis (Figure 4, from Equation (11)). For $\beta \ge {10}^{-2}$ the eigenvalues become complex conjugate at $P>P_{th}$, i.e., in the upper region of the characteristic S-curve of laser emission (cf. Figure 5). The new quantum-mechanical model [68] also predicts the appearance of the coherent field bifurcation close to the upper branch, signalling a displacement of the threshold towards larger pump values. This strengthens the case for a strong role of photon bursts in the transition between spontaneous and coherent emission. Extensions based on the statistical theory of phase transitions, instead, fail, as they predict a threshold at the mid-point of the steeper region of growth (i.e., $\frac{P}{P_{th}}=1$) [67]).

Figure 6 shows the equivalent eigenvalues for a borderline microlaser ($\beta ={10}^{-4}$) and for a macroscopic laser ($\beta ={10}^{-6}$), even though not a very large one (a large semiconductor, for instance, or a solid state microdevice). The difference is striking, as in the macrosopic laser one eigenvalue comes much closer to zero than in all other devices, proving the progressive convergence towards the thermodynamic limit. As in Figure 4, the microlaser displays a (small) dip at pump values close to “threshold”, while the macroscopic one reduces its stability in this region, inverting the trend observed at the micro- and nanoscale and approaching the thermodynamic limit.

While the lessening of the stability with decreasing $\beta$ is not surprising when seen from the perspective of the thermodynamic limit, intuitive considerations could have also justified the opposite conclusion. Based on the fact that the relative amount of spontaneous emission coupled into the lasing mode increases with $\beta$ (i.e., going towards the nanoscale) one could have argued for a nanolaser’s accrued sensitivity to noise and, with that, for a decrease in stability. The lsa belies this conclusion and advances potentially interesting consequences in applications, for instance in telecommunications [121]. This consideration has the merit of clarifying an important difference: noise and intrinsic stability are not equivalent. We can therefore conclude that nanolasers are intrinsically noisier devices, due to their low photon number, but they are structurally more dynamically robust than their micro- and macroscopic counterparts.

6.2. Eigenvector Analysis

The origin of spontaneous spiking (photon bursts) in the transition from a purely spontaneous emission regime to the coherent one can be better understood from the analysis of the eigenvector [84]. Figure 7 shows the normalized component of the eigenvector which matches the photon number n (i.e., the $\nu$ component in Equation (12)) for the least stable of the two eigenvalues (Figure 4) for different values of $\beta$ ranging from nano- to microlasers. As can be easily evinced from the curves, the other component ($\mu$) has an amplitude close to 1 (except for $\beta =1$ and $\frac{P}{P_{thr}}>1$), given that the eigenvector is normalized. The second eigenvector (not shown), matching the more negative eigenvalue, is (also) almost entirely aligned with the population variable (N) [121], thus the two eigenvectors are nearly parallel below threshold. This observation has far-reaching implications, since it proves that, in spite of their origin ($\nu$ or $\mu$) fluctuations are strongly decoupled from the photon number variable: noise affects the population inversion and can make it deviate strongly from its equilibrium position, with only a weak transfer onto the photon field. This implies that the population inversion can grow quite far from its stationary value with a practically negligible consequence on the photon number. In other words, the transfer of a fluctuation onto the photon number is an unlikely process which takes place only occasionally, thus hindering the stimulated emission process.

The (near) absence of coupling to the photon field allows for the growth of population fluctuations of considerable amplitude. Thus, when a “transfer” towards the photon field takes place, the accumulated excess population enables the violent growth of the photon number through stimulated emission, and a photon burst ensues, in a way similar to a laser Q-switch [50]. This is the origin of the observed pulses.

Physical considerations on the spontaneous emission can be used to give an alternative interpretation of this same picture. It is well-known that the spontaneous coupling of emitting dipoles to the radiation field is very weak, due to their extremely small size compared to the wavelength ($O\left({10}^{-3}\right))$, which renders them extremely inefficient antennas. The well-known consequence is the weak population’s relaxation rate (also known as fluorescence rate) which, for the systems we consider here, is about five to six orders of magnitude smaller than the absorption (and stimulated emission [1]) rate. This is the reason why below threshold—i.e., in a regime where stimulated emission is disfavoured—the population can grow to excessively large amounts. It is this built-up population excess which enables the transient ignition of stimulated emission (cf. bilinear term in Equations (7) and (8)) responsible for the photon bursts.

Comparison of the photon component of the least stable eigenvector for different laser sizes is also illuminating. For the extreme nanolaser ($\beta =1$), where all spontaneous emission is channeled into the lasing mode (black curve in Figure 7) the relative weight of the photon eigendirection is stronger. This can be understood in terms of the transfer efficiency between population inversion and photon number, given that all spontaneous emission ends up into the lasing mode. From a more mathematical point of view, this remark matches the fact that the coupling coefficient in Equations (7) and (8) is larger thanks to $\beta =1$. As $\beta$ decreases there is a rapid reduction in coupling between the two variables, represented by the ever smaller component of the eigenvector projection along the photon axis. This holds true even close to the transition—identified by the end of the line traced in each figure—which corresponds to the transformation from a real into a complex eigenvector, or to the appearance of an imaginary part in the eigenvalue. In microlasers (e.g., $\beta ={10}^{-3}$) the amplitude of the photon number component of the eigenvector is only 1% even at threshold (Figure 7).

The weak stability, which leads to the true phase transition in the thermodynamic limit, can be visualized by the transformation of a very large amount of stored energy into the field, giving rise to the (nearly) discontinuous transition. This is the picture that we normally use to describe threshold crossing by macroscopic lasers.

Figure 8 compares the photon component of the least stable eigenvector, as in Figure 7, for a microlaser ($\beta ={10}^{-4}$) and a macrolaser ($\beta ={10}^{-6}$). The emerging feature is that the photon component remains zero until very close to threshold for the macroscopic laser (it is always very small for the microlaser) and that its value remains quite small (well below 1%) even at the transition. In addition, a rapid rotation of the eigenvector in its plane appears through a sign switch in the components for the microlaser (Figure 9, green line—the diagonal lines join consecutive points). The macroscopic device shows a double rotation (dashed orange line), where the first signals the threshold crossing, and the second the end of the region where the eigenvalue is real (even above threshold). The fact that class B lasers [117] possess a narrow region with real eigenvalues (i.e., no relaxation oscillations) above threshold has been known for a long time [122], but can be observed only in devices where the relative time constants (${\mathsf{\Gamma }}_c$ and $\gamma$) are sufficiently close to permit it (i.e., not the CO₂ lasers considered in [122]).

6.3. Topological Conclusions

The combined information coming from the eigenvalues and the eigenvector analysis prove that the origin of the sudden photon spikes is dynamical and resides in the overall weak coupling between photons and population inversion below threshold—something which is to be expected, since the laser does not operate in that regime. The transition, however, is more or less sharp and sudden depending on the laser parameters: a nanolaser, more subject to intrinsic noise, is nonetheless less unstable and is expected therefore to display smaller and more frequent photon spikes in the so-called ASE region.

An interesting consequence of this analysis is that relaxation oscillations, believed not to exist in the thresholdless laser [56] actually do occur even in these limiting devices, albeit only at large relative pump values $\left(\frac{P}{P_{thr}}\gtrsim 2.1\right)$, as shown by the eigenvalues (Figure 4). The physical argument advanced in favour of the lack of oscillations [56]—absence of energy storing and immediate transformation of all the population inversion into photons—does not hold and is only a misinterpretation of the insufficient amount of coupling to initiate steady lasing at $\frac{P}{P_{thr}}=1$ (Figure 4). We also see, through the very small coupling at low pump rate ($P\ll P_{thr}$) that the zero-threshold connotation for $\beta =1$ devices [64] does not make any sense. This name originally came from the belief that the straight line relationship between input and output originated from the position of threshold at virtually zero pump. Although this is no longer considered to be true, the lsa gives clear evidence for a presence of threshold at $\frac{P}{P_{thr}}>2.1$.

7. Symmetry Break between Spontaneous and Stimulated Processes

As already mentioned in Section 5, differential models with Langevin noise do not predict the existence of photon bursts. Yet, the introduction of a phenomenological asymmetry in the relaxation constants, intended to model the aforementioned correlations in Quantum Dot devices, appears to show (small) bursts (Figure 5 in [104]). Given the unusual nature of this result, it is worth trying to understand its origin, at least from a topological point of view. For this purpose, we transpose it onto the Quantum Well REs, such as Equations (7) and (8) studied in Section 6, so as to compare the changes introduced by the phenomenological assumption to the standard case we have examined in detail:

$$\begin{array}{ccc}\hfill \dot{n}& =& -{\mathsf{\Gamma }}_{c}n+\beta \gamma Nn+\beta {\gamma }_{s}N,\hfill \end{array}$$

(16)

$$\begin{array}{ccc}\hfill \dot{N}& =& P-\beta \gamma Nn-\gamma N,\hfill \end{array}$$

(17)

where $\gamma$ now corresponds to the stimulated process and ${\gamma }_s$ to the spontaneous one. The symmetry is now (artificially) broken in the equation for the photon balance, since the stimulated and spontaneous rates are phenomenologically chosen to be different (the total rate in the equation for the population stays the same). We outline the changes, relative to Section 6, by giving the equivalent expressions, which can be easily deduced from Equations (16) and (17):

$$\begin{array}{ccc}\hfill \overline{n}& =& \frac{1}{\beta }\left\{\frac{C-1}{2}+\sqrt{{\left(\frac{C-1}{2}\right)}^2+\beta C\xi }\right\},\hfill \end{array}$$

(18)

$$\begin{array}{ccc}\hfill \overline{N}& =& \frac{\frac{P}{\gamma }}{1+\beta \overline{n}},\hfill \end{array}$$

(19)

$$\begin{array}{ccc}\hfill C& =& \frac{\beta }{{\mathsf{\Gamma }}_c}P,P_{th}=\frac{{\mathsf{\Gamma }}_c}{\beta },\hfill \end{array}$$

(20)

where $\xi =\frac{{\gamma }_s}{\gamma }$ [104] introduces the symmetry break ($\xi >1$: superradiance; $\xi <1$: subradiance). In the presence of the rate asymmetry the stability matrix becomes:

$$\begin{array}{ccc}\hfill \overline{\overline{\mathcal{S}}}& =& \left(\begin{array}{cc}\beta \gamma \overline{N}-\lambda -{\mathsf{\Gamma }}_c& \beta \gamma (\overline{n}+\xi )\\ -\beta \gamma \overline{N}& -\gamma (\beta \overline{n}+1)-\lambda \end{array}\right).\hfill \end{array}$$

(21)

Concentrating on the case $\beta ={10}^{-1}$, for concreteness, we look at the influence of $\xi$ on the eigenvalues and on the “photon number component” of the least stable eigenvector, as in Section 6. Figure 10 shows the real part of the eigenvalue pair, which possess the same characteristic features as the standard REs, for different values of asymmetry $\xi$. The red curve matches the corresponding one in Figure 4 since $\xi =1$ corresponds to the symmetric rate configuration studied in Section 6. Superradiance ($\xi >1$) stabilizes somewhat the nanolaser by rendering more negative the eigenvalue closer to 0 (green curve), while subradiance ($\xi <1$) renders it a little more susceptible to noise by bringing it closer to 0 (black curve).

The eigenvector analysis confirms the destabilizing quality of subradiance (Figure 11) as opposed to the superradiance-induced stabilization. The amplitude of the normalized photon component of the least stable eigenvector (matching the upper eigenvalue in Figure 10) becomes progressively smaller as the symmetry break proceeds from super- to subradiant interactions (colour coding as in Figure 10). As already discussed in Section 6 this amounts to saying that the component of this eigenvector aligned with the photon number variable n is small (extremely small in the subradiant case) over a broad range of pump values. Hence, this eigenvector is nearly aligned with the population variable N (the other eigenvector—not shown—is also aligned with N). Thus, the fluctuations which occur in this eigendirection—due to the closeness to 0 of the eigenvalue (Figure 10)—influence almost exclusively the population N, which may undergo large excursions, since the only relaxation channel is the spontaneous relaxation (partially inhibited by subradiance). As discussed at length in Section 6, if the weak coupling to the photon variable takes place in the presence of a large excess in N, then a photon burst takes place; more readily in the case of subradiant interaction.

The analysis shows that the symmetry break quantitatively affects the phase space structure and the photon burst appearance; no qualitative—e.g., structural—changes are introduced into the modified phase space. For the standard REs (for Quantum Wells) this would amount to larger photon bursts (more frequent depending on the parameter details). However, since photon bursts and superthermal statistics were already predicted under these conditions [72,84,114,115,116,119], the symmetry break does not seem to bring anything new. On the other hand, it is possible that for a sufficiently large asymmetry the integration of the REs model may also produce bursts, thanks to the laser’s closeness to the instability threshold which may be reached even with perturbations of Langevin type [123].

For completeness, it is important to remark that in Equations (16) and (17) we have attributed the asymmetry only to the decay into the lasing mode (no specific indication is given in [104] as to the choice made). The extension of the asymmetry (in particular the subradiant case, $\xi <1$ for our purposes) to the whole relaxation from the excited state (i.e., also to the last term of Equation (17)), would have lowered even more strongly the stability of the device, both in the eigenvalue and in the eigenvector components (results not shown). This way, the small amount of Langevin noise—proportional to the photon number (very small below threshold), could even more easily produce photon bursts.

8. Conclusions

The objective of this contribution has been the presentation of a summary of the current observations of photon bursts and their comparison with the properties of ASE. No conclusion is drawn about the true nature of these bursts, whence the quotes around Amplified Spontaneous Emission in the title, which undoubtedly require further evidence and investigation.

Photon bursts are seen to precede the establishment of coherence in micro- and nanolaser and therefore take a significance which is not necessarily present in their macroscopic counterparts. Even though their role is not fully characterised, they appear as an instance of a nascent instability, as shown through the analysis of the phase space properties of the most basic physical model. An interesting question, not yet fully answered, is the inability of differential models of predicting the appearance of photon bursts—up to the recent exception [104] which probably benefits from the destabilization found in Section 7—while the intrinsic granularity and randomness arising from numerical stochastic approaches give an excellent match to the observations, independently of the model details. The different aspects of the stochastic predictions are summarized and compared to the main conclusions which can be drawn from the current experimental knowledge of photon spikes. The experimentally relevant question of the identification of photon bursts through the second-order autocorrelation—the most widespread detection tool—is addressed with the help of a simple model, which explains the role of the various parameters (burst duration, relative height of background to peak, filling factor in the observation time interval) on the actual identification of a superthermal statistics.

Devices with very few QDs are now consistently built, with good control of their numbers and properties [124] and limitations exist on the minimum number of emitters necessary for lasing [111,112]. Interesting questions arise in the dynamical interaction among photons and emitters in the below-threshold region, given the very restricted number of QDs actually interacting (as matter) with the thermal or pseudo-thermal radiation inside the cavity. In other words, it would be interesting to understand whether the thermodynamic limits taken in macroscopic out-of-equilibrium systems hold [44]. This question is certainly one that will need to be addressed in a near future in order to shed further light on the physics of radiation in interaction with matter.

On the list of forthcoming work on this topic the following items ought to appear: a better characterization of photon bursts, including their coherence time and their statistical properties (such as repetition rate, amplitude statistics to probe for possible systematic or deterministic aspects); the evolution of the photon bursts into the cw (noisy) coherent emission; the possible relationship between burst features and cavity parameters, currently hinted to by stochastic modelling; the possible role that these bursts may play as a connection between the radiation statistics in thermodynamic equilibrium below and above the transparency threshold and the coherent, lasing regime.