Abstract
Lifetime calculations of Th II J = 1.5 and 2.5 odd states are performed with configuration–interaction many-body perturbation theory (CI-MBPT). For many J = 2.5 states, lifetimes are quite accurate, but two pairs of J = 2.5 odd states and many groups of J = 1.5 states are strongly mixed, making theoretical predictions unreliable. To solve this problem, a method based on intensities is used. To relate experimental intensities to lifetimes, two parameters, one an overall coefficient of proportionality for transition rates and one temperature of the Boltzmann distribution of populations, are introduced and fitted to minimize the deviation between theoretical and intensity-derived lifetimes. For strongly mixed groups of states, the averaged lifetimes obtained from averaged transition rates were used instead of individual lifetimes in the fit. Close agreement is obtained. Then intensity branching ratios are used to extract individual lifetimes for the strongly mixed states. The resulting lifetimes are compared to available directly measured lifetimes and reasonable agreement is found, considering limited accuracy of intensity measurements. The method of intensity-based lifetime calculations with fit to theoretical lifetimes is quite general and can be applied to many complex atoms where strong mixing between multiple states exists.
1. Introduction
The age of the Galaxy can be estimated using a thorium–uranium cosmochronometer [1]. Substantial uncertainty comes from the oscillator strengths of Th II and U II lines used in the abundance calculations. Oscillator strengths determination usually requires experimental lifetimes, using which and intensity branching ratios, they can be found with some level of accuracy. Historically, Th II oscillator strengths initially were obtained by Corliss and Bozman in 1962 from relative intensities in arc spectra [2]. In 1979, Corliss [3] used a lifetime of one level measured by Andersen and Petkov [4] with 15% accuracy to correct systematic errors arising from the incorrect population distribution of the excited levels to obtain oscillator strengths of 35% accuracy derived from 30% accurate intensity measurements. Lifetime measurements for 18 levels were performed by Simonsen et al., in 1988 [5]. In 2002, new measurements of lifetimes and derived oscillator strengths were reported by Nilsson et al. [6]. These oscillator strengths are considered to be most accurate. Oscillator strength calculations of Th II were performed very recently using pseudorelativistic Hartree-Fock with core polarization (HFR-CPOL) method by Gamrath et al. [7], which previously showed promising results for strong U II lines [8].
Motivated by Th nuclear clock search, the method of valence configuration–interaction (CI) with all-order valence-core corrections was used by M. S. Safronova et al. [9] to calculate energies of Th I, Th II, and Th III, but unfortunately transition probabilities or lifetimes for Th II were not presented. This could be due to complexity and strong mixing of Th II levels that require precision beyond available in ab initio theory. Th II has also been investigated using CI and CI-MBPT approaches. Flambaum and Dzuba [10] showed that the number of states in Th II, as well as in Th I, grows exponentially, which is a useful property for nuclear clocks, while it also indicates the complexity of the spectrum, making the precise calculations difficult. Another study showed that the nuclear clock transition can be enhanced through the electronic bridge process [11].
While a large number of Th I and Th II levels are cataloged and included in atlases for calibration, the lifetimes and oscillator strengths are available only for a small number of states [6], which involve states with relatively high energies, more difficult for theory. This work focused on how low-energy states will fill the gap. We present theoretical calculations of lifetimes and most importantly a method that can replace measurements of lifetimes with lifetime calculations for obtaining transition probabilities and related properties from intensities. The theoretical framework is parametric relativistic configuration-interaction many-body perturbation theory (CI-MBPT).
Previously this theory was applied to similar atoms [12,13], and transition probabilities of Si I [14], La II [15], and La I [16] were found in excellent agreement with experiment, although some pairs of levels of La I needed to be adjusted to correct the pair-wise mixing. The method for mixing-angle correction was developed for strong mixing of two pairs of levels, but in general, more levels can strongly interact, which is the case of Th II. The mixing in La II and La I occurred for quite high-energy levels, and a large number of levels could be calculated accurately without any problem. Th II has substantial mixing between levels even at low energy, so it is a more challenging atom than La I, although the number of valence electrons is the same. The main difference is that the actinide core is larger, and stronger valence–core interactions lead to larger correlation corrections. Because reliable experimental lifetimes are available for relatively high energy levels, many of which strongly mixed, a new method was needed to treat them.
Here we theoretically investigated lifetimes of J = 1.5 and J = 2.5 odd Th II states. These particular states were chosen for the following reason. First, J = 1.5 odd states were chosen because they have significant mixing of more than 2 states (see Table 2), so our previous method based on one mixing angle to improve La I transitions for pairs of mixed states [16] would not work and a more general method had to be developed and demonstrated. Lifetimes for many J = 1.5 odd Th II states were precisely measured [6] and constitute a test of the theory. Second, J = 2.5 odd Th II states have more unmixed states for which the theory without mixing complications should give good accuracy (see Table 3). Thus it is possible by comparison to attribute inaccuracy of the theory of J = 1.5 odd states for individual transitions to the mixing problem, and not to the problem of other nature: limited inclusion of correlations, etc.
2. CI-MBPT Calculations
2.1. CI-MBPT Method
To calculate Th II energies, a CI+MBPT method developed for open-shell atoms with multiple valence electrons is used (see for example [17]). The effective CI+MBPT Hamiltonian for Th II is split into two parts:
The one-electron contribution
in addition to the Dirac-Hartree-Fock (DHF) potential contains the valence electron self-energy correction, [18]. In the current CI+MBPT program, the self-energy correction is calculated with the second-order MBPT. The term is scaled with seven factors for one-electron relativistic angular momentum numbers: , , , , ,, . These factors both take into account some high-order MBPT corrections and relativistic effects, including the one-particle Hartree–Fock Breit term. The two-electron Hamiltonian is
where is the Coulomb interaction screening term arising from the presence of the core [19], which is calculated in the second order of MBPT. Fitting with three additional scaling factors is introduced for zero-, first- and second-order multipolarity of the Coulomb interaction. Further details on the CI+MBPT approach can be found in Ref. [20]. In numerical calculations, first, the DHF V potential is calculated (the closed-shell Th V ion). Second, the basis in the frozen V potential is calculated using a B-spline subroutine, with a cavity of radius a.u. chosen for the ion. In this basis, the CI+MBPT terms of Equation (1) are evaluated. The final step in the energy states and wavefunctions calculation is the the solution of eigen-value problem for the effective Hamiltonian matrix.
The program can generate a set of configurations by single-, double-, etc. excitations of the input configurations limited by a given maximum angular momentum and . In case of Th II, we chose single and double excitations limited by: for s and p states, for d states, 9 for f states. The effective Hamiltonian matrix generation is repeated multiple times for different scaling factors and the optimization procedure described below is used until some optimum is reached. The electric dipole matrix elements are evaluated only. Random-phase approximation (RPA) corrections are added to take into account core-polarization corrections for the matrix elements.
2.2. Optimization of and Parameters
Seven and three parameters (the parameter’s definition is provided in the previous section) were found using a random walk method, with one parameter fixed to 0.8, about the average value of the other parameters. The meaning of this procedure is that by scaling the second-order energy corrections, more accurate single valence electron and screened Coulomb interaction can be obtained. Value 1 means just ab initio second-order MBPT corrections in CI-MBPT, while 0 means only valence-valence CI, with core-polarization effects ignored. Values close to 1, such as 0.8, means that the perturbation theory convergences, and high-order corrections constitute only 20% of the second-order corrections.
Initially guessed parameters were modified by some small random values at the same time and the energies and g-factors were compared between old and new sets, with the minimization of error used as the optimization goal. The g-factor errors were weighted with some factors to regulate how accurately g-factors need to be improved. If the error between theory and experiment was reduced, the new set was accepted, or if not, the old set was kept, and the iterations were repeated many times. The smaller number of configurations was initially used, but then it was increased and the parameters were re-optimized. The final optimal values of parameters and configurations are shown in Table 1. The parameter for s and p states substantially deviate from unity, meaning significant higher-order effects, owing to deeper penetration of these valence electrons into the core. Some differences for different values of J can be observed. This can be partially due to differences in energies of different J states and hence level of correlations.

Table 1.
Optimized parameters. Single and double excitations of basic configurations “Basic Conf.” were limited by 11s,11p,10d,9f. In the basic configurations listed “s” means 7s, “p” means 7p, f means “5f”, and “d” means 6d. The core states are the same.
In this paper, we focused on lifetimes of J = 1.5 and J = 2.5 odd states, so the optimization was done for these and the even states to which transitions are allowed. The basic set of configurations explicitly shown in the table was extended by single and double excitations which included 7s–11s, 7p–11p, 6d–10d, and 5f–9f electrons.
The energies were found in close agreement with the experiment, with the error on the order 100 cm. Table 2 shows J = 1.5 odd states for which experimental and theoretical lifetimes will be compared in the next section. These states are quite strongly mixed, so despite a close agreement for energies, g factors show significant differences, which are often due to small distances between levels. We found that g factors for some mixed states can be added together (or averaged, as in the table), and then the agreement between theory and experiment becomes much improved. Such addition or averaging will be used later for lifetimes to show similar significant improvement.

Table 2.
Energies (cm) and g-factors for optimized parameters presented in Table 1 for J = 1.5 odd states. The experimental energies and g-factors are taken from NIST database [21].
J = 2.5 odd states (Table 3), for which we present lifetime calculations, are less mixed than J = 1.5 odd states, at least for low-energy states. The averaging for g factors is shown only for two mixing groups. Thus it is expected that theoretical lifetimes will be reliable for most states listed in the table.

Table 3.
Energies (cm) and g-factors for optimized parameters presented in Table 1 for J = 2.5 odd states. The experimental energies and g-factors are taken from NIST database [21].
Mixing for even states is less important for lifetime calculations, which involve summation over multiple even states. Because the mixing occurs for almost degenerate states, their contributions to the total radiative decay rate of the upper odd states will be only weakly dependent on the mixing. The sum of oscillator strengths is an invariant and if energy differences are small, the sum of transition probabilities becomes invariant, too. In Table 4 CI-MBPT energies and g factors are compared with experiment for J = 1.5 even states. Many g factors have a good agreement, indicating relatively weak mixing. A similar situation is in J = 2.5 even states, for which CI-MBPT calculations are shown in Table 5. In general, we can conclude that the accuracy of even states is sufficient for lifetime calculations of the odd states.

Table 4.
Energies (cm) and g-factors for optimized parameters presented in Table 1 for J = 1.5 even states. The experimental energies and g-factors are taken from NIST database [21].

Table 5.
Energies (cm) and g-factors for optimized parameters presented in Table 1 for J = 2.5 even states. The experimental energies and g-factors are taken from NIST database [21].
2.3. Lifetime of J = 1.5 and 2.5 Odd States
Experimental intensities are proportional to , where is the upper state degeneracy, and the populations of the upper levels, which are not known accurately, and this is the major source of error for the extraction of transition probabilities. So very often experimental lifetimes are used to exclude the populations:
and
We assumed that the intensities are normalized, which is approximately true for the same discharge source and for a calibrated detector. The NIST database contains normalized intensities when possible and they will be used here for comparison of theoretical lifetimes with lifetimes derived from intensities.
With the help of LTE level populations for different levels can be related, so only one coefficient and one temperature are needed to obtain the radiative decay rates for different levels i:
The radiative decay rate can be related to lifetimes, , so
The fitting parameters k and T can be found from comparison with theoretical lifetimes,
In this work, we test this method, which practically is realized by fitting parameters in Equation (7) to match theoretical lifetimes, Equation (8).
One problem with the theory of complex atoms, such as Th II, is that multiple states are significantly mixed and the mixing coefficients, since they are very sensitive to small corrections, are not easy to predict. One indication of this problem is a disagreement between theoretical and experimental g-factors, which in non-relativistic approximation are related to the spin and angular momentum of the states, or terms, so the disagreement for transition matrix elements is also expected.
For example, mixing between the second, third, fourth, and fifth J = 1.5 odd states (Table 2) leads to significant differences between theoretical and experimental g-factors of each state, but the sum or average, that is the sum divided by the number of mixed states, shows a very close agreement. This leads us to believe that the theory predicts quite accurately the lifetimes averaged by transition rates,
while individual lifetimes are not accurate, but they can be improved by using experimental fraction ratios. The accuracy of the theory is also reduced for smaller values of transition matrix elements due to cancellation effects. Thus we can recommend the theoretical values of lifetimes for the averaged values defined above of mixed or individual unmixed states and the experimental branching ratios to predict mixing and individual lifetimes of the mixed states. The odd J = 1.5 states have many groups of mixed states, while the lowest even J = 2.5 states are not much mixed.
In Figure 1 we show that lifetimes derived from experimental NIST intensities are closely correlated with lifetimes derived from theory, with two groups (11–13 and 16–17) of mixed states averaged. The correlation for independently obtained theoretical and experimental lifetimes is a good test of theory and experiment, with the error given by the difference.
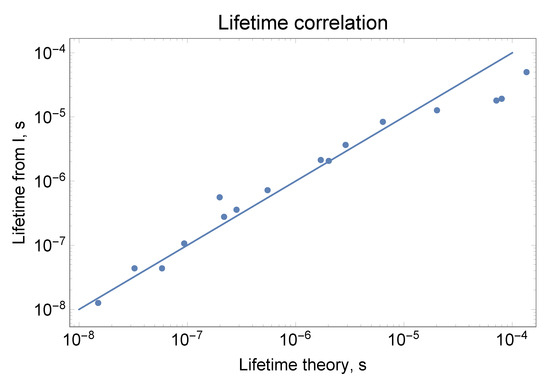
Figure 1.
Comparison between theory and experiment for lifetimes of J = 2.5 odd states. Because of strong mixing for the 20,120, 20,310, 20,686 cm states and 24,463 cm and 24,873 cm states, their average lifetimes were plotted with the average energy used in LTE equation. The lifetimes derived from experimental intensities “Lifetimes from I” (the sum of intensities given by NIST for a transitions from a specific level) were scaled with Boltzmann factor Exp[-E/T] and multiplied by a coefficient for best match: T = 4000 cm and k = 32. The data are also presented in Table 6.
Once the temperature and coefficient of proportionality are found from the fit, the experimental values can be used to find lifetimes derived from intensities. Table 6 shows the values both theoretical and those derived from intensities. The graph has already illustrated close agreement for most states. At very low energies, the agreement becomes worse, but it can be attributed to experimental issues, since theory, in general, is expected to predict more accurately lifetimes for lowest states. Thus we list recommended values as theoretical ones. The error of 10% is assigned from the comparison at higher energies. However, starting with energy 14,545 cm, the agreement between theoretical and intensity-derived lifetimes becomes quite close, and the recommend values are chosen as the average between the two, with the error taken as the difference between the average and the theory. For high enough energy levels, directly measured experimental lifetimes are available, and they are compared with our recommend values. While the agreement is not perfect, nevertheless it is quite acceptable, considering quite large uncertainties in the intensities from multiple sources. Furthermore, the theory might not be very accurate for higher excited states, even after mixing corrections.

Table 6.
Comparison between lifetimes “” calculated with configuration–interaction many-body perturbation theory (CI-MBPT) and lifetimes derived from the sum of intensities for J = 2.5 odd Th II states. The difference allows us to estimate the error of calculations. When strong mixing occurs, the average lifetimes are compared (below the horizontal line), and the intensities are used to obtain individual lifetimes (*) from branching ratios. Theoretical lowest-energy lifetimes are expected to be quite reliable, so the intensities were not used for the recommended value, especially because some systematic effects can be present. A 10% error is assigned from the analysis of the data at higher energies. The directly-measured experimental lifetimes are taken from: [5], [6], [4]. In case of mixing, one averaged experimental lifetime (**) was compared with the averaged recommended lifetime.
Figure 2 shows similar comparison for J = 1.5 odd states as Figure 1 for J = 2.5 odd states. Because more groups of mixed states can be found for these states, fewer points are shown on the graph since many individual lifetimes are replaced with averaged values. Still enough points exist that the temperature and the coefficient of proportionality can be extracted. However, the theoretical uncertainty is expected to be larger. In Table 7 we show theoretical and intensity-derived lifetimes for J = 1.5 odd states. Because of strong mixing for many levels, the lifetimes derived from intensities are recommended. We omitted some theoretical values where a very strong mixing is present since those values are not accurate. The error of 10% is somewhat arbitrary, estimated from the analysis of agreement between theory and experiment when mixing is not present or when the averaged values over the group of strongly mixed states are used. Of course theory does not predict well mixing and correctness of lifetimes for mixed states relies completely on the accuracy of branching ratios.
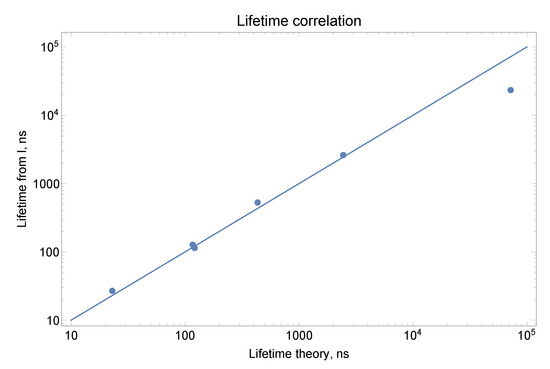
Figure 2.
Comparison between theory and experiment for lifetimes of J = 1.5 odd states. Because of strong mixing for many groups of states (#2-5, #6-8, #9-14, #15-16, #17-18), their average lifetimes were plotted with the average energy used in the LTE equation. The lifetimes derived from experimental intensities “Lifetimes from I” (the sum of intensities given by NIST for a transition from a specific level) were scaled with Boltzmann factor Exp[-E/T] and multiplied by a coefficient for the best match: T = 4500 cm and k = 500. The data are also presented in Table 7.

Table 7.
Lifetime calculations for J = 1.5 odd states using CI-MBPT “” and comparison with lifetimes derived from the sum of intensities. The difference allows us to estimate the error of calculations. When strong mixing occurs, the individual lifetimes derived from intensities are recommended instead of theoretical values, which become incorrect. The lowest-energy lifetime is expected to be more reliable than that derived from intensities. A 10% error can be assigned to from the analysis of the data (see Figure 2). The directly measured experimental lifetimes are taken from: S—[5], N—[6].
3. Discussion
The NIST [21] database provides extensive data for intensities of Th II with references to sources (see for example: [22,23,24,25,26]), but only a small number of transition probabilities, lifetimes or oscillator strengths [6] are given in the literature, and mostly for quite highly excited states. In order to compare theory with experiment, it is necessary to analyze highly excited odd parity states where strong mixing occurs and the results are very sensitive to small theoretical corrections. On the other hand, the theory is expected to be more accurate for low-energy states, where mixing is not strong. Thus we supplement lifetime data for high-energy levels with theoretical data for low-energy states. The quality of the data is evaluated by comparison with lifetimes derived from intensities. The close agreement indicates that theoretical data are reliable and that the method of extraction of lifetimes from intensities can be used in the case when experimental lifetimes are not available. Once the lifetimes are found, specific transition probabilities can be found from branching ratios for a given set of intensities for transitions starting from a specific level for which the lifetime is known.
The case of odd J = 1.5 state is more problematic due to the fact that the majority of the states are strongly mixed in groups. Nevertheless, it is still possible to extract the individual lifetimes from branching ratios of experimental intensities.
While we focused on specific J = 2.5 and J = 1.5 odd states of Th II, the method is quite general and can be used for many complex atoms where strong mixing is present, including actinides. For reliable extraction of lifetimes from intensities, it is necessary that the LTE assumption is accurate and intensities are properly calibrated.
Recently, calculations of oscillator strengths from high-energy excited states to low-energy and ground state were reported [7]. A graphical comparison shows that the core-polarization effects are important and HFR+CPOL calculations are compared with MCDF and experiment. Substantial differences are observed, as expected, since strong mixing makes even strong transitions sensitive to small corrections. Unfortunately, no theoretical lifetime data are presented for comparison with the current work.
It is possible to use our lifetimes and intensities to extract oscillator strengths for some transitions analyzed in [7]. However, the odd states already have lifetimes measured and corresponding oscillator strengths calculated, so this work does not add much to the accuracy. For example, we have calculated J = 2.5 odd state with energy 28,245 cm and obtained a quite accurate agreement with the experiment, 14 ns vs. 11.5(7) [6]. Because in some cases the largest contributions come from the transitions to the ground state or low-energy states which do not have strong mixing, theoretical oscillator strengths should be more or less adequate. Just as an example, we calculated J = 2.5 odd (28,245 cm) to the ground state transition and obtained gf = 0.225, while Nilsson et al. [6] reported experimental gf of 0.287 and Gamrath et al. [7] HFR+CPOL gf of 0.331. Both theoretical values are in some agreement with the experiment of [6], although on the opposite sides of deviation. Thus our approach can be also used for calculations of oscillator strengths of strong lines. However, we did not optimize our parameters for such high energy levels and we postpone a more rigorous treatment for the future. In passing we note that it is important not only to have large matrix elements but also minimal mixing with nearby states for both odd and even states to have reliable theoretical oscillator strengths. Otherwise, a similar procedure of using intensities can be employed to extract more accurate oscillator strengths or transition probabilities from experimental intensities. In order to reduce errors in intensities, it is important to have calibration using for example some known atomic lines.
4. Conclusions
We have presented CI-MBPT parametric calculations of lifetimes for J = 1.5 and J = 2.5 odd states. Because J = 2.5 odd low-energy states are not strongly mixed, pure theoretical values are expected to be accurate. The accuracy was demonstrated by comparison with lifetimes derived from intensities and directly measured. However, because two groups of J = 2.5 odd states and many groups of J = 1.5 odd states were mixed, a procedure was introduced to extract more accurate lifetimes using intensities. The resulting intensity-derived lifetimes are in agreement with measured lifetimes even for the cases where many states are mixed. We tabulated recommended lifetimes which can be used to extract oscillator strengths using calibrated intensities. The method of intensity-derived lifetimes is quite general and can be used for calculations of highly excited states where theory fails to predict configuration mixing. This method can supplement the approach where experimental lifetimes are used for the same purpose. An additional issue can be that the observed spectrum can be limited and not include all strong lines. Th II has an extensive tabulation of lines and in this respect is a perfect system for the intensity-based lifetime calculations.
Funding
This research received no external funding.
Acknowledgments
Research presented in this article was supported by the Laboratory Directed Research and Development program of Los Alamos National Laboratory under the project number 20180125ER. The author is grateful to Dzuba for making the CI-MBPT code available for this work.
Conflicts of Interest
The author declares no conflict of interest.
References
- Cayrel, R.; Hill, V.; Beers, T.C.; Barbuy, B.; Spite, M.; Spite, F.; Plez, B.; Anderson, J.; Bonifacio, P.; Francois, P.; et al. Measurement of stellar age from uranium decay. Nature 2001, 409, 691–692. [Google Scholar] [CrossRef]
- Corliss, C.H.; Bozman, W.R. NBS Monograph; US Govt Printing Office: Washington, DC, USA, 1962; Volume 53.
- Corliss, C.H. Oscillator strengths for lines of ionized thorium (Th II). Mon. Not. R. Astr. Soc. 1979, 189, 607. [Google Scholar] [CrossRef][Green Version]
- Andersen, T.; Petkov, A.P. Th II Meanlife and the Solar Thorium Abundance. Astron. Astrophys. 1975, 45, 237. [Google Scholar]
- Simonsen, H.; Worm, T.; Jessen, P.; Poulsen, O. Lifetime Measurements and Absolute Oscillator Strengths for Single Ionized Thorium (ThII). Phys. Scripta 1988, 38, 370–373. [Google Scholar] [CrossRef]
- Nilsson, H.; Zhang, Z.G.; Lundberg, H.; Johansson, S.; Nordström, B. Experimental oscillator strengths in Th II. Astron. Astrophys. 2002, 382, 368. [Google Scholar] [CrossRef][Green Version]
- Gamrath, S.; Godefroid, M.R.; Palmeri, P.; Quinet, P.; Wang, K. Spectral line list of potential cosmochronological interest deduced from new calculations of radiative transition rates in singly ionized thorium (Th II). Mon. Not. R. Astron. Soc. 2020, 496, 4507. [Google Scholar] [CrossRef]
- Gamrath, S.; Palmeri, P.; Quinet, P. Calculated oscillator strengths for the strongest lines of cosmochronological interest in the visible spectrum of singly ionized uranium (U II). Mon. Not. R. Astron. Soc. 2018, 480, 4754. [Google Scholar] [CrossRef]
- Safronova, M.S.; Safronova, U.I.; Clark, C.W. Relativistic all-order calculations of Th, Th+, and Th2+ atomic properties. Phys. Rev. A 2014, 90, 032512. [Google Scholar] [CrossRef]
- Dzuba, V.A.; Flambaum, V.V. Exponential Increase of Energy Level Density in Atoms: Th and Th II. PRL 2010, 104, 213002. [Google Scholar] [CrossRef]
- Porsev, S.G.; Flambaum, V.V. Electronic bridge process in 229Th+. Phys. Rev. A 2010, 81, 042516. [Google Scholar] [CrossRef]
- Savukov, I.M. Parametric CI+MBPT calculations of Th I energies and g-factors for even states. J. Phys. B At. Mol. Opt. Phys. 2017, 50, 165001. [Google Scholar] [CrossRef]
- Savukov, I.; Safronova, U.I.; Safronova, M.S. Relativistic configuration interaction plus linearized-coupled-cluster calculations of U2+ energies, g factors, transition rates, and lifetimes. Phys. Rev. A 2015, 92, 052516. [Google Scholar] [CrossRef]
- Savukov, I.M. Configuration-interaction plus many-body-perturbation-theory calculations of Si i transition probabilities, oscillator strengths, and lifetimes. Phys. Rev. A 2016, 93, 022511. [Google Scholar] [CrossRef]
- Savukov, I.M.; Anisimov, P.M. Configuration-interaction many-body perturbation theory for La ii electric-dipole transition probabilities. Phys. Rev. A 2019, 99, 032507. [Google Scholar] [CrossRef]
- Filin, D.; Savukov, I. Accurate CI-MBPT calculation of radiative lifetimes and transition probabilities of neutral lanthanum (La I) odd states with J = 3/2. Phys. Scr. 2020. accepted to publication. [Google Scholar] [CrossRef]
- Dzuba, V.A. Calculation of the energy levels of Ge, Sn, Pb, and their ions in the VN−4 approximation. Phys. Rev. A 2005, 71, 062501. [Google Scholar] [CrossRef]
- Dzuba, V.A.; Flambaum, V.V.; Silvestrov, P.G.; Sushkov, O.P. Calculation of parity non-conservation in thallium. J. Phys. B 1987, 20, 3297. [Google Scholar] [CrossRef]
- Dzuba, V.A.; Flambaum, V.V.; Sushkov, O.P. Summation of the high orders of perturbation theory for the parity nonconserving E1-amplitude of the 6s–7s transition in the caesium atom. Phys. Lett. A 1989, 140, 493. [Google Scholar] [CrossRef]
- Dzuba, V.A.; Flambaum, V.V.; Kozlov, M.G. Combination of the many-body perturbation theory with the configuration-interaction method. Phys. Rev. A 1996, 54, 3948. [Google Scholar] [CrossRef]
- Kramida, A.; Ralchenko, Y.; Reader, J.; NIST ASD Team. NIST Atomic Spectra Database (Ver. 5.7); National Institute of Standards and Technology: Gaithersburg, MD, USA, 2019. Available online: https://physics.nist.gov/asd (accessed on 21 July 2020).
- Kerber, F.; Nave, G.; Sansonetti, C.J. The Spectrum of Th-Ar Hollow Cathode Lamps in the 691–5804 nm Region: Establishing Wavelength Standards Calibration of Infrared Spectrographs. Astrophys. J. Suppl. Ser. 2008, 178, 374–381. [Google Scholar] [CrossRef]
- Palmer, B.A.; Engleman, R., Jr. Atlas of the Thorium, Spectrum; Report LA-9615; Los Alamos National Lab: Los Alamos, NM, USA, 1983; p. 333.
- Zalubas, R.; Corliss, C.H. Energy Levels and Classified Lines in the Second Spectrum of Thorium (Th II). J. Res. Natl. Bur. Stand. (U.S.) Sect. A 1974, 78, 163–246. [Google Scholar] [CrossRef]
- Redman, S.L.; Nave, G.; Sansonetti, C.J. The Spectrum of Thorium from 250 nm to 5500 nm: Ritz Wavelengths and Optimized Energy Levels. Astrophys. J. Suppl. Ser. 2014, 211, 4. [Google Scholar] [CrossRef]
- Lovis, C.; Pepe, F. A New List of Thorium and Argon Spectral Lines in the Visible. Astron. Astrophys. 2007, 468, 1115–1121. [Google Scholar] [CrossRef]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2020 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).