On Laser-Modified Rutherford Scattering

Abstract

We present a theoretical analysis of a charged-particle scattering by a Coulomb potential in the presence of laser radiation. The effect of a laser field is studied using our recently developed nonperturbative parabolic quasi-Sturmian approach for solving the system of coupled Lippmann–Schwinger–Floquet equations in the Kramers–Henneberger frame. We calculate the ratio of multiphoton differential cross sections to the Rutherford cross section in the case of a laser-assisted electron-proton scattering process. Our results are compared with predictions of the Bunkin–Fedorov, Kroll–Watson, and Coulomb–Volkov analytical approximations: marked discrepancies are found for different net numbers of exchanged photons and different orientations of the laser-field polarization vector. Our findings clearly demonstrate deficiencies of those well-known approximations for describing laser-modified Rutherford scattering processes.

1. Introduction

The Rutherford scattering, i.e., scattering of a charged particle in a Coulomb potential, is a fundamental phenomenon in atomic physics that played a historical role in establishing the planetary and, eventually, the Bohr model of the atom. This process is well understood in quantum mechanics: a closed-form solution of the corresponding Schrödinger equation—the Coulomb scattering state—is known exactly (see, e.g., the textbook [1]), and the angular differential cross section is given by the famous Rutherford formula.

In contrast, the Rutherford scattering in the presence of a laser field is much less understood. This largely owes to the fact that the Schrödinger equation for a charged particle moving in combined Coulomb and laser fields does not have closed-form solutions. Within given approximations, valid in certain conditions, analytical results can be obtained. Well known are the Bunkin–Fedorov approach [2], the low-frequency approximation of Kroll and Watson [3], and the result based on the Coulomb–Volkov function [4,5]. In the search for laser dressed atom effects, the Kroll–Watson approximation, for example, resulted in being sufficient to explain the experimental data on laser-assisted elastic electron scattering off neutral atoms (see, for instance, [6,7]). In a similar way, one might expect that the main features of the laser-modified Rutherford scattering can also be described already by means of one of these analytical descriptions and that more advanced methods, which are purely numerical and free of approximations, bring about only minor corrections. In this work we show that such an expectation is wrong: for a chosen set of physical parameters that could be envisaged in an experiment, the indicated approximations yield results which markedly differ from advanced numerical calculations. For this purpose, we use our recently developed nonperturbative approach for computing laser-modified Coulomb scattering states [8], which we already have successfully utilized in the theoretical treatment of the laser-assisted $(e,2e)$ process of atomic hydrogen [9]. Our method makes use of quasi-Sturmian (QS) basis functions [10] taken in parabolic coordinates to solve the system of coupled Lippmann–Schwinger–Floquet equations in the Kramers–Henneberger representation [11]. Because of the adequate asymptotic behavior of the parabolic QS functions, from the obtained solution one can easily extract the scattering amplitude for a given net number of exchanged photons.

The paper is organized as follows. In Section 2, we deliver a general formulation and outline the basic features of our approach for calculating multiphoton cross sections of laser-modified Rutherford scattering. The analytical results for the cross sections within the Bunkin–Fedorov, Kroll–Watson, and Coulomb–Volkov approximations are also briefly recalled. In Section 3, we present and discuss numerical calculations obtained with our nonperturbative QS approach in comparison with those obtained using such customary approximations. The conclusions are drawn in Section 4. Atomic units (a.u., $\hslash =e=m_e=1$) are used throughout unless otherwise stated.

2. Theoretical Formulation

Without loss of generality, we will consider electron scattering in a Coulomb potential of a nucleus in the presence of linearly polarized monochromatic laser radiation with the vector potential

$$\mathbf{A}\left(t\right)={\mathbf{A}}_{0}cos\omega t.$$

(1)

The laser field of frequency $\omega$ is assumed to switch on adiabatically at $t=-\infty$.

The electron dynamics are governed by the time-dependent Schrödinger equation

$$i\frac{\partial }{\partial t}\mathsf{\Psi }(\mathbf{r},t)=\left[\frac{1}{2}{\left(-i\mathsf{\nabla }+\frac{1}{c}\mathbf{A}\left(t\right)\right)}^2+V\left(\mathbf{r}\right)\right]\mathsf{\Psi }(\mathbf{r},t),$$

(2)

with the electron-nucleus Coulomb potential $V\left(\mathbf{r}\right)=-Z/r$ (the nucleus of charge $Z>0$ is assumed to be infinitely heavy as compared to the electron mass). In the accelerated, or space-translated, Kramers–Henneberger frame [11], Equation (2) is transformed into

$$i\frac{\partial }{\partial t}\psi (\mathbf{r},t)=\left(-\frac{1}{2}\Delta +V[\mathbf{r}+\mathbf{a}\left(t\right)]\right)\psi (\mathbf{r},t),$$

(3)

where

$$\psi (\mathbf{r},t)=exp\left[\mathbf{a}\left(t\right)·\mathsf{\nabla }+\frac{i}{2c^2}\underset{-\infty }{\overset{t}{\int }}d{t}^{\prime }{A}^2\left(t^{\prime }\right)\right]\mathsf{\Psi }(\mathbf{r},t),$$

(4)

and

$$\begin{array}{c}\hfill \mathbf{a}\left(t\right)=\frac{1}{c}\underset{-\infty }{\overset{t}{\int }}d{t}^{\prime }\mathbf{A}\left(t^{\prime }\right)={\mathbf{a}}_{0}sin\omega t\end{array}$$

(5)

is the displacement vector of a classical electron, with ${\mathbf{a}}_0={\mathbf{A}}_0/\omega c$ called the quiver amplitude.

Within the Hermitian Floquet theory (see, e.g., [12]), one seeks the solution of Equation (3) in the form

$$\psi (\mathbf{r},t)=e^{-iEt}\sum _{\ell =-\infty }^{\infty }{e}^{-i\ell \omega t}{F}_{\ell }(E,\mathbf{r}),$$

(6)

where E is a real quantity called the Floquet quasi-energy of the state. The harmonic components $F_{\ell }$ satisfy an infinite set of time-independent equations:

$$\left(H_{\ell }+{\tilde{V}}_0({\mathbf{a}}_0,\mathbf{r})-E\right)F_{\ell }(E,\mathbf{r})+\sum _{{\ell }^{\prime }\ne \ell }{V}_{\ell -{\ell }^{\prime }}({\mathbf{a}}_0,\mathbf{r})F_{{\ell }^{\prime }}(E,\mathbf{r})=0,\ell =0,\pm 1,\pm 2,\dots$$

(7)

Here

$$H_{\ell }=H_C-\ell \omega ,H_C=-\frac{1}{2}\Delta -\frac{Z}{r},{\tilde{V}}_0({\mathbf{a}}_0,\mathbf{r})=V_0({\mathbf{a}}_0,\mathbf{r})+\frac{Z}{r},$$

(8)

and $V_{\ell }$ are the Fourier components of the space-translated Coulomb potential $V[\mathbf{r}+\mathbf{a}(t\left)\right]$,

$$\begin{array}{ccc}\hfill V_{\ell }({\mathbf{a}}_0,\mathbf{r})& =& \frac{1}{T}\underset{0}{\overset{T}{\int }}dtexp(i\ell \omega t)V\left[\mathbf{r}+\mathbf{a}\left(t\right)\right],\hfill \end{array}$$

(9)

where $T=2\pi /\omega$ denotes the optical period.

2.1. The Parabolic QS Approach

Let us briefly outline our nonperturbative approach [8] that we employ to obtain differential cross sections for the laser-modified electron-nucleus scattering. We express the Floquet components $F_{\ell }$ in the form

$$F_{\ell }(E,\mathbf{r})={\tilde{F}}_{\ell }(E,\mathbf{r})+{\delta }_{\ell 0}{\psi }_C^{(+)}\left(\mathbf{r}\right),$$

(10)

where

$${\psi }_C^{(+)}\left(\mathbf{r}\right)=\frac{e^{-\frac{1}{2}\pi \beta }}{{\left(2\pi \right)}^{3/2}}\Gamma (1+i\beta )e^{i\mathbf{k}\mathbf{r}}{}_1{F}_1(-i\beta ,1;i(kr-\mathbf{k}\mathbf{r}))$$

represents the electron state in the absence of a laser field, i.e., a Coulomb wave [1] describing the incident electron of momentum $\mathbf{k}$ and characterized by the Sommerfeld parameter $\beta =-Z/k$. The use of form (10) recasts the system of coupled Floquet equations (7) into a system of coupled Lippmann–Schwinger–Floquet equations (see details in Ref. [8]). Further, introducing the parabolic coordinates ($\xi$,$\eta$,$\varphi$) with the z axis directed along $\mathbf{k}$,

$$x=\sqrt{\xi \eta }cos\varphi ,y=\sqrt{\xi \eta }sin\varphi ,z=\frac{1}{2}(\xi -\eta ),$$

we employ for the components ${\tilde{F}}_{\ell }$ the expansion

$${\tilde{F}}_{\ell }(E,\mathbf{r})=\sum _{m=-M}^M\sum _{n_1,n_2=0}^{N-1}{C}_{n_1{n}_{2}m}^{\ell }{Q}_{n_1{n}_{2}m}^{(+)}\left(k_{\ell };\xi ,\eta ,\varphi \right).$$

(11)

on the parabolic QS functions $Q_{n_1{n}_{2}m}^{(+)}$ subject to the appropriate boundary conditions as defined in Ref. [10], and with momenta given by

$$k_{\ell }=\left\{\begin{array}{c}\sqrt{2(E+\ell \omega )},E+\ell \omega \ge 0,\\ i\sqrt{-2(E+\ell \omega )},E+\ell \omega <0.\end{array}\right.$$

(12)

Let ${\beta }_{\ell }=-Z/k_{\ell }$ be the corresponding Sommerfeld parameter.

One representation of the QS functions is

$$Q_{n_1{n}_{2}m}^{(+)}(k_{\ell };\xi ,\eta ,\varphi )=\frac{e^{im\varphi }}{\sqrt{2\pi }}{\mathcal{P}}_{n_1{n}_2}^{\left|m\right|}(k_{\ell };\xi ,\eta ),$$

(13)

with the ‘radial’ part presented as

$$\begin{array}{cc}\hfill {\mathcal{P}}_{n_1{n}_2}^{\left|m\right|}(k_{\ell };\xi ,\eta )=& 2(1+\zeta )\sqrt{\frac{n_1!n_2!}{(n_1+\left|m\right|)!(n_2+\left|m\right|)!}}{\left(2b\sqrt{\xi \eta }\right)}^{\left|m\right|}{e}^{-b(\xi +\eta )}\hfill \\ \hfill & \times \underset{0}{\overset{1}{\int }}ds{(1-s)}^{i{\beta }_{\ell }+\left|m\right|}{\left(1-\zeta s\right)}^{-i{\beta }_{\ell }+\left|m\right|}{\left(1-s-\zeta s\right)}^{n_1+n_2}exp\left[2b(\xi +\eta )\frac{\zeta s}{(1+\zeta )}\right]\hfill \\ \hfill & \times L_{n_1}^{\left|m\right|}\left(2b\xi \frac{(1-s)(1-\zeta s)}{(1-s-\zeta s)}\right)L_{n_2}^{\left|m\right|}\left(2b\eta \frac{(1-s)(1-\zeta s)}{(1-s-\zeta s)}\right),\hfill \end{array}$$

(14)

where $L_n^{\left|m\right|}$ are the associated Laguerre polynomials with scale parameter b, and the parameter $\zeta$ is defined by

$$\zeta =\frac{b+i\frac{k_{\ell }}{2}}{b-i\frac{k_{\ell }}{2}}.$$

(15)

This representation allows one to ensure the proper asymptotic behavior of expansion (11). Indeed, the parabolic QS functions (13) behave asymptotically as

$${\mathcal{Q}}_{n_1{n}_{2}m}^{(+)}(k_{\ell };\xi ,\eta ,\varphi )\underset{r\to \infty }{⟶}\frac{e^{im\varphi }}{\sqrt{2\pi }}{\mathcal{A}}_{n_1{n}_2}^{\left|m\right|}\left(\theta \right)\frac{exp\left\{i\left[k_{\ell }r-{\beta }_{\ell }ln\left(2k_{\ell }r\right)\right]\right\}}{r},$$

(16)

with

$$\begin{array}{cc}\hfill {\mathcal{A}}_{n_1{n}_2}^{\left|m\right|}\left(\theta \right)=& \frac{i}{k}\sqrt{\frac{n_1!n_2!}{(n_1+\left|m\right|)!(n_2+\left|m\right|)!}}{\zeta }^{-i{\beta }_{\ell }}{e}^{-\frac{\pi {\beta }_{\ell }}{2}}{\left(\frac{1}{\zeta }-\zeta \right)}^{\left|m\right|+1}{\left(\frac{sin\theta }{2}\right)}^{\left|m\right|}{(-\zeta )}^{n_1+n_2}\hfill \\ \hfill & \times \sum _{{\nu }_1=0}^{n_1}\sum _{{\nu }_2=0}^{n_2}{c}_{{\nu }_1}^{(n_1,|m\left|\right)}{c}_{{\nu }_2}^{(n_2,|m\left|\right)}\Gamma (i{\beta }_{\ell }+\left|m\right|+{\nu }_1+{\nu }_2+1){(1-{\zeta }^{-2})}^{{\nu }_1+{\nu }_2},\hfill \\ \hfill & \times {\left(cos\frac{\theta }{2}\right)}^{2{\nu }_1}{\left(sin\frac{\theta }{2}\right)}^{2{\nu }_2},\hfill \end{array}$$

(17)

where the coefficients $c_{\nu }^{(n,|m\left|\right)}$ are defined by [13]

$$c_{\nu }^{(n,|m\left|\right)}={(-1)}^{\nu }\frac{(n+|m\left|\right)!}{(n-\nu )!(\nu +|m\left|\right)!\nu !}.$$

(18)

From the asymptotic behavior of the Floquet components (10) one can derive the ℓ-photon angular differential cross sections, i.e., the cross sections corresponding to a net number ℓ of photons ($\ell ={\ell }_a-{\ell }_e$, where ${\ell }_{a\left(e\right)}$ is the total number of absorbed (emitted) photons) exchanged between the electron and laser field:

$$\frac{d{\sigma }_{\ell }}{d\mathsf{\Omega }}=\frac{k_{\ell }}{k}{\left|{\delta }_{\ell 0}{f}_C\left(\theta \right)+2\pi \sum _{m=-M}^M{e}^{im\varphi }\sum _{n_1,n_2=0}^{N-1}{C}_{n_1{n}_{2}m}^{\ell }{\mathcal{A}}_{n_1{n}_2}^{\left|m\right|}\left(\theta \right)\right|}^2.$$

(19)

The Coulomb amplitude

$$f_C\left(\theta \right)=-\frac{\beta }{2k{sin}^2\frac{\theta }{2}}{e}^{-i\beta ln\left({sin}^2\frac{\theta }{2}\right)}\frac{\Gamma (1+i\beta )}{\Gamma (1-i\beta )}$$

(20)

provides the field-free Coulomb differential cross section, given by the Rutherford formula

$$\frac{d{\sigma }_C}{d\mathsf{\Omega }}={\left|f_C\left(\theta \right)\right|}^2=\frac{Z^2}{16E^2{sin}^4\frac{\theta }{2}}.$$

(21)

In what follows, we will study the ratio

$$R=\frac{\frac{d{\sigma }_{\ell }}{d\mathsf{\Omega }}}{\frac{d{\sigma }_C}{d\mathsf{\Omega }}},$$

(22)

which conveniently quantifies the effect of the laser field on the Coulomb scattering process.

2.2. The Customary Analytical Approximations

It is well known that one obtains the exact cross section (21) for the field-free Coulomb scattering already in the first Born approximation. By treating the Coulomb interaction in the first Born approximation and using electron states in a laser field, which are given by Volkov functions [14], one arrives at the well-known approach to the laser-assisted electron scattering which was originally proposed by Bunkin and Fedorov [2] and later independently formulated by Kroll and Watson [3] as the weak-potential approximation. The Bunkin–Fedorov approximation, valid when the potential is weak compared to the laser strength and can be treated as a perturbation, yields for the quantity (22) the following expression:

$$R=\frac{k_{\ell }}{k}{\left|J_{\ell }\left({\mathbf{q}}_{\ell }{\mathbf{a}}_0\right)\right|}^2{\left(\frac{q}{q_{\ell }}\right)}^4,$$

(23)

where $J_{\ell }$ is a Bessel function of order ℓ, ${\mathbf{q}}_{\ell }=\mathbf{k}-{\mathbf{k}}_{\ell }$, ${\mathbf{k}}_{\ell }$ is the final electron momentum, and $q=2ksin(\theta /2)$. It should be noted that one obtains the same expression when using the low-frequency (or soft-photon) approximation of Kroll and Watson [3], even though this approach treats the Coulomb interaction nonperturbatively (see Ref. [12] for details).

Another well-known analytical approximation that treats both the Coulomb and laser interactions nonperturbatively is the use of a Coulomb–Volkov function [4,5]. It approximates the exact electron state in combined Coulomb and laser fields by

$${\psi }_{\mathrm{CVF}}^{(+)}(\mathbf{r},t)=\frac{e^{-\frac{1}{2}\pi \beta }}{{\left(2\pi \right)}^{3/2}}\Gamma (1+i\beta )e^{-i(Et-\mathbf{k}\mathbf{r})}{}_1{F}_1(-i\beta ,1;i[k{r}^{\prime }\left(t\right)-\mathbf{k}{\mathbf{r}}^{\prime }\left(t\right)]),$$

where ${\mathbf{r}}^{\prime }\left(t\right)=\mathbf{r}+\mathbf{a}\left(t\right)$. Using its asymptotic form at $r\to \infty$, we derive the ratio [12]

$$R={\left|J_{\ell }\left(\mathbf{q}{\mathbf{a}}_0\right)\right|}^2,$$

(24)

where $\mathbf{q}=\mathbf{k}-k{\widehat{\mathbf{k}}}_{\ell }$, with ${\widehat{\mathbf{k}}}_{\ell }={\mathbf{k}}_{\ell }/k_{\ell }$.

Expressions (23) and (24) coincide when $\ell =0$, but are different otherwise.

3. Results and Discussion

As indicated in the Introduction, we wish to show that the well-known analytical approximations do not give a proper account of laser-modified Rutherford scattering. For this purpose we consider the case of the laser-assisted electron-proton scattering process

$$e^{-}+p+\ell \omega \to e^{-}+p.$$

We calculate the ratio (22) within our nonperturbative QS approach and compare with the predictions of the Bunkin–Fedorov/Kroll–Watson, and Coulomb–Volkov approximations recalled above.

The laser field is taken with the polarization vector directed along the y axis (i.e., perpendicular to the incident electron momentum $\mathbf{k}$), a quiver amplitude $a_0=5$ and a frequency $\omega =0.05=1.36$ eV, values which are close to those in the laser-assisted $(e,2e)$ experiment of Höhr et al. [15,16] ($I=4\times {10}^{12}\mathrm{W}/{\mathrm{cm}}^2$ and $\omega =1.17$ eV). The incident electron momentum is set to $k=0.93$, which represents a characteristic value of the ejected electron momentum in the experiment of Höhr et al. It can be seen that the corresponding electron energy $E=k^2/2$ obeys the low-frequency regime $E\gg \omega$, for which the Kroll–Watson approximation is supposed to be valid. Though the corresponding Sommerfeld parameter $\beta =-1/k$ does not satisfy the formal condition $\left|\beta \right|\ll 1$ of the perturbative regime in the case of Coulomb collisions (let us note that one obtains the Rutherford formula for Coulomb scattering both in the exact treatment and in the Born approximation, i.e., in the lowest order of perturbation theory), we point out once again that the Bunkin–Fedorov approach based on the weak-potential approximation and the nonperturbative Kroll–Watson approach yield the same analytical expression (23), irrespective of the values of the Sommerfeld and laser parameters. One may question whether our choice of kinematical and laser parameters allows one to consider the Coulomb–Volkov approximation. We recall that a Coulomb–Volkov function can be considered as a reasonable interpolation between the well-known solutions of the Schrödinger equation in the pure Coulomb field and in the pure laser field. However, in spite of wide applications, the range of applicability (and thus their accuracy) of Coulomb–Volkov functions remains mostly undetermined; our present analysis can help to shed some light on this issue.

In the numerical calculations using our QS approach, we set the Laguerre basis scale parameter to $b=0.6$. We take the ansatz (11) with the maximum projection of the angular momentum $M=7$ and restrict ourselves to $N=16$ ‘radial’ parabolic basis functions along both axes $\xi$ and $\eta$ (this means a basis size of 3840). A more detailed description of our numerical scheme, including its efficiency and convergence, can be found in Ref. [8].

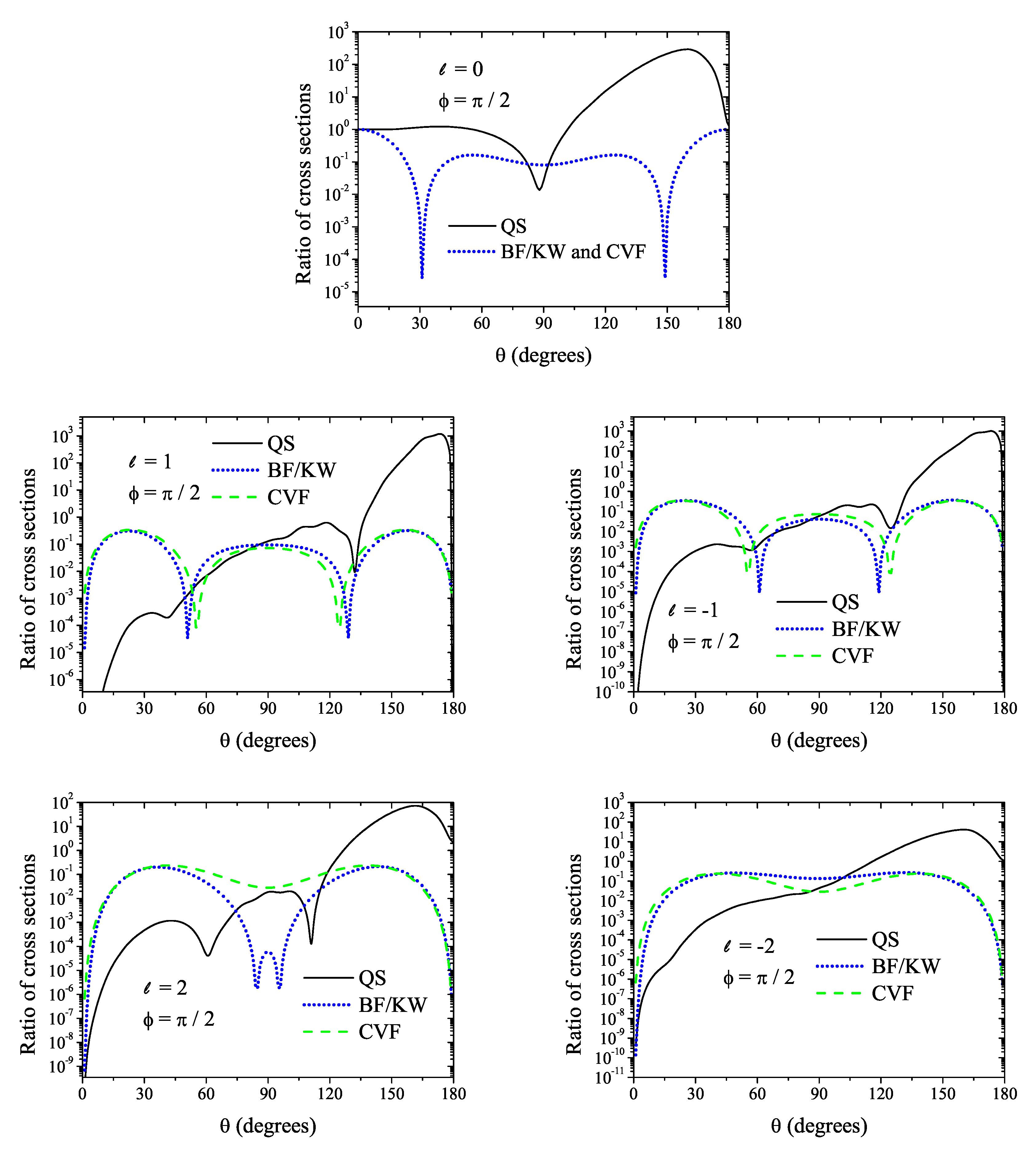
Figure 1 shows numerical values for ℓ-photon differential cross sections normalized to the field-free, Rutherford scattering cross section (21). For all inspected photon numbers we find marked discrepancies, both in shape and in magnitude, between our numerical QS approach and the analytical approximations. The latter, on the contrary, exhibit a rather close agreement with each other. This can be readily explained by the fact that for small ℓ values the differences between the results (23) and (24) are not significant. Note that due to ${\left|J_{\ell }\left(x\right)\right|}^2\le 1$, the analytical approximations yield a ratio $R\lesssim 1$, while in our QS approach the ratio can exceed unity by orders of magnitude, especially at large scattering angles. The only common feature of the QS approach and analytical approximations is found in the vicinity of the forward scattering direction when $\ell =0$, where the cross section ratio is very close to unity. This feature owes to the dominating role of the long-range Coulomb potential $V_C=-1/r$ at small scattering angles (with the cross section going to infinity as $\theta \to 0$), as compared to the role of the ‘short-range’ part of the potential ${\tilde{V}}_0({\mathbf{a}}_0,\mathbf{r})$.

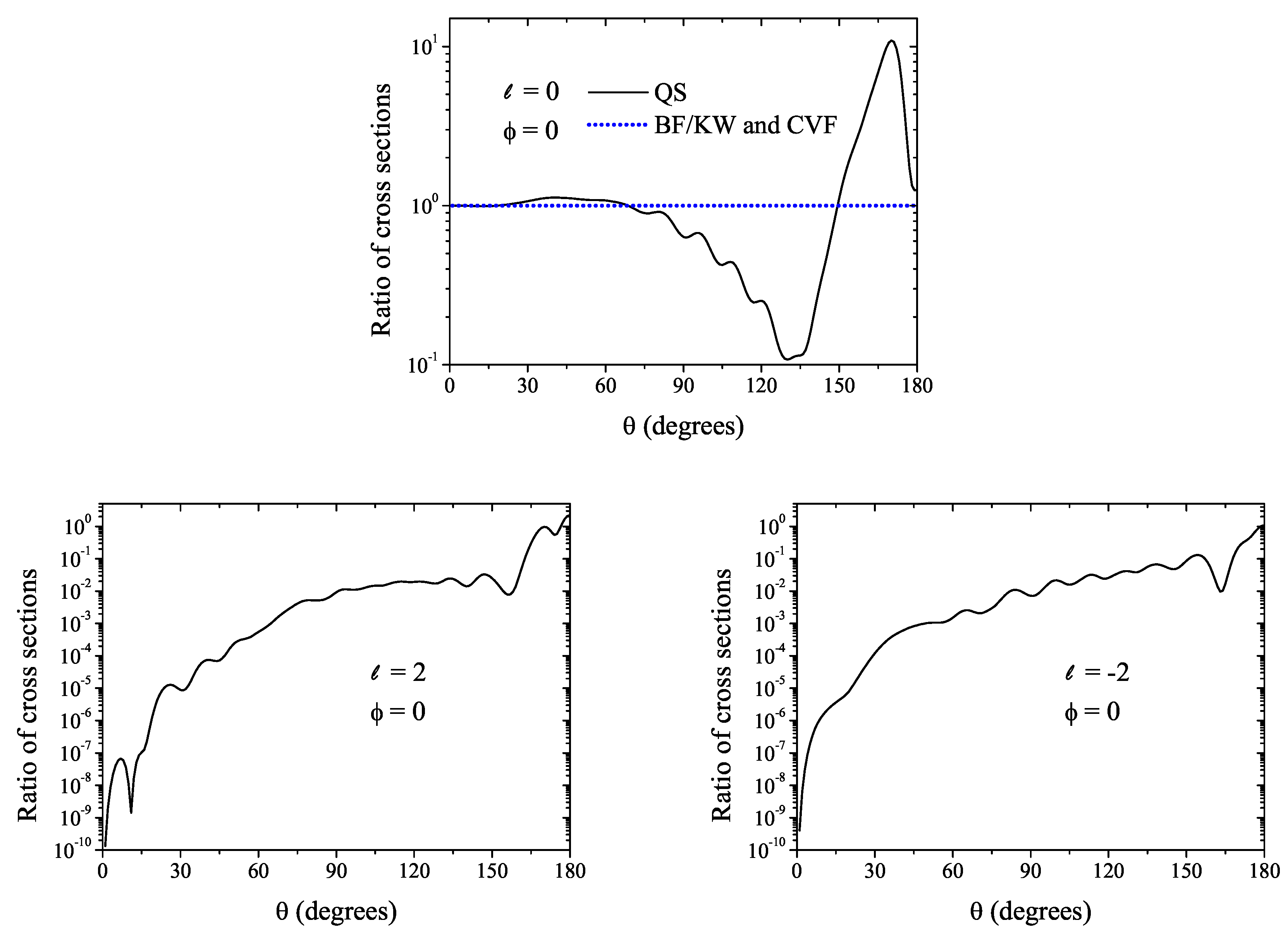
The results presented in Figure 1 are for the case when the laser field lies in the scattering plane. The difference between our nonperturbative QS approach and the analytical approximations becomes even more pronounced if the laser field is perpendicular to the scattering plane, as illustrated by the ratios shown in Figure 2. When $\ell =0$, the laser field has no effect on the scattering process within the analytical approximations. On the contrary, the results using the QS approach exhibit a substantial effect in the angular region $\theta \gtrsim {90}^{\circ }$. Further, according to the selection rule discussed in [17], the ℓ-photon cross sections vanish in the considered geometry when ℓ is odd. We have verified that this requirement is met with a very high accuracy in our QS calculations for $\ell =\pm 1$. While the analytical approximations (23) and (24) formally obey the selection rule, they predict vanishing values (due to $J_{\ell }\left(0\right)={\delta }_{\ell 0}$ [13]) not only for odd ℓ but for all $\ell \ne 0$. As can be seen from the $\ell =\pm 2$ QS results in Figure 2, the cross sections for even ℓ are clearly nonzero.

Small ripples are observed in the QS curves in Figure 2, and to a lesser extent in Figure 1. We cannot associate them with any simple physical explanation. In addition, they are not due to some numerical instability and/or insufficient size of the QS basis. At the same time, even if they were related to the representation of the Floquet components with a finite QS expansion, these ripples do not modify our general observation of marked discrepancies between the QS approach and analytical approximations.

4. Summary and Conclusions

We have presented a theoretical investigation of laser-modified Coulomb scattering. We have employed our recently developed nonperturbative QS approach to solve numerically the system of coupled Lippmann–Schwinger–Floquet equations in the Kramers–Henneberger frame. On this basis we have calculated ℓ-photon differential cross sections for a laser-assisted electron-proton scattering process. We have compared the ratio of these cross sections to the field-free Rutherford cross section with the results obtained within the Bunkin–Fedorov/Kroll–Watson and Coulomb–Volkov approximations. Two orientations of the laser polarization vector have been studied: (i) when this vector lies in the scattering plane and is perpendicular to the incident electron momentum and (ii) when it is perpendicular to the scattering plane. In both geometries, we have found marked discrepancies between our QS approach and the customary approximations both in terms of shape and in terms of magnitude. Particularly strong disagreements have been observed when the laser field is perpendicular to the scattering plane, in which case the approximate treatments predict no laser-field effect at all, namely they predict the Rutherford cross section for $\ell =0$ and vanishing cross sections for all $\ell \ne 0$.

The results of our study clearly demonstrate the deficiency of the customary approximations in describing laser-modified Rutherford scattering processes. The only situation where their results appear to be more or less reliable is the scattering in the vicinity of the forward direction when $\ell =0$. This is explained by the dominance of the field-free Coulomb scattering mechanism in such a case. The effect of a laser field on the scattering dynamics grows with increasing scattering angle and net number of exchanged photons. We thus expect larger inaccuracies of the analytical approximations in such situations and, hence, a proper treatment of the laser field effect becomes essential, in general, with increasing the laser-field strength. Note that in our analysis we inspected the absolute Sommerfeld-parameter value $\left|\beta \right|\approx 1$ that is rather far off the perturbative regime ($\left|\beta \right|\ll 1$) for Coulomb collisions. Larger inaccuracies of the analytical approximations are also anticipated for larger $\left|\beta \right|$.

For an accurate theoretical treatment of laser-assisted Coulomb scattering processes, we thus advocate the use of nonperturbative numerical approaches such as the one used here, or the R-matrix-Floquet theory [18] and the close-coupling method [19,20,21]. It would be interesting, though, to understand when the analytical approximations could still provide some acceptable results. To properly answer this question, the laser-modified Rutherford scattering process should be further investigated, exploring the multi-parameter space by systematically varying the field strength, the laser frequency, the electron energy and the Coulomb charge. This is part of our current investigations. Along these lines, in our study of the laser-assisted $(e,2e)$ process of atomic hydrogen [9], we have played with both the field strength and the laser frequency (actually, maintaining the same Keldysh parameter) and observed the varying effect on the differential cross sections.