The Allure of High Total Angular Momentum Levels in Multiply-Excited Ions
Abstract
1. Introduction
2. General Remarks and Earlier Work
2.1. Satellites to Diagram Lines in He-Like Ion Spectra
2.2. High-J Levels in Li-Like Ions with n > 2: 1s2p3d 4
2.3. Al-Like Ions: The 3s3p3d 4 Level
2.4. Na-Like Ions: The 2p53s3p 4 – 2p53s3d 4 Transition
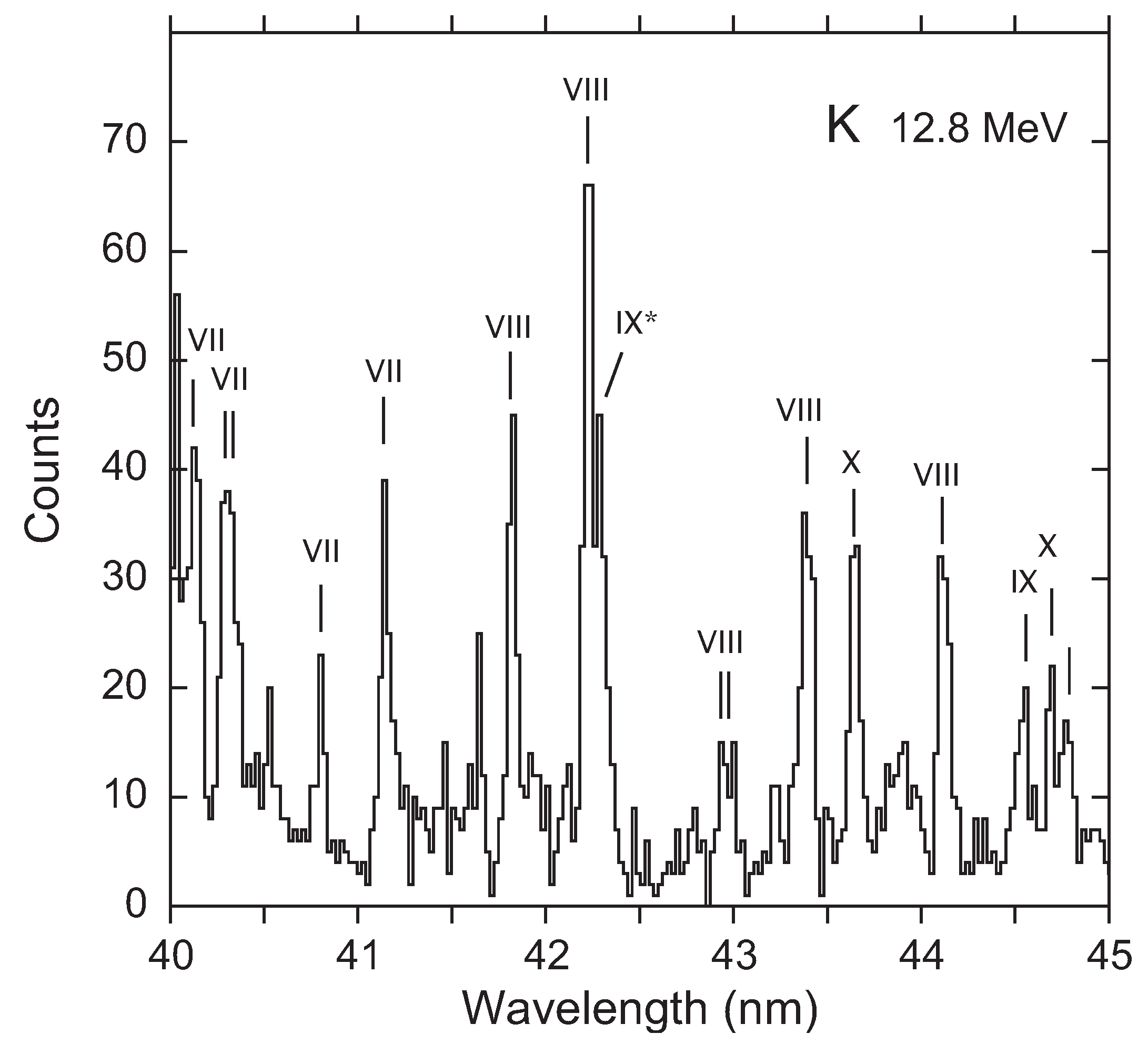
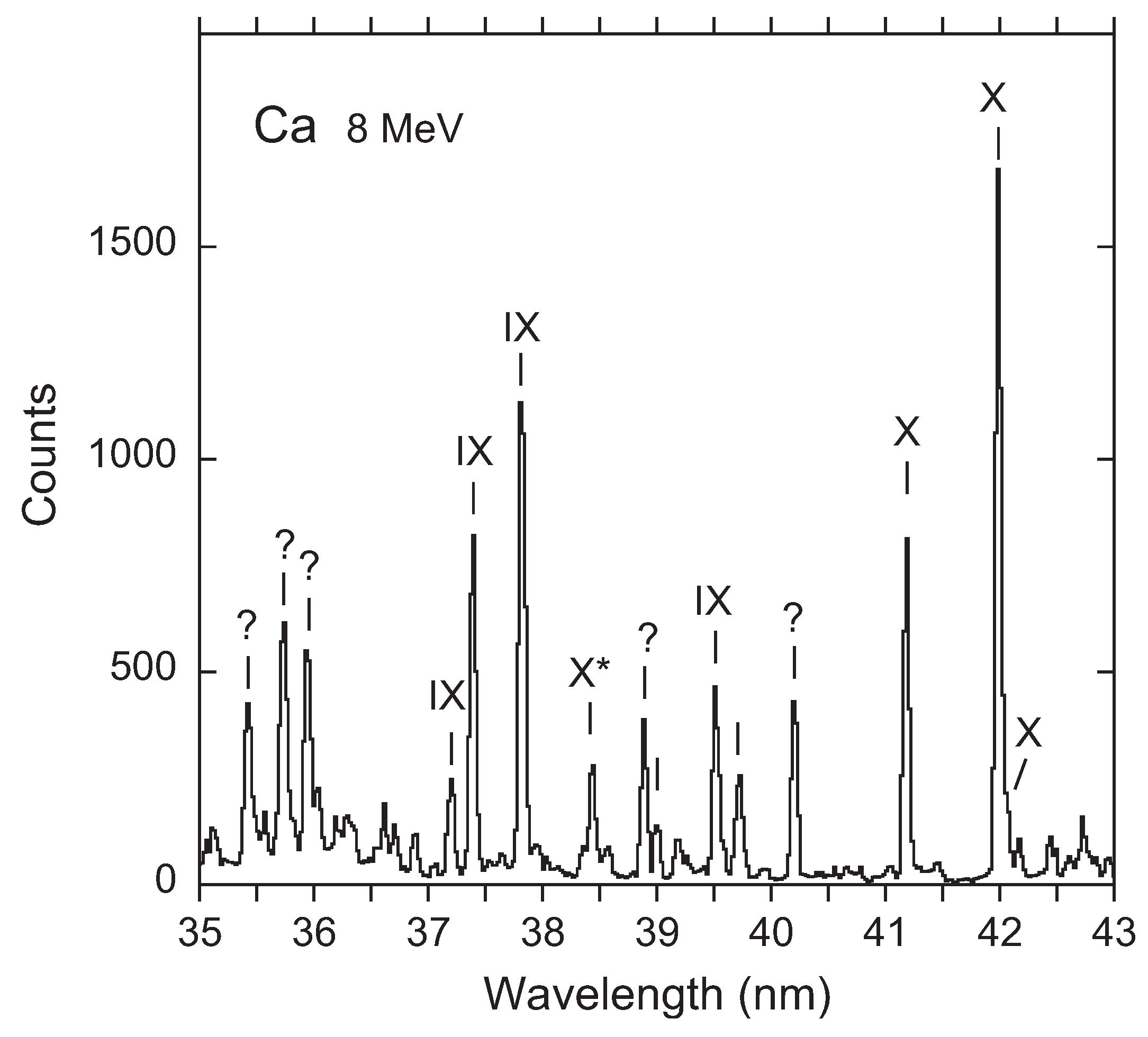
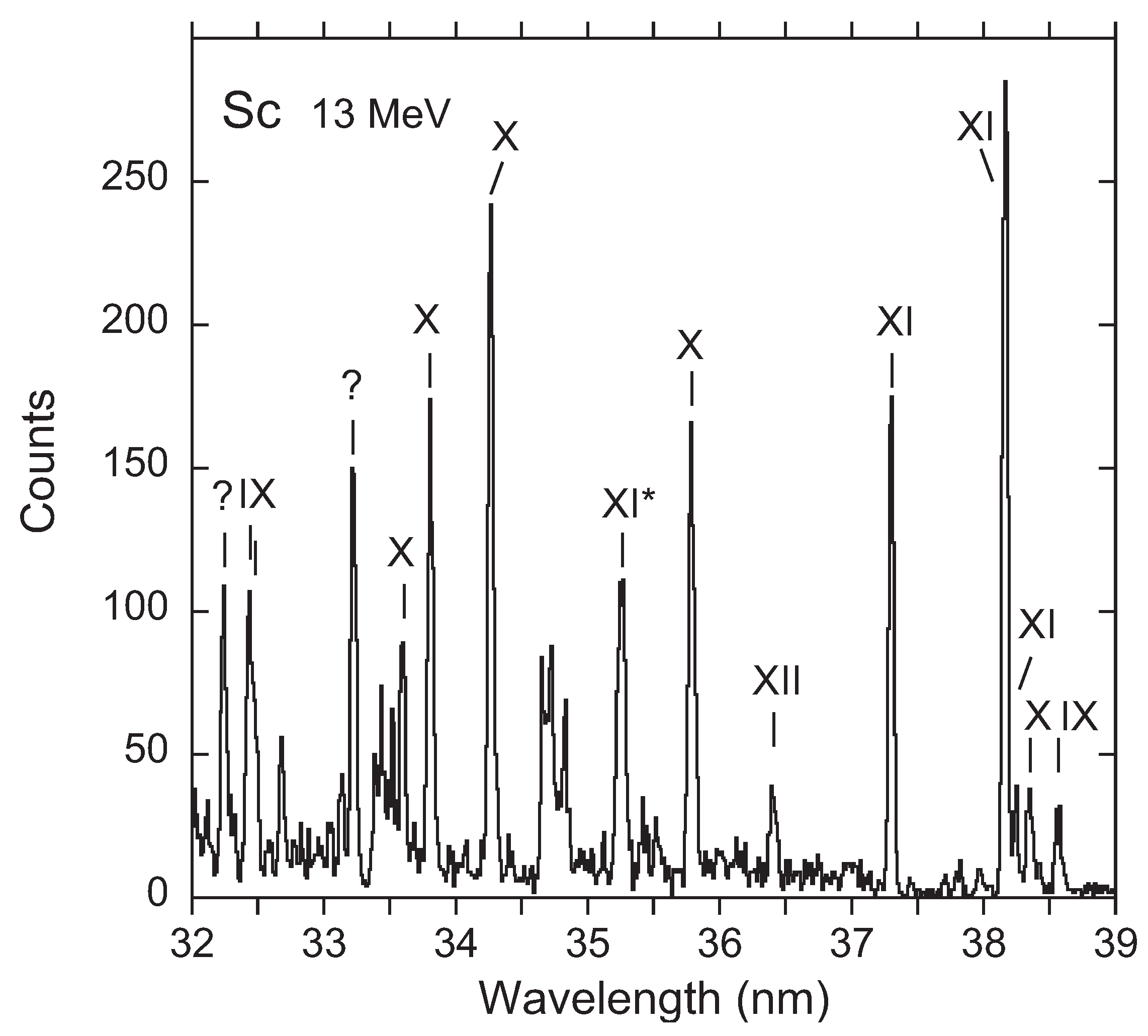
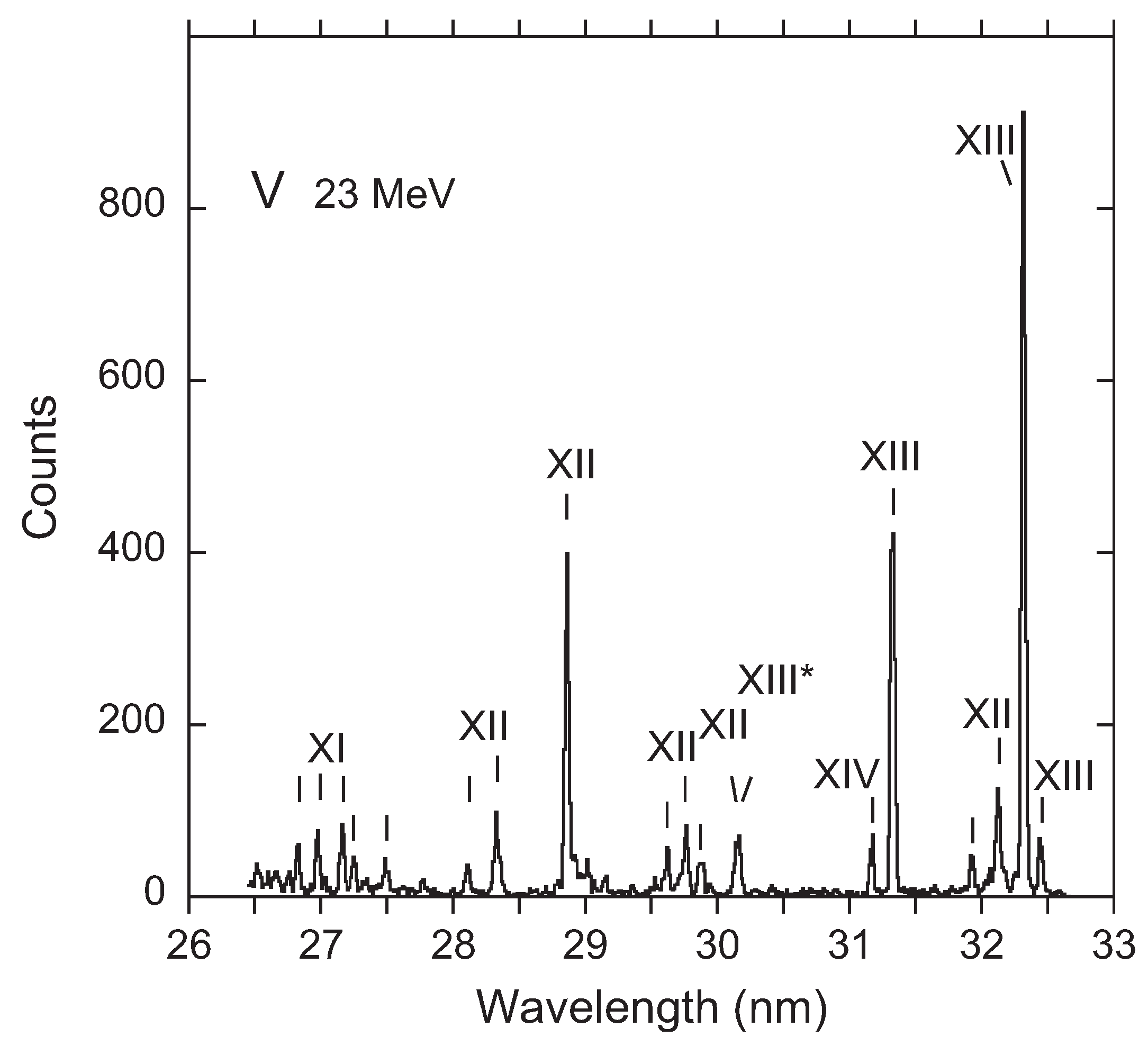
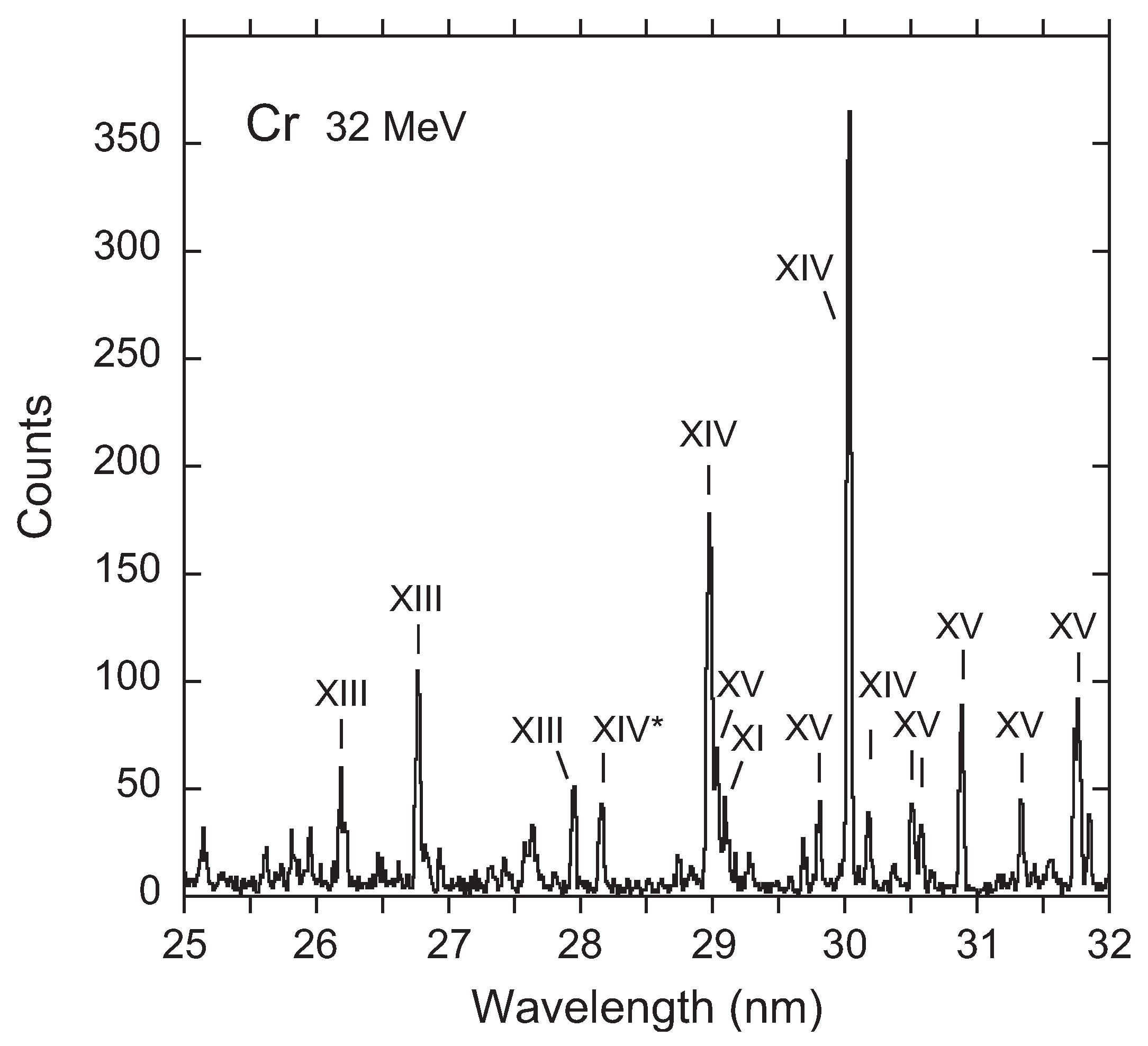
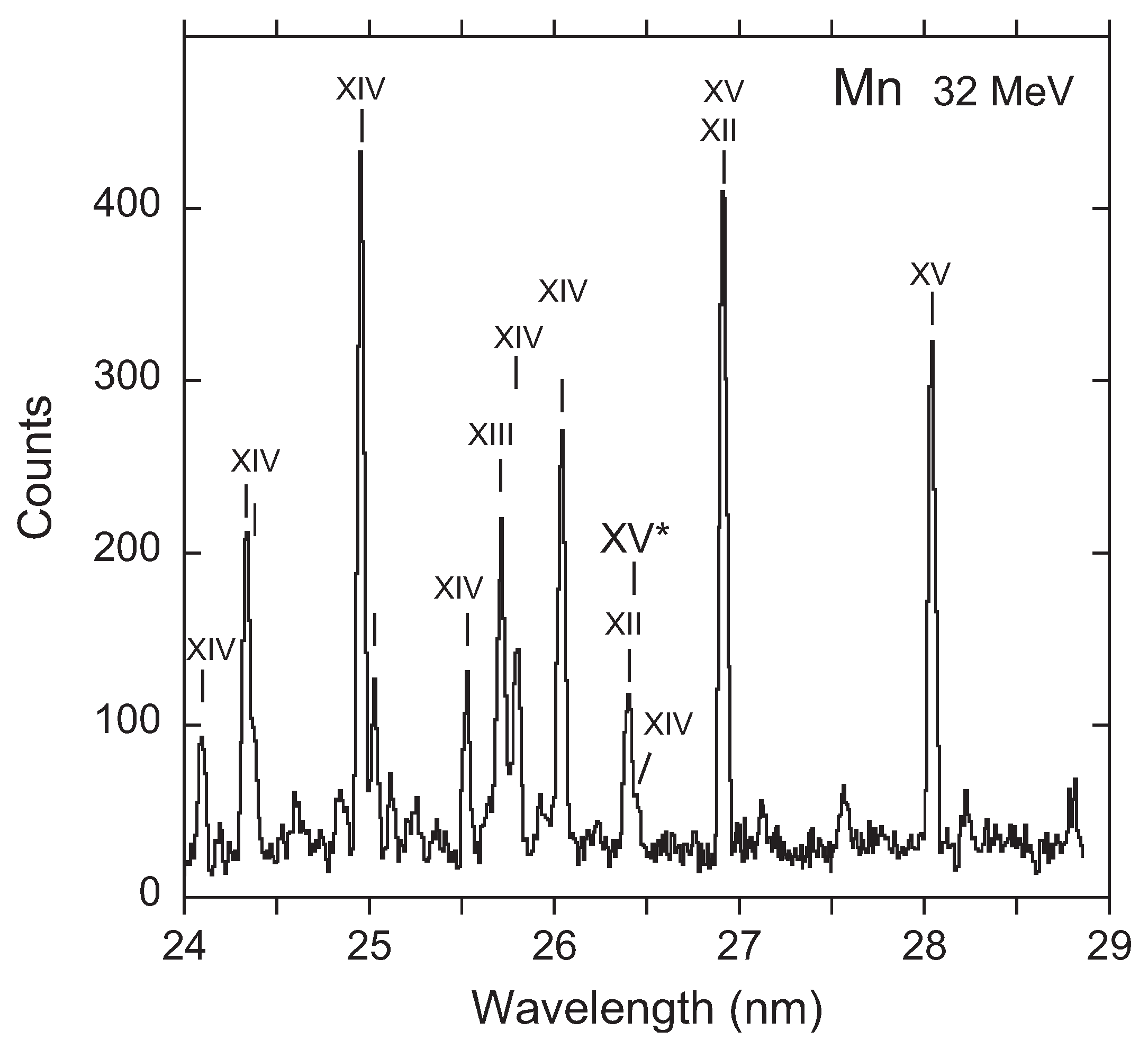
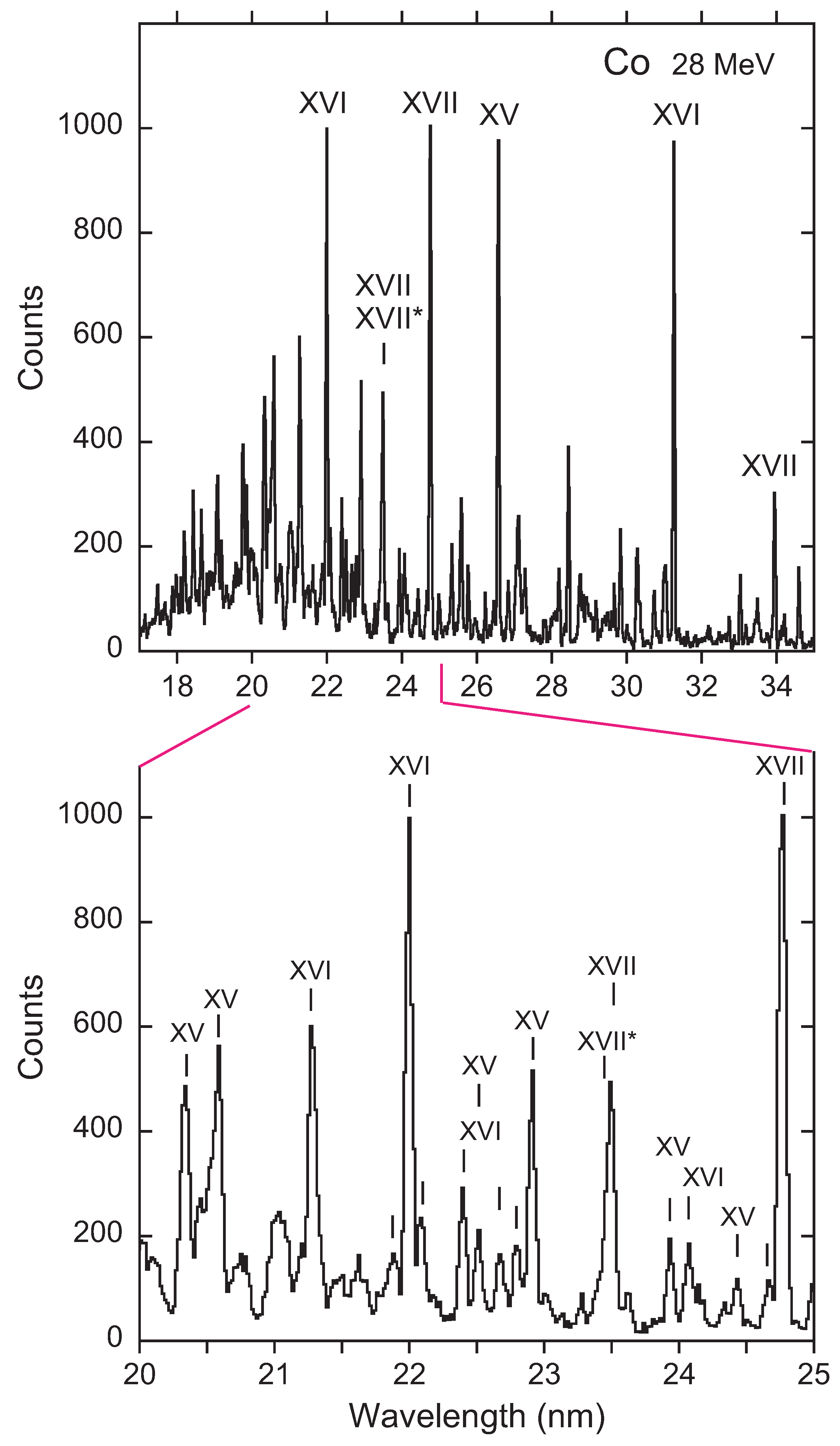
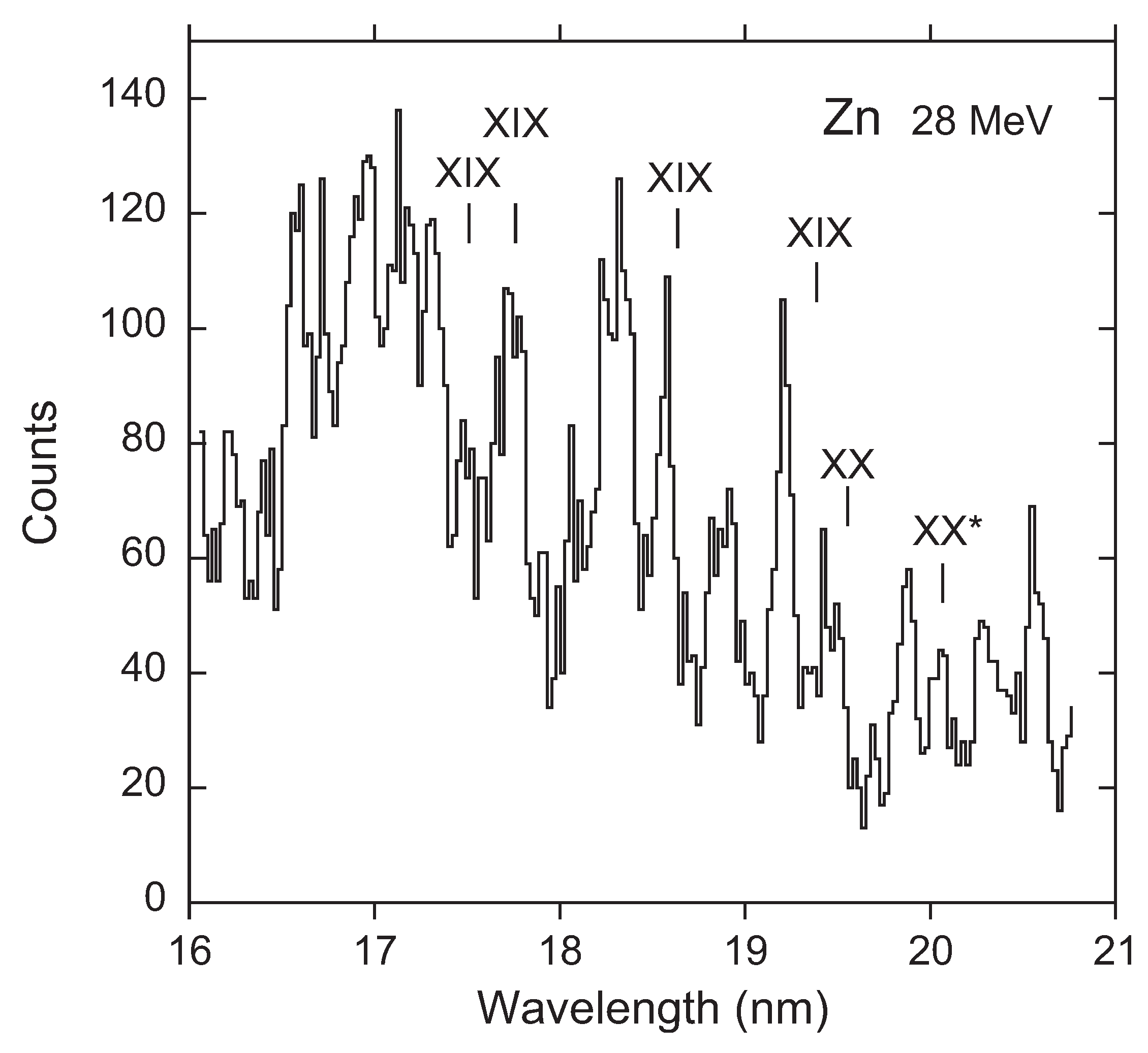
3. Recent Work on the 23s3p 4–2p53s3d 4 Transition
Available Data
4. Discussion and Outlook
Acknowledgments
Conflicts of Interest
References
- Edlén, B. Atomic Spectra. In Encyclopedia of Physics; Flügge, S., Ed.; Springer: Berlin, Germany, 1964; Volume 27. [Google Scholar]
- Wu, T.-Y. Auto-ionization in doubly excited helium and the λ 320.4 and λ 357.5 lines. Phys. Rev. 1944, 66, 291. [Google Scholar] [CrossRef]
- Pietenpol, J.R. Auto-ionization of the (1s2s2p) 4P5/2 level in Li and He−. Phys. Rev. Lett. 1961, 7, 64. [Google Scholar] [CrossRef]
- Gabriel, A.H. Dielectronic satellite spectra for highly-charged helium-like ion lines. Mon. Not. R. Astron. Soc. 1972, 160, 99–119. [Google Scholar] [CrossRef]
- Kay, L. A van de Graaff beam as a source of atomic emission spectra. Phys. Lett. 1963, 5, 36–37. [Google Scholar] [CrossRef]
- Bashkin, S.; Meinel, A.B. Laboratory excitation of the emission spectrum of a nova. Astrophys. J. 1964, 139, 413–415. [Google Scholar] [CrossRef]
- Bashkin, S. Optical spectroscopy with Van De Graaff accelerators. Nucl. Instrum. Meth. 1964, 28, 88–96. [Google Scholar] [CrossRef]
- Bashkin, S. A new method for studying the atom. Science 1965, 148, 1047–1053. [Google Scholar] [CrossRef]
- Kay, L. On the origins of beam-foil spectroscopy—I. Nucl. Instrum. Methods Phys. Res. Sect. B 1985, 9, 544–545. [Google Scholar] [CrossRef]
- Bashkin, S. On the origins of beam-foil spectroscopy—II. Nucl. Instrum. Methods Phys. Res. Sect. B 1985, 9, 546–548. [Google Scholar] [CrossRef]
- Berry, H.G. Multiply-excited states in beam-foil spectroscopy. Phys. Scr. 1975, 12, 5–20. [Google Scholar] [CrossRef]
- Berry, H.G. Beam-foil spectroscopy. Rep. Prog. Phys. 1977, 40, 155–217. [Google Scholar] [CrossRef]
- Mannervik, S. Optical studies of multiply excited states. Phys. Scr. 1989, 40, 28–52. [Google Scholar] [CrossRef]
- Träbert, E. Radiative-Lifetime Measurements on Highly-Charged Ions. In Accelerator-Based Atomic Physics Techniques and Applications; Shafroth, S.M., Austin, J.C., Eds.; American Institute of Physics: Washington, DC, USA, 1997; pp. 567–607. [Google Scholar]
- Bruch, R.; Paul, G.; Andrä, J.; Fricke, B. Auger transitions in Li-like and Be-like ions. Phys. Lett. A 1975, 53, 293–294. [Google Scholar] [CrossRef]
- Schneider, D.; Bruch, R.; Schwarz, W.H.E.; Chang, T.C.; Moore, C.F. Identifications of Auger spectra from 2-MeV foil-excited carbon ions. Phys. Rev. A 1977, 15, 926–934. [Google Scholar] [CrossRef]
- Bruch, R.; Rødbro, M.; Bisgaard, P.; Dahl, P. Time-delayed Li, Be and B autoionization spectra excited in low-energy (200 keV) single gas collisions. Phys. Rev. Lett. 1977, 39, 801–803. [Google Scholar] [CrossRef]
- Dohmann, H.-D.; Liesen, D.; Pfeng, H. High resolution spectroscopy of prompt and metastable decaying levels in highly ionized argon, especially of the metastable 3P2-state of Ar16+ and the 4P5/2-state of Ar15+. Z. Phys. A 1978, 285, 171–176. [Google Scholar] [CrossRef]
- Beiersdorfer, P.; Bitter, M.; Hey, D.; Reed, K.J. Identification of the 1s2s2p 4P5/2→ 1s22s 2S1/2 magnetic quadrupole inner-shell satellite line in the Ar16+ K-shell X-ray spectrum. Phys. Rev. A 2002, 66, 032504. [Google Scholar] [CrossRef]
- Träbert, E. Lifetimes of lowest even-parity quartet levels of three-electron ions. Z. Phys. A 1985, 321, 51–55. [Google Scholar] [CrossRef]
- Träbert, E. The lifetime of the 1s2p2 4P state, Li0 - Si11+; a comment on available data and suggestions for a recommended set of data. Nucl. Instrum. Methods Phys. Res. Sect. B 1987, 23, 287–290. [Google Scholar] [CrossRef]
- Träbert, E.; Curtis, L.J. Comment on finestructure data of three-electron quartet states. Phys. Scr. 1985, 32, 599–601. [Google Scholar] [CrossRef]
- Hellmann, H.; Träbert, E. Beam-foil spectroscopical study of the 1s2s2p and 1s2p2 quartet levels of Mg9+ and Al10+. Nucl. Instrum. Methods Phys. Res. Sect. B 1985, 9, 611–613. [Google Scholar] [CrossRef]
- Engström, L.; Hutton, R.; Reistad, N.; Martinson, I.; Huldt, S.; Mannervik, S.; Träbert, E. A new measurement of the 1s2s2p 4Po–1s2p2 4P transitions in C IV: Wavelengths, fine structure intervals and lifetimes. Phys. Scr. 1987, 36, 250–254. [Google Scholar] [CrossRef]
- Buchet, J.P.; Buchet-Poulizac, M.C.; Denis, A.; Désesquelles, J.; Druetta, M.; Martin, S.; Ouerdane, Y. Fine structure of the 1s2s2p 4Po and 1s2p2 4P doubly excited states of lithiumlike Si XII. J. Phys. (Paris) Coll. Suppl. Au 1988, 49, 111–114. [Google Scholar]
- Mannervik, S.; Short, R.T.; Sonnek, D.; Träbert, E.; Möller, G.; Lodwig, V.; Heckmann, P.H.; Blanke, J.H.; Brand, K. Bound triply excited states in neutral lithium. Phys. Rev. A 1989, 39, 3964–3968. [Google Scholar] [CrossRef]
- Träbert, E.; Heckmann, P.H.; Doerfert, J.; Granzow, J. Search for the spectrally narrow radiative decay of 2p3 4S3/2o. J. Phys. B At. Mol. Opt. Phys. 1992, 25, L353–L358. [Google Scholar] [CrossRef]
- Knystautas, E.J. Observation of a triply excited state in He−. Phys. Rev. Lett. 1992, 69, 2635–2637. [Google Scholar] [CrossRef]
- Winter, H.; Aumayr, F. Hollow atoms. J. Phys. B At. Mol. Opt. Phys. 1999, 32, R39. [Google Scholar] [CrossRef]
- Rosmej, F.B.; Dachicourt, R.; Deschaud, B.; Khaghani, D.; Dozières, M.; Šmìd, M.; Renner, O. Exotic X-ray emission from dense plasmas. J. Phys. B: At. Mol. Opt. Phys. 2015, 48, 224005. [Google Scholar] [CrossRef]
- Träbert, E.; Armour, I.A.; Bashkin, S.; Jelley, N.A.; O’Brien, R.; Silver, J.D. The X-ray spectra of H-like, He-like and Li-like silicon ions after foil excitation. J. Phys. B At. Mol. Phys. 1979, 12, 1665–1676. [Google Scholar] [CrossRef]
- Träbert, E.; Fawcett, B.C. Identification of satellite lines in the X-ray spectrum of foil-excited silicon. J. Phys. B At. Mol. Phys. 1979, 12, L441–L447. [Google Scholar] [CrossRef]
- Armour, I.A.; Fawcett, B.C.; Silver, J.D.; Träbert, E. X-ray spectra and satellite classification of foil-excited Mg and Al. J. Phys. B At. Mol. Phys. 1980, 13, 2701–2709. [Google Scholar] [CrossRef]
- Träbert, E.; Fawcett, B.C.; Silver, J.D. One- and two-electron one-photon satellite transitions in the X-ray spectrum of foil-excited F and Si. J. Phys. B At. Mol. Phys. 1982, 15, 3587–3597. [Google Scholar] [CrossRef]
- Bunge, C.F. Identification of bound states of core-excited negative lithium atoms in beam-foil experiments. Phys. Rev. Lett. 1980, 44, 1450–1452. [Google Scholar] [CrossRef]
- Mannervik, S.; Astner, G.; Kisielinski, M. An optical transition in the negative lithium ion. J. Phys. B At. Mol. Phys. 1980, 13, L441–L444. [Google Scholar] [CrossRef]
- Lodwig, V.; von Buttlar, H. Lifetime of the 1s2p3 5So level in the negative lithium ion. Phys. Scr. 1989, 39, 586–591. [Google Scholar] [CrossRef]
- Hardis, J.E.; Berry, H.G.; Curtis, L.J.; Livingston, A.E. The 1s2s2p2 5P1,2,3–1s2p3 5 transition in Ne VII. Phys. Scr. 1984, 30, 189–193. [Google Scholar] [CrossRef]
- Träbert, E.; Blanke, J.H.; Heckmann, P.H.; Hellmann, H.M.; Möller, G. Ruhr-Universität Bochum, Dynamitron Tandem Laboratory. Unpublished work. 1986. [Google Scholar]
- Brage, T.; Froese Fischer, C. The 1s2s2p2 5P–1s2p3 5S transition in Be I-like ions. J. Phys. B At. Mol. Opt. Phys. 1988, 21, 2563–2569. [Google Scholar] [CrossRef]
- Kwong, T.; Chung, K.T. 1s2s2p2 5P–1s2p3 5So transition and fine structure of Be-like systems. Phys. Rev. A 1989, 40, 4203–4208. [Google Scholar]
- Hata, J.; Grant, I.P. The 1s2s2p2 5P–1s2p3 5S transitions in the beryllium isoelectronic sequence. J. Phys. B At. Mol. Phys. 1983, 16, L125–L128. [Google Scholar] [CrossRef]
- Chung, K.T.; Davis, B.F. Transition wavelength and fine structure for the quartet states of Be+. Phys. Rev. A 1984, 29, 1871–1877. [Google Scholar] [CrossRef]
- Davis, B.F.; Chung, K.T. Transition wavelengths and fine structure for the doublet states of Be+. Phys. Rev. A 1984, 29, 2586–2590. [Google Scholar] [CrossRef]
- Davis, B.F.; Chung, K.T. Spin-induced autoionization and radiative transition rates for the (1s2p2p) 4PJ states in lithiumlike ions. Phys. Rev. A 1988, 37, 111–118. [Google Scholar] [CrossRef] [PubMed]
- Davis, B.F.; Chung, K.T. Spin-induced autoionization and radiative transition rates for the (1s2s2p) 4 states in lithiumlike ions. Phys. Rev. A 1989, 39, 3942–3955. [Google Scholar] [CrossRef] [PubMed]
- Aspromallis, G.; Nicolaides, C.A.; Komninos, Y. Multichannel relativistic autoionisation of negative ions: The 1s2s2p3 6 metastable state of Be−. J. Phys. B At. Mol. Phys. 1985, 18, L545–L549. [Google Scholar] [CrossRef]
- Blanke, J.H.; Fricke, B.; Heinemann, D.; Sepp, W.-D.; Thies, B.; Göbenli, T.; Heckmann, P.; Möller, G.; Träbert, E. Study of 3d 4f and 3d 5f quartet and doublet transitions of doubly excited three-electron ions. Z. Phys. D 1989, 13, 1–7. [Google Scholar] [CrossRef]
- Blanke, J.H.; Fricke, B.; Sepp, W.-D.; Heckmann, P.H.; Möller, G.; Wagner, C. Transitions between quintet states of doubly excited four-electron ions: Experiment and MCDF theory along the isoelectronic sequence. Phys. Scr. 1990, 42, 522–529. [Google Scholar] [CrossRef][Green Version]
- Blanke, J.H.; Fricke, B.; Heinemann, D.; Heckmann, P.H.; Möller, G.; Träbert, E. Further investigations on doubly excited four-electron ions: Beam-foil experiment and MCDF theory. Phys. Scr. 1991, 44, 436–441. [Google Scholar] [CrossRef]
- Blanke, J.H.; Fricke, B.; Heckmann, P.H.; Träbert, E. First results of experimental and theoretical investigations on sextet states of doubly-excited five-electron ions. Phys. Scr. 1992, 45, 430–435. [Google Scholar] [CrossRef]
- Chen, M.H.; Crasemann, B. Lifetime of the 1s2p3d 4F9/2 metastable state of Li-like ions. Phys. Rev. A 1987, 35, 4839–4841. [Google Scholar] [CrossRef]
- Désesquelles, J.; Buchet-Poulizac, M.C.; Bernard, J.; Brédy, R.; Chen, L.; Denis, A.; Martin, S.; Berry, H.G. Collision spectroscopy of normal and displaced terms for boronlike O3+, F4+ and Ne5+ ions. Phys. Scr. 2001, T92, 290–293. [Google Scholar]
- Zouros, T.J.M.; Sulik, B.; Gulyás, L.; Orbán, A. Production of projectile 1s2s2p 4P states by transfer-loss in collisions of O5+ and F6+ ions with H2 and He targets. J. Phys. B At. Mol. Opt. Phys. 2006, 39, L45–L52. [Google Scholar] [CrossRef]
- Benis, E.P.; Zouros, T.J.M. Determination of the 1s2ℓ2ℓ’ state production ratios 4Po/2P, 2D/2P and 2P+/2P− from fast (1s2, 1s2s 3S) mixed- state He-like ion beams in collisions with H2 targets. J. Phys. B At. Mol. Opt. Phys. 2016, 49, 235202. [Google Scholar] [CrossRef]
- Miecznik, G.; Brage, T. J-dependent lifetimes of the 2s2p3p 4De and 2s2p3d 4Fo terms in the boron isoelectronic sequence. J. Phys. B At. Mol. Opt. Phys. 1995, 28, 4233–4247. [Google Scholar] [CrossRef]
- Johnson, B.M.; Jones, K.W.; Gregory, D.C.; Kruse, T.H.; Träbert, E. Beam-foil lifetimes of n = 3 levels in Fe XIII to Fe XVI; I. Experiment using position sensitive detection. Phys. Lett. A 1981, 86, 285–288. [Google Scholar] [CrossRef]
- Träbert, E.; Suleiman, J.; Cheng, S.; Berry, H.G.; Dunford, R.W.; Kanter, E.W.; Kurtz, C.; Livingston, A.E.; Kukla, K.W.; Serpa, F.G.; et al. Experimental transition probabilities of intercombination transitions in Mg-like and Al-like ions of bromine. Phys. Rev. A 1993, 47, 3805–3809. [Google Scholar] [CrossRef]
- Churilov, S.S.; Levashov, V.E. The 3p23d and 3s3d2 configurations in aluminium-like K VII-Ni XVI. Phys. Scr. 1993, 48, 425–435. [Google Scholar] [CrossRef]
- Träbert, E.; Wagner, C.; Heckmann, P.H.; Möller, G.; Brage, T. A beam-foil study of the 3s3p3d 4F levels in the Al-like ions of Ti, Fe and Ni. Phys. Scr. 1993, 48, 593–597. [Google Scholar]
- Träbert, E.; Hoffmann, J.; Krantz, C.; Wolf, A.; Ishikawa, Y.; Santana, J.A. Atomic lifetime measurements on forbidden transitions of Al-, Si-, P- and S-like ions at a heavy-ion storage ring. J. Phys. B At. Mol. Opt. Phys. 2009, 42, 025002. [Google Scholar] [CrossRef]
- Nemouchi, M.; Godefroid, M.R. Irreducible tensor form of the relativistic corrections to the M1 transition operator. L. Phys. B At. Mol. Opt. Phys. 2009, 42, 175002. [Google Scholar] [CrossRef]
- Schneider, D.; Bruch, R.; Shlyaptseva, A.; Brage, T.; Ridder, D. Auger decay of Na-like Si3+ (2p5 3ℓ3ℓ’) states formed in slow Si5+→ He and Ar ion atom collisions. Phys. Rev. A 1995, 51, 4652–4661. [Google Scholar] [CrossRef]
- Jupén, C.; Engström, L.; Hutton, R.; Träbert, E. Identification of the core-excited 2p5 3s3p 4D7/2–2p5 3s3d 4F9/2 transition in Na-like ions ranging from S VI to Cu XIX. J. Phys. B At. Mol. Phys 1988, 21, L347–L351. [Google Scholar] [CrossRef]
- Jupén, C.; Engström, L.; Hutton, R.; Reistad, N.; Westerlind, M. Analysis of core-excited n = 3 configurations in S VI, Cl VII, Ar VIII and Ti XII. Phys. Scr. 1990, 42, 44–50. [Google Scholar] [CrossRef]
- Cowan, R.D. The Theory of Atomic Structure and Spectra; University of California Press: Berkeley, CA, USA, 1981. [Google Scholar]
- Kramida, A. Cowan code: 50 years of growing impact on atomic physics. Atoms 2019, 7, 64. [Google Scholar] [CrossRef]
- Chen, M.H. Effects of relativity and configuration interaction on L-shell Auger and radiative decays of the doubly excited 3ℓ3ℓ’ states of sodiumlike ions. Phys. Rev. A 1989, 40, 2365–2372. [Google Scholar] [CrossRef]
- Møller, C.; Plesset, M.S. Note on an approximation treatment for many-electron systems. Phys. Rev. 1934, 46, 618–622. [Google Scholar] [CrossRef]
- Vilkas, M.J.; Ishikawa, Y. High-accuracy calculations of term energies and lifetimes of silicon-like ions with nuclear charges Z = 24–30. J. Phys. B At. Mol. Opt. Phys. 2004, 37, 1803–1816. [Google Scholar] [CrossRef]
- Vilkas, M.J.; Ishikawa, Y. Relativistic many-body perturbation calculations on extreme ultraviolet and soft-X-ray transition energies in siliconlike iron. Phys. Rev. A 2004, 69, 062503. [Google Scholar] [CrossRef]
- Vilkas, M.J. (University of Puerto Rico, San Juan, Puerto Rico, USA); Ishikawa, Y. (University of Puerto Rico, San Juan, Puerto Rico, USA). Personal communication, 2005.
- Delaunay, B. Heavy-ion stripping. Nucl. Instrum. Meth. 1977, 146, 101–113. [Google Scholar] [CrossRef]
- Shima, K.; Kuno, N.; Yamanouchi, M.; Tawara, H. Equilibrium charge fractions of ions of Z = 4–92 emerging from a carbon foil. At. Data Nucl. Data Tab. 1992, 51, 173–241. [Google Scholar] [CrossRef]
- Kramida, A.; Ralchenko, Y.; Reader, J.; NIST ASD Team. NIST Atomic Spectra Database (Version 5.7); National Institute of Standards and Technology: Gaithersburg, MD, USA, 2019. Available online: https://physics.nist.gov/asd (accessed on 10 October 2019).
- Kelly, R.L. Atomic and ionic spectrum lines below 2000 Angstroms. J. Phys. Chem. Ref. Data 1987, 16 (Suppl. 1), 1371–1678. [Google Scholar]
- Del Zanna, G.; Dere, K.P.; Young, P.R.; Landi, E.; Mason, H.E. CHIANTI—An atomic database for emission lines. Astron. Astrophys. 2015, 582, A56. [Google Scholar] [CrossRef]
- Träbert, E.; Beiersdorfer, P.; Lepson, J.K.; Reinke, M.L.; Rice, J.E. EUV spectra and line ratios of multiply ionized calcium and argon atoms in a laboratory plasma. Astrophys. J. 2018, 865, 148. [Google Scholar] [CrossRef]
- Beiersdorfer, P.; Lisse, C.M.; Olson, R.E.; Brown, G.V.; Chen, H. X-ray velocimetry of solar wind ion impact on comets. Astrophys. J. 2001, 549, L147–L150. [Google Scholar] [CrossRef]
- Beiersdorfer, P.; Boyce, K.R.; Brown, G.V.; Chen, H.; Kahn, S.M.; Kelley, R.L.; May, M.; Olson, R.E.; Porter, F.S.; Stahle, C.K.; et al. Laboratory simulation of charge exchange-produced X-ray emission from comets. Science 2003, 300, 1558–1559. [Google Scholar] [CrossRef] [PubMed]
- Beiersdorfer, P.; Schweikhard, L.; Liebisch, P.; Brown, G.V. X-ray signature of charge exchange in the spectra of L-shell iron ions. Astrophys. J. 2008, 672, 726–732. [Google Scholar] [CrossRef]
- Frankel, M.; Beiersdorfer, P.; Brown, G.V.; Gu, M.F.; Kelley, R.L.; Kilbourne, C.A.; Porter, F.S. X-ray signature of charge exchange in L-shell sulfur ions. Astrophys. J. 2009, 702, 171–177. [Google Scholar] [CrossRef]
- Leutenegger, M.A.; Betancourt-Martinez, G.L.; Beiersdorfer, P.; Brown, G.V.; Kelley, R.L.; Kilbourne, C.A.; Porter, F.S. Charge exchange measurements with an X-ray calorimeter at an electron beam ion trap. Phys. Scr. 2013, T156, 014006. [Google Scholar] [CrossRef]
- Träbert, E.; Beiersdorfer, P.; Pinnington, E.H.; Utter, S.B.; Vilkas, M.J.; Ishikawa, Y. Experiment and theory in interplay on high-Z few-electron ion spectra from foil-excited ion beams and electron beam ion traps. J. Phys. Conf. Ser. 2007, 58, 93–96. [Google Scholar]
- Träbert, E. Extreme ultraviolet spectra of highly charged Fe ions in the laboratory versus the excitation of spectra in astrophysical environments. Can. J. Phys. 2017, 95, 777–782. [Google Scholar] [CrossRef]
- Beiersdorfer, P.; Schweikhard, L.; Crespo López-Urrutia, J.; Widmann, K. The magnetic trapping mode of an electron beam ion trap: New opportunities for highly charged ion research. Rev. Sci. Instrum. 1996, 67, 3818–3826. [Google Scholar] [CrossRef]
| Z | Experiment | HF a | Fit a | MR-MP b |
|---|---|---|---|---|
| 17 | 53.270 ± 0.010 a | 52.75 | 53.267 | 53.307 |
| 18 | 47.134 ± 0.005 a | 46.71 | 47.122 | 47.213 |
| 19 | 42.29 ± 0.01 c | 41.97 | 42.305 | 42.391 |
| 20 | 38.420 ± 0.005 c | 38.13 | 38.415 | 38.473 |
| 21 | 35.20 ± 0.01 c | 34.96 | 35.198 | 35.252 |
| 22 | 32.487 ± 0.002 a | 32.28 | 32.489 | 32.488 |
| 23 | 30.17 ± 0.01 c | 29.98 | 30.169 | 30.179 |
| 24 | 28.167 ± 0.005 a | 27.99 | 28.160 | 28.170 |
| 25 | 26.40 ± 0.01 c | 26.25 | 26.398 | 26.407 |
| 26 | 24.836 ± 0.005 a | 24.71 | 24.839 | 24.848 |
| 27 | 23.44 ± 0.01 c | 23.33 | 23.448 | 23.458 |
| 28 | 22.200 ± 0.010 a | 22.09 | 22.198 | 22.209 |
| 29 | 21.070 ± 0.005 a | 20.97 | 21.068 | 21.079 |
| 30 | - | 19.95 | 20.039 | 20.051 |
© 2019 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Träbert, E. The Allure of High Total Angular Momentum Levels in Multiply-Excited Ions. Atoms 2019, 7, 103. https://doi.org/10.3390/atoms7040103
Träbert E. The Allure of High Total Angular Momentum Levels in Multiply-Excited Ions. Atoms. 2019; 7(4):103. https://doi.org/10.3390/atoms7040103
Chicago/Turabian StyleTräbert, Elmar. 2019. "The Allure of High Total Angular Momentum Levels in Multiply-Excited Ions" Atoms 7, no. 4: 103. https://doi.org/10.3390/atoms7040103
APA StyleTräbert, E. (2019). The Allure of High Total Angular Momentum Levels in Multiply-Excited Ions. Atoms, 7(4), 103. https://doi.org/10.3390/atoms7040103





