Critical Stability of the Negatively Charged Positronium-Like Ions with Yukawa Potentials and Varying Z
Abstract
1. Introduction
2. Calculations
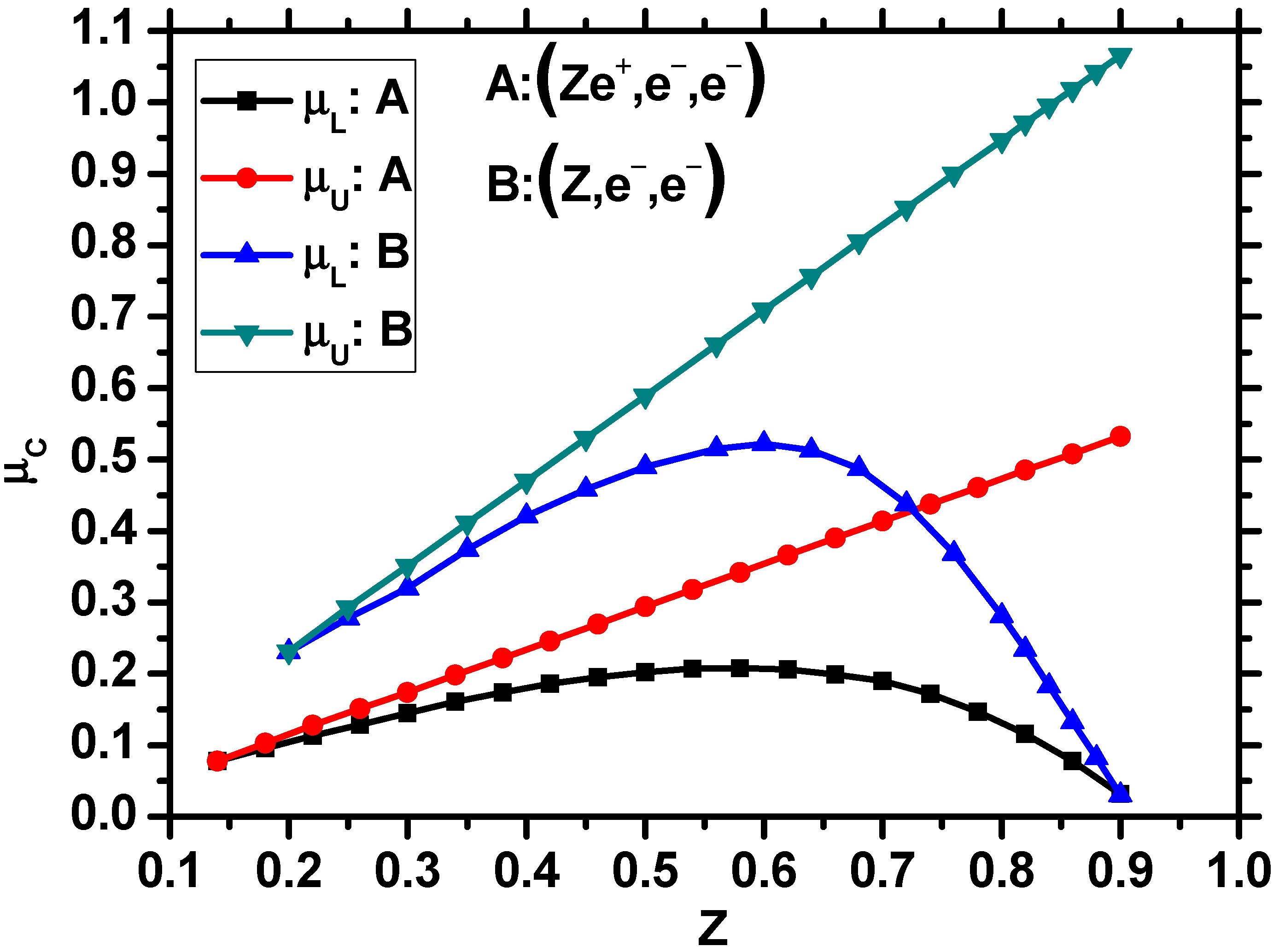
3. Results and Discussion
4. Conclusions
Supplementary Materials
Author Contributions
Funding
Conflicts of Interest
References
- Kais, S.; Shi, Q. Quantum criticality and stability of three-body Coulomb systems. Phys. Rev. A 2000, 62, 060502. [Google Scholar] [CrossRef]
- Stillinger, F.H. Ground-state energy of two-electron atoms. J. Chem. Phys. 1966, 45, 3623. [Google Scholar] [CrossRef]
- Stillinger, F.H.; Stillinger, D.K. Nonlinear variational study of perturbation theory for atoms and ions. Phys. Rev. A 1974, 10, 1109. [Google Scholar] [CrossRef]
- Reinhardt, W.P. Dilatation analyticity and the radius of convergence of the 1/Z perturbation expansion: Comment on a conjecture of Stillinger. Phys. Rev. A 1977, 15, 802. [Google Scholar] [CrossRef]
- Baker, J.D.; Freund, D.E.; Hill, R.N.; Morgan, J.D. Radius of convergence and analytic behavior of the 1/Z expansion. Phys. Rev. A 1990, 41, 1247. [Google Scholar] [CrossRef]
- Ivanov, I.A. References Radius of convergence of the 1/Z expansion for the ground state of a two-electron atom. Phys. Rev. A 1995, 51, 1080. [Google Scholar] [CrossRef] [PubMed]
- Armour, E.A.G.; Richard, J.-M.; Varga, K. Stability of few-charge systems in quantum mechanics. Phys. Rep. 2005, 413, 1–90. [Google Scholar] [CrossRef][Green Version]
- Zamastil, J.; Cizek, J.; Skala, L.; Simanek, M. Convergence study of the 1/Z expansion for the energy levels of two-electron atoms. Phys. Rev. A 2010, 81, 032118. [Google Scholar] [CrossRef]
- Guevara, N.L.; Turbiner, A.V. Heliumlike and lithiumlike ionic sequences: Critical charges. Phys. Rev. A 2011, 84, 064501. [Google Scholar] [CrossRef]
- Estienne, C.S.; Busuttil, M.; Moini, A.; Drake, G.W.F. Critical nuclear charge for two-electron atoms. Phys. Rev. Lett. 2014, 112, 173001. [Google Scholar] [CrossRef] [PubMed]
- Moini, A. Critical Nuclear Charge of Quantum Mechanical Three-Body Problem. Electronic Master’s Thesis, University of Windsor, Windsor, ON, Canada, 2014. [Google Scholar]
- Pilón, H.O.; Turbiner, A.V. Nuclear critical charge for two-electron ion in Lagrange mesh method. Phys. Lett. A 2015, 379, 688. [Google Scholar] [CrossRef]
- Sen, K.D.; Katriel, J.; Montgomery, H.E., Jr. A comparative study of two-electron systems with screened Coulomb potentials. Ann. Phys. 2018, 397, 192. [Google Scholar] [CrossRef]
- Montgomery, H.E., Jr.; Sen, K.D.; Katriel, J. Critical screening on one- and two-electron Yukawa atoms. Phys. Rev. A 2018, 97, 022503. [Google Scholar] [CrossRef]
- Kar, S.; Wang, Y.-S.; Ho, Y.K. Critical stability for the two-electron ions with Yukawa potentials and Varying Z. Phys. Rev. A 2019, 99, 042514. [Google Scholar] [CrossRef]
- Yukawa, H. On the interaction of elementary particles. Proc. Phys. Math. Soc. Jpn. 1935, 17, 48–57. [Google Scholar]
- Debye, P.; Hückel, E. The theory of electrolytes. I. Lowering of freezing point and related phenomena. Phys. Z. 1923, 24, 185–206. [Google Scholar]
- Mills, A.P., Jr. Observation of the positronium negative ion. Phys. Rev. Lett. 1981, 46, 717. [Google Scholar] [CrossRef]
- Ho, Y.K. Atomic resonances involving positrons. Nucl. Instr. Meth. Phys. Res. B 2008, 266, 516. [Google Scholar] [CrossRef]
- Nagashima, Y. Experiments on positronium negative ions. Phys. Rept. 2014, 545, 95. [Google Scholar] [CrossRef]
- Kar, S.; Ho, Y.K. Excitons and the positronium negative ion: Comparison in spectroscopic properties. In Excitons; Pyshkin, S.L., Ed.; INTECH: London, UK, 2018; Chapter 5; pp. 69–90. [Google Scholar]
- Kar, S.; Ho, Y.K. Two-photon double-electron D-wave resonant excitation in the positronium negative ion. Euro. Phys. J. D 2018, 72, 193. [Google Scholar] [CrossRef]
- Michishio, K.; Kanai, T.; Kuma, S.; Azuma, T.; Wada, K.; Mochizuki, I.; Hyodo, T.; Yagishita, A.; Nagashima, Y. Observation of a shape resonance of the positronium negative ion. Nat. Commun. 2016, 7, 11060. [Google Scholar] [CrossRef]
- Cassidy, D.B. Experimental progress in positronium laser physics. Eur. Phys. J. D 2018, 72, 53. [Google Scholar] [CrossRef]
- Kar, S.; Wang, Y.-S.; Wang, Y.; Ho, Y.K. Polarizability of negatively charged helium-like ions interacting with Coulomb and screened Coulomb potentials. Int. J. Quantum Chem. 2018, 118, e25515. [Google Scholar] [CrossRef]
- Sil, A.N.; Canuto, S.; Mukherjee, P.K. Spectroscopy of Confined Atomic Systems: Effect of Plasma. Adv. Quantum. Chem. 2009, 58, 115. [Google Scholar]
- Kar, S.; Ho, Y.K. Effect of screened Coulomb potentials on the resonance states of two-electron highly stripped atoms using the stabilization method. J. Phys. B 2009, 42, 044007. [Google Scholar] [CrossRef]
- Janev, R.K.; Zhang, S.; Wang, J. Review of quantum collision dynamics in Debye plasmas. Matter Radiat. Extrem. 2016, 1, 23. [Google Scholar] [CrossRef]
- Kar, S.; Wang, Y.S.; Jiang, Z.; Wang, Y.; Ho, Y.K. Potential-screening on atomic wavelengths. Chin. J. Phys. 2018, 56, 3085. [Google Scholar] [CrossRef]
- Ho, Y.K. The Combined Screened Coulomb and Varying Charge Effects on Doubly Excited Resonance States in the Positronium Negative Ion. JPS Conf. Proc. 2017, 18, 011027. [Google Scholar]
- Katriel, J.; Montgomery, H.E., Jr.; Sen, K.D. Hund’s rule in the (1s2s )1,3S states of the two-electron Debye atom. Phys. Plasmas 2018, 25, 092111. [Google Scholar] [CrossRef]
- Dubau, J.; Ivanov, I.A. Numerical calculation of the complex energy of the 1s2 resonance of a two-electron atom with nuclear charge below the threshold value. J. Phys. B 1998, 31, 3335–3344. [Google Scholar] [CrossRef]
- Kar, S.; Ho, Y.K. Borromean windows for H2+ with screened Coulomb potentials. Phys. Rev. A 2012, 506, 282. [Google Scholar] [CrossRef]
- Dutta, S.; Saha, J.K.; Bhattacharyya, S.; Mukherjee, P.K.; Mukherjee, T.K. Exotic systems under screened Coulomb interactions: A study on Borromean windows. Phys. Scr. 2014, 89, 015401. [Google Scholar] [CrossRef]
- Naidon, P.; Endo, S. Efimov physics: A review. Rep. Prog. Phys. 2017, 80, 056001. [Google Scholar] [CrossRef]
- Kar, S.; Ho, Y.K. Positron annihilation in the dense-plasma-embedded Ps−. Chem. Phys. Lett. 2006, 424, 403. [Google Scholar] [CrossRef]
- Efimov, V. Energy levels arising from resonant two-body forces in a three-body system. Phys. Lett. B 1970, 33, 563. [Google Scholar] [CrossRef]
- Efimov, V. Weakly-bound states of three-resonantly interacting particles. Sov. J. Nucl. Phys. 1970, 12, 589. [Google Scholar]
- Ho, Y.K. The method of complex coordinate rotation and its applications to atomic collision processes. Phys. Rep. 1983, 99, 1. [Google Scholar] [CrossRef]
- Mann, R. An Introduction to Particle Physics and the Standard Model; CRC Press: Boca Raton, FL, USA, 2009; 614p. [Google Scholar]
- De-Picciotto, R.; Reznikov, M.; Heiblum, M.; Umansky, V. Direct observation of a fractional charge. Nature 1997, 389, 182. [Google Scholar] [CrossRef]
- Saminadayar, L.; Glattli, D.C.; Jin, Y.; Eitenne, B. Observation of the e/3 fractionally charged Laughlin quasiparticle. Phys. Rev. Lett. 1997, 79, 2526. [Google Scholar] [CrossRef]
- Martin, J.; Ilani, S.; Verdene, B.; Smet, J.; Umansky, V.; Mahalu, D.; Schuh, D.; Abstreiter, G.; Yacoby, A. Localization of fractionally charged quasi-particles. Science 2004, 305, 980. [Google Scholar] [CrossRef]
- Laughlin, R.B. Anomalous quantum Hall effect: An incompressible quantum fluid with fractionally charged excitations. Phys. Rev. Lett. 1983, 50, 1395. [Google Scholar] [CrossRef]
- Tsui, D.C.; Stormer, H.L.; Gossard, A.C. Two-dimensional magnetotransport in the extreme quantum limit. Phys. Rev. Lett. 1983, 48, 1559. [Google Scholar] [CrossRef]
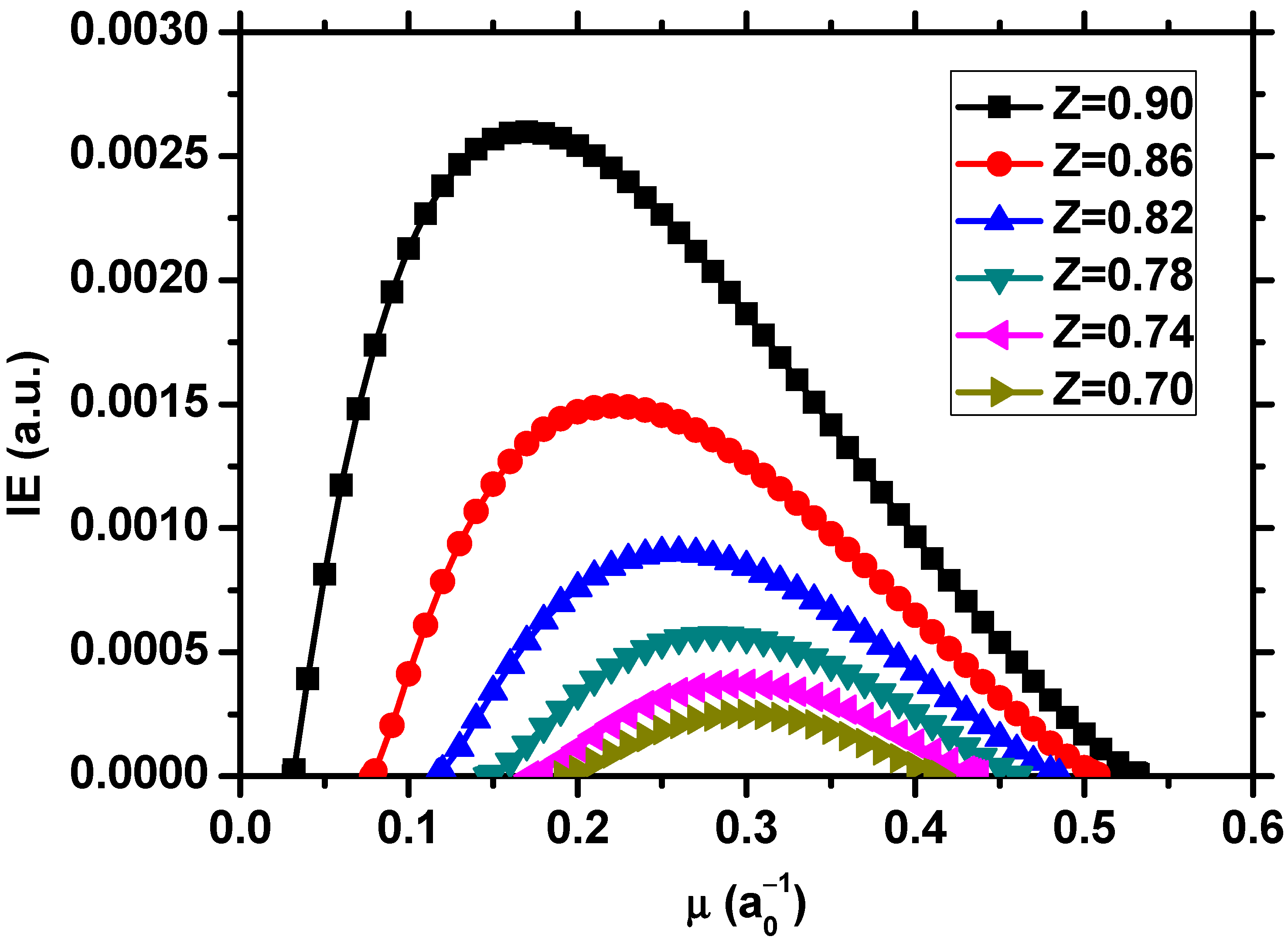
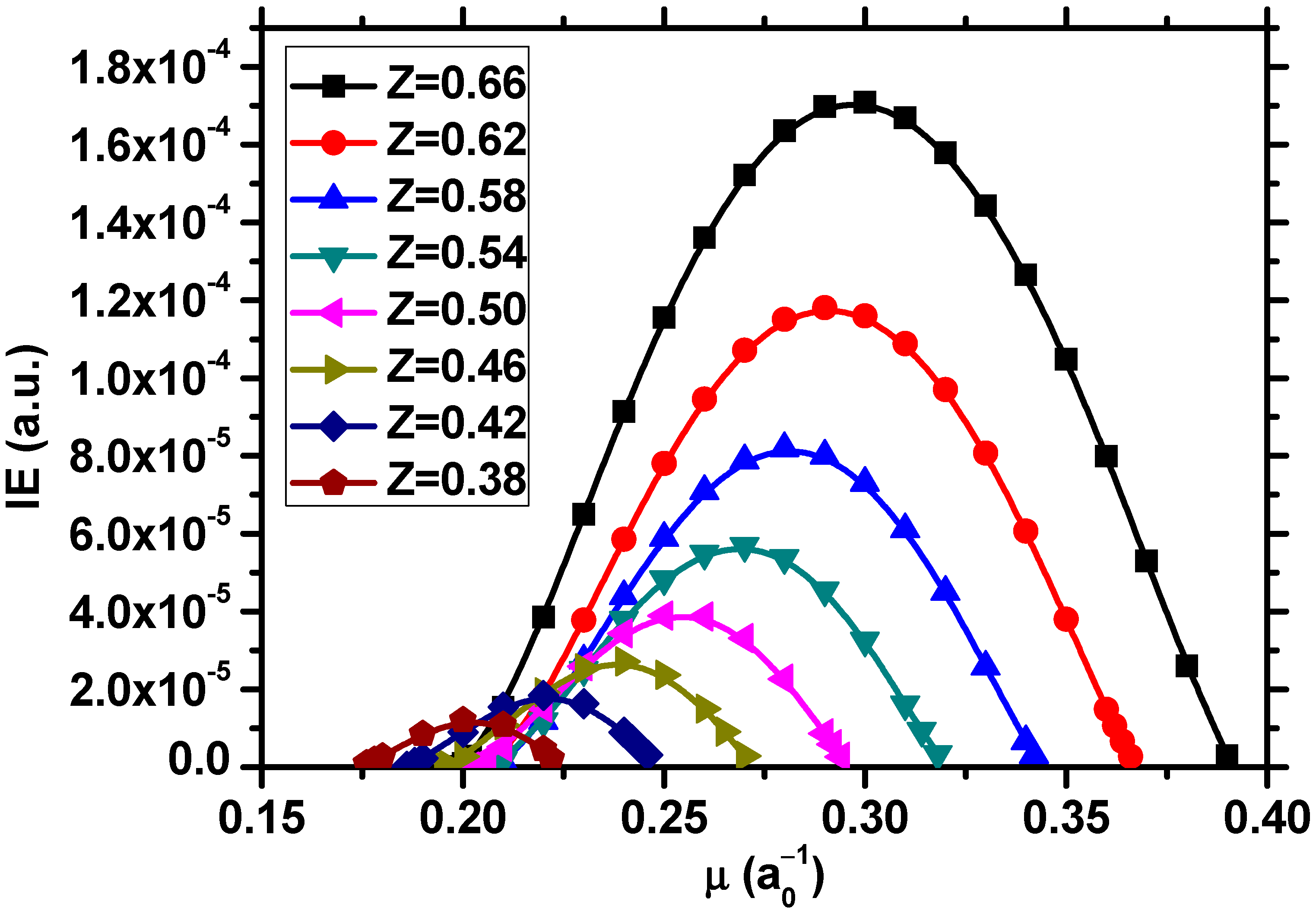
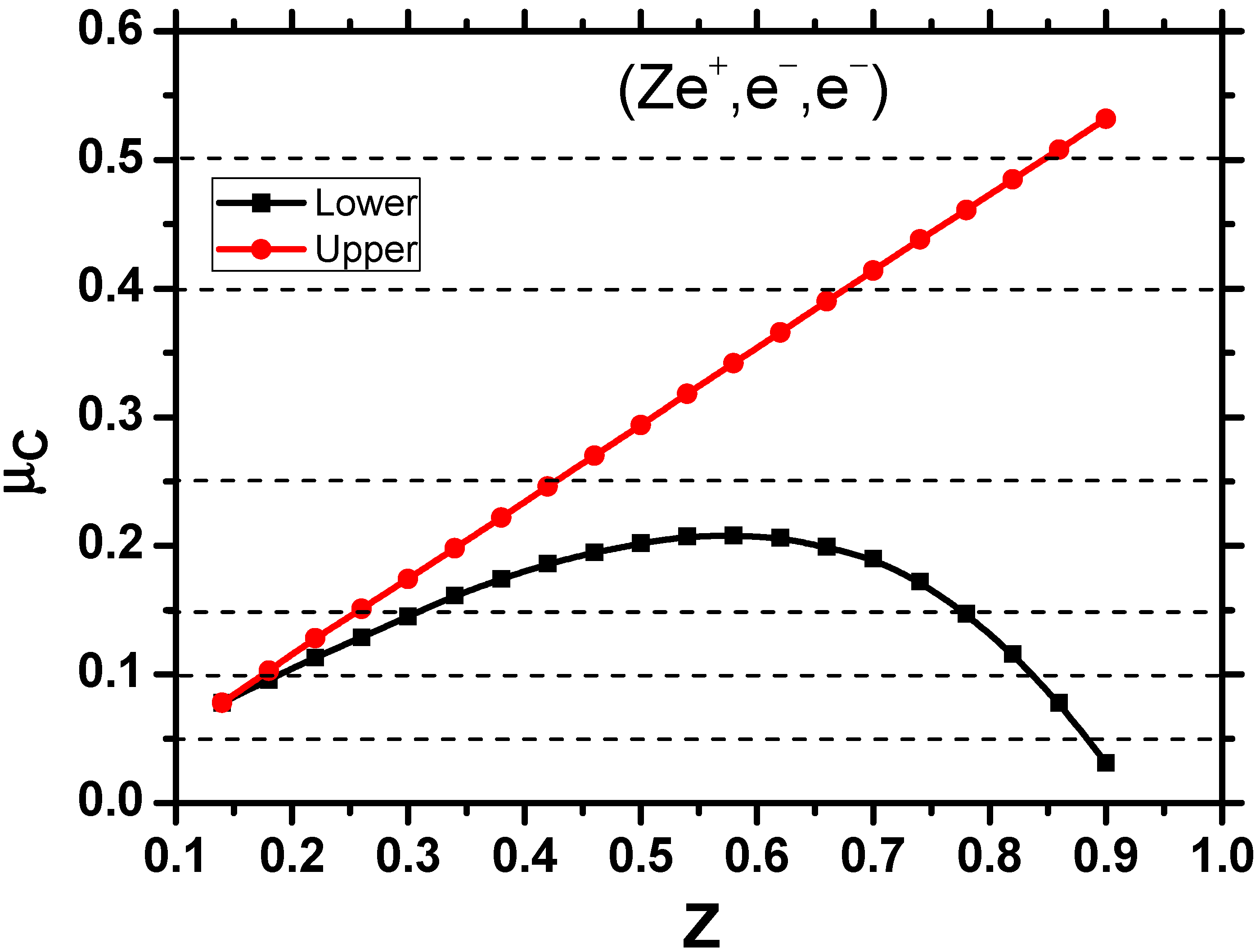
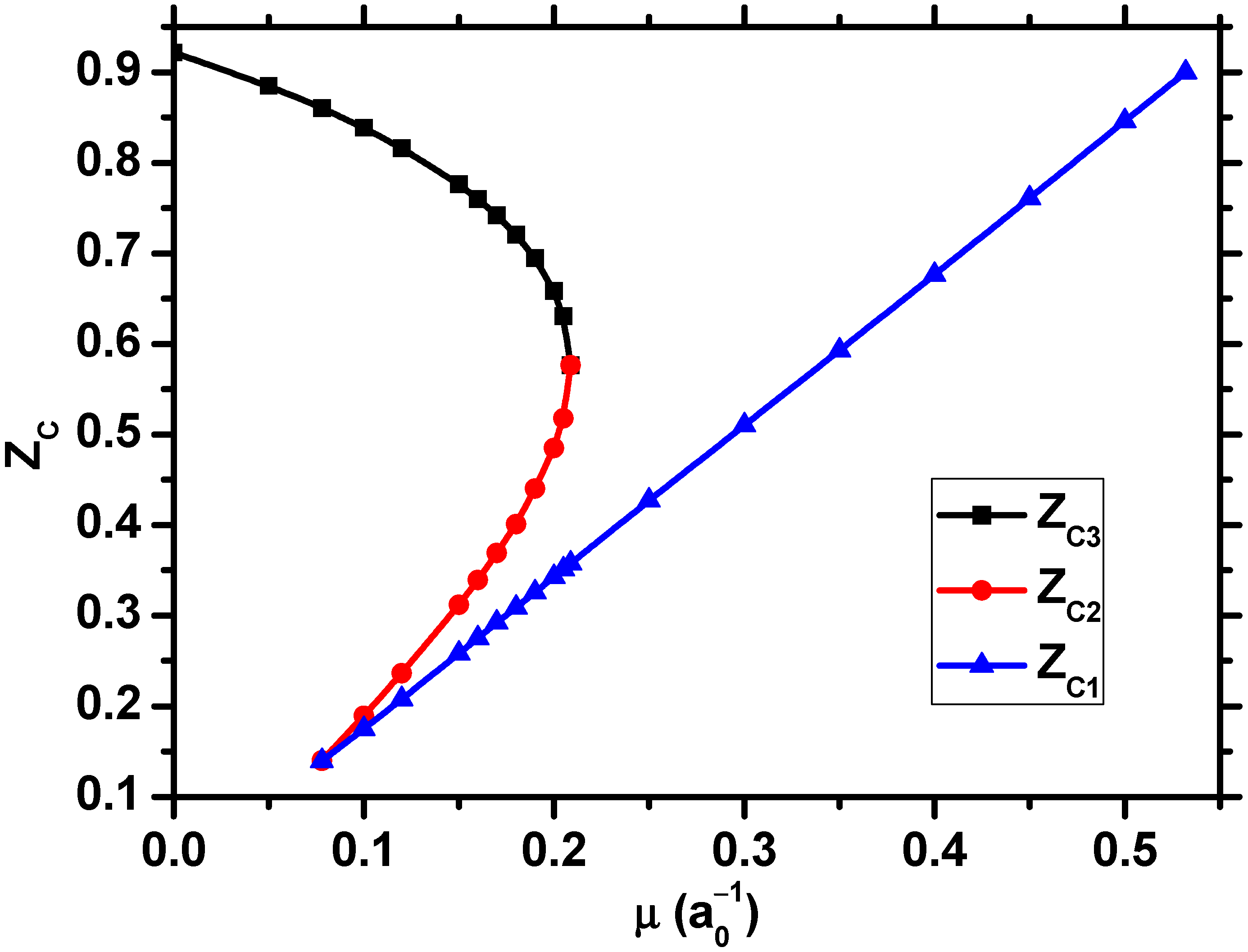
| 1.0 | −0.2620050702325 a | −0.2500000000000 |
| 0.98 | −0.248636029841 | −0.2401000000000 |
| 0.95 | −0.229443708915 | −0.2256250000000 |
| 0.93 | −0.21726201089 | −0.2162250000000 |
| 0.921803 | −0.21243026065 | −0.2124301927023 |
| 0.92180250 | −0.21242996923 | −0.2124299622516 |
| 0.92180245 | −0.21242994009 | −0.2124299392065 |
| 0.921802445 | −0.21242993719 | −0.2124299369020 |
| 0.921802444 | −0.21242993659 | −0.2124299364411 |
| 0.921802443 | −0.21242993600 | −0.2124299359802 |
| 0.9218024426 | −0.21242993576 | −0.2124299357958 |
| 0.9218024425 | −0.21242993571 | −0.2124299357497 |
| 0.9218024424 | −0.21242993565 | −0.2124299357037 |
| 0.921802442 | −0.21242993543 | −0.2124299355193 |
| 0.92180244 | −0.21242993424 | −0.2124299345975 |
| Z | |||||||
|---|---|---|---|---|---|---|---|
| 0.14 | 0.078 | 0.078 | 0.078 | 0.00 | 0.921802443 | ||
| 0.18 | 0.096 | 0.103 | 0.10 | 0.05 | 0.88479 | ||
| 0.22 | 0.113 | 0.128 | 0.12 | 0.07798 | 0.86032 | 0.14001 | |
| 0.26 | 0.129 | 0.151 | 0.14 | 0.07815 | 0.86016 | 0.14040 | 0.14001 |
| 0.30 | 0.145 | 0.174 | 0.16 | 0.10 | 0.83862 | 0.18970 | 0.17500 |
| 0.34 | 0.161 | 0.198 | 0.18 | 0.12 | 0.81638 | 0.23648 | 0.20790 |
| 0.38 | 0.174 | 0.222 | 0.20 | 0.15 | 0.77627 | 0.31192 | 0.25823 |
| 0.42 | 0.186 | 0.246 | 0.22 | 0.16 | 0.76018 | 0.33942 | 0.27515 |
| 0.46 | 0.195 | 0.27 | 0.24 | 0.17 | 0.74198 | 0.36885 | 0.29264 |
| 0.50 | 0.202 | 0.294 | 0.25 | 0.18 | 0.72076 | 0.40109 | 0.30905 |
| 0.54 | 0.207 | 0.318 | 0.27 | 0.19 | 0.69466 | 0.44036 | 0.32601 |
| 0.58 | 0.208 | 0.342 | 0.28 | 0.20 | 0.65864 | 0.48474 | 0.34294 |
| 0.62 | 0.206 | 0.366 | 0.29 | 0.205 | 0.63067 | 0.51803 | 0.35140 |
| 0.66 | 0.199 | 0.39 | 0.30 | 0.20865 | 0.57632 | 0.57632 | 0.35757 |
| 0.70 | 0.190 | 0.414 | 0.30 | 0.25 | 0.42707 | ||
| 0.74 | 0.172 | 0.438 | 0.29 | 0.30 | 0.51025 | ||
| 0.78 | 0.147 | 0.461 | 0.28 | 0.35 | 0.59307 | ||
| 0.82 | 0.116 | 0.485 | 0.26 | 0.40 | 0.67642 | ||
| 0.86 | 0.078 | 0.508 | 0.22 | 0.45 | 0.76090 | ||
| 0.90 | 0.0313 | 0.532 | 0.17 | 0.50 | 0.84609 | ||
| 0.53198 | 0.89999 | ||||||
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Kar, S.; Wang, Y.-S.; Wang, Y.; Ho, Y.K. Critical Stability of the Negatively Charged Positronium-Like Ions with Yukawa Potentials and Varying Z. Atoms 2019, 7, 53. https://doi.org/10.3390/atoms7020053
Kar S, Wang Y-S, Wang Y, Ho YK. Critical Stability of the Negatively Charged Positronium-Like Ions with Yukawa Potentials and Varying Z. Atoms. 2019; 7(2):53. https://doi.org/10.3390/atoms7020053
Chicago/Turabian StyleKar, Sabyasachi, Yu-Shu Wang, Yang Wang, and Yew Kam Ho. 2019. "Critical Stability of the Negatively Charged Positronium-Like Ions with Yukawa Potentials and Varying Z" Atoms 7, no. 2: 53. https://doi.org/10.3390/atoms7020053
APA StyleKar, S., Wang, Y.-S., Wang, Y., & Ho, Y. K. (2019). Critical Stability of the Negatively Charged Positronium-Like Ions with Yukawa Potentials and Varying Z. Atoms, 7(2), 53. https://doi.org/10.3390/atoms7020053







