Degree-Distance Based Topological Indices of Crystal Cubic Carbon Structure

Abstract

Chemical graph theory comprehends the basic properties of an atomic graph. The sub-atomic diagrams are the graphs that are comprised of particles called vertices and the covalent bond between them are called edges. The eccentricity ${ϵ}_u$ of vertex u in an associated graph G, is the separation among u and a vertex farthermost from u. In this article, we consider the precious stone structure of cubic carbon and registered Eccentric-connectivity index $\xi \left(G\right)$, Eccentric connectivity polynomial $ECP(G,x)$ and Connective Eccentric index $C^{\xi }\left(G\right)$ of gem structure of cubic carbon for n-levels.

1. Introduction

A branch of scientific chemistry is Chemical graph hypothesis, which relates to the nontrivial utilizations of graph hypothesis for taking care of the atomic issues. Its pioneers are Alexandru Balaban [1], Ante Graovac [2], Ivan Gutman [3], Milan Randić [4] and Nenad Trinajstić [5]. Chemical graph theory utilizes mathematical invariants to limit the structure of a particle into a solitary number which signifies the energy of molecule, structural sections, sub-atomic stretching and electronic structures. These graph theoretic invariants are utilized to connect with physical perceptions ascertained by experiments. In [6], chemical graph hypothesis ought to be seen not just as equivalent to different branches of theoretical chemistry but also as corresponding and essential for better comprehension of the idea of the compound structure.

There are sure synthetic intensifies that are valuable for the survival of living things. Carbon, oxygen, hydrogen and nitrogen are the primary components that aide in the creation of cells in the living things. Carbon is a fundamental component for human life. It is valuable in the development of proteins, starches and nucleic acids. It is imperative for the development of plants as carbon dioxide. The carbon particles can bond together in different ways, called allotropes of carbon. The notable structures are graphite and precious stone. As of late, numerous new structures have been found including nanotubes, buckminsterfullerene and sheets, precious stone cubic structure, and so on. The utilizations of various allotropes of carbon are talked about in detail in [7,8,9].

A molecular graph is a straight forward graph speaking to the carbon atom skeleton of a organic molecule. In the molecular graph, the vertices speak to the carbon molecules and the edges speak to the carbon-carbon bonds.

Consider $G(V,E)$ as a fundamental basic graph, where V and E address the course of action of vertices and the game plan of edges. The amount of parts in V is known as the request of the diagram G and the amount of segments in E is known as the extent of the chart G. The amount of vertices neighboring the vertex $v\in V$ is known as the level of v and is connoted as $d_v$. On the off chance that no vertices in $u–v$ walk are reiterated, then it is called $u–v$ way in chart G. The length of a way is the amount of edges in it. The separation $d(u,v)$ from vertex u to vertex v is the length of a most constrained $u–v$ way in a chart G where $u,v\in G.$ In an associated diagram $G$, the flightiness ${ϵ}_u$ of vertex u is the separation among u and a vertex most removed from u in $G$.

A graph can be seen by a numeric number, a polynomial, a gathering of numbers or a system. A topological index (molecular structure descriptor) is a numerical regard related with manufactured constitution for relationship of substance structure with various physical properties, compound reactivity or natural activity. There are some noteworthy classes of topological files, for instance, separate-based topological lists, flightiness-based topological records, degree-based topological lists and tallying related polynomials and lists of diagrams.

The primary topological record is the Wiener list which was proposed in 1947 when Harold wiener [10] was taking a shot at the breaking point of paraffin. It was the main topological record which relied on the idea of separation between two vertices in a chart. Wiener considered it the way number. In any case, after that it was renamed as Wiener file and it is signified by W. The hypothesis of topological files began from the Wiener record. Wiener portrayed the way number as the total of the quantity of bonds between all combinations of particles [10], and is defined as pursues:

$$W\left(G\right)=\frac{1}{2}\sum _{(u,v)}d(u,v),$$

where $(u,v)$ is any discretionary match of vertices in G and $d(u,v)$ is $u–v$ the length of most limited way among u and v. The Eccentric-connectivity index $\xi \left(G\right)$ which was proposed by Sharma, Goswami and Madan characterized as [11]:

$$\xi \left(G\right)=\sum _{u\in V\left(G\right)}{d}_u{ϵ}_u,$$

(1)

Alaeiyan, Mojarad and Asadpour define the Eccentric connectivity polynomial of a graph G as [12]:

$$ECP(G,x)=\sum _{u\in V\left(G\right)}{d}_u{x}^{{ϵ}_u},$$

(2)

where value of x is greater than 1. The relationship between eccentric connectivity polynomial and eccentric-connectivity index is given by

$$ECP(G,x)=\xi (G,1),$$

(3)

where $\xi (G,1)$ is the principal subsidiary of $ECP(G,x)$ [13]. Another essential Eccentricity based topological record is Connective Eccentric index $C^{\xi }\left(G\right)$ which was proposed by Gupta et al. [14]. The Connective Eccentric index is characterized as:

$$C^{\xi }=\sum _{u\in V\left(G\right)}\frac{d_u}{{ϵ}_u},$$

(4)

For more information and properties of Eccentricity based topological index, see [15,16,17,18,19,20,21,22].

2. Methods

To compute our results, we utilized an approach for combinatorial enrolling, a vertex portion strategy, an edge allocate, outline hypothetical instruments, consistent structures, a degree-counting procedure, and a degrees of neighbors framework. Additionally, we used Matlab for intelligent estimations and attestations. We also utilized Maple for plotting numerical results.

3. Eccentric Index of Crystal Structure of Cubic Carbon

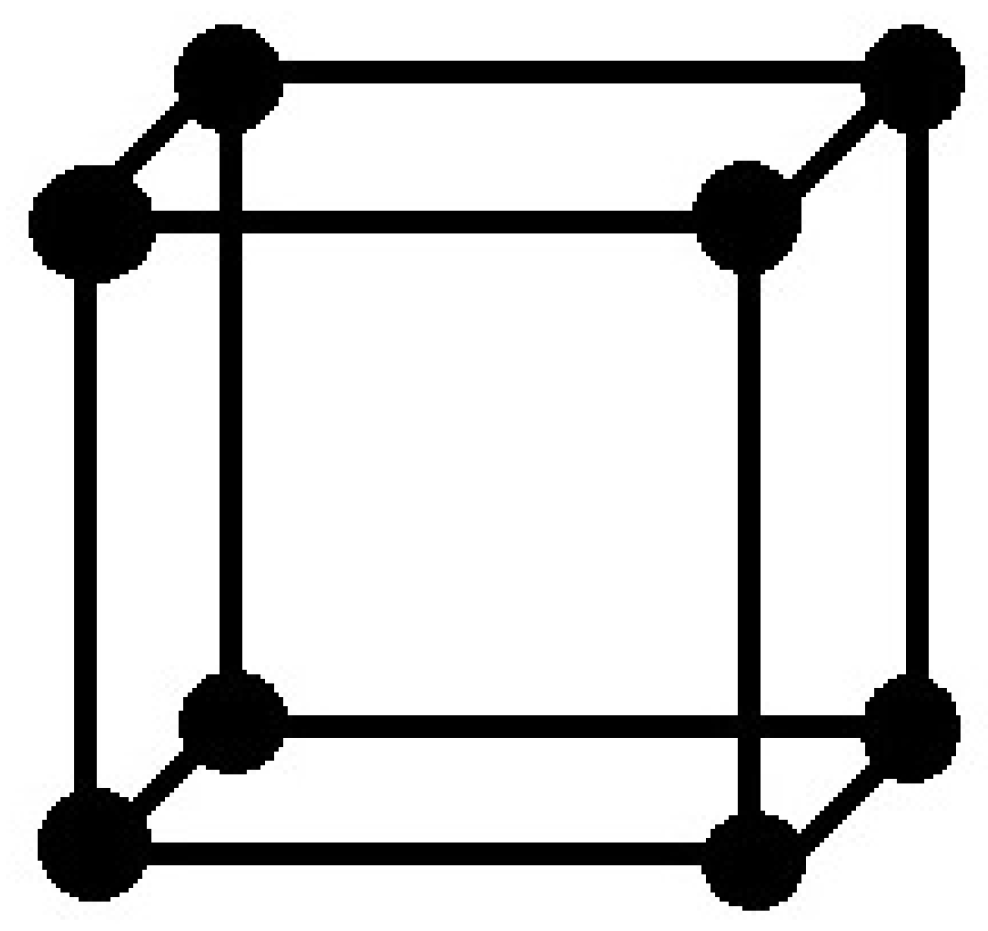
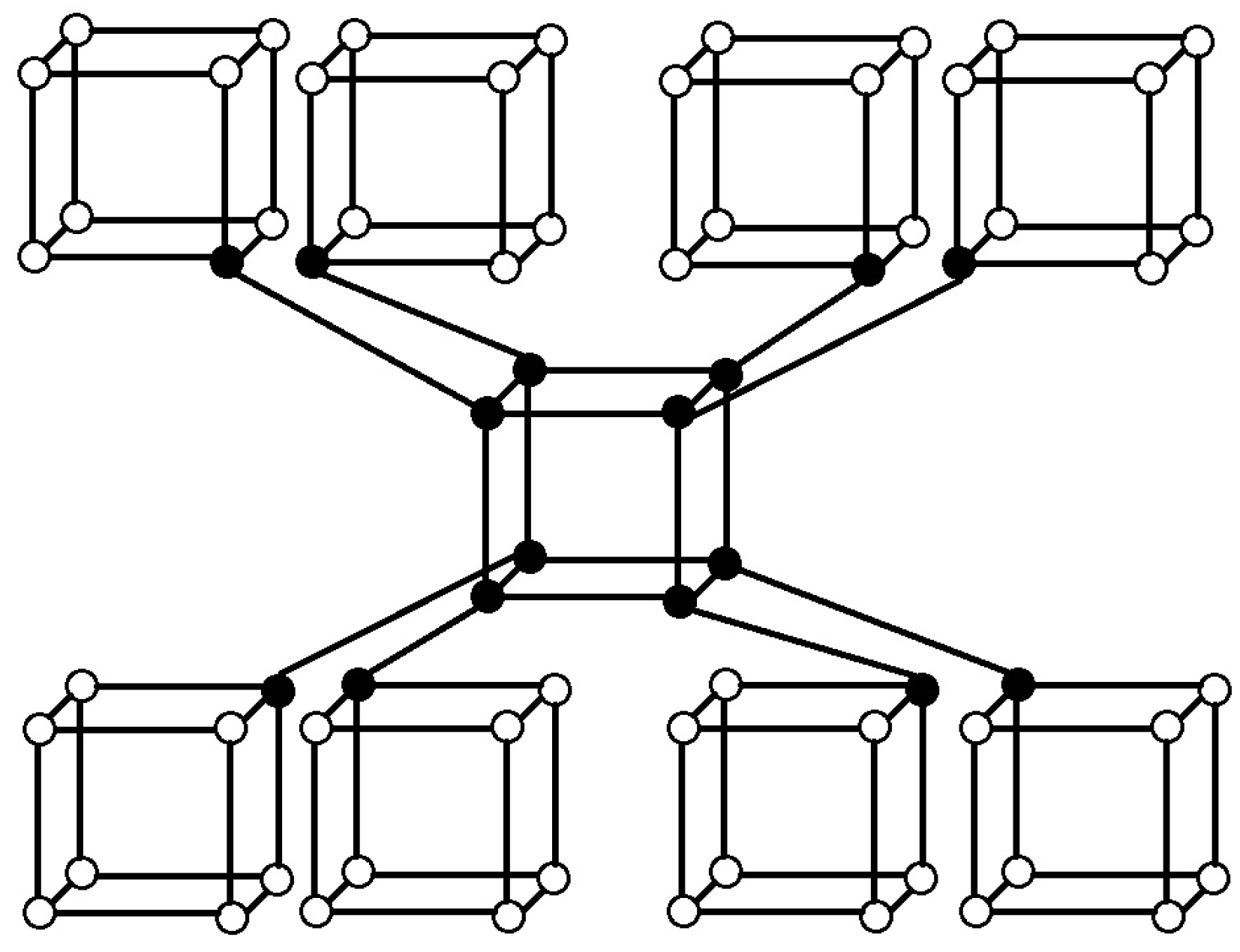
The structure of precious stone cubic carbon (or gem structure of cubic carbon ) is comprised of 3D squares and was talked about in [23]. The atomic chart of precious stone cubic carbon $CCC\left(n\right)$ for the first level is portrayed in Figure 1. For second level, new 3D shapes are joined at each end vertex of degree 3 of first level. The second level of $CCC\left(n\right)$ is portrayed in Figure 2. Additionally, this method is rehashed to get the following level et cetera. The cardinality of vertices and edges in $CCC\left(n\right)$ are given beneath separately.

$$\left|V\left(CCC\left(n\right)\right)\right|=2\left\{24\sum _{r=3}^n{(2^3-1)}^{r-3}+31{(2^3-1)}^{n-2}+2\sum _{r=0}^{n-2}{(2^3-1)}^r+3\right\}.$$

(5)

$$\left|E\left(CCC\left(n\right)\right)\right|=4\left\{24\sum _{r=3}^n{(2^3-1)}^{r-3}+24{(2^3-1)}^{n-2}+2\sum _{r=0}^{n-2}{(2^3-1)}^r+3\right\}.$$

(6)

Let $Q_k$ be the set of all cubic free vertices in $CCC\left(k\right)$ at the k-th level with $k\ge 2$, where we say that a vertex is cubic free if its degree is 3 at the k-th level. Let $v\in Q_k,$ be an arbitrary element, in $(k+1)$-th level, we partition the new coming vertices in four sets. The number of new vertices at every $(k+1)$-th level is $448{(2^3-1)}^{k-3}$. The partition of these vertices is given as follows:

$S_1^k$ is the set of vertices at distance 1 from any $v\in Q_k$ with number of such vertices is $56{(2^3-1)}^{k-3}$, $S_2^k$ is the set of vertices at distance 2 from v with cardinality $|S_2^k|=168{(2^3-1)}^{k-3}$, $S_3^k$ is the set of vertices at distance 3 from v with cardinality $|S_3^k|=168{(2^3-1)}^{k-3}$ and $S_4^k$ is the set of vertices at distance 4 from v with cardinality $|S_4^k|=56{(2^3-1)}^{k-3}$. In addition, we denote another set as $S^k$, which is the set of vertices of $ccc\left(1\right)$ that is the initial vertices in each k-th level, so cardinality $|S^k|=8$. This partition is also described in

Table 1. Vertex partition of new coming vertices at $(k+1)$-th level.

Set	Number of Vertices	Distance from Arbitrary $\mathit{v}\in {\mathit{Q}}_{\mathit{k}}$
$S_1$	$56{(2^3-1)}^{k-3}$	1
$S_2$	$168{(2^3-1)}^{k-3}$	3
$S_3$	$168{(2^3-1)}^{k-3}$	3
$S_4$	$56{(2^3-1)}^{k-3}$	1

.

In

Table 2. Vertex partition of $CCC\left(n\right)$ based on degree and eccentricity of each vertex.

Representative	Degree	Eccentricity	Frequency	Range
$v\in S^k$	4	$3+4(n-1)$	8	$2\le k\le n$
$v\in S_1^k$	4	$4(n+k-2)$	$56{(2^3-1)}^{k-3}$	$2\le k\le n$
$v\in S_2^k$	4	$4(n+k)-7$	$168{(2^3-1)}^{k-3}$	$2\le k\le n-1$
$v\in S_2^k$	3	$8n-7$	$168{(2^3-1)}^{k-3}$	$k=n$
$v\in S_3^k$	4	$4(n+k)-6$	$168{(2^3-1)}^{k-3}$	$2\le k\le n-1$
$v\in S_3^k$	3	$8n-6$	$168{(2^3-1)}^{k-3}$	$k=n$
$v\in S_4^k$	4	$4(n+k)-5$	$56{(2^3-1)}^{k-3}$	$2\le k\le n-1$
$v\in S_4^k$	3	$8n-5$	$56{(2^3-1)}^{k-3}$	$k=n$

we give the partition of all the vertices of $CCC\left(n\right)$ based on degree, eccentricity and the membership to the sets $S_1,S_2,S_3$ and $S_4$.

In the coming Theorems, we have computed Eccentric-connectivity index $\xi \left(G\right)$, Eccentric connectivity polynomial $ECP(G,x)$ and Connective Eccentric index $C^{\xi }\left(G\right)$ for crystal structure of cubic carbon $CCC\left(n\right)$.

Theorem 1.

Consider the graph $G\cong CCC\left(n\right)$ with $n\ge 2$, then its Eccentric-connectivity index is equal to

$$\xi \left(G\right)=\frac{(2^6\times 3\times 7\times 13n-2^5\times 503)7^n}{3^2\times 7^2}-\frac{2^7}{3}n+\frac{2^5\times 29}{3^2}.$$

(7)

Proof. 

Let $G\cong CCC\left(n\right)$ be the crystal structure of cubic carbon. The vertex partition of $CCC\left(n\right)$ based on degrees of vertices and eccentricities with their frequencies is given in Table 2. Then by using Table 2 and Equation (1), the Eccentric-connectivity index can be calculated as follows:

$$\begin{array}{ccc}\hfill \xi \left(G\right)& =& \sum _{u\in V\left(G\right)}{d}_u{ϵ}_u\hfill \\ \hfill \xi \left(G\right)& =& 8\left(4(3+4(n-1\left)\right)\right)+4\times \sum _{k=2}^{n}56{(2^3-1)}^{k-3}4(n+k-2)\hfill \\ & +& 4\times \sum _{k=2}^{n-1}168{(2^3-1)}^{k-3}(4(n+k)-7)+3\times 168{(2^3-1)}^{n-3}(8n-7)\hfill \\ & +& 4\times \sum _{k=2}^{n-1}168{(2^3-1)}^{k-3}(4(n+k)-6)+3\times 168{(2^3-1)}^{n-3}(8n-6)\hfill \\ & +& 4\times \sum _{k=2}^{n-1}56{(2^3-1)}^{k-3}(4(n+k)-5)+3\times 56{(2^3-1)}^{n-3}(8n-5)\hfill \end{array}$$

After, some easy computations, we get:

$$\xi \left(G\right)=\frac{(2^6\times 3\times 7\times 13n-2^5\times 503)7^n}{3^2\times 7^2}-\frac{2^7}{3}n+\frac{2^5\times 29}{3^2}.$$

(8)

 ☐

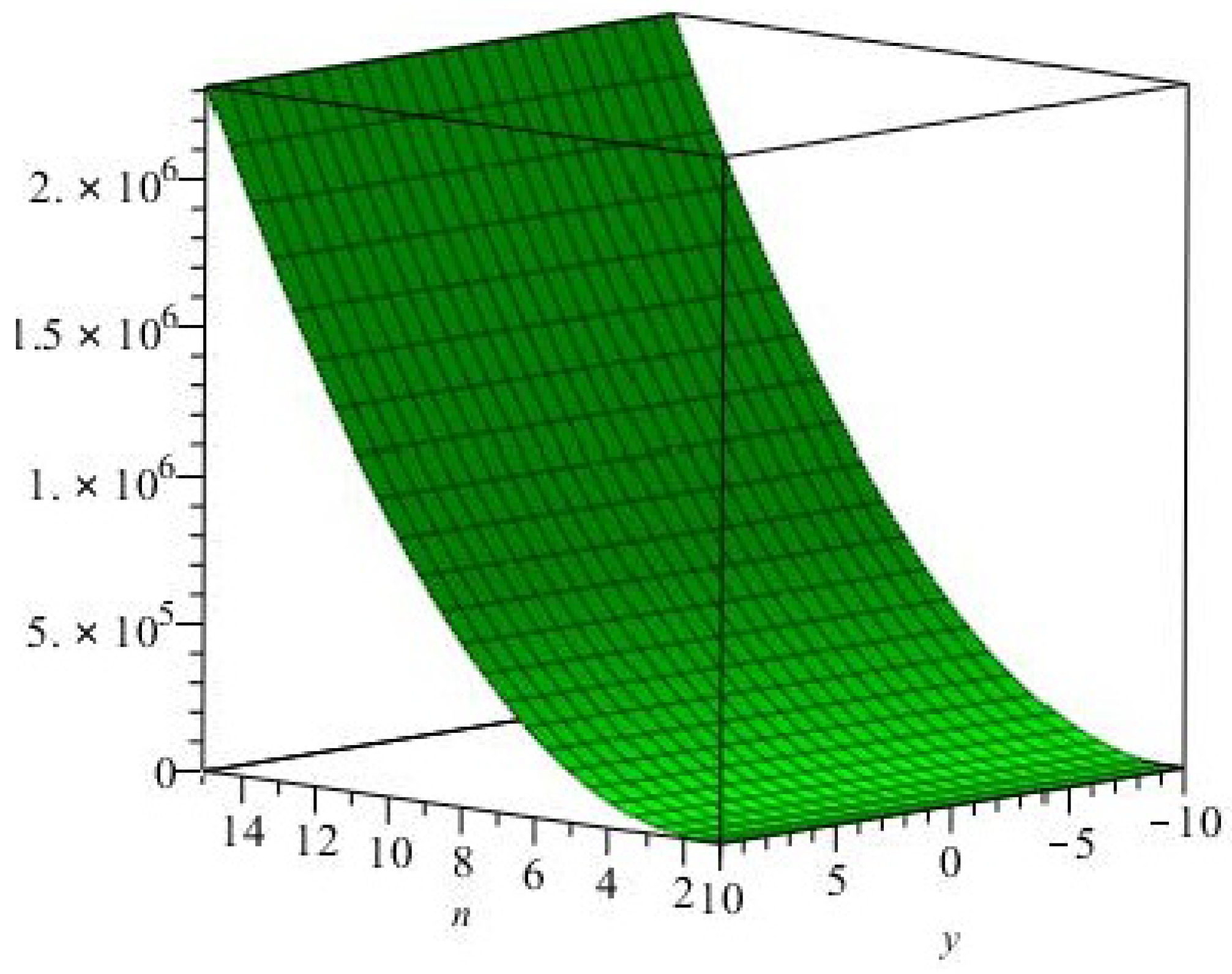
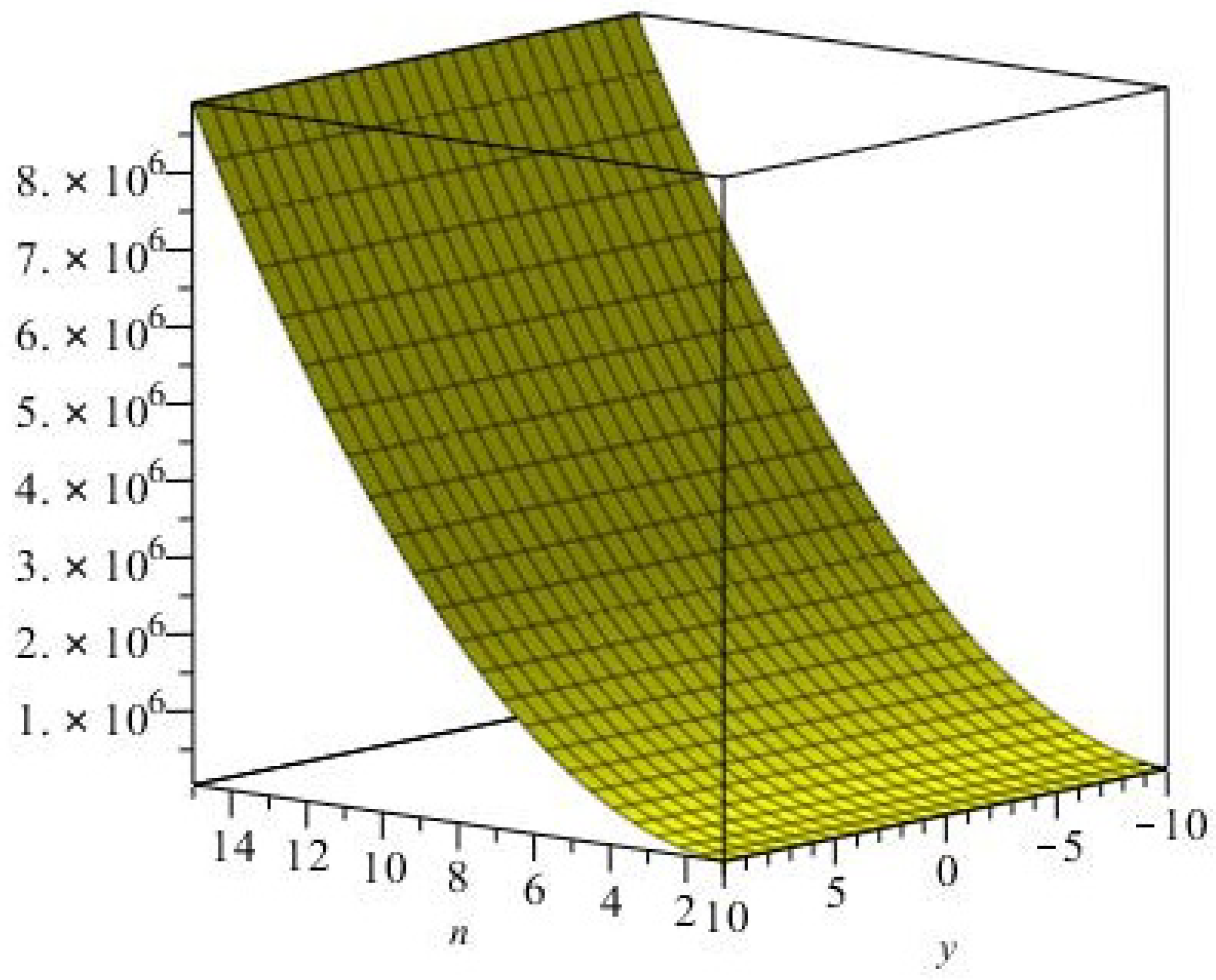
The $3D-$graphical representation of the Eccentric-connectivity index is depicted in Figure 3.

Theorem 2.

Consider the graph $G\cong CCC\left(n\right)$ with $n\ge 2$, then its Eccentric connectivity polynomial is equal to

$$\begin{array}{ccc}\hfill ECP(G,x)& =& 32x^{(4n-1)}+168{\left(7\right)}^{n-3}{x}^{8n-5}+504{\left(7\right)}^{n-3}{x}^{8n-6}+504{\left(7\right)}^{n-3}{x}^{8n-7}\hfill \\ & +& 224\times \sum _{k=2}^n{\left(7\right)}^{k-3}{x}^{4(n+k-2)}+672\times \sum _{k=2}^{n-1}{\left(7\right)}^{k-3}{x}^{4(n+k)-7}\hfill \\ & +& 672\times \sum _{k=2}^{n-1}{\left(7\right)}^{k-3}{x}^{4(n+k)-6}+224\times \sum _{k=2}^{n-1}{\left(7\right)}^{k-3}{x}^{4(n+k)-5}.\hfill \end{array}$$

Proof. 

Let $G\cong CCC\left(n\right)$ be the crystal structure of cubic carbon. Then by using Table 2 and Equation (2) the Eccentric connectivity polynomial is given by:

$$\begin{array}{ccc}\hfill ECP(G,x)& =& \sum _{u\in V\left(G\right)}{d}_u{x}^{{ϵ}_u}\hfill \\ \hfill ECP(G,x)& =& 8\times 4x^{3+4(n-1)}+4\times \sum _{k=2}^{n}56{(2^3-1)}^{k-3}{x}^{4(n+k-2)}\hfill \\ & +& 4\times \sum _{k=2}^{n-1}168{(2^3-1)}^{k-3}{x}^{4(n+k)-7}+3\times 168{(2^3-1)}^{n-3}{x}^{8n-7}\hfill \\ & +& 4\times \sum _{k=2}^{n-1}168{(2^3-1)}^{k-3}{x}^{4(n+k)-6}+3\times 168{(2^3-1)}^{n-3}{x}^{8n-6}\hfill \\ & +& 4\times \sum _{k=2}^{n-1}56{(2^3-1)}^{k-3}{x}^{4(n+k)-5}+3\times 56{(2^3-1)}^{n-3}{x}^{8n-5}.\hfill \end{array}$$

After an easy calculation, we get:

$$\begin{array}{ccc}\hfill ECP(G,x)& =& 32x^{(4n-1)}+168{\left(7\right)}^{n-3}{x}^{8n-5}+504{\left(7\right)}^{n-3}{x}^{8n-6}+504{\left(7\right)}^{n-3}{x}^{8n-7}\hfill \\ & +& 224\times \sum _{k=2}^n{\left(7\right)}^{k-3}{x}^{4(n+k-2)}+672\times \sum _{k=2}^{n-1}{\left(7\right)}^{k-3}{x}^{4(n+k)-7}\hfill \\ & +& 672\times \sum _{k=2}^{n-1}{\left(7\right)}^{k-3}{x}^{4(n+k)-6}+224\times \sum _{k=2}^{n-1}{\left(7\right)}^{k-3}{x}^{4(n+k)-5}.\hfill \end{array}$$

 ☐

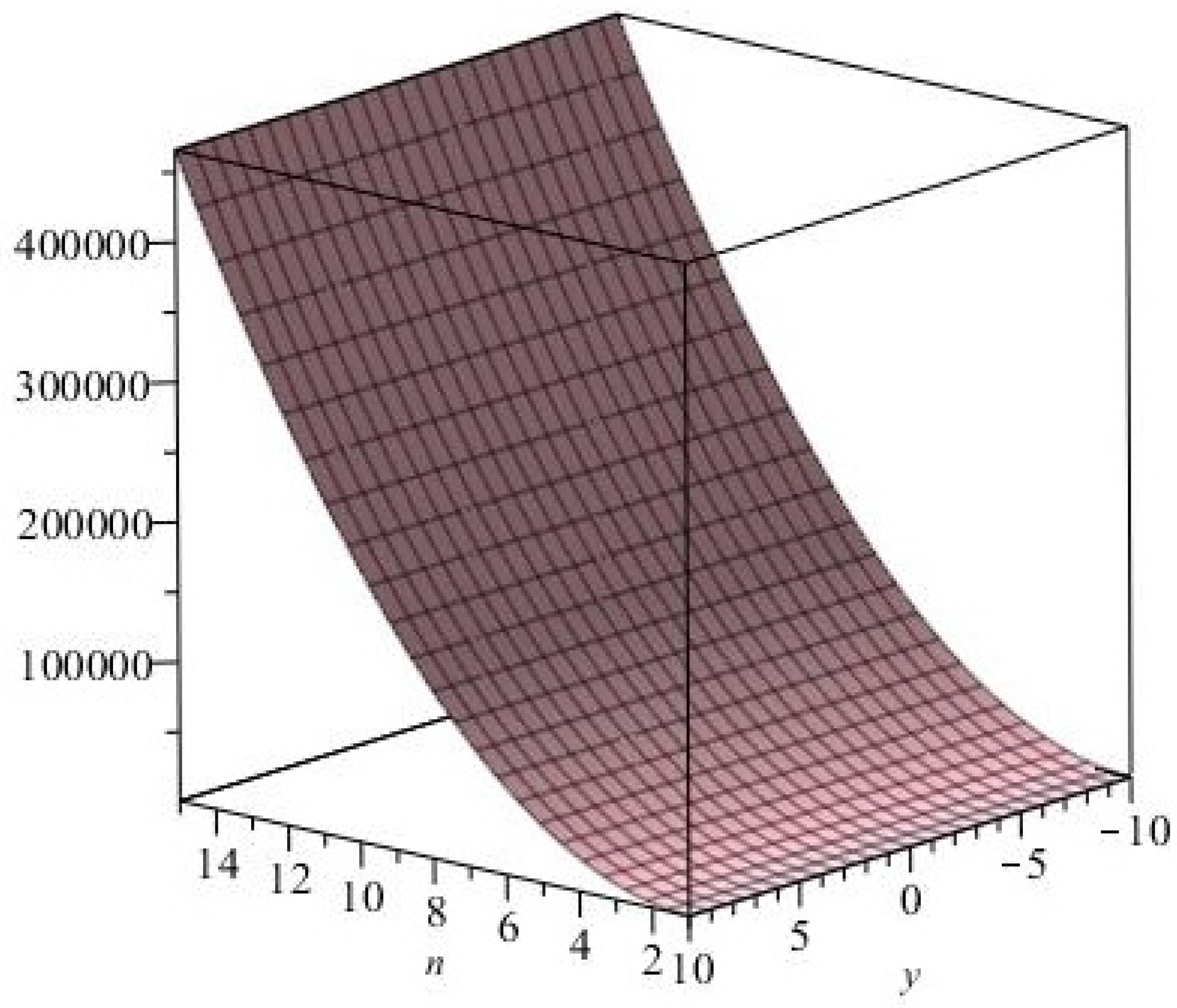
The $3D-$graphical representation of the Eccentric connectivity polynomial is depicted in Figure 4.

Theorem 3.

Consider the graph $G\cong CCC\left(n\right)$ with $n\ge 2$, then its Connective Eccentric index is equal to

$$\begin{array}{ccc}\hfill C^{\xi }\left(G\right)& =& \frac{32}{(4n-1)}+\frac{{727}^n}{(392n-343)}+\frac{{367}^n}{(196n-147)}+\frac{{247}^n}{(392n-245)}\hfill \\ & +& 224\times \sum _{k=2}^n\frac{{\left(7\right)}^{k-3}}{4(n+k-2)}+672\times \sum _{k=2}^{n-1}\frac{{\left(7\right)}^{k-3}}{4(n+k)-7}+672\times \sum _{k=2}^{n-1}\frac{{\left(7\right)}^{k-3}}{\left(4\right(n+k)-6)}\hfill \\ & +& 224\times \sum _{k=2}^{n-1}\frac{{\left(7\right)}^{k-3}}{4(n+k)-5}.\hfill \end{array}$$

Proof. 

Let $G\cong CCC\left(n\right)$ be the crystal structure of cubic carbon. Then by using Table 2 and Equation (4) the Connective Eccentric index is calculated as:

$$\begin{array}{ccc}\hfill C^{\xi }\left(G\right)& =& \sum _{u\in V\left(G\right)}\frac{d_u}{{ϵ}_u}\hfill \\ \hfill C^{\xi }\left(G\right)& =& \frac{32}{3+4(n-1)}+4\times \sum _{k=2}^n\frac{56{(2^3-1)}^{k-3}}{4(n+k-2)}+4\times \sum _{k=2}^{n-1}\frac{168{(2^3-1)}^{k-3}}{4(n+k)-7}\hfill \\ & +& 168{(2^3-1)}^{n-3}\times \frac{3}{8n-7}+4\times \sum _{k=2}^{n-1}\frac{168{(2^3-1)}^{k-3}}{\left(4\right(n+k)-6)}+168{(2^3-1)}^{n-3}\times \frac{3}{8n-6}\hfill \\ & +& 4\times \sum _{k=2}^{n-1}\frac{56{(2^3-1)}^{k-3}}{4(n+k)-5}+56{(2^3-1)}^{n-3}\times \frac{3}{8n-5}\hfill \end{array}$$

After an easy calculation, we get:

$$\begin{array}{ccc}\hfill C^{\xi }\left(G\right)& =& \frac{32}{(4n-1)}+\frac{{727}^n}{(392n-343)}+\frac{{367}^n}{(196n-147)}+\frac{{247}^n}{(392n-245)}\hfill \\ & +& 224\times \sum _{k=2}^n\frac{{\left(7\right)}^{k-3}}{4(n+k-2)}+672\times \sum _{k=2}^{n-1}\frac{{\left(7\right)}^{k-3}}{4(n+k)-7}+672\times \sum _{k=2}^{n-1}\frac{{\left(7\right)}^{k-3}}{\left(4\right(n+k)-6)}\hfill \\ & +& 224\times \sum _{k=2}^{n-1}\frac{{\left(7\right)}^{k-3}}{4(n+k)-5}.\hfill \end{array}$$

 ☐

The $3D-$graphical representation of the Connective Eccentric index is depicted in Figure 5.

4. Numerical and Graphical Comparison of Computed Indices

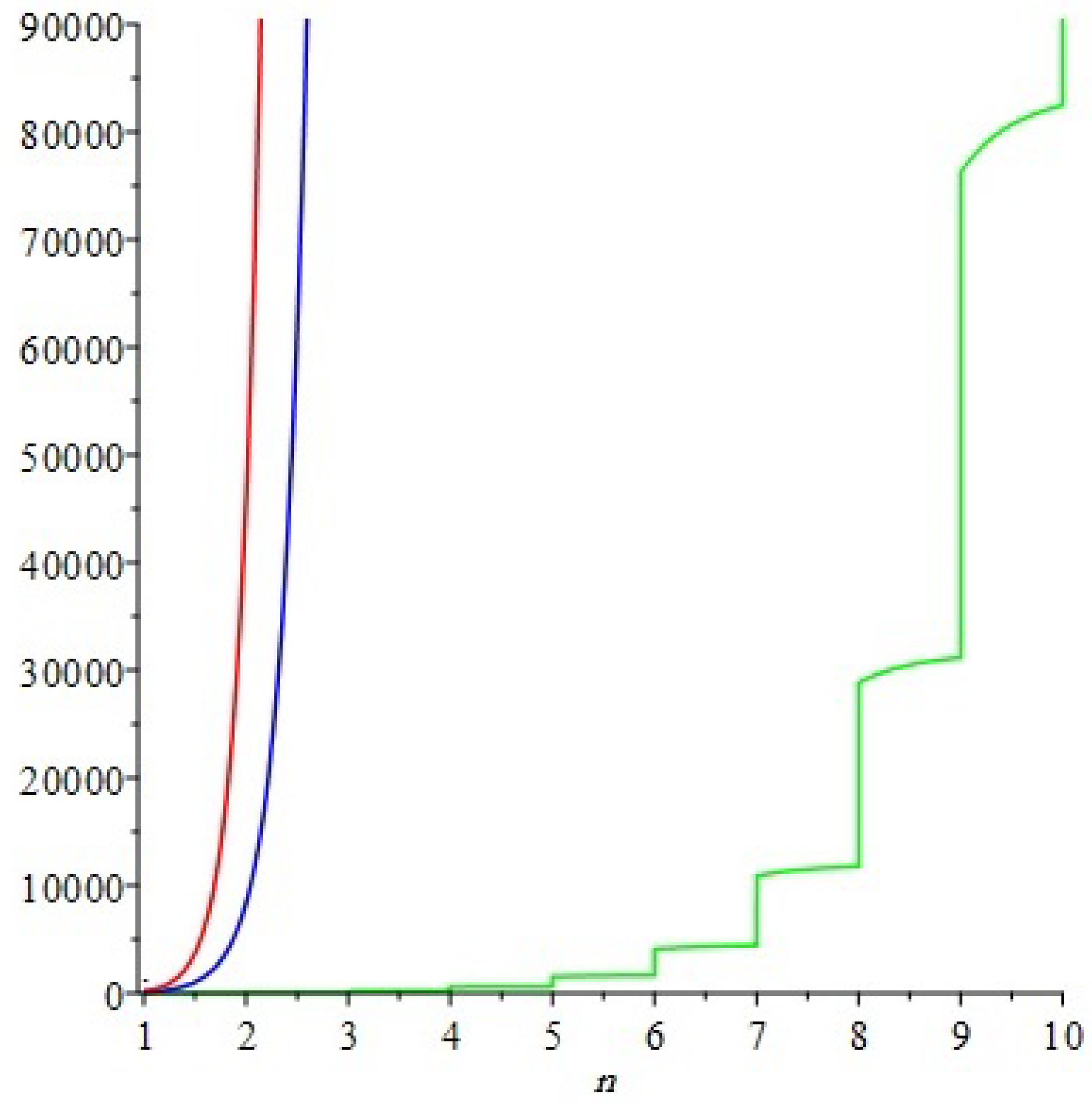
In this section we shall compare Eccentric-connectivity index, Eccentric connectivity polynomial and Connective Eccentric index of $CCC\left(n\right)$, both numerically and graphically. The

Table 3. Comparison of the $\xi \left(G\right)$, $C^{\xi }\left(G\right)$ and $ECP(G,x)$ of $G\cong CCC\left(n\right)$.

n	$\mathit{\xi }\left(\mathit{G}\right)$	${\mathit{C}}^{\mathit{\xi }}\left(\mathit{G}\right)$	$\mathit{ECP}(\mathit{G},\mathit{x})$
			Approx.
2	$5457.60$	9352	$\mathrm{32,038.4}$
3	$\mathrm{533,337.60}$	$\mathrm{538,880}$	$\mathrm{3,224,281.6}$
4	$\mathrm{4,183,459.20}$	$\mathrm{31,716,640}$	$\mathrm{242,651,430.4}$
5	$\mathrm{30,899,311.808}$	$\mathrm{2,065,600,096}$	$\mathrm{1,612,928,748.80}$
6	$\mathrm{22,891,814.30464}$	$\mathrm{62,224,801,952}$	$\mathrm{100,242,075,452.16}$
7	$\mathrm{8,645,581,788.7936}$	$\mathrm{7,559,088,080,480}$	$\mathrm{5,974,731,403,050.24}$
8	$\mathrm{541,359,817,758.7904}$	$\mathrm{225,395,825,441,440}$	$\mathrm{346,142,855,211,733.76}$
9	$\mathrm{34,985,496,157,764.4224}$	$\mathrm{7,144,399,013,120,096}$	$\mathrm{196,480,917,540,735.5008}$
10	$\mathrm{239,376,206,786,041.20768}$	$\mathrm{401,075,576,608,315,552}$	$\mathrm{10,983,346,993,039,897.4848}$

shows a numerical comparison of the described indices and the polynomial. The graphical representation of the numerical comparison is depicted in Figure 6.

The next graph shows the graphical comparison of Eccentric-connectivity index, Eccentric connectivity polynomial and Connective Eccentric index of $CCC\left(n\right)$.

5. Conclusions

In this article, we have discussed the Eccentric Connectivity index, Eccentric connectivity polynomial and Connective Eccentric index. We consider the molecular graph of crystal structure cubic carbon $CCC\left(n\right)$ and we have computed Connective Eccentric index, Eccentric connectivity polynomial and Connective Eccentric index of crystal structure of cubic carbon $CCC\left(n\right)$ chemical graphs for n-levels.