Abstract
Semi-empirical transition probabilities for magnetic dipole (M1) and electric quadrupole (E2) emission lines have been derived from parametric studies of experimental energy levels in Tm3+ (Tm IV), Yb4+ (Yb V), and Er3+ (Er IV), using Cowan codes. Results are compared with those existing from ab initio calculations or from more sophisticated semi-empirical calculations. Satisfactory agreements show that simple parametric calculations can provide good predictions on line intensities, provided that experimental levels are available, allowing reliable fits of energy parameters.
1. Introduction
The radiative properties of lanthanide ions have since long attracted interest because of the numerous applications of these ions in solid-state laser materials, photonics, or the lighting industry (see [1] and references therein for example). Radiative transitions were observed in doped crystals or in solution with small displacements relative to free ions, and their interpretation was helped by the knowledge of free ion structures and transition probabilities [2,3]. In astrophysics, Hubble Space Telescope observations of spectra of chemically peculiar stars show the presence of lanthanide ions up to doubly charged stages (see [4] for example). More recently, simultaneously observed emissions of electromagnetic waves and gravitational waves during two neutron stars merging increased the interest for radiative properties of higher charged lanthanide ions [5,6].
Due to the presence of 4f open shell electrons, lanthanide ions have very complex spectra, which can be untangled only by high-resolution laboratory studies. Systematic comparison of variation trends in energy parameters along isoelectronic or isoionic sequences is also a necessary help. During the past years, our collaborating team has carried out analyses of high-resolution spectra of several lanthanide ions in the vacuum ultra-violet (VUV) region [7,8,9,10,11,12,13,14], which contains essentially the fourth and fifth spectra and partially the third spectra. Experimental spectra were produced using high-voltage vacuum spark sources. Their interpretations in terms of atomic structures were supported by parametric calculations of energies and transition probabilities using the COWAN program package RCN/RCN2/RCG/RCE [15] in its Windows version [16]. As the analysis makes progress and experimental level energies become known, an iterative least-squares fit of energy parameters, i.e., the radial integrals, is performed in the RCE code, minimizing the differences between the calculated and the experimental energy values. In all of our previous works, this semi-empirical approach was shown to provide constantly improved predictions for unknown energy levels, and for observed intensities of spectral lines.
In the plasma of vacuum sparks, observed emitted lines are electric dipole (E1) transitions, the electron density being too high (around 1018 cm−3) for the observation of forbidden transitions such as magnetic dipole (M1) or electric quadrupole (E2) transitions. However, these transitions become observable in low density astrophysical or laboratory plasmas. It is therefore worth the effort to obtain good predictions for them. Early in the 1960s, Carnall et al. [2,3] already investigated spectral intensities within the ground-state 4fn configurations of the trivalent lanthanides in solution, in relation to theoretical calculations of transition probabilities by Judd [17] and Ofelt [18]. Recently, Dodson and Zia [19] reported ab initio calculations of emission rates and oscillator strengths for the M1 and E2 transitions in triply ionized lanthanide ions (Ce IV–Yb IV). The authors of [19] used a detailed free ion Hamiltonian, including electrostatic and spin-orbit terms as well as two-body, three-body, spin-spin, spin-other-orbit, and electrostatically correlated spin-orbit interactions. Semi-empirical calculations are possible when experimental level energies are available. Enzonga Yoca and Quinet [20] introduced the experimental level energies from Meftah et al. [11] into semi-empirical calculations for Tm IV, and reported the radiative decay rates for E1, M1, and E2 transitions obtained by the pseudo-relativistic Hartree-Fock (HFR) approach, including configuration interactions and core-polarization effects. Li et al. [21] reported semi-empirical radiative rates for M1 and E2 transitions of Ba-like ions within the 4f2 configuration, and also of Yb V within the 4f12 configuration. The authors fitted the experimental energy levels from Meftah et al. [12] to a standard f-shell Hamiltonian, including not only the major electrostatic and spin-orbit terms, but also various minor contributions like two-body, spin-spin, and spin-other orbit terms [21].
The main purpose of our present work is to explore the reliability of semi-empirical forbidden (M1 and E2) transition probabilities that we may derive from our spectral analyses of allowed transitions in a rather simple way by using Cowan codes; in particular, for the recently analyzed Er IV spectrum. Furthermore, the results are compared with ab initio results by Dodson and Zia [19]. The cases of Tm IV and Yb V are also studied for a comparison of our results to the previous results obtained by more sophisticated semi-empirical methods respectively, in Enzonga Yoca and Quinet [20] and Li et al. [21].
2. Experimental and Theoretical Methods
The present semi-empirical calculations were based on experimental level energies resulting from high-resolution studies of high voltage vacuum spark emission spectra recorded on the 10 m vacuum spectrograph of the Meudon Observatory (3600 lines/mm holographic concave grating, linear dispersion 0.25 Å/mm in the focal plane, resolution 0.008 Å in a wavelength range of 200–3000 Å). The overall uncertainty on the measured wavelengths varied between ± 0.003 and 0.005 Å. Analyses of these spectra with the resolution of fine structures, based on the Ritz combination principle, led to the determination of energy levels of the studied ion. The energy values of the levels were optimized by the least-squares fit, minimizing differences between the experimental wavenumbers and the calculated (Ritz) wavenumbers [22]. The uncertainty on the experimental energies could be estimated as ± 0.3–1 cm−1 in most cases. More experimental details can be found in previous publications (see Ref [12] for example).
The parametric calculations supporting the analyses are based on the standard Central Field Approximation and the Perturbation Theory. The Hamiltonian can be written as: H = H0 + H1, where H0 is the zero-order central field Hamiltonian and H1 = Q + Λ, the perturbation Hamiltonian, with the terms of the electrostatic interactions Q and the terms of the spin-orbit interactions Λ. The calculations were performed using the COWAN program package RCN/RCN2/RCG/RCE. A first step consisted of Hartree-Fock calculations of radial integrals, including relativistic corrections (HFR) performed by running RCN and RCN2. In this step, atomic orbitals and average energies of configurations EAv were optimized. Then, the Hamiltonian matrix was diagonalized in RCG, leading to energy values and eigenvectors of levels in intermediate coupling. The diagonalization took place in a basis, generally in a LS-coupling scheme, including the close configurations of a given parity, which possibly undergo mutual configuration interactions (CI). Each matrix element of H1 was written as a sum of products: , where are angular coefficients that are derived from angular momentum algebra and are radial integrals, which are also designated as energy parameters. Explicit configuration interactions are described by off-diagonal matrix elements between interacting configurations. Two-body electrostatic interactions from far configurations are taken into account by the introduction of effective parameters. When experimental energies are available, RCE is run for iterative least-squares fits minimizing the differences between the calculated and experimental energies, where the radial integrals are used as fitted parameters. The mean error of the fit is defined by , where Ni is the number of known experimental energies and Np is the number of free parameters. To avoid too large a number of free parameters, some constraints on parameters could be introduced by fixing their values or by fixing their ratios to their HFR values. After convergence, the final parameters were used in a final diagonalization, providing the best predictions for unknown energy levels. The corresponding level compositions in the intermediate coupling scheme are used for the calculations of the Landé factors and the radiative transition probabilities, log gf (g: statistical weight of the lower level, f: the absorption oscillator strength) and gA (g: statistical weight of the upper level, A: the Einstein spontaneous emission coefficient). These quantities are thus semi-empirical values based on experimental energies, and they hopefully represent better predictions than ab initio ones. The consistency between the observed intensities and calculated gA values for electric dipole transitions was also a criterion for the reliability of transition identifications. The RCG code output displayed a cancellation factor (CF), along with the gA value of a spectral line, which is defined by Equation (14.107), p. 432 in [15]. The CF is an indication of possible destructive interference effects in line strength calculations involving amplitudes in wavefunctions with intermediate-coupling and configuration–interaction mixings. According to Cowan [15], “Computed line strengths may be expected to show large percent errors when CF is smaller than about 0.1 or 0.05”. However, this limit seems to be rather restrictive, since in the case of Dy I quoted by Cowan [15], a good correlation between the observed intensities and the computed gf values for CF of greater than about 0.02 was found.
With the final fitted energy parameters, the Cowan programs could be run for calculations of magnetic dipole (M1) and electric quadrupole (E2) transition probabilities with specific options involving the matrix elements of the corresponding operators. We carried out these calculations for three lanthanide ions for which we have experimental energies derived from our previous analyses, i.e., Tm3+ (Tm IV) [11], Yb4+ (Yb V) [12], and Er3+ (Er IV) [14]. The reliability of our results was checked by comparison with available results from other calculations, either ab initio or semi-empirical. In the following, the results of Tm IV were compared with ab initio results by Dodson and Zia [19] and semi-empirical ones from Enzonga Yoca and Quinet [20]. Results on Yb V were compared with semi-empirical ones from Li et al. [21]. For Er IV, the present work reported the first semi-empirical results and compared them with ab initio ones by Dodson and Zia [19].
In each case, the comparison was carried out on the one hand, for the values of transition rate gA, and on the other hand, for the line strengths S, so to eliminate the wavelength dependences. Indeed, in different codes, the primary calculated quantity for each transition was the line strength. Transition rate is proportional to the line strength, with a factor varying over (λ)−3 for a M1 emission line, and over (λ)−5 for an E2 emission line [15]. A consistent comparison between the different calculations should involve line strengths. It is also possible to scale the gA values to the experimental wavelengths. The Ritz wavelengths derived from fitted energies (λRitz_Fit) were rather close to the ones that were derived from experimental energies (λRitz_Exp), but this was not the case for ab initio calculated wavelengths (λcalc). The numerical factors of conversion between gA (s−1) and S (a.u.), with λ in angström, can be found in the NIST Atomic Spectra Database [23]:
M1 lines: S = 3.707342 × 10−14 λ3 gA;
E2 line: S = 8.928970 × 10−19 λ5 gA.
3. Results and Discussion
3.1. Tm IV
The Tm IV case is a favorable one to commence comparisons. The analysis of the Tm3+ free ion spectrum [11] in the 700–2320 Å range resulted in the determination of 10 levels of the ground-state configuration 4f12, together with 9, 33, and 157 levels of, respectively, the 4f116s, 4f116p, and 4f115d-excited configurations. The parametric interpretation of the configurations reported in [11] involved a basis of three even configurations 5p64f12, 5p64f116p, and 5p54f13, and a basis of three odd configurations 5p64f115d, 5p64f116s, and 5p54f125d. Progress was made [24] since the last publication, with one more experimental level in the ground-state configuration 4f12 (3P J = 1), localized at E = 36,763.8 cm−1. Thus a new parametric calculation was performed in the present work, including as well a fourth even configuration 5p54f126p into the basis allowing calculations of gA values for the M1 and E2 transition with the new set of parameters. Table 1 reports the final parameter values of the fit for the even parity levels of 5p64f12 and 5p64f116p configurations, although they are only slightly different from the set reported in Table 5 of [11]. The set of electrostatic (Fk, Gk) and spin-orbit parameters (ζ) was completed by effective parameters α, β, and γ related to two-body excitation in fn subshells, and by “illegal” Slater parameters F1(f,p) and G3(f,p) acting on the (S, L) terms of the fnp configurations, which drastically improve the calculated energies. The perturbing configurations 5p54f13 and 5p54f126p were experimentally unknown. They were introduced in the basis set with all relevant parameters (scaled HFR) and Eav(5p54f13) = 235,589 cm−1, and Eav(5p54f126p) = 361,860 cm−1 fixed. All the configuration interaction parameters Rk were fixed to their HFR values. The corresponding mean error of the fit was 46 cm−1.

Table 1.
Parameter values (in cm−1) for 4f12 and 4f116p in Tm IV from a least-squares fit including four even configurations. Experimental energy values are from [11,24]. The perturbing configurations 5p54f13 and 5p54f126p are introduced in the basis set with all relevant parameters (scaled HFR), and Eav(5p54f13) = 235,589 cm−1 and Eav(5p54f126p) = 361,860 cm−1 fixed. The constrained parameters are indicated in the columns “St. Dev” by ‘r’ (linked by a constant ratio) and by ‘f’ (fixed).
Table 2 shows the comparison between different calculations of the M1 and E2 transition probabilities. Following the presentation of [20] where the authors listed the transition probabilities gA that were greater than 0.01 s−1 for M1 and E2 decays within the 4f12 ground-state configuration, and compared them to the ab initio calculations by Dodson and Zia [19], we listed the corresponding results from the present work. The first column displays the predicted Ritz wavelengths λRitz_Exp of the M1 and E2 lines derived from experimental level energies [11]. All the gA values (col. 5–7) have been converted into line strengths S (col. 8–10) using the wavelengths involved in the corresponding calculations, i.e., the ab initio calculated wavelengths for conversion of ab initio gA values [19] (col. 6) and Ritz wavelengths derived from our fitted energies for conversion of our gA values (col. 7). The corresponding wavelengths are respectively listed in col. 11 and col. 12 of Table 2. As for the gA values of Enzonga Yoca and Quinet (col. 5) [20], we used the λRitz_Exp for conversion in the absence of indications on the authors’ wavelengths. This is reasonable, since, as already mentioned, λRitz_Fit were very close to λRitz_Exp, and the factors (λRitz_fit/λRitz_exp)3 or (λRitz_fit/λRitz_Exp)5 would produce changes of less than 3%.

Table 2.
Transition probabilities gA (s−1) and line strengths for magnetic dipole (M1) and electric quadrupole (E2) transitions within the Tm IV ground-state configuration 4f12. Comparison with existing results. All wavelengths are in vacuum.
Figure 1 shows the distribution of M1 and E2 line strengths of Table 2 versus experimental wavelengths for Tm IV. One can see that for M1 transitions, our parametric calculations led to results that are in good agreement with the semi-empirical calculations in [20], and with the ab initio calculations in [19]. The standard deviation is about 2% between our results and the previous semi-empirical results [20], and is about 9% between our results and the ab initio results [19]. The predicted line at 4266 Å, a mixture of M1 and E2, had a M1 line strength showing a large discrepancy with the ab initio value [19]. The corresponding gA value was not explicitly given in [20]. For this line, the cancellation factor (CF) derived in our calculations from Cowan codes was 0.00, meaning an unreliable result. For E2, the three calculations give more scattered results. However, for the lines at 3039, 3847, 4437, 4721, 5759, 6402 and 7968 Å, indicated in [20] as having large discrepancies with ab initio values, our values are much closer to the values in [20]. One may note that in Tm IV, the E2 transitions have line strengths of two orders of magnitude lower than the M1 transitions. The cancellation factors calculated in this work were on average smaller for E2 than for the M1, meaning that the gA values are less reliable for E2 transitions.
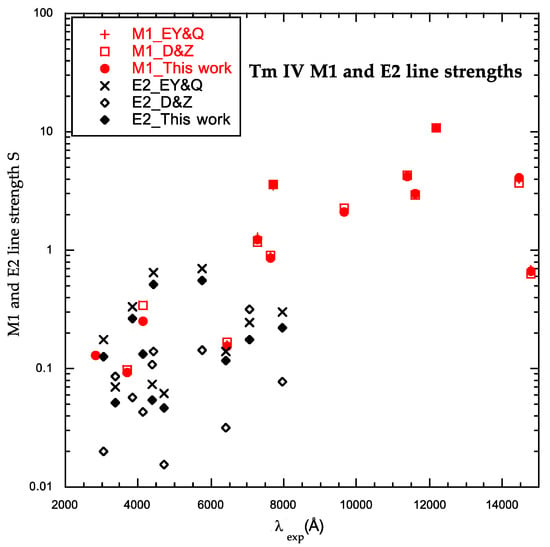
Figure 1.
Magnetic dipole (M1) and electric quadrupole (E2) line strengths in Tm IV for lines between 2000 and 15,000 Å.
3.2. Yb V
The analysis of the Yb V spectrum, isoelectronic to Tm IV, was achieved by Meftah et al. [12] with the determination of all 13 energy levels of the ground-state configuration 4f12, and respectively, 174, 12, and 43 levels of the excited configurations 4f115d, 6s, and 6p. The parametric study of the even parity included 4f12, 4f116p, and the unknown core-excited configurations 5p54f13 and 5p54f126p. The least-squares fit minimizing the differences between calculated and experimental energies involved 56 even parity levels and resulted in a mean error of 55 cm−1. In the present work, using the final fitted values of parameters reported in Table 5 of [12], we calculated the transition probabilities gA for the forbidden M1 and E2 transitions within the ground-sate configuration 4f12 of Yb V, and compared them in Table 3 with the results from semi-empirical calculations by Li et al. [21]. We also converted gA to line strengths S, as described above. The cancellation factors are listed in the last column, and all but three values are smaller than 0.02.

Table 3.
Transition probabilities gA (s−1) and line strengths for magnetic dipole (M1) and electric quadrupole (E2) transitions within the Yb V ground-state configuration 4f12. Comparison with existing results (ordered by increasing upper level energies). All wavelengths are in vacuum. CF is the cancellation factor as defined by Equation (14.107), p. 432 in [15], and derived from our calculations.
Figure 2 displays the M1 and E2 line strengths in Yb V in the wavelength range reduced to 2000–8000 Å for clarity. One can see that the two sets of line strengths are in good agreement, with relative differences less than 3% for M1 lines, except for 3810 Å and 28,836 Å, and less than 10% for E2 lines, except for the lines et 2702, 3810, and 4133 Å. It can be noticed in Table 3 that each of these transitions involved one level with a strong mixing of LS components. Indeed, for the levels 6112.03 cm−1 (4), 24,192.89 cm−1 (4), and 43,119.5 cm−1 (2), Meftah et al [12] reported the main LS components with the percentage compositions of 62% 1G, 56% 3H, and 56% 1D (4f12), respectively. The calculated gA could be rather sensitive to small changes in these percentages.
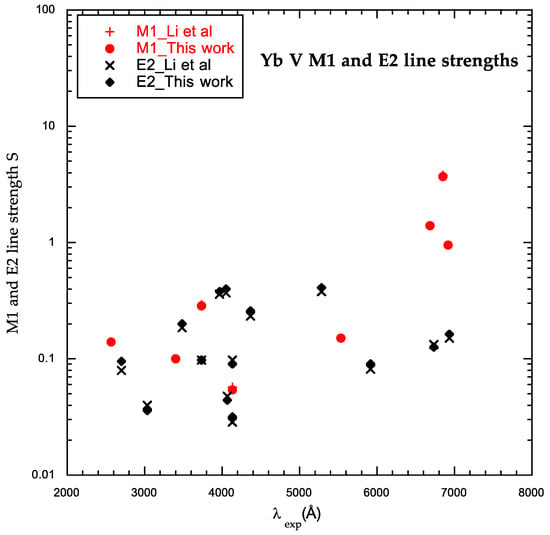
Figure 2.
Magnetic dipole (M1) and electric quadrupole (E2) line strengths in Yb V for lines between 2000 and 8000 Å.
3.3. Er IV
The recent analysis [14] of Er IV, isoionic of Tm IV, led to the determination of 120 energy levels belonging to the lower parts of the four configurations 4f11, 4f105d, 6s, and 6p. Unfortunately, the experimental energies of the 4f11 ground-state configuration that comprises 41 levels were less completely known than in Tm IV and Yb V cases. However, in the parametric study of the odd-parity configurations, the least-squares fit with 11 free parameters upon respectively nine and 29 known levels of 4f11 and 4f106p resulted in a mean error of 41 cm−1, which was quite satisfactory for the average energies of respectively Eav(4f11) = 35,997 cm−1 and Eav(4f106p) = 207,022 cm−1. Using the parameters of the final fit given in Table 4 of [14], we calculated the semi-empirical transition probabilities for M1 and E2 transitions within the ground-state configuration 4f11 of Er IV. Table 4 reports the present results on M1 transitions between 3000 Å and 17,000 Å, the ab initio values of which are available in Dodson and Zia [19] to make a comparison possible. Table 5 reports similar results for E2 transition probabilities. Figure 3a,b display respectively the M1 and E2 line strengths from the present work versus the ab initio results from [19].

Table 4.
Semi-empirical transition probabilities gA (s−1) and line strengths for magnetic dipole (M1) transitions within the Er IV ground-state configuration 4f11. Comparison with ab initio results from Dodson and Zia [19]. All wavelengths are in vacuum. Each energy level is specified by its energy value, followed by the quantum number J between parentheses [14]. CF is the cancellation factor as defined by Equation (14.107), p. 432 in [15] and derived from our calculations.

Table 5.
Semi-empirical transition probabilities gA (s−1) and line strengths for electric quadrupole (E2) transitions within the Er IV ground-state configuration 4f11. Comparison with ab initio results from Dodson and Zia [19]. All wavelengths are in vacuum. Each energy level is specified by its energy value, followed by the quantum number J between the parentheses [14]. CF is the cancellation factor as defined by Equation (14.107), p. 432 in [15] and derived from our calculations.
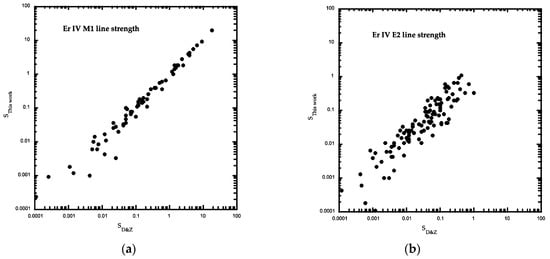
The large number of spectral lines in Er IV encourages an examination of possible correlation between discrepancies with ab initio results and cancellation factors (CF). These are listed in the last columns of Table 4 and Table 5. Figure 3a shows that the M1 line strengths are in good agreement. Most of the M1 line strengths have a relative discrepancy of less than 5%, except for the eight lines. Three of them (4623, 5868, 6016 Å) have a CF of 0.00, four others (2975, 3660, 4094, 10,328 Å) have CF between 0.02 and 0.04, and one (13,752 Å) has a CF of 0.08. For the E2 transitions, the results are more scattered, with 90 in 113 lines showing discrepancies of less than 15%. Three lines (4608, 5233, and 14,568 Å) have been discarded on the figure since their line strengths differ by one or two orders of magnitude. Discrepancies are also more or less correlated to cancellation factors without an absolute rule. In the absence of CF values from the ab initio calculations [19], the CF values listed in Table 4 and Table 5 only characterize the present results and they do not fully explain the discrepancies observed.
It is worth examining the particular case of the M1 line at 1.5 μm, which is widely used for fiber amplifiers in optical communication. The Ritz wavelength derived from the experimental energies of the ground state 4f11 4I15/2 and the first excited state 4f11 4I13/2 [14] is λRitz_Exp = 15,366.3 Å, and it should be the best wavelength prediction for the free ion. As for the transition probabilities, our semi-empirical prediction is λRitz_Fit = 15,231.3 Å, gA = 144.4 s−1 and S = 18.92 a.u., whereas the ab initio calculations report λD&Z = 15,280 Å, gA = 142.8 s−1 and S = 18.89 a.u. The relative discrepancy on gA is ∆(gA)/gA = 1.1 × 10−2 and only ∆S/S = 1.6 × 10−3 on line strength. It means that uncertainties on wavelengths propagate into gA values. A scaling of calculated values of gA with a factor (λcalc./λRitz_exp)3 or (λcalc./λRitz_exp)5 could lead to an improvement in applications. Emission in aqueous solution was predicted [3] at 15,129 Å, with a magnetic dipole oscillator strength of 30.82 × 10−8, i.e., gA = 143.7 s−1 and S = 18.45 a.u.
3.4. Scaling Factors of Energy Parameters as Derived from Least-Squares Fits
As explained in our previous parametric studies, in order to obtain a meaningful least-squares fit of the energy parameters and consequently reliable energy predictions, we strived to reduce the number of free parameters by applying constraints on some parameters, either by fixing their values or by fixing their ratios to their HFR values. The choice of good initial values of the parameters is therefore important. Table 6 shows a comparison of scaling factors among several neighboring spectra of lanthanide ions. The first four columns were already discussed in [25], and the more recent results on Yb V and Er IV confirm the consistency of these scaling factors, which helps for the choice of their initial values, including the effective parameters that are used for taking interactions with far unknown configurations into account.

Table 6.
Consistency of scaling factor (SF) values of energy parameters SF = Pfit/PHFR among neighboring spectra of lanthanide ions. An example of effective CI parameter F1(4f,5d) values is given.
4. Conclusions
We have shown that it is possible to perform rather simple calculations using Cowan codes [15] to obtain reliable transition probabilities for forbidden transitions such as magnetic dipole (M1) and electric quadrupole transitions (E2) within the ground-state configurations of the lanthanide ions, provided that experimental level energies are known and good parametric studies can be carried out. The good agreement between our results and the results of existing ab initio and semi-empirical calculations in Tm IV and Yb V allow for confidence in the first parametric calculations for Er IV. Generally speaking, agreements between different calculations are more satisfactory for the magnetic dipole transitions than for the electric quadrupole transitions. In the absence of experimental data for a systematic investigation of the reliability of calculations, the cancellation factor, as defined by Cowan [15], is the only possible criterion. A good correlation between observed intensities and the computed gf values for CF that are greater than about 0.02, was found in the case of Dy I as quoted by Cowan [15]. Furthermore, in a discussion about oscillator strength determination for rare-earth elements and ions, Biémont set the limit to 0.01, under which the transition may be affected by severe cancellation effects [26]. Being aware that these considerations are based on the observed intensities of allowed electric dipole transitions, one may apply with caution the criterion of |CF|> 0.01 or 0.02 to forbidden transitions. Unfortunately, for the last, meaningful conclusions can be drawn only if systematic comparison of observed intensities and calculated transition probabilities becomes possible.
Author Contributions
All authors had equal contribution.
Funding
Financial support of the French CNRS–Stellar Physics National Program (PNPS) is acknowledged. This work is part of the Plas@Par LabEx project managed by the ANR (ANR-11-IDEX-0004-02). A.M. and S.A.M. wish to acknowledge supports from University Mouloud Mammeri, Tizi-Ouzou, Algeria, and from the project CNEPRU D00520110032, Algeria.
Acknowledgments
The authors are grateful to A. Kramida for maintaining the Windows version of the Cowan codes and for helpful answers about their operations. WULTB wishes to thank T. Brage and R. Hutton for useful discussions at the ExTra workshop in Fudan University.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Wybourne, B.G. The fascination of the rare earths—Then, now and in the future. J. Alloys Compd. 2004, 380, 96–100. [Google Scholar] [CrossRef]
- Carnall, W.T.; Fields, P.R.; Wybourne, B.G. Spectral intensities of the trivalent lanthanides and actinides in solution. I. Pr3+, Nd3+, Er3+, Tm3+, and Yb3+. J. Chem. Phys. 1965, 42, 3797–3806. [Google Scholar] [CrossRef]
- Carnall, W.T.; Fields, P.R.; Wybourne, B.G. Spectral intensities of the trivalent lanthanides and actinides in solution. II. Pm3+, Sm3+, Eu3+, Gd3+, Tb3+, Dy3+, and Ho3+. J. Chem. Phys. 1968, 49, 4412–4423. [Google Scholar] [CrossRef]
- Ryabchikova, T.; Ryabtsev, A.N.; Kochukov, O.; Bagnulo, S. Rare-earth elements in the atmosphere of the magnetic chemically peculiar star HD 144897. New classification of the Nd III spectrum. Astron. Astrophys. 2006, 456, 329–338. [Google Scholar] [CrossRef]
- Kasen, D.; Badnell, N.R.; Barnes, J. Opacities and spectra of the r-process ejecta from neutron star mergers. Astrophys. J. 2013, 774, 25. [Google Scholar] [CrossRef]
- Fontes, C.J.; Fryer, C.L.; Hungerford, A.L.; Hakel, P.; Colgan, J.; Kilcrease, D.P.; Sherrill, M.E. Relativistic opacities for astrophysical applications. High Energy Density Phys. 2015, 16, 53–59. [Google Scholar] [CrossRef]
- Wyart, J.-F.; Meftah, A.; Bachelier, A.; Sinzelle, J.; Tchang-Brillet, W.-Ü.L.; Champion, N.; Spector, N.; Sugar, J. Energy levels of 4f3 in the Nd3+ free ion from emission spectra. J. Phys. B Mol. Opt. Phys. 2006, 39, L77. [Google Scholar] [CrossRef]
- Wyart, J.-F.; Meftah, A.; Tchang-Brillet, W.-Ü.L.; Champion, N.; Lamrous, O.; Spector, N.; Sugar, J. Analysis of the free ion Nd3+ spectrum (Nd IV). J. Phys. B At. Mol. Opt. Phys. 2007, 40, 3957–3972. [Google Scholar] [CrossRef]
- Wyart, J.-F.; Meftah, A.; Sinzelle, J.; Tchang-Brillet, W.-Ü.L.; Spector, N.; Judd, B. Theoretical study of ground-state configurations 4fN in Nd IV, Pr IV and Nd V. J. Phys. B At. Mol. Opt. Phys. 2008, 41, 085001. [Google Scholar] [CrossRef]
- Wyart, J.-F.; Meftah, A.; Sinzelle, J.; Tchang-Brillet, W.-Ü.L.; Champion, N.; Spector, N.; Sugar, J. Spectrum and energy levels of the Nd4+ free ion (Nd V). Phys. Scr. 2008, 77, 055302. [Google Scholar]
- Meftah, A.; Wyart, J.-F.; Champion, N.; Tchang-Brillet, W.-Ü.L. Observation and interpretation of the Tm3+ free ion spectrum. Eur. Phys. J. D 2007, 44, 35–45. [Google Scholar] [CrossRef]
- Meftah, A.; Wyart, J.-F.; Tchang-Brillet, W.-Ü.L.; Blaess, C.; Champion, N. Spectrum and energy levels of the Yb4+ free ion (Yb V). Phys. Scr. 2013, 88, 045305. [Google Scholar] [CrossRef]
- Deghiche, D.; Meftah, A.; Wyart, J.-F.; Champion, N.; Blaess, C.; Tchang-Brillet, W.-Ü.L. Observation of core-excited configuration in four-time ionized neodymium Nd4+ (Nd V). Phys. Scr. 2015, 90, 095402. [Google Scholar] [CrossRef]
- Meftah, A.; Ait Mammar, S.; Wyart, J.-F.; Tchang-Brillet, W.-Ü.L.; Champion, N.; Blaess, C.; Deghiche, D.; Lamrous, O. Analysis of the free ion spectrum of Er3+ (Er IV). J. Phys. B At. Mol. Opt. Phys. 2016, 49, 165002. [Google Scholar] [CrossRef]
- Cowan, R.D. The Theory of Atomic Structure and Spectra; University of California Press: Berkeley, CA, USA, 1981. [Google Scholar]
- Kramida, A. A Suite of Atomic Structure Codes Originally Developed by R. D. Cowan Adapted for Windows-Based Personal Computers. Available online: http://das101.isan.troitsk.ru/COWAN (accessed on 5 May 2017).
- Judd, B.R. Optical absorption intensities of rare-earth ions. Phys. Rev. 1962, 127, 750–761. [Google Scholar] [CrossRef]
- Ofelt, G.S. Intensities of crystal spectra of rare-earth ions. J. Chem. Phys. 1962, 37, 511–520. [Google Scholar] [CrossRef]
- Dodson, C.M.; Zia, R. Magnetic dipole and electric quadrupole transitions in the trivalent lanthanide series: Calculated emission rates and oscillator strengths. Phys. Rev. B 2012, 86, 126102. [Google Scholar] [CrossRef]
- Enzonga Yoca, S.; Quinet, P. Radiative decay rates for electric dipole, magnetic dipole and electric quadrupole transitions in triply ionized Thulium (Tm IV). Atoms 2017, 5, 28. [Google Scholar] [CrossRef]
- Li, H.; Kuang, X.-Y.; Yeung, Y.Y. Semi-empirical calculations of radiative rates for parity-forbidden transitions within the 4f2 configuration of Ba-like ions La+, Ce2+, Pr3+ and Nd4+ and 4f12 configuration of Dy-like Yb4+. J. Phys. B At. Mol. Opt. Phys. 2014, 47, 145002. [Google Scholar] [CrossRef]
- Kramida, A.E. The program LOPT for least-squares optimization of energy levels. Comput. Phys. Commun. 2010, 182, 419–434. [Google Scholar] [CrossRef]
- Kramida, A.; Ralchenko, Y.; Reader, J. NIST ASD Team. NIST Atomic Spectra Database; version 5.5.6; National Institute of Standards and Technology: Gaithersburg, MD, USA, 2018. Available online: https://physics.nist.gov/asd (accessed on 7 August 2018).
- Meftah, A. (Observatoire de Paris-Meudon, PSL Research University, Meudon, France and Université Mouloud Mammeri, Tizi-Ouzou, Algeria). Personal communication, 2017.
- Wyart, J.-F. On the interpretation of complex atomic spectra by means of the parametric Racah-Slater method and Cowan codes. Can. J. Phys. 2011, 89, 451–456. [Google Scholar] [CrossRef]
- Biémont, E. Recent advances and difficulties in oscillator strength determination for rare-earth elements and ions. Phys. Scr. 2005, T119, 55–60. [Google Scholar] [CrossRef]
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).