Studying Antimatter Gravity with Muonium
Abstract
1. Introduction
2. Method
- Development of improved low-velocity muon and muonium beams;
- Development of a sufficiently precise interferometer; and
- Development of a sufficiently precise interferometer alignment and calibration technique.
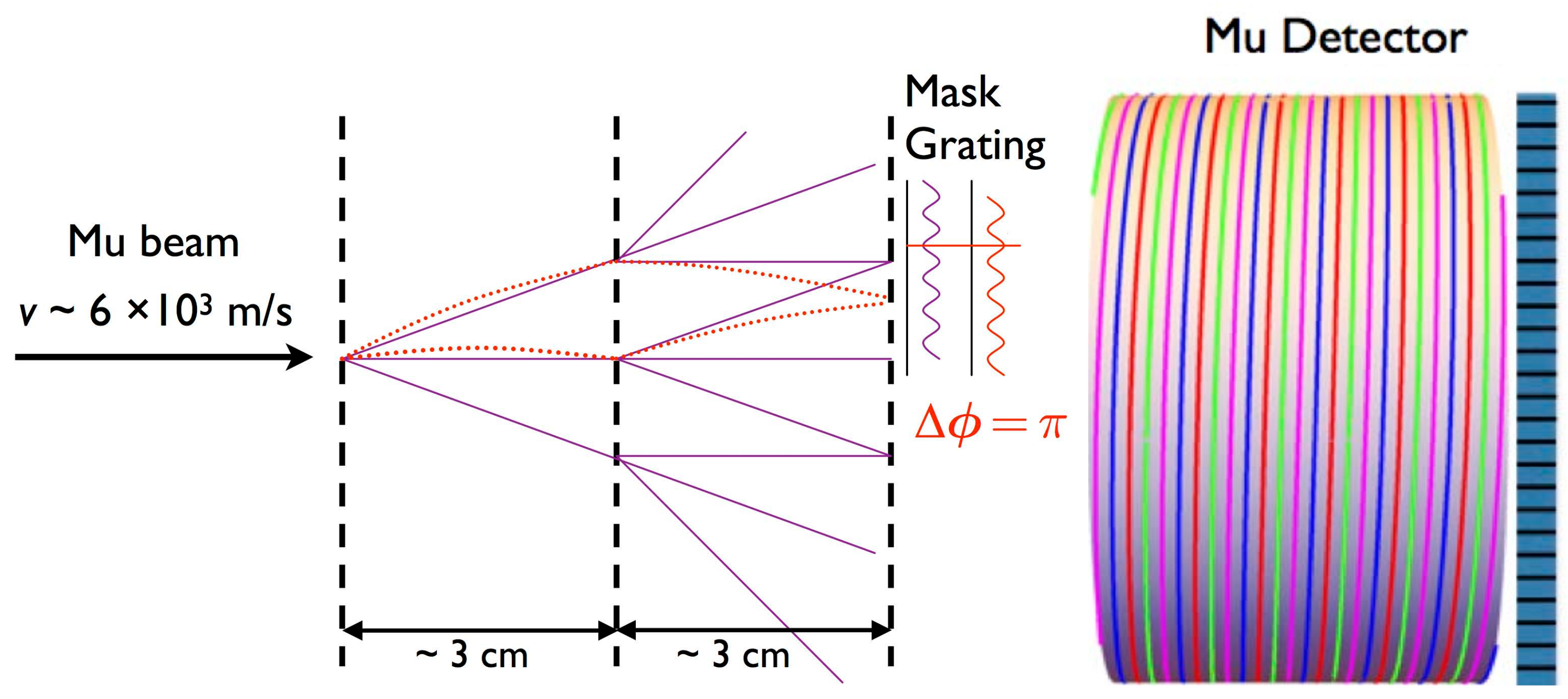
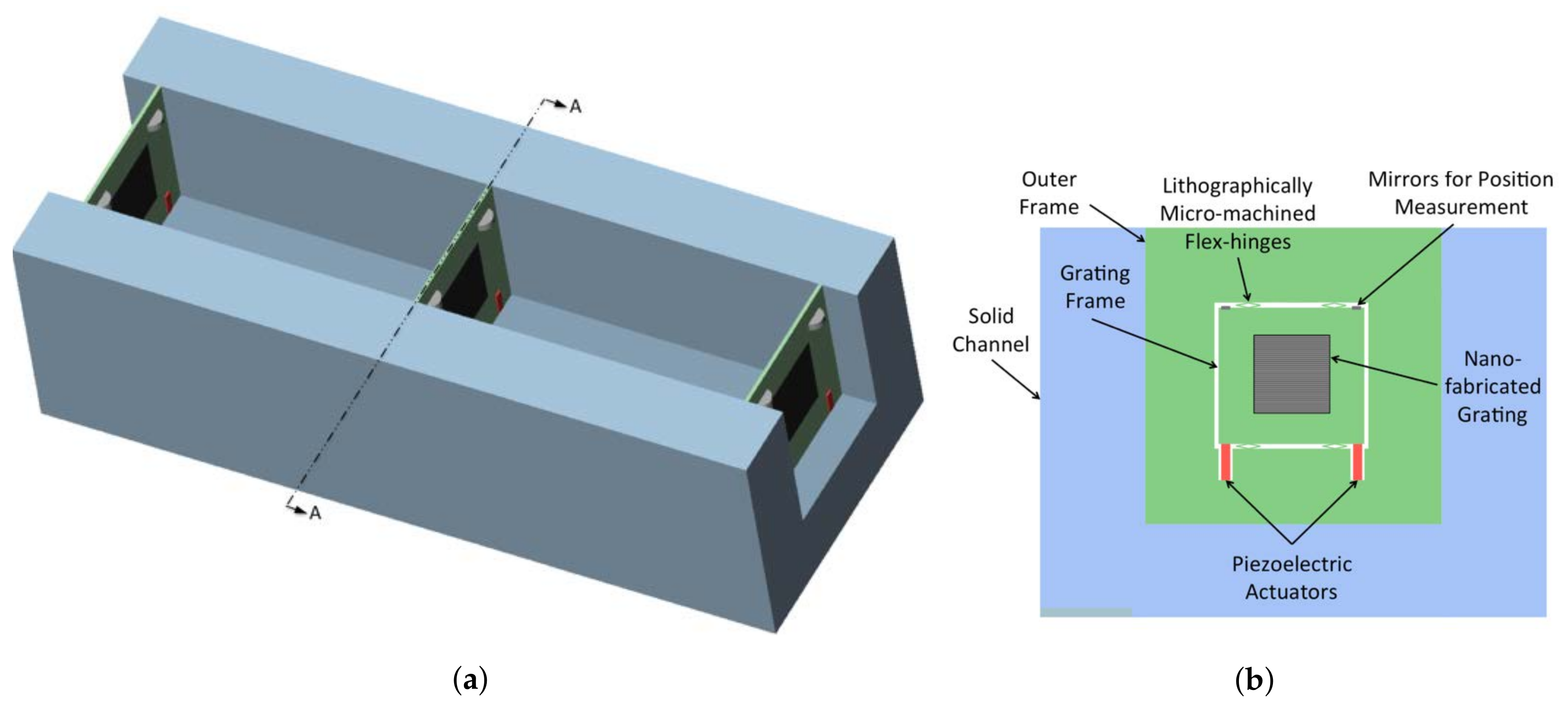
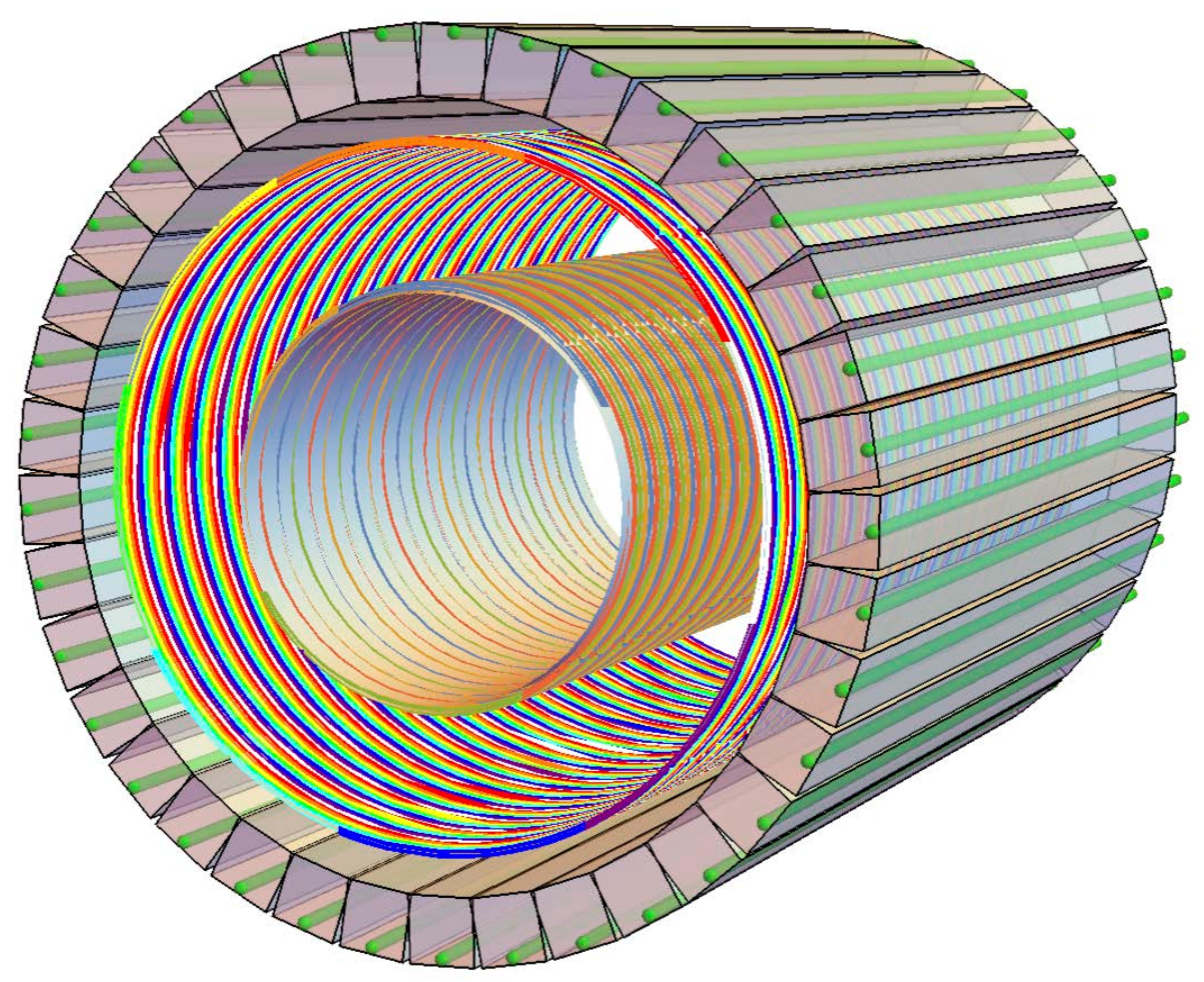
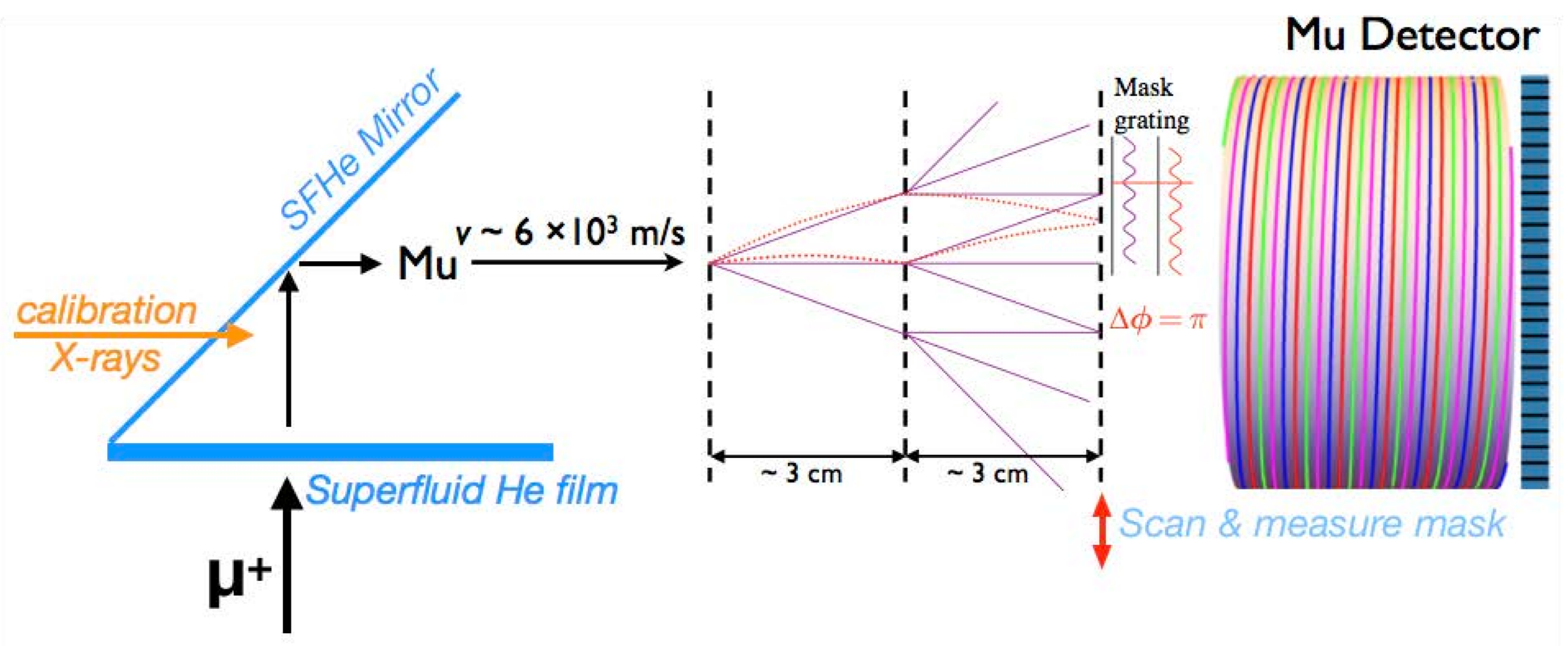
2.1. Interferometer
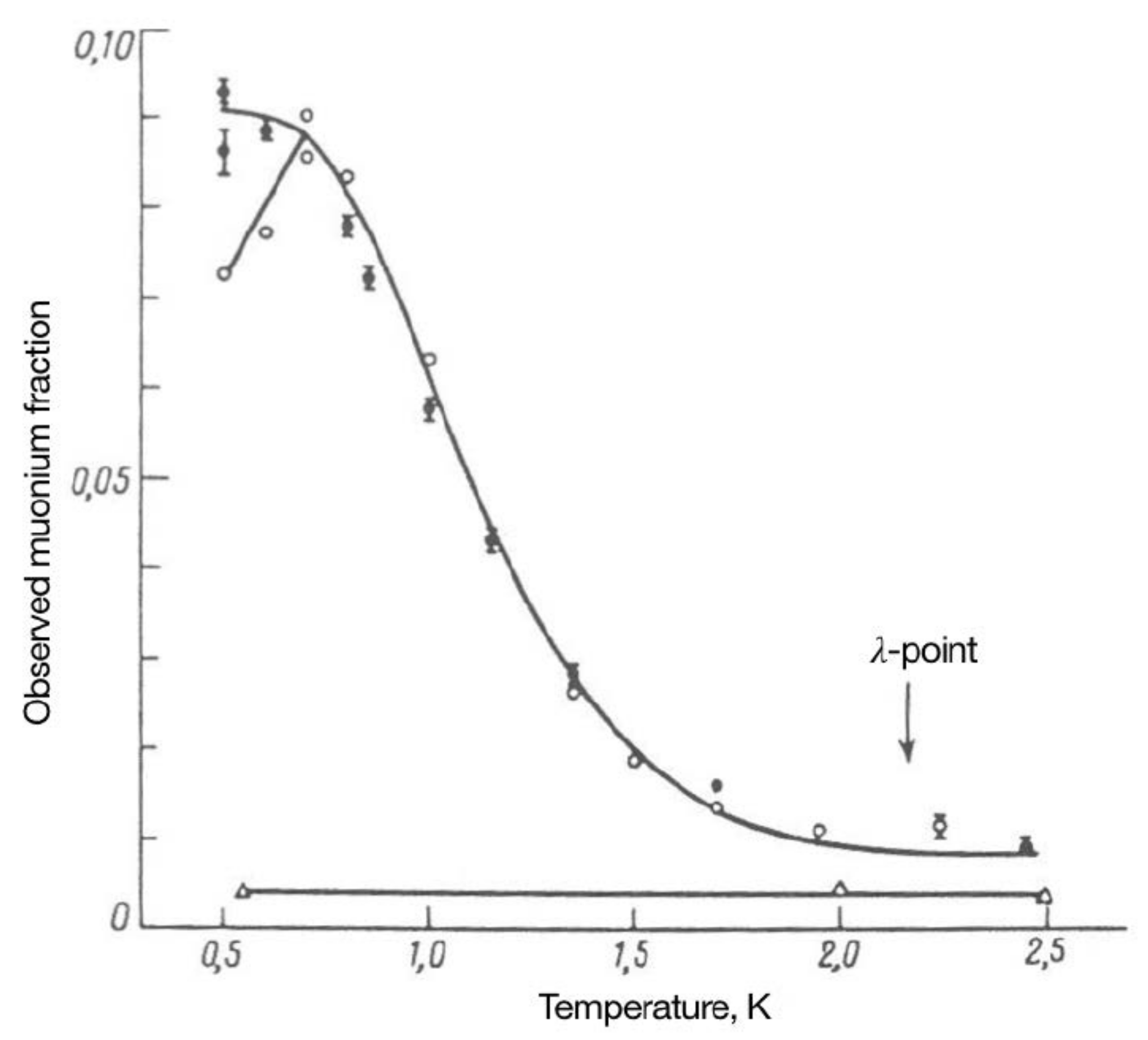
2.2. Muonium Beam
2.3. Interferometer Alignment and Calibration
3. Systematic Uncertainties
4. Prospects
Acknowledgments
Author Contributions
Conflicts of Interest
Abbreviations
| CNM | the Center for Nanoscale Materials at Argonne National Laboratory |
| FWHM | full-width at half maximum |
| , g | the gravitational acceleration at the earth’s surface of antimatter and matter, respectively |
| GR | general relativity |
| IIT | Illinois Institute of Technology |
| IPRO | Inter-Professional Project |
| IR | infrared |
| MAGE | the Muonium Antimatter Gravity Experiment |
| MCP | microchannel plate |
| MDPI | Multidisciplinary Digital Publishing Institute |
| Mu | muonium |
| muCool | cooled muon beam R&D program at PSI |
| PBS | polarizing beam splitter |
| PSI | Paul Scherrer Institute |
| RMS | root-mean-square |
| SFHe | superfluid helium |
| TFG | tracking frequency gauge |
| UNCD | ultrananocrystalline diamond |
| vdWE | van der Waals effect |
References
- Morrison, P. Approximate Nature of Physical Symmetries. Am. J. Phys. 1958, 26, 358. [Google Scholar] [CrossRef]
- Nieto, M.M.; Goldman, T. The Arguments Against “Antigravity” and the Gravitational Acceleration of Antimatter. Phys. Rep. 1991, 205, 221–281. [Google Scholar] [CrossRef]
- Fischler, M.; Lykken, J.; Roberts, T. Direct Observation Limits on Antimatter Gravitation. Tech. Rep. FERMILAB-FN-0822-CD-T. arXiv, 2008; arXiv:0808.3929. [Google Scholar]
- Amole, C.; Ashkezari, M.D.; Baquero-Ruiz, M.; Bertsche, W.; Butler, E.; Capra, A.; Cesar, C.L.; Charlton, M.; Eriksson, S.; Fajans, J.; et al. Description and first application of a new technique to measure the gravitational mass of antihydrogen. Nat. Commun. 2013, 4, 1–9. [Google Scholar] [CrossRef] [PubMed]
- Kellerbauer, A.; Aghion, S.; Amsler, C.; Ariga, A.; Ariga, T.; Bonomi, G.; Bräunig, P.; Bremer, J.; Brusa, R.S.; Cabaret, L.; et al. Probing antimatter gravity—The AEGIS experiment at CERN. In Proceedings of the 4th International Conference on New Frontiers in Physics (ICNFP 2015), Crete, Greece, 23–30 August 2015; Bravina, L., Foka, Y., Kabana, S., Eds.; EPJ Web of Conf. EDP Sciences: Les Ulis, France, 2016; Volume 126, p. 02016. [Google Scholar]
- Drobychev, G.; Nedelec, P.; Sillou, D.; Gribakin, G.; Walters, H.; Ferrari, G.; Prevedelli, M.; Tino, G.M.; Doser, M.; Canali, C.; et al. Proposal for the AEGIS Experiment at the CERN Antiproton Decelerator. Tech. Rep., CERN-SPSC-2007-017, CERN. June 2007. Available online: http://doc.cern.ch//archive/electronic/cern/preprints/spsc/public/spsc-2007-017.pdf (accessed on 1 February 2018).
- Perez, P.; Sacquin, Y. The GBAR experiment: gravitational behaviour of antihydrogen at rest. Class. Quantum Gravity 2012, 29, 184008. [Google Scholar] [CrossRef]
- Cassidy, D.B.; Hogan, S.D. Atom control and gravity measurements using Rydberg positronium. Int. J. Mod. Phys. Conf. Ser. 2014, 30, 1460259. [Google Scholar] [CrossRef]
- Wagner, T.A.; Schlamminger, S.; Gundlach, J.H.; Adelberger, E.G. Torsion-balance tests of the weak equivalence principle. Class. Quantum Gravity 2012, 29, 184002. [Google Scholar] [CrossRef]
- Touboul, P.; Métris, G.; Rodrigues, M.; André, Y.; Baghi, Q.; Bergé, J.; Boulanger, D.; Bremer, S.; Carle, P.; Chhun, R.; et al. The MICROSCOPE mission: First results of a space test of the Equivalence Principle. Phys. Rev. Lett. 2017, 119, 231101. [Google Scholar] [CrossRef] [PubMed]
- Alves, D.S.M.; Jankowiak, M.; Saraswat, P. Experimental constraints on the free fall acceleration of antimatter. arXiv, 2009; arXiv:0907.4110. [Google Scholar]
- Ulmer, S.; Smorra, C.; Mooser, A.; Franke, K.; Nagahama, H.; Schneider, G.; Higuchi, T.; Van Gorp, S.; Blaum, K.; Matsuda, Y.; et al. High-precision comparison of the antiproton-to-proton charge-to-mass ratio. Nature 2015, 524, 196–199. [Google Scholar] [CrossRef] [PubMed]
- Hughes, R.J.; Holzscheiter, M.H. Constraints on the gravitational properties of antiprotons and positrons from cyclotron-frequency measurements. Phys. Rev. Lett. 1991, 66, 854–857. [Google Scholar] [CrossRef] [PubMed]
- Gabrielse, G.; Fei, X.; Orozco, L.A.; Tjoelker, R.L.; Haas, J.; Kalinowsky, H.; Trainor, T.A.; Kells, W. Thousandfold Improvement in the Measured Antiproton Mass. Phys. Rev. Lett. 1990, 65, 1317–1320. [Google Scholar] [CrossRef] [PubMed]
- Good, M.L. and the Equivalence Principle. Phys. Rev. 1961, 121, 311. [Google Scholar] [CrossRef]
- Gabrielse, G.; Khabbaz, A.; Hall, D.S.; Heimann, C.; Kalinowsky, H.; Jhe, W. Precision Mass Spectroscopy of the Antiproton and Proton Using Simultaneously Trapped Particles. Phys. Rev. Lett. 1999, 82, 3198. [Google Scholar] [CrossRef]
- Smorra, C.; Sellner, S.; Borchert, M.J.; Harrington, J.A.; Higuchi, T.; Nagahama, H.; Tanaka, T.; Mooser, A.; Schneider, G.; Bohman, M.; et al. A parts-per-billion measurement of the antiproton magnetic moment. Nature 2017, 550, 371–374. [Google Scholar] [CrossRef] [PubMed]
- Karshenboim, S.G. K0 meson physics in the gravitation field: A constraint on the equivalence principle. arXiv, 2008; arXiv:0811.1009. [Google Scholar]
- Kostelecký, V.A.; Tasson, J. Matter-gravity couplings and Lorentz violation. Phys. Rev. D 2010, 83, 016013. [Google Scholar] [CrossRef]
- Tasson, J.D. Gravity effects on antimatter in the standard-model extension. Int. J. Mod. Phys. Conf. Ser. 2014, 30, 1460273. [Google Scholar] [CrossRef]
- Tasson, J.D. The standard-model extension and gravitational tests. Symmetry 2016, 8, 111. [Google Scholar] [CrossRef]
- Glashow, S.L.; Guadagnoli, D.; Lane, K. Lepton Flavor Violation in B Decays? Phys. Rev. Lett. 2015, 114, 091801. [Google Scholar] [CrossRef] [PubMed]
- Buttazzo, D.; Greljo, A.; Isidori, G.; Marzocca, D. B-physics anomalies: A guide to combined explanations. arXiv, 2017; arXiv:1706.07808.Unpublished work. [Google Scholar]
- Abbott, B.P.; Abbott, R.; Abbott, T.D.; Abernathy, M.R.; Acernese, F.; Ackley, K.; Adams, C.; Adams, T.; Addesso, P.; Adhikari, R.X.; et al. Observation of Gravitational Waves from a Binary Black Hole Merger. Phys. Rev. Lett. 2016, 116, 061102. [Google Scholar] [CrossRef] [PubMed]
- Parker, L.; Toms, D. Quantum Field Theory in Curved Spacetime: Quantized Fields and Gravity; Cambridge Monographs on Mathematical Physics: Cambridge, UK, 2009. [Google Scholar]
- Chardin, G. Motivations for antigravity in general relativity. Hyperfine Int. 1997, 109, 83–94. [Google Scholar] [CrossRef]
- Villata, M. The matter-antimatter interpretation of Kerr spacetime. Ann. Phys. 2015, 527, 507–512. [Google Scholar] [CrossRef]
- Arcos, H.I.; Pereira, J.G. Kerr-Newman solution as a Dirac particle. Gen. Rel. Grav. 2004, 36, 2441–2464. [Google Scholar] [CrossRef]
- Burinskii, A. The Dirac-Kerr-Newman electron. Gravit. Cosmol. 2008, 14, 109–122. [Google Scholar] [CrossRef]
- Burinskii, A. Gravitational strings beyond quantum theory: Electron as a closed heterotic string. J. Phys. Conf. Ser. 2012, 361, 012032. [Google Scholar] [CrossRef]
- Boyer, R.H.; Lindquist, R.W. Maximal Analytic Extension of the Kerr Metric. J. Math. Phys. 1967, 8, 265–281. [Google Scholar] [CrossRef]
- Kowitt, M. Gravitational repulsion and Dirac antimatter. Int. J. Theor. Phys. 1996, 35, 605–631. [Google Scholar] [CrossRef]
- Blanchet, L.; Le Tiec, A. Model of dark matter and dark energy based on gravitational polarization. Phys. Rev. D 2008, 78, 024031. [Google Scholar] [CrossRef]
- Blanchet, L.; Le Tiec, A. Dipolar dark matter and dark energy. Phys. Rev. D 2009, 80, 023524. [Google Scholar] [CrossRef]
- Cabbolet, M.J.T.F. Elementary Process Theory: A formal axiomatic system with a potential application as a foundational framework for physics supporting gravitational repulsion of matter and antimatter. Ann. Phys. 2010, 522, 699–738. [Google Scholar] [CrossRef]
- Hajdukovic, D.S. Is dark matter an illusion created by the gravitational polarization of the quantum vacuum? Astrophys. Space Sci. 2011, 334, 215–218. [Google Scholar] [CrossRef]
- Villata, M. CPT symmetry and antimatter gravity in general relativity. Europhys. Lett. 2011, 94, 20001. [Google Scholar] [CrossRef]
- Benoit-Lévy, A.; Chardin, G. Introducing the Dirac-Milne universe. Astron. Astrophys. 2012, 537, A78. [Google Scholar] [CrossRef]
- Hajdukovic, D. Quantum vacuum and virtual gravitational dipoles: the solution to the dark energy problem? Astrophys. Space Sci. 2012, 339, 1–5. [Google Scholar] [CrossRef]
- Villata, M. “Dark energy” in the Local Void. Astrophys. Space Sci. 2012, 339, 7–12. [Google Scholar] [CrossRef]
- Villata, M. On the nature of dark energy: The lattice Universe. Astrophys. Space Sci. 2013, 345, 1–9. [Google Scholar] [CrossRef]
- Drell, P.; Albrecht, A.; Aronson, S.; Baker, K.; Bagger, J.; Calder, N.; Gates, E.; Gilman, F.; Jackson, J.; Kahn, S.; et al. Quantum Universe; DOE/NSF: Washington, DC, USA, 2006. Available online: http://www.quantumuniversereport.org/ (accessed on 1 February 2018).
- Fixsen, D.J. The Temperature of the Cosmic Microwave Background. Astrophys. J. 2009, 707, 916–920. [Google Scholar] [CrossRef]
- Peacock, J.A. Cosmological Physics; Cambridge University Press: Cambridge, UK, 1998; ISBN 978-0-521-42270-3. [Google Scholar]
- Riess, A.G.; Filippenko, A.V.; Challis, P.; Clocchiattia, A.; Diercks, A.; Garnavich, P.M.; Gilliland, R.M.; Hogan, C.J.; Jha, S.; Kirshner, R.P.; et al. Observational Evidence from Supernovae for an Accelerating Universe and a Cosmological Constant. Astron. J. 1998, 116, 1009. [Google Scholar] [CrossRef]
- Perlmutter, S.; Aldering, G.; Goldhaber, G.; Knop, R.A.; Nugent, P.; Castro, P.G.; Deustua, S.; Fabbro, S.; Goobar, A.; Groom, D.E.; et al. Measurements of Ω and Λ from 42 High-Redshift Supernovae. Astrophys. J. 1999, 517, 565–586. [Google Scholar] [CrossRef]
- Chaboyer, B.; Demarque, P.; Kernan, P.J.; Krauss, L.M. The Age of Globular Clusters in Light of Hipparcos: Resolving the Age Problem? Astrophys. J. 1998, 494, 96. [Google Scholar] [CrossRef]
- Nielsen, J.T.; Guffanti, A.; Sarkar, S. Marginal evidence for cosmic acceleration from Type Ia supernovae. Sci. Rep. 2016, 6, 35596. [Google Scholar] [CrossRef] [PubMed]
- Blanchet, L. Gravitational polarization and the phenomenology of MOND. Class. Quant. Gravity 2007, 24, 3529. [Google Scholar] [CrossRef]
- Bekenstein, J.; Milgrom, M. Does the missing mass problem signal the breakdown of Newtonian gravity? Astrophys. J. 1984, 286, 7–14. [Google Scholar] [CrossRef]
- McGaugh, S.S. A Novel Test of the Modified Newtonian Dynamics with Gas Rich Galaxies. Phys. Rev. Lett. 2011, 106, 121303. [Google Scholar] [CrossRef] [PubMed]
- Weinberg, S. The cosmological constant problem. Rev. Mod. Phys. 1989, 61, 1–23. [Google Scholar] [CrossRef]
- Czarnecki, A.; Lepage, G.P.; Marciano, W.J. Muonium decay. Phys. Rev. D 2000, 61, 073001. [Google Scholar] [CrossRef]
- Hammond, T.D. Atom Interferometry: Dispersive Index of Refraction and Rotation Induced Phase Shifts for Matter-Waves. Ph.D. Thesis, MIT, Cambridge, MA, USA, February 1997. [Google Scholar]
- McMorran, B.; Cronin, A.D. Model for partial coherence and wavefront curvature in grating interferometers. Phys. Rev. A 2008, 78, 013601. [Google Scholar] [CrossRef]
- Phillips, T.J. Antimatter gravity studies with interferometry. Hyp. Int. 1997, 109, 357–365. [Google Scholar] [CrossRef]
- Kirch, K. Testing Gravity with Muonium. arXiv, 2007; arXiv:physics/0702143. [Google Scholar]
- Oberthaler, M.K. Anti-matter wave interferometry with positronium. Nucl. Instrum. Methods Phys. Res. B 2002, 192, 129–134. [Google Scholar] [CrossRef]
- Keith, D.W.; Ekstrom, C.R.; Turchette, Q.A.; Pritchard, D.E. An interferometer for atoms. Phys. Rev. Lett. 1991, 66, 2693. [Google Scholar] [CrossRef] [PubMed]
- Brezger, B.; Hackermüller, L.; Uttenthaler, S.; Petschinka, J.; Arndt, M.; Zeilinger, A. Matter-wave interferometer for large molecules. Phys. Rev. Lett. 2002, 88, 100404. [Google Scholar] [CrossRef] [PubMed]
- Chang, B.J.; Alferness, R.; Leith, E.N. Space-invariant achromatic grating interferometers: Theory. Appl. Opt. 1975, 14, 1592–1600. [Google Scholar] [CrossRef] [PubMed]
- Cronin, A.D.; Schmiedmayer, J.; Pritchard, D.E. Optics and interferometry with atoms and molecules. Rev. Mod. Phys. 2009, 81, 1051. [Google Scholar] [CrossRef]
- Hornberger, K.; Gerlich, S.; Haslinger, P.; Nimmrichter, S.; Arndt, M. Quantum interference of clusters and molecules. Rev. Mod. Phys. 2012, 84, 157. [Google Scholar] [CrossRef]
- Ekstrom, C.R. Experiments with a Separated-Beam Atom Interferometer. Ph.D. Thesis, MIT, Cambridge, MA, USA, September 1993. [Google Scholar]
- Wojcik, M.J.; Mancini, D.C.; Divan, R.; Ocola, L.E. X-ray zone plate with 25 aspect ratio using a 2-μm-thick ultrananocrystalline diamond mold. Microsyst. Technol. 2014, 20, 10. [Google Scholar] [CrossRef]
- Wojcik, M.J. Fabrication and Characterization of High Aspect Ratio Hard X-ray Zone Plates with Ultrananocrystalline Diamond Molds. Ph.D. Thesis, Illinois Institute of Technology, Chicago, IL, USA, 2013. [Google Scholar]
- Zhang, L.; Lee, W.-K.; Wulff, M.; Eybert, L. The performance of a cryogenically cooled monochromator for an in-vacuum undulator beamline. J. Synchrotron Radiat. 2003, 10, 313–319. [Google Scholar] [CrossRef] [PubMed]
- Swenson, C.A. Recommended values for the thermal expansivity of silicon from 0 to 1000 K. J. Phys. Chem. Ref. Data 1983, 12, 179. [Google Scholar] [CrossRef]
- Thapa, R.; Phillips, J.D.; Rocco, E.; Reasenberg, R.D. Subpicometer length measurement using semiconductor laser tracking frequency gauge. Opt. Lett. 2011, 36, 3759–3761. [Google Scholar] [CrossRef] [PubMed]
- Reasenberg, R.D.; Lorenzini, E.C.; Patla, B.R.; Phillips, J.D.; Popescu, E.; Rocco, E.; Thapa, R. A quick test of the WEP enabled by a sounding rocket. Class. Quant. Gravity 2011, 28, 094014. [Google Scholar] [CrossRef]
- Reasenberg, R.D.; Patla, B.R.; Phillips, J.D.; Thapa, R. Design and characteristics of a WEP test in a sounding-rocket payload. Class. Quant. Gravity 2012, 29, 184013. [Google Scholar] [CrossRef][Green Version]
- Drever, R.W.P.; Hall, J.L.; Kowalski, F.V.; Hough, J.; Ford, G.M.; Munley, A.J.; Ward, H. Laser Phase and Frequency Stabilization Using an Optical Resonator. Appl. Phys. B 1983, 31, 97–105. [Google Scholar] [CrossRef]
- Kaplan, D.M.; Roberts, T.J.; Phillips, J.D.; Reasenberg, R.D. Improved performance of semiconductor laser tracking frequency gauge. J. Instrum. 2018, 13, P03008. [Google Scholar] [CrossRef]
- Matthias, B.E.; Ahn, H.E.; Badertscher, A.; Chmely, F.; Eckhause, M.; Hughes, V.W.; Jungmann, K.P.; Kane, J.R.; Kettell, S.H.; Kuang, Y.; et al. New search for the spontaneous conversion of muonium to antimuonium. Phys. Rev. Lett. 1991, 66, 2716–2719. [Google Scholar] [CrossRef] [PubMed]
- Roberts, T.J. G4beamline (a “Swiss Army knife” for Geant4, Optimized for Simulating Beamlines). Available online: http://g4beamline.muonsinc.com (accessed on 1 February 2018).
- Abela, R.; Herlach, D.; Morenzoni, E.; Solt, G.; Zimmermann, U.; Gygax, F.N.; Schenk, A.; Eshchenko, D.G.; Krasnoperov, E.P.; Melikjov, E.E. Muonium in liquid helium isotopes. JETP Lett. 1993, 57, 157. [Google Scholar]
- Bao, Y.; Aldognini, A.; Bertl, W.; Hildebrandt, M.; Khaw, K.S.; Kirch, K.; Papa, A.; Petitjean, C.; Piegsa, F.M.; Ritt, S.; et al. Muon cooling: Longitudinal compression. Phys. Rev. Lett. 2014, 112, 224801. [Google Scholar] [CrossRef] [PubMed]
- Kirch, K.; Khaw, K.S. Testing antimatter gravity with muonium. Int. J. Mod. Phys. Conf. Ser. 2014, 30, 1460258. [Google Scholar]
- Eggenberger, A.; Belosevic, I.; Wichmann, G. Development of a low-energy, high-brightness μ+ beam line. In Proceedings of the Seventh Meeting on CPT and Lorentz Symmetry (CPT’16), Bloomington, IN, USA, 20–24 June 2016; Kostelecký, V.A., Ed.; World Scientific: Singapore, 2017; p. 235. [Google Scholar]
- Eggenberger, A. Development of a Novel Low-Energy, High-Brightness μ+ Beam Line. Ph.D. Thesis, ETH Zürich, Zürich, Switzerland, 2016. [Google Scholar]
- Taqqu, D. Compression and Extraction of Stopped Muons. Phys. Rev. Lett. 2006, 97, 194801. [Google Scholar] [CrossRef] [PubMed]
- Reynolds, M.W.; Hayden, M.E.; Hardy, W.N. Hyperfine resonance of atomic deuterium at 1 K. J. Low Temp. Phys. 1991, 84, 87–108. [Google Scholar] [CrossRef]
- Krotscheck, E.; Zillich, R.E. Hydrogen and 3He atoms on 4He surfaces: Bound states and scattering features. Phys. Rev. B 2008, 77, 094507. [Google Scholar] [CrossRef]
- Taqqu, D. Ultraslow Muonium for a Muon beam of ultra high quality. Phys. Procedia 2011, 17, 216. [Google Scholar] [CrossRef]
- Luppov, V.G.; Kaufman, W.A.; Hill, K.M.; Raymond, R.S.; Krisch, A.D. Focusing a Beam of Ultracold Spin-Polarized Hydrogen Atoms with a Helium-Film-Coated Quasiparabolic Mirror. Phys. Rev. Lett. 1993, 71, 2405. [Google Scholar] [CrossRef] [PubMed]
- Afach, S.; Ayres, N.J.; Ban, G.; Bison, G.; Bodek, K.; Chowdhuri, Z.; Daum, M.; Fertl, M.; Franke, B.; Griffith, W.C.; et al. Observation of Gravitationally Induced Vertical Striation of Polarized Ultracold Neutrons by Spin-Echo Spectroscopy. Phys. Rev. Lett. 2015, 115, 162502. [Google Scholar] [CrossRef] [PubMed]
- Perreault, J.D.; Cronin, A.D. Observation of Atom Wave Phase Shifts Induced by Van Der Waals Atom-Surface Interactions. Phys. Rev. Lett. 2005, 95, 133201. [Google Scholar] [CrossRef] [PubMed]
- Perreault, J.D.; Cronin, A.D.; Savas, T.A. Using atomic diffraction of Na from material gratings to measure atom-surface interactions. Phys. Rev. A 2005, 71, 053612. [Google Scholar] [CrossRef]
- Interprofessional Projects Program at Illinois Institute of Technology. Available online: http://ipro.iit.edu (accessed on 1 February 2018).
| 1. | |
| 2. | The only published direct test so far [4] has yielded the limit . |
| 3. | |
| 4. | This also suggests a solution to what has been called “the worst prediction in physics”: that the gravitational zero-point energy of the universe seems to exceed the size of the cosmological constant by a factor [52]. |
| 5. | |
| 6. | An alternative derivation in an accelerated reference frame, in which the beam travels in a straight, horizontal line and the interferometer accelerates upwards at g, may be somewhat easier to follow and leads to the same conclusion. |
| 7. | For overlapped interferometer beams as in our case, the optimal open fractions have been shown to be (0.60, 0.43, 0.37) [54], which can feasibly be fabricated in our proposed approach. |
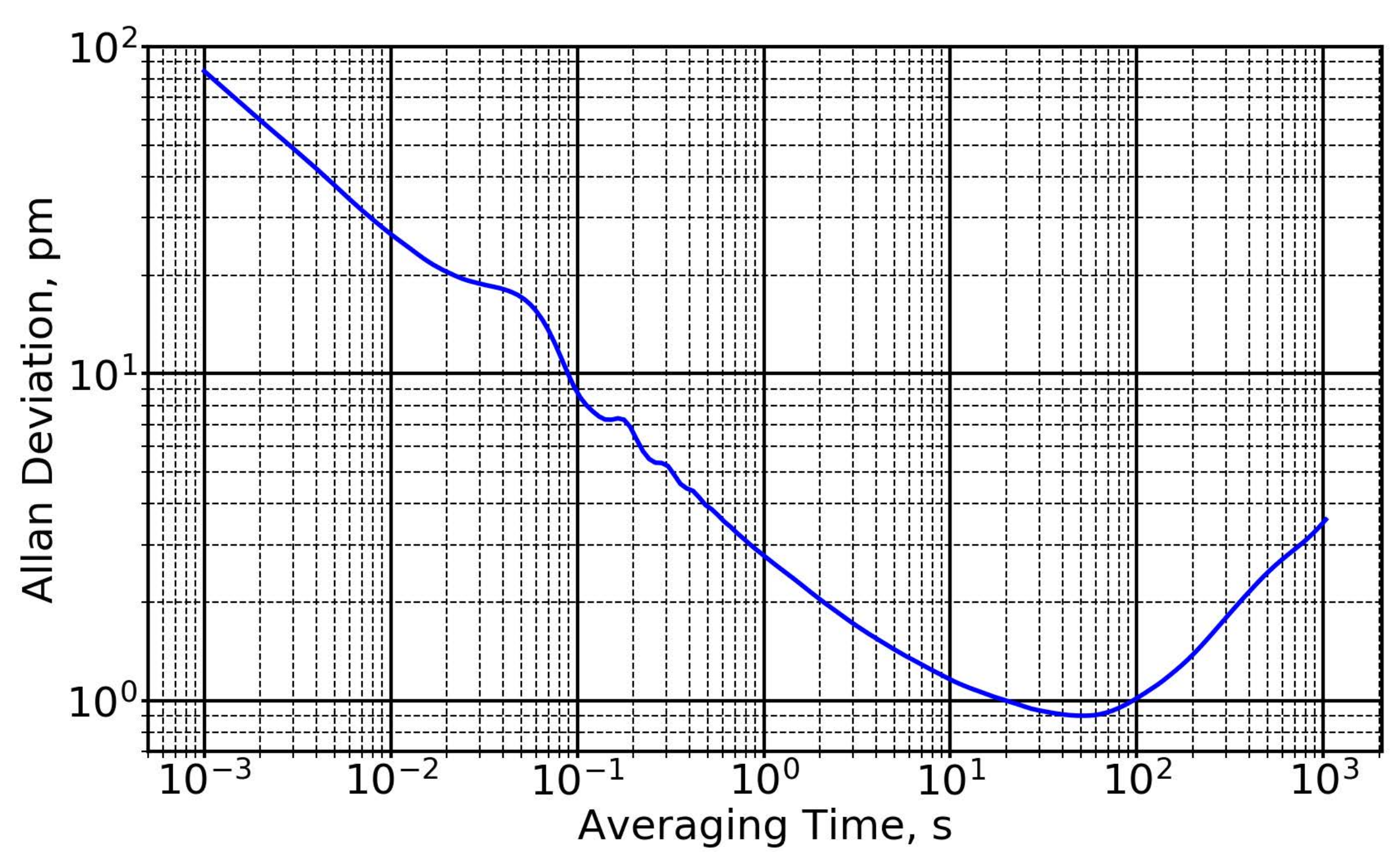
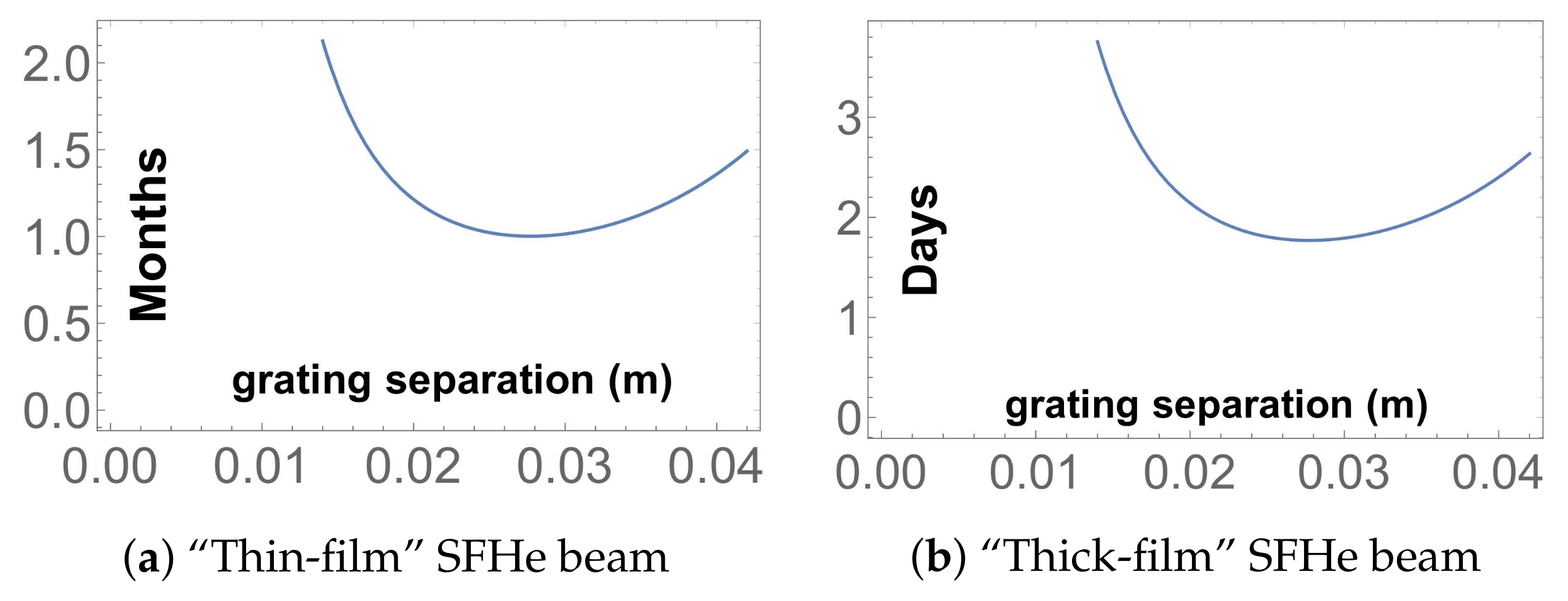
| 8. | Note that the sensitivities of Figure 7 are somewhat more pessimistic than that of Equation (1), due to inclusion of estimated decay losses from the Mu source to the first grating. The size of this effect will depend on the final source–interferometer distance, which will depend on cryostat engineering details yet to be determined. |
| 9. | The “obvious” solution of comparing muonium and antimuonium beams is unfortunately not feasible, since it is impractical to produce a sufficiently positron-rich stopping medium. |
| 10. | If necessary, to eliminate the possible ambiguity between Mu and X-ray events, the accelerating potential can be turned off during calibration runs. |

| Cause | Size | Parameter | Value | Effect (g) |
|---|---|---|---|---|
| E gradient | 100 V/m | m | 0.04 * | |
| B gradient | <1 nT/mm | J/T | <0.005 |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Antognini, A.; Kaplan, D.M.; Kirch, K.; Knecht, A.; Mancini, D.C.; Phillips, J.D.; Phillips, T.J.; Reasenberg, R.D.; Roberts, T.J.; Soter, A. Studying Antimatter Gravity with Muonium. Atoms 2018, 6, 17. https://doi.org/10.3390/atoms6020017
Antognini A, Kaplan DM, Kirch K, Knecht A, Mancini DC, Phillips JD, Phillips TJ, Reasenberg RD, Roberts TJ, Soter A. Studying Antimatter Gravity with Muonium. Atoms. 2018; 6(2):17. https://doi.org/10.3390/atoms6020017
Chicago/Turabian StyleAntognini, Aldo, Daniel M. Kaplan, Klaus Kirch, Andreas Knecht, Derrick C. Mancini, James D. Phillips, Thomas J. Phillips, Robert D. Reasenberg, Thomas J. Roberts, and Anna Soter. 2018. "Studying Antimatter Gravity with Muonium" Atoms 6, no. 2: 17. https://doi.org/10.3390/atoms6020017
APA StyleAntognini, A., Kaplan, D. M., Kirch, K., Knecht, A., Mancini, D. C., Phillips, J. D., Phillips, T. J., Reasenberg, R. D., Roberts, T. J., & Soter, A. (2018). Studying Antimatter Gravity with Muonium. Atoms, 6(2), 17. https://doi.org/10.3390/atoms6020017





